Behera and Panda defined a balancing number as a number b for which the sum of the numbers from \(1\) to \(b – 1\) is equal to the sum of the numbers from \(b + 1\) to \(b + r\) for some r. They also classified all such numbers. We define two notions of balancing numbers for Farey fractions and enumerate all possible solutions. In the stricter definition, there is exactly one solution, whereas in the weaker one all sufficiently large numbers work. We also define notions of balancing numbers for levers and mobiles, then show that these variants have many acceptable arrangements. For an arbitrary mobile, we prove that we can place disjoint consecutive sequences at each of the leaves and still have the mobile balance. However, if we impose certain additional restrictions, then it is impossible to balance a mobile.
In 1999, Behera and Panda [1] defined a balancing number as a number \(b\) for which there exists a number \(r\) such that \[1 + 2 + \cdots + (b – 1) = (b + 1) + (b + 2) + \cdots + (b + r).\] They then showed that \(b\) is balancing exactly when \(8b^2 + 1\) is a square. (An alternate characterization is that \(b^2\) is triangular.) Over the course of the next \(25\) years, many mathematicians wrote papers on balancing numbers. (For a recent survey, see [2].)
Some authors found additional properties of balancing numbers. Liptai proved that \(1\) is the only Fibonacci balancing number [3] and that there are no Lucas balancing numbers [4]. Kovács, Liptai, and Olajos [5] showed that for any positive integer \(k\), there are only finitely many balancing numbers which are the product of \(k\) consecutive integers. They also showed that \(6\) is is only solution for \(k = 2, 3\) and that there are no solutions for \(k = 4\). Tengely [6] then proved that there are no solutions for \(k = 5\).
Numerous authors have also “balanced” different sets of numbers. For example, Panda and Panda [7] defined a \(k\)-circular balancing number as a number \(n\) for which the equation \[(1 + 2 + \cdots + (k – 1)) + ((n + 1) + (n + 2) + \cdots + m) = (k + 1) + (k + 2) + \cdots + (n – 1)\] holds for some \(m\). In other words, if we arrange the numbers from \(1\) to \(m\) in a circle and remove the numbers \(n\) and \(k\), then the two remaining arcs have the same sum. Panda and Panda then showed that \(n\) is \(k\)-circular balancing when \(8(n^2 – k^2) + 1\) is a square.
Let \(y\), \(k\), and \(\ell\) be positive integers. Liptai, Luca, Pintér, and Szeley [8] defined a \((k, \ell)\)-power numerical center for \(y\) as a number \(x\) satisfying the equation \[1^k + 2^k + \cdots + (x – 1)^k = (x + 1)^\ell + (x + 2)^\ell + \cdots + (y – 1)^\ell\] and proved that there are only finitely many \((k, \ell)\)-power numerical centers for a given \(k, \ell\) with \(k > 1\). Kovács, Liptai, and Olajos [5] defined an \((a, b)\)-balancing number as a number \(m = an + b\) for which \[(a + b) + (2a + b) + \cdots + (a(n – 1) + b) = (a(n + 1) + b) + (a(n + 2) + b) + \cdots + (a(n + r) + b)\] for some \(r\) and proved several results about these numbers.
Szakács [9] defined a multiplying balancing number as a number \(n\) for which the equation \[1 \cdot 2 \cdots n = (n + 1)(n + 2) \cdots + (n + r)\] has a solution for some positive \(r\). He then showed that \(7\) is the only multiplying balancing number [9,Thm. 1]. Szakács also generalized this definition to powers. The number \(n\) is a \((k, \ell)\)-power multiplying balancing number if the equation \[(1 \cdot 2 \cdots (n – 1))^k = ((n + 1)(n + 2) \cdots m)^\ell\] has a solution. Szakács [9,Thm .3] also proved that \((n, k, \ell) = (7, 11, 1)\) is the only solution to the previous equation satisfying \(n \geq 4\).
Given that so many different sequences have been balanced, it is natural to balance some more. In this note, we define notions of balancing numbers for Farey sequences, levers, and mobiles.
Let \(F_n\) be the Farey sequence of order \(n\), i.e., the sequence of fractions with denominator \(\leq n\) in the interval \([0, 1]\). We can define a notion of balancing Farey fractions analogous to balancing numbers. In addition, we break the interval \([0, 1]\) into \(k\) parts, rather than just \(2\).
Definition 1. Fix an integer \(k \geq 2\). The number \(n\) is \(k\)-Farey balancing if there exists an increasing sequence of numbers \(r_1, r_2, \ldots, r_{k – 1} \in (0, 1)\) such that \[\sum_{x \in F_n \cap [0, r_1]} x = \sum_{x \in F_n \cap (r_1, r_2]} x = \cdots = \sum_{x \in F_n \cap (r_{k – 2}, r_{k – 1}]} x = \sum_{x \in F_n \cap (r_{k – 1}, 1]} x.\] In other words, the sums of the Farey fractions in the intervals \([0, r_1], (r_1, r_2], \ldots, (r_{k – 1}, 1]\) are all equal. When \(k = 2\), we simply refer to \(n\) as a Farey balancing number.
We can prove that \(n = 4\) is Farey balancing as follows: \[0 + \frac{1}{4} + \frac{1}{3} + \frac{1}{2} + \frac{2}{3} = \frac{3}{4} + 1.\] We show that this is the only \(n\) for which this is possible.
Theorem 1. The number \(4\) is the only Farey balancing number.
For larger \(k\), we obtain a similar result.
Theorem 2. There are no \(k\)-Farey balancing numbers for any \(k > 2\).
Given that there are so few numbers satisfying these conditions, it is tempting to weaken our definitions so that we obtain more solutions.
Definition 2. The number \(n\) is weakly Farey balancing if there exists a set \(S \subseteq F_n\) such that \[\sum_{x \in S} x = \sum_{x \in F_n \backslash S} x.\] In this case, the sum of the fractions in \(S\) is equal to the sum of the fractions which belong to \(F_n\), but not \(S\).
Clearly \(4\) is weakly Farey balancing because it is Farey balancing. In fact, we show a much stronger result.
Theorem 3. All numbers greater than \(3\) are weakly Farey balancing.
We can see that being Farey balancing is a very strong condition and that being weakly Farey balancing is a very weak one. In light of this, we consider properties in between these two conditions. Instead of letting \(S\) be any subset of \(F_n\), we let \(S\) be the intersection of \(F_n\) and a specific interval. Unfortunately, we were unable to find numbers \(n\) for which we can let \(S\) be such a set.
Conjecture 1. Fix \(n > 4\). There do not exist disjoint intervals \(I_1, I_2 \subseteq [0, 1]\) such that both \(F_n \cap I_1\) and \(F_n \cap I_2\) are non-empty and \[\sum_{x \in F_n \cap I_1} x = \sum_{x \in F_n \cap I_2} x.\]
Nevertheless, we can show that there are only finitely many solutions for certain pairs of intervals \((I_1, I_2)\) satisfying a few weak conditions.
Theorem 4. Let \(I_1 = [\alpha_1, \beta_1]\) and \(I_2 = [\alpha_2, \beta_2]\) be disjoint subintervals of \([0, 1]\) for which the set \(\{1, \alpha_1, \beta_1, \alpha_2, \beta_2\}\) is linearly independent over \(\mathbf{Z}\) or \(\beta_1^2 – \alpha_1^2 \neq \beta_2^2 – \alpha_2^2\). Then the equation \[\sum_{x \in F_n \cap I_1} x = \sum_{x \in F_n \cap I_2} x\] only holds for finitely many values of \(n\).
In Section \(3\), we consider a different balancing configuration. Rather than balance numbers in a line, we balance them on a lever. We put the number \(b\) at the fulcrum and the lever and have the other numbers from \(1\) to \(b + r\) balance on top. The numbers further from \(b\) exert more torque, which we need to account for.
Definition 3. The number \(b\) is lever balancing if there exists a number \(r\) such that \[(b – 1) \cdot 1 + (b – 2) \cdot 2 + \cdots + 1 \cdot (b – 1) = 1 \cdot (b + 1) + 2 \cdot (b + 2) + \cdots + r \cdot (b + r).\]
Lever balancing numbers are surprisingly common.
Theorem 5. The number \(b\) is lever balancing exactly when it is odd.
We can also generalize our previous definition as follows. Instead of just placing \(b\) at the fulcrum, we also remove the \(k – 1\) numbers closest to \(b\) on each side. (A similar concept already exists for ordinary balancing numbers. We say that \(b\) is a \(k\)-gap balancing number if there exists a number \(r\) such that \(1 + 2 + \cdot + (b – k) = (b + k) + (b + k + 1) + \cdots + (b + k + r)\). For more information on gap balancing numbers, see [10-12].)
Definition 4. Fix a non-negative integer \(k\). The number \(b\) is a \(k\)-lever balancing number if there exists an \(r\) such that \[(b – 1) \cdot 1 + (b – 2) \cdot 2 + k \cdot (b – k) = k \cdot (b + k) + (k + 1) \cdot (b + k + 1) + \cdots + r \cdot (b + r).\]
Because we have been unable to find any \(k\)-lever balancing numbers for \(k > 1\), we write the following conjecture.
Conjecture 2. There are no \(k\)-lever balancing numbers for any \(k > 1\).
Though we cannot prove this result, we did obtain a slightly weaker statement.
Theorem 6. For all \(k > 1\), there are only finitely many \(k\)-lever balancing numbers.
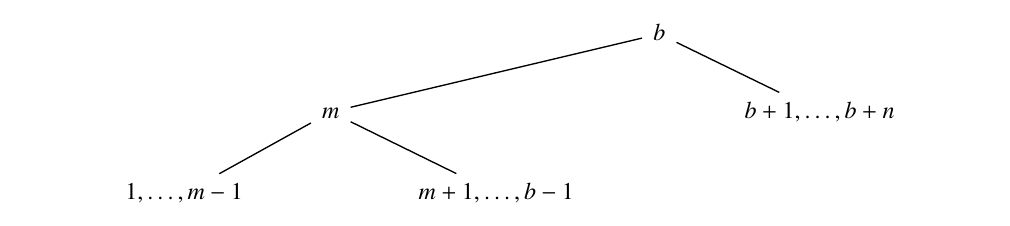
Instead of balancing numbers in a line, we can also balance them on a mobile. We say that \(b\) is left-mobile balancing if there exist \(m\) and \(n\) such that \[\begin{aligned} 1 + 2 + \cdots + (m – 1) & = (m + 1) + (m + 2) + \cdots + (b – 1), \\ 1 + 2 + \cdots + (b – 1) & = (b + 1) + (b + 2) + \cdots + (b + n). \end{aligned}\] In other words, the following mobile balances:
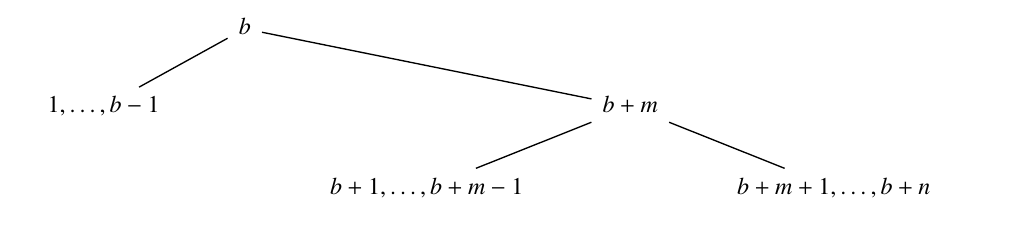
Likewise, we say that \(b\) is right-mobile balancing if the “reflection” of this mobile balances:
We show that it is impossible to balance these mobiles.
Theorem 7. Left- and right-mobile balancing numbers do not exist.
However, we can weaken our definitions. Instead of trying to balance specific sets of consecutive numbers, we can let the leaves contain any set of consecutive numbers. Loosening this restriction allows us to select sets of consecutive numbers in order to balance any given mobile, which we discuss in more detail in Section \(4\). For example, consider the following mobile.
This mobile balances in the sense that if we add up all of the numbers in the leaves to on the left and right subtrees of the root, we obtain the same value. In addition, the right subtree also balances in this sense. We have \(1 + 2 + \cdots + 20 = (34 + 35 + 36) + (52 + 53)\) and \(34 + 35 + 36 = 52 + 53\). Finally, note that all of the leaves contain consecutive sequences of numbers. We will provide an algorithm for labelling the roots of any mobile with disjoint consecutive sequences which cause each subtree to balance.
We now classify the \(k\)-Farey balancing numbers. The basic idea is to show that for large values of \(n\), one of our two intervals has to be much longer than the other, then use the fact that short subintervals do not contain too many elements of \(F_n\).
Definition 5. Let \(S\) be a finite subset of the interval \([a, b]\). The discrepancy of \(S\) is \[D_S = \sup_{a \leq c < d \leq b} \left|\frac{\# (S \cap [c, d])}{\# S} – (d – c)\right|.\]
Lemma 1 ([13,p. 348]). The set \(F_n\) has discrepancy \(2/n\).
Finally, we need a few results on prime gaps.
Theorem 8 ([14,p. 180]). If \(n \geq 9\), then the interval \([n, (4/3)n)\) contains at least one prime.
For larger \(n\), much stronger results are known [15]. (See [16] for the current lower bound on the largest gap between two consecutive primes \(\leq x\).)
Corollary 1. For all \(n \geq 11\), the interval \((n/2, n]\) contains at least two primes.
Proof. The smallest element of \((n/2, n]\) is \(\lfloor (n/2) + 1 \rfloor\). If \(n \geq 16\), then \(\lfloor (n/2) + 1 \rfloor \geq 9\) and \((4/3)^2 \lfloor (n/2) + 1 \rfloor \leq n\). In this case, \((n/2, n]\) contains at least two primes. If \(n\) is \(11\), \(12\), or \(13\), then \(7, 11 \in (n/2, n]\). If \(n\) is \(14\) or \(15\), then \(11, 13 \in (n/2, n]\). ◻
We now prove Theorems 1 and 2, which we write as one result.
Theorem 9. If \(n\) is a \(k\)-Farey balancing number for some \(k \geq 2\), then \(n = 4\) and \(k = 2\).
Proof. Suppose that \(n\) is \(k\)-Farey balancing for a given \(k \geq 2\). We may break \([0, 1]\) into \(k\) disjoint intervals \(S_1, S_2, \ldots, S_k\) where the sum of the elements of \(F_n \cap S_i\) is constant for all \(i \leq k\). We write \(S_1 = [0, r_1)\), \(S_i = [r_{i – 1}, r_i)\) for all \(i \in [2, k – 1]\), and \(S_k = [r_{k – 1}, 1]\), where \(0 < r_1 < r_2 < \cdots < r_{k – 1} < 1\). If \(d | k\), then we can combine groups of \(k/d\) consecutive intervals. We have now split \([0, 1]\) into \(d\) consecutive intervals with the same sum. In other words, if \(n\) is \(k\)-Farey balancing, then \(n\) is also \(d\)-Farey balancing for all \(d | k\). Hence, if \(n\) is not \(p\)-Farey balancing for any prime \(p\), then it is not \(k\)-Farey balancing for any \(k\). From on, we assume that \(k\) is prime.
In addition, \(F_n \cap S_i\) must be non-empty for all \(i\) because it is non-empty for some \(i\). Therefore, \(\# F_n \geq k\). However, \(\# F_n \leq n^2\), which implies that \(n \geq \sqrt{k}\). We also showed that if \(n \leq 10\) and \(n\) is \(k\)-Farey balancing for some \(k\), then \(n = 4\) and \(k = 2\) using the code in the appendix. From here on, we assume that \(n \geq \max(\sqrt{k}, 11)\).
Because \(n \geq 11\), the interval \((n/2, n]\) contains at least two primes. Let \(p \in (n/2, n]\) be a prime which does not equal \(k\). For each \(i \in [1, k]\), let \(a_i\) be the largest number satisfying \(a_i/p \in S_i\). (We also let \(a_0 = 0\).) Because \(p > n/2\), the only elements of \(F_n\) whose denominator is a multiple of \(p\) are the fractions with denominator \(p\). For all \(i \leq k\), \[\sum_{x \in F_n \cap S_i} x = \left(\frac{a_{i – 1}}{p} + \frac{a_{i – 1} + 1}{p} + \cdots + \frac{a_i}{p}\right) + \frac{b_i}{c_i} = \frac{(a_i (a_i + 1) – a_{i – 1} (a_{i – 1} + 1))/2}{p} + \frac{b_i}{c_i}\] for some \(b_i, c_i \in \mathbf{Z}\) with \(p \nmid c_i\). Because the sum is constant for all \(i\), we have \[\begin{aligned} \frac{a_1 (a_1 + 1) – a_0 (a_0 + 1)}{2} & \equiv \frac{a_2 (a_2 + 1) – a_1 (a_1 + 1)}{2} \\ & \equiv \cdots \\ & \equiv \frac{a_k (a_k + 1) – a_{k – 1} (a_{k – 1} + 1)}{2} \textrm{ mod } p. \end{aligned}\] For all \(j\), we have \[\begin{aligned} k(a_j (a_j + 1) – a_{j – 1} (a_{j – 1} + 1)) & \equiv \sum_{i = 1}^k (a_i (a_i + 1) – a_{i – 1} (a_{i – 1} + 1)) \\ & \equiv a_k (a_k + 1) – a_0 (a_0 + 1) \\ & \equiv 0 \textrm{ mod } p. \end{aligned}\] Recall that \(k\) and \(p\) are distinct primes. Therefore, \(p \nmid k\), which implies that \[a_j (a_j + 1) – a_{j – 1} (a_{j – 1} + 1) \equiv 0 \textrm{ mod } p.\] Let \(m\) be the smallest number satisfying \(a_m \neq 0\). Then, \(a_m (a_m + 1)\) is a multiple of \(p\). Because \(a_m \leq p\), we have \(a_m = p\) or \(a_m = p – 1\). Either way, \(1/p, 2/p, \ldots, (p – 1)/p \in F_n \cap S_m\). In addition, \(p \geq 7\) because \(n \geq 11\) and \(p > n/2\). Therefore, \[F_n \cap \left[\frac{1}{7}, \frac{6}{7}\right] \subseteq F_n \cap \left[\frac{1}{p}, \frac{p – 1}{p}\right] \subseteq F_n \cap S_m.\]
We now show that the sum of the elements of \(F_n \cap [1/7, 6/7]\) is more than half of the sum of the elements of \(F_n\). This would imply that the sum of the elements of \(F_n \cap S_m\) is greater than the sum of the elements of \(F_n \cap S_i\) for any \(i \neq m\).
For every \(a/b \in F_n\), \(1 – (a/b)\) is also an element of \(F_n\). Therefore, \[\sum_{x \in F_n} x = \frac{1}{2} \# F_n.\] Similarly, if \(a/b \in F_n \cap [1/7, 6/7]\), then so is \(1 – (a/b)\). This implies that \[\sum_{x \in F_n \cap [1/7, 6/7]} x = \frac{1}{2} \# \left(F_n \cap \left[\frac{1}{7}, \frac{6}{7}\right]\right).\] By Lemma 1, \[\#\left(F_n \cap \left[\frac{1}{7}, \frac{6}{7}\right]\right) \geq \left(\frac{5}{7} – \frac{2}{n}\right) \# F_n \geq \left(\frac{5}{7} – \frac{2}{11}\right) \# F_n = \frac{41}{77} \# F_n.\] Putting everything together gives us \[\sum_{x \in F_n \cap S_m} x \geq \sum_{x \in F_n \cap [1/7, 6/7]} x \geq \frac{41}{154} \# F_n > \frac{1}{4} \# F_n = \frac{1}{2} \sum_{x \in F_n} x.\] So, the sum of the elements of \(F_n \cap S_m\) is greater than the sum of the elements of \(F_n \cap S_i\) for any \(i \neq m\). Hence, \(n\) is not \(k\)-Farey balancing. ◻
Here is an alternate condition for balancing numbers. We say that a number \(n\) is weakly Farey balancing if we can split \(F_n\) into two disjoint subsets with equal sum. Clearly, \(n = 4\) is weakly Farey balancing because it is also Farey balancing. It is also easy to show that numbers less than \(4\) do not have this property. We show that all numbers greater than \(4\) are weakly Farey balancing.
Proof of Theorem 3. We proceed by induction. We already know that \(n = 4\) is weakly Farey balancing. Suppose we know that \(n\) is weakly Farey balancing and we want to show that \(n + 1\) is as well. By assumption, there exist two disjoint subsets \(S_1, S_2 \subseteq F_n\) such that \(S_1 \cup S_2 = F_n\) and the elements of \(S_1\) and \(S_2\) have the same sum. There are two cases.
First, suppose that \(\varphi(n + 1)\) is a multiple of \(4\). We may split the fractions with denominator \(n + 1\) (when written as a reduced fraction) into \(\varphi(n + 1)/2\) pairs, each with sum \(1\). We then put \(\varphi(n + 1)/4\) of these pairs into \(S_1\) and the \(\varphi(n + 1)/4\) pairs into \(S_2\). Our sets still have equal sums.
Now suppose \(4 \nmid \varphi(n + 1)\). Because \(n + 1 > 2\), \(\varphi(n + 1)\) is still even. We still have \(\varphi(n + 1)/2\) pairs with sum \(1\). Without loss of generality, let \(1/2 \in S_1\). This time, we put \((\varphi(n + 1) + 1)/2\) pairs into \(S_1\) and \((\varphi(n + 1) – 1)/2\) pairs into \(S_2\). We then move \(1/2\) from \(S_1\) to \(S_2\) in order to balance the sums. ◻
Rather than considering Farey balancing numbers, we can investigate a slightly weaker condition. Instead of the sums of the elements of \(F_n \cap [0, r]\) and \(F_n \cap (r, 1]\) being equal, we can replace \([0, r]\) and \((r, 1]\) with arbitrary disjoint subintervals of \([0, 1]\). Even still, we have been unable to find any solutions. We rewrite Conjecture 1 from the Introduction.
Conjecture 3. Fix \(n > 4\). There do not exist disjoint intervals \(I_1, I_2 \subseteq [0, 1]\) such that the sets \(F_n \cap I_1\) and \(F_n \cap I_2\) are both non-empty and \[\sum_{x \in F_n \cap I_1} x = \sum_{x \in F_n \cap I_2} x.\]
Though we cannot prove Conjecture 3, we can prove Theorem 4 using the following results.
Definition 6. Let \(f: [0, 1] \to \mathbf{R}\) be a function. The variation of \(f\) is given by the formula \[V(f) = \sup_{0 = x_1 < x_2 < \cdots < x_n = 1} \sum_{i = 1}^{n – 1} |f(x_{i + 1}) – f(x_i)|.\]
The next result is the one-dimensional case of the Koksma-Hlawka Inequality [17,Thm. 5.1], which is an upper bound on the sum of a function over certain sets.
Theorem 10. Let \(P\) be a finite subset of \([0, 1]\) with discrepancy \(D(P)\) and let \(f: [0, 1] \to \mathbf{R}\) be a function with bounded variation. Then, \[\left|\frac{1}{\# P} \sum_{x \in P} f(x) – \int_0^1 f(x) dx\right| \leq \frac{1}{2} V(f) D(P).\]
We write a lemma which will allow us to prove our desired results.
Lemma 2. Let \(I_1\) and \(I_2\) be disjoint subintervals of \([0, 1]\) and fix \(n \geq 1\). For a given \(m\), let \(P_m\) be the set \(\{1/m, 2/m, \ldots, 1\}\). If \[\sum_{x \in F_n \cap I_1} x = \sum_{x \in F_n \cap I_2} x,\] then \[\left|\sum_{x \in P_m \cap I_1} x – \sum_{x \in P_m \cap I_2} x\right| < 8\] for all \(m \leq n\).
Proof. Define the function \(f: [0, 1] \to \mathbf{R}\) as \[f(x) = \left\{\begin{array}{rl} x, & \textrm{if } x \in I_1, \\ -x, & \textrm{if } x \in I_2, \\ 0, & \textrm{otherwise.} \end{array}\right.\] The variation of \(f\) is \[V(f) = 2\left(\max_{x \in I_1} x + \max_{x \in I_2} x\right) < 4.\] Theorem 10 implies that \[\left|\frac{1}{\# F_n} \sum_{x \in F_n} f(x) – \int_0^1 f(x) dx\right| \leq V(f) D(F_n) < \frac{4}{n}.\] By assumption, the sum of \(f(x)\) over all \(x \in F_n\) is \(0\). Therefore, \[\left|\int_0^1 f(x) dx\right| < \frac{4}{n}.\]
We apply a similar argument to \(P_m\). It is straightforward to show that \(D(P_m) = 2/m\). We now have \[\left|\frac{1}{\# P_m} \sum_{x \in P_m} f(x) – \int_0^1 f(x) dx\right| \leq \frac{V(f) D(P_m)}{2} < \frac{4}{m}.\] Note that \(\# P_m = m\). Our bound on the integral of \(f(x)\) implies that \[\left|\sum_{x \in P_m} f(x)\right| < m\left(\frac{4}{m} + \frac{4}{n}\right) \leq 8. \] ◻
We are now ready to prove Theorem 4, which we break into two parts for readability.
Theorem 11. Let \(I_1 = [\alpha_1, \beta_1]\) and \(I_2 = [\alpha_2, \beta_2]\) be disjoint subintervals of \([0, 1]\) with \(\beta_1^2 – \alpha_1^2 \neq \beta_2^2 – \alpha_2^2\). Then the equation \[\sum_{x \in F_n \cap I_1} x = \sum_{x \in F_n \cap I_2} x\] only holds for finitely many values of \(n\).
Proof. Fix \(I_1\) and \(I_2\) and suppose that the equation in the theorem holds for infinitely many \(n\). Let \(n\) be a large solution and \(p\) be a prime in the interval \((n/2, n]\). Let \(P_p\) be the set of fractions \(a/p \in (0, 1]\). If \(a/p \in I_1\), then \(\alpha_1 \leq a/p \leq \beta_1\), which implies that \(\alpha_1 p \leq a \leq \beta_1 p\). We assume that \(p\) is sufficiently large so that \(\alpha_i p\) and \(\beta_i p\) are non-integral for \(i = 1, 2\). So, \(\lfloor \alpha_1 p \rfloor + 1 \leq a \leq \lfloor \beta_1 p \rfloor\). Similarly, if \(a/p \in I_2\), then \(\lfloor \alpha_2 p \rfloor + 1 \leq a \leq \lfloor \beta_2 p \rfloor\). So, \[\sum_{x \in P_p \cap I_1} x – \sum_{x \in P_p \cap I_2} x = \frac{\lfloor \beta_1 p \rfloor (\lfloor \beta_1 p \rfloor + 1) – \lfloor \alpha_1 p \rfloor (\lfloor \alpha_1 p \rfloor + 1) – \lfloor \beta_2 p \rfloor (\lfloor \beta_2 p \rfloor + 1) + \lfloor \alpha_2 p \rfloor (\lfloor \alpha_2 p \rfloor + 1)}{2p}.\]
The previous lemma implies that the absolute value of this quantity is less than \(8\). In addition, it must also be an integer because none of the elements of \(F_n \backslash P_p\) have a denominator which is a multiple of \(p\). So, there exists an integer \(k\) with \(|k| < 16\) for which \[\lfloor \beta_1 p \rfloor (\lfloor \beta_1 p \rfloor + 1) – \lfloor \alpha_1 p \rfloor (\lfloor \alpha_1 p \rfloor + 1) – \lfloor \beta_2 p \rfloor (\lfloor \beta_2 p \rfloor + 1) + \lfloor \alpha_2 p \rfloor (\lfloor \alpha_2 p \rfloor + 1) = kp.\] For a given real number \(r\), we write \(\{r\} = r – \lfloor r \rfloor\) for the fractional part of \(r\). In particular, we have \(\lfloor r \rfloor = r – \{r\}\). So, \[\begin{aligned} kp & = (\beta_1 p – \{\beta_1 p\})(\beta_1 p – \{\beta_1 p\} + 1) – (\alpha_1 p – \{\alpha_1 p\})(\alpha_1 p – \{\alpha_1 p\} + 1) \\ & -(\beta_2 p – \{\beta_2 p\})(\beta_2 p – \{\beta_2 p\} + 1) + (\alpha_2 p – \{\alpha_2 p\})(\alpha_2 p – \{\alpha_2 p\} + 1) \\ & = (\beta_1^2 – \alpha_1^2 – \beta_2^2 + \alpha_2^2)p^2 + (\beta_1 – 2\beta_1 \{\beta_1 p\} – \alpha_1 + 2\alpha_1 \{\alpha_1 p\} – \beta_2 + 2\beta_2 \{\beta_2 p\} + \alpha_2 – 2\alpha_2 \{\alpha_2 p\}) p \\ & – \{\beta_1 p\} + \{\beta_1 p^2\} + \{\alpha_1 p\} – \{\alpha_1 p\}^2 + \{\beta_2 p\} – \{\beta_2 p\}^2 – \{\alpha_2 p\} + \{\alpha_2 p\}^2. \end{aligned}\] However, \(\{r\}\) always lies in the interval \([0, 1)\). As \(p \to \infty\), we have \[(\beta_1^2 – \alpha_1^2 – \beta_2^2 + \alpha_2^2) p^2 + O(p) = kp.\] This equation only holds when \(\beta_1^2 + \alpha_1^2 – \beta_2^2 + \alpha_2^2 = 0\). ◻
From here, we can prove the second half of Theorem 4.
Theorem 12. Let \(I_1 = [\alpha_1, \beta_1]\) and \(I_2 = [\alpha_2, \beta_2]\) with \(\beta_1 < \alpha_2\). If the set \(\{1, \alpha_1, \beta_1, \alpha_2, \beta_2\}\) is linearly independent in \(\mathbf{Z}\), then the equation \[\sum_{x \in F_n \cap I_1} x = \sum_{x \in F_n \cap I_2} x\] still only holds for finitely many values of \(n\).
Proof. Suppose that there are infinitely many possible values of \(n\). The previous theorem shows that \(\beta_1^2 – \alpha_1^2 = \beta_2^2 – \alpha_2^2\). In the previous proof, we obtained an expression for \(kp\). Dividing both sides of this equation by \(p\) and letting \(p \to \infty\) gives us \[k = 2(-\beta_1 \{\beta_1 p\} + \alpha_1 \{\alpha_1 p\} + \beta_2 \{\beta_2 p\} – \alpha_2 \{\alpha_2 p\}) + (\beta_1 – \alpha_1 – \beta_2 + \alpha_2) + O(1/p).\] By assumption, \(\beta_1^2 – \alpha_1^2 = \beta_2^2 – \alpha_2^2\), which implies that \[(\beta_1 – \alpha_1)(\beta_1 + \alpha_1) = (\beta_2 – \alpha_2)(\beta_2 + \alpha_2).\] Because \(\beta_1 + \alpha_1 < \beta_2 + \alpha_2\), we have \(\beta_1 – \alpha_1 > \beta_2 – \alpha_2\). Let \(\gamma = \beta_1 – \alpha_1 – \beta_2 + \alpha_2\). Then, \(\gamma \in (0, 1)\). In addition, \[k = 2(-\beta_1 \{\beta_1 p\} + \alpha_1 \{\alpha_1 p\} + \beta_2 \{\beta_2 p\} – \alpha_2 \{\alpha_2 p\}) + \gamma + O(1/p),\] giving us \[2(\beta_1 \{\beta_1 p\} – \alpha_1 \{\alpha_1 p\} + \beta_2 \{\beta_2 p\} – \alpha_2 \{\alpha_2 p\}) \equiv \gamma + O(1/p) \textrm{ mod } 1.\] Fix a small \(\epsilon > 0\). For a given real number \(r\), let \(\lfloor r \rceil\) be the integer closest to \(r\). In the proof of [18, Thm. 4], Harman shows that if \(n\) is sufficiently large, then there exists a prime \(p \in (n/2, n]\) for which \[\max(|\alpha_1 p – \lfloor \alpha_1 p \rceil|, |\alpha_2 p – \lfloor \alpha_2 p \rceil|, |\beta_1 p – \lfloor \beta_1 p \rceil|, |\beta_2 p – \lfloor \beta_2 p \rceil|) < \epsilon.\] For this value of \(p\), we have \[\{\alpha_1 p\}, \{\beta_1 p\}, \{\alpha_2 p\}, \{\beta_2 p\} \in (0, \epsilon) \cup (1 – \epsilon, 1).\] In particular, there exist constants \(a_{1, p}, a_{2, p}, b_{1, p}, b_{2, p} \in \{0, 1\}\) such that \(|\{\alpha_i p\} – a_{i, p}|\) and \(|\{\beta_i p\} – b_{i, p}|\) are both less than \(\epsilon\) for \(i = 1, 2\). Thus, \[|2(\beta_1 \{\beta_1 p\} – \alpha_1 \{\alpha_1 p\} + \beta_2 \{\beta_2 p\} – \alpha_2 \{\alpha_2 p\}) – 2(\beta_1 b_{1, p} – \alpha_1 a_{1, p} + \beta_2 b_{2, p} – \alpha_2 a_{2, p})| < 8\epsilon,\] which implies that \[\gamma \equiv 2(\beta_1 b_{1, p} – \alpha_1 a_{1, p} + \beta_2 b_{2, p} – \alpha_2 a_{2, p}) + O(\epsilon + (1/p)) \textrm{ mod } 1.\]
Even though \(p\) can be arbitrarily large, the tuple \((a_{1, p}, b_{1, p}, a_{2, p}, b_{2, p})\) can only take on one of \(16\) possible values. Therefore, there exist \(A_1, B_1, A_2, B_2 \in \{0, 1\}\) such that for infinitely many \(p\), the equations \(a_{1, p} = A_1\), \(b_{1, p} = B_1\), \(a_{2, p} = A_2\), and \(b_{2, p} = B_2\) hold simultaneously. For all \(\epsilon > 0\), we have the congruence \[\gamma \equiv 2(B_1 \beta_1 – A_1 \alpha_1 + B_2 \beta_2 – A_2 \alpha_2) + O(\epsilon) + o(1) \textrm{ mod } 1.\] Because this congruence must hold for all positive \(\epsilon\), we must have \[\gamma \equiv 2(B_1 \beta_1 – A_1 \alpha_1 + B_2 \beta_2 – A_2 \alpha_2) \textrm{ mod } 1.\] Recall that \(\gamma = \beta_1 – \alpha_1 – \beta_2 + \alpha_2\). So, \[(2B_1 – 1)\beta_1 – (2A_1 – 1)\alpha_1 + (2B_2 + 1)\beta_2 – (2A_2 + 1) \equiv 0 \textrm{ mod } 1.\] However, the coefficients of each \(\alpha_i\) and \(\beta_i\) are non-zero, which is impossible because \(1\), \(\alpha_1\), \(\beta_1\), \(\alpha_2\), and \(\beta_2\) are linearly independent. Hence, there can only be finitely many possible values of \(n\). ◻
Rather than balancing numbers in a line, we can balance them on a lever. In addition to being the center of the lever, the number \(b\) is now the fulcrum, i.e., the point on which the lever balances. The Law of the Lever states that the force required to lift an object with a lever is proportional to its mass and its distance from the fulcrum. For a given integer \(m\) on the lever, we set its mass to \(m\) and its distance from the fulcrum to \(|m – b|\). For a lever with fulcrum \(b\) to balance, there must exist a number \(r\) for which \[(b – 1) \cdot 1 + (b – 2) \cdot 2 + \cdots + 1 \cdot (b – 1) = 1 \cdot (b + 1) + 2 \cdot (b + 2) + \cdots + r \cdot (b + r).\] We call numbers \(b\) for which such an \(r\) exists lever balancing numbers. We show that a number is lever balancing exactly when it is odd.
Proof of Theorem 5. Let \(b > 1\) be an integer. We have \[\begin{aligned} (b – 1) \cdot 1 + (b – 2) \cdot 2 + \cdots + 1 \cdot (b – 1) &=\sum_{i = 1}^{b – 1} i(b – i) \\ &= b \sum_{i = 1}^{b – 1} i – \sum_{i = 1}^{b – 1} i^2 \\ &= \frac{b^2 (b – 1)}{2} – \frac{b(b – 1)(2b – 1)}{6} \\ &= \frac{b(b – 1)(b + 1)}{6}, \end{aligned}\] \[\begin{aligned} 1 \cdot (b + 1) + 2 \cdot (b + 2) + \cdots + r(b + r) & = \sum_{i = 1}^r i(b + i) \\ & = b\sum_{i = 1}^r i + \sum_{i = 1}^r i^2 \\ & = \frac{br(r + 1)}{2} + \frac{r(r + 1)(2r + 1)}{6} \\ & = \frac{r(r + 1)(3b + 2r + 1)}{6}. \end{aligned}\] The only numbers \(r\) satisfying \(b(b – 1)(b + 1)/6 = r(r + 1)(3b + 2r + 1)/6\) are \(r = -(b + 1), -b, (b – 1)/2\). The only positive solution is \((b – 1)/2\), which is only an integer when \(b\) is odd. ◻
Instead of removing one number from the sequence and balancing the entire lever on that number, we can remove a sequence of numbers.
Definition 7. Fix a positive integer \(k\). The number \(b\) is a \(k\)-lever balancing number if the corresponding lever balances after we remove the \(k – 1\) terms closest to \(b\) on both sides. In other words, we have \[(b – 1) \cdot 1 + (b – 2) \cdot 2 + \cdots + k \cdot (b – k) = k \cdot (b + k) + (k + 1) \cdot (b + k + 1) + \cdots + r \cdot (b + r).\]
Theorem 13. For all \(k > 1\), there are finitely many \(k\)-lever balancing numbers.
Proof. Suppose \(b\) is \(k\)-lever balancing for a fixed \(k > 1\). The lefthand side of the equation in the previous definition is \[\begin{aligned} \sum_{i = 1}^{b – k} i(b – i) & = \frac{b(b – k)(b – k + 1)}{2} – \frac{(b – k)(b – k + 1)(2b – 2k + 1)}{6} \\ & = \frac{(b – k)(b – k + 1)(b + 2k – 1)}{6} \end{aligned}\] and the right side is \[\begin{aligned} \sum_{i = k}^r i(b + i) & = \frac{br(r + 1) – bk(k – 1)}{2} + \frac{r(r + 1)(2r + 1) – k(k – 1)(2k – 1)}{6} \\ & = \frac{r(r + 1)(3b + 2r + 1) – k(k – 1)(3b + 2k – 1)}{6}. \end{aligned}\] Setting these values equal to each other and treating them as polynomials in \(r\), we obtain \[2r^3+3(b+1)r^2+(3b+1)r +(b-b^3)= 2k-6k^2+4k^3.\] We shall let the polynomial on the left be \(g_b(r)\) and the constant on the right be \(C_k\). Note that \(g_b(r)\) is a cubic polynomial with roots at \(r=-1-b,-b, (b-1)/2\). Also, \(g'_b(r)>0\) for \(r\ge0\). Therefore, there is at most one positive value of \(r\) for which \(g_b(r)=C_k\). We also note that \(C_k>0\) for \(k>1\). Finally, we note that \(g_b((b – 1)/2)=0\) and \(g_b(b/2)=(6b+9b^2)/4\), which means that as soon as \(b\) is large enough so that this last quantity exceeds \(C_k\), the unique solution (in \(r\)) to \(g_b(r)=C_k\) must be between \((b-1)/2\) and \(b/2\), and so is not an integer. Thus there are only finitely many \(k\)-lever balancing numbers. ◻
We generalize the concept of balancing numbers to balancing mobiles.
Definition 8. To construct a mobile, take a rooted tree and assign each node a (possibly empty) set of numbers.
Interestingly, mobiles have another definition in combinatorics. Bergeron, Labelle, and Leroux [19,Ex. VII.5] define a mobile as a class of labelled rooted trees. Two mobiles are equivalent if one can turn one mobile into another by cyclic shifts of the subtrees of a given node.
Definition 9. We say that a mobile is terminal if only the leaves have non-empty sets of numbers.
All mobiles in this section are terminal.
Definition 10. In a consecutive mobile, the set corresponding to each leaf is a consecutive set of positive integers.
For the trees in this section, the leaves will be labelled. In particular, they appear in a specific order and we will impose the additional restriction that the largest element of one leaf is smaller than the smallest element of the next. When we provide an image of a mobile, the leaves will be labelled from left to right.
Definition 11. The weight of a mobile is equal to the sum of the elements of all of the nodes.
Definition 12. Let \(M\) be a mobile with vertex set \(V\). For each \(v \in V\), let \(M_v\) be the subtree of \(M\) which consists of \(v\) and every vertex below \(v\). A mobile \(M\) is balancing if for every \(v \in V\), the weight of \(M_c\) is constant for all children \(c\) of \(v\).
In this section, we investigate balancing consecutive mobiles. For example, consider the following mobile.
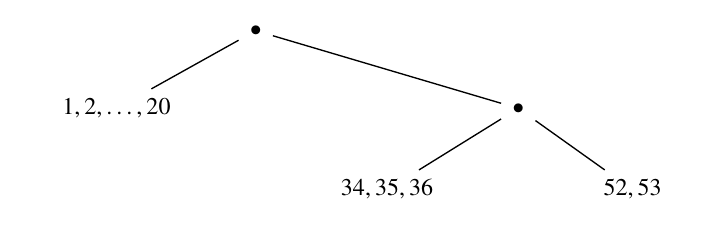
The left and right halves both have weight \(210\). In addition, the right half also splits into two parts, both of which have weight \(105\). Both the entire mobile and the smaller mobile making up the right half balance. In addition, every node consists of a set of consecutive integers. Hence, we have a balancing consecutive mobile.
Lemma 3. Let \(M\) be a mobile with \(k\) leaves and weight \(w\). There exists a sequence of positive real numbers \((r_1, r_2, \ldots, r_k)\) such that \(M\) is balancing exactly when the weight of the \(i\)th leaf is \(w/r_i\) for all \(i \leq k\).
Proof. We prove this result by induction on the number of layers of \(M\). This result clearly holds if there is one layer as the only possible mobile consists of a single point. In this case, we use \(r_1 = 1\).
Suppose we already have the result for \(\leq \ell\) layers and we want to prove it for \(\ell + 1\) layers. Let \(c_1, c_2, \ldots, c_t\) be the children of the root. The mobiles \(M_{c_1}, \ldots, M_{c_t}\) must all have the same weight \(w' := w/t\). Let \(m_i\) be the number of leaves in \(M_{c_i}\). By assumption, there exists a sequence \(r_{i, 1}, \ldots, r_{i, m_i}\) such that the weight of the \(j\)th leaf of \(M_{c_i}\) is \(w'/r_{i, j}\). In particular, the weight of this leaf is \(w/(tr_{i, j})\). ◻
Lemma 4. Every consecutive mobile corresponds to an integer \(k\) and three \(k\)-tuples of positive integers \((r_1, r_2, \ldots, r_k)\), \((a_1, a_2, \ldots, a_k)\), and \((b_1, b_2, \ldots, b_k)\). If \(b_i + a_i \leq b_{i + 1}\) for all \(i < k\), then the sequences on the nodes are disjoint. This mobile is balancing if the quantity \[r_i (a_i + (a_i + 1) + \cdots + (a_i + b_i – 1))\] is constant for all \(i \leq k\).
Proof. Let \(M\) be a balancing consecutive mobile with \(k\) leaves. Let the sequence at the \(i\)th leaf be \(a_i, a_i + 1, \ldots, a_i + b_i – 1\) and let \(S_i\) be the sum of these numbers. The previous lemma implies that for \(M\) to balance, the weight at each leaf must be a specific proportion of the total weight of the mobile. In other words, there is a sequence of positive numbers \(r_1, r_2, \ldots, r_k\) such that \(r_i S_i\) is constant for all \(i\). By assumption, the largest element of \(S_i\) is less than the smallest element of \(S_{i + 1}\). So, \(a_i + b_i – 1 < a_{i + 1}\) for all \(i\). ◻
We prove the following result.
Theorem 14. For every integer \(k\) and \(k\)-tuple \((r_1, \ldots, r_k)\), there exist infinitely many pairs of \(k\)-tuples \((a_1, \ldots, a_k)\) and \((b_1, \ldots, b_k)\) satisfying the conditions of the previous lemma.
Because every mobile obeying the conditions of Lemma 4 is a balancing consecutive mobile, we can choose sets of disjoint consecutive numbers to balance a given rooted tree. In order to obtain this result, we write a few theorems about consecutive sequences. Sylvester [20, §46] showed that the number of partitions of a number \(n\) into consecutive parts is equal to the number of odd divisors of \(n\). Mason [21] (see also [22]) strengthened this result as follows.
Theorem 15. The number of partitions of \(n\) into an odd number of consecutive parts is equal to the number of odd divisors of \(n\) less than \(\sqrt{2n}\). In addition, the number of partitions of \(n\) into an even number of consecutive parts is equal to the number of odd divisors of \(n\) greater than \(\sqrt{2n}\).
This result already implies that there exist numbers which we can write as sums of consecutive parts in arbitrarily many ways. Suppose we want to express \(n\) as a sum of an odd number of consecutive parts. Then we write \(n = (2k + 1)a\) and note that \[n = (a – k) + (a – k + 1) + \cdots + (a + k).\] This sequence has \(2k + 1\) terms and the middle term is \(a\).
Lemma 5. Fix a number \(k\) and a constant \(c > 1\). Then there exist infinitely many numbers \(n\) which we can write as a sum of an odd number of consecutive integers in \(k\) different ways. In addition, we may impose the following condition. Let the sequences be \(S_1, S_2, \ldots, S_k\), when written in increasing order of smallest element. For all \(i < k\), the smallest element of \(S_{i + 1}\) is more than \(c\) times greater than the largest element of \(S_i\).
Proof. Let \(n = t^m\) with \(t > 3c\) odd and \(m \geq 2(k – 1)\). For all \(\ell \in [\lceil m/2 \rceil, m]\), we have \[n = \left(t^\ell – \frac{t^{m – \ell} – 1}{2}\right) + \cdots + \left(t^\ell + \frac{t^{m – \ell} – 1}{2}\right).\] Because \(m \geq 2k\), we can express \(n\) as a sum of consecutive parts in at least \(m – \lceil m/2 \rceil + 1 \geq k\) different ways.
By assumption, \(c < t/3\). Therefore, \[c\left(t^\ell + \frac{t^{m – \ell} – 1}{2}\right) < \frac{t}{3} \cdot \frac{3t^\ell}{2} = \frac{t^{\ell + 1}}{2} < t^{\ell + 1} – \frac{t^{m – \ell + 1} – 1}{2}.\] Because \(n\) can be any number of the form \(t^m\) with \(t\) and \(m\) sufficiently large and \(t\) odd, there are infinitely many possible values of \(n\). ◻
We are now ready to prove Theorem 14.
Proof of Theorem 14. Let \(M\) be a balancing mobile with \(t\) leaves and weight \(w\). Lemma 4 implies for some sequence of real numbers \((r_1, \ldots, r_k)\), the weight of the \(i\)th leaf is \(w:= w/r_i\). Let \(c\) be the largest possible value of \(r_i/r_{i + 1}\). The previous lemma implies that there exists an integer \(n\) which we can write as a sum of an odd number of consecutive integers in \(k\) different ways. Let these sums be \(S_1, S_2, \ldots, S_m\). We can also guarantee that the ratio between the smallest element of \(S_{i + 1}\) and the largest element of \(S_i\) is greater than \(c\) for all \(i < m\).
Let \(S_i\) be the sequence \(a_i – c_i, a_i – c_i + 1, \ldots, a_i + c_i\). Each sequence has the same sum. If we multiply every element of \(S_i\) by \(r_i\), then the ratios of the sum of the sequences will be the same as the ratios between the weights of the leaves of \(M\). Unfortunately, this new sequence is no longer consecutive. The \(i\)th sequence is now \(r_i (a_i – c_i), r_i (a_i – c_i + 1), \ldots, r_i (a_i + c_i)\). However, replacing this sequence with \(r_i a_i – c_i, r_i a_i – c_i + 1, \ldots, r_i a_i + c_i\) keeps the sum the same and makes the sequence consecutive. For each \(i < k\), we have \(r_i a_i + c_i < r_{i + 1} a_{i + 1} – c_{i + 1}\) because the gaps between the original sequences \(S_i\) and \(S_{i + 1}\) were sufficiently large. ◻
Our proof of Theorem 14 is constructive. We close this section with an example. Specifically, we label the following rooted tree so that it becomes a balancing consecutive mobile.
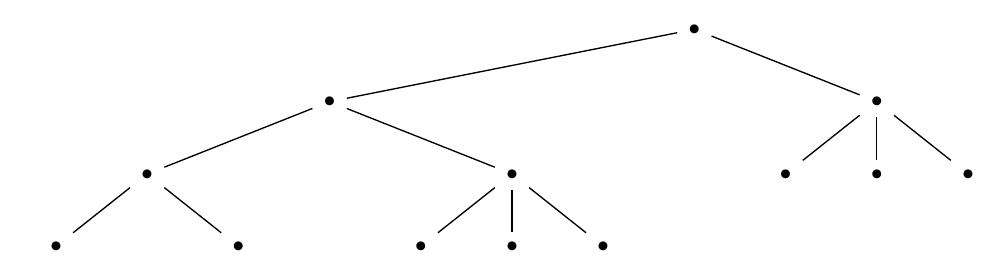
Let \(S_1, S_2, \ldots, S_8\) be the sums of the sequences at leaves of the mobile. For the mobile to balance, the sums of the \(S_i\)’s must have the ratio \(3 : 3 : 2 : 2 : 2 : 4 : 4 : 4\). The largest value of \(S_i/S_{i + 1}\) is \(3/2\), which occurs at \(i = 2\). By the proof of Lemma 5, we need to let \(n = t^m\), where \(t\) is an odd number greater than \(3(3/2) = 9/2\) and \(m \geq 2(8 – 1) = 14\). So, we let \(n = 5^{14}\).
We express \(5^{14}\) as a sum of consecutive integers in \(8\) different ways: \[\left(5^7 – \frac{5^7 – 1}{2}\right) + \cdots + 5^7 + \cdots + \left(5^7 + \frac{5^7 – 1}{2}\right),\] \[\left(5^8 – \frac{5^6 – 1}{2}\right) + \cdots + 5^8 + \cdots + \left(5^8 + \frac{5^6 – 1}{2}\right),\] \[\ldots\] \[5^{14}.\] However, we don’t want the sums to be the same. We want them to have a specific ratio. So, we multiply the center element by the desired amount and keep the length of each sequence the same. Because the endpoints of each sum are sufficiently far apart, we do not have to worry about our new sums overlapping. The sums on our leaves are as follows: \[\left(3 \cdot 5^7 – \frac{5^7 – 1}{2}\right) + \cdots + 3 \cdot 5^7 + \cdots + \left(3 \cdot 5^7 + \frac{5^7 – 1}{2}\right),\] \[\left(3 \cdot 5^8 – \frac{5^6 – 1}{2}\right) + \cdots + 3 \cdot 5^8 + \cdots + \left(3 \cdot 5^8 + \frac{5^6 – 1}{2}\right),\] \[\left(2 \cdot 5^9 – \frac{5^5 – 1}{2}\right) + \cdots + 2 \cdot 5^9 + \cdots + \left(2 \cdot 5^9 + \frac{5^5 – 1}{2}\right),\] \[\left(2 \cdot 5^{10} – \frac{5^4 – 1}{2}\right) + \cdots + 2 \cdot 5^{10} + \cdots + \left(2 \cdot 5^{10} + \frac{5^4 – 1}{2}\right),\] \[\left(2 \cdot 5^{11} – \frac{5^3 – 1}{2}\right) + \cdots + 2 \cdot 5^{11} + \cdots + \left(2 \cdot 5^{11} + \frac{5^3 – 1}{2}\right),\] \[\left(4 \cdot 5^{12} – \frac{5^2 – 1}{2}\right) + \cdots + 4 \cdot 5^{12} + \cdots + \left(4 \cdot 5^{12} + \frac{5^2 – 1}{2}\right),\] \[\left(4 \cdot 5^{13} – \frac{5 – 1}{2}\right) + \cdots + 4 \cdot 5^{13} + \cdots + \left(4 \cdot 5^{13} + \frac{5 – 1}{2}\right),\] \[4 \cdot 5^{14}.\]
While our algorithm generates consecutive mobiles, these mobiles are not necessarily minimal in any sense. We are unaware of any way to minimize either the largest number in a given mobile or the gaps between elements of consecutive leaves.
In addition to considering balancing mobiles, we can also impose the additional restriction that when we combine the various nodes, we obtain a sequence of consecutive numbers.
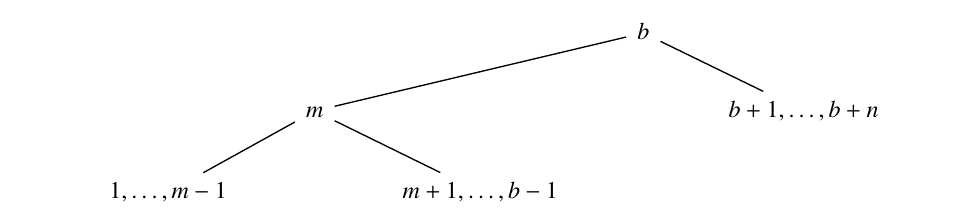
Definition 13. The number \(b\) is a left-mobile balancing number if there exist \(m\) and \(n\) such that
\(1 + 2 + \cdots + (m – 1) = (m + 1) + (m + 2) + \cdots + (b – 1),\)
\(1 + 2 + \cdots + (b – 1) = (b + 1) + (b + 2) + \cdots + (b + n).\)
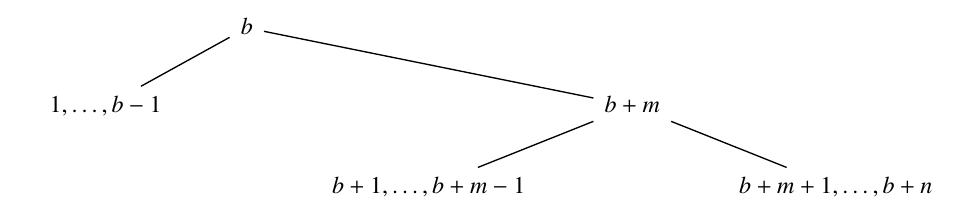
In addition, \(b\) is a right-mobile balancing number if there exist \(m\) and \(n\) such that
\(1 + 2 + \cdots + (b – 1) = (b + 1) + (b + 2) + \cdots + (b + n),\)
\((b + 1) + (b + 2) + \cdots + (b + m – 1) = (b + m + 1) + (b + m + 2) + \cdots + (b + n).\)
If \(b\) is left-mobile balancing, then the following mobile balances for some \(m, n\):
For a right mobile balancing number, we use this one:
We prove both halves of Theorem 7 separately.
Theorem 16. Left-mobile balancing numbers do not exist.
Proof. Suppose \(b\) is a left-mobile balancing number and suppose that \(m\) satisfies Condition \((1)\) of the definition. Because \(m\) is balancing, \(8m^2 + 1\) is a square and \[b = \frac{1 + \sqrt{8m^2 + 1}}{2}.\] From here on, we let \(r^2 = 8m^2 + 1\). In addition, Condition \((2)\) implies that \(b\) is balancing. So, \(8b^2 + 1\) is a square as well. We have \[8b^2 + 1 = 8\left(\frac{r + 1}{2}\right)^2 + 1 = 2(r + 1)^2 + 1 = 2r^2 + 4r + 3.\]
The previous equation implies that \(2r^2 + 4r + 3\) is a square. We also have \(2r^2 – 2 = 16m^2\). To summarize, both \(2r^2 – 2\) and \(2r^2 + 4r + 3\) are squares. We can show that there are no solutions.
Let \(c = \sqrt{2r^2 – 2}\) and suppose that \((c + k)^2 = 2r^2 + 4r + 3\). There are two possibilities based on the size of \(k\).
Suppose \(k = 1\). We have \((c + 1)^2 = 2r^2 – 1 + 2\sqrt{2r^2 – 2} = 2r^2 + 4r + 3\), which has no solutions because \(2\sqrt{2(r^2 – 1)} – 1 < (2\sqrt{2})r < 4r + 3\).
Suppose \(k > 1\). Then, \[2r^2 + 4r + 3 = (c + k)^2 \geq (c + 2)^2 = 2r^2 + 2 + 4\sqrt{2(r^2 – 1)},\] which implies that \[\sqrt{2(r^2 – 1)} \leq r – (1/4),\] which is impossible for \(r \geq 2\).
Because \(2r^2 – 2\) and \(2r^2 + 4r + 3\) cannot both be squares for \(r \geq 3\), left-mobile balancing numbers do not exist. ◻
Before discussing right-mobile balancing numbers, we write a few notes about Pell equations. Let \(D\) be an integer which is not a square. Every solution to the Pell equation \(x^2 – Dy^2 = 1\) satisfies the equation \(x + y\sqrt{D} = \pm u^k\), where \(u\) is a fixed element of \(\mathbf{Z}[\sqrt{D}]\) known as the fundamental unit. When we want to solve the equation \(x^2 – Dy^2 = n\), we use the following result.
Theorem 17 ([23, p.244]). Let \(u = a + b\sqrt{D}\) be the fundamental unit of \(\mathbf{Z}[\sqrt{D}]\). Then every integral solution to \(a^2 – Db^2 = n\) satisfies the equation \(a + b\sqrt{D} = (a' + b' \sqrt{D}) u^k\) for some integer \(k\), with \[|a'| \leq \frac{u + |n|}{2}, \quad |b'| \leq \frac{u + |n|}{2\sqrt{D}}.\]
We can now write our final theorem on mobiles.
Theorem 18. Right-mobile balancing numbers do not exist.
Proof. Because \(b\) is balancing, \(8b^2 + 1\) is a square and \[b + n = \frac{-1 + \sqrt{8b^2 + 1}}{2}.\] We can rewrite Condition \((2)\) of the definition as \[T(b + n) = 2T(b + m) – T(b) – (b + m),\] where \(T(k)\) is the \(k\)th triangular number. Expanding out the triangular terms and multiplying by \(2\) gives us \[(b + n)(b + n + 1) = 2(b + m)^2 – b(b + 1).\] In addition, \[(b + n)(b + n + 1) = 2b^2,\] which implies that \[2(b + m)^2 = 2b^2 + b(b + 1) = 3b^2 + b.\]
To summarize, \(8b^2 + 1\) and \(6b^2 + 2b\) must both be squares. By completing the square, we obtain \[6b^2 + 2b = 6\left(b + \frac{1}{6}\right)^2 – \frac{1}{6}.\] Let \(c = b + (1/12)\). There exist \(x\) and \(y\) satisfying the equations \[\begin{aligned} 8\left(c – \frac{1}{12}\right)^2 – x^2 & = & 1, \\ 6\left(c + \frac{1}{12}\right)^2 – y^2 & = & \frac{1}{6}. \end{aligned}\] We scale both equations to make every coefficient an integer: \[\begin{aligned} (12c – 1)^2 – 18x^2 & = 18, \\ (12c + 1)^2 – 24y^2 & = 4. \end{aligned}\] Finally, we replace \((12c, 3x, 2y)\) with \((c, x, y)\): \[\begin{aligned} (c – 1)^2 – 2x^2 & = 18, \\ (c + 1)^2 – 6y^2 & = 4. \end{aligned}\]
A classic theorem in number theory states that a pair of distinct Pell equations can only have finitely many solutions. (For an upper bound on the size of the solutions, see [24].) However, we can show that these equations have no simultaneous solutions through a short congruence argument.
The fundamental units of \(a^2 – 2b^2 = 1\) and \(a^2 – 6b^2 = 1\) are \(3 \pm 2\sqrt{2}\) and \(5 \pm 2\sqrt{6}\), respectively. Using the upper bound in the previous theorem, we can see that the only non-negative solutions to \(a'^2 – 2b'^2 = 18\) and \(a'^2 – 6b'^2 = 4\) are \((a', b') = (6, 3)\) and \((a', b') = (2, 0)\), respectively. Therefore, the non-negative solutions to \(a^2 – 2b^2 = 18\) have the form \(a + b\sqrt{2} = (6 + 3\sqrt{2})(3 + 2\sqrt{2})^m\) and the non-negative solutions to \(a^2 – 6b^2 = 4\) have the form \(a + b\sqrt{6} = 2(5 + 2\sqrt{6})^n\), for some \(m, n \geq 0\), respectively.
To summarize, \(c\), \(x\), and \(y\) must satisfy \[\begin{aligned} (c – 1) + x\sqrt{2} & = (6 + 3\sqrt{2})(3 + 2\sqrt{2})^m, \\ (c + 1) + y\sqrt{6} & = 2(5 + 2\sqrt{6})^n, \end{aligned}\] for some \(m, n \geq 0\). Let \(A_m\) and \(B_n\) be the integral parts of \((6 + 3\sqrt{2})(3 + 2\sqrt{2})^m\) and \(2(5 + 2\sqrt{6})^n\), respectively. By definition, \(c – 1 = A_m\) and \(c + 1 = B_n\) for some \(m\) and \(n\). Our goal is to show that the equation \(A_m = B_n – 2\) has no solutions.
We consider \(A_m\) and \(B_n\) mod \(5\) and \(7\). Note that these variables satisfy the following recurrences: \[A_m = 6A_{m – 1} – A_{m – 2}, \quad A_0 = 6, A_1 = 30,\] \[B_n = 10B_{n – 1} – B_{n – 2}, \quad B_0 = 2, B_1 = 10.\] For any given modulus \(r\), the sequences \(A_0, A_1, \ldots\) and \(B_0, B_1, \ldots\) are cyclic mod \(r\). The values of \(A_m\) mod \(5\) cycle through the numbers \[1, 0, 4, 4, 0, 1.\] Similarly, \(B_n\) mod \(5\) cycles through \[2, 0, 3, 0.\] We can see that \(A_m \equiv B_n – 2 \textrm{ mod } 5\) is only possible when \(n\) is even.
Modulo \(7\), we have \[6, 2, 6\] for \(A_m\) and \[2, 3, 0, 4, 5, 4, 0, 3\] for \(B_n\). In this case, \(A_m \equiv B_n – 2 \textrm{ mod } 7\) implies that \(n \equiv 3, 5 \textrm{ mod } 8\). But, this contradicts the result we obtained when we considered the problem mod \(5\). So, \(A_m \neq B_n – 2\) for all \(m, n\). (In particular, \(A_m \equiv B_n – 2 \textrm{ mod } 35\) has no solutions.) There are no right-mobile balancing numbers because no value of \(x\) works for both of our Pell equations. ◻
In the proof of Theorem 9, we stated that if \(n \leq 10\) is \(k\)-Farey balancing for some \(k\), then \(n = 4\) and \(k = 2\). We now discuss how we obtained that result. Suppose \(n\) is \(k\)-Farey balancing. By definition, we may break \([0, 1]\) into \(k\) intervals \(I_1, I_2, \ldots, I_k\) such that the sum of the elements of \(F_n \cap I_i\) is constant for all \(i \leq k\). In particular, the sum of the elements of \(F_n \cap I_1\) is equal to the sum of the elements of \(F_n \cap I_k\). We also observe that \(I_1\) is an interval with minimum element \(0\) and \(I_k\) is an interval with maximum element \(1\).
The code works as follows. First, we list all elements of \(F_n \backslash \{1\}\) in increasing order and call this list \(S\). We also define two variables left and right, which represent the sums of the elements of \(I_1\) and \(I_k\). Initially, left \(= 0\) and right \(= 1\). (We don’t set right to \(0\) to ensure that left \(\neq\) right initially.) If left \(<\) right, we add the smallest element of \(S\) to left and remove it from \(S\). We repeat this process until left \(=\) right or \(S = []\). If left \(\neq\) right, then \(n\) is not \(k\)-Farey balancing. If left \(=\) right and \(S = []\), then \(n\) is \(k\)-Farey balancing exactly when \(k = 2\). Finally, if left \(=\) right and \(S \neq []\), we cannot conclude anything.

When we run this code for \(n = 4\), the output is “\(k\)-Farey balancing exactly when \(k = 2\)“. For all other \(n \leq 10\), the code outputs “not \(k\)-Farey balancing for any \(k\)“.
The authors declare no conflicts of interest.
There is no conflict of interest related to this work.