Let \( G \) be a graph and let \( 0 \leq p, q \) and \( p + q \leq 1 \). Suppose that each vertex of \( G \) gets a weight of \( 1 \) with probability \( p \), \( \frac{1}{2} \) with probability \( q \), and \( 0 \) with probability \( 1-p-q \), and vertex weight probabilities are independent. The \textit{fractional vertex cover reliability} of \( G \), denoted by \( \operatorname{FRel}(G;p,q) \), is the probability that the sum of weights at the end-vertices of every edge in \( G \) is at least \( 1 \). In this article, we first provide various computational formulas for \( \operatorname{FRel}(G;p,q) \) considering general graphs, basic graphs, and graph operations. Secondly, we determine the graphs which maximize \( \operatorname{FRel}(G;p,q) \) for all values of \( p \) and \( q \) in the classes of trees, connected unicyclic and bicyclic graphs with fixed order, and determine the graphs which minimize it in the classes of trees and connected unicyclic graphs with fixed order. Our results on optimal graphs extend some known results in the literature about independent sets, and the tools we developed in this paper have the potential to solve the optimality problem in other classes of graphs as well.
There are many probabilistic measures of network reliability that have been extensively studied in the literature. For example, the classic all terminal edge reliability [1] computes the probability that operational edges form a connected spanning subgraph of a given graph assuming that each edge is operational with some fixed probability and all the vertices are always operational. Some other types of reliabilities include the node cop-win reliability [2], two-terminal reliability [3,4] and pair-connected reliability [5]. Yatauro [6] studied the edge cover reliability, that is, the probability that operational edges form an edge cover of the graph when each edge is operational with some fixed probability and vertices always operational. The focus of this note will be a new bivariate reliability polynomial defined via fractional vertex covers.
In this article, we assume that all graphs are finite, simple and undirected. A subset of vertices \(S\) is called a vertex cover of \(G\) if every edge is incident to some vertex in \(S\). Vertex covers are also known as transversals [7]. The cardinality of a minimum vertex cover is called the vertex cover number of \(G\), it is denoted by \(\tau(G)\).
Let \(\operatorname{vc}_k(G)\) be the number of vertex covers of \(G\) which contain exactly \(k\) vertices. The vertex cover polynomial [8] of graph of order \(n\) is given by \[\operatorname{VC}(G,x)=\sum_{k=\tau(G)}^n\operatorname{vc}_k(G)x^k.\] A subset of mutually non-adjacent vertices is called an independent set of the graph. It is clear that a subset of vertices \(S\) is a vertex cover of \(G\) if and only if \(V(G)\setminus S\) is an independent set of \(G\). Therefore, if \(i_t(G)\) is the number of independent sets with \(t\) vertices, then \(\operatorname{vc}_k(G)=i_{n-k}(G)\) for all \(k\). Thus, the well-known independence polynomial \(I(G,x)=\sum_k i_k(G)x^k\) and the vertex cover polynomial are related by the following identity \[\operatorname{VC}(G,x)=x^nI(G,1/x).\]
A fractional vertex cover is a function \(f:V(G)\to [0,1]\) such that for every edge \(e=uv\) in \(G\), \(f(u)+f(v)\geq 1\). Note that if the range of \(f\) consists of only \(0\) and \(1\), then \(f\) is simply a vertex cover. In this article, we will consider fractional vertex covers \(f\) such that \(f:V(G)\to \{0,1,\frac{1}{2}\}\) and we will assume that the range of \(f\) consists of only \(0\), \(1\) and \(\frac{1}{2}\) unless otherwise stated. Such fractional vertex covers play an important role in computation of the fractional matching number, \(\mu_f(G)\), which is one of the basic core fractional graph parameters, see [7] for a definition of \(\mu_f(G)\). It was shown in [7] that for every graph \(G\), there exists a fractional vertex cover \(g\) for which \[\sum_{v\in V(G)}g(v)=\mu_f(G)\] such that \(g(v)\in \{0,\frac{1}{2},1\}\) for all \(v\in V(G)\).
Suppose that vertices of a graph are independently operational with some fixed probability \(p\), where \(0\leq p\leq 1\), and edges are always operational. We define the vertex cover reliability, \(\operatorname{VCRel}(G,p)\) as the probability that operational vertices form a vertex cover of \(G\). It is clear that \(\operatorname{VCRel}(G,p)\) is a polynomial function in the variable \(p\) because \[\operatorname{VCRel}(G,p)=\sum_{k} \operatorname{vc}_k(G)\,p^k\,(1-p)^{n-k}\] and it can be obtained from the vertex cover polynomial under the following simple transformation \[\operatorname{VCRel}(G,p)=(1-p)^n\,\operatorname{VC}\left(G,p/(1-p)\right).\] We introduce a bivariate form of this type of reliability as follows. Let \(0\leq p,q\) and \(p+q\leq 1\). Suppose that each vertex of \(G\) gets a weight of \(1\) with probability \(p\), \(\frac{1}{2}\) with probability \(q\) and \(0\) with probability \(1-p-q\). The fractional vertex cover reliability of \(G\), denoted by \(\operatorname{FRel}(G;p,q)\), is the probability that operational vertices form a fractional vertex cover (that is, for each edge the sum of weights at the end-vertices is at least \(1\)). Fractional reliability also has potential to model practical problems on transportation networks. Consider a network of roads where vertices represent cities and edges represent the roads between them. Vertices are weighted \(1\) if they can maintain the roads they are incident to, \(0\) if they cannot, and \(\frac{1}{2}\) if they are willing to share maintenance with neighboring cities. A fractional vertex cover then models a maintained network of roads and fractional reliability measures the probability of the network being maintained.
A main problem studied in many reliability models [1-6,9] is to show whether optimal graphs exist and determine them if they exist in various classes of graphs. For two graphs \(G\) and \(H\), we say that \(G\) is at least as reliable as \(H\) if \(\operatorname{FRel}(G;p,q)\geq \operatorname{FRel}(H;p,q)\) for all \(0\leq p,q\) and \(p+q \leq 1\), and in this case we say \(G\) is more reliable than \(H\) if \(\operatorname{FRel}(G;p,q)>\operatorname{FRel}(H;p,q)\) for some \(p,q\). This relation induces a partially ordered set on graphs. As such, we use \(G\succeq H\) and \(G\succ H\) to denote \(G\) being at least as reliable or more reliable than \(H\) respectively. Similarly, we define that \(G\) is at most as reliable as \(H\) (\(G\preceq H\)) if \(H\succeq G\), and \(G\) is less reliable than \(H\) (\(G\prec H\)) if \(H\succ G\). Let \(\mathfrak{F}\) be a class of graphs. We say that \(G\) is a most optimal graph in \(\mathfrak{F}\) if \(G\succeq H\) for all \(H\in \mathfrak{F}\). We say that \(G\) is a least optimal graph in \(\mathfrak{F}\) if \(G\preceq H\) for all \(H\in \mathfrak{F}\).
This article is structured as follows. First, in Section 2, we present some basic results about fractional reliability that will be used in the latter sections. In Section 3, we address computational aspects. We provide three different formulas to compute the fractional reliability of an arbitrary graph (Theorems 1, 2,3) and a recursive formula for graphs which contain a vertex with a clique neighborhood (Theorem 4). We give formulas for fractional reliability of join of graphs (Theorem 5) and subdivision of graphs (Theorem 6) in terms of fractional reliabilities of input graphs. We also obtain results for fundamental graphs such as complete graphs (Corollary 1, complete bipartite graphs (Corollary 3), paths (Theorem 7) and cycles (Theorem 8). In Section 4,we investigate the problem of determining most or least optimal graphs. We develop two graph transformation techniques and our techniques allow us to find the most or least optimal graphs in the classes of trees (Theorems 9 and 10), unicyclic graphs (Theorems 11 and 12) of fixed order, and most optimal graphs in the classes of bicyclic graphs (Theorem 13) of fixed order. Our results on optimal graphs provide a fractional generalization of some results about enumeration of independent sets in [10,11]. In Section 5, we conclude with some future research directions.
For a graph \(G\), we write \(V(G)\) and \(E(G)\), or simply \(V\) and \(E\) respectively when the graph is clear from the context, for the vertex and edge set of \(G\). Since all graphs in this paper are undirected, an edge comprising vertices \(u\) and \(v\) will be denoted \(uv\). The open neighborhood of \(v\) in \(G\), denoted by \(N_G(v)\), consists of neighbors of \(v\) in \(G\), and the closed neighborhood of \(v\) in \(G\) is \(N_G[v]=N_G(v)\cup \{v\}\). For a subset of vertices \(S\) of \(G\), we define \(N_G(S)=\cup_{v\in S}N_G(v)\) and \(N_G[S]=S\cup N_G(S)\). We write \(\overline{G}\) for the complement of the graph \(G\). The complete graph \(K_r\) will be called the \(r\)–clique. For \(e=uv\) in \(E(G)\), the subgraph \(G\setminus uv\) is obtained from \(G\) by deleting the edge \(e\); \(V(G \setminus uv) = V(G)\), and \(E(G\setminus uv) = E(G) \setminus \{uv\}\). For a subset of vertices \(S\), \(G\setminus S\) is the subgraph induced by \(V(G)\setminus S\); that is, \(G \setminus S\) is the graph obtained by deleting all vertices of \(S\) (and the edges incident to those vertices). The union of \(G\) and \(H\), denoted by \(G\cup H\), is the graph consisting of disjoint copies of \(G\) and \(H\). The join of \(G\) and \(H\), denoted by \(G\vee H\), is obtained by taking a copy of each of \(G\) and \(H\), and adding an edge between every vertex of \(G\) and every vertex of \(H\). Given a graph \(G\) with an edge \(uv\), the subdivision of \(G\) obtained by subdividing \(uv\) is the graph \(H\) with \(V(H)=V(G)\cup\{w\}\) and \(E(H)=(E(G)\setminus \{uv\})\cup \{uw,vw\}\).
For an event \(A\), let \(\operatorname{\mathbb{P}}(A)\) denote the probability that \(A\) occurs. The conditional probability is defined to be \(\operatorname{\mathbb{P}}(A|B)=\operatorname{\mathbb{P}}(A\cap B)/\operatorname{\mathbb{P}}(B)\) when \(\operatorname{\mathbb{P}}(B)\) is nonzero. We say that a graph \(G\) is reliable if a random assignment of weights \(1,\frac{1}{2},0\) to vertices with probabilities \(p\), \(q\) and \(1-p-q\) yields a fractional vertex cover. Let \(v\to \alpha\) denote the event that the vertex \(v\) gets weight \(\alpha\) and \(\operatorname{FRel}(G;p,q|\,v\rightarrow \alpha)\) be the conditional probability that \(G\) is reliable given that the weight of \(v\) is \(\alpha\). Then, the probability that \(G\) is reliable is equal to \[\operatorname{FRel}(G;p,q)=\sum_{\alpha \in \{0,\frac{1}{2},1\}} \operatorname{\mathbb{P}}(v\to \alpha )\operatorname{FRel}(G;p,q|\,v\rightarrow \alpha)\] for any vertex \(v\).
A fractional vertex cover is called an \(i,j\)–fractional vertex cover if exactly \(i\) vertices have weight \(1\) and exactly \(j\) vertices have weight \(\frac{1}{2}\). Let \(\operatorname{fvc}_{i,j}(G)\) be the number of \(i,j\)-fractional vertex covers of \(G\). It is clear that \[\label{eqn:frel_equiv_fvc} \operatorname{FRel}(G;p,q)=\sum_{i=0}^{n}\sum_{j=0}^{n-i}\operatorname{fvc}_{i,j}(G)\,p^iq^j(1-p-q)^{n-i-j}, \tag{1}\] and \(\operatorname{FRel}(G;p,q)\) is a polynomial function in variables \(p\) and \(q\). From equation (1) we prove the following two lemmas which will be useful in Section 4 for finding optimal graphs.
Lemma 1. Let \(G\) and \(H\) be graphs. If \(\operatorname{fvc}_{i,j}(G)\le\operatorname{fvc}_{i,j}(H)\) for all \(i,j\), then \(G\) is at most as reliable as \(H\). Moreover, in this case if for some \(i,j\), \(\operatorname{fvc}_{i,j}(G)<\operatorname{fvc}_{i,j}(H)\), then \(G\) is less reliable than \(H\).
Proof. Let \(G\) and \(H\) be graphs with \(\operatorname{fvc}_{i,j}(G)\le\operatorname{fvc}_{i,j}(H)\) for all \(i,j\). Let \(0\le p,q\le 1\) and consider that by equation (1), \[\begin{align} \operatorname{FRel}(G;p,q)&=\sum_{i=0}^{n}\sum_{j=0}^{n-i}\operatorname{fvc}_{i,j}(G)p^iq^i(1-p-q)^{n-i-j}\\& \le\sum_{i=0}^{n}\sum_{j=0}^{n-i}\operatorname{fvc}_{i,j}(H)p^iq^i(1-p-q)^{n-i-j} \\ &=\operatorname{FRel}(H;p,q). \end{align}\tag{2}\] Moreover, in this case if there is some \(i,j\) such that \(\operatorname{fvc}_{i,j}(G)<\operatorname{fvc}_{i,j}(H)\), then the inequality (2) holds strictly and we conclude \(G\) is less reliable than \(H\). ◻
Lemma 2. Let \(G\) and \(H\) be graphs belonging to an arbitrary class \(\mathfrak{F}\) of graphs. If \(\operatorname{fvc}_{i,j}(G)\le\operatorname{fvc}_{i,j}(H)\) (respectively \(\operatorname{fvc}_{i,j}(G)\ge\operatorname{fvc}_{i,j}(H)\)) for all \(i,j\) and \(H\in \mathfrak{F}\), then \(G\) is a least (respectively most) reliable graph in \(\mathfrak{F}\).
Proof. Assume \(G\in \mathfrak{F}\) is such that \(\operatorname{fvc}_{i,j}(G)\le\operatorname{fvc}_{i,j}(H)\) for all \(i,j\) and \(H\in \mathfrak{F}\). Then it follows from Lemma 1 that \(\operatorname{FRel}(G;p,q)\le\operatorname{FRel}(H;p,q)\) for all \(H\in \mathfrak{F}\) and \(0\le p,q\le1\), thus making \(G\) a least reliable graph of \(\mathfrak{F}\).
The proof that \(G\) is a most optimal graph of \(\mathfrak{F}\) if \(\operatorname{fvc}_{i,j}(G)\ge\operatorname{fvc}_{i,j}(H)\) for all \(i,j\) and all \(H\in\mathfrak{F}\) is nearly identical. ◻
These lemmas naturally lead us to the following observation:
Proposition 1. If \(e\) is an edge of \(G\), then \(G\) is more reliable than \(G-e\).
Proof. Consider that all fractional vertex covers of \(G\) are also fractional vertex covers of \(G-e\). Thus \(\operatorname{fvc}_{i,j}(G)\le\operatorname{fvc}_{i,j}(G-e)\) for all \(i,j\). Moreover, consider the fractional vertex cover of \(G\) in which the endpoints of \(e\) are assigned weight \(0\), and all other vertices \(1\). As no edge is incident to both of the vertices with weight \(0\), this is a fractional vertex cover of \(G-e\), however applying the same weights to vertices in \(G\) fails to be a fractional vertex cover as the weights on endpoints of \(e\) sum to \(0\). Thus \(\operatorname{fvc}_{n-2,0}(G)<\operatorname{fvc}_{n-2,0}(G-e)\), and by Lemma 1 \(G\) is less reliable than \(G-e\). ◻
Proposition 1 implies that every proper spanning subgraph of \(G\) is less reliable than \(G\).
In this section, we provide three different formulas to compute the fractional reliability of an arbitrary graph by conditioning on vertices which get a particular weight. We also provide a recursive formula to compute fractional reliability of graphs which contain a vertex whose closed neighborhood is an \(r\)-clique, for some \(r\).
Theorem 1. Let \(G\) be a graph of order \(n\). Then, \[\operatorname{FRel}(G;p,q)=\sum_{\substack{S\in \mathfrak{I}(G)}}(1-p-q)^{|S|}\, p^{|N_G(S)|}\, (p+q)^{n-|N_G[S]|}\] where \(\mathfrak{I}(G)\) denotes the set of all independent sets of \(G\).
Proof. Let \(S\) be the set of all vertices which receive the weight \(0\). First note that \(S\) must form an independent set in \(G\) and the probability that all vertices in a set \(S\) get the same weight \(0\) is \((1-p-q)^{|S|}\). To cover the edges incident to vertices in \(S\), all vertices in \(N_G (S)\) must be of weight \(1\), giving a probability of \(p^{|N_G(S)|}\). Every other vertex in \(V(G)\setminus N_G[S]\) can then be either of value \(1\), or of value \(\frac{1}{2}\) which gives a probability of \((p + q)^{|n – N_G[S]|}\). All of these conditions must occur for each independent set of vertices that can take on the value of \(0\) in order for G to be reliable, so they are multiplied and then each case of a unique independent set is added together to cover every way in which \(G\) can be reliable. Thus, we obtain the result. ◻
Theorem 2. Let \(G\) be a graph of order \(n\) with no isolated vertices. Then, \[\operatorname{FRel}(G;p,q)=\sum_{S\subseteq V(G)}p^{|S|}\sum_{U\in \xi(S)}(1-p-q)^{|U|}q^{n-|S|-|U|}\] where \(\xi(S)=\{U:\ U\subseteq N_G(S)\ \text{and}\ N_G(U)\subseteq S\}\).
Proof. Let \(S\) consists of all vertices which get weight \(1\). By definition, every vertex outside of \(S\) must get weight \(0\) or \(\frac{1}{2}\). Since there are no isolated vertices, if some vertex \(v\) gets weight \(0\) then it must be in \(N(S)\) and all neighbors of \(v\) must be in \(S\). The subset of vertices that have weight \(0\) must then be elements of some \(U \in \xi(S)\). This leaves the remaining vertices to be of weight \(\frac{1}{2}\), of which there are \(n – |S| – |U|\). Every vertex of weight \(0\) must be adjacent to some vertex of weight \(1\) in \(S\), and so all ways to get a fractional vertex cover are represented by allowing these zeroes to be some subset \(U\) of \(\xi(S)\). This leaves the remaining vertices to be of weight \(\frac{1}{2}\), of which there must be \(n – |S| – |U|\) of them. This leaves a summation across all ways to have \(S\), of which there is a probability \(p^{|S|}\), and then this is multiplied by all the ways a reliable vertex cover could be completed, of which there are \(U \in \xi(S)\) ways where we have the probability of \((1 – p – q)^{|U|} q^{n – |S|-|U|}\). ◻
The following theorem relates the fractional vertex cover reliability of a graph to its vertex cover reliability.
Theorem 3. For every graph \(G\), \[\operatorname{FRel}(G;p,q)=\sum_{S\subseteq V(G)}q^{|S|}p^{|N_G(S)\setminus S|}\, \operatorname{VCRel}(G\setminus N_G[S],p).\]
Proof. We calculate the fractional reliability by conditioning on vertices which get weight \(\frac{1}{2}\). If \(S\) consists of all vertices of weight \(\frac{1}{2}\), then all all vertices in \(N_G(s)\) must get weight \(1\), and so we have the probability \(p^{|S|}\, q^{|N_G(S)\setminus S|}\). Every edge incident to some vertex in \(N_G(S)\) is covered and no vertex outside \(S\) gets weight \(\frac{1}{2}\). So, given these conditions, the probability that the subgraph \(G\setminus N_G[S]\) is reliable is equal to vertex cover reliability of \(G\setminus N_G[S]\). ◻
Theorem 4. Let \(u\) be a vertex of \(G\) such that \(N(u)\) induces an \(r\)-clique in \(G\). Then, \(\operatorname{FRel}(G; p, q)\) is equal to \[\begin{aligned} & p\operatorname{FRel}(G\setminus u;p,q)+(1-p-q)p^r\operatorname{FRel}(G\setminus N[u];p,q)\\ & + q\left(\operatorname{FRel}(G\setminus u;p,q)-\sum_{v\in N(u)}(1-p-q)p^{|N(v)\setminus \{u\}|}\operatorname{FRel}(G\setminus N[v];p,q)\right). \end{aligned}\]
Proof. The probability that \(G\) is reliable and the vertex \(u\) gets weight \(1\) (respectively \(0\)) is equal to \(p\operatorname{FRel}(G\setminus u;p,q)\) (respectively \((1-p-q)p^r\operatorname{FRel}(G\setminus N[u];p,q)\)). The probability that \(G\) is reliable given that vertex \(u\) gets weight \(\frac{1}{2}\) is equal to the probability that \(G\setminus u\) is reliable and no vertex in \(N_G(u)\) gets weight \(0\). Since \(N(u)\) is a clique, at most one vertex in \(N(u)\) may get weight \(0\) when \(G\setminus u\) is reliable. The probability that \(G\setminus u\) is reliable and a given vertex \(v\in N(u)\) gets weight \(0\) is equal to \((1-p-q)p^{|N(v)\setminus \{u\}|}\operatorname{FRel}(G\setminus N[v];p,q)\). Thus, \(\operatorname{FRel}(G\setminus u;p,q)-\sum_{v\in N(u)}(1-p-q)p^{|N(v)\setminus \{u\}|}\operatorname{FRel}(G\setminus N[v];p,q)\) gives the probability that \(G\setminus u\) is reliable and no vertex in \(N_G(u)\) gets weight \(0\). ◻
We consider three basic graph operations such as disjoint union, join and subdivision. First, observe that the disjoint union of \(G\) and \(H\), denoted by \(G\cup H\), is reliable if and only if both of \(G\) and \(H\) are reliable. So,
\[\operatorname{FRel}(G\cup H;p,q)=\operatorname{FRel}(G;p,q)\operatorname{FRel}(H;p,q).\]
Theorem 5. Let \(G\) and \(H\) be two graphs with \(|V(G)|=n_1\), \(|V(H)|=n_2\) and \(n=n_1+n_2\). Then, \(\operatorname{FRel}(G\vee H;p,q)\) is equal to \[(p+q)^{n}+p^{n_2}(\operatorname{FRel}(G;p,q)-(p+q)^{n_1})+p^{n_1}(\operatorname{FRel}(H;p,q)-(p+q)^{n_2}).\]
Proof. The probability that \(G\vee H\) is reliable and no vertex gets weight \(0\) is equal to \((p+q)^n\). If some vertex \(v\) of \(G\) gets weight \(0\), then, in order to cover edges from \(v\) to \(H\), all vertices of \(H\) must get weight \(1\). The probability that \(G\) is reliable with at least one vertex weight \(0\) is equal to \(\operatorname{FRel}(G,p,q)-(p+q)^{n_1}\). Hence, the probability that \(G\vee H\) is reliable and at least one vertex of \(G\) gets weight is equal to \(p^{n_2}(\operatorname{FRel}(G;p,q)-(p+q)^{n_1})\). Similarly, the probability that \(G\vee H\) is reliable and at least one vertex of \(H\) gets weight is equal to \(p^{n_1}(\operatorname{FRel}(H;p,q)-(p+q)^{n_2})\). ◻
In the next theorem, we will simply write \(\operatorname{FRel}(G)\) for \(\operatorname{FRel}(G;p,q)\).
Theorem 6. Let \(e=uv\) be an edge of \(G\) and let \(H\) be the graph obtained from \(G\) by subdividing the edge \(e\). Then, \[\begin{aligned} \operatorname{FRel}(H)&=p\operatorname{FRel}(G\setminus e)+(1-p-q)p^2\operatorname{FRel}(G\setminus \{u,v\})+q\operatorname{FRel}(G)\\ & -q(1-p-q)\sum_{x\in\{u,v\}}p^{|N_G[x]|}\operatorname{FRel}(G\setminus N_G[x]). \end{aligned}\]
Proof. Let \(w\) be the new vertex which is adjacent to both \(u\) and \(v\) in \(H\). The probability that \(H\) is reliable and the vertex \(w\) gets weight \(1\) is equal to \(\operatorname{\mathbb{P}}(w\rightarrow 1)\operatorname{FRel}(H|\,w\rightarrow 1)=p\,\operatorname{FRel}(G\setminus e)\), as \(w\) does not cover any edge other than \(uw\) and \(vw\). If \(w\) gets weight \(0\), then both \(u\) and \(v\) must get weight \(1\) in order for \(H\) to be reliable and in this case all edges incident to \(u\) or \(v\) are covered. So, the probability that \(H\) is reliable and \(w\) gets weight \(0\) is equal to \(\operatorname{\mathbb{P}}(w\rightarrow 0)\operatorname{FRel}(H|\,w\rightarrow 0)=(1-p-q)p^2\,\operatorname{FRel}(G\setminus \{u,v\})\). Lastly, the probability that \(H\) is reliable and the vertex \(w\) gets weight \(\frac{1}{2}\) is equal to \(q\operatorname{FRel}(H|\,w\rightarrow \frac{1}{2})\). So, it remains to compute \(\operatorname{FRel}(H|\,w\rightarrow \frac{1}{2})\). \[\begin{aligned} \operatorname{FRel}(H|\,w\rightarrow \frac{1}{2}) & =\operatorname{\mathbb{P}}(G\ \text{is reliable and neither $u$ nor $v$ receives weight $0$})\\ &= \operatorname{FRel}(G)-\operatorname{\mathbb{P}}(\text{$G$ is reliable and exactly one of $u$ or $v$ gets weight $0$ })\\ &= \operatorname{FRel}(G)-(1-p-q)\sum_{x\in\{u,v\}}p^{|N_G[x]|}\operatorname{FRel}(G\setminus N_G[x]) \end{aligned}\] and the last equality follows because all neighbors of a zero weighted vertex must receive weight \(1\) in order for the graph to be reliable. ◻
Note that in an empty graph, there is no edge that needs to be covered and so, \(\operatorname{FRel}(\overline{K}_n;p,q)=1\). Recall that \(\mathfrak{I}(G)\) denotes the set of all independent vertex subsets of \(G\). Next, we consider complete graphs.
Corollary 1. For every \(n\geq 1\), \[\operatorname{FRel}(K_n; p,q) = n\cdot (1- p – q)p^{n-1} + (p + q)^{n}.\]
Proof. In a complete graph \(K_n\), non-empty independent sets are precisely the singletons, that is \(\mathfrak{I}(G)\setminus \varnothing=\{\{v\}\, : v\in V(G)\}\). For each nonempty \(S\in \mathfrak{I}(G)\), we have \(|S|=1\), \(|N_G(S)|=n-1\) and \(|N_G[S]|=n\) and \(|\varnothing|=0\), \(|N_G(\varnothing)|=0\). Thus, the result follows from Theorem 1. ◻
We also have the following recursive formula for \(K_n\) which follows immediately from Theorem 5, as \(K_n\) is the join of \(K_{n-1}\) and \(K_1\).
Corollary 2. For every \(n\geq 1\), \[\operatorname{FRel}(K_n;p,q)=p\operatorname{FRel}(K_{n-1};p,q)+(1-p-q)p^{n}+q(p+q)^n.\]
Theorem 5 also gives us the following explicit formula for the fractional reliability of complete bipartite graphs.
Corollary 3. For every \(r\) and \(s\), \[\operatorname{FRel}(K_{r,s};p,q)=(p+q)^{r+s}+p^{s}(1-(p+q)^{r})+p^{r}(1-(p+q)^{s}).\]
Next, we give a recursive formula for the fractional reliability of path graphs.
Theorem 7. For every \(n\geq 4\), \(\operatorname{FRel}(P_n;p,q)\) is equal to \[(p+q)\operatorname{FRel}(P_{n-1};p,q)+p(1-p-q)\operatorname{FRel}(P_{n-2};p,q)-pq(1-p-q)\operatorname{FRel}(P_{n-3};p,q).\]
Proof. Let \(u\) be a leaf vertex of \(P_n\) and let \(v\) be the unique neighbor of \(u\). The probability that \(P_n\) is reliable and \(u\) has weight \(1\) is equal to \(\operatorname{\mathbb{P}}(u\rightarrow 1)\operatorname{FRel}(P_n;p,q|\,u\rightarrow 1)=p\,\operatorname{FRel}(P_{n-1};p,q)=p\operatorname{FRel}(P_{n-1};p,q)\) because \(u\) covers the edge \(uv\). Similarly, the probability that \(P_n\) is reliable and \(u\) has weight \(0\) is equal to \(p(1-p-q)p\operatorname{FRel}(P_{n-2};p,q)\) because this case requires the vertex \(v\) to have weight \(1\), and so both edges incident to \(v\) are covered by \(v\). Lastly, the event that \(u\) has weight \(\frac{1}{2}\) and \(P_n\) is reliable occurs if and only if \(u\) has weight \(\frac{1}{2}\), \(v\) has non-zero weight and \(P_n\setminus u\) is reliable. Considering the complementary event, we find that the probability that \(P_n\setminus u\) is reliable and \(v\) has weight \(0\) is equal to \(\operatorname{FRel}(P_{n-1})-p(1-p-q)\operatorname{FRel}(P_{n-3};p,q)\). Thus, the probability that \(P_n\) is reliable and \(u\) has weight \(\frac{1}{2}\) is equal to \(q\left(\operatorname{FRel}(P_{n-1};p,q)-p(1-p-q)\operatorname{FRel}(P_{n-3};p,q)\right)\). ◻
Lastly, we obtain a formula for the fractional reliability of a cycle graph in terms of fractional reliability of path graphs.
Theorem 8. For every \(n\geq 7\), \[\begin{aligned} \operatorname{FRel}(C_n;p,q) &= \operatorname{FRel}(P_{n};p,q)-p(1-p-q)(p(1-p-q)-2pq-2q^2)\operatorname{FRel}(P_{n-4};p,q)\\ & +2p^2q^2(1-p-q)^2\operatorname{FRel}(P_{n-6};p,q). \end{aligned}\]
Proof. Let \(e=uv\) be an edge in \(C_n\). First observe that \(C_n\) is reliable if and only if \(C_n\setminus e\) is reliable and the sum of weights of \(u\) and \(v\) is at least \(1\). We will consider the event that \(C_n\setminus e\) is reliable but the sum of weights of \(u\) and \(v\) is less than \(1\).
The probability that \(C_n\setminus e\cong P_n\) is reliable and both \(u\) and \(v\) get weight \(0\) is equal to \(p^2(1-p-q)^2\operatorname{FRel}(P_{n-4};p,q)\) because weight \(0\) on \(u\) and \(v\) requires their neighbors in \(C_n\setminus e\) to receive weight \(1\).
Next, consider the case when \(u\) gets weight \(0\), \(v\) gets weight \(\frac{1}{2}\) and \(C_n\setminus e\) is reliable. In this case the neighbor of \(u\) in \(C_n\setminus e\) is required to receive weight \(1\), and the neighbor of \(v\) in \(C_n\setminus e\), say \(v'\), may get either \(\frac{1}{2}\) or \(1\). If \(v\) gets weight \(1\), the fractional reliability is equal to \(p^2q(1-p-q)\operatorname{FRel}(P_{n-4};p,q)\). If \(v\) gets weight \(\frac{1}{2}\), then the problem reduces to the fractional reliability of \(P_{n-3}\) with one leaf having weight \(\frac{1}{2}\), and the latter can be calculated by using the last line in the proof of Theorem 7. Thus, the probability that \(C_n\setminus e\) is reliable with the given vertex weights is equal to \(pq^2(1-p-q)\left[q\left(\operatorname{FRel}(P_{n-4};p,q)-p(1-p-q)\operatorname{FRel}(P_{n-6};p,q)\right)\right]\). Now, \(\operatorname{\mathbb{P}}(u\to 0, v\to \frac{1}{2}, C_n\setminus e \ \text{is reliable})=\operatorname{\mathbb{P}}(u\to \frac{1}{2}, v\to 0, C_n\setminus e \ \text{is reliable})\). Thus, \[\begin{aligned} \operatorname{FRel}(C_n;p,q) &= \operatorname{FRel}(P_{n};p,q)-p^2(1-p-q)^2\operatorname{FRel}(P_{n-4};p,q)-2p^2q(1-p-q)\operatorname{FRel}(P_{n-4};p,q)\\ & -2pq^2(1-p-q)\left[q\left(\operatorname{FRel}(P_{n-4};p,q)-p(1-p-q)\operatorname{FRel}(P_{n-6};p,q)\right)\right] \end{aligned}\] and the result follows after the simplification of the above. ◻
If \(G\) is a graph on \(n\) vertices and is not isomorphic to \(\overline{K}_n\) or \(K_n\), then \(\overline{K}_n\) is a subgraph of \(G\) and \(G\) is a subgraph of \(K_n\). By Proposition 1 \(K_n\) is the least reliable graph on \(n\) vertices, and \(\overline{K}_n\) is the most reliable. In this section we consider restricted classes of graphs, and, within those classes, determine which are most and least reliable.
Definition 1 and 2 describe transformations on graphs that strictly increase or strictly decrease the number of fractional vertex covers of a given graph.
Definition 1. Transformation A. Let \(G\) be a graph with a path \(v_1,v_2,\dots,v_k\) with \(\deg(v_1)=1\), \(\deg(v_i)=2\) for all \(2 \le i < k\) and \(\deg(v_k)\ge 3\), and let \(u\) be a neighbor of \(v_k\) other than \(v_{k-1}\). Let \(G^|\) be the graph with \(V(G^|)=V(G)\) and \(E(G^|)=\left(E(G)\setminus v_{k}u\right) \cup v_{1}u\). See Figure 1 in which the dashed edge indicates a path of arbitrary length, the dotted edge is either in \(G\) or not, and within the circle are all other vertices and edges of \(G\).
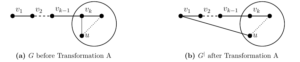
Lemma 3. If \(G\) is a graph with structure amenable to Transformation A of Definition 1 and \(G^|\) is the graph obtained from \(G\) via Transformation A then, \(G^|\) is strictly less reliable than \(G\).
Proof. Let \(G\) and \(G^|\) be as specified. Let \(P\) be the path \(v_1,\dots,v_k\). We use Transformation A to show that there is a non-surjective injection from \(i,j\)-fractional vertex covers of \(G^|\) to \(i,j\)-fractional vertex covers of \(G\). We then show that for some \(i,j\) and \(i,j\)-fractional vertex cover of \(G\), there is no preimage for it among \(i,j\)-fractional vertex covers of \(G^|\).
Let \(\mu^|:V(G)\to\{0,\frac{1}{2},1\}\) be a
fractional vertex cover of \(G^|\). We
consider two cases depending on whether \(\mu^|(v_1)+\mu^|(u) \ge 1\).
Case 1. \(\mu^|(v_1)+\mu^|(u) \ge
1\).
The only edge in \(G\) which is not
in \(G^|\) is \(v_{k}u\). Because in this case this edge is
covered by \(\mu^|\), we map \(\mu^|\) to \(\mu\) with \(\mu=\mu^|\).
Case 2. \(\mu^|(v_1)+\mu^|(u) <
1\).
Let \(\mu:V(G)\to\{0,\frac{1}{2},1\}\) be defined by \[\mu(w)=\begin{cases} \mu^|(v_{k-i+1})&w=v_i\\ \mu^|(w)&\text{otherwise} \end{cases}.\] We claim that \(\mu\) is an \(i,j\)-fractional vertex cover of \(G\). To prove this, we verify all edges of \(G\) are covered by \(\mu\). Because \(\mu^|(w)=\mu(w)\) if \(w\ne v_i\) for any \(i\), all edges not incident to any \(v_i\) have the same weights under \(\mu\) as they do under \(\mu^|\), hence \(\mu\) covers all edges not incident to \(P\). Similarly, we can verify that for some edge \(v_{i}v_{i+1}\) in \(P\), \[\mu(v_i)+\mu(v_{i+1})=\mu^|(v_{k-i+1})+\mu^|(v_{k-i})\ge1,\] and hence \(\mu\) covers \(P\).
It remains to verify the edges incident to \(v_k\) are covered by \(\mu^|\). Since \(\mu^|\) is an \(i,j\)-fractional vertex cover of \(G^|\), and by assumption, \[\mu^|(v_1)+\mu^|(u)\ge 1 > \mu^|(v_k)+\mu^|(u).\] Further, this implies \[\mu^|(v_1)>\mu^|(v_k)\] and \[\mu(v_k)>\mu(v_1).\] Hence all edges \(v_kw\) present in both \(G^|\) and \(G\) are covered in \(G\). Finally, consider that for \(uv_k\), the only edge in \(G\) which is not in \(G^|\), \[\mu(v_k)+\mu(u)=\mu^|(v_1)+\mu^|(u)\ge 1.\] Therefore \(\mu\) is an \(i,j\)-fractional vertex cover of \(G\).
\[\mu_1(v_1)+\mu_1(u)\ge 1 > \mu_2(v_1) + \mu_2(u),\] Now we show that any \(\mu_1\) that is an image of the injection and as described in Case 1, is different than any \(\mu_2\) which is an image of the injection and is as described in Case 2. Suppose \(\mu_1\) and \(\mu_2\) are such \(i,j\)-fractional vertex covers. Consider that \[\mu_1(v_1)+\mu_1(u)\ge 1 > \mu_2(v_1) + \mu_2(u),\] hence \(\mu_1\ne \mu_2\) for any \(\mu_1\) and \(\mu_2\), as desired.
Now we describe, for some \(i,j\), an \(i,j\)-fractional vertex cover of \(G\) that is not the image of the injection.
To this end, we define \[\mu(w)=\begin{cases} 0&w=v_1\\ \frac{1}{2}&w\in N_G(v_k)\setminus\{v_{k-1}\}\\ 1&\text{otherwise} \end{cases}.\]
We claim \(\mu\) is a fractional vertex cover of \(G\). To wit, the only vertex with weight \(0\) is \(v_1\), and its only neighbor, \(v_2\), has weight \(1\). All other edges of \(G\) are incident to two vertices with weight at least \(\frac{1}{2}\) and are therefore covered by \(\mu\). Further, \(\mu\) is not a fractional vertex cover of \(G^|\) as \(\mu(v_1)+\mu(u)=\frac{1}{2}\). Therefore, if \(\mu\) is the image of a cover of \(G^|\), it must be a cover \(\mu_2\) as described in Case 2.
But then the preimage of \(\mu\) must have had the weights on \(v_1, \dots, v_k\) reversed; that is, assuming \(\mu^|\) is the preimage of \(\mu\) then
\[\mu^|=\begin{cases} 0&w=v_k\\ \frac{1}{2}&w\in N_G(v_k)\setminus\{v_{k-1}\}\\ 1&\text{otherwise} \end{cases}.\] Since \(\deg_G(v_k)\) was assumed to be at least \(3\), there is some \(x\in N_G(v_k)\setminus\{v_{k-1}, u\}\). Consider that \(v_kx\in E(G^|)\), however \[\mu^|(v_k)+\mu^|(x)=\frac{1}{2},\] and hence \(\mu^|\) is not a fractional vertex cover of \(G^|\). Therefore, \(\mu\) is a fractional vertex cover of \(G\) which is not the image of any fractional vertex cover of \(G^|\). Therefore, by Lemma 1 we conclude \(G\) is strictly more reliable than \(G^|\). ◻
Now we define a transformation that, as will be shown in Lemma 4, increases reliability of graphs on which it acts.
Definition 2(Transformation B). Let \(G\) be a connected graph with vertices \(u\) and \(v\) such that \(N_G(u)\not\subseteq N_G[v]\) and \(N_G(v)\not\subseteq N_G[u]\). In particular this implies that \(N_G(u)\setminus N_G[v]\) and \(N(v)\setminus N_G[u]\) are nonempty and disjoint, and we will refer to vertices in these sets as the private neighbors of \(u\) and \(v\), respectively. Define \(W = N_G(u) \setminus N_G[v]\). Let \(G^*\) be defined by \(V(G^*)=V(G)\) and \(E(G^*) = E(G)\setminus\{uw:w\in W\}\cup\{vw:w\in W\}\). Equivalently, \(G^*\) is the graph obtained by disconnecting \(u\) from all of its private neighbors, and connecting them to \(v\).
See Figure 2 in which the privet neighborhood of \(u\) in \(G\) is denoted \(W\) as above, the common neighborhood of \(u\) and \(v\) is denoted \(X\), the private neighborhood of \(v\) in \(G\) is \(Y\). The dotted edge indicates an edge that may or may not be present in \(G\), while solid edges denote that \(u\) or \(v\) are adjacent to all vertices of the corresponding set. \(G\) may have any other vertices or edges in the larger oval containing \(W,X,\) and \(Y\).

Note that if \(G\) is connected, and \(u\) and \(v\) are chosen such that either \(uv\in E(G)\) or \(N(u)\cap N(v)\) is nonempty, then the resulting \(G^*\) is also connected.
Lemma 4. If \(G\) is a graph with structure amenable to Transformation B of Definition 2, and \(G^*\) is the graph obtained from \(G\) by Transformation B, then \(G^*\) is more reliable than \(G\).
Proof. Let \(G\), \(u\), \(v\), and \(W\), be as described in Definition 2, and \(G^*\) is obtained from \(G\) by the action of Transformation B. As in the proof of Lemma 3, we show that there is a injection of \(i,j\)-fractional vertex covers of \(G\) into \(i,j\) fractional vertex covers of \(G^*\) that is not surjective. But note that we are considering the injection to map from the \(i,j\)-fractional vertex covers of \(G\), the graph on which Transformation B operates to the set of \(i,j\)-fractional vertex covers of the graph produced by the transformation. Then we describe an \(i,j\)-fractional vertex cover of \(G^*\) that is not the image of of the injection, and appealing to Lemma 1 will yield the result.
Let \(\mu:V(G)\to\{0,\frac{1}{2},1\}\) be an
\(i,j\)-fractional vertex cover of
\(G\). For the injection, we map each
\(i,j\)-fractional vertex cover \(\mu\) of \(G\) to a unique \(i,j\)-fractional vertex cover \(\mu^*\) of \(G^*\). We need to consider two cases,
depending on whether \(\mu(v) + \mu(w) \ge
1\) for all \(w \in W\).
Case 1. \(\mu(v)+\mu(w)\ge 1\)
for all \(w\in W\).
In this case \(\mu\) also is an \(i,j\)-fractional vertex cover of \(G^*\) since it covers all the edges which are in \(G^*\). In this case, we let \(\mu^*=\mu\).
Case 2. \(\mu(v)+\mu(w)<1\) for some \(w\in W\).
Let \(\mu^*:V(G)\to\{0,\frac{1}{2},1\}\) be defined by \[\mu^*(x)=\begin{cases} \mu(u)&x=v\\ \mu(v)&x=u\\ \mu(x)&\text{otherwise} \end{cases}.\]
We claim that \(\mu^*\) is an \(i,j\)-fractional vertex cover of \(G^*\). Clearly, \(\mu^*\) covers all edges not incident to \(u\) or \(v\) since the weights of those edges are those of \(\mu\). As \(u\) is only incident to the edge \(uv\) and edges between \(u\) and \(s \forall s \in S\), it is straightforward to calculate \(\mu^*(u)+\mu^*(v)=\mu(v)+\mu(u)\ge 1\), and \(\mu^*(u)+\mu^*(s)=\mu(v)+\mu(s)\ge 1\). For the edges incident to \(v\) we begin with neighbors in \(W\). For all \(w\in W\), \[\mu^*(v)+\mu^*(w)=\mu(u)+\mu(v)\ge1.\] To show the remaining edges are covered it is helpful to note that because \(\mu(u)+\mu(w)\ge 1>\mu(v)+\mu(w)\) for some \(w\), \(\mu(u)>\mu(v)\). It follows for all \(x\in N_{G^*}(v)\diagdown (W\cup\{u\})\), \[\mu^*(v)+\mu^*(x)=\mu(u)+\mu(x)>\mu(v)+\mu(x)\ge 1.\] Therefore, \(\mu^*\) covers all edges of \(G^*\), and is an \(i,j\)-fractional vertex cover of \(G^*\). Further, because there is some \(w\in W\) such that \[\mu^*(u)+\mu^*(w)=\mu(v)+\mu(w)<1,\] the \(\mu^*\) provided in case \(2\) is different from any \(\mu*\) as in case \(1\).
Therefore, there is an injection from \(i,j\)-fractional vertex covers of \(G\) to \(i,j\)-fractional vertex covers of \(G^*\), and hence \(\operatorname{fvc}_{i,j}(G)\le \operatorname{fvc}_{i,j}(G^*)\).
To show that \(G^*\) is more reliable than \(G\), we will demonstrate that for some \(i\) and \(j\), \(\operatorname{fvc}_{i,j}(T) < \operatorname{fvc}_{i,j}(K_{1,n-1})\) and the result will follow from Lemma 1. Let \(i = |V(G)| – 3\) and \(j = 2\). Let \(w\in N_G(u)\setminus N_G[v]\) and \(y\in N_G(v)\setminus N_G[u]\). Consider the following function \(\mu^*\) on \(G^*\): \[\mu^*(x)=\begin{cases} 0&x=u\\ \frac{1}{2}&x\in\{w,y\}\\ 1&\text{otherwise} \end{cases}.\]
The function \(\mu^*\) is a fractional vertex cover of \(G^*\) because \(u\) is the only vertex with weight \(0\), and \(w,y\) are not adjacent to \(u\). It follows that all neighbors of \(u\) in \(G^*\) have weight \(1\), and all edges of \(G^*\) are covered. Now we will show that this \(i,j\)-fractional vertex cover is not the image of any \(i,j\)-fractional vertex cover of \(G\). Assume that \(\mu\) is a \(|V|-3,2\)-fractional vertex cover of \(G\) which is the image of \(\mu^*\) under the given injection. Recall that \(\mu\) and \(\mu^*\) only differ in their values on \(u\) and \(v\). Because \(u\) and \(v\) have \(w\) and \(y\) as neighbors with a weight of \(\frac{1}{2}\) in \(G\), and because either \(\mu(u)=0\) or \(\mu(v)=0\), there must be an edge with one endpoint weighted \(0\) and the other only \(\frac{1}{2}\). Thus \(\mu\) cannot be a fractional vertex cover of \(G\), and we conclude the fractional vertex cover \(\mu^*\) cannot be the image of any fractional vertex cover of \(G\).
Thus, there exists an \(i\) and \(j\) such that an \(i,j\)-fractional vertex cover in \(G^*\) is not the image of a fractional vertex cover in \(G\). Therefore, by Lemma 1, \(G\) is strictly less reliable than \(G^*\). ◻
Recall that a connected graph with no cycles is a tree. In this section, we will determine the most and least optimal graphs among all trees of fixed order. It was shown in [11] that the star graph \(K_{1,n-1}\) maximizes and the path graph \(P_n\) minimizes \(i_k(G)\) (or equivalently maximizes \(vc_k(G)\)) for all \(k\) among all trees on \(n\) vertices. Our results about trees (Theorems 9 and 9) generalize these results from vertex covers to fractional vertex covers, as \(\operatorname{fvc}_{k,0}(G)=vc_k(G)\).
Theorem 9. \(P_n\) is the unique least optimal tree of order \(n\).
Proof. Let \(T\) be a tree on \(n\) vertices. If \(T\ne P_n\), then \(T\) has a vertex with degree at least \(3\). Because all trees have a vertex of degree \(1\), the transformation described in Lemma 3 can be executed by letting \(v_1\) be a vertex with degree \(1\), \(v_2,\dots,v_{k-1}\) be the vertices with degree \(2\) leading up to some vertex with degree at least three, \(v_k\). Let \(T^|\) be \(T\) transformed as described in Lemma 3.
Consider that all vertices in \(T\) and \(T^|\) have the same degree except \(v_1\) and \(v_k\). In particular, \(\deg_{T^|}(v_1)=\deg_T(v_1)+1=2\), and \(\deg_{T^|}(v_k)=\deg_T(v_k)-1\ge2\). This implies that \(T^|\) has exactly one fewer degree-one vertex than \(T\). It follows that if \(T\) has \(\ell\) vertices of degree-one, then \(\ell-2\) iterations of the transformation applied to \(T\) will yield a tree with only two vertices of degree 1 which must be a path because among trees only paths have exactly two degree 1 vertices. Because Lemma 3 implies every iteration of Transformation A strictly decreases the number of fractional vertex covers, we conclude the desired result. ◻
Theorem 10. \(K_{1,n-1}\) is the unique most optimal tree of order \(n\).
Proof. Let \(T\) be a tree. If \(T\) is not \(K_{1,n-1}\), there exists some edge \(uv\) with \(\deg(u)>1\) and \(\deg(v)>1\). Because \(T\) is acyclic, this implies \(u\) and \(v\) have distinct neighbors and Transformation B can be applied. Let \(W=N_T(u)\diagdown N_T[v]\) and let \(T^*\) be \(T\) with Transformation B applied to \(uv\).
Consider that all vertices in \(T\) and \(T^*\) have the same degree except \(u\) and \(v\). In particular, \(\deg_{T^*}(u)=1\), and \(\deg_{T^*}(v)=\deg_T(v)+\deg_T(u)-1\). This implies that \(T^*\) has exactly one more degree-one vertex than \(T\). It follows that if \(T\) has \(\ell\) vertices of degree-one, then \(n-1-\ell\) iterations of Transformation B applied to \(T\) will yield a \(K_{1,n-1}\). By Lemma 4 each iteration of this flip strictly increases the reliability of \(T\). This implies \(T\) is less reliable than \(K_{1,n-1}\) and the proof is complete. ◻
Lastly, we note that the number of \(i,j\)-fractional vertex covers of the most optimal tree \(K_{1,n-1}\) can be calculated as follows.
\[\operatorname{f}_{i,j}(K_{1,n-1})= \begin{cases} {\binom{n}{i}} & \text{if } i+j=n\\ {\binom{n-1}{i-1}}{\binom{n-i}{j}}%={n-1\choose i-1,j,n-i-j} & \text{if } i+j<n \ \text{and} \ i,j\geq 1\\ 0 & \text{if } i+j<n\ \text{and} \ i=0\\ vc_i(K_{1,n-1}) & \text{if } i\geq 1\ \text{and} \ j=0\\ \end{cases}\]
A graph is called unicyclic if it contains exactly one cycle. A connected graph \(G\) is unicyclic if and only if \(|E(G)|=|V(G)|\). Using the same tactics as above, we also determine the least and most reliable graphs among all unicyclic connected graphs.
Theorem 11. \(C_n\) is uniquely the least reliable graph among all connected unicyclic graphs.
Proof. We will show that if some unicyclic graph \(G\) is not \(C_n\), then \(G\) is strictly more reliable than \(C_n\). The proof will proceed by induction on the number of degree \(1\) vertices in \(G\). Consider first that if \(G\) has \(0\) vertices with degree \(1\), \(G\) must be \(C_n\).
Next, assume for some \(\ell\ge0\) that all unicyclic graphs with \(\ell\) vertices of degree \(1\) are either \(C_n\) or strictly more reliable than \(C_n\). Consider some unicyclic \(G\) with \(\ell+1\) vertices with degree \(1\), and let \(v_1\) be one of those degree \(1\) vertices. Because the average degree of any unicyclic graph is \(2\), and \(v_1\) has degree less than \(2\), somewhere in \(G\) there is a vertex with degree at least \(3\). Let \(v_1,\dots,v_k\) be the unique path from \(v_1\) to a vertex \(v_k\) where \(\deg(v_k)\ge 3\) and \(\deg(v_i)=2\) for all \(0<i<k\). Let \(u\) be a neighbor of \(v_k\) other than \(v_{k-1}\). Let \(G^|\) be the result of applying Transformation A from Definition 1 with \(v_1,\dots,v_k\) and \(u\) as specified. Consider that among \(G\) and \(G^|\) all vertices have the same degree except \(v_1\) and \(v_k\), and that \(\deg_{G^|}(v_1)=2\) and \(\deg_{G^|}(v_k)\ge 2\). This implies that \(G^|\) has exactly one fewer vertex of degree \(1\) than \(G\) does. By the result of Lemma 3, \(G^|\) is strictly less reliable than \(G\). Further, \(G^|\) has \(\ell\) vertices of degree \(1\). Thus, by the induction assumption \(G^|\) is at least as reliable as \(C_n\), and \(G\succ C_n\). Therefore, by the principle of mathematical induction, \(C_n\) is uniquely the least reliable unicyclic graph. ◻
The lollipop graph \(L_{n,3}\) which is the unique connected unicyclic graph on \(n\) vertices with a \(C_3\) subgraph and exactly one vertex of degree \(1\). We note that it was proved in [10] that among all connected unicyclic graphs with fixed order, both \(C_n\) and \(L_{n,3}\) minimize the total number of their independent sets. One result of Theorem 12 is that there is no \(i\) for which \(\operatorname{fvc}_{i,0}(L_{n,3})<\operatorname{fvc}_{i,0}(C_n)\). It follows that in order to achieve the same total of independent sets, \(\operatorname{vc}_i(L_{n-3})=\operatorname{vc}_i(C_n)\) for all \(i\). Thus in the non-fractional case of reliability, \(C_n\) and \(L_{n,3}\) are both least optimal connected unicyclic graphs. In this case, the fractional result differs as \(L_{n,3}\) can still be transformed to \(C_n\) via Transformation A as depicted above in Figure 1.
Theorem 12. \(K_1\vee(K_2\cup\overline{K}_{n-3})\) is uniquely the most optimal graph among all connected unicyclic graphs.
Proof. As in the proof of Theorem 11 we will show if \(G\ne K_1\vee(K_{2}\cup \overline{K}_{n-3})\), then \(G\) is less reliable than \(K_1\vee(K_{2}\cup \overline{K}_{n-3})\).
Let \(G\) be a connected unicyclic graph on \(n\) vertices. We claim that if \(G\) has a vertex of degree \(n-1\), then \(G=K_1\vee(K_2\cup \overline{K}_{n-3})\).
Proof of Claim: Assume \(G\) has a vertex of degree \(n-1\). Then \(G=K_1\vee H\) for some \(H\) with \(n-1\) vertices and \(n-(n-1)=1\) edge. It follows that \(H=K_{2}\cup \overline{K}_{n-3}\). Thus \(G=K_1\vee(K_2\cup \overline{K}_{n-3})\).
We now assume \(G\) is not \(K_1\vee(K_2\cup \overline{K}_{n-3})\), and thus must not have a vertex of degree \(n-1\). Let \(v\) be a vertex of maximum degree in \(G\). Because \(G\) is connected, and \(\deg_G(v)<n-1\), there must be some vertex \(w\notin N_G[v]\) such that \(N_G(w)\cap N_G(v)\ne\varnothing\). Let \(u\in N_G(w)\cap N_G(v)\). Because \(v\) has maximum degree in \(G\), and \(w\in N_G(u)\setminus N_G[v]\), we conclude \(N_G(v)\setminus N_G[u]\ne \varnothing\), and we can apply Transformation B to \(G\) with \(u\) and \(v\) as selected to produce a new graph \(G^*\). Consider that because \(u\in N_G(v)\), \(G^*\) is connected, and also has \(n\) edges, \(G^*\) is a unicyclic connected graph. By Lemma 4, \(G^*\) is more reliable than \(G\). Further, we observe that \(d_G(v)<d_{G^*}(v)\).
Because the degree of \(v\) increased in the above process, repeating this process at most \(n-1-\deg_G(v)\) times will produce a graph, \(H\), with \(\deg_H(v) = n-1\). In this case \(H=K_1\vee(K_2\cup\overline{K}_{n-3})\), and because every iteration of Transformation B strictly increases reliability by Lemma 4, we conclude \(G\prec K_1\vee(K_1\cup\overline{K}_{n-3})\). Thus \(K_1\vee(K_2\cup \overline{K}_{n-3})\) is uniquely the most reliable connected unicyclic graph. ◻
A connected graph of order \(n\) is called bicyclic if it contains exactly \(n+1\) edges. We now provide a unique most optimal graph among connected bicyclic graphs with fixed order. Similar to the proof of Theorem 12, we first note the following structural property of bicyclic graphs.
Proposition 2. \(K_1\vee(P_3\cup\overline{K}_{n-4})\) is the unique connected bicyclic graph with a vertex of degree \(n-1\) and a vertex of degree \(3\).
Proof. Assume \(G\) has a vertex \(v\) of degree \(n-1\) and a vertex \(u\) of degree \(3\). Then \(G\) can be expressed as \({v}\vee H\) for some \(H\) subgraph. Because \(\deg_H(w)=\deg_G(w)-1\) for all \(w\in V(G)\setminus{v}\), we affirm \(\deg_H(u)=2\). Because \(H\) is a graph on \(n-1\) vertices with exactly two edges and a vertex with degree \(2\), \(H\) must be \(P_3\cup \overline{K}_{n-4}\). Thus, \(G\simeq K_1\vee(P_3\cup \overline{K}_{n-4})\). ◻
Theorem 13. \(K_1\vee(P_3\cup\overline{K}_{n-4})\) is uniquely the most optimal graph among all connected bicyclic graphs.
Proof. We first claim that \(K_1\vee(P_3\cup\overline{K}_{n-4})\) is the most optimal graph among all bicyclic connected graphs with a vertex of degree \(n-1\).
Proof of Claim: Let \(G\) be a connected bicyclic graph with a vertex \(w\) of degree \(n-1\). We again consider that for some \(H\) on \(n-1\) vertices with two edges, \(G\simeq K_1\vee H\). If the two edges have a common endpoint, then \(G\simeq K_1\vee (P_3\cup \overline{K}_{n-4})\). Otherwise, \(H\simeq P_2\cup P_2\cup\overline{K}_{n-5}\). Let \(u\) and \(v\) each be an endpoint of a different edge in \(H\). Because the two edges are non-incident, \(u\) and \(v\) have unique neighbors relative to each other, and we can apply Transformation B. Let \(G^*\) be the graph obtained by applying Transformation \(B\) to \(G\).
Consider that \(G\) and \(G^*\) both necessarily have the same number of edges, and \(w\) is a common neighbor of \(u\) and \(v\). It follows that \(G^*\) is connected and bicyclic. Further, the vertex \(w\) is not a unique neighbor of \(u\) and \(v\), and is thus unchanged by Transformation \(B\), and we determine \(\deg_{G^*}(w)=n-1\). Finally we consider that \(v\) has one more neighbor in \(G^*\) as compared to \(G\), and thus \(\deg_{G^*}(v)=3\). Thus, as \(G^*\) is a connected bicyclic graph with a vertex of degree \(n-1\) and a vertex of degree \(3\), \(G^*\simeq K_1\vee(P_3\cup\overline{K}_{n-4})\). By Lemma 4 \(G^*\succ G\), and thus \(K_1\vee(P_3\cup\overline{K}_{n-4})\) is the unique most reliable graph among all connected bicyclic graphs with a vertex of degree \(n-1\).
We next assume \(\Delta(G)<n-1\). Let \(v\) be a vertex of maximum degree in \(G\). Because \(G\) is connected and \(\deg_G(v)<n-1\), there must be some vertex \(w\notin N_G[v]\) such that \(N_G(w)\cap N_G(v)\ne\varnothing\). Let \(u\in N_G(w)\cap N_G(v)\). Because \(v\) has maximum degree in \(G\), and \(w\in N_G(u)\setminus N_G[v]\), we conclude \(N_G\setminus N_G[u]\ne\varnothing\). Thus \(u\) and \(v\) have unique neighbors relative to each other and we can construct \(G^*\) by applying Transformation B to \(G\) with \(u\) and \(v\) as specified. We observe that because \(u\) and \(v\) are adjacent in \(G\), \(G^*\) is connected and has \(n+1\) edges. Thus \(G^*\) is a connected bicyclic graph. Further, by Lemma 4, \(G^*\) is strictly more reliable than \(G\), and \(\Delta(G)<\Delta(G^*)\).
Because the above process strictly increased the maximum degree of \(G\), it follows that repeating the above process a finite number of times will yield a connected bicyclic graph with a vertex of degree \(n-1\). Thus \(G\) is strictly less reliable than some connected bicyclic graph \(G'\) with a vertex of degree \(n-1\), and by the previous claim, \(G'\preceq K_1\vee(P_3\cup\overline{K}_{n-4})\). Therefore, \(K_1\vee(P_3\cup\overline{K}_{n-4})\) is the unique most optimal connected bicyclic graph. ◻
While we determined the most optimal connected bicyclic graph, the subject of least optimal connected bicyclic graphs remains an open problem. The tactics used among trees and connected unicyclic graphs fail to provide a least reliable connected bicyclic graph. The proof of Theorem 13 works similarly to the proof of Theorem 12 because the number of graphs with degree \(n-1\) remains small. In the case of a least optimal connected bicyclic graph, we could well apply Transformation A and Lemma 3 as in the proof of Theorem 11. This only serves to reduce the graphs under consideration to connected bicyclic graphs with no leaf vertices, and these prove to be far more numerous than connected bicyclic graphs with a vertex of degree \(n-1\). In general, connected bicyclic graphs with no leaves can be divided into subdivisions of the three graphs shown in Figure 3. It is unknown which of these subdivisions may be a least optimal graph, and how much each edge should be subdivided to produce it. Based on direct computations on some small graphs, we believe that the stretched bowtie graph \(B_n\), which is obtained from the subdivisions of the left-most graph in Figure 3 using the edge \(uv\), is the least optimal graph. Hence, we posit the following conjecture.

Conjecture 1. \(B_n\) is the unique most optimal connected bicyclic graph of order \(n\).
A lexicographical graph, \(L(n,m)\), is the graph with vertex set \(\{1,\dots,n\}\) and whose edge set is the first \(m\) edges sorted lexicographically; that is, with \(i<j\) and \(k<\ell\), edge \(ij\) precedes edge \(k\ell\) lexicographically if \(i<k\) or, \(i=k\) and \(j<\ell\). The most optimal trees, connected unicyclic graphs, and connected bicyclic graphs in this document all are in the class of lexicographical graphs. We thus make the following conjecture.
Conjecture 2. For any positive integers \(n\) and \(m\ge n-1\), the lexicographical graph \(L(n,m)\) is the unique most optimal connected graph with order \(n\) and size \(m\).
Archer, K., Graves, C. and Milan, D., 2019. Classes of uniformly most reliable graphs for all-terminal reliability. Discrete Applied Mathematics, 267, 12–29.
Pedersen, A. S. and Vestergaard, P. D., 2005. The number of independent sets in unicyclic graphs. Discrete Applied Mathematics, 152(1-3), 246–256.
Wingard, G., 1995. Properties and Applications of the Fibonacci Polynomial of a Graph (Doctoral dissertation, University of Mississippi).