For a graph \(G\) and a positive integer \(k\), a royal \(k\)-edge coloring of \(G\) is an assignment of nonempty subsets of the set \(\{1, 2, \ldots, k\}\) to the edges of \(G\) that gives rise to a proper vertex coloring in which the color assigned to each vertex \(v\) is the union of the sets of colors of the edges incident with \(v\). If the resulting vertex coloring is vertex-distinguishing, then the edge coloring is a strong royal \(k\) coloring. The minimum positive integer \(k\) for which a graph has a strong royal \(k\)-coloring is the strong royal index of the graph. The primary emphasis here is on strong royal colorings of trees.
For a connected graph \(G\) of order 3 or more and a positive integer \(k\), let \(c: E(G) \to [k]=\{1, 2, \ldots, k\}\) be an unrestricted edge coloring of \(G\). In particular, adjacent edges of \(G\) may be assigned the same color. We write \(\mathcal{P}^*([k])\) for the set consisting of the \(2^k-1\) nonempty subsets of \([k]\). The edge coloring \(c\) gives rise to the vertex coloring \(c': V(G) \to \mathcal{P}^*([k])\) where \(c'(v)\) is the set of colors of the edges incident with \(v\). If \(c'\) is a proper vertex coloring of \(G\), then \(c\) is a majestic \(k\)-edge coloring and the minimum positive integer \(k\) for which \(G\) has a majestic \(k\)-edge coloring is the majestic index \(\mathop{\rm maj}(G)\) of \(G\). If \(c'\) is vertex-distinguishing (that is, \(c'(u)\ne c'(v)\) for every two distinct vertices \(u\) and \(v\) of \(G\)), then \(c\) is a strong majestic \(k\)-edge coloring and the minimum positive integer \(k\) for which \(G\) has a strong majestic \(k\)-edge coloring is the strong majestic index \(\mathop{\rm smaj}(G)\) of \(G\). Majestic edge colorings were introduced by Györi, Horňák, Palmer, and Woźnick [1] under different terminology and studied further in [2,3]. Strong majestic edge colorings were introduced by Harary and Plantholt [4] in 1985, also using different terminology, and studied further by others (see [5,6,7]).
The following is an immediate observation concerning these indexes.
Proposition 1. Every connected graph \(G\) of size \(m \ge 2\) has a strong majestic coloring and therefore a majestic coloring. Furthermore,
\(2\le \mathop{\rm maj}(G) \le \mathop{\rm smaj}(G)\le m.\)
Proof. For a connected graph \(G\) with \(E(G)=\{e_1, e_2, \ldots, e_m\}\), define an edge coloring \(c: E(G) \to [m]\) by \(c(e_i)=i\) for \(1 \le i \le m\). Since the sets of edges incident with distinct vertices are distinct, it follows that \(c\) is a strong majestic \(m\)-coloring of \(G\), producing the desired inequalities.
The following results were obtained by Harary and Plantholt [4] on complete graphs \(K_n\), complete bipartite graphs \(K_{s, t}\), paths \(P_n\), cycles \(C_n\), and hypercubes \(Q_n\).
Theorem 1. [4] For every integer \(n\ge 3\), \[\mathop{\rm smaj}(K_n) = \mathop{\rm maj}(K_n) = 1+ \left\lceil{\log_2 n}\right\rceil.\]
Theorem 2. [4] For integers \(s\) and \(t\) with \(2\le s \le t\), then \[\mathop{\rm smaj}(K_{s, t}) \le 2+ \left\lceil{\log_2 t}\right\rceil.\] In particular, \(1 + \left\lceil{\log_2 t}\right\rceil \le \mathop{\rm smaj}(K_{t, t}) \le 2+ \left\lceil{\log_2 t}\right\rceil\) for each integer \(t \ge 2\).
Theorem 3. [4] For each integer \(n \ge 3\), \[\begin{aligned} \mathop{\rm smaj}(P_n) &=& \min\left\{2\left\lceil{\frac{1+ \sqrt{8n-9}}{4}} \ \right\rceil-1, \ 2\left\lceil{\sqrt{\frac{n-1}{2}}} \ \right\rceil \right\}, \\ \mathop{\rm smaj}(C_n) &=& \min\left\{2\left\lceil{\frac{1+ \sqrt{8n+1}}{4}} \ \right\rceil-1, \ 2\left\lceil{\sqrt{\frac{n}{2}}} \ \right\rceil \right\}. \end{aligned}\]
Theorem 4. [4] For each integer \(n \ge 2\), \(\mathop{\rm smaj}(Q_n) = n+1\).
Theorem 5. [4] For each integer \(k \ge 2\), the largest order \(M(k)\) of a tree with strong majestic index \(k\) is \[M(k)= \left\{\begin{array}{cl} \frac{k^2 +3k-4}{2} & \mbox{ if $k \ge 2$ and $k \ne 4$}\\[.2cm] 11 & \mbox{ if $k = 4$.} \end{array}\right.\]
The following is a consequence of Theorem 5.
Conjecture 1. If \(T\) is a tree of order \(n \ge 3\) and \(\mathop{\rm smaj}(T) \ne 4\), then \[\mathop{\rm smaj}(T) \ge \left\lceil{\frac{\sqrt{8n+25}-3}{2}}\right\rceil.\]
Proof. Let \(T\) be a tree of order \(n \ge 3\) with \(\mathop{\rm smaj}(T) = k\ne 4\). It then follows by Theorem 5 that \(n \le \frac{k^2 +3k-4}{2}\) and so \(k^2+3k-2n-4 \ge 0\), producing the desired inequality.
While an edge coloring \(c\) of a graph \(G\) typically uses colors from the set \([k]\) for some positive integer \(k\) resulting in \(c(e)=i\) for some \(i \in [k]\), we might equivalently define \(c(e)=\{i\}\) as well. In this case, both the edge coloring \(c\) and the induced vertex coloring \(c'\) assign subsets of \([k]\) to both the edges and the vertices of \(G\), where the color assigned to an edge by \(c\) is a singleton subset of \([k]\). Looking at \(c\) in this manner suggests the idea of studying edge colorings \(c\) where both \(c\) and its derived vertex coloring \(c'\) assign nonempty subsets of \([k]\) to the elements (edges and vertices) of a graph \(G\) such that the color assigned to an edge of \(G\) by \(c\) is not necessarily a singleton subset of \([k]\). This observation gives rise to the primary concepts of this paper.
In a majestic edge coloring of a graph \(G\), the colors assigned to the edges of \(G\) are the elements of some set \([k]\) for a positive integer \(k\), which results in a proper vertex coloring of \(G\) where the color of a vertex \(v\) is the set of colors of the edges incident with \(v\). If the vertex coloring is vertex-distinguishing, then the edge coloring is a strong majestic edge coloring of \(G\). Here, we consider edge colorings, called royal colorings and strong royal colorings, where the colors assigned to the edges of a graph are nonempty subsets of a set \([k]\) rather than elements of \([k]\).
For a connected graph \(G\) of order 3 or more, let \(c: E(G) \to \mathcal{P}^*([k])\) be an unrestricted edge coloring of \(G\) for some positive integer \(k\). The edge coloring \(c\) produces the vertex coloring \(c': V(G) \to \mathcal{P}^*([k])\) defined by \[c'(v)=\bigcup_{e \in E_v} c(e),\] where \(E_v\) is the set of edges of \(G\) incident with \(v\). If \(c'\) is a proper vertex coloring of \(G\), then \(c\) is called a royal \(k\)-edge coloring of \(G\). An edge coloring \(c\) is a royal coloring of \(G\) if \(c\) is a royal \(k\)-edge coloring for some positive integer \(k\). The minimum positive integer \(k\) for which a graph \(G\) has a royal \(k\)-edge coloring is the royal index \(\mathop{\rm roy}(G)\) of \(G\). If \(c'\) is vertex-distinguishing, then \(c\) is a strong royal \(k\)-edge coloring of \(G\). An edge coloring \(c\) is a strong royal coloring of \(G\) if \(c\) is a strong royal \(k\)-edge coloring for some positive integer \(k\). The minimum positive integer \(k\) for which a graph \(G\) has a strong royal \(k\)-coloring is the strong royal index \(\mathop{\rm sroy}(G)\) of \(G\). While no royal coloring exists for the graph \(K_2\), such a coloring exists for every connected graph of order at least 3. Since every strong majestic edge coloring is a strong royal coloring and every majestic edge coloring is a royal coloring, the following is a consequence of Proposition 1.
Proposition 2. Every connected graph \(G\) of order \(3\) or more has a strong royal coloring and therefore a royal coloring. Furthermore,
\(2\le \mathop{\rm roy}(G) \le \mathop{\rm maj}(G)\le \mathop{\rm smaj}(G)\) and \(\mathop{\rm roy}(G) \le \mathop{\rm sroy}(G) \le \mathop{\rm smaj}(G)\).
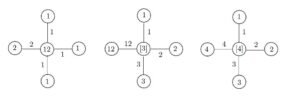
If \(G\) is a connected graph of order \(3\), then either \(G = P_3\) or \(G= K_3\). It is easy to see that \(\mathop{\rm smaj}(P_3) =\mathop{\rm smaj}(P_3) =2\) and \(\mathop{\rm smaj}(K_3) = \mathop{\rm smaj}(K_3)= 3\). Since \(|\mathcal{P}^*([2])| = 3\), it follows that \(\mathop{\rm sroy}(G) \ge 3\) for every connected graph \(G\) of order \(n \ge 4\). Thus, \(P_3\) is the only connected graph with strong royal index 2. In what follows, we consider only connected graphs of order at least 4. For example, consider the star \(G= K_{1, 4}\) of size 4. Figure 1 shows a royal \(2\)-edge coloring, a strong royal \(3\)-edge coloring, and a strong majestic \(4\)-edge coloring of \(G\), where, for simplicity, we write the set \(\{a\}\) as \(a\), \(\{a, b\}\) as \(ab\), and \(\{a, b, c\}\) as \(abc\). In fact, \(\mathop{\rm roy}(G)=2, \mathop{\rm sroy}(G)=3\), and \(\mathop{\rm smaj}(G)=4\) for this graph \(G\). Thus, the values of the three parameters \(\mathop{\rm roy}(G)\), \(\mathop{\rm sroy}(G)\), and \(\mathop{\rm smaj}(G)\) can be different for a graph \(G\). In fact, the value of \(\mathop{\rm smaj}(G) – \mathop{\rm sroy}(G)\) can be arbitrarily large for a connected graph \(G\) (as we will see in Section 3). On the other hand, it can occur that \(\mathop{\rm smaj}(G) = \mathop{\rm sroy}(G)\) for connected graphs \(G\) of order 4 or more.
Proposition 3. For every integer \(n \ge 4\), \[\mathop{\rm smaj}(K_{n}) = \mathop{\rm smaj}(K_n) = 1+ \left\lceil{\log_2 n}\right\rceil.\]
Proof. Since \(\mathop{\rm sroy}(K_{n}) \le 1+ \left\lceil{\log_2 n}\right\rceil\) by Theorem 1 and Proposition 1, it remains to show that \(\mathop{\rm sroy}(K_{n}) \ge 1+ \left\lceil{\log_2 n}\right\rceil\). Suppose that \(\mathop{\rm sroy}(K_n) = k\) for an integer \(n \ge 4\). Then there exists a strong royal \(k\)-edge coloring \(c: E(K_n) \to \mathcal{P}^*([k])\) of \(K_n\) such that the induced vertex coloring \(c': V(K_n) \to \mathcal{P}^*([k])\) is vertex-distinguishing. Thus, \(c'(u)\ne c'(v)\) for every two distinct vertices \(u\) and \(v\) of \(K_n\). However, since \(c'(u)\) and \(c'(v)\) both contain the color \(c(uv)\), it follows that \(c'(u) \cap c'(v) \ne \emptyset\). Thus, if \(A \subseteq [k]\) such that \(c'(x) = A\) for some vertex \(x\) of \(K_n\), then \(c'(y) \not\subseteq \overline{A}= [k]-A\) for every vertex \(y\) of \(K_n\) distinct from \(x\). Hence, there are at most \(2^{k-1}\) possible colors for the \(n\) vertex colors of \(K_n\). Thus, \(n \le 2^{k-1}\) and so \(\log_2 n \le k-1\). Therefore, \(\mathop{\rm sroy}(K_n) = k \ge 1+ \left\lceil{\log_2 n}\right\rceil\) and so \(\mathop{\rm sroy}(K_n)=1+ \left\lceil{\log_2 n}\right\rceil\).
There are other connected graphs \(G\) for which \(\mathop{\rm smaj}(G) = \mathop{\rm sroy}(G)\). First, we present a lower bound for the strong royal index of any connected graph of order 4 or more in term of its order.
Proposition 4. If \(G\) is a connected graph of order \(n \ge 4\), then
\(\mathop{\rm sroy}(G) \ge \left\lceil{\log_2 (n+1)}\right\rceil = 1 + \lfloor{\log_2 n}\rfloor.\)
Proof. Suppose that \(\mathop{\rm sroy}(G)=k\) and let \(c: E(G) \to \mathcal{P}^*([k])\) be a strong royal \(k\)-edge coloring of \(G\). Then the induced coloring \(c': V(G) \to \mathcal{P}^*([k])\) is vertex-distinguishing. Since \(c'(v) \ne\emptyset\) for each vertex \(v\) of \(G\) and \(| \mathcal{P}^*([k])| = 2^{k}-1\), it follows that \(n \le 2^k- 1\) and so \(\mathop{\rm sroy}(G) = k \ge \left\lceil{\log_2 (n+1)}\right\rceil=1 + \lfloor{\log_2 n}\rfloor\).
For the hypercubes \(Q_n\), \(n \ge 3\), of order \(2^n\), we have \(\mathop{\rm sroy}(Q_{n}) \le \mathop{\rm smaj}(Q_n) =n+1\) by Propositions 1 and 1. Since the order of \(Q_n\) is \(2^n\), it follows by Proposition 4 that \(\mathop{\rm sroy}(Q_n) \ge \left\lceil{\log_2 (2^n+1)}\right\rceil =n+1\). These observations provide the following result.
Proposition 5. For an integer \(n \ge 3\), \[\mathop{\rm sroy}(Q_{n}) = \mathop{\rm smaj}(Q_n) = \left\lceil{\log_2 (2^n+1)}\right\rceil = n+1.\]
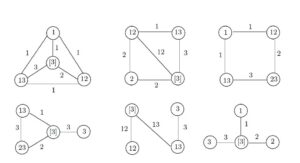
If \(G\) is a connected graph of order 4, then
\(G \in \{K_4, K_4 – e, (K_2+K_1)\vee K_1, C_4, P_4, K_{1, 3}\}\).
By Proposition 4, \(\mathop{\rm sroy}(G) \ge 3\). Figure 2 shows a strong royal \(3\)-edge coloring for each of these graphs. Thus, \(\mathop{\rm sroy}(G) = 3 = \left\lceil{\log_2 (n+1)}\right\rceil\) for every connected graph \(G\) of order \(n=4\). Furthermore, \(\mathop{\rm smaj}(G)=\mathop{\rm sroy}(G)= 3\) for these six graphs \(G\). In fact, for each integer \(n \ge 4\), there is a connected graph \(G\) of order \(n \ge 4\) such that \(\mathop{\rm sroy}(G) = \left\lceil{\log_2 (n+1)}\right\rceil\), as we will see in Section 3.
In Proposition 4, a lower bound for the strong royal index of a connected graph \(G\) was presented in terms of its order. Next, we present an upper bound for the strong royal index of \(G\) in terms of the strong royal indexes of the connected spanning subgraphs of \(G\). This bound shows the value of determining the strong royal indexes of trees.
Proposition 6. If \(G\) is a connected graph of order \(4\) or more, then \[\mathop{\rm sroy}(G) \le 1+ \min\{\mathop{\rm sroy}(H): \mbox{ $H$ is a connected spanning subgraph of~$G$}\}.\] In particular, \[\label{spanningtree} \mathop{\rm sroy}(G) \le 1+ \min\{\mathop{\rm sroy}(T): \mbox{ $T$ is a spanning tree of~$G$}\}.\tag{1}\]
Proof. Among all connected spanning subgraphs of \(G\), let \(H\) be one having the minimum strong royal index, say \(\mathop{\rm sroy}(H)=k\). Let \(c_H: E(H) \to \mathcal{P}^*([k])\) be a strong royal \(k\)-edge coloring of \(H\). Then \(c'_H(x)\neq c'_H(y)\) for every two distinct vertices \(x\) and \(y\) of \(H\). We extend \(c_H\) to an edge coloring \(c_G:E(G) \to \mathcal{P}^*([k+1])\) of \(G\) by defining \[c_G(e) =\left\{\begin{array}{ll} c_H(e) & \mbox{ if $e\in E(H)$ }\\[.1cm] \{k+1\} & \mbox{ if $ e\in E(G)-E(H)$.} \end{array} \right.\] Since either \(c'_G(x) = c'_H(x)\subseteq [k]\) or \(c'_G(x)= c'_H(x) \cup \{k+1\}\) for each \(x\in V(G)\) and \(c'_H\) is vertex-distinguishing, it follows that \(c'_G\) is vertex-distinguishing. Therefore, \(c_G\) is a strong royal \((k+1)\)-edge coloring of \(G\) and so \(\mathop{\rm sroy}(G)\leq k +1 = \mathop{\rm sroy}(H)+1\). The inequality (\ref{spanningtree}) follows immediately.
As a consequence of Proposition 6, if we know the strong royal indexes of all spanning trees of a connected graph \(G\), then we have an upper bound for \(\mathop{\rm sroy}(G)\). Consequently, we now turn to investigating the strong royal indexes of trees of order 4 or more. By Proposition 4, if \(T\) is a tree of order \(n \ge 4\), then \(\mathop{\rm sroy}(T) \ge \left\lceil{\log_2 (n+1)}\right\rceil.\) We show that there is equality for this bound when \(T\) is either a star or a path.
Proposition 7. For every integer \(n \ge 4\), \[\mathop{\rm sroy}(K_{1, n-1}) = \left\lceil{\log_2 (n+1)}\right\rceil.\]
Proof. Let \(k = \left\lceil{\log_2 (n+1)}\right\rceil \ge 3\) and let \(G = K_{1, n-1}\) be a star of order \(n\), where \(V(G)\)\(=\){\(v\), \(v_1\), \(v_2\), \(\ldots\), \(v_{n-1}\)} and \(\deg_G v = n-1\). By Proposition 4, it suffices to show that \(G\) has a strong royal \(k\)-edge coloring. Since \(k = \left\lceil{\log_2 (n+1)}\right\rceil\ge 3\), it follows that
\(2^{k-1}-1 \le n-1 \le 2^k-2\).
Let \(S_1, S_2, \ldots, S_{2^k-2}\) be the \(2^k-2\) distinct nonempty proper subsets of \([k]\), where \(S_i = \{i\}\) for \(1 \le i \le k\). Define the coloring \(c:E(G) \to \mathcal{P}^*([k])\) by \(c(vv_i)= S_i\) for \(1 \le i \le n-1\). Since \(c'(v_i) = S_i\) \(1 \le i \le n-1\) and \(c'(v)= [k]\), it follows that \(c'\) is vertex-distinguishing. Therefore, \(c\) is a strong royal \(k\)-edge coloring of \(G\) and so \(\mathop{\rm sroy}(G) = \left\lceil{\log_2 (n+1)}\right\rceil.\)
Theorem 6. For every integer \(n \ge 4\), \(\mathop{\rm sroy}(P_n) = \left\lceil{\log_2 (n+1)}\right\rceil.\)
Proof. Let \(k = \left\lceil{\log_2 (n+1)}\right\rceil \ge 3\). Then \(2^{k-1} \le n \le 2^k-1\). By Proposition 4, it suffices to show that \(G\) has a strong royal \(k\)-edge coloring. For \(4 \le n \le 7\), there is a strong royal \(3\)-edge coloring of \(P_n\) (shown in Figure 3) and so \(\mathop{\rm sroy}(P_n) = 3= \left\lceil{\log_2 (n+1)}\right\rceil\). We may therefore assume that \(n \ge 8\).
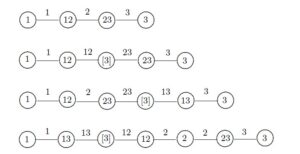
First, we construct strong royal \(4\)-edge colorings of \(P_8\) and \(P_9\) from a strong royal \(3\)-edge coloring of \(P_4\) as follows. Let \(P_8\) be constructed from two copies of \(P_4\), namely \((u_1, u_2, u_3, u_4)\) and \((v_1, v_2, v_3, v_4)\), by adding the edge \(u_4v_4\) and let \(P_9\) be obtained from \(P_8\) by adding a new vertex \(v_0\) and the new edge \(v_0v_1\). (That is, \(P_9\) is constructed from \(P_4=(u_1, u_2, u_3, u_4)\) and \(P_5=(v_0, v_1, v_2, v_3, v_4)\) by adding the edge \(u_4v_4\).) Let \(c_{4}\) be a strong royal \(3\)-edge coloring of \(P_4\). Define the strong royal \(4\)-edge coloring \(c_8: E(P_8) \to \mathcal{P}^*([4])\) of \(P_8\) as follows: \[c_8(e) = \left\{ \begin{array}{ll} c_4(e) & \mbox{ if $e = u_iu_{i+1}$ for $1 \le i \le 3$}\\[.1cm] c_4(u_3u_4) & \mbox{ if $e = u_4v_4$}\\[.1cm] c_4( u_iu_{i+1}) \cup \{4\} & \mbox{ if $e = v_iv_{i+1}$ for $1 \le i \le 3$.} \end{array}\right.\] Since \(c_8'(u_i) = c_4' (u_i)\) and \(c_8'(v_i) = c_4' (u_i) \cup \{4\}\) for \(1 \le i \le 4\), it follows that \(c_8'\) is vertex-distinguishing. Thus, \(c_8\) is a strong royal \(4\)-edge coloring of \(P_8\). Next, we extend this strong royal \(4\)-edge coloring \(c_8\) of \(P_8\) to a strong royal \(4\)-edge coloring \(c_9\) by assigning \(\{4\}\) to the edge \(v_0v_1\). Since \(c_9'(v_0) =\{4\}\) and \(c_9'(x) = c_8'(x)\ne \{4\}\) if \(x \ne v_0\), it follows that \(c_9'\) is vertex-distinguishing. Hence, \(c_9\) is a strong royal \(4\)-edge coloring of \(P_9\). Thus, \(\mathop{\rm sroy}(P_8) = \mathop{\rm sroy}(P_9) = 4\). These two colorings are illustrated in Figure 4. Similarly, for \(t = 5, 6, 7\), we can construct strong royal \(4\)-edge colorings of \(P_{2t}\) and \(P_{2t+1}\) from a strong royal \(3\)-edge coloring of \(P_t\). Therefore, if \(8 \le n \le 15\), then \(\mathop{\rm sroy}(P_{n}) = 4\).

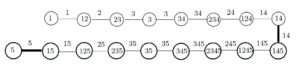
Suppose for an integer \(n\ge 8\) such that \(2^{k-1} \le n \le 2^k-1\) for some integer \(k\) that \(\mathop{\rm sroy}(P_n)=k\). Let \(c_n: E(P_n)\to \mathcal{P}^*([k])\) be a strong royal \(k\)-edge coloring of \(P_n\). Since \(2^{k-1} \le n \le 2^k-1\), it follows that \(2^k \le 2n < 2^{k+1} – 1\) and \(2^k < 2n + 1 \le 2^{k+1} – 1\). Hence, \(\left\lceil{\log_2 (2n+1)}\right\rceil = \left\lceil{\log_2 (2n+2)}\right\rceil = k+1\). We construct strong royal \((k+1)\)-edge colorings of \(P_{2n}\) and \(P_{2n+1}\) from the strong royal \(k\)-edge coloring \(c_n\) of \(P_n\) as follows. Let \(P_{2n}\) be constructed from two copies of \(P_n\), namely \((u_1, u_2, \ldots, u_n)\) and \((v_1, v_2, \ldots, v_n)\), by adding the edge \(u_nv_n\) and let \(P_{2n+1}\) be obtained from \(P_{2n}\) by adding a new vertex \(v_0\) and the new edge \(v_0v_1\). Define the edge coloring \(c_{2n}: E(P_{2n}) \to \mathcal{P}^*([k+1])\) of \(P_{2n}\) as follows: \[c_{2n}(e) = \left\{ \begin{array}{ll} c_n(e) & \mbox{ if $e = u_iu_{i+1}$ for $1 \le i \le n-1$}\\[.1cm] c_n(u_{n-1}u_n) & \mbox{ if $e = u_nv_n$}\\[.1cm] c_n(u_iu_{i+1}) \cup \{k+1\} & \mbox{ if $e = v_iv_{i+1}$ for $1 \le i \le n-1$.} \end{array}\right.\] Since \(c_{2n}'(u_i) = c_n' (u_i)\) and \(c_{2n}'(v_i) = c_n' (u_i) \cup \{k+1\}\) for \(1 \le i \le n\), it follows that \(c_{2n}'\) is vertex-distinguishing. Thus, \(c_{2n}\) is a strong royal \((k+1)\)-edge coloring of \(P_{2n}\). Next, we extend this strong royal \((k+1)\)-edge coloring \(c_{2n}\) of \(P_{2n}\) to a strong royal \((k+1)\)-edge coloring \(c_{2n+1}\) of \(P_{2n+1}\) by assigning \(\{k+1\}\) to the edge \(v_0v_1\). Since \(c_{2n+1}'(v_0) =\{k+1\}\) and \(c_{2n+1}'(x) = c_{2n}'(x)\ne \{k+1\}\) if \(x \ne v_0\), it follows that \(c_{2n+1}'\) is vertex-distinguishing. Hence, \(c_{2n+1}\) is a strong royal \((k+1)\)-edge colorings of \(P_{2n+1}\). This is illustrated in Figure 5 for \(n = 8\) and \(k = 4\), where a strong royal \(5\)-edge coloring of \(P_{17}\) is constructed from a strong royal \(4\)-edge coloring of \(P_{8}\). Deleting the vertex labeled 5 from \(P_{17}\), we obtain a strong royal \(5\)-edge coloring of \(P_{16}\).
Therefore, \(\mathop{\rm sroy}(P_n) = \left\lceil{\log_2 (n+1)}\right\rceil\) for each integer \(n \ge 4\).
By Proposition 4, \(\mathop{\rm sroy}(T) \ge 3\) for a tree \(T\) of order \(n\) where \(4 \le n \le 7\). In fact, the following result can be readily verified.
Proposition 8. If \(T\) is a tree of order \(n\) where \(4 \le n\le 7\), then
\(\mathop{\rm sroy}(T)= 3\).
We now consider a familiar class of trees, namely the double stars. A double star is a tree of diameter 3.
Theorem 7. If \(T\) is a double star of order \(n \ge 4\), then \[\mathop{\rm sroy}(T) = \left\lceil{\log_2 (n+1)}\right\rceil.\]
Proof. By Proposition 1, we may assume that \(T\) is a double star of order \(n \ge 8\). Let \(k = \left\lceil{\log_2 (n+1)}\right\rceil \ge 4\). Then \(2^{k-1} \le n \le 2^k-1\). By Proposition 4, it suffices to show that \(T\) has a strong royal \(k\)-edge coloring. Let \(u\) and \(v\) be the central vertices of \(T\) where \(\deg_T u = a\) and \(\deg_T v = b\). Suppose that \(u\) is adjacent to the end-vertices \(u_1,u_2,\ldots,u_{a-1}\) and \(v\) is adjacent to the end-vertices \(v_1,v_2,\ldots,v_{b-1}\). We may assume that \(2\le a \le b\). Since \(2^{k-1} \le n = a+b \le 2^k-1\), \(2\le a \le b\), and \(k \ge 4\), it follows that \[\label{royaldoublestarab} \mbox{$1\le a-1 \le 2^{k-1}-2$ and $k-1 \le b-1 \le 2^k-a-2$.}\tag{2}\] We consider two cases, according to \(a \le k\) or \(a \ge k+1\).
Case \(1\). \(2 \le a \le k\). Let \(p = a-1\). Then \(1\le p \le k-1\) and \(b-1 \le 2^k-p-3\) by (\ref{royaldoublestarab}). For each integer \(i\) with \(1 \le i \le p\), let \(X_i = \{i\}\) for \(1 \le i \le p\). Next, let
\(Y = \mathcal{P}^*([k])-\left(\{[p], [k]\} \cup \{X_i: \ 1 \le i \le p\}\right)\).
Then \(|Y| = 2^k – p – 3\). Let \(Y_1, Y_2, \ldots, Y_{2^k – p – 3}\) be the \(2^k – p – 3\) distinct elements of \(Y\) such that \(Y_j=\{j, k\}\) for \(1 \le j \le k-1\). Define an edge coloring \(c: E(T) \to \mathcal{P}^*([k])\) by \[c(e)=\left\{\begin{array}{cl} X_1 & \mbox{ if $e = uv$ or $e = uu_1$}\\[.1cm] X_i & \mbox{ if $e = uu_i$ for $2 \le i \le p$}\\[.1cm] Y_j & \mbox{ if $e = vv_i$ for $1 \le j \le b-1 \le 2^k-p-3$.} \end{array}\right.\] Since \(p = a-1 \le k-1\) and \(b-1 \ge k-1\), it follows that \(c'(u) =[p]\ne [k] = c'(v)\). In fact, the induced vertex coloring \(c': V(T) \to \mathcal{P}^*([k])\) of \(T\) is given by \[c'(x)=\left\{\begin{array}{cl} X_i & \mbox{ if $x= u_i$ for $1 \le i \le p$}\\[.1cm] [p] & \mbox{ if $x = u$}\\[.1cm] [k] & \mbox{ if $x = v$}\\[.1cm] Y_j & \mbox{ if $x = v_j$ for $1 \le j \le b-1 \le 2^k-p-3$.} \end{array}\right.\] Since \(c'\) is vertex-distinguishing, \(c\) is a strong royal \(k\)-edge coloring of \(T\).
Case \(2\). \(k +1 \le a \le 2^{k-1}-1\). Let \(p = a-1\). It follows that
\(k \le p \le 2^{k-1}-2 = |\mathcal{P}^*([k-1]) -\{[k-1]\}|\).
Let \(X_1\), \(X_2\), \(\ldots\), \(X_{p}\) be distinct elements of \(\mathcal{P}^*([k-1]) -\{[k-1]\}\) such that \(X_i = \{i\}\) for \(1 \le i \le k-2\). Next, let
\(Y = \mathcal{P}^*([k])-\left(\{[k-1], [k]\} \cup \{X_i: \ 1 \le i \le p\}\right)\).
Then \(|Y|=2^k-3 – p\). Let \(Y_1, Y_2, \ldots, Y_{2^k – p – 3}\) be the \(2^k – p – 3\) distinct elements of \(Y\) such that \(Y_j=\{j, k\}\) for \(1 \le j \le k-1\). Define an edge coloring \(c: E(T) \to \mathcal{P}^*([k])\) by \[c(e)=\left\{\begin{array}{cl} X_1& \mbox{ if $e = uv$ or $e = uu_1$}\\[.1cm] X_i & \mbox{ if $e = uu_i$ and $2 \le i \le p$}\\[.1cm] Y_j & \mbox{ if $e =vv_i$ for $1 \le i \le b-1 \le2^{k-1}-p-3$.} \end{array}\right.\] Since \(p=a-1 \ge k\) and \(b-1 \ge k-1\), it follows that \(c'(u)=[k-1]\) and \(c'(v)=[k]\). The induced vertex coloring \(c': V(T) \to \mathcal{P}^*([k])\) is given by \[c'(x)=\left\{\begin{array}{cl} X_i & \mbox{ if $x= u_i$ for $1 \le i \le p$}\\[.1cm] [k-1] & \mbox{ if $x = u$}\\[.1cm] [k] & \mbox{ if $x = v$}\\[.1cm] Y_j & \mbox{ if $x = v_j$ for $1 \le j \le b-1 \le 2^k-p-3$.} \end{array}\right.\] Since \(c'\) is vertex-distinguishing, \(c\) is a strong royal \(k\)-edge coloring of \(T\).
Based on the information obtained thus far on the strong royal indexes of trees, it is reasonable to make the following conjecture.
Conjecture 2. If \(T\) is a tree of order \(n \ge 4\), then \(\mathop{\rm sroy}(T) = \left\lceil{\log_2 (n+1)}\right\rceil.\)
For an integer \(n\ge 4\), let \(k\) be the unique integer such that \(2^{k-1} \le n \le 2^k-1\). We construct a graph \(G_k\) of order \(2^k-1\) as follows. The vertices of \(G_k\) are labeled with the \(2^k-1\) distinct elements of \(\mathcal{P}^*([k])\). For each \(v \in V(G_k)\), let \(\ell(v)\) denote the label of \(v\). Thus, \(\{\ell(v): \ v \in V(G_k)\} = \mathcal{P}^*([k]).\) Two vertices \(u\) and \(v\) of \(G_k\) are adjacent in \(G_k\) if and only if \(\ell(u) \cap \ell(v) \ne \emptyset\). The graph \(G_3\) of order \(7=2^3 -1\) is shown in Figure 6.
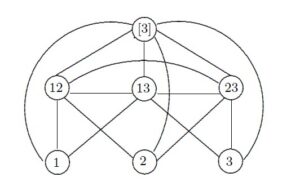
Conjecture 2 is true if and only if for every tree \(T\) of order \(n\ge 4\), where \(2^{k-1} \le n \le 2^k-1\), there is a subgraph \(H\) of \(G_k\) isomorphic to \(T\) having the property that every edge \(uv\) of \(H\) is assigned the color \(c(uv) = \ell(u) \cap \ell(v)\) and every vertex \(v\) of \(H\) is assigned the color \(c'(v)=\bigcup_{e \in E_{H}(v)} c(e)\), where \(E_{H}(v)\) is the set of the edges of \(H\) incident with \(v\), such that \(c'(v) =\ell(v)\).
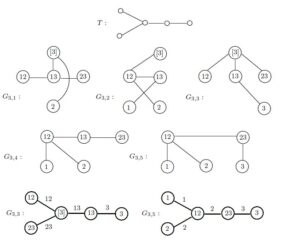
For example, consider the tree \(T\) of order \(5\) in Figure 7 and the graph \(G_3\) in Figure 6. Figure 7 also shows five subgraphs \(G_{3, 1}, G_{3, 2}, G_{3, 3}, G_{3, 4}, G_{3, 5}\) of \(G_3\), each isomorphic to \(T\) with the corresponding edge colors and vertex colors described above. Two of these subgraphs, namely \(G_{3,3}\) and \(G_{3, 5}\), result in a strong royal \(3\)-edge coloring of \(T\), which verifies Conjecture 2 for this tree \(T\). This also shows that there are two distinct ways to give a strong royal \(3\)-edge coloring of \(T\).
We have seen that Conjecture 2 is true for all trees of order \(n\) with \(4 \le n\le 7\) as well as all paths, stars, and double stars. Hence, it remains to show that Conjecture 2 is true for every tree of order \(n \ge 8\) that is not a path, star, or double star. A caterpillar is a tree \(T\) of order 3 or more, the removal of whose leaves produces a path (called the spine of \(T\)). A star is therefore a caterpillar of diameter \(2\) whose spine is a trivial path of order 1 and a double star is a caterpillar of diameter \(3\) whose spine is a path of order 2. We now move on to the next step by showing that Conjecture 2 is true as well if \(T\) is a caterpillar whose spine has order 3, that is, \(T\) has diameter \(4\). In the proof, we assume that the spine of \(T\) is \((x, y, z)\); so \(T\) contains a path \(P=(s, x, y, z, t)\), where \(\deg_T s=\deg_T t= 1\) and \(\deg_T x \ge 2\), \(\deg_T y \ge 2\), and \(\deg_T z \ge 2\).
Theorem 8. If \(T\) is a caterpillar of order \(n \ge 8\) and diameter \(4\), then
\(\mathop{\rm sroy}(T) = \left\lceil{\log_2 (n+1)}\right\rceil.\)
Proof. Let \(k = \left\lceil{\log_2 (n+1)}\right\rceil\ge 4.\) Then \(2^{k-1} \le n \le 2^k-1\). By Proposition 4, it suffices to show that \(T\) has a strong royal \(k\)-edge coloring. We consider three cases, beginning with the case when only one of \(x, y\), and \(z\) has degree exceeding \(2\).
Case \(1\). Exactly one of \(x, y\) and \(z\) has degree exceeding \(2\). We may assume that exactly one of \(x\) and \(y\) is adjacent to \(n-5 \ge 3\) vertices not on \(P\).
Subcase \(1.1\). \(x\) is adjacent to \(n-5\) vertices not on \(P\). Let \(x_1, x_2, \ldots, x_{n-5}\) be the neighbors of \(x\) not on \(P\) and let \(e_i=xx_i\) for \(1 \le i \le n-5\). Let \(S_1 =\{1, k\}\), \(S_2=[2, k]\) and let \(S_3, S_4, \ldots, S_{n-5}\) be distinct nonempty proper subsets of \([k]\) different from \(\{1\}\), \(\{2 \}\), \(\{3\}\), \(\{2, 3\}\), \(\{1, k\}\), \([2, k]\). Define an edge coloring \(c: E(T) \to \mathcal{P}^*([k])\) by \[c(e)=\left\{\begin{array}{cl} \{1\} & \mbox{ if $e = sx$}\\[.1cm] \{2\} & \mbox{ if $e = xy$ or $e= yz$}\\[.1cm] \{3\} & \mbox{ if $e = zt$}\\ S_i & \mbox{ if $e = e_i$ for $1 \le i \le n-5$.} \end{array}\right.\] Then \(c'(s)=\{1\}\), \(c'(x)=[k]\), \(c'(y)=\{2\}\), \(c'(z)=\{2, 3\}\), \(c'(t)=\{3\}\), and \(c'(x_i)= S_i\) for \(1 \le i \le n-5\). Since \(c'\) is vertex-distinguishing, \(c\) is a strong royal \(k\)-edge coloring of \(T\).
Subcase \(1.2\). \(y\) is adjacent to \(n-5 \ge 3\) vertices not on \(P\). Let \(y_1, y_2, \ldots, y_{n-5}\) be the neighbors of \(y\) not on \(P\) and let \(e_i=yy_i\) for \(1 \le i \le n-5\). Let \(S_1 =\{1, k\}\), \(S_2=[2, k]\) and let \(S_3, S_4, \ldots, S_{n-5}\) be distinct nonempty proper subsets of \([k]\) different from \(\{1\}\), \(\{3\}\), \(\{1, 2\}\), \(\{2, 3\}\), \(\{1, k\}\), \([2, k]\). Define an edge coloring \(c: E(T) \to \mathcal{P}^*([k])\) by \[c(e)=\left\{\begin{array}{cl} \{1\} & \mbox{ if $e = sx$}\\[.1cm] \{2\} & \mbox{ if $e = xy$ or $e= yz$}\\[.1cm] \{3\} & \mbox{ if $e = zt$}\\ S_i & \mbox{ if $e = e_i$ for $1 \le i \le n-5$.} \end{array}\right.\] Then \(c'(s)=\{1\}\), \(c'(x)=\{1, 2\}\), \(c'(y)=[k]\), \(c'(z)=\{2, 3\}\), \(c'(t)=\{3\}\), and \(c'(x_i)= S_i\) for \(1 \le i \le n-5\). Since \(c'\) is vertex-distinguishing, \(c\) is a strong royal \(k\)-edge coloring of \(T\).
Case \(2\). Exactly two of \(x, y\) and \(z\) have degree exceeding \(2\). We may assume that \(x\) has degree exceeding \(2\) and exactly one of \(y\) and \(z\) has degree exceeding \(2\).
Subcase \(2.1\). \(x\) and \(z\) have degree exceeding \(2\). We may assume that \(x\) is adjacent to the \(p\) vertices \(x_1, x_2, \ldots, x_{p}\) not on \(P\) and \(z\) is adjacent to the \(q\) vertices \(z_1, z_2, \ldots, z_{q}\) not on \(P\), where \(1 \le p \le q\) and \(p+q=n-5\). Then \(p \le \frac{1}{2}(n-5) \le \frac{1}{2}(2^k-6)\) and so \(p \le 2^{k-1}-3\). Let \(S_1, S_2, \ldots, S_{p}\) be distinct nonempty proper subsets of \([k-1]\) where \(S_1=[2, k-1]\) such that \(S_i \ne \{1\}\) for \(2 \le i \le p\). Let \(T_1, T_2, \ldots, T_{p}\) be distinct nonempty proper subsets of \([k]\) different from \(S_1, S_2, \ldots, S_p\) such that \(T_1=[2, k]\), \(T_2=\{1\} \cup [3, k]\) and \(T_i \ne \{1\}, \{k\}, \{1, k\}, [k-1]\) for \(3 \le i \le q\). Thus, for \(1 \le i \le p\),
\(S_i \in \mathcal{P}^*([k-1])-\{\{1\}, [k-1]\}\)
and for \(1 \le i \le q\),
\(T_i \in \mathcal{P}^*([k])- \left[\{S_i: 1 \le i \le p\} \cup\{\{1\}, \{k\}, \{1, k\}, [k-1], [k]\}\right]\)
Define an edge coloring \(c: E(T) \to \mathcal{P}^*([k])\) by \[c(e)=\left\{\begin{array}{cl} \{1\} & \mbox{ if $e = sx$ or $e=xy$ }\\[.1cm] \{k\} & \mbox{ if $e = yz$ or $e= zt$}\\[.1cm] S_i & \mbox{ if $e = xx_i$ for $1 \le i\le p$}\\ T_i & \mbox{ if $e = zz_i$ for $1 \le i \le q$.} \end{array}\right.\] Then \(c'(s)=\{1\}\), \(c'(x)=[k-1]\), \(c'(y)=\{1, k\}\), \(c'(z)=[k]\), \(c'(t)=\{k\}\), \(c'(x_i)= S_i\) for \(1 \le i \le p\) and \(c'(z_i) = T_i\) for \(1\le i \le q\). Since \(c'\) is vertex-distinguishing, \(c\) is a strong royal \(k\)-edge coloring of \(T\).
Subcase \(2.2\). \(x\) and \(y\) have degree exceeding \(2\). Suppose that \(x\) is adjacent to the \(p\) vertices \(x_1, x_2, \ldots, x_{p}\) not on \(P\) and \(y\) is adjacent to the \(q\) vertices \(y_1, y_2, \ldots, y_{q}\) not on \(P\). Then \(p, q \ge 1\) and \(p+q=n-5\). There are two subcases, according to whether \(p \le q\) or \(p > q\). Observe that
Subcase \(2.2.1\). \(p \le q\). Then
\(p \le \frac{1}{2}(n-5) \le \frac{1}{2}(2^k-6)=2^{k-1}-3 = |\mathcal{P}^*([k-1])-\{\{1\}, [k-1]\}|\).
Let \(S_1, S_2, \ldots, S_{p}\) be distinct elements of \(\mathcal{P}^*([k-1])-\{\{1\}, [k-1]\}\) where \(S_1=[2, k-1]\) and let \(T_1, T_2, \ldots, T_{q}\) be distinct elements of
\(\mathcal{P}^*([k]) – \left[\{S_i: \ 1 \le i \le p\} \cup \{\{1\},\{1, k-1, k\}, \{k-1, k\}, [k-1], [k]\}\right]\)
where \(T_1=[2, k]\). Define an edge coloring \(c: E(T) \to \mathcal{P}^*([k])\) by \[c(e)=\left\{\begin{array}{cl} \{1\} & \mbox{ if $e \in \{sx, xy, yz\}$ }\\[.1cm] \{k-1, k\} & \mbox{ if $e= zt$}\\[.1cm] S_i & \mbox{ if $e = xx_i$ for $1 \le i\le p$}\\ T_i & \mbox{ if $e = yy_i$ for $1 \le i \le q$.} \end{array}\right.\] Then \(c'(s)=\{1\}\), \(c'(x)=[k-1]\), \(c'(y)=[k]\), \(c'(z)=\{1, k-1, k\}\), \(c'(t)=\{k-1, k\}\), \(c'(x_i)= S_i\) for \(1 \le i \le p\) and \(c'(y_i) = T_i\) for \(1\le i \le q\). Since \(c'\) is vertex-distinguishing, \(c\) is a strong royal \(k\)-edge coloring of \(T\).
Subcase \(2.2.2\). \(p > q\). Then
\(q < \frac{1}{2}(n-5) \le \frac{1}{2}(2^k-6)=2^{k-1}-3 = |\mathcal{P}^*([k-1])-\{\{1\}, [k-1]\}|\).
Let \(S_1, S_2, \ldots, S_{q}\) be distinct elements of \(\mathcal{P}^*([k-1])-\{\{1\}, [k-1]\}\) where \(S_1=[2, k-1]\) and let \(T_1, T_2, \ldots, T_{p}\) be distinct elements of
\(\mathcal{P}^*([k]) – \left[\{S_i: \ 1 \le i \le p\} \cup \{\{1\},\{1, k-1\}, [k-1], [k]\}\right]\)
where \(T_1=[2, k]\). Define an edge coloring \(c: E(T) \to \mathcal{P}^*([k])\) by \[c(e)=\left\{\begin{array}{cl} \{1\} & \mbox{ if $e = xy$ or $e=zt$ $$ }\\[.1cm] \{k-1\} & \mbox{ if $e = yz$ }\\[.1cm] \{k\} & \mbox{ if $e = sx$}\\[.1cm] T_i & \mbox{ if $e = xx_i$ for $1 \le i\le p$}\\ S_i & \mbox{ if $e = yy_i$ for $1 \le i \le q$.} \end{array}\right.\] Then \(c'(s)=\{k\}\), \(c'(x)=[k]\), \(c'(y)=[k-1]\), \(c'(z)=\{1, k-1\}\), \(c'(t)=\{1\}\), \(c'(x_i)= T_i\) for \(1 \le i \le p\) and \(c'(y_i) = S_i\) for \(1\le i \le q\). Since \(c'\) is vertex-distinguishing, \(c\) is a strong royal \(k\)-edge coloring of \(T\).
Case \(3\). Each of \(x, y\), and \(z\) has degree \(3\) or more. Suppose that \(x\) is adjacent to the \(p\) vertices \(x_1, x_2, \ldots, x_{p}\) not on \(P\), \(y\) is adjacent to the \(q\) vertices \(y_1, y_2, \ldots, y_{q}\) not on \(P\), and \(z\) is adjacent to the \(r\) vertices \(z_1, z_2, \ldots, z_{r}\) not on \(P\). Then \(p, q, r \ge 1\) and \(p+q+r = n-5\). We consider three subcases, according to the values of \(p, q\), and \(r\).
Subcase \(3.1\). \(1\le p \le q \le r\). Then
\(p \le \frac{1}{3}(2^k-6) = \frac{2^k }{3} – 2\) and \(p+q \le\frac{2}{3}(2^k-6)= \frac{2^{k+1}}{3} – 4\).
Since \(|\mathcal{P}([k-2])-\{[k-2]\}|=2^{k-2}-1\), there are \(2^{k-2}-1\) distinct subsets in \(\mathcal{P}^*([k-2]\cup \{k\})-\{[k-2]\cup \{k\}\}\) that contain \(k\). (Note that it is possible that \(p \ge 2^{k-2}\).) Let \(S_1, S_2, \ldots, S_{p}\) be \(p\) distinct subsets of \(\mathcal{P}^*([k-2]\cup \{k\})-\{[k-2]\cup \{k\}\}\) such that \(S_1=[2, k-2]\cup \{k\}\), \(k \in S_i\) for \(2 \le i \le p\) if \(p \le 2^{k-2}-1\) and \(k\in S_i\) for \(2 \le i \le 2^{k-2}-1\) if \(p \ge 2^{k-2}\), let \(T_1, T_2, \ldots, T_{q}\) be \(q\) distinct subsets of \(\mathcal{P}^*([k-1])- \{\{1\}, [k-1]\}\) different from \(S_1, S_2, \ldots, S_p\) such that \(T_1=[2, k-1]\), and let \(R_1, R_2, \ldots, R_{r}\) be \(r\) distinct subsets of \(\mathcal{P}^*([k])\) different from \(\{1\}\), \([k-2]\cup \{k\}\), \([k-1]\), \([k]\), \(\{k-1, k\}\), \(S_1\), \(S_2\), \(\ldots\), \(S_p\), \(T_1\), \(T_2\), \(\ldots\), \(T_q\) such that \(R_1=[2, k]\). Since there are \(2^{k-2}-1\) distinct subsets in \(\mathcal{P}^*([k-2]\cup \{k\})-\{[k-2]\cup \{k\}\}\) that contain \(k\) and \(|\mathcal{P}^*([k-1])- \{\{1\}, [k-1]\}| = 2^{k-1}-3\), it follows that at least
\((2^{k-2}-1) + (2^{k-1}-3)= 3\cdot 2^{k-2}-4\)
subsets of \(\mathcal{P}^*([k])\) are available for \(S_1, S_2, \ldots, S_p, T_1, T_2, \ldots, T_q\). Because
\(p+q \le \frac{2^{k+1}}{3} – 4 \le 3 \cdot 2^{k-2}-4\),
these \(p+q\) distinct subsets \(S_1, S_2, \ldots, S_p, T_1, T_2, \ldots, T_q\) of \(\mathcal{P}^*([k])\) exist. Define an edge coloring \(c: E(T) \to \mathcal{P}^*([k])\) by \[c(e)=\left\{\begin{array}{cl} \{1\} & \mbox{ if $e \in \{sx, xy, yz\}$ }\\[.1cm] \{k-1, k\} & \mbox{ if $e = zt$ }\\[.1cm] S_i & \mbox{ if $e = xx_i$ for $1 \le i\le p$}\\ T_i & \mbox{ if $e = yy_i$ for $1 \le i \le q$} \\ R_i & \mbox{ if $e = zz_i$ for $1 \le i\le r$.} \end{array}\right.\] Then \(c'(s)=\{1\}\), \(c'(x)=[k-2]\cup\{k\}\), \(c'(y)=[k-1]\), \(c'(z)=[k]\), \(c'(t)=\{k-1, k\}\), \(c'(x_i)= S_i\) for \(1 \le i \le p\), \(c'(y_i) = T_i\) for \(1\le i \le q\) and \(c'(z_i)=R_i\) for \(1 \le i \le r\). Since \(c'\) is vertex-distinguishing, \(c\) is a strong royal \(k\)-edge coloring of \(T\).
Subcase \(3.2\). \(q < \min\{p, r\}\). We may assume that \(q< p \le r\). Then
\(q \le \frac{1}{3}(2^k-6) = \frac{2^k }{3} – 2\) and \(p+q \le\frac{2}{3}(2^k-6)= \frac{2^{k+1}}{3} – 4\).
Let \(S_1, S_2, \ldots, S_{q}\) be distinct subsets of \(\mathcal{P}^*([k-2]\cup \{k\})-\{[k-2]\cup \{k\}\}\) such that \(S_1=[2, k-2]\cup \{k\}\), \(k \in S_i\) for \(2 \le i \le q\) if \(q \le 2^{k-2}-1\) and \(k\in S_i\) for \(2 \le i \le 2^{k-2}-1\) if \(q \ge 2^{k-2}\), let \(T_1, T_2, \ldots, T_{p}\) be distinct subsets of \(\mathcal{P}^*([k-1])- \{\{1\}, [k-1]\}\) different from \(S_1, S_2, \ldots, S_q\) such that \(T_1=[2, k-1]\), and let \(R_1, R_2, \ldots, R_{r}\) be distinct subsets of \(\mathcal{P}^*([k])\) different from \(\{1\}\), \([k-2]\cup \{k\}\), \([k-1]\), \([k]\), \(\{k-1, k\}\), \(S_1\), \(S_2\), \(\ldots\), \(S_q\), \(T_1\), \(T_2\), \(\ldots\), \(T_p\) such that \(R_1=[2, k]\). Since there are \(2^{k-2}-1\) distinct subsets in \(\mathcal{P}^*([k-2]\cup \{k\})-\{[k-2]\cup \{k\}\}\) that contain \(k\) and \(|\mathcal{P}^*([k-1])- \{\{1\}, [k-1]\}| = 2^{k-1}-3\), it follows that at least
\((2^{k-2}-1) + (2^{k-1}-3)= 3\cdot 2^{k-2}-4\)
subsets of \(\mathcal{P}^*([k])\) are available for \(S_1, S_2, \ldots, S_q, T_1, T_2, \ldots, T_p\). Since
\(p+q \le \frac{2^{k+1}}{3} – 4 \le 3 \cdot 2^{k-2}-4\),
these \(p+q\) distinct subsets \(S_1, S_2, \ldots, S_q, T_1, T_2, \ldots, T_p\) exist. Define an edge coloring \(c: E(T) \to \mathcal{P}^*([k])\) by \[c(e)=\left\{\begin{array}{cl} \{1\} & \mbox{ if $e \in \{sx, xy, yz\}$ }\\[.1cm] \{k-1, k\} & \mbox{ if $e = zt$ }\\[.1cm] T_i & \mbox{ if $e = xx_i$ for $1 \le i\le p$}\\ S_i & \mbox{ if $e = yy_i$ for $1 \le i \le q$} \\ R_i & \mbox{ if $e = zz_i$ for $1 \le i\le r$.} \end{array}\right.\] Then \(c'(s)=\{1\}\), \(c'(x)=[k-1]\), \(c'(y)=[k-2]\cup\{k\}\), \(c'(z)=[k]\), \(c'(t)=\{k-1, k\}\), \(c'(x_i)= T_i\) for \(1 \le i \le p\), \(c'(y_i) = S_i\) for \(1\le i \le q\) and \(c'(z_i)=R_i\) for \(1 \le i \le r\). Since \(c'\) is vertex-distinguishing, \(c\) is a strong royal \(k\)-edge coloring of \(T\).
Subcase \(3.3\). \(q > \max\{p, r\}\). We may assume that \(p\le r < q\). Then
\(p \le \frac{1}{3}(2^k-6) = \frac{2^k }{3} – 2\) and \(p+r \le\frac{2}{3}(2^k-6)= \frac{2^{k+1}}{3} – 4\).
Let \(S_1, S_2, \ldots, S_{p}\) be distinct subsets of \(\mathcal{P}^*([k-2]\cup \{k\})-\{[k-2]\cup \{k\}\}\) such that \(S_1=[2, k-2]\cup \{k\}\), \(k \in S_i\) for \(2 \le i \le p\) if \(p \le 2^{k-2}-1\) and \(k\in S_i\) for \(2 \le i \le 2^{k-2}-1\) if \(p \ge 2^{k-2}\), let \(T_1, T_2, \ldots, T_{r}\) be distinct subsets of \(\mathcal{P}^*([k-1])- \{\{1\},\{1, k-1\}, [k-1]\}\) different from \(S_1, S_2, \ldots, S_p\) such that \(T_1=[2, k-1]\), and let \(R_1, R_2, \ldots, R_{q}\) be distinct subsets of \(\mathcal{P}^*([k])\) different from \(\{1\}\), \([k-2]\cup \{k\}\), \([k-1]\), \([k]\), \(\{1, k-1\}\), \(S_1\), \(S_2\), \(\ldots\), \(S_p\), \(T_1\), \(T_2\), \(\ldots\), \(T_r\) such that \(R_1=[2, k]\). Since there are \(2^{k-2}-1\) distinct subsets in \(\mathcal{P}^*([k-2]\cup \{k\})-\{[k-2]\cup \{k\}\}\) that contain \(k\) and \(|\mathcal{P}^*([k-1])- \{\{1\}, \{1, k-1\}, [k-1]\}| = 2^{k-1}-4\), it follows that at least
\((2^{k-2}-1) + (2^{k-1}-4)= 3\cdot 2^{k-2}-5\)
subsets of \(\mathcal{P}^*([k])\) are available for \(S_1, S_2, \ldots, S_p, T_1, T_2, \ldots, T_r\). Since
\(p+r \le \frac{2^{k+1}}{3} – 4 \le 3 \cdot 2^{k-2}-5\),
these \(p+r\) distinct subsets \(S_1, S_2, \ldots, S_p, T_1, T_2, \ldots, T_r\) exist. Define an edge coloring \(c: E(T) \to \mathcal{P}^*([k])\) by \[c(e)=\left\{\begin{array}{cl} \{1\} & \mbox{ if $e \in \{sx, xy, yz\}$ }\\[.1cm] \{1, k-1\} & \mbox{ if $e = zt$ }\\[.1cm] S_i & \mbox{ if $e = xx_i$ for $1 \le i\le p$}\\ R_i & \mbox{ if $e = yy_i$ for $1 \le i \le q$} \\ T_i & \mbox{ if $e = zz_i$ for $1 \le i\le r$.} \end{array}\right.\] Then \(c'(s)=\{1\}\), \(c'(x)=[k-2]\cup\{k\}\), \(c'(y)=[k]\), \(c'(z)=[k-1]\), \(c'(t)=\{k-1, k\}\), \(c'(x_i)= S_i\) for \(1 \le i \le p\), \(c'(y_i) = R_i\) for \(1\le i \le q\) and \(c'(z_i)=T_i\) for \(1 \le i \le r\). Since \(c'\) is vertex-distinguishing, \(c\) is a strong royal \(k\)-edge coloring of \(T\).
If Conjecture 2 is true, then, for a connected graph \(G\) of order \(n\ge 4\), there are only two possible values for \(\mathop{\rm sroy}(G)\) (namely \(\left\lceil{\log_2 (n+1)}\right\rceil\) and \(\left\lceil{\log_2 (n+1)}\right\rceil +1\)) by Propositions 4 and 6. Consequently, we have the following conjecture.
Conjecture 3. If \(G\) is a connected graph of order \(n \ge 4\), then \[\left\lceil{\log_2 (n+1)}\right\rceil \le \mathop{\rm sroy}(G) \le \left\lceil{\log_2 (n+1)}\right\rceil + 1.\]
Since we know that the lower bound for \(\mathop{\rm sroy}(G)\) is true in Conjecture 3, this conjecture is equivalent to the following conjecture.
Conjecture 4. If \(G\) is a connected graph of order \(n \ge 4\) where \(2^{k-1} \le n \le 2^k-1\) for some integer \(k\), then there exists a strong royal \((k+1)\)-edge coloring of \(G\).
We have seen numerous examples of connected graphs \(G\) of order \(n \ge 4\) where \(\mathop{\rm sroy}(G) = \left\lceil{\log_2 (n+1)}\right\rceil\). Indeed, every tree of order \(n \ge 4\) has either been shown to have strong royal index \(\left\lceil{\log_2 (n+1)}\right\rceil\) or has been conjectured to have this value for its strong royal index. By Proposition 3, if \(n\ge 4\) is an integer with \(2^k < n < 2^{k+1}\) for some integer \(k \ge 2\), then \(\mathop{\rm sroy}(K_{n}) = \left\lceil{\log_2 (n+1)}\right\rceil + 1\). Thus, both bounds in Conjecture 3 are attainable. Hence, if Conjectures 3 and 4 are true, then the resulting theorem cannot be improved. The only question that would remain then is for a given connected graph \(G\) of order \(n \ge 4\), which of these two values is the strong royal index of \(G\)?
The author declares no conflict of interests.