In the new era characterized by the modernization of national governance, fair competition is the inherent requirement of building a modern market system. However, the abuse of administrative power by administrative organs to excessively interfere in free-market competition is widespread, seriously damaging the market competition order in China. To avoid the unreasonable intervention of administrative organs in the market economy, restrain the administrative acts of administrative organs, and form a highly “competitive” market environment, the fair competition review system came into being. With the rapid development of blockchain technology, new ideas are provided for the research of fair-trade protocols. Aiming at the system performance bottleneck and high-cost problems caused by centralized processing in traditional fair transaction schemes based on trusted third parties, a fair transaction scheme based on fuzzy signature is proposed. In the proposed scheme, the signature model uses concurrent signature, and both parties hold their own key numbers, which are released through blockchain transactions to bind their signatures. In the whole process, both parties can complete the contract signing without the assistance of a centralized third party. Based on analyzing the security of the proposed scheme, the performance of the proposed scheme is further compared with other similar schemes of the same kind, which shows that the proposed scheme has higher computational efficiency.
Fair competition review system is an important competition system to realize that the market plays a decisive role in resource allocation. Since China entered the period of the “Fourteenth Five Year Plan”, it is an important task for our government to establish a high standard market system, continue to promote the construction of the market system, and form a unified domestic market that is equal, fair, orderly, honest, efficient, standardized, and fair in competition. In the “Fourteenth Five Year Plan”, it was again proposed to establish and improve the fair competition review mechanism, strengthen the important role of anti-monopoly law enforcement and justice in improving the comprehensive market supervision ability, which has played a “strong shot” for the continuous promotion of the fair competition review system in China.
However, since the establishment and implementation of the fair competition review system, China has implemented a long-term planned economy before the establishment of the socialist market economy system. The idea of state intervention in the economy, which is dominated by the state planned management economy, is deeply rooted, and excessive administrative intervention still plays a strong leading role in market competition, damaging the fair market competition environment [1]. Whether it is the Anti Unfair Competition Law or the Anti-monopoly Law, it has played a positive role in regulating the competition behavior of market subjects. However, as Professor Zhang Zhanjiang pointed out, compared with the damage to market competition caused by enterprises, the government’s unreasonable intervention is more harmful.
The government’s abuse of administrative power to eliminate and restrict competition has become an important feature of China’s competitive ecology. It has seriously damaged the market competition order and the socio-economic order. Although Chapter 5 of the Anti-monopoly Law stipulates that the administrative authorities eliminate and restrict competition, the power of China’s competition legal system is still insufficient in the face of the increasingly complex restrictions on competition by the administrative authorities, and the efficiency of competition law enforcement and judicial protection also encounter great obstacles [2]. Therefore, in order to implement the spirit of the Fifth Plenary Session of the 19th Central Committee and establish a high standard market system, it is necessary to improve the fair competition review system at the legislative, law enforcement, and judicial levels in order to ensure a fair competition market environment and a legal environment.
With the rapid development of Internet technology, e-commerce is becoming an important part of people’s business activities. People can purchase and sell goods or services through the Internet, conduct electronic voting/election, complete contract signing and other activities [3]. Obviously, in a dynamic and open Internet environment, because there is no physical connection between the two parties involved in the transaction, the participants may not trust each other, which will make the transaction deadlocked, thus hindering the development of these applications.
When the buyer buys some goods in the physical store, it is irrelevant whether the seller hands over the goods to the buyer or the buyer pays first because the on-site transaction reduces the distrust between entities [4, 5]. However, if the transaction occurs online, this situation is unfavorable to the party who executes the first step. Fair trade protocol is designed to solve this kind of problem. It has various forms, including not only ensuring fair trade of electronic contracts after digitizing contract data involving “multiple interests and responsibilities” [6]. It also includes the problem of fair payment between the buyer and the seller in outsourcing services with the rapid development of cloud computing and fog computing.
At present, with the rapid development of blockchain technology in recent years, new research ideas have been provided in a wide range of research fields [7]. In the field of fair-trade research, many schemes based on blockchain technology have also been proposed [8]. This is mainly due to its distributed and decentralized characteristics. In blockchain based outsourcing services, service fees are directly transferred between users and cloud service providers, who do not need the help of a third party. In the transaction protocol of electronic contracts based on blockchain, the fair transaction of contracts can be completed without the need for a third party by combining with other cryptographic technologies.
This paper mainly studies the fair transaction mechanism based on the blockchain, and the main work is as follows: First, to not introduce trusted third parties in the protocol, but also to meet fairness, this paper proposes a fair transaction scheme based on the blockchain [9]. Secondly, considering the need to ensure the confidentiality of contract data transmission in some applications, a fair transaction scheme with signing function is proposed based on the above fair transaction scheme. Finally, the performance of this scheme is compared with that of other schemes of the same type. This scheme still has high efficiency and relatively low computational overhead in the current network environment.
In China, the theoretical research and practical operation of the fair competition review system have just started and are not yet very mature [10]. However, the research and practice of this system in many countries and regions in the world have been very mature. The appellation, concept expression, and definition of the fair competition review system vary internationally. OECD believes that the fair competition review system (competition assessment) refers to the assessment of whether public policies have or may have anti-competitive effects in market economy activities. In addition, alternative policy plans with less negative impact on anti-competition policies should be considered [11]. In South Korea, the fair competition review system (competition assessment) is defined as: to achieve certain policy objectives, policy-making organs evaluate the policy measures to be implemented or being implemented and strive to minimize the negative impact of the policy measures on market competition. The EU established the fair competition review system early, and the operation of the European Community has always adhered to the basic principle of “fair competition” to maintain the stability and order of the market competition order [12]. It believes that the fair competition review system (state aid system) refers to all policies that a government gives enterprises various preferential policies, such as finance, taxation, subsidies, etc., to promote enterprises to make profits or avoid economic losses. From the published documents and relevant theoretical research in China, we cannot get a unified and clear definition of the concept of the fair competition review system. Some scholars believe that the fair competition review system refers to preventing or reducing the interference of administrative power on market competition through certain evaluation standards and procedures [13]. Some scholars believe that the fair competition review system refers to a system that conducts external or internal review, substitution, and even suppression of regulations, normative documents, and other policy measures related to market economic activities formulated by policy-making organs in accordance with statutory competition standards. Other scholars believe that the fair competition review system aims to ensure that market subjects have equal opportunities for competition and various factors of production and avoid excessive interference in market competition by administrative organs [14].
There are significant differences in the emergence, development, and operability of the fair competition review system at home and abroad. However, from a historical perspective, the process of the fair competition review system at home and abroad has generally gone through three stages: germination, formation, and development [15]. In addition, in the process of development, China’s fair competition review system has been constantly adapted and integrated with China’s national conditions and has finally become a top-level system design with Chinese characteristics and innovation [16].
The development history of the foreign fair competition review system is as follows.
Foreign fair competition review system originated from government regulation [17]. In the middle and late 19th century, western developed countries, which had long believed in laissez-faire market economy, gradually realized that appropriate government regulation could effectively correct market failure under the background of market failure [18]. The so-called regulation means that “the government restricts the free choice of individuals and organizations through legal deterrence. At the same time, according to the different fields and purposes of intervention,” economic regulation “and” social regulation “become two major categories of regulation [19]. The field of economic regulation is mainly natural monopoly industries. The government regulates the production and operation activities of enterprises through a series of means and tools; And social regulation is obviously social; its main purpose is to eliminate the negative impact of economic activities, so as to improve public welfare.
The world economic crisis that broke out in 1929 was the fuse to fully implement government regulation and strengthen government intervention in the market. Since the 1930s, the regulatory policies implemented by the U.S. government have expanded to many important industries, and the U.S. government’s regulatory philosophy has been borrowed by countries around the world, and the development of regulatory policies has reached the peak. However, in the 1970s, economic stagflation occurred in western capitalist countries, and the theory of government intervention was questioned. The liberal market economy was once again valued by all countries. Countries around the world have “loosened” the market economy and gradually reduced government regulation in many industries [20].
From the 1970s to the 1990s, there were two changes in the deregulation activities carried out by countries around the world: first, the restriction of competition was changed to the promotion of competition, and the competitive objectives were included in the regulatory policies. The government’s regulatory approach gradually changed from direct intervention in market economic activities to strengthening cooperation with enterprises and society [21]. Second, the government regulation has changed in the field, which is mainly reflected in the fact that although the United States and other countries have relaxed the economic regulation of natural monopoly industries and financial industries, they have strengthened the social regulation of health, safety, and environmental quality.
In the mid-1990s, countries around the world set off a wave of government regulation reform again. Currently, the focus of reform was to pursue and optimize the concept of government regulation and attach importance to the quality of regulation reform [22]. After the world economic crisis in the 1930s and economic stagflation in the 1970s, western capitalist countries gradually realized that the complete laissez-faire of the market economy and excessive government regulation would affect the development of their own economies. Only by balancing market competition and government regulation can we promote the benign development of the market economy [23].
In 1998, at the “Symposium on Regulatory Innovation” held by the Asia Pacific Economic Cooperation (APEC), the participants pointed out that the government should take the responsibility to promote competition and not “compete” with the market, thus forming “high-quality regulation”. Since then, in the pursuit of such “high-quality regulation” (Australia calls it “professional regulation”), countries have begun to assess the impact of regulation. Many countries have even proposed to conduct a special competition assessment of regulation, to ensure that regulation will not interfere with the market competition order [24].
In the process of government regulation reform, although it is possible to conduct judicial review of government regulation that affects competition, as judicial review is an ex post regulatory measure, in practice, economically developed European and American countries have adopted more competition evaluation systems with the characteristics of ex ante regulation to solve government regulation problems. In 1980, the Federal Trade Commission of the United States began to conduct a competitive evaluation of federal regulations involving international trade, health care, transportation, and other fields [25]. In the 1990s, Australia, which was highly regulated by the government, began to implement competition assessment policies. Based on the negative impact of state-owned enterprises on market competition at that time, it formulated the principle of competition neutrality for state-owned enterprises. As of 2005, Australia has made remarkable achievements in competition assessment. It has not only basically completed the assessment of the policies and measures being implemented but also revised or abolished more than 18000 laws and regulations restricting competition. In addition, OECD has also played a positive role in the development of the competition evaluation system. In 2007, the OECD launched the Competition Assessment Toolkit, which specifies the methods and procedures of the competition assessment system in detail and recommends that all member countries establish competition assessment systems. So far, most developed countries in the world have taken the lead in establishing competition assessment systems, and some developing countries have followed suit to gradually introduce competition assessment systems, thus creating a good market competition environment.
Blockchain is a distributed accounting technology jointly maintained by many participants, which uses a variety of cryptography technologies to ensure the security of its transmission and access and realizes the consistent storage of data, tamper-proof, and non-repudiation. Blockchain stores data in the form of a block chain. Bitcoin is the most mature application of blockchain technology. This paper constructs a transaction scheme based on Bitcoin and then takes Bitcoin as the specific introduction object.
In the Bitcoin system, the issue of currency is realized by the nodes (miners) in the network through the completion of the consensus mechanism. In this process, miners will compete to solve a mathematical problem, which will consume a lot of computing power of miners. This process is called Proof of Work. The first miner to solve this problem will get the right to chain up the transactions in the packaging network, that is, the bookkeeping right. At the same time, miners will get a certain amount of Bitcoin as incentives, so that new currencies will be issued to the network. At the same time, it is also an important means to ensure the network security of Bitcoin and a key point to prevent currency from being double-spent.
P2SH was introduced into the Bitcoin system in 2012 as a new, powerful transaction type that can greatly simplify complex transaction scripts. Although the multi-signature function in Bitcoin is very powerful, it is inconvenient to use. In addition, multi-signature may contain a very long public key, which will also cause additional costs for users. P2SH can not only realize the multi-signature function but also be as simple as paying directly to the Bitcoin address. The reason is that researchers replace the complex multi-signature locking script with a simple hash value. If you want to use such a transaction output later, you must provide the script corresponding to the hash value.
To provide more flexibility, the Bitcoin system provides the time lock function. Transactions with the time lock function can only be disbursed after the specified time. Bitcoin has multiple levels of time locks, and transaction-level time locks define the earliest effective time of transactions. However, the transaction-level time lock can only guarantee that the transaction receiver cannot complete the transaction for realization before the specified time, but it cannot guarantee that the transaction initiator will not make dual payments before the specified time. To solve this problem, time locks must be placed on UTXO (Unspent Transaction Outputs), so that each transaction output can be specified at what time before redemption. Check Lock Time Verify is designed to achieve this function. CLTV operation codes can be added to the redemption script so that the output can only be redeemed after a specified time.
Fair trade plays a key role in the field of e-commerce and e-government, such as contract signing. Taking contract signing as an example, traditional paper contracts are signed by both parties face to face in the same physical environment, and signed by both parties under mutual supervision, so there is almost no unfairness. In the network environment, because there is no trust foundation between the parties signing the contract, how to ensure the rights and interests of both parties, especially fairness, is an important problem faced by e-commerce, e-government, and other fields.
Traditional fair-trade protocols are usually implemented based on trusted third parties. According to the degree of dependence on TTP in the protocol, TTP can be divided into three forms: In-line TTP, Online TTP, and Offline TTP. However, no matter how involved TTP is, as the core of the whole system, whether in computing, communication, or storage, it will become the bottleneck of the system. To solve this problem, this paper proposes a fair transaction scheme based on blockchain, which can achieve fairness without the participation of TTP.
The fair-trade scheme proposed in this paper has the following characteristics:
No trusted third party participates. The fairness of this scheme does not depend on a trusted third party.
Non-forgeability. The signature scheme in this scheme cannot be forged under the adaptive selection message attack.
Fairness. Under the random oracle model, the scheme meets the fairness requirements.
Tamper-proof. The transaction in this scheme is tamper-proof.
Verifiability. The key number verification in this scheme can be publicly verified on the Bitcoin network.
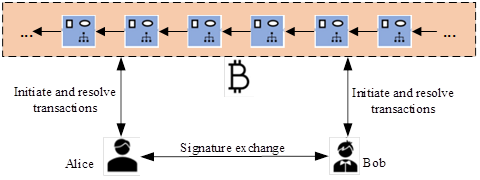
The system model of the fair transaction scheme designed based on blockchain technology in this paper is shown in Figure 1. The system includes the transaction initiator, transaction receiver, and blockchain. In the following description, we use Alice and Bob to represent the initiator and receiver of the signature protocol, respectively. For the sake of brevity, we only include the main steps of the protocol in Figure 1.
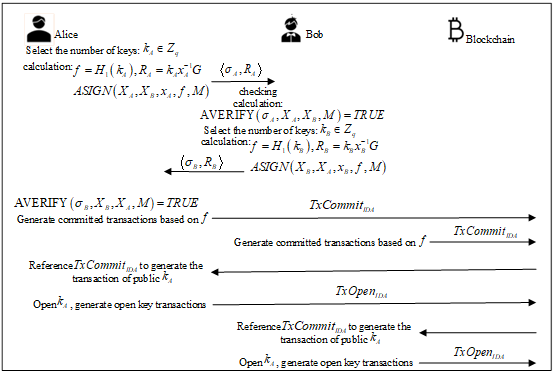
Alice, as the initiator of the protocol, selects her key number and generates the corresponding hash value of the key number. She generates a fuzzy signature through the fuzzy signature algorithm and sends the fuzzy signature to Bob. After receiving Alice’s fuzzy signature, Bob will check the signature accordingly. If it passes, Bob will generate his fuzzy signature and send it to Alice as required by the protocol. Similarly, Alice verifies after receiving Bob’s fuzzy signature. If successful, Alice will generate a P2SH transaction based on Bob’s key number hash value, and Bob will do the same. This type of transaction aims to force the other party to disclose the key number. After that, Alice and Bob will refer to the transaction sent by the other party to create a transaction that exposes their key numbers.
| Symbol | Meaning |
|---|---|
| l | security parameter |
| q | Large prime number |
| Elliptic curve addition group | |
| Elliptic curve multiplication group | |
| G | Generators for |
| One way hash function: |
|
| E | Bilinear mapping |
| private key | |
| User Public Key | |
| M | Message to be signed |
| K | Key number |
| F | Key number hash value |
| Fuzzy signature |
The main symbols used in this paper’s transaction scheme and their corresponding definitions are shown in Table 1.
This section first gives the specific structure of the concurrent signature algorithm based on bilinear pairing. The details (SETUP, ASIGN, AVERIFY, VERIFY) are as follows:
SETUP: Given the security parameter
ASIGN: The algorithm takes
Algorithm output:
Algorithm check: Formulas [eq4] and [eq5]
This scheme is a fair transaction scheme based on the blockchain proposed by the signature algorithm. Without losing generality, the protocol is initiated by Alice and responded to by Bob. The scheme is divided into four stages, namely, fuzzy signature transaction stage, transaction stage, open stage, and transaction verification stage. The overall transaction process is shown in Figure 2.
The contract signing business in the field of e-commerce has greatly improved the rapidity and convenience of transactions. However, in the complex and open Internet environment, it also brings risks that do not exist in traditional business activities. In application scenarios with higher security requirements, the confidentiality of the contract to be traded must be guaranteed. In the process of fair trading, it must be ensured that no information of the contract will be disclosed, and the receiver can verify its correctness.
To solve this problem, this paper proposes a fair-trade scheme that can ensure the confidentiality of the contract and meet other security features. This scheme has the following characteristics:
No trusted third party participates. The implementation of fairness in this scheme does not depend on the trusted third party.
Fairness. The contract signed by both parties involved in this scheme can be traded fairly.
Nonrepudiation. After both parties of the transaction execute the data transaction of the agreement according to the provisions of the agreement, neither party can deny the message sent or received.
Confidentiality. This scheme ensures the confidentiality of contract information, which is ensured by the elliptic curve discrete logarithm problem.
Timeliness. If both parties execute the agreement, the agreement will end at the effective time.
This scheme is applicable to the contract signing business in e-commerce. The system consists of three entities: the transaction initiator, transaction receiver, and blockchain network. For the sake of brevity, Alice represents the initiator of the transaction, and Bob represents the receiver of the transaction in the later description of this article.
Alice first completes the encryption of the contract message
Alice, like Bob, checks the received ciphertext. After verification,
Alice and Bob jointly perform zero knowledge proof, and Alice proves to
Bob that she has secret value
Alice accepts the certificate and initiates a committed transaction
(Tomita), then launches a public transaction (Topeka)
according to Commit, used to disclose the secret value
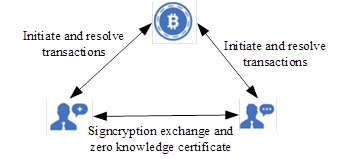
This scheme is a verifiable encryption inscription scheme based on signature and verifiable encryption signature. Schnarr signature is provably secure in the random oracle model. The reduction algorithm used in the scheme evolved from inscription specification to Schnarr signature specification proposed by elliptic curve discrete logarithm problem to discrete logarithm problem.
The scheme is divided into five stages: system generation stage, inscription transaction stage, transaction initiation stage, secret disclosure stage, and transaction verification stage. In the system generation phase, the public parameters of the system and the public and private keys of Alice and Bob, the transaction participants, will be determined. Alice and Bob will sign the ciphertext of the transaction respectively and verify it during the signing phase.
In the transaction initiation stage, Alice and Bob mutually prove zero knowledge to prove that they know the relevant secret value, and finally launch TX Commit transaction to support redemption. In the secret disclosure stage, Alice and Bob disclose the secret value by initiating a TX Open transaction.
At the transaction verification stage, the transaction process has ended, and the transaction results will be verified to verify whether the transaction results are legal. The main symbols and their definitions used in this scheme are shown in Table 2.
| Symbol | meaning |
|---|---|
| Q | A large prime number |
| Elliptic curve addition group | |
| Elliptic curve multiplication group | |
| P | Generators of |
| One way hash function: | |
| One way hash function: | |
| One way hash function: | |
| One way hash function: | |
| One way hash function: | |
| e | Bilinear mapping |
| private key | |
| User Public Key | |
| Epimorphic homomorphic algorithm |
To sign the contract
At this time, Alice’s ciphertext
Finally, Alice’s verifiable signature document
Check the contract message
If
Finally, Bob sends the encrypted message
Check the contract message. If
If
Comparing the performance of the scheme in this paper with the
existing fair transaction signature scheme, considering that there is no
article completely based on blockchain and concurrent signature at
present, the fair transaction scheme selected in this paper is
implemented by verifiable encryption signature. The performance analysis
mainly includes the system generation phase, which only considers the
generation of users that are necessary in a signature, the fuzzy
signature phase, the fuzzy signature verification phase, and the
signature verification phase. The simulation experiments in this stage
are carried out on a laptop configured with Intel i5-8300H 2.30GHz, 16GB
of memory and running Windows 10 1909 system. The JPBC library is used
to complete the algorithm implementation. Due to the low time
consumption of finite field multiplication and hash operation, they are
not considered in the comparison. For convenience,
| stage | System generation stage | Fuzzy signature stage/encrypted signature stage | Fuzzy signature verification stage | Signature verification stage/signature extraction stage |
|---|---|---|---|---|
| Literature 1 | ||||
| Literature 2 | ||||
| Literature 3 | ||||
| Scheme |
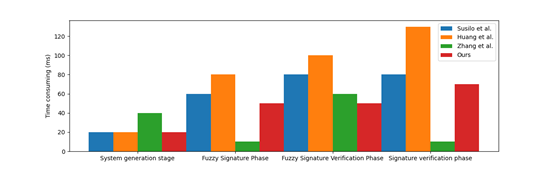
The time consumption at different stages of each scheme is shown in Figure 4. For the total time of each scheme, the total time of Literature 1 is 238.04 ms, the total time of Literature 2 is 326.45 ms, the total time of Literature 3 is 125.63 ms, and the total time of this scheme is 215.38 ms. Compared with the other two schemes implemented by the concurrent signature algorithm, this scheme has a slight advantage in computing time consumption at each stage. In the system generation phase, the calculation consumption of each scheme is roughly the same. In the fuzzy signature phase, the calculation consumption of this scheme is significantly lower than that of the other two concurrent signature schemes. In the fuzzy signature verification phase, the signature verification phase is significantly better than the comparison scheme. Since the scheme in Literature 3 is not implemented by concurrent signature, its time consumption in each phase is lower than that of other comparison schemes. However, it needs to construct complex smart contracts, and the calculation consumption in this part is not counted.
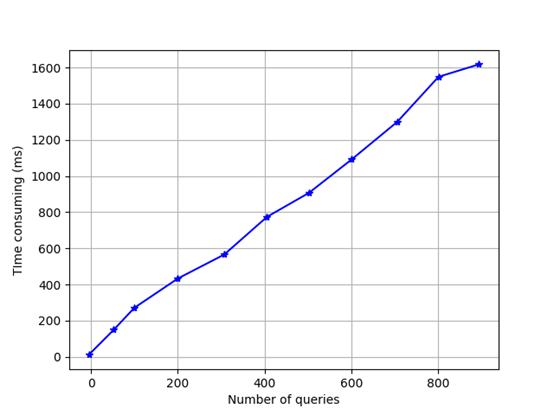
The scheme in this paper involves the analysis of transaction information in the blockchain. The main time is spent reading transactions from the main chain. The other is to check the hash value carried in the transaction. In this section, the retest test network provided by Bitcoin Core is used for the experiment of reading transaction information. The experimental data is shown in Figure 5. For nodes that have synchronized transaction information locally, each query transaction takes about 1 ms on average, which is not the main consumption compared with other calculations in the stage. Considering that in the blockchain environment, the time from the initiation of a transaction to the final confirmation of the transaction is huge compared to the time consumed in computing. The main reason is that the verification needs to be completed on the public chain. In the process of verification, we need to wait for the nodes in the blockchain to confirm.
However, in the comparison scheme, the protocol is not asymmetric, and it is difficult to achieve full fairness. Only when the signature initiator releases the key number can the fuzzy signature be bound to the real signer. If the signature initiator is malicious, he can construct the key number in his favor or publish the key number at a favorable time. In the traditional scheme based on the trusted third party, when there are dishonest participants, honest participants need to contact the trusted third party to resolve conflicts, and from this perspective, the cost will be greatly increased. This scheme is a fair transaction scheme based on blockchain. Without the participation of a trusted third party, it can achieve security, fairness, and availability. In general, since there is no traditional trusted third party, the server computing and storage pressure will no longer be a problem. All computing pressures will be shared by all nodes. This scheme has high efficiency in the current computing environment, and the computing overhead is kept at a low level.
The scheme in this paper will be compared with some existing
fair-trade schemes. The simulation experiments conducted in this section
are carried out on a laptop configured with Intel i5-8300H 2.30GHz, 16GB
memory, and running Windows 10 1909 system. Bilinear operations are
implemented using JPBC library. Due to the low time consumption of hash
operation, finite field multiplication, and other operations, they are
not considered in this comparison. For the convenience of description,
Each scheme will adopt different methods to achieve fair transactions according to their needs. The scheme realizes fair transactions of signing ciphertext based on concurrent signature technology. In case of dispute, it can sue for compensation to the legal department according to the evidence obtained, which can achieve weak security. Fair contract signing protocols are implemented based on blockchain and verifiable cryptographic signature.
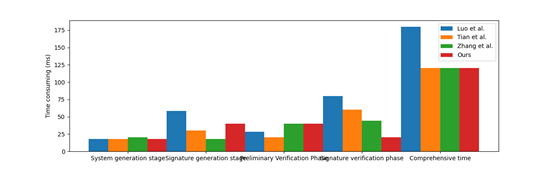
The scheme in this paper is a fair signed ciphertext transaction protocol based on blockchain and verifiable encryption signature technology. Although there are some differences in details, they can be summarized into four stages, and both fuzzy signature verification and verifiable encrypted signature verification are agreed upon as preliminary signature verification. The specific calculation cost corresponding to each phase of each scheme is shown in Table 4:
| stage | System generation stage | Sign off (name) generation phase | Preliminary validation stage | Signature verification stage | |
|---|---|---|---|---|---|
| Literature 1 | |||||
| Literature 2 | |||||
| Literature 3 | |||||
| Scheme |
The time consumption of each scheme is shown in Figure 6. Each scheme has its own advantages and disadvantages at each stage. In general, there is little difference. Considering that this scheme not only realizes the verifiability of data but also ensures the confidentiality of data, it requires a certain amount of additional computation.
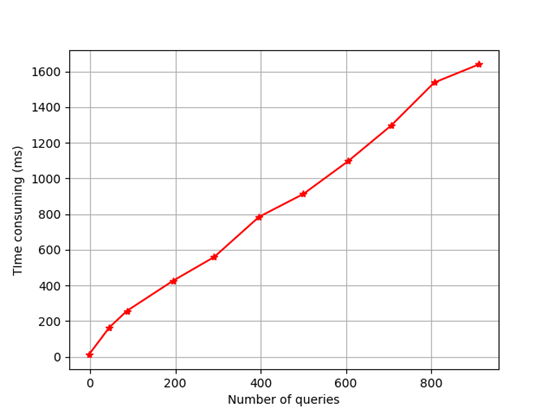
All the schemes in this paper are fair trading schemes based on the blockchain system, requiring the participation of the blockchain network in the protocol. Generating blockchain transactions is a necessary process. In the Zaida scheme, the Bitcoin network is required to support additional bilinear pair verification operations, and relatively complex smart contracts need to be constructed in the scheme. The scheme in this paper can only be implemented by the native Bitcoin system, which can be considered an advantage. Additionally, although the scheme does not require the participation of the blockchain, it needs to introduce a trusted third party to resolve disputes. In this scheme, the analysis of Bitcoin transaction information is involved, and the main time consumption is to read the transaction information from the main chain. This section uses the retest provided by Bitcoin Core to test the network to read the transaction information. The experimental results are shown in Figure 7. In the real network, the time consumption is heavily dependent on the network environment. For participants who have synchronized the transaction information locally, each query transaction takes about 1ms on average, which is not the main consumption compared with other calculations. In the blockchain environment, the time taken for a transaction from initiation to final confirmation is far greater than its computational cost. However, compared with the traditional scheme of fair transaction based on the trusted third party, when there are dishonest participants, honest participants need to contact the trusted third party to resolve their disputes. From this perspective, the cost will be greatly increased. In this scheme, the Bitcoin transaction status is introduced as a part of the verification conditions, avoiding the limitation of using a large amount of Bitcoin as a guarantee and expanding the scope of use. This scheme can achieve confidentiality, fairness, and availability without the participation of a trusted third party. In general, because traditional trusted third parties are not involved, the storage and computing pressure of the server will no longer be the bottleneck of the system. All the computing pressure will be shared by all nodes. This scheme still has high efficiency in the current network environment, and the computing cost remains at a relatively low level.
With the popularization of online services such as e-commerce and e-government, the demand for fair transactions between two parties, such as contract signing, has emerged. In a dynamic and open Internet environment, due to the lack of a trust foundation between business parties, fair transactions face challenges. The key to solving these problems is to design relevant fair-trade agreements. This paper designs two fair-trade protocols based on blockchain technology. The first fair transaction protocol based on the blockchain uses Bitcoin P2SH and time-locking technology, incorporating Bitcoin script diversion to ensure the fairness of transactions. Security and performance analyses demonstrate that the scheme maintains ideal performance while ensuring unforgeability and fairness. Second, we utilize P2SH and transaction output time-lock technology in Bitcoin and include the transaction status of Bitcoin in the final transaction verification to ensure fairness by leveraging the tamper resistance of Bitcoin transactions. The security and performance analyses show that this scheme also maintains ideal performance while realizing many security features.
The experimental data used to support the findings of this study are available from the corresponding author upon request.
The author declares that they have no conflicts of interest regarding this work.
1970-2025 CP (Manitoba, Canada) unless otherwise stated.