Radio Antipodal Labeling of Mongolian Tent and Torus Grid Graphs

1. Introduction

Wireless communication has become one of the fastest-growing industry segments in recent years. Due to rapid growth in wireless communication services and the corresponding scarcity and high cost of radio spectrum bandwidth, it has become increasingly important for cellular network operators to maximize spectrum efficiency. Such efficiency can be achieved by optimal frequency reuse. The effective reuse of the radio spectrum with less or no interference can be achieved by studying channel allocation problems in wireless mesh networks [1]. This can be easily achieved by using graph theory techniques.

Graph theory is a branch of mathematics concerned with networks (graphs) of points (vertices) connected by lines (edges). It has grown into a significant area of mathematical research, with applications in chemistry, operations research, social sciences, computer science etc. Some of the research topics in graph theory are listed in [2,3,4,5,6,7,8]. One of the important areas in graph theory is Graph labeling. The graph labeling or valuation of a graph [9] is an assignment of integers to vertices or edges or both subject to certain conditions.

Radio labeling of graphs was introduced in 2001 by Chartrand et al. [10] as they were motivated by regulations for frequency (channel) assignments of FM radio stations. In a frequency assignment problem, the task is to assign the radio frequencies to the transmitters at different locations without causing interference and minimizing the span. Here, the span is the largest label assigned to the transmitters. This problem was first formulated as a Graph coloring problem in 1980 by Hale [11], who introduced the notion of T-Coloring of a graph. In a graph model of this problem, the transmitters are represented by the vertices, and the link between every pair of transmitters is represented by edges. Radio labeling is a function from the graph’s vertices to some subset of non-negative integers.

The radio\(\ k\) -labeling [12] of a graph \(G\) is an assignment of positive integers to the vertices of \(G\) such that \(d\left(u,v\right)+\left|f\left(u\right)-f(v)\right|\ge \ k+1\), where \(\ d(u,v)\) denotes the distance between every pair of distinct vertices \(u\) and \(v\ \)of\(\ G\) and \(k\) is a positive integer. Based on the value of k,, the radio labeling is classified as follows. The radio labeling is a radio\(\ k\)-labeling [13] when\(\ k=diam(G)\). If \(k=diam\left(G\right)-1\ \), it is called radio antipodal labeling [14,15]. In other words, an antipodal labeling for a graph G is a function \(f:V(G)\to \left\{0,1,2,\dots \right\}\) such that \(d\left(u,v\right)+\left|f\left(u\right)-f(v)\right|\ge \ diam(G)\). The span of the function\(\ f\) is\(\ sp\left(f\right)=\mathrm{max}\mathrm{}\{\left|f\left(u\right)-f\left(v\right)\right|:u,v\in V(G)\}\). The radio antipodal number for G, denoted by \(an\left(G\right)\ \), is the minimum span of an antipodal labeling admitted by G. Radio labeling is a one-to-one function, while in antipodal labeling, two vertices of distance \(diam(G)\) apart may receive the same label. It is computationally complex to calculate the radio number on the general graph. Determining the radio number of a general graph with diameter 2 is NP-hard, and its complexity is unknown in general [16].

Several authors have studied the antipodal number for different families of graphs. The antipodal coloring of graphs was first studied by Chartrand, Erwin and Zhang, [15]. They gave general bounds for the antipodal number of a graph. Also, they have studied the radio antipodal labeling for path and cycle [12,14]. But the exact value of the radio antipodal number of a path has been found in [17]. Juan and Liu, [18] have determined the radio antipodal number of cycles. Khennoufa and Togni, [19] studied the radio antipodal number and the radio number of the hypercube, which was determined by a generalization of binary gray codes.

Radio labeling and antipodal labeling of trees with orders up to eight were obtained by Zheng [20]. The multi-level labeling of generalized Petersen graphs \(P\ (4k+\ 2,\ 2)\) related graphs was investigated by Kang et al. [21]. Saha and Panigrahi, [22] obtained the antipodal number of some powers of cycles. The radio number and radio antipodal number of circulant graphs \(G\left(4k+2;\left\{1,2\right\}\right)\) was investigated by Saima Nazeer et al. [23]. William and Robert, [24] obtained an upper bound for the radio antipodal number of the hexagonal mesh and grid. The radio antipodal number of the Circulant graph was studied in [25,26]. In this paper, the antipodal number of Mongolian tents and Torus grid has been studied.

Definition 1.[27] The Ladder graph \({\ L}_n\) is obtained by the Cartesian product of two path graphs \({\ P}_2\) and\({\ P}_n,\ n\ge 2\). It has \(2n\ \)vertices and \(n+2(n-1)\) edges.

Definition 2.[27] A Mongolian tent graph \(MT(n)\) is a simple connected graph that is obtained by joining all the vertices in the upper row of the ladder graph with a single vertex \((z)\) which is not in the ladder.

The number of vertices of \(MT(n)\) for \(n\ge 2\) is \(2n+1\), and the number of edges is\(\ 4n-2\). A generalized Mongolian tent of order \(n\) is shown in Figure 1.

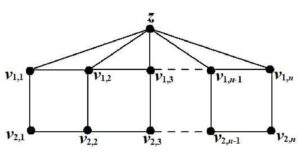
Remark 1. For our convenience, we call the row \(v_{1,j},\ j=1,2,\dots ,n\) as top row and \(v_{2,j},\ j=1,2,\dots ,n\) as bottom row.

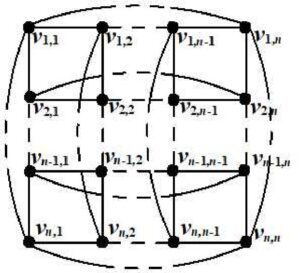
Definition 3.[9] A Torus Grid Graph \(T\left(n\times n \right)\)is obtained from Grid graph. In addition, the leftmost and rightmost nodes of each row are adjacent, and the uppermost and lowermost nodes of each column are adjacent.

It has \(n^2\) vertices, \(2n^2\) edges and its diameter is \(2\lfloor {n}/{2}\rfloor.\ \) It is a 4-regular graph. For example, see Figure 2.

2. Antipodal number for Mongolian tent graph

In this section, we establish the antipodal number of Mongolian tent graph \(MT(n)\) for \(n\ge 6.\)

Remark 2. Let \(f\) be an optimum antipodal labeling of graph \(G=MT(n)\) and \(\left\{z,\ v_{i,1,}v_{i,2}\dots v_{i,n};i=1,2\right\}\) be the vertices of \(G\). The vertices of \(MT(n)\) are labeled as follows. The single vertex z is labeled as 1. In antipodal labeling, the diametrically opposite vertices receive the same label. If \(d\left(v_{i,j}\ ,v_{i,j+1}\right)=\ diam\left(G\right)\ \) then the difference of their labeling is zero, hence \( f(v_{i,j+1})\ –\ f(v_{i,j})=0\). To find a lower bound for \(an(G)\), we assume that there are at most \(x\) pairs of vertices that are diametrically opposite in a graph \(G\) with smallest diameter, then there will be \(\left(2n-x\right)\) vertices in the top row and bottom row of \(MT(n)\) and their labeling will be different from x pairs and is based on antipodal condition. In this case, we have

where \(y_k\) is the remaining number of vertices in the top row and bottom row of \(MT(n)\).

Theorem 1.

• a) The antipodal number of \(MT(2)\) is 3.
• b) The antipodal number of \(MT(3)\) is 9.
• c) The antipodal number of \(MT(4)\) is 13.

Proof. Let \(\left\{z,\ v_{i,1,}v_{i,2}\dots v_{i,n};i=1,2\right\}\) be the vertices of\(\ MT(n)\). The lower bound of the antipodal number of \(MT\left(n\right),\ \) for \(n=2,3,4\) is determined first. The vertices of \(\ MT(n)\) are labeled as given by Remark 2.1. Let \(f\) be an optimum antipodal labeling of \(MT(n)\). We investigate the maximum number of pairs (\(v_{i,j},v_{i,j+1}\)) which are diametrically opposite, so that by antipodal condition \(f(v_{i,j+1})\ –\ f(v_{i,j})=0.\)

Take \(f(z)\ =1\). Then label vertex \(v_{11}\). From \(v_{11}\), labeled the vertex, which is at diametric distance. Then again from \(v_{11}\), label the vertices \(v_{21}\)and \(v_{12}\). Then from \(v_{21}\)and\(v_{12}\), label all the adjacent vertices. This pattern continues until all the remaining vertices of \(MT(n)\) are labeled.

The upper bounds for the antipodal number of the considered graphs have been illustrated in Figure 3.

Case (a) The graph \(MT(2)\) has \(5\) vertices, \(6\) edges and its diameter is 2. By \(\left(1\right),\) \[an\left(MT(2)\right)\ge \ 1+\ 2\left(0\right)+2(1)=1+2=3.\]

From Figure 3(a), \(an\left(MT\left(2\right)\right)\le \ 3\ \). Hence \(an\left(MT\left(2\right)\right)=3.\)

Case (b) The graph\(\ MT(3)\) has \(7\) vertices, \(10\) edges and its diameter is \(3\). By (1), \(an\left(MT\left(3\right)\right)\ge \ 1+2\left(0\right)+4\left(2\right)\ge 9.\) From Figure 3(b), \(an\left(MT\left(3\right)\right)\le \ 9\ \).

Hence \(an\left(MT\left(3\right)\right)=9.\)

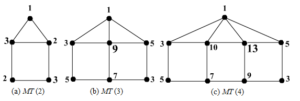
By (1), \[an\left(MT\left(4\right)\right)\ge 1+2\left(0\right)+6\left(2\right)\ge 13.\] From Figure 3(c), \(an\left(MT\left(4\right)\right)\le \ 13\ \). Hence \(an\left(MT\left(4\right)\right)=13\).

Theorem 2. The antipodal number of \(MT\left(5\right)\) is 15.

Proof.

The graph \(MT(5)\) has 11 vertices and 18 edges, and its diameter is 4. The vertices of \(MT(5)\)are labeled as follows. The single vertex z is labeled as 1. The vertices \(v_{\mathrm{11}}\) and \(v_{\mathrm{21}}\)are labeled using antipodal condition. The remaining vertices in the top row and bottom row of \(MT(5)\) are labeled using the antipodal condition, and the distance between the pair of vertices is as follows.

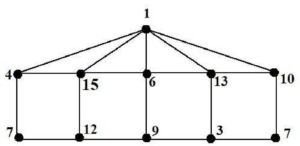
Here\(\ d\left(v_{\mathrm{2,1}},v_{\mathrm{2,5}}\right)=4\), i.e., \(v_{\mathrm{21}}\) and \(v_{\mathrm{25}}\) are at diametric distance. Hence\(\ f\left(v_{\mathrm{2,1}}\right)=f(v_{\mathrm{2,5}}\mathrm{)}\); now\(\ d\left(v_{\mathrm{1,1}},v_{\mathrm{2,4}}\right)\mathrm{=3}\), so \(v_{\mathrm{24}}\) is labeled. Then\({\ v}_{\mathrm{13}}\mathrm{\ }\)and \(v_{23}\) are labeled as\(\ d\left(v_{\mathrm{1,1}},v_{\mathrm{1,3}}\right)\mathrm{=}d\left(v_{2,1},v_{2,3}\right)=2\).

As \(\ d\left(v_{2,3},v_{1,5}\right)=3\), \(v_{15}\) is labeled. Now,\(\ d\left(v_{1,5,},v_{2,2}\right)=3\), so \(v_{22}\) is labeled. \(d\left(v_{2,2},v_{1,4}\right)=3\). Hence \(v_{1,4}\) is labeled.

Finally vertex \(v_{1,2}\) was labeled from vertex \(\ v_{1,4}\).

By (1), \(an(MT(5))\ \ge 1+1\left(0\right)+4\left(1\right)+2\left(2\right)+2\left(3\right)=15.\) The antipodal labeling \(MT(5)\) is given in Figure 4. This implies\(\ an\left(MT\left(5\right)\right)\le \ 15\ \). Hence \(an(MT(5))=15.\)

Theorem 3. The antipodal number of n \({}^{th}\) dimension of Mongolian tent \(MT(n)\ \)is \(an(MT(n))\ \ge \ \ 2n+8\),\(n\ge 6\).

Proof. Let be \(\left\{z,\ v_{i,1,}v_{i,2}\dots v_{i,n};i=1,2\right\}\) be the vertex set of Mongolian tent \(MT(n)\). These vertices are labeled as follows. The single vertex z of \(MT(n)\) is labeled as 1. The vertices \(v_{\mathrm{1,1}}\) and \(v_{\mathrm{2,1}}\)are labeled using antipodal condition. The remaining vertices in the top row and bottom row of \(MT(n)\) are labeled respectively based on their maximum distance from \(v_{\mathrm{1,1}}\) and \(v_{\mathrm{2,1}}.\)

Clearly, d (\(v_{2,1},v_{2,j}\)) = 4, \(j>4\), that is there are \((n-4)\) vertices of distance 4 from \(v_{\mathrm{21}}\). These vertices are labeled, starting from \(v_{2,5}\ \)to\({\ v}_{2,n}\) in the cyclic manner as follows,

\begin{align*} &f\left(v_{2,4j+1}\right)=f\left(v_{21}\right)+4;\&f\left(v_{2,4j+2}\right)=f\left(v_{21}\right)-2\&f\left(v_{2,4j+3}\right)=f\left(v_{21}\right)+2;\&f\left(v_{2,4j+4}\right)=f\left(v_{21}\right)-4,\ j=1,2\dots \end{align*}

Now \(\left|f(v_{2,1})-f(v_{2,j})\right|=0.\)

Consider the vertices in the top row. Clearly, d (\(v_{1,1},v_{1,j}\)) = 2, \(j>2\). There are \(n-1\) pairs of vertices in the top row at two distances from \({\ v}_{11}\). The vertices in the odd positions are labeled as follows, \[f(v_{13}) =f\left(v_{1,1}\right)+2;\ \ f\left(v_{1,5}\right)=f\left(v_{1,1}\right)+4;\ \ f\left(v_{1,7}\right)=f\left(v_{1,1}\right)+8\] If n is even the vertices at the odd position in a top row starting from \(v_{1,9}\) to \(v_{1,n-1}\) are labeled using the relation \(f\left(v_{1,2j+7}\right)=f\left(v_{1,2j+5}\right)+2,\ j=1,2\dots \) If n is odd, then the vertices at odd position in the top row from \(v_{1,9}\ \ \)to\(\ \ v_{1,n}\) are labeled using the above relation.

The vertices in even position of top row from \(v_{1,2}\ \ \)to\(\ \ v_{1,n-1}\) are labeled as follows.

When \(n\ \) is odd, \(f(v_{1,2}\)) \(=f\left(v_{1,n}\right)+2,\)

when \(\ n\ \ \)is even, \(\ f\left(v_{1,4}\right)=f\left(v_{1,n-1}\right)+2\) and \(f\left(v_{1,2j+4}\right)=f\left(v_{1,2j+2}\right)+2,\ j=1,2\dots .\) Now \(\left|{f(v}_{1,2j+3})-f(v_{1,2j+1})\right|\ge 2\) and \(\left|{f(v}_{1,2j+2})-f(v_{1,2j})\right|\ge 2.\) Hence the total number of labeled vertices of MT ( n) is \(3+\left(n-4\right)+\left(n-1\right)=2n-2\). Then the number of unlabeled vertices in \(MT(n)\) is (\(2n+1)-\ \left(2n-3\right)=3.\) From these 3 vertices, consider three pairs in which two pairs are adjacent and one pair at a distance 3. Therefore, the difference between the label of these vertices must satisfy \(\left|{f(v}_{2,j+1}){-f(v}_{2,j})\right|\ge 3,j=1,2.\ \) and \(\left|f(v_{2,4})-f(v_{1,2})\right|\ge 1\).

The antipodal number is \(an\left(MT\left(n\right)\right)\ge 3+\left(n-4\right)\left(0\right)+\left(n-1\right)\left(2\right)+2\left(3\right)+1\left(1\right)\) Hence,\(\ \ an\left(MT\left(n\right)\right)\ge 2n+8\).

Theorem 4. For \(n\ \ge \ 6\), the antipodal number of Mongolian tent is \(an\left(MT\left(n\right)\right)\le 2n+6\ \mathrm{for\ }n\equiv 2\ \left(mod\ 4\right)\) and \[an\left(MT\left(n\right)\right)\le 2n+8\ \mathrm{ for}\ n\equiv 3\ \left(mod\ 4\right),\ \ n\ \equiv 0\left(mod\ 4\right)\ \mathrm{ \& }\ \ n\ \equiv 1\ (mod4).\]

Proof. Let \(\ V(MT(n))\ =\ \{v_{i,j}\ 1\le \ i\ \le \ 2,\ 1\le \ j\ \le \ n\}\cup \{z\}\) and \[E(MT(n))=\ \{v_{i,j}v_{i,j+1},v_{i,j}uv_{i+1,j}:i=1\mathrm{and}\ 2;\ 1\le j\le n-1\}\cup \{zv_{i,j}:\] \(i=1\),\(1\le j\le n\}\) be the vertex and edge set of the Mongolian tent graph.

The antipodal labeling \(f:V(MT(n))\to \{0,1,2,3\dots .\}\) should satisfy the condition \[d(u,v)+|f(u)-f(v)|\ge diam(G).\] The vertices of \(MT\left(n\right)\), \(n\ge 6\) are labeled as follows;

Take \(f\left(z\right)=\ 1;\ f\left(v_{1,1}\right)=4;\ f(v_{2,1})=7.\)

The vertices of the bottom row, except \(v_{21}\) is labeled using the following relation \[f\left(v_{2,j}\right)=f\left(v_{2,j-1}\right)+{\left(-1\right)}^jd+{\left(-1\right)}^j.2\ (\ j\ mod\left(2\right))\ \mathrm{for}\ 2\le j\le 5\] and \[f\left(v_{2,j}\right)=f\left(v_{2,j-4}\right)\ \ \mathrm{for}\ j\ge 6.\]

The vertices in the top row are labeled based on whether n is even or odd.

Case(i): Suppose \(n\) is even\(\ \ j=2r\ ;\ r=1,2\dots ,\left\lfloor \frac{n}{2}-1\right\rfloor \). We divide this case into two sub cases.

Case(a). When \(n\equiv 2\left(mod4\right)\)

\begin{align*} &f\left(v_{1,n}\right)=2d\&if\ r=1,\ \ f\left(v_{1,2r}\right)=f\left(v_{1,n}\right)+n;\ \ f\left(v_{1,2r+1}\right)=f\left(v_{1,n}\right)+2n-2\&if\ r>1,\ \ f\left(v_{1,2r}\right)=f\left(v_{1,2r-2}\right)-2;\ f\left(v_{1,2r+1}\right)=f\left(v_{1,2r-1}\right)-2\\ \end{align*}

Case(b). When \(\ n\ \equiv \ 0(mod\ 4)\)

\begin{align*} &f\left(v_{1,n}\right)=3d \ if\ r=1,\&f(v_{1,2r})=f(v_{1,n})+n-2;f(v_{1,2r+1})=f(v_{1,n})+2(n-2) \ if\ r>1,\&f\left(v_{1,2r}\right)=f\left(v_{1,2r-2}\right)-2;\ f\left(v_{1,2r+1}\right)=f\left(v_{1,2r-1}\right)-2 \end{align*}

Case(ii): Suppose \(n\) is odd \[j=2r,\ \ r=1,2….,\left\lfloor \frac{n-2}{2}\right\rfloor \]

We divide this case into two sub-cases.

Case(a). When \(n\equiv 3\left(mod4\right)\)

\begin{align*} &f\left(v_{1,n}\right)=2d\&if\ r=1,\ \ f\left(v_{1,2r}\right)=f\left(v_{1,n}\right)+6;\ f(v_{1,2r+1})=f(v_{1,n-1})+2 \ if\ r>1,\&f\left(v_{1,2r}\right)=f\left(v_{1,2r-2}\right)+2;\ f\left(v_{1,2r+1}\right)=f\left(v_{1,2r-1}\right)+2\&if r=\left\lceil \frac{n-2}{2}\right\rceil ,\ f\left(v_{1,2r}\right)=f\left(v_{1,2r-2}\right)+2 \end{align*}

Case(b). When \(n\ \equiv \ 1\left(mod\ 4\right)\)

\begin{align*} & f\left(v_{1,n}\right)=3d\& if\ r=1,\ \ f\left(v_{1,2r}\right)=f\left(v_{1,n}\right)+2;\ f(v_{1,2r+1})=f(v_{1,n-1})+2\& if\ r>1, f\left(v_{1,2r}\right)=f\left(v_{1,2r-2}\right)+2;\ f(v_{1,2r+1})=f(v_{1,2r-1})+2\& if r=\left\lceil \frac{n-2}{2}\right\rceil ,\ f\left(v_{1,2r}\right)=f\left(v_{1,2r-2}\right)+2 \end{align*} Hence, the antipodal labeling of \(MT(n)\) is obtained. Thus span of an antipodal labeling \(\mathrm{f}\mathrm{\ }\)is max \(\{|\mathrm{f}\left(\mathrm{u}\right)-\mathrm{\ }\mathrm{f}\ (\mathrm{v})|:\mathrm{u},\ \mathrm{v}\ \in \ \mathrm{V(G)}\}.\) The antipodal number of \(MT(n)\) for different values of n is \(an\left(MT\left(n\right)\right)\le 2n+6\ \mathrm{for\ }n\equiv 2\ \left(mod\ 4\right)\) and \[an\left(MT\left(n\right)\right)\le 2n+8\mathrm{\ for}\ n\equiv 3\ \left(mod\ 4\right),\ \ n\ \equiv 0\left(mod\ 4\right)\ \mathrm{\&}\ \ n\ \equiv 1\ (mod4)\]

Remark 3. By Theorem 4, \(an(MT(n)\)) \(\mathrm{\le}\) \(2n+8,n\ge 6\).

Theorem 5. The antipodal number of Mongolian tent is \(\ 2n+8,\ n\ge 6\ \).

Proof. For \(n\ \ge 6\ \), from Theorem 3, \(an(MT(n))\ge 2n+8\) and by Remark 3 \(an(MT(n)\)) \(\mathrm{\le}\) \(2n+8\). Hence, \(an(MT(n))\ =\ 2n+8\).

3. Antipodal number for Torus graph

In this section, we found an antipodal number of \(T(3\times 3)\) and establish the upper bound of \(T\left(n\times n\right),n>3\).

Theorem 6. The antipodal number of \(T(3\times 3)\) is 4.

Proof.

The graph \(T(3\times 3)\) has nine vertices and 18 edges. Its diameter is 2. By antipodal condition we label all the vertices \(v_{i,j}\),\(i.j=1,2,3\)

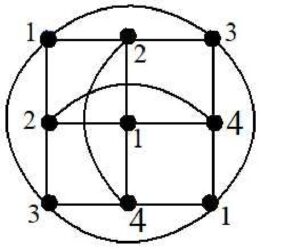
Let \(f\left(v_{1,1}\right)=1.\) Vertices \(v_{1,2},v_{1,3},v_{2,1}\) and \(v_{3,1}\) are adjacent to \(v_{1,1}\). So label them as follows.

\[{f(v}_{1,2})=f{(v}_{2,1})=2\] \[f\left(v_{1,3}\right)=f\left(v_{3,1}\right)=3\] Now \(v_{2,2},v_{2,3},v_{3,2},\mathrm{and}\ v_{3,3}\) are diametrically opposite to \(v_{1,1}\). So by antipodal condition, either vertices \(v_{2,2}\) and \(v_{3,3}\) or \(v_{2,3}\) and \(v_{3,2}\) can be labeled as 1. Suppose \({f(v}_{2,2})=f{(v}_{3,3})=1\). Then \({f(v}_{2,3})=f{(v}_{3,2})=4\). Hence \[an(T(3\times 3))\ge 4.\] The antipodal number of \(T(3\times 3)\) is given in Figure 5. This implies \(an(T(3\times 3))\ \le 4.\ \) Hence \(\ an\left(T\left(3\times 3\right)\right)=4\)

Theorem 7. For \(n\ \ge \ 3\), the antipodal number of torus graph \(T(n\times n\)) is \[an(T(n\times n))\ \ \le \ \left[n^2\ +(d-3)\ n^2/ 2\ \ +(d/n)\ \right]\;\;\; \textrm{if n is even.}\] \[an\left(T\left(n\times n\right)\right)\le \ \left[n^2\ \ +\frac{d^2}{2}\left(d-2\right)-(n+d-1)\right] \;\;\; if\;n\; is\; odd.\]

Proof. Let the vertex set V and the edge set E of \(T(n\times n\)) be defined as follows: \(V\ =\{v_{i,j}\ /\ 1\le \ i,j\le \ n\}\) and \(E\ =\) \(\mathrm{\{}\) \(v_{i,j}v_{i+1,j},v_{i,j}v_{i,j+1};1\le \ i,j\le \ n-1\}\cup \{v_{i,1}v_{i,n},v_{1,j}v_{n,j}\ \mathrm{;}1\le i,j\le n\) \(\mathrm{\}}\).

The function of antipodal labeling of the torus grid graph is defined by the mapping \[f\ :\ V\left(T\left(n\times n\right)\right)\rightarrow \{0,1,2\dots .\}\]

The vertices of the torus grid graph \(T(n\times n\)) are labeled using the relation \[\ f{(v}_{i,j})=\lfloor{(n}/{2)}-1\rfloor\ d\left(i\ -1\right)+\ i\ +\ \left(d\ -1\right)\left(j\ -1\right),\ i\ ,j=1,2\dots n.\] Hence, the antipodal number of \(T(n\times n)\) is obtained as follows:

\[an(T(n\times n))\ \ \le \ \left[n^2\ +(d-3)\ n^2/2\ \ +(d/n)\ \right]\;\;\; \textrm{if n is even.}\] \[an\left(T\left(n\times n\right)\right)\le \ \left[n^2\ \ +\frac{d^2}{2}\left(d-2\right)-(n+d-1)\right] \;\;\; if\;n\; is\; odd.\]

4. Conclusion

The usage of wireless networks in daily life has increased significantly since the last decade, and without wireless mobile devices, the existence of life itself is unimaginable. Communication in wireless networks without interference can be done by suitably assigning different channels to all the transmitters in that network. The assignment of channels to transmitters is said to be a channel assignment problem, and this can be done by studying radio labeling and radio antipodal labeling. The radio number and radio antipodal number were investigated for many graphs. In this paper, we have determined the radio antipodal number of Mongolian tent and provided the upper bound for the Torus grid graph. The problem of finding an antipodal number for many networks is still open.

Acknowledgments : The authors wish to thank the referees for the valuable comments and suggestions which led to an improved version of the paper. Also, the authors would like to thank the management of SSN College of Engineering for their continuous support and encouragement.

Conflicts of Interest:

The authors declare no conflict of interest.