A dominating broadcast of a graph \(G\) is a function \(f : V(G) \rightarrow \lbrace 0, 1, 2, \dots ,\text{diam}(G)\rbrace\) such that \(f(v) \leqslant e(v)\) for all \(v \in V(G)\), where \(e(v)\) is the eccentricity of \(v\), and for every vertex \(u \in V(G)\), there exists a vertex \(v\) with \(f(v) > 0\) and \(\text{d}(u,v) \leqslant f(v)\). The cost of \(f\) is \(\sum_{v \in V(G)} f(v)\). The minimum of costs over all the dominating broadcasts of \(G\) is called the broadcast domination number \(\gamma_{b}(G)\) of \(G\). A graph $G$ is said to be radial if \(\gamma_{b}(G)=\text{rad}(G)\). In this article, we give tight upper and lower bounds for the broadcast domination number of the line graph \(L(G)\) of \(G\), in terms of \(\gamma_{b}(G)\), and improve the upper bound of the same for the line graphs of trees. We present a necessary and sufficient condition for radial line graphs of central trees, and exhibit constructions of infinitely many central trees \(T\) for which \(L(T)\) is radial. We give a characterization for radial line graphs of trees, and show that the line graphs of the \(i\)-subdivision graph of \(K_{1,n}\) and a subclass of caterpillars are radial. Also, we show that \(\gamma_{b}(L(C))=\gamma(L(C))\) for any caterpillar \(C\).
Broadcast domination is a variety of distance related domination parameter. For a radio station, the range and the cost of a broadcasting tower depends on the capacity of the tower. Tactical installation of broadcasting towers of varying capacities at different locations of a region so that the whole region can hear the broadcast from the radio station is one of the real-life instances of the application of the broadcast domination.
Formally, a broadcast of a graph \(G\) is a function \(f : V(G) \rightarrow \{0, 1, 2, \dots, \text{diam}(G)\}\) such that \(f(v)\) is at most the eccentricity of \(v\) for all \(v \in V(G)\). The cost of \(f\) is \(\sum_{v \in V(G)} f(v)\) and is denoted by \(\sigma(f)\). A vertex \(v\) is a broadcasting vertex if \(f(v) \geqslant 1\), and the set of all broadcasting vertices is denoted by \(V_{f}^{+}(G)\) or simply \(V_{f}^{+}\). A vertex \(u \in V(G)\) is said to be \(f\)-dominated by a broadcasting vertex \(v\) if \(d(u,v) \leqslant f(v)\). It is clear that a broadcasting vertex is \(f\)-dominated by itself. A vertex \(u \in V(G)\) is said to be over-\(f\)-dominated or overdominated (when the broadcast is clear from the context) by a broadcasting vertex \(v\) if \(d(u,v)< f(v)\). A vertex \(u\) is said to be a boundary vertex of a broadcasting vertex \(v\) if \(d(u,v)= f(v)\), and the set of all boundary vertices of a broadcasting vertex \(v\) is denoted by \(B_{f}(v)\). For each vertex \(v \in V_{f}^{+}\), the closed f-neighborhood \(N_{f}[v]\) of \(v\) is the set \(\lbrace u \in V(G) : d(u,v) \leqslant f(v) \rbrace\). A broadcast \(f\) is a dominating broadcast if \(\bigcup_{v \in V_{f}^{+}} N_{f}[v] = V(G)\), and the minimum of costs over all the dominating broadcasts of \(G\) is called the broadcast domination number \(\gamma_{b}(G)\) of \(G\). A dominating broadcast \(f\) of \(G\) is said to be an optimal dominating broadcast if \(\sigma(f) = \gamma_{b}(G)\). A dominating broadcast \(f\) of \(G\) is said to be an efficient dominating broadcast if every vertex of \(G\) is \(f\)-dominated by exactly one broadcasting vertex. From now onwards, we use \(DB\) and \(ODB\) in place of dominating broadcast and optimal dominating broadcast, respectively. In a graph \(G\), a set \(S \subseteq V(G)\) is said to be a dominating set if every vertex in \(G\) is either belongs to \(S\) or adjacent to some vertex of \(S\). The domination number \(\gamma(G)\) is the minimum size of a dominating set in \(G\).
The concept of the line graph of a graph was first introduced by [1] but the formal studies on the line graph itself was by [1]. Two edges in a simple graph are said to be adjacent if they are incident on a common vertex. For a given simple graph \(G\) with at least one edge, the line graph \(L(G)\) is defined as the graph such that \(V(L(G))=E(G)\) and two vertices of \(L(G)\) are adjacent if the corresponding edges are adjacent in \(G\).
In this paper, every graph, unless mentioned, is simple and connected. For any two vertices \(u\) and \(v\) in a graph, \(u \sim v\) is written for “\(u\) and \(v\) are adjacent”. An edge with end vertices \(u\) and \(v\) is denoted as \(uv\). If \(H\) is a subgraph of a connected graph \(G\), then for any vertex \(u \in V(G)\), \(d_{G}(u,H)\) or simply \(d(u,H)\) is \(\min \left\{d_{G}(u,x) : x \in V(H)\right\}\). A caterpillar \(C\) is a tree of order at least \(3\) such that deletion of all the leaves yield a path called the spine. A vertex of spine is called stem if it is adjacent to a pendant vertex and a vertex of spine is called trunk if it is not adjacent to any pendant vertex. It is clear that the first and last vertices of the spine are necessarily stem vertices. In a graph \(G\), the \(i^{th}\)-subdivision of an edge \(uv\) is an operation of deleting the edge \(uv\), introducing an \(x,y\)-path of order \(i\), and making \(u\) and \(v\) adjacent to \(x\) and \(y\), respectively. For any graph \(G\), the \(i\)-subdivision graph of \(G\), denoted by \(S_{i}(G)\), is the graph obtained from \(G\) by considering \(i^{th}\)-subdivision for every edge of \(G\).
The concept of broadcast domination was first presented by [3]. For a graph \(G\), [3] gave bounds for \(\gamma_{b}(G)\) in terms of the diameter, the radius and the domination number of \(G\).

Theorem 1. [3] For a non-trivial connected graph \(G\), \(\left\lceil \frac{diam(G) + 1}{3} \right\rceil \leqslant \gamma_{b}(G) \leqslant \min \lbrace \gamma(G), rad(G) \rbrace\).
In the light of the upper bound given in Theorem 1, [4] proposed the following classification of graphs and related studies can be found in [3,6,78]. A graph \(G\) is
Type I or \(1\)-cap graph if \(\gamma_{b}(G)=\gamma(G)\).
Type II or radial graph if \(\gamma_{b}(G)=\text{rad}(G)\).
Type III if \(\gamma_{b}(G) < \min \lbrace \gamma(G), \text{rad}(G) \rbrace\).
[4] proved that every graph has an efficient \(ODB\). [6] characterized radial trees. If \(P\) is a diametrical path of a tree \(T\), then a set \(M\) of edges of \(P\) is said to be a split-P-set if end vertices of every edge of \(M\) have degree two and for every component \(T^{\prime}\) of \(T-M\), the path \(P \cap T^{\prime}\) is a diametrical path of \(T^{\prime}\) with even positive length. A tree is said to have a split-set if it has a split-\(P\)-set for some diametrical path \(P\). In Figure 1, the set \(\{x_{1}y_{1}, x_{2}y_{2}\}\) is a split-set of \(T\) corresponding to the diametrical path induced by the black colored vertices.

Theorem 2. [6] A tree is radial if and only if it has no non-empty split-set.
Let \(G\) be any graph of order \(n\) and \(H_{1},H_{2},H_{3}, \dots, H_{n}\) be any graphs. Then, the generalized corona \(G \circ (H_{1},H_{2},H_{3}, \dots, H_{n})\) is the graph obtained by making adjacent the \(i^{th}\) vertex of \(G\) with all the vertices of \(H_{i}\).
Theorem 3. [6] For any connected graph \(G\) of order \(n\) and for any graphs \(H_{1},H_{2},H_{3}, \dots, H_{n}\), the graph \(G \circ (H_{1},H_{2},H_{3}, \dots, H_{n})\) is radial.
[9] observed that for any spanning subgraph \(H\) of \(G\), \(\gamma_{b}(G) \leqslant \gamma_{b}(H)\). [1] showed that the broadcast domination number of a graph is the minimum of the broadcast domination numbers of its spanning trees. [6] proved that the broadcast domination number of a graph of order \(n\) is at most \(\left\lceil\frac{n}{3}\right\rceil\). For an efficient \(ODB\) \(f\) of \(G\), [11] defined the domination graph \(G_{f}\), where \(V(G_{f})=V_{f}^{+}\) and \(uv \in E(G_{f})\) if \(N(N_{f}[u]) \cap N_{f}[v] \neq \emptyset\). Further, they proved the result below.
Theorem 4. [11] For any graph \(G\), there exists an efficient optimal dominating broadcast \(f\) such that \(G_{f}\) is either a path or a cycle.
For trees \(T\), the above theorem can be restated as, there exists an efficient \(ODB\) \(f\) such that \(T_{f}\) is a path.
[10] was the first author to characterize line graphs. For a brief survey on line graphs, one may look into [2].
Theorem 5. [10] A graph \(G\) is a line graph of some connected graph if and only if \(G\) has a clique decomposition such that every vertex of \(G\) lies in at most two cliques.
For a graph \(G\), a collection \(\mathcal{K}\) of subgraphs is said to be a Krausz decomposition if it has the following three properties.
Each element of \(\mathcal{K}\) is a complete graph.
Every edge of \(G\) belongs to exactly one element of \(\mathcal{K}\).
Every vertex of \(G\) belongs to exactly two elements of \(\mathcal{K}\).
Considering \(K_{1}\) also as a clique, Theorem 5 can be restated as, a graph \(G\) is a line graph of a connected graph if and only if \(G\) has a Krausz decomposition. For any graph \(G\), the edges incident on each vertex form a clique in \(L(G)\) and the collection of all those cliques is a Krausz decomposition of \(L(G)\). In a Karusz decomposition, we say a clique as a trivial clique if it is \(K_{1}\). The theorem below implies that for any tree \(T\) except \(K_{1,3}\), \(L(T)\) has a unique Krausz decomposition.
Theorem 6. [2] Every connected line graph \(G\), other than the line graphs of \(K_{1,3}, K_{1,3}+e, K_{4}-e\) and \(K_{4}\), has a unique Krausz decomposition.
Our contributions start from Section 2. In Subsection 2.1, we prove that \(\frac{\gamma_{b}(G)}{2} \leqslant \gamma_{b}(L(G)) \leqslant 2\gamma_{b}(G)\) for any connected graph \(G\) and the upper bound is further improved to \(\gamma_{b}(L(T))\) for trees \(T\). As \(\gamma_{b}(L(T))\neq\gamma_{b}(T)\) for any bicentral and radial tree \(T\), for central trees \(T\), we show that \(L(T)\) is radial if and only if \(T\) is radial and \(\gamma_{b}(L(T))=\gamma_{b}(T)\). We give a characterization for radial line graphs of trees in Subsection 2.2, by defining a concept of separating-set for trees. Further, we give the value of \(\gamma_{b}(L(T))\) involving the maximum size of a separating-set in \(T\). We denote the class of central trees \(T\) with \(L(T)\) is radial as \(\mathcal{T}_{R}\) and endow a couple of constructions of infinitely many trees of \(\mathcal{T}_{R}\). We study the broadcast domination in line graphs of caterpillars and \(i\)-subdivision graph of \(K_{1,n}\) in Subsection 2.3. We prove that the line graphs of caterpillars are Type I, and show that a subclasss of caterpillars and \(i\)-subdivision graph of \(K_{1,n}\) belong to \(\mathcal{T}_{R}\).
In this subsection, we present a relation between \(\gamma_{b}(G)\) and \(\gamma_{b}(L(G))\). In the line graph \(L(G)\) of \(G\), we denote the vertex corresponding to the edge \(e\) of \(G\) as \(v_{e}\). Conversely, the edge of \(G\) corresponding to the vertex \(u\) in \(L(G)\) is denoted as \(e_{u}\).
Theorem 7. For any connected graph \(G\), \(\frac{\gamma_{b}(G)}{2} \leqslant \gamma_{b}(L(G)) \leqslant 2\gamma_{b}(G)\).
Proof. Let \(f\) be an efficient \(ODB\) of \(L(G)\) and \(\{u_{1},u_{2},u_{3},\dots, u_{k}\}=V_{f}^{+}(L(G))\). Then, we define a broadcast \(g\) of \(G\) as below. \[g(x) = \begin{cases} f(u_{i})+1 & \text{when $x=x_{i}$, where $e_{u_{i}}=x_{i}y_{i}$, $1 \leqslant i \leqslant k$},\\ 0 & \text{otherwise}. \end{cases}\] It is easy to see that \(g\) is a \(DB\) of \(G\) with cost \(\sigma(f) + |V_{f}^{+}(L(G))|\). Therefore, \(\frac{\gamma_{b}(G)}{2} \leqslant \gamma_{b}(L(G))\).
Let \(f'\) be an efficient \(ODB\) of \(G\) and \(\{v_{1},v_{2},v_{3},\dots, v_{l}\}=V_{f'}^{+}(G)\). Let \(e_{j}\) be an edge incident on \(v_{j}\), \(1 \leqslant j \leqslant l\). Now, we define a \(DB\) \(g'\) of \(L(G)\) as follows. \[g'(x) = \begin{cases} f'(v_{j})+1 & \text{when $x=v_{e_{j}}$, $1 \leqslant j \leqslant l$},\\ 0 & \text{otherwise}. \end{cases}\] Therefore, \(\gamma_{b}(L(G)) \leqslant \sigma(f') + |V_{f'}^{+}|\). Hence, \(\gamma_{b}(L(G)) \leqslant 2\gamma_{b}(G)\).
A bistar graph \(B(m,n)\) is a graph obtained by joining centers of two star graphs \(K_{1,m}\) and \(K_{1,n}\) by an edge. A wheel graph \(W_{n}\) is a graph on \(n+1\) vertices which contains a cycle \(C_{n}\) and all the vertices of \(C_{n}\) are adjacent to a single vertex. It is easy to verify that \(\frac{\gamma_{b}(B(m,n))}{2} = \gamma_{b}(L(B(m,n)))\) and \(\gamma_{b}(L(W_{n})) = 2\gamma_{b}(W_{n})\).
From the proof of Theorem 7, it is evident that, working on an efficient \(ODB\)s with minimum number of broadcasting vertices give better bounds. Since, for any tree, there exists no edge between two boundary vertices of a broadcasting vertex and there exists a unique path between two broadcasting vertices, the upper bound given in Theorem 7 is improved for trees in Theorem 9.
For any shortest path \(u_{1}u_{2}u_{3}\dots u_{k}\) of order \(k\) in a graph \(G\), there exists a shortest \(v_{e_{1}},v_{e_{k-1}}\)-path \(v_{e_{1}}v_{e_{2}}v_{e_{3}}\dots v_{e_{k-1}}\) of order \(k-1\) in \(L(G)\), where \(e_{i}=u_{i}u_{i+1}\), \(i=1,2,3,\dots, k-1\). Conversely, for every shortest \(w_{1},w_{l}\)-path \(w_{1}w_{2}w_{3}\dots w_{l}\) of order \(l\) in \(L(G)\), there exists a shortest \(u_{1},u_{l+1}\)-path \(u_{1}e_{w_{1}}u_{2}e_{w_{2}}u_{3}e_{w_{3}}u_{4}\dots u_{l}e_{w_{l}}u_{l+1}\) of order \(l+1\) in \(G\). Hence, we have the following observation. We say a tree is central (bicentral) if its center is \(K_{1}\) (\(K_{2}\)).
Observation 8. If \(T\) is a central tree, then \(\text{rad}(L(T))=\text{rad}(T)\), and if \(T\) is a bicentral tree, then \(\text{rad}(L(T))=\text{rad}(T)-1\).
Theorem 9. For any tree \(T\), \(\gamma_{b}(L(T)) \leqslant \gamma_{b}(T)\).
Proof. For radial trees, it is easy to observe from Theorem 1 and Observation 8 that \(\gamma_{b}(L(T)) \leqslant \gamma_{b}(T)\). For any non-radial tree \(T\), every \(ODB\) of \(T\) has at least two broadcasting vertices. Let \(f\) be an efficient \(ODB\) of \(T\) such that \(T_{f}\) is a path. Let \(\{v_{1},v_{2},v_{3},\dots, v_{k}\}=V_{f}^{+}(T)\) and \(T_{f} : v_{1}v_{2}v_{3}\cdots v_{k}\). Then, there is a \(v_{1},v_{k}\)-path in \(T\) containing all the broadcasting vertices. Let \(e_{i}\) be the edge incident on \(v_{i}\) and lie on \(v_{i},v_{i+1}\)-subpath of \(v_{1},v_{k}\)-path in \(T\), \(1 \leqslant i \leqslant k-1\). Let \(e_{k}\) be the edge incident on \(v_{k}\) and lie on \(v_{k-1},v_{k}\)-subpath of \(v_{1},v_{k}\)-path in \(T\). Let \(g\) be a \(DB\) of \(L(T)\) defined as follows. \[g(x) = \begin{cases} f(v_{i}) & \text{when $x=v_{e_{i}}$, for $1 \leqslant i\leqslant k$},\\ 0 & \text{otherwise}. \end{cases}\] Therefore, \(\gamma_{b}(L(T)) \leqslant \gamma_{b}(T)\).
It is straightforward from Theorem 9 and Observation 8 that if a tree \(T\) is radial and bicentral, then \(\gamma_{b}(L(T))<\gamma_{b}(T)\). Hence, if a tree \(T\) is radial and bicentral, then \(L(T)\) can be radial or non-radial. Therefore, if a radial tree \(T\) has the property \(\gamma_{b}(T)=\gamma_{b}(L(T))\), then \(T\) must be central. The following result is a direct implication of Theorem 9 and Observation 8.
Corollary 1. For a central tree \(T\), \(L(T)\) is radial if and only if \(T\) is radial and \(\gamma_{b}(T)=\gamma_{b}(L(T))\).
In this subsection, we characterize those line graphs of trees that are radial. Further, we construct infinitely many radial line graphs of central trees. Before advancing, we give some results that we use in the subsequent part of the paper.
Observation 10. In the line graph \(L(T)\) of any tree \(T\), there exists a unique shortest path between every pair of vertices.
Proof. Since every shortest path in \(L(T)\) implies a path in \(T\), we have the proof.
Lemma 1. For any tree \(T\), the line graph \(L(T)\) has an efficient optimal dominating broadcast \(f\) such that \((L(T))_{f}\) is a path.
Proof. Let \(g\) be an efficient \(ODB\) of \(L(T)\) such that \((L(T))_{g}\) is a cycle. Let \((L(T))_{g}\) be \(v_{1}v_{2}v_{3}\dots v_{n}v_{1}\), where \(\{v_{1},v_{2},v_{3}, \dots, v_{n}\}=V_{g}^{+}(L(T))\). Now, the shortest \(v_{i},v_{i+1}\)-paths for \(1 \leqslant i \leqslant n-1\), and the shortest \(v_{n},v_{1}\)-path together form a cycle \(C^{*}\) in \(L(T)\). Then, the end vertices of the edges in \(T\) corresponding to the vertices of \(C^{*}\) form a cycle in \(T\), which is a contradiction. Therefore, \(L(T)\) has no efficient \(ODB\) \(g\) such that \((L(T))_{g}\) is a cycle. By Theorem 4, \(L(T)\) has an efficient \(ODB\) \(f\) such that \((L(T))_{f}\) is a path.
Theorem 11. The line graph \(L(T)\) of a tree \(T\) has an efficient optimal dominating broadcast \(f\) such that the broadcasting vertices lie on a diametrical path of \(L(T)\). Moreover, the end vertices of the diametrical path are not over-\(f\)-dominated if one of the following conditions hold.
\(T\) is bicentral.
\(T\) is central and \(L(T)\) is non-radial.
Proof. We divide our proof into two cases. For any two
vertices \(u\) and \(v\), we denote a shortest \(u,v\)-path as \(u
– v\). A broadcast \(f\) of a
graph \(G\) is a radial
broadcast if \(f(v) =
\text{rad}(G)\) for some central vertex \(v\), and \(f(u)=0\) if \(u
\neq v\).
Case 1: \(L(T)\)
is radial
As \(L(T)\) is radial, the radial
broadcast \(f\) of \(L(T)\) is an efficient \(ODB\) of \(L(T)\) with the broadcasting vertex lying
on a diametrical path in \(L(T)\). One
can note that for any diametrical path in \(T\), there is a diametrical path of length
\(\text{diam}(T)-1\) in \(L(T)\), and vice versa. If \(T\) is bicentral, then there is a unique
central vertex in \(L(T)\) and \(\text{diam}(L(T))\) is even, and hence, the
end vertices of the diametrical path are not over-\(f\)-dominated.
Case 2: \(L(T)\)
is non-radial
Every \(ODB\) of \(L(T)\) has at least two broadcasting
vertices. By Lemma 1, let \(g\)
be an efficient \(ODB\) of \(L(T)\) such that \((L(T))_{g}\) is a path. Let \((L(T))_{g}\) be \(v_{1}'v_{2}'v_{3}'\dots
v_{n}'\), where \(\{v_{1}',v_{2}',v_{3}', \dots,
v_{n}'\}=V_{g}^{+}(L(T))\). Let \(x_{1}\) and \(x_{2}\) be boundary vertices of \(v_{1}'\) and \(v_{n}'\), respectively, and \(x_{j}\) and \(x_{j}'\) be two distinct boundary
vertices of \(v_{j}\) for \(j=2,3,4, \dots, n-1\) such that \(x_{1} \sim x_{2}\) and \(x_{j}' \sim x_{j+1}\), \(j=2,3,4, \dots, n-1\). Let \(Q\) be the shortest \(v_{1}',v_{n}'\)-path in \(L(T)\) described as below (see Figure 2). The
dashed circle around \(v_{j}'\) in
Figure 2 is \(N_{g}[v_{j}']\). \[v_{1}'-x_{1}x_{2}-v_{2}'-x_{2}'x_{3}-v_{3}'-x_{3}'x_{4}-
\dots
-x_{n-2}'x_{n-1}-v_{n-1}'-x_{n-1}'x_{n}-v_{n}'\]
Let \(X_{1}\) (\(X_{2}\)) be the set of farthest vertices from \(v_{1}'\) (\(v_{n}'\)) in \(N_{g}[v_{1}']\) (\(N_{g}[v_{n}']\)). If there exists a vertex \(u_{1}' \in X_{1}\) (\(u_{2}' \in X_{2}\)) such that \(d(u_{1}',v_{n}')=d(u_{1}',v_{1}')+d(v_{1}',v_{n}')\) (\(d(u_{2}',v_{1}')=d(u_{2}',v_{n}')+d(v_{n}',v_{1}')\)), then the path \(u_{1}'-Q -u_{2}'\) is the diametrical path of \(L(T)\) which contains all the broadcasting vertices of \(g\). If for every vertex \(x \in X_{1}\), \(d(x,v_{n}')< d(x,v_{1}')+d(v_{1}',v_{n}')\) but the vertex \(u_{2}'\) exists in \(X_{2}\), then let \(u_{1}''\) be a vertex in \(X_{1}\) such that \(u_{1}''-v_{1}'\) does not intersect \(Q\). Then, the broadcast \(g'\) defined as \(g'(w_{1})=g(v_{1}'),~ g'(v_{1}')=0\) and \(g'(x)=g(x)\) for all \(x \in V(L(T)) \setminus \{w_{1},v_{1}'\}\), where \(w_{1}\) is the neighbor of \(v_{1}'\) in \(v_{1}'-u_{1}''\), is an efficient \(ODB\) of \(L(T)\). If \(w_{1}'\) is the neighbor of \(v_{1}'\) in \(Q\), then the path \(u_{1}''-w_{1}w_{1}' -v_{n}'-u_{2}'\) is the diametrical path of \(L(T)\) which contains all the broadcasting vertices of \(g'\). If for every vertex \(y \in X_{2}\), \(d(y,v_{1}')< d(y,v_{n}')+d(v_{n}',v_{1}')\) but the vertex \(u_{1}'\) exists in \(X_{1}\), then, for a vertex \(u_{2}'' \in X_{2}\) with \(u_{2}''-v_{n}'\) does not intersect \(Q\), we can define an efficient \(ODB\), similar to \(g'\), whose broadcasting vertices lie on the diametrical path \(u_{1}'-v_{1}'-w_{2}'w_{2}-u_{2}''\), where \(w_{2}\) and \(w_{2}'\) are the neighbors of \(v_{n}'\) in \(v_{n}'-u_{2}''\) and \(Q\), respectively. If for every vertex \(x \in X_{1}\) and \(y \in X_{2}\), \(d(x,v_{n}')< d(x,v_{1}')+d(v_{1}',v_{n}')\) and \(d(y,v_{1}')< d(y,v_{n}')+d(v_{n}',v_{1}')\), then we can choose two vertices \(u_{1}''' \in X_{1}\) and \(u_{2}''' \in X_{2}\) such that \(u_{1}'''-v_{1}'\) and \(u_{2}'''-v_{n}'\) do not intersect \(Q\). Then, similar to the above, we can get an efficient \(ODB\) whose broadcasting vertices lie on the diametrical path \(u_{1}'''-w_{1}''w_{1}'-w_{2}'w_{2}''-u_{2}'''\), where \(w_{1}''\) (\(w_{2}''\)) is the neighbor of \(v_{1}'\) (\(v_{n}'\)) in \(v_{1}'-u_{1}'''\) (\(v_{n}'-u_{2}'''\)). As \(g\) is an \(ODB\) of \(L(T)\), it is not possible that for every vertex \(x \in X_{1}\) (\(y \in X_{2}\)), \(d(x,v_{n}')< d(x,v_{1}')+d(v_{1}',v_{n}')\) (\(d(y,v_{1}')< d(y,v_{n}')+d(v_{n}',v_{1}')\)) and \(x-v_{1}'\) (\(y-v_{n}'\)) intersects \(Q\); else we can define a \(DB\) \(g''\) of \(L(T)\) as \(g''(w_{1}')=g(v_{1}')-1, ~g''(w_{2}')=g(v_{n}')-1,~ g''(v_{1}')=0,~g''(v_{n}')=0\) and \(g''(x)=g(x)\) for all \(x \in V(L(T)) \setminus \{v_{1}',v_{n}',w_{1}',w_{2}'\}\) such that \(\sigma(g'') < \sigma(g)=\gamma_{b}(L(T))\), which is not possible.
For the ease of analysis in the latter part of the proof, we rename the efficient \(ODB\) whose broadcasting vertices lie on a diametrical path, as \(f\); the broadcasting vertices as \(v_{1},v_{2},v_{3}, \dots, v_{n}\) with \((L(T))_{f}: v_{1}v_{2}v_{3}\dots v_{n}\); the shortest \(v_{1},v_{n}\)-path in \(L(T)\), as described earlier, as \(P\). Let \(P': u_{1}-P-u_{2}\) be the diametrical path of \(L(T)\). Let \(\tilde{v_{1}}\) and \(\tilde{v_{n}}\) be the neighbors of \(v_{1}\) and \(v_{2}\) in \(P\), respectively.
If both \(u_{1}\) and \(u_{2}\) are not over-\(f\)-dominated, then \(f\) is our desired efficient \(ODB\) and \(P'\) is our desired diametrical path in \(L(T)\). Suppose that at least one of \(u_{1}\) and \(u_{2}\) is over-\(f\)-dominated. If \(u_{1}\) is over-\(f\)-dominated, then \(d(u_{1},v_{1})=f(v_{1})-1\), else we have another \(DB\) \(f'\) defined by \(f'(\tilde{v_{1}})=f(v_{1})-1, ~f'(v_{1})=0\) and \(f'(x)=f(x)\) otherwise, having \(\sigma(f')<\gamma_{b}(L(T))\) which is not possible. Similarly, if \(u_{2}\) is over-\(f\)-dominated, then \(d(u_{2},v_{n})=f(v_{n})-1\).
Suppose \(u_{1}\) is overdominated by \(v_{1}\), and \(u_{2}\) is not overdominated by \(v_{2}\). Then, we perform a couple of modifications on \(f\) to have a new efficient \(ODB\) whose broadcasting vertices lie on \(P'\) and \(u_{1}\) is not overdominated. Let \(f'\) be the \(ODB\) defined as \(f'(\tilde{v_{1}})=f(v_{1}),~ f'(v_{1})=0\) and \(f'(x)=f(x)\) for all \(x \in V(L(T)) \setminus \{v_{1},\tilde{v_{1}}\}\). Then, \(u_{1}\) is not over-\(f'\)-dominated and all the broadcasting vertices lie on \(P'\). Now, \(N_{f'}[\tilde{v_{1}}] \cap N_{f'}[v_{2}] \neq \emptyset\) with \(f'(\tilde{v_{1}})+f'(v_{2})=d(\tilde{v_{1}},v_{2})\). Then, there exists a vertex \(w\) on \(\tilde{v_{1}},v_{2}\)-subpath of \(P\) such that \(d(\tilde{v_{1}},w)=f'(v_{2})\) and \(d(w,v_{2})=f'(\tilde{v_{1}})\). Now, we modify \(f'\) to \(f''\) as \(f''(w)=f'(\tilde{v_{1}})+f'(v_{2}), f''(x)=0\) for \(x=\tilde{v_{1}},v_{2}\), and \(f''(y)=f'(y)\) for all \(y \in V(L(T))\setminus \{w,\tilde{v_{1}},v_{2}\}\). It is easy to verify that \(f''\) is an efficient \(ODB\). If \(u_{2}\) is over-\(f\)-dominated but not \(u_{1}\) or both \(u_{1}\) and \(u_{2}\) are over-\(f\)-dominated, then, in a similar manner, we can get an efficient \(ODB\) \(h\) whose broadcasting vertices lie on a diametrical path, and \(u_{1}\) and \(u_{2}\) are not over-\(h\)-dominated.
Motivated by the concept of a split-set in a tree, we define separating-set, a collection of vertices in a tree, and prove that the radialness of \(L(T)\) depends on the existence of a separating-set in a tree \(T\). Later, we show a relation between a split-set and a separating-set of a tree. For any diametrical path of \(T\), let \(v_{i}\) and \(v_{j}\) be two vertices on that path such that \(\text{deg}(v_{i})\) and \(\text{deg}(v_{j})\) are less than or equal to \(2\), and \(P\) denotes the \(v_{i},v_{j}\)-path in \(T\). We define \(T_{i,j}\) is the subtree of \(T\) induced by \(S= \cup_{v \in V(P)} \{w \in V(T) : d_{T}(w,P)=d_{T}(w,v)\}\).
Definition 1. Let \(T\) be a tree and \(P: v_{1}v_{2}v_{3}\dots v_{n}\) be a diametrical path of it. We say a collection \(F=\{v_{i_{1}},v_{i_{2}},v_{i_{3}},\dots,v_{i_{t}}\}\), \(i_{1} < i_{2} < i_{3} < \dots < i_{t}\), of vertices of \(P\) is a separating-\(P\)-set if
\(\text{deg}(v_{i_{j}})=2\), for \(j=1,2,3,\dots, t\),
\(d(v_{i_{j-1}},v_{i_{j}})\), \(1 \leqslant j \leqslant t+1\), is odd and greater than one, where \(v_{i_{0}}=v_{1}\) and \(v_{i_{t+1}}=v_{n}\), and
\(v_{i_{j-1}},v_{i_{j}}\)-path is a diametrical path of the subtree \(T_{i_{j-1},i_{j}}\), for \(j=1,2,3,\dots, t+1\).
We say a tree has a separating-set if \(T\) has a separating-\(P\)-set for some diametrical path \(P\).
Example 1. In Figure 3, the collection \(\{v_{4},v_{7}\}\) is a separating-set of the tree corresponding to the diametrical path \(v_{1}v_{2}v_{3}v_{4}v_{5}v_{6}v_{7}v_{8}v_{9}v_{10}\).

Theorem 12. For any tree \(T\), \(L(T)\) is radial if and only \(T\) has no separating-set.
Proof. We prove the contrapositive of the statement. Let \(T\) be a tree with a diametrical path \(P:u_{1}e_{1}u_{2}e_{2}u_{3}e_{3}u_{4}\dots u_{n-1}e_{n-1}u_{n}\). Then, the path \(P':v_{e_{1}}v_{e_{2}}v_{e_{3}}\dots v_{e_{n-1}}\) is a diametrical path of \(L(T)\). Suppose \(T\) has a separating-\(P\)-set \(\{u_{i_{1}},u_{i_{2}},u_{i_{3}},\dots,u_{i_{t}}\}\), \(i_{1} < i_{2} < i_{3} < \dots < i_{t}\), and let \(u_{i_{0}}=u_{1}\) and \(u_{i_{t+1}}=u_{n}\). Let \(f\) be a broadcast defined as follows. \[\label{eq1} f(x) = \begin{cases} \dfrac{i_{j}-i_{j-1}-1}{2} & \text{when $x=v_{e_{(i_{j}+i_{j-1}-1)/2}}$ for $1 \leqslant j \leqslant t+1$}, \\ 0 & \text{otherwise}. \end{cases}\] As for each \(j \in \{1,2,3,\dots, t+1\}\), \(u_{i_{(j-1)}},u_{i_{j}}\)-path is a diametrical path of the subtree \(T_{i_{(j-1)},i_{j}}\) of odd length, the corresponding \(v_{e_{i_{(j-1)}}}, v_{e_{(i_{j}-1)}}\)-subpath of \(P'\) is the diametrical path of the subgraph \(L(T_{i_{(j-1)},i_{j}})\) of even length. Moreover, since the broadcast assigns label \(\text{rad}(L(T_{i_{(j-1)},i_{j}}))\) to the middle vertex of the \(v_{e_{i_{(j-1)}}}, v_{e_{(i_{j}-1)}}\)-subpath for each \(j \in \{1,2,3,\dots, t+1\}\), \(f\) is a \(DB\) of \(L(T)\) with \(\sigma(f)=\frac{n-t-2}{2} < \frac{n-2}{2} \leqslant \left\lceil \frac{n-2}{2} \right\rceil = \text{rad}(L(T))\). Therefore, \(L(T)\) is not radial.
Conversely, suppose \(L(T)\) is not a radial graph. By Theorem 11, there exists an efficient \(ODB\) \(g\) of \(L(T)\) such that all the broadcasting vertices lie on a diametrical path, say \(Q\), and none of the end vertices of \(Q\) are over-\(g\)-dominated. If \(Q\) is \(w_{1}w_{2}w_{3}\dots w_{n}\), then the corresponding path \(Q': v_{1}e_{w_{1}}v_{2}e_{w_{2}}v_{3}e_{w_{3}}v_{4}\dots v_{n-1}e_{w_{n-1}}v_{n}e_{w_{n}}v_{n+1}\) is a diametrical path in \(T\). Let the set of broadcasting vertices of \(g\) be \(\{w_{i_{1}},w_{i_{2}},w_{i_{3}}, \dots, w_{i_{m+1}}\}\), \(i_{1} < i_{2} < i_{3} < \dots < i_{m+1}\), and \(w_{1}\) and \(w_{n}\) be the boundary vertices of \(w_{i_{1}}\) and \(w_{i_{m+1}}\), respectively. For every consecutive pair of broadcasting vertices \(w_{i_{j}}\) and \(w_{i_{j+1}}\), there exists a pair of adjacent vertices \(x^{2}_{i_{j}}\) and \(x^{1}_{i_{j+1}}\) such that \(x^{2}_{i_{j}} \in B_{g}(w_{i_{j}})\) and \(x^{1}_{i_{j+1}} \in B_{g}(w_{i_{j+1}})\), where \(1 \leqslant j \leqslant m\). If \(v_{k_{j}}\) is the common end vertex of \(e_{x^{2}_{i_{j}}}\) and \(e_{x^{1}_{i_{(j+1)}}}\) in \(T\) for \(1 \leqslant j \leqslant m\), then we consider the set \(F=\{v_{k_{1}},v_{k_{2}},v_{k_{3}},\dots,v_{k_{m}}\}\). Moreover, \(k_{1} < k_{2} < k_{3} < \dots < k_{m}\).
Now, we prove that the set \(F\) is indeed a separating-\(Q'\)-set of \(T\). It is clear that the degree of each vertex in \(F\) is \(2\). Let \(v_{1}=v_{k_{0}}\) and \(v_{n+1}=v_{k_{m+1}}\). As each broadcasting vertex \(g\)-dominates exactly odd number of vertices of \(Q\) in \(L(T)\), \(d(v_{k_{j-1}},v_{k_{j}})\), \(1 \leqslant j \leqslant m+1\), is odd and greater than one. Moreover, since \(g\) is an efficient \(ODB\) of \(L(T)\) such that none of the end vertices of \(Q\) are over-\(g\)-dominated, \(v_{k_{j-1}},v_{k_{j}}\)-subpath is a diametrical path of the subtree \(T_{k_{j-1},k_{j}}\), for \(j=1,2,3,\dots, m+1\). Therefore, the set \(F\) is a separating-\(Q'\)-set of \(T\).
Remark 1.
It is easy to observe that if \(\text{diam}(T) \leqslant 5\), then the tree \(T\) cannot have a separating-set and hence \(L(T)\) is radial.
If \(P\) is a diametrical path of \(T\) and \(T\) has a split-\(P\)-set \(\{x_{1}y_{1},x_{2}y_{2},x_{3}y_{3}, \dots, x_{t}y_{t}\}\) \((t \geqslant 2)\) of size at least two, then \(T\) has a separating-\(P\)-set \(\{x_{2},x_{3},x_{4}, \dots, x_{t}\}\). [6] have proved that if a central tree is not radial, then the maximum size of a split-set is at least two. So, it is straightforward that if a central tree \(T\) is not radial, then \(L(T)\) is not radial. If the maximum size of a split-set in \(T\) is one, then \(T\) may or may not have a separating-sets.
For any non-radial \(L(T)\) of a tree \(T\) with \(\text{diam}(T)=n-1\), let \(g\) be an efficient \(ODB\) of \(L(T)\) such that all the broadcasting vertices lie on a diametrical path of \(L(T)\) and none of the end vertices are over-\(g\)-dominated, and \(F_{g}\) be the corresponding separating-set of \(T\) obtained in the proof of Theorem 12. Then, \(\gamma_{b}(L(T))=\sigma(g)=\frac{n-|F_{g}|-2}{2}\). If \(F_{g}\) is not of maximum size, then there exists a separating-set of \(T\) of size more than \(|F_{g}|\) and the corresponding \(DB\) defined in Equation \(\eqref{eq1}\) of the proof of Theorem 12, in \(L(T)\), has cost less than \(g\), which is a contradiction. Therefore, we have the following result.
Theorem 13. Let \(T\) be a tree of diameter \(n-1\). Then, \[\gamma_{b}(L(T)) = \begin{cases} \left\lfloor \frac{n-1}{2} \right\rfloor & \text{when $L(T)$ is radial},\\ \frac{n-t-2}{2} & {\begin{aligned}[c] \text{when}~L(T)~ \text{is non-radial and}~ t~ \text{is the maximum size}\\ \text{of a separating-set of}~ T. \end{aligned}} \end{cases}\]
Remark 1. In order to determine \(\gamma_{b}(L(T))\) when \(L(T)\) is non-radial, finding the maximum of the sizes of all the separating-sets of \(T\) is the key task. One of the naive approaches is to find a separating-set of maximum size for every diametrical path and then find the separating-set of maximum cardinality among all such separating-sets. It is to be observed that for a diametrical path \(P: v_{1}v_{2}v_{3}\dots v_{n}\), if the set \(F=\{v_{i_{1}},v_{i_{2}},v_{i_{3}},\dots,v_{i_{t}}\}\), \(i_{1} < i_{2} < i_{3} < \dots < i_{t}\), is a separating-\(P\)-set, then \(i_{2k-1}\) is always even and \(i_{2k}\) is always odd, for \(k=1,2,3,\dots\). One can exploit this property to obtain a separating-set of maximum size for a tree.
Theorem 14. For a central tree \(T\), the following statements are equivalent.
\(T\) is radial and \(\gamma_{b}(L(T))=\gamma_{b}(T)\).
\(L(T)\) is radial.
\(T\) has no separating-set.
\(L(T)\) has no efficient optimal dominating broadcast \(f\) such that all the broadcasting vertices lie on a diametrical path and the end vertices of the diametrical path are not over-\(f\)-dominated.
Proof. The equivalencies of 1, 2 and 3 are straightforward from Corollary 1 and Theorem 12. From Theorem 11, if \(L(T)\) is non-radial, then \(L(T)\) has an efficient \(ODB\) \(f\) such that all the broadcasting vertices lie on a diametrical path and the end vertices of the diametrical path are not over-\(f\)-dominated. Therefore, 4 implies 2. Let \(g\) be an efficient \(ODB\) of \(L(T)\) such that all the broadcasting vertices lie on a diametrical path and the end vertices of the diametrical path are not over-\(g\)-dominated. As \(T\) is central, \(L(T)\) has two adjacent minimum eccentricity vertices on any diametrical path. So, \(|V_{g}^{+}(L(T))| \geqslant 2\). Then, by the second part of the proof of Theorem 12, \(T\) has a separating-set and hence, by Theorem 12, \(L(T)\) is non-radial. Therefore, 2 implies 4.
We denote the class of central trees \(T\) for which \(L(T)\) is radial as \(\mathcal{T}_{R}\). Now, we give some types of constructions of infinitely many trees of \(\mathcal{T}_{R}\).
Theorem 15. For any central tree \(H\) of order \(t\), if \(T=H \circ (\overline{K}_{n_{1}},\overline{K}_{n_{2}},\overline{K}_{n_{3}},\dots,\overline{K}_{n_{t}})\) (\(n_{i}\geqslant 1\) for \(i=1,2,3,\dots, t\)), then \(T \in \mathcal{T}_{R}\).
Proof. As \(H\) is central, \(T\) is also central, and by Observation 8, \(\text{rad}(L(T))=\text{rad}(T)\). As degree of each non-pendant vertex of \(H\) is at least \(3\) in \(T\), \(T\) has no separating-set. So, by Theorem 12, \(L(T)\) is radial. Hence, we have the proof.
Next, we present a construction of a bigger tree of \(\mathcal{T}_{R}\) from a tree of \(\mathcal{T}_{R}\). Let \(T\) be a central tree and \(v\) be its central vertex. A new tree \(T'\) is obtained from \(T\) by merging a leaf of \(K_{1,n}\) (\(n \geqslant 2\)) to a leaf \(u\) of \(T\) such that \(d(u,v) \neq \text{rad}(T)-1\) (Method \(1\)), or by merging the center of \(K_{1,n}\) (\(n \geqslant 2\)) to a leaf \(u\) of \(T\) such that \(d(u,v) \neq \text{rad}(T)\) (Method \(2\)). In Figure 4, examples of Method \(1\) and Method \(2\) are given. The tree \(T'\) is obtained using Method \(1\) from \(T\) by merging vertices marked with \(\star\) in \(T\) and \(K_{1,4}\), and the tree \(T''\) is obtained using Method \(2\) from \(T\) by merging vertices marked with \(\blacktriangle\) in \(T\) and \(K_{1,4}\).
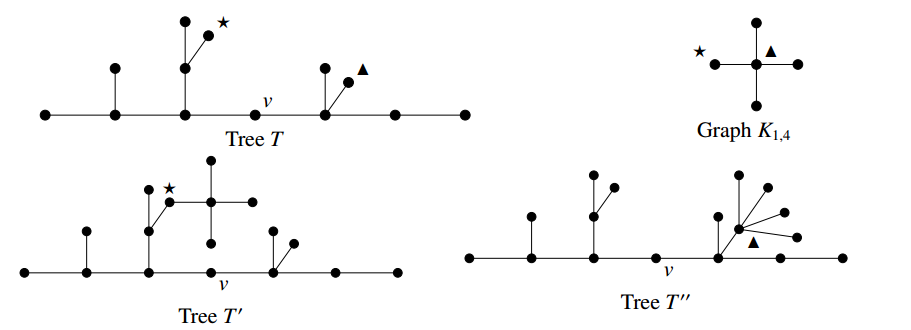
Theorem 16. If \(T'\) is a tree obtained from a tree \(T \in \mathcal{T}_{R}\) by Method \(1\) or Method \(2\) of construction, then \(T' \in \mathcal{T}_{R}\).
Proof. The constructed tree \(T'\) is always a central tree, and its
radius, with respect to \(T\), depends
on the position of merging of a vertex of \(K_{1,n}\). Further, as the tree \(T\) is a subtree of the tree \(T'\), \(L(T)\) is a subgraph of \(L(T')\). Let \(v\) be the central vertex of \(T\) and \(u\) be the leaf of \(T\) where the merging of a vertex of \(K_{1,n}\) has happened. We use the
equivalencies of Theorem 14 to prove our claim.
Case 1: \(\text{rad}(T')=\text{rad}(T)\)
Let \(f\) be an efficient \(ODB\) of \(L(T')\). Then, the broadcast \(g\) of \(L(T)\) defined as
\[g(x) =
\begin{cases}
f(v) & { \text{if for some $v \in V_{f}^{+}(L(T'))$,
$d_{L(T')}(v,x) = d_{L(T')}(v,L(T))$}},\\
0 & { \text{otherwise}.}
\end{cases}\] is a \(DB\) of cost \(\gamma_{b}(L(T'))\). So, \(\gamma_{b}(L(T)) \leqslant
\gamma_{b}(L(T'))\). As \(\text{rad}(L(T')) \geqslant
\gamma_{b}(L(T')) \geqslant \gamma_{b}(L(T)) = \text{rad}(L(T))
=\text{rad}(T)=\text{rad}(T')=\text{rad}(L(T'))\), \(L(T')\) is radial. Therefore, \(T' \in \mathcal{T}_{R}\).
Case 2: \(\text{rad}(T')=\text{rad}(T)+1\)
Let \(f\) be an efficient \(ODB\) of \(L(T')\) such that every broadcasting
vertex lie on a diametrical path of \(L(T')\). Then, there exists a
broadcasting vertex \(v\) which \(f\)-dominates the vertices of \(L(K_{1,n})\). Let \(w\) be the neighbor of \(v\) on the diametrical path, such that
\(d_{L(T')}(w,L(K_{1,n}))
=d_{L(T')}(v,L(K_{1,n}))+1\). Then, we define a \(DB\) \(g\)
of \(L(T)\) such that \(g(w)=f(v)-1\), \(g(v)=0\) (if \(v
\in V(L(T))\)) and \(g(x)=f(x)\)
for other vertices of \(L(T)\). Hence,
\(\gamma_{b}(L(T))+1 \leqslant
\gamma_{b}(L(T'))\). As, \(\text{rad}(L(T')) \geqslant
\gamma_{b}(L(T')) \geqslant \gamma_{b}(L(T))+1 = \text{rad}(L(T))+1
=\text{rad}(T)+1=\text{rad}(T')=\text{rad}(L(T'))\),
\(L(T')\) is radial. Therefore,
\(T' \in \mathcal{T}_{R}\).
In this subsection, we explore the line graphs of two classes of graphs, namely, caterpillar graph and \(i\)-subdivision graph of star graph. First, we show that the line graph of caterpillar is Type I.
Theorem 17. For any caterpillar \(C\) of order at least \(3\), \(\gamma_{b}(L(C))=\gamma(L(C))\).
Proof. Let \(f\) be an efficient \(ODB\) of \(L(C)\). A broadcasting vertex \(v\) \(f\)-dominates all the vertices of at most \(2f(v)\) cliques. Then, it can be observed from Figure 5 that those vertices can be dominated by at most \(f(v)\) vertices of \(S_{v}=\{u_{1},u_{2},\dots u_{(f(v)-1)},u_{f(v)}\}\). The dashed circles in Figure 5 represent cliques of \(L(C)\) in its Krausz decomposition. Then, the set \(\bigcup_{v \in V_{f}^{+}(L(C))}S_{v}\) forms a dominating set of \(L(C)\) of size at most \(\gamma_{b}(L(C))\). Hence, \(\gamma(L(C)) \leqslant \gamma_{b}(L(C))\). Therefore, by Theorem 1, we have the proof.

Let the spine of a caterpillar \(C\) be \(v_{1}v_{2}v_{3}\dots v_{n}\). Ignoring all the leaves, except one leaf each attached to \(v_{1}\) and \(v_{n}\), we get a diametrical path of \(C\). Then, if exists, finding a separating-set of maximum size on this diametrical path is enough to find \(\gamma_{b}(L(C))\). Hence, by Theorem 17, we can determine the domination number of \(L(C)\). Now, we give a subclass of caterpillars \(C\) which satisfy the equality \(\gamma_{b}(L(C))=\gamma_{b}(C)\).
Proposition 1. Let \(C\) be a caterpillar with the spine \(v_{1}v_{2}v_{3}\dots v_{n}\), \(n\) is odd. If each \(v_{2i+1}\), \(i=1,2,3,\dots, \frac{n-3}{2}\), is a stem, then \(\gamma_{b}(L(C))=\gamma_{b}(C)\).
Proof. As \(C\) has odd number of spine vertices, \(C\) is central. Moreover, it is not hard, due to the way \(C\) is defined, to observe that it has no separating-set. Hence, by Theorem 12, \(L(C)\) is radial. Therefore, by Theorem 14, \(\gamma_{b}(L(C))=\gamma_{b}(C)\).
Finally, we show that \(L(S_{i}(K_{1,n}))\) is radial.
Theorem 18. For \(n\geqslant3\), \(\gamma_{b}(L(S_{i}(K_{1,n})))=\gamma_{b}(S_{i}(K_{1,n}))\).
Proof. It is easy to observe that \(S_{i}(K_{1,n})\) is central, and let \(v\) be the central vertex. Let \(P\) be a diametrical path of \(S_{i}(K_{1,n})\). As \(S_{i}(K_{1,n})\) has at least three diametrical paths and \(v\) lies on every diametrical path, due to 1 of Definition [def], \(S_{i}(K_{1,n})\) cannot have a separating-set. Hence, by Theorem 12, \(L(S_{i}(K_{1,n}))\) is radial, and by Theorem 14, we have the proof.
We conclude the article with some remarks which require further investigation.
In this article, we gave a characterization of line graphs of trees to be radial, by introducing the concept of separating-set on trees. One may generalize the concept to graphs to deal with the radialness of line graphs.
The next interesting problem is to characterize Type I line graphs of trees.
In this article, for radial trees \(T\), we completely settled the case when \(\gamma_{b}(T)= \gamma_{b}(L(T))\). The same problem is open for non-radial trees.
We show that the line graphs of caterpillars are \(1\)-cap graphs, and in Proposition 1, we present a subclass of caterpillars whose line graphs are radial. So, we propose to determine the complete subclass of caterpillars whose line graphs are both radial and \(1\)-cap.
The authors declare no conflict of interests.
1970-2025 CP (Manitoba, Canada) unless otherwise stated.