The geometrical properties of a plane determine the tilings that can be built on it. Because of the negative curvature of the hyperbolic plane, we may find several types of groups of symmetries in patterns built on such a surface, which implies the existence of an infinitude of possible tiling families. Using generating functions, we count the vertices of a uniform tiling from any fixed vertex. We count vertices for all families of valence \(5\) and for general vertices with valence \(6\), with even-sized faces. We also give some general results about the behavior of the vertices and edges of the tilings under consideration.
Although tilings are present in many constructions of different civilizations, a mathematical study of tilings began in 1619, with the work Harmonices Mundi by Johannes Kepler, where regular and semi-regular tilings of the Euclidean plane are studied.
At the beginning of the 19th century, we see the appearance of new geometries. Lobachevsky and Bolyai, in parallel, developed and published the concepts of hyperbolic geometry. Gauss had already developed the same theory, but he did not publish his results. Riemann made important contributions to elliptic geometry and later unified and generalized the three types of geometry through Riemannian geometry.
Only in 1891, the Russian Fyodorov ([1]) demonstrate that there are only 17 possibilities for the symmetry group of a periodic tiling of the Euclidean plane. With the development of the other geometries, it was proved that there are 14 possibilities for symmetry groups of periodic tilings of the sphere and infinite symmetry groups for periodic tilings of the hyperbolic plane.
Uniform tilings are those formed by regular faces with transitive vertices due to the action of a symmetry group. The size of a regular polygon is its number of edges, and the type of a vertex \(v\) is the sequence of the sizes of all polygons adjacent to \(v\). Consider a uniform tiling with vertex type \(a = [a_1, a_2, \cdots, a_n]\) with \(n \geq 3\), \(n \in \mathbb{N}\). Because of the hyperbolic plane’s properties, regular polygons of sizes \(a_1,\cdots,a_n\) with the same edge size can be build according to \(a\) around a vertex. However, there is not always a group of symmetries able to tessellate the hyperbolic plane to obtain a uniform tiling with the desired vertex type.
The works [2-4] study the classification of uniform tiling. The complete classifications of uniform tiling of valences \(5, 6\) and \(7\) are given in [4], along with some general cases.
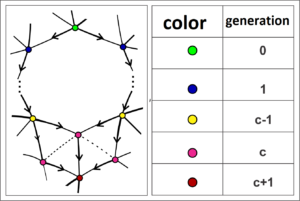
Given a uniform tiling of valence \(k\), we fix any vertex \(v\) and define the generation \(n\) as the set formed by the vertices that are at a distance \(n\) from the vertex \(v\), where the distance between two vertices is measured by the number of edges of the shortest path between these two points. We denote the number of elements of the \(n\) generation by \(v_n\). A way to obtain \(v_n\) is to use combinatorial derivations to get a rational generating function \(V(z) = \sum_{n\geq 0} v_n z^n\) for the sequence \(v_0, v_1,\ldots\).
To our knowledge, the first works using generating functions to study the growth of elements in a tiling were [5,6], where the author studied growth functions for cocompact hyperbolic groups and Coxeter groups. After that, in [7,8] the authors used geometric and combinatorial results to obtain their results. [9] makes some generalizations by demonstrating that the denominator of \(V(z)\) is a reciprocal Salem polynomial. In [10] the author investigated an algorithmical approach to calculating the sequence of \(v_n\).
The non-regular uniform case has been little studied in the literature. We also call attention to the fact that in [11], the authors study growth series for hyperbolic tilings given by polygons with alternating inner angles, which they call “semi-regular tessellations”, but these are not unifom.
In the paper [12], the authors present an innovative and simpler method of counting vertices in regular tilings, using generating functions.
In this work, we extend the method used in [12] for the case of uniform tilings. The generating functions will be derived from the recurrence relations in a standard way, as we can see in [13]. To avoid a lengthy work, we will examine all cases of valence \(5\) and some particular cases of valence \(6\). All other valences can be obtained using the same reasonings.
The work is divided into five sections. In Section 2, we introduce the basic terminology and concepts used in our work and provide the results that guarantee the existence of the tilings under consideration. In Section 3, we give the vertex counting method and also give some general results about the behavior of the vertices and edges of the tessellations under consideration. In Section 4, we count vertices in all cases of uniform tilings of valence \(5\). In Section 5, we count the vertices of uniform tilings of valence 6, where we are considering the cases with even parameters.
In this section basic terminology and concepts are provided, mainly taken from [3] and [4].
A plane is a simply connected Riemann surface \(X\) without boundaries. An isometry of the plane \(X\) is a distance-preserving bijection from \(X\) to \(X\).
A plane tessellation or tiling consists of a countable family \(\mathcal{T} = (A_1, \cdots, A_n, \cdots)\) of connected closed subsets of the plane called tiles, such that the union of sets \(A_i\) is the entire plane and the interiors of two distinct sets \(A_i\) and \(A_j\) are disjoint.
The arcs of the elements \(A_i\) are the edges of the tiling. The vertices in a tiling are the intersection and final points of the arcs. The boundary of a tile is its topological boundary and can be divided into a sequence of edges separated by vertices.
Each edge connects two vertices and separates two tiles. The number of incident edges on a vertex \(v\) is referred to as the vertex’s degree or valence. A tiling face is the topological interior of a tile of \(\mathcal{T}\).
In particular, we will be working with tilings where the tiles are regular polygons, all with the same edge size.
A symmetry of a tiling is an isometry of the plane that leaves the tiling globally invariant. A tiling is considered uniform when its group of symmetries \(S\) is transitive on the set of vertices (i.e., there exists a symmetry \(\gamma\) such that \(\gamma(v_1) = v_2\) for each pair of vertices \(v_1\) and \(v_2\)) and its tiles are regular polygons. If the tiling is uniform and has only one kind of tile, then it is classified as regular. On the other hand, a semi-regular tessellation of the plane is one in which each polygon is regular and the type of vertex is identical for each vertex. From the definition, both regular and semi-regular tessellations are uniform tessellations, and we will use this terminology in our current work.
A tiling \(\mathcal{T}\) is locally finite if all compact sets of the plane intersect a finite number of tiles of the tiling. Every compact subset in this case has a finite number of edges and vertices of \(\mathcal{T}\), and the degree of the vertex is finite. Each tessellation may be represented as follows: \(\mathcal{T} = (V, E, F)\), where \(V,\)E, and \(F\) are the sets of vertices, edges, and faces, respectively. We draw attention to the fact that in our current work, we are only considering locally finite tessellations, which means that each vertex has a finite number of faces.
Two faces are adjacent if their boundaries have an edge or a vertex in common. The size of a face is the number of vertices along its boundary. This paper focuses only on faces of finite size, called finite.
Consider the set of all faces incident to a vertex \(v\), and let \([a_1; \cdots; a_d]\) be a vector containing the faces’ sizes, listed in cyclic order around \(v\). This vector is a type vector or a type of vertex for \(v\).
Given a natural number \(n \geq 3\) and a vector of natural numbers \(a = [a_1; a_2; \cdots; a_n]\), a necessary condition for \(a\) to be a type of tiling vertex is that they satisfy the condition \[\label{cond} \sum_{i =1}^n\frac{(a_i-2)\pi}{a_i}>2\pi .\tag{1}\]
For valences \(3\) and \(4\) we have the following result, (see [3]).
Proposition 1. For degree \(3\), the possible types are \([n;n;n]\), \([n;2m;2m]\) and \([2n; 2m; 2p]\), where the sizes are greater than or equal to \(3\). For degree \(4\), we have four type vectors: \[\{[n;m;n;m], [n; 3m; 3m; 3m], [n; 2m; p;2m], [2n; 2m; 2p; 2q]\} \,,\] where in all cases the parameters satisfy 1.
The following results from [4] guarantee the cases that we will count.
Theorem 1. Given a natural number \(n\geq 3\), there exists a uniform tessellation of the hyperbolic plane with vertex type \[[2a_1;\;2a_2;\;\cdots;\;2a_n],\] where \(a_1,\cdots,a_n\) satisfy the condition (1), and \(2 a_i \geq 3\) for all \(i = 1,\ldots,n\).
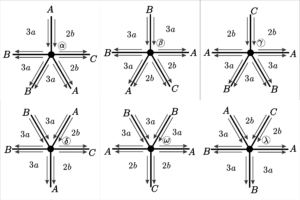
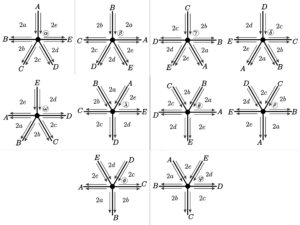
Theorem 2. Let \(a = [a_1;\;a_2;\;a_3;\;a_4;\;a_5]\) be a vector with valence \(5\), satisfying the condition (1). Then, \(a\) is a type of vertex valid for an uniform tessellation of the hyperbolic plane if and only if \(a\) is a particular case of one of the following families:
|
|
|
Since we are working with uniform tilings, it follows that there is only one type of vertex. However, by assigning an order, we obtain vertex subtypes, which are here called vertex positions. We select a vertex position and disregard its reflection (vertex type reverse), since we are only interested in the produced vertices and faces and these two positions generate the same elements.
We include here only the necessary content for the understanding of the work; however, several applications of generating functions can be found in [13]
Each vertex position is denoted by a Greek letter, and then we check the positions that can be generated by each of them. Thus, we obtain recurrence formulas that give the number of vertices at each position in a generation.
Generator functions are powerful tools in discrete mathematics and can be used to facilitate the manipulation of sequences. Instead of working with an infinite sequence, the idea is to use a function that encodes the sequence. Given a sequence \((a_n)\), the function does not return the \(n-\)th term, but rather a power series whose term \(a_n\) of the sequence is the coefficient of the power \(z^n\).
To avoid a lengthy and repetitive work, we will examine all cases of valence 5 given in Theorem 2, as well as the general even case of valence 6. The reasoning used in these cases allows us to analyze any other valence.
We use the method presented in [13] to find the unknown sequence corresponding to a recurring formula. Given a recurrence formula, to find the sequence using the equivalent generating function, we must perform the following steps:
Check the values for which the recurrence formula is valid.
Name the generating function we are looking for and write this function in terms of the unknown sequence (for example, denote the function by \(A(z)\), and set \(A(z) = \sum_{n\geq 0}a_n\)).
Multiply both sides of the recurrence by \(z^n\) and add for which the recurrence holds.
Express both sides of the resulting equation in terms of the generating function \(A(z)\).
Solve the resulting equation for the unknown generating function \(A(z)\).
To obtain an exact formula for the defined sequence, one must expand \(A(z)\) by a power series.
Thus, our objective is to use the described method to obtain the sequence \((v_n)\) of the number of vertices of each generation. The term \(v_n\) corresponds to the coefficient of the power \(z^n\) in the generating function \(V(z) = \sum_{n\geq0}v_nz^n\) expanded by power series.
The counting of the vertices of a uniform tiling begins with the selection of any vertex \(v\). We can predict the behavior of tiling starting from \(v\) because we have a single type of vertex. Using the distance defined by the number of edges on the shortest path connecting two vertices, we denote by \(v_n\) the number of vertices with a distance equal to \(n\) from the vertex \(v\), and we say that these vertices form the generation \(n\).
Let \((v_n)\) be the sequence given by the number of vertices in each generation. We want to count all the vertices of the tiling, ensuring that no vertices are counted twice and that none are left uncounted. We know that \(v_0 = 1\) when we consider the vertex \(v\), and we begin counting the vertices as they move away from \(v\).
Given a vertex \(w\), arrival edges are the edges that connect \(w\) to vertices from the previous generation, departure edges are the edges that connect \(w\) to vertices from the next generation, and fraternal edges are the edges that connect vertices from the same generation.
As an example, we have Figure 1 which shows the face positions for regular tilings of valence \(5\) with odd-sized faces. Note that, as all edges are symmetric, we rely on a single type of edge, implying that we have only one vertex position with one arriving edge, one vertex position with two arriving edges, and one position with a fraternal edge.

To count the vertices of a tiling, first examine its formation from \(v\). The construction of a face is done in two ways, starting from a vertex or a fraternal edge. In fact, we start the tiling from \(v\), with consecutive edges forming faces. Given a face \(f\) incident to \(v\), each edge of \(f\) in \(v\) constructs a path departing from \(v\) (at the same speed) and terminating at the end of the face, either at a vertex or on a fraternal edge. We cannot have consecutive fraternal edges at a vertex, so the following edges of a fraternal edge that ends a face must move away, forming a new face.
Thus, if a face of size \(m\) begins at a vertex in generation \(t\), it will end at a vertex in generation \(t+\frac{m}{2}\) for even \(m\) or on a fraternal edge with final vertices in generation \(t+\frac{m-1}{2}\) for odd \(m\). If the face begins on a fraternal edge with endpoints in generation \(t\) and has size \(m\), it will end on a fraternal edge with endpoints in generation \(t+\left(\frac{m}{2}- 1\right)\) if \(m\) is even, or at a vertex of generation \(t+\frac{m-1}{2}\) if \(m\) is odd.
Note that in a vertex position, faces that have both arrival and departure edges are being constructed, faces with only arrival edges are closed, and faces with only departure edges start at this vertex.
We begin the counting process by considering all possible face formations beginning with \(v\). Through this analysis, we are able to determine all the positions of tiling vertices, including those that have fraternal edges (when they exist), since the tiling vertices are at the beginning, middle, or end of the faces.
We list the faces that start at each vertex position. Furthermore, we consider that all positions generate vertices with only one arrival edge (not containing fraternal edges). Note that this does not always happen, but our procedure has the idea of counting all the vertices that could be created and disregarding the vertices that cease to exist due to the presence of positions containing fraternal edges or closing faces.
Let \(\alpha\) be a vertex position with only one arriving edge (which does not contain a fraternal edge). We denote the number of vertices in position \(\alpha\) in generation \(n\) by \(y_n\) and the number of possible positions \(\alpha\) generated by all positions in generation \(n-1\) by \(\alpha_n\). If the leading edge of \(\alpha\) is one of the leading edges of some closing position, \(\theta\), we have to subtract \(\theta_n\) from \(y_n\). Vertex positions with fraternal edges that have the same arrival edge as \(\alpha\) must also be discounted from the \(y_n\) estimate. So we get \(\alpha_n\) by subtracting all of these possible cases.
If \(\theta\) is a close position of a face denoted by \(P\), by analyzing the face size, we find the generation \(m\) in which the face was started to be closed in the generation \(n\) and then \(\theta_n\) is the sum of the number of faces \(P\) created in the \(m\) generation.
Thus, we obtain a recurrence formula for each position of the vertex, and, using the method of generating functions, we have a generating function for each of them. Our goal is to obtain the function \(V(z) = \sum_{n\geq0}v_nz^n\). We know that \(v_0 = 1\) and that all vertex positions exist beginning with generation \(1\). \(V(z) = 1 + \sum_{n\geq1}v_nz^n\), where \(v_n\) is the sum of all vertex positions in the generation \(n\). Therefore, the desired function will be the sum of \(1\) plus the generating function obtained as the sum of the functions associated with all vertex positions.
The following results will be of great help in ensuring that we are considering all possible vertex positions for each general vertex type.
Lemma 1. Let \(\mathcal{T}\) be a uniform tiling of valence \(n\), with \(n\geq 6\), and \(v\) be any fixed vertex of \(\mathcal{T}\). Considering the construction of tiling from \(v\), no vertex has more than two arrival edges.
Proof. By construction, the arrival edges of all vertices are consecutive and are equivalent to closing faces. Also, as we start from a vertex, the neighboring edges to a fraternal edge must have the same direction, that is, every fraternal edge in a vertex must be between a arriving edge and a leaving edge.
The vertex \(v\) does not have any arriving edges, while each vertex of generation \(1\) has only \(1\) such edge. Suppose, by absurd, that there are vertices with more than \(2\) arrival edges. Let \(m\) be the first generation where we have vertices with more than \(2\) arrival edges and \(w\) one of these vertices from the generation \(m\). We consider \(3\) of the incoming edges of \(w\) and denote by \(f_1\) and \(f_2\) the faces enclosed in such edges. We select, without loss of generality, the face \(f_1\) and check its behavior.
We have two possibilities for \(f_1\): either \(f_1\) starts at a fraternal edge between vertices of generation \(m-1\), or \(f_1\) has a size greater than \(3\) and starts at a generation earlier than \(m-1\). We denote by \(A\) the edge between \(f_1\) and \(f_2\) and by \(p\) the end of \(A\) in the generation \(m-1\). Note that \(p \neq v\). In fact, if \(p = v\), \(w\) is in generation \(1\), but this is an absurd because \(w\) has more than \(2\) arriving edges, and vertices in generation \(1\) have only \(1\) edge of this category. Therefore, \(p\) has some arriving edge.
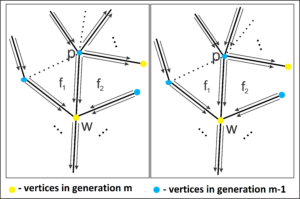
Suppose \(p\) has only one arriving edge. In this way, we have a maximum of \(3\) edges of \(p\) marked: \(A\), the arrival edge of \(p\) and the fraternal edge of \(f_1\) (in case \(f_1\) is a triangle). Since \(n \geq 6\), there are at least \(3\) edges left in \(p\), where we can have at most one fraternal edge and the other edges must be starting. Therefore, the face \(f_2\) starts between two starting edges of \(p\), implying that the construction path of the face \(f_2\) passes through points of the generation \(m\) followed by points of the generation \(m-1\), which it is an absurd. Thus, \(p\) cannot have only one arriving edge.
Now consider that \(p\) has two arriving edges. Thus, these edges are consecutive and one of them is used in the construction of the face \(f_1\) or the face connected to \(f_1\), in case \(f_1\) is a triangle. Thus, we mark at most \(4\) edges: \(A\), \(2\) arrival edges and the sister edge of \(f_1\) (if \(f_1\) is a triangle). Considering that \(n\geq 6\), there are still at least two edges at the vertex \(p\), having at most one fraternal edge (next to an incoming edge) and the other edges of the starting type. We get the same absurdity found in the previous case, implying that \(p\) cannot have only two arriving edges. Therefore, \(p\) has more than \(2\) arriving edges, but this is an absurd, since \(p\) is in the \(m-1\) generation and \(m\) is the first generation with vertices that have more than \(2\) arriving edges.
We conclude that there is no vertex with type \(w\) and, thus, all vertices of tiling have at most two arriving edges. ◻
We emphasize that the presence of triangular faces in a tiling entails the presence of particular vertex positions. An example of this type of vertex position can be seen in the result below.
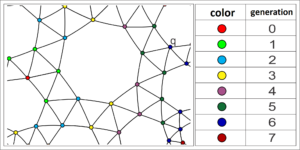
Theorem 3. Let \(\mathcal{T}\) be a uniform tiling of valence \(5\) of the hyperbolic plane. Consider the construction of the tiling from a fixed vertex \(v\) of \(\mathcal{T}\). Then, there exists a vertex with three arrival edges in \(\mathcal{T}\) if and only if the vertex type of \(\mathcal{T}\) is a particular case of the general case \([3;\;3;\;3;\; 3;\;b]\). ]
Proof. Suppose tiling \(\mathcal{T}\) has vertex type \([3;\;3;\;3;\;3;\;b]\). So it falls under the type \([3a;\;3a;\;b;\;3a;\;c]\) and we can use rotational points to create this tiling. If \(b\) is even, then there exists \(c\in \mathbb{N}\) such that \(b = 2c\). A face of size \(b\) that starts at \(v\) ends at a vertex in generation \(c\) and there is a point in generation \(c+1\) with more than two arriving edges.
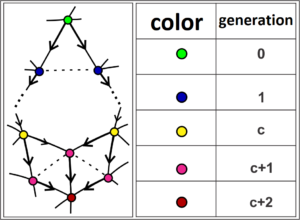
If \(b\) is odd, there is \(c \in \mathbb{N}\) such that \(b = 2c+1\). Thus, taking the first triangle enclosed by a fraternal edge with ends in generation \(1\) and connected to a face of size \(b\), we construct a face that starts at a fraternal edge of vertices contained in generation \(1\) and ends at a vertex in the \(c+1\) generation. We obtain a vertex with more than two arrival edges in the generation \(c+2\). Therefore, if the vector type of \(\mathcal{T}\) is a particular case of the general vertex type \([3;\; 3;\; 3;\; 3;\; b]\), then there is a vertex with more than two arriving edges.
Conversely, suppose that \(w\) is a vertex in the generation \(m\) with \(3\) arrival edges, where \(m\) is the smallest generation that contains vertices with this characteristic. Let \(f_1\) and \(f_2\) be the faces enclosed in \(w\), \(A\) the edge separating \(f_1\) and \(f_2\), and \(p\) the endpoint of \(A\) in the generation \(m-1\). Note that \(f_1\) and \(f_2\) must be triangles. In fact, if \(f_1\) is not a triangle, then, as \(p\) has at most \(2\) arriving edges (since it is in the \(m-1\) generation), we have that at least two edges must be starting or fraternal. Thus, it is not possible to construct the face \(f_2\) so that it ends in \(w\), as we can see in the proof of Lemma 1. It follows, analogously, that \(f_2\) must be a triangle. Thus, to enable the formation, we must have in \(p\) two arrival edges, two fraternal edges, and a departure edge (\(A\)).
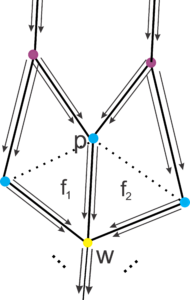
At all extremities of fraternal edges of \(f_1\) and \(f_2\) we have arrival edges. Since \(p\) encloses a face, the arrival edges in \(p\) are used in the construction of this face. Note that we can only have triangles or squares connected to the faces \(f_1\) and \(f_2\), since we can use on each face a starting edge of \(p\) (which forms a triangle), or a fraternal edge of \(p\) (forming a square). If we use a fraternal edge to form a square on the side of \(f_1\), the next edge (clockwise) must be a arriving edge. Since the arriving edges are consecutive, and we are at a vertex in the \(m-2\) generation, the last edge of the vertex can only be a fraternal edge, and thus \(p\) closes a triangle. So the vertex type in \(p\) is \([3;\;3;\;4;\;3;\;b]\), where \(b\) can only be \(4\) or \(3\), which is absurd , as these face measurements do not satisfy the condition (1) for tiling the hyperbolic plane. So, we can only build a triangle next to \(f_1\). Analogously, we conclude that the face attached to \(f_2\) must be a triangle. Thus, we obtain in \(p\) a type of vertex \([3;\;3;\;3;\;3;\;b]\), where \(b>4\). ◻
In Figure 6 we see a hyperbolic uniform tiling of vertex type \([3;\; 3;\; 3;\;3;\; 8]\). Considering the construction of the tiling from the red vertex, we have that the vertex \(q\), in the \(6\) generation, has three arrival edges.
Corollary 1. Let \(\mathcal{T}\) be a uniform tiling of the hyperbolic plane with valence \(5\). Consider the construction of the tiling from a fixed vertex \(v\) of \(\mathcal{T}\). So, there is no vertex with four arrival edges in \(\mathcal{T}\).
Proof. Suppose by absurd that there are vertices with \(4\) arrival edges. Let \(w\) be a vertex of \(\mathcal{T}\) in the generation \(m\) with \(4\) arriving edges. In particular, \(w\) has \(3\) arriving edges and, by the Theorem 3, the vertex type of \(\mathcal{T}\) can be written as \([3;\;3;\;3;\;3; \;b]\). Therefore, the only starting edge will be an edge that forms a triangle, but this is absurd, since, by construction, we cannot form a triangle having two edges in the same direction. Therefore, there is no vertex \(w\) with 4 arriving edges. ◻
Corollary 2. Let \(\mathcal{T}\) be a uniform tiling of the hyperbolic plane of valence \(5\), where all faces have sizes greater than \(3\). Consider the construction of the tiling starting from a vertex \(v\) of fixed \(\mathcal{T}\). Then:
No vertex of \(\mathcal{T}\) that has only one arriving edge has two fraternal edges;
No vertex of \(\mathcal{T}\) that has exactly two arriving edges can have a fraternal edge.
Proof. For \((1)\) suppose that there is a vertex \(w\) in \(\mathcal{T}\) in the generation \(m\) containing, between its edges, two fraternal edges and exactly one arriving edge. We denote by \(p\) the vertex of the generation \(m-1\) of the arrival edge in \(w\).
Since we are constructing the faces on both sides of the arrival edge in \(w\), we must have two arrival edges in \(p\). So we have \(4\) edges in \(p\), and we have one edge left to add. We cannot place the edge on the faces being constructed as we would have to insert starting edges and these would provide faces of size 3.
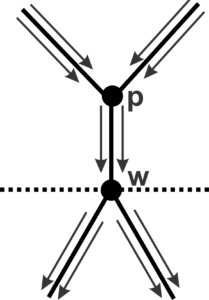
Thus, we have to insert an edge between the arrival edges of \(p\). But the only edge that can be added at this position is an incoming edge, since incoming edges are consecutive at the vertex. Therefore, \(p\) has \(3\) arriving edges, which is absurd, as it contradicts the Theorem 3, since all faces of \(\mathcal{T}\) are greater than \(3\).
Now, let us consider \((2)\). Suppose that there is a vertex \(w\) in \(\mathcal{T}\) in the generation \(m\) containing, between its edges, a fraternal edge and exactly two arriving edges. Let \(p\) be the vertex of the \(m-1\) generation of the arrival edge in \(w\) that is building the face with the fraternal edge.
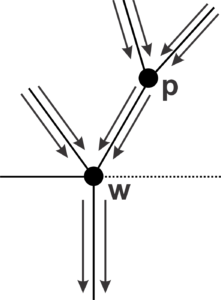
Due to the presence of the fraternal edge, we add an arriving edge in \(p\), as we cannot add a starting edge and form a triangle, since the tiling has no triangular faces. Since \(w\) closes a face and it is not triangular, we add another arriving edge to \(p\). The only place we can insert the missing edge of \(p\) is between the arriving edges. Since this type of edge appears consecutively, we have to add an arriving edge. By the Theorem 3, the tiling is of the type \([3;\;3;\;3;\;3;\;b]\), which is absurd, since \(\mathcal{T}\) has no triangular faces. Therefore, there is no vertex with two arrival edges and a fraternal edge. ◻
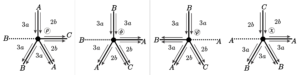
From the results of Section \(3\) we have that a hyperbolic uniform tiling of valence \(5\) must have a vertex type of one of the following families below.
|
|
|
Note that the values assigned in each tiling family (to obtain a vertex type) have no restrictions on parity, but only on the plane to be tessellated. However, if we consider a construction order, we must consider parity, as this interferes with the position of the final vertex of the face, or in some cases, the presence of fraternal edges.
Given a general vertex type containing \(p\) parameters to determine a vertex type, we have \(2^p\) cases to analyze, based on possible parity combinations. Thus, we would have to consider \(70\) cases to determine the vertex counting in tilings of valence \(5\). However, we can disregard \(31\) cases associated with family \(6\) and analyze a single case, because in this situation parity only influences the reflection of the final position and not on the type of vertex position found. Similarly, we exclude other cases that do not add factors other than those already considered and conclude that there are \(20\) essential cases.
| Item | Tessellation family | Even parameters | Odd parameters |
|---|---|---|---|
| 1 | \([a;\; a;\; a;\; a;\; a]\) | \(a\) | – |
| 2 | \([a;\; a;\; a;\; a;\; a]\) | – | \(a\) |
| 3 | \([3a;\; 3a;\; 3a;\; 2b;\; 2b]\) | \(a\), \(b\) | – |
| 4 | \([3a;\; 3a;\; 3a;\; 2b;\; 2b]\) | \(b\) | \(a\) |
| 5 | \([3a;\; 3a;\; 3a;\; 2b;\; 2b]\) | – | \(a\), \(b\) |
| 6 | \([3a ;\; 3a;\; b;\; 3a;\; c]\) | \(a, b\), \(c\) | – |
| 7 | \([3a ;\; 3a;\; b;\; 3a;\; c]\) | \(a\), \(b\) | \(c\) |
| 8 | \([3a ;\; 3a;\; b;\; 3a;\; c]\) | \(a\) | \(b\), \(c\) |
| 9 | \([3a ;\; 3a;\; b;\; 3a;\; c]\) | \(b\), \(c\) | \(a\) |
| 10 | \([3a ;\; 3a;\; b;\; 3a;\; c]\) | \(c\) | \(a\), \(b\) |
| 11 | \([3a ;\; 3a;\; b;\; 3a;\; c]\) | – | \(a, b\), \(c\) |
| 12 | \([2a;\; 2b ;\; 2b ;\; 2a ;\; c]\) | \(a, b\), \(c\) | – |
| 13 | \([2a;\; 2b ;\; 2b ;\; 2a ;\; c]\) | \(a\) | \(b\), \(c\) |
| 14 | \([2a;\; 2b ;\; 2b ;\; 2a ;\; c]\) | \(b\) | \(a\), \(c\) |
| 15 | \([2a;\; 2b ;\; 2b ;\; 2a ;\; c]\) | – | \(a, b\), \(c\) |
| 16 | \([4a;\; b;\; 4a;\; 2c;\; 2d]\) | \(a, b, c\), \(d\) | – |
| 17 | \([4a;\; b;\; 4a;\; 2c;\; 2d]\) | \(b, c\), \(d\) | \(a\) |
| 18 | \([4a;\; b;\; 4a;\; 2c;\; 2d]\) | \(a, c\), \(d\) | \(b\) |
| 19 | \([4a;\; b;\; 4a;\; 2c;\; 2d]\) | \(c\), \(d\) | \(a\), \(b\) |
| 20 | \([2a;\; 2b;\; 2c;\; 2d;\; 2e]\) | \(a, b, c, d\), \(e\) | – |
We know that every case where there are only even parameters can be written as particular cases of the family \([2a;\; 2b;\; 2c;\; 2d;\; 2e]\), however, we counted these cases in order to obtain simpler formulas for situations in which even vectors fit into the families presented.
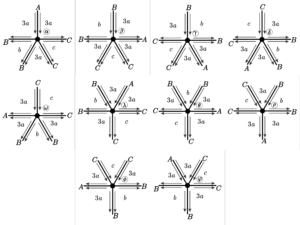
In the analysis of each family, from Item \(4\) onwards, we built two tables: one presenting what each vertex position can generate (in general), and another analyzing the behavior of the faces, taking into account the different types of face formation.
Based on the tables, we set up formulas to determine the number of vertices of each position present in the \(n\) generation. Then we use generating functions and obtain a system of \(p\) variables and \(p\) functions, where \(p\) is the number of vertex positions present in the tiling. With the help of Wolfram Mathematica Software [Mathematica], we solve the system and add the generating functions corresponding to all the positions of vertices present in the tiling, plus \(1\) vertex of the origin and we obtain the function that provides all the quantities of vertices of the tiling separated by generations. We simplify the obtained functions, whenever possible, in order to observe what the properties of the vertex interfere in the final function.
We carry out the procedure in detail for the first semi-regular case and, for the other cases, we only include the tables mentioned above and the function we obtain to count the tiling vertices. For each general vertex type, we denote in the same way the faces starting at a vertex, regardless of the parity considered. We proceed in this way so we do not need to repeat information already presented.
The functions obtained here are valid for counting vertices of uniform tilings with faces greater than \(3\), as our analysis is based on the Corollary 2. We can analyze tilings with triangular faces considering the existence of the vertex positions stated in the mentioned result and verifying the properties generated by the presence of triangles in the tiling. We now start the process for the \(20\) cases found:
1. \([a;\;a;\;a;\;a;\;a]\), para \(a = 2r\) com \(r \in \mathbb{N}\).
The vertex with \(5\) symmetric faces has the \(5\) symmetric edges and these will be denoted by \(A\). Fixing any vertex \(v\), we have two possibilities of vertex positions.
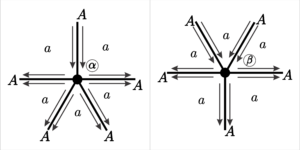
Denoting by \(T_1\) the face that begins between two edges \(A\), we have that \(T_1\) ends \(r\) generations after its initial vertex, between the edges \(A\). Therefore, to determine the number of vertices \(\beta_n\) we must consider the number of faces \(T_1\) starting in the generation \(n-r\), considering that \(\beta\) can only be the end point of the face \(T_1\).
| Vertex position | Generated vertices | Generated faces |
|---|---|---|
| \(\alpha\) | \(4\alpha\) | \(3T_1\) |
| \(\beta\) | \(3\alpha\) | \(2T_1\) |
Table 2 does not take into account the edges used to form the position \(\beta\). For each \(\beta\) position in the generation \(n\), we no longer have \(2\) vertices in the \(\alpha\) position. Defining \(\alpha_n\) and \(\beta_n\) as the number of position vertices \(\alpha\) and \(\beta\) in the \(n\) generation, respectively, we have: \[\alpha_n = 4\alpha_{n-1}+3\beta_{n-1}-2\beta_n, \quad \alpha_1 = 5 \quad \mbox{and}\] \[\beta_n = 3\alpha_{n-r}+2\beta_{n-r},\quad \beta_1=\cdots=\beta_{r-1} = 0, \beta_r = 5.\] Let \(v_n\) be the number of vertices in the generation \(n\). So \(v_0 = 1\) and \(v_n = \alpha_n + \beta_n\) for \(n\geq 1\). Thus, if we define \(V(z) = \sum_{n\geq0}v_nz^n\), we have that \[V(z) = v_0 + \sum_{n\geq1}v_nz^n = 1 + \sum_{n\geq1}\alpha_nz^n+\sum_{n\geq1}\beta_nz^n.\] Denoting \(A(z) = \sum_{n\geq1}\alpha_nz^n\) and \(B(z) = \sum_{n\geq1}\beta_nz^n\), we have: \[V(z) = 1 + A(z) + B(z).\] By means of generating functions, we obtain the system:
\[\begin{aligned} (4z-1)A(z)+(3z-2)B(z)&=& -5z,\nonumber \\ 3z^rA(z) + (2z^r-1)B(z) & = & -5z^r, \nonumber \end{aligned}\] which has as a solution, \[A(z) = \frac{5 \left(z^{r+1}-2 z^r+z\right)}{1-4z+4z^r-z^{r+1}} \quad \mbox{and} \quad B(z) = \frac{5(1-z)z^r}{1-4z+4z^r-z^{r+1}}.\] Therefore, \[V(z) = \frac{(1+z)(1-z^r)}{1-4z+4z^r-z^{r+1}}.\]
2. \([a;\;a;\;a;\;a;\;a]\), para \(a = 2r+1\) onde \(r \in \mathbb{N}\).
For the case where \(a\) is odd, we have \(3\) possible vertex positions.

Since \(a\) is odd, we have that the face \(T_1\) that starts between edges \(A\) ends \(r\) generations later at \(2\) vertices with position \(\beta\) and a fraternal edge \(A\). The face \(T_2\) starting at fraternal edge \(A\) ends \(r\) generations later, between edges \(A\) at position \(\gamma\).
| Vertex position | Generated vertices | Generated faces |
|---|---|---|
| \(\alpha\) | \(4\alpha\) | \(3T_1\) |
| \(\beta\) | \(3\alpha\) | \(2T_1 + T_2\) |
| \(\gamma\) | \(3\alpha\) | \(2T_1\) |
We obtain the following recurrence formulas for the vertex positions: \[\alpha_n = 4\alpha_{n-1}+3\beta_{n-1}+3\gamma_{n-1}-2\gamma_n-\beta_n, \quad \alpha_1 = 5,\] \[\beta_n = 6\alpha_{n-r} + 4\beta_{n-r}+4\gamma_{n-r},\quad \beta_1 = \cdots=\beta_{r-1} = 0, \beta_r = 10\mbox{\;\;e\;}\] \[\gamma_n = \frac{\beta_{n-r}}{2}, \quad \gamma_1=\cdots=\gamma_{2r-1}=0, \gamma_{2r} = 5.\] Defining \(A(z) = \sum_{n\geq1}\alpha_nz^n\), \(B(z)= \sum_{n\geq1}\beta_nz^n\) e \(C(z) = \sum_{n\geq1}\gamma_nz^n\), we obtain \[V(z) = 1 + A(z) + B(z) + C(z).\] Thus, using generating functions, we obtain the system
\[\begin{aligned} (4z-1)A(z)+(3z-1)B(z)+(3z-2)C(z) & = & -5z, \nonumber \\ 6z^rA(z) + (4z^r-1)B(z) +4z^rC(z) & = & -10z^r, \nonumber \\ z^rB(z)-2C(z)&=&0, \nonumber \vspace{-0.4cm} \end{aligned}\] which has as solution \[A(z) = \frac{5 \left(1+z^r\right)\left(z-2z^r+z^{r+1}\right)}{1-4z+2z^r-2z^{r+1} + 4z^{2r}-z^{2r+1}},\] \[B(z) = \frac{10(1-z)z^r}{1-4z+2z^r-2z^{r+1} + 4z^{2r}-z^{2r+1}} \,\, \mbox{and}\] \[C(z) = \frac{5(1-z)z^{2r}}{1-4z+2z^r-2z^{r+1} + 4z^{2r}-z^{2r+1}}.\] We concluded that \[V(z) = \frac{1+z+2z^r-2z^{r+1}-z^{2r}-z^{2r+1}}{1-4z +2z^r-2z^{r+1}+4z^{2r}-z^{2r+1}}.\]
3. \([3a;\;3a;\;3a;\;2b;\;2b]\), com \(a = 2r\) e \(b = 2s\).
This type of vector has vertex symmetry, which implies that we have symmetry between the edges, which allows us to denote edges only by the letters \(A, B\), and \(C\).
Analyzing the symmetries of tiling, we found that the face \(T_1\) starting between edges \(A\) and \(B\) ends three generations later, between edges \(A\) and \(B\) at position \(\delta\); face \(T_2\) starting between edges \(B\)s ends after three generations, between edges \(B\) at position \(\omega\) and face \(T_3\) starting between edges \(A\) and \(C\) ends \(b\) generations later between edges \(A\) and \(C\) at position \(\lambda\).
| Vertex position | Generated vertices | generated faces |
|---|---|---|
| \(\alpha\) | \(\alpha + 2\beta + \gamma\) | \(T_1+T_2+T_3\) |
| \(\beta\) | \(2\alpha+ \beta + \gamma\) | \(T_1 + 2T_3\) |
| \(\gamma\) | \(2\alpha + 2\beta\) | \(2T_1 + T_2\) |
| \(\delta\) | \(\alpha + \beta + \gamma\) | \(T_1+T_3\) |
| \(\omega\) | \(2\alpha + \gamma\) | \(2T_3\) |
| \(\lambda\) | \(\alpha + 2\beta\) | \(T_1+T_2\) |
Note that \(\delta\), \(\omega\) and \(\lambda\) can only be obtained as endpoints of the faces \(T_1\), \(T_2\) and \(T_3\). Furthermore, a vertex at position \(\delta\) implies one less vertex from position \(\alpha\) and one less from position \(\beta\); one vertex at position \(\omega\) implies two less vertices at position \(\beta\) and a vertex at position \(\lambda\) removes a vertex from each position \(\alpha\) and \(\gamma\). We get the following recurrence formulas:
\[\alpha_n = \alpha_{n-1}+2\beta_{n-1}+2\gamma_{n-1}+\delta_{n-1}+2\omega_{n-1}+\lambda_{n-1}-\delta_n – \lambda_n,\quad \alpha_1=2,\] \[\beta_n = 2\alpha_{n-1}+\beta_{n-1}+2\gamma_{n-1}+\delta_{n-1}+2\lambda_{n-1}-\delta_n-2\omega_n, \quad \beta_1= 2,\] \[\gamma_n = \alpha_{n-1}+\beta_{n-1}+\delta_{n-1}+\omega_{n-1}-\lambda_n, \quad \gamma_1=1,\] \[\delta_n = \alpha_{n-3r} + \beta_{n-3r} + 2\gamma_{n-3r} + \delta_{n-3r} + \lambda_{n-3r},\quad \delta_1=\cdots=\delta_{3r-1}=0, \quad\delta_{3r}=2,\] \[\omega_n = \alpha_{n-3r}+\gamma_{n-3r}+\lambda_{n-3r}, \quad \omega_1=\cdots=\omega_{3r-1}=0, \omega_{3r}=1 \mbox{\;\;and}\] \[\lambda_n = \alpha_{n-b}+2\beta_{n-b}+\delta_{n-b}+2\omega_{n-b}, \quad \lambda_1=\cdots=\lambda_{b-1}=0, \quad \lambda_b= 2.\] Defining \(A(z) = \sum_{n\geq1}\alpha_nz^n\), \(B(z) = \sum_{n\geq1}\beta_nz^n\), \(C(z) = \sum_{n\geq1}\gamma_nz^n\), \(D(z) = \sum_{n\geq1}\delta_nz^n\), \(E(z) = \sum_{n\geq1}\omega_nz^n\) e \(F(z) = \sum_{n\geq1}\lambda_nz^n\) we get \[V(z) = 1 + A(z) + B(z) + C(z) + D(z) + E(z) + F(z).\] Through the method based on generating functions, we obtain the system below.
\[\begin{aligned} z(2B(z)+2C(z)+2E(z))-(z-1)(A(z)+D(z)+F(z)) &=&-2z, \nonumber \\ z(2A(z)+2C(z)+2F(z))+(z-1)(B(z)+D(z))-2E(z) &=& -2z,\nonumber \\ z(A(z)+B(z)+D(z)+E(z))-C(z)-F(z)&=&-z,\nonumber \\ z^{3r}(A(z)+B(z)+2C(z)+F(z))+(z^{3r}-1)D(z)&=&-2z^{3r},\nonumber\\ z^{3r}(A(z)+C(z)+F(z))-E(z)&=&-z^{3r} \quad\mbox{e}\nonumber \\ z^b(A(z)+2B(z)+D(z)+2E(z))-F(z)&=&-2z^b. \nonumber \end{aligned}\] This system has as solution: \[\begin{aligned} &A(z) = \frac{2(z-z^{3r}-z^{2s}+2z^{3r+2s}-z^{3r+2s+1})}{1-4z+(2z+1)z^{2s}+(2+z)z^{3r}-4z^{3r+2s}+z^{3r+2s+1}},& \nonumber \\ &B(z)=\frac{2(z-2z^{3r}+z^{3r+1})(1-z^{2s})}{1-4z+(2z+1)z^{2s}+(2+z)z^{3r}-4z^{3r+2s}+z^{3r+2s+1}},& \nonumber \\ &C(z) = \frac{(1-z^{3r})(z-2z^{2s}+z^{2s+1})}{1-4z+(2z+1)z^{2s}+(2+z)z^{3r}-4z^{3r+2s}+z^{3r+2s+1}},& \nonumber \\ &D(z) = \frac{2(1-z)z^{3r}(1-z^{2s})}{1-4z+(2z+1)z^{2s}+(2+z)z^{3r}-4z^{3r+2s}+z^{3r+2s+1}},& \nonumber \\ &E(z) = \frac{(1-z)z^{3r}(1-z^{2s})}{1-4z+(2z+1)z^{2s}+(2+z)z^{3r}-4z^{3r+2s}+z^{3r+2s+1}}&\quad \nonumber \\ &F(z) = \frac{2(1-z)(1-z^{3r})z^{2s}}{1-4z+(2z+1)z^{2s}+(2+z)z^{3r}-4z^{3r+2s}+z^{3r+2s+1}}. & \nonumber \end{aligned}\] Therefore, the vertices of this tiling can be counted using the following function \[V(z) =\frac{(1+z)(1-z^{3r})(1-z^{2s})}{1-4z+(1+2z)z^{2s}+(2+z)z^{3r}-4z^{3r+2s}+z^{3r+2s+1}}.\] For the next cases, since we have a similar reasoning, we present only the data necessary to obtain the vertex count formulas, in order not to make the work tiring and extensive.
4. \([3a;\; 3a;\; 3a;\; 2b;\; 2b]\), para \(a= 2r +1\) e \(b = 2s + 2\), onde \(r, s \in \mathbb{N}\).
Due to the presence of odd parameters, we have face positions containing fraternal edges. Thus, we have all the positions shown in Figure 11 and also the positions shown in Figure 12.
| Face | Start of the edges | Size | End of the edges | End of the vertices |
|---|---|---|---|---|
| \(T_1\) | between edges \(A\) and \(B\) | \(3a\) | fraternal edge \(B\) | \(\phi + \rho\) |
| \(T_4\) | fraternal edge \(B\) | \(3a\) | between edges \(A\) and \(B\) | \(\delta\) |
| \(T_2\) | between edges \(B\) and \(B\) | \(3a\) | fraternal edge \(A\) | \(2\varphi\) |
| \(T_5\) | fraternal edge \(A\) | \(2b\) | fraternal edge \(A\) | \(2\chi\) |
| \(T_6\) | fraternal edge \(A\) | \(3a\) | between edges \(B\) and \(B\) | \(\omega\) |
| \(T_3\) | between edges \(A\) and \(C\) | \(2b\) | between edges \(A\) and \(C\) | \(\lambda\) |
| Vertex position | Generated positions | Generated faces |
|---|---|---|
| \(\rho\) | \(\alpha + \beta + \gamma\) | \(T_1 + T_3\) |
| \(\phi\) | \(2\alpha + \gamma\) | \(2T_3\) |
| \(\varphi\) | \(\alpha + \beta + \gamma\) | \(T_1 + T_3\) |
| \(\chi\) | \(\alpha + 2 \beta\) | \(T_1 + T_2\) |
Since we need vertices at positions \(\phi\) and \(\rho\) to enclose a face of type \(T_1\), it follows that the numbers of vertices at these two positions in one generation must be equal. Thus, we choose one of the two positions of the vertex to determine the generating function, and when adding all the vertices to obtain the general formula, we multiply the obtained function by \(2\) to add all the vertices of the positions \(\phi\) and \(\rho\). Using the information presented in Tables 5 and 6, we built recurrence formulas for the positions of vertices and found the corresponding generating functions. We concluded that,
\(V(z) = ((1+z)(1-z^b)(-z^{9 r} (z^{2 s+4}-z^{2 s+6})-z^{12 r} (-z^{2 s+5}-2 z^{2 s+6}-z^{2 s+7})-z^{6 r} (3 z^{2 s+3}+z^{2 s+5}+3 z^4+z^2)-(z^3-z) z^{3 r}+z^2+2 z+1)/((-z^{10}+2 z^9+7 z^8+4 z^7) z^{12 r+4 s}+(-z^9-2 z^8+z^7+2 z^6) z^{9 r+4 s}+(-z^8-4 z^7-5 z^6-2 z^5) z^{12 r+2 s}+(-z^8-4 z^7-3 z^6-4 z^5) z^{6 r+4 s}+(-z^7+4 z^6+z^5-4 z^4) z^{9 r+2 s}+(2 z^7-6 z^6+6 z^4-2 z^3) z^{6 r+2 s}+(4 z^6-z^5-4 z^4+z^3) z^{3 r+2 s}+(-2 z^4-z^3+2 z^2+z) z^{3 r}+(4 z^5+3 z^4+4 z^3+z^2) z^{6 r}+(2 z^5+5 z^4+4 z^3+z^2) z^{2 s}-4 z^3-7 z^2-2 z+1)\).
5. \([3a;\;3a;\;3a;\;2b;\;2b]\), where \(a = 2r+1\), \(b = 2s+1\), for \(r,s \in \mathbb{N}\).
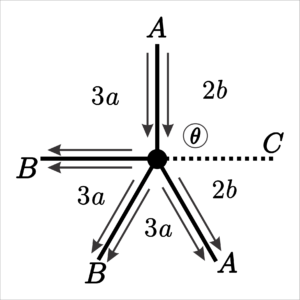
The vertex positions for this uniform tiling are shown in Figures 11, 12 and 13. There are \(7\) possible face vectors, according to Table 7.
| Face | Star of the edges | Size | End of the edges | End of the vertices |
|---|---|---|---|---|
| \(T_1\) | between edges \(A\) and \(B\) | \(3a\) | fraternal edge \(B\) | \(\phi + \rho\) |
| \(T_4\) | fraternal edge \(B\) | \(3a\) | between edges \(A\) and \(B\) | \(\delta\) |
| \(T_2\) | between edges \(B\) and \(B\) | \(3a\) | fraternal edge \(A\) | \(2\varphi\) |
| \(T_5\) | fraternal edge \(A\) | \(2b\) | fraternal edge \(C\) | \(2\theta\) |
| \(T_6\) | fraternal edge \(C\) | \(2b\) | fraternal edge \(A\) | \(2x\) |
| \(T_7\) | fraternal edge \(A\) | \(3a\) | between edges \(B\) and \(B\) | \(\omega\) |
| \(T_3\) | between edges \(A\) and \(C\) | \(2b\) | etween edges \(A\) and \(C\) | \(\lambda\) |
We start the analysis by checking the positions generated by the positions present in the previous generation. We record this information in the Table 8.
| Vertex position | Generated position | Start faces |
|---|---|---|
| \(\chi\) | \(\alpha+2\beta\) | \(T_1+T_2\) |
In addition to the faces described in Table 8, we have the faces that start at fraternal edges: \(\phi + \rho\) generate \(T_2\), \(2\varphi\) generate \(T_4\), \(2\theta\) generate \(T_5\) and \(2x\) generate \(T_6\). Solving the system from the recurrence functions and summing the vertices of all positions, we obtain
\(V(z)=((1+z)(1-z^b)((z^5-z^3) z^{9 r+4 s}+(z^6+2 z^5+z^4) z^{12 r+4 s}+(z-z^3) z^{3 r}+(-3 z^4-z^2) z^{6 r}+z^2+2 z+1))/((-z^8+2 z^7+7 z^6+4 z^5) z^{12 r+6 s}+(-z^7-4 z^6-5 z^5-2 z^4) z^{12 r+4 s}+(-z^7-2 z^6+z^5+2 z^4) z^{9 r+6 s}+(2 z^6-9 z^5-2 z^4-3 z^3) z^{6 r+2 s}+(-z^6+4 z^5+z^4-4 z^3) z^{9 r+4 s}+(-z^6-4 z^5-3 z^4-4 z^3) z^{6 r+6 s}+(4 z^5-z^4-4 z^3+z^2) z^{3 r+2 s}+(3 z^5+2 z^4+9 z^3-2 z^2) z^{6 r+4 s}+(-2 z^4-z^3+2 z^2+z) z^{3 r}+(4 z^5+3 z^4+4 z^3+z^2) z^{6 r}+(2 z^4+5 z^3+4 z^2+z) z^{2 s}-4 z^3-7 z^2-2 z+1)\).
6. \([3a;\;3a;\;b;\;3a;\;c]\), for \(a = 2r\), \(b = 2s\) e \(c = 2t\), where \(r, s, t \in \mathbb{N}\).
Since we only have even parameters, we do not have fraternal edges, which implies that we only have face-to-vertex closing. Thus, the tiling presents only the vertex positions presented in 14.
This tiling presents \(5\) types of face formations, presented in Table 9.
| Face | Start of the edges | Size | End o the edges | End of the vertex |
|---|---|---|---|---|
| \(T_1\) | between edges \(A\) and \(B\) | \(3a\) | between edges \(A\) and \(B\) | \(\lambda\) |
| \(T_2\) | between edges \(B\) and \(B\) | \(b\) | between edges \(B\) and \(B\) | \(\theta\) |
| \(T_3\) | between edges \(B\) and \(C\) | \(3a\) | between edges \(B\) and \(C\) | \(\rho\) |
| \(T_4\) | between edges \(C\) and \(C\) | \(c\) | between edges \(C\) and \(C\) | \(\phi\) |
| \(T_5\) | between edges \(A\) and \(C\) | \(3a\) | between edges \(C\) and \(A\) | \(\varphi\) |
| Vertex position | Generated position | Started faces |
|---|---|---|
| \(\alpha\) | \(\beta + \gamma + \delta + \omega\) | \(T_2 + T_3 + T_4\) |
| \(\beta\) | \(\alpha + \beta + \delta + \omega\) | \(T_3+ T_4 + T_5\) |
| \(\gamma\) | \(\alpha+\gamma + \delta + \omega\) | \(T_1+T_4 + T_5\) |
| \(\delta\) | \(\alpha+\beta+\gamma+\delta\) | \(T_1+T_2 + T_5\) |
| \(\omega\) | \(\alpha+\beta+ \gamma + \omega\) | \(T_1+ T_2 + T_3\) |
| \(\lambda\) | \(\beta + \delta + \omega\) | \(T_3 + T_4\) |
| \(\theta\) | \(\alpha+\delta + \omega\) | \(T_4 + T_5\) |
| \(\rho\) | \(\alpha+\gamma+ \delta\) | \(T_1+T_5\) |
| \(\phi\) | \(\alpha+\beta+\gamma\) | \(T_1 + T_2\) |
| \(\varphi\) | \(\beta+\gamma+ \omega\) | \(T_2+T_3\) |
Therefore, using information from Table 10, we obtain that the number of vertices is determined by the following function,
\(V(z) = ((1+z)(1-z^{3r})(1-z^s)(1-z^t))/(1-4z+ 3z(z^s+z^t)-(1+2z)z^{s+t}+(2+z)z^{3r} -3(z^{3r+s}+z^{3r+t})+ 4z^{3r+s+t}-z^{3r+s+t+1})\).
7. \([3a ;\; 3a;\; b;\; 3a;\; c]\), for \(a = 2r+2\), \(b = 2s+2\) and \(c = 2t +1\), where \(r, s, t \in \mathbb{N}\).
We have \(14\) face positions in this tiling, shown in Figures 14 and 15. Thus, we get the recurring formulas of vertex positions using the informations of Tables 9 and 10.
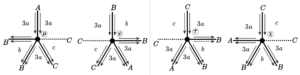
| Face | Start of the edges | Size | End of the edges | End of the vertices |
|---|---|---|---|---|
| \(T_1\) | between edges \(A\) and \(B\) | \(3a\) | between edges \(A\) and \(B\) | \(\lambda\) |
| \(T_2\) | between edges \(B\) and \(B\) | \(b\) | between edges \(B\) and \(B\) | \(\theta\) |
| \(T_3\) | between edges \(B\) and \(C\) | \(3a\) | between edges \(B\) and \(C\) | \(\rho\) |
| \(T_4\) | between edges \(C\) and \(C\) | \(c\) | fraternal edge \(C\) | \(\tau + \chi\) |
| \(T_6\) | fraternal edge \(C\) | \(3a\) | fraternal edge \(C\) | \(\mu + \psi\) |
| \(T_7\) | fraternal edge \(C\) | \(c\) | between edges \(C\) an \(C\) | \(\phi\) |
| \(T_5\) | between edges \(A\) and \(C\) | \(3a\) | between edges \(A\) and \(C\) | \(\varphi\) |
| Vertex position | Position generated | Initiated faces |
|---|---|---|
| \(\mu\) | \(\beta + \gamma + \omega\) | \(T_2 + T_3\) |
| \(\psi\) | \(\alpha + \gamma + \delta\) | \(T_1 + T_5\) |
| \(\tau\) | \(\alpha+ \beta + \gamma\) | \(T_1 + T_2\) |
| \(\chi\) | \(\alpha + \beta + \gamma\) | \(T_1 + T_2\) |
Putting together the formulas, we find the generating functions for each position of the vertex, and we conclude that the function that provides the numbers of vertices of this tiling is given by:
\[\begin{aligned} V(z) = &((1+z) (1-z^{3r+3}) (1-z^{s+1}) (1+z-2 z^{t+1}+2z^{3r+t+2}-z^{3r+2t+2}-z^{3 r+2 t+3}))/(1-3z\\ \notag &-4 z^2+6 z^{t+2}+2 z^{3 r+t+2}-8 z^{3 r+t+3} -(3 z+3) (z^{3 r+s+4}-z^{3 r+2 t+3}+z^{6 r+2 t+5}-z^{s+2})\\ \notag &-(2 z^2+3 z+1) z^{3 r+s+2 t+3}+(2 z^2+4 z) z^{6 r+t+5}+(z^2+3 z+2) z^{3 r+3}-(4 z^2+2 z) z^{s+t+1}\\ \notag &+6 (z^{3 r+s+t+4}-z^{3 r+t+4})+8z^{3 r+s+t+5}-2 z^{3 r+s+t+6}-6 z^{6 r+s+t+6}+4 z^{6 r+s+2 t+6}+3 z^{6 r+s+2 t+7}\\ \notag &-z^{6 r+s+2 t+8}). \end{aligned}\]
8. \([3a ;\; 3a;\; b;\; 3a;\; c]\), para \(a = 2r+2\), \(b = 2s+1\) e \(c = 2t+1\), onde \(r, s, t \in \mathbb{N}\).
This tiling has \(18\) types of vertices, which can be seen in Figures 14, 15 and 16. Information about these vertices is contained in Tables 10, 12 and 14.

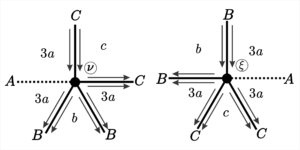
| Face | Start of the edge | Size | End of the edge | End of the vertice |
|---|---|---|---|---|
| \(T_1\) | between edges \(A\) and \(B\) | \(3a\) | between edges \(A\) and \(B\) | \(\lambda\) |
| \(T_2\) | between edges \(B\) and \(B\) | \(b\) | fraternal edge \(B\) | \(\eta + \sigma\) |
| \(T_3\) | between edges \(B\) and \(C\) | \(3a\) | between edges \(B\) and \(C\) | \(\rho\) |
| \(T_4\) | between edges \(C\) and \(C\) | \(c\) | fraternal edge \(C\) | \(\tau + \chi\) |
| \(T_6\) | fraternal edge \(C\) | \(3a\) | fraternal edge \(C\) | \(\mu + \psi\) |
| \(T_7\) | fraternal edge \(C\) | \(c\) | between edges \(C\) and \(C\) | \(\phi\) |
| \(T_5\) | between edges \(A\) and \(C\) | \(3a\) | between edges \(A\) and \(C\) | \(\varphi\) |
| \(T_8\) | fraternal edge \(B\) | \(3a\) | fraternal edge \(B\) | \(\kappa + \epsilon\) |
| \(T_9\) | fraternal edge \(B\) | \(b\) | between edges \(B\) and \(B\) | \(\theta\) |
| Vertex position | Generated position | Started faces |
|---|---|---|
| \(\kappa\) | \(\beta + \delta + \omega\) | \(T_3 + T_4\) |
| \(\eta\) | \(\alpha + \delta + \omega\) | \(T_4 + T_5\) |
| \(\sigma\) | \(\alpha+ \delta + \omega\) | \(T_4 + T_5\) |
| \(\epsilon\) | \(\alpha + \gamma + \delta\) | \(T_1 + T_5\) |
By the method given above, we obtain generating functions for each vertex position and, by adding all these functions plus \(1\) (the initial vertex), we find the generating function that determines the numbers of vertices in each generation, which has the following form,
\(V(z) = ((1+z) (1-z^{3 r+3}) (-2 z^{s+1}+2 z^{3 r+s+2}-z^{3 r+2 s+2}-z^{3 r+2 s+3}+z+1) (-2 z^{t+1}+2 z^{3 r+t+2}-z^{3 r+2 t+2}-z^{3 r+2 t+3}+z+1))/((4 z^8+8 z^7) z^{9 r+s+t}+(-6 z^8-6 z^7) (z^{9 r+2 s+t}+z^{9 r+s+2 t})+(2 z^7+6 z^6+4 z^5) (z^{6 r+s}+z^{6 r+t})+(-3 z^7-6 z^6-3 z^5) (z^{6 r+2 s}+z^{6 r+2 t})+(-4 z^6+16 z^5+24 z^4) z^{3 r+s+t}+(-24 z^6-16 z^5+4 z^4) z^{6 r+s+t}+(3 z^5+6 z^4+3 z^3) (z^{3 r+2 s}+z^{3 r+2 t})+(-4 z^5-6 z^4-2 z^3) (z^{3 r+2 s+t}+z^{3 r+s+2 t})+(-z^{10}+2 z^9+7 z^8+4 z^7) z^{9 r+2 s+2 t}+(-2 z^8+6 z^7+14 z^6+6 z^5) (z^{6 r+2 s+t}+z^{6 r+s+2 t})+(-2 z^7-5 z^6-4 z^5-z^4) z^{6 r+2 s+2 t}+(-6 z^5-14 z^4-6 z^3+2 z^2) (z^{3 r+s}+z^{3 r+t})+(z^6+4 z^5+5 z^4+2 z^3) z^{3 r}+(-8 z^3-4 z^2) z^{s+t}+(6 z^3+6 z^2) (z^s+z^t)-4 z^3-7 z^2-2 z+1)\).
9. \([3a ;\; 3a;\; b;\; 3a;\; c]\), for \(a = 2r + 1\), \(b = 2s+2\) and \(c = 2t+2\), onde \(r, s, t \in \mathbb{N}\).
The last two possible vertex positions for tilings with vertex type \([3a ;\; 3a;\; B;\; 3a;\; c]\) (and faces greater than \(3\)) are shown in Figure 17. We then have \(20\) different vertex positions.
| Face | Start of the edge | Size | End of the edge | End of the vertex |
|---|---|---|---|---|
| \(T_1\) | between edges \(A\) and \(B\) | \(3a\) | fraternal edge \(C\) | \(\mu + \psi\) |
| \(T_2\) | between edges \(B\) and \(B\) | \(b\) | between edges \(B\) and \(B\) | \(\theta\) |
| \(T_3\) | between edges \(B\) and \(C\) | \(3a\) | fraternal edge \(A\) | \(\nu + \xi\) |
| \(T_4\) | between edges \(C\) and \(C\) | \(c\) | between edges \(C\) and \(C\) | \(\phi\) |
| \(T_6\) | fraternal edge \(C\) | \(c\) | fraternal edge \(C\) | \(\tau + \chi\) |
| \(T_7\) | fraternal edge \(C\) | \(3a\) | between edges \(A\) and \(B\) | \(\lambda\) |
| \(T_5\) | between edges \(A\) and \(C\) | \(3a\) | fraternal edge \(B\) | \(\kappa + \epsilon\) |
| \(T_8\) | fraternal edge \(A\) | \(3a\) | between edges \(B\) and \(C\) | \(\rho\) |
| \(T_9\) | fraternal edge \(B\) | \(b\) | fraternal edge \(B\) | \(\eta + \sigma\) |
| \(T_{10}\) | fraternal edge \(B\) | \(3a\) | between edges \(A\) and \(C\) | \(\varphi\) |
| Vertex position | Generated position | Started faces |
|---|---|---|
| \(\nu\) | \(\beta + \gamma + \omega\) | \(T_2 + T_3\) |
| \(\zeta\) | \(\beta + \delta + \omega\) | \(T_3 + T_4\) |
Taking into account a group that can be used to produce a tiling with this type of vertex, we are able to know how each face ends up, depending on the parity. We take all of this into account to actually consider all face options. For this case, we get the following vertex count formula,
\(V(z) = ((1-z^{s+1})(1-z^{t+1})(-(z+1)^3 z^{18 r+s+t+6}+2 z^{9 r} (z^{s+t+3}-z^{s+t+4}-z^{s+4}+z^{s+5}-z^{t+4}+z^{t+5}-z^6+z^5)-(z+1) z^{6 r+2} (z^{s+t}+z^{s+2}+2 z^s+z^{t+2}+2 z^t+4 z^2+1)+(z+1) z^{12 r} (4 (z^2+1) z^{s+t+4}+(2 z^2+1) z^4 (z^s+z^t)+z^6)+(z+1)^3))/((z^4-12 z^3+2 z^2+4 z-1) (z^s+z^t) z^{6 r+2}+(-2 z^3-5 z^2-4 z-1) z^{s+t+2}+(-5 z^5+15 z^4-7 z^3-4 z^2+2 z-1) z^{6 r+s+t+2}+6 (z^2-1) (z^s+z^t) z^{3 r+3}+(-2 z^4-3 z^2-3 z-1) (z^{2 s}+z^{2 t}) z^{6 r+3}+2 (-z^4-z^3+4 z^2-z-1) (z^s+z^t) z^{9 r+3}+2 (2 z^2-z-1) z^{9 r+4}+2 (1-z^3) (z^{2 s}+z^{2 t}) z^{9 r+4}+2 (z^4+z^3-4 z^2+1 z+1) (z^{2 s+t}+z^{s+2 t}) z^{9 r+4}+(-z^2-4 z-1) (z^s+z^t) z^{12 r+4}+6 (z^4-3 z^3+3 z-1) z^{9 r+s+t+4}+(z^2+4 z+1) (z^{2 s+t}+z^{s+2 t}) z^{6 r+5}+(z^3+3 z^2+3 z+2) (z^{2 s}+z^{2 t}) z^{12 r+5}+(z^4-4 z^3-2 z^2+12 z-1) (z^{2 s+t}+z^{s+2 t}) z^{12 r+5}+2 (z^2+z-2) z^{9 r+2 s+2 t+5}+6 (z^2-1) (z^{2 s+t}+z^{s+2 t}) z^{15 r+6}+(z^3+4 z^2+5 z+2) z^{18 r+s+t+6}+3 (-z^2-2 z-1) (z^{2 s+t}+z^{s+2 t}) z^{18 r+7}+(3 z^5+11 z^4+z^3) z^{6 r}+(-z^7-2 z^6) z^{12 r}+(z^9-2 z^8+4 z^7+7 z^6-15 z^5+5 z^4) z^{12 r+s+t}+(2 z^5+z^4) z^{6 r+2 s+2 t}+(-z^8-11 z^7-3 z^6) z^{12 r+2 s+2 t}+(-z^{11}+2 z^{10}+7 z^9+4 z^8) z^{18 r+2 s+2 t}-4 z^3+3 (z^2+2 z+1) (z^s+z^t) z^2-7 z^2-2 z+6 (1-z^2) (z^{3 r+2}+z^{3 r+s+t+4}+z^{15 r+s+t+5}+z^{15 r+2 s+2 t+7})+1)\).
10. \([3a ;\; 3a;\; b;\; 3a;\; c]\), para \(a = 2r + 1\), \(b = 2s + 1\) e \(c = 2t+2\), onde \(r, s, t \in \mathbb{N}\).
All possible vertex positions have already been checked. So this case does not add any new type of vertex position, but it forms faces in a different way since it has parameters with different parity.
| Face | Start of the edge | Size | End of the edge | End of the vertex |
|---|---|---|---|---|
| \(T_1\) | between edges \(A\) and \(B\) | \(3a\) | fraternal edge \(C\) | \(\mu + \psi\) |
| \(T_2\) | between edges \(B\) and \(B\) | \(b\) | fraternal edge \(B\) | \(\eta + \sigma\) |
| \(T_3\) | between edges \(B\) and \(C\) | \(3a\) | fraternal edge \(A\) | \(\nu + \xi\) |
| \(T_4\) | between edges \(C\) and \(C\) | \(c\) | between edges \(C\) and \(C\) | \(\phi\) |
| \(T_6\) | fraternal edge \(C\) | \(c\) | fraternal edge \(C\) | \(\tau + \chi\) |
| \(T_7\) | fraternal edge \(C\) | \(3a\) | between edges \(A\) and \(B\) | \(\lambda\) |
| \(T_5\) | between edges \(A\) and \(C\) | \(3a\) | fraternal edge \(B\) | \(\kappa + \epsilon\) |
| \(T_8\) | fraternal edge \(B\) | \(3a\) | between edges \(A\) and \(C\) | \(\varphi\) |
| \(T_9\) | fraternal edge \(A\) | \(3a\) | between edges \(B\) and \(C\) | \(\rho\) |
| \(T_{10}\) | fraternal edge \(B\) | \(b\) | between edges \(B\) and \(B\) | \(\theta\) |
| Face | Start of the edge | Size | End of the edge | End of the veertex |
|---|---|---|---|---|
| \(T_1\) | between edges \(A\) and \(B\) | \(3a\) | fraternal edge \(C\) | \(\mu + \psi\) |
| \(T_2\) | between edges \(B\) and \(B\) | \(b\) | fraternal edge \(B\) | \(\eta + \sigma\) |
| \(T_3\) | between edges \(B\) and \(C\) | \(3a\) | fraternal edge \(A\) | \(\nu + \xi\) |
| \(T_4\) | between edges \(C\) and \(C\) | \(c\) | fraternal edge \(C\) | \(\xi + \tau\) |
| \(T_5\) | fraternal edge \(C\) | \(c\) | between edges \(C\) and \(C\) | \(\phi\) |
| \(T_6\) | fraternal edge \(B\) | \(3a\) | between edges \(A\) and \(C\) | \(\varphi\) |
| \(T_7\) | between edges \(A\) and \(C\) | \(3a\) | fraternal edge \(B\) | \(\kappa + \epsilon\) |
| \(T_8\) | fraternal edge \(A\) | \(3a\) | between edges \(B\) and \(C\) | \(\rho\) |
| \(T_9\) | fraternal edge \(C\) | \(3a\) | between edges \(A\) and \(B\) | \(\lambda\) |
| \(T_{10}\) | fraternal edge \(B\) | \(b\) | e between edges \(B\) and \(B\) | \(\theta\) |
Applying the method to the information contained in the table, we obtain the following function to determine the number of vertices in the tiling,
\(V(z) = ((1-z^{1+t})(((z ((z+1) (2 z (2 z-5)+5) z^{6 r+1}-(z-1)^2 (z+1)^3 z^{12 r+3}-(z-1) (z (2 z^2+z-4)+3) z^{3 r}+2 z+1)-1) z^{2 s}+(z (-(z-1) (z (z (1-2 z)^2+6)-5) z^{6 r+1}-(z-1)^2 (z (2 z^2+z-5)+4) z^{3 r}+(z^2-1)^2 z^{12 r+3}+(2 z^2+z-7) z+5)-1) z^s+z ((z^2 (z^3-3 z+3)-1) z^{3 r}+(z+1) (2 z^3-3 z^2+z+1) z^{6 r+2}-(z (z+2)-2) z+1)-2) z^{6 r+t+2}-3 z^{2 (3 r+s+1)}+3 z^{6 r+s+2}+z^{2 (6 r+s+2)}-7 z^{6 r+s+3}+4 z^{2 (6 r+s+3)}+3 z^{6 r+s+4}-4 z^{2 (6 r+s+4)}+15 z^{6 r+s+5}-24 z^{6 r+s+6}+10 z^{6 r+s+7}+7 z^{9 r+s+4}-25 z^{9 r+s+5}+35 z^{9 r+s+6}-23 z^{9 r+s+7}+6 z^{9 r+s+8}-z^{12 r+s+4}+3 z^{12 r+s+5}-7 z^{12 r+s+6}+5 z^{12 r+s+7}+2 z^{12 r+s+8}-2 z^{12 r+s+9}+4 z^{6 r+2 s+3}-4 z^{6 r+2 s+5}+2 z^{6 r+2 s+6}-z^{6 r+2 s+7}-5 z^{9 r+2 s+4}+13 z^{9 r+2 s+5}-13 z^{9 r+2 s+6}+5 z^{9 r+2 s+7}-2 z^{12 r+2 s+5}+3 z^{12 r+2 s+9}-4 z^{6 r+4}+6 z^{6 r+5}+5 z^{6 r+6}-5 z^{6 r+7}+2 z^{9 r+4}-z^{9 r+5}-5 z^{9 r+6}+7 z^{9 r+7}-3 z^{9 r+8}-2 z^{12 r+7}-z^{12 r+8}+z^{12 r+9}-2 z^{s+1}-2 z^{s+2}+4 z^{s+3}+z^{s+4}-2 z^{s+5}+z^s+z^5+z^4-2 z^3-2 z^2+z+1))/((-(7 z^s-2 z^{2 s}-35 z^{s+1}+61 z^{s+2}-47 z^{s+3}+23 z^{s+4}-12 z^{s+5}+3 z^{s+6}+18 z^{2 s+1}-39 z^{2 s+2}+20 z^{2 s+3}-4 z^{2 s+5}+z^{2 s+6}-z^6+2 z^5+z^4+3 z^3-z^2+z+1) z^{t+4}+(2 z^s+3 z^{2 s}-13 z^{s+1}+14 z^{s+2}+8 z^{s+3}-14 z^{s+4}+3 z^{s+5}+4 z^{2 s+1}-19 z^{2 s+2}+7 z^{2 s+3}+2 z^{2 s+4}+3 z^4-2 z^3-z^2+2 z+1) z^{2 t+5}-(-z^s+2 z^{2 s}+z^{s+1}-2 z^{s+2}+z^{s+3}+3 z^{s+4}-2 z^{s+5}-z^{2 s+3}+z^{2 s+4}+z^{2 s+5}+z^5-4 z^3) z^4) z^{12 r}-(z-1)^2 (-4 z^s+4 z^{s+1}+11 z^{s+2}-12 z^{s+3}+2 z^{t+1}+6 z^{t+2}-2 z^{t+3}-6 z^{t+4}+4 z^{s+t+1}-5 z^{s+t+2}-8 z^{s+t+3}+10 z^{s+t+4}+7 z^3+z^2-7 z-1) z^{3 r+1}+(z^s+z^{2 s}+5 z^{s+1}-31 z^{s+2}+41 z^{s+3}-16 z^{s+4}+z^{2 s+1}-z^{2 s+2}+2 z^{2 s+5}-(z^s-5 z^{s+1}+27 z^{s+2}-72 z^{s+3}+80 z^{s+4}-37 z^{s+5}+6 z^{s+6}+2 z^{2 s+2}+4 z^{2 s+3}-3 z^{2 s+4}+2 z^{2 s+5}+z^{2 s+6}+10 z^5-23 z^4+z^3+13 z^2-9 z+2) z^t+(-z^{2 s}+2 z^{s+1}-z^{s+2}-4 z^{s+3}+z^{s+4}+2 z^{s+5}+4 z^{2 s+2}-z^5-2 z^4+z^3+2 z^2-3 z) z^{2 t+1}+3 z^5+4 z^4-19 z^3+7 z^2+2 z) z^{6 r+2}-(z-1)^2 (-z^s+3 z^{2 s}-2 z^{s+1}-z^{s+2}+4 z^{s+3}-3 z^{2 s+3}+3 z^t+z^{t+1}-7 z^{t+2}+2 z^{t+3}+2 z^{t+4}+5 z^{s+t}-19 z^{s+t+1}+2 z^{2 (s+t+1)}+25 z^{s+t+2}-12 z^{s+t+3}+3 z^{s+t+4}+2 z^{2 s+t}+2 z^{2 s+t+1}-9 z^{2 s+t+2}+4 z^{2 s+t+3}+2 z^{2 s+t+4}-2 z^{2 t+1}-2 z^{2 t+2}+2 z^{2 t+3}+2 z^{2 t+4}-z^{s+2 t+1}+6 z^{s+2 t+2}-2 z^{s+2 t+3}-5 z^{s+2 t+4}-5 z^{2 s+2 t+1}+2 z^{2 s+2 t+3}-5 z^3+2 z^2+2 z) z^{9 r+3}+(z-1)^2 (7 z^s-6 z^{s+2}-z^{s+4}+6 z^{t+1}-3 z^{t+2}-5 z^{t+3}+z^{t+4}-7 z^{s+t+1}-z^{s+t+2}+7 z^{s+t+3}+z^{s+t+4}+z^4-z^3+3 z^2+4 z-6) z^{15 r+s+t+5}+(z-1)^2 (z+1) (3 z^s+3 z^{s+1}+3 z^{t+1}-4 z^{s+t+1}-3 z^{s+t+2}+z^{s+t+3}-z-2) z^{18 r+s+t+6}-(z-1)^2 (z+1) (3 z^{s+1}-6 z^{s+2}-3 z^{t+2}-3 z^{t+3}-z^{s+t+1}+4 z^{s+t+3}+4 z^2+3 z-1))\).
11. \([3a ;\; 3a;\; b;\; 3a;\; c]\), para \(a = 2r + 1\), \(b = 2s + 1\) e \(c = 2t + 1\), onde \(r, s, t \in \mathbb{N}\).
Since no face has even size, no face formation that starts at a vertex will end at a vertex.
We analyze face formations to determine the system needed to calculate the generating functions, considering in which generation each face starts and ends. Due to the odd parameters and the lack of symmetry at the vertex, the formula obtained is extensive and here we make a simplification,
\(V(z) = (z (-z^{6 r+1}-z^{6 r+2}-4 z^{6 r+3}-4 z^{6 r+4}+2 z^{9 r+4}-2 z^{9 r+5}+z^{12 r+5}+z^{12 r+6}-2 z^s-4 z^{s+1}-2 z^{s+2}+4 z^{6 r+s+1}+2 z^{6 r+s+2}+z^{2 (6 r+s+2)}+2 z^{6 r+s+3}+2 z^{2 (6 r+s+3)}+8 z^{6 r+s+4}+4 z^{9 r+s+3}-8 z^{9 r+s+4}+4 z^{9 r+s+5}-2 z^{12 r+s+3}-4 z^{12 r+s+5}-2 z^{12 r+s+6}-2 z^{6 r+2 s+1}-2 z^{6 r+2 s+2}-z^{6 r+2 s+3}-z^{6 r+2 s+4}-2 z^{9 r+2 s+3}+2 z^{9 r+2 s+4}+z^{12 r+2 s+3}+2 z^{12 r+2 s+5}+2 (z (2 z^{6 r}+z^{6 r+1}+z^{6 r+2}+4 z^{6 r+3}+2 z^{9 r+2}-4 z^{9 r+3}+2 z^{9 r+4}-z^{12 r+2}-2 z^{12 r+4}-z^{12 r+5}+2 (-(z (4 z^2-2 z+3)+1) z^{6 r}-2 (z-1)^3 z^{9 r+1}+(z (z (z+3)-2)+4) z^{12 r+2}-(z+1) z^{18 r+4}+z+1) z^s+(z (-2 (z-1)^2 z^{3 r}-(2 z^3+z^2+z+4) z^{6 r+1}+(z+1)^2 z^{12 r+3}+z^2+2)+1) z^{2 (3 r+s)}-z-2)-1) z^t+(2 (z-1) z^{3 r+2}+(z+1) (2 z^2+1) z^{6 r+2}+2 (z (-2 (z-1)^2 z^{3 r}-(2 z^3+z^2+z+4) z^{6 r+1}+(z+1)^2 z^{12 r+3}+z^2+2)+1) z^s+(z (-2 (z-1) z^{3 r}+(z+1) (z^2+4) z^{6 r+1}-(z+1)^3 z^{12 r+3}-1)-1) z^{2 s}-(z^2+z+2) z-2) z^{6 r+2 t+1}+z^2+3 z+3)+1)/(z (6 z^{3 r+1}-6 z^{3 r+3}+z^{6 r+2}+11 z^{6 r+3}+3 z^{6 r+4}-2 z^{9 r+3}-2 z^{9 r+4}+4 z^{9 r+5}-2 z^{12 r+5}-z^{12 r+6}+6 z^{s+1}+6 z^{s+2}+2 z^{3 r+s}-6 z^{3 r+s+1}-6 z^{3 r+s+2}+10 z^{3 r+s+3}-2 z^{6 r+s+2}-3 z^{2 (6 r+s+2)}-20 z^{6 r+s+3}-z^{2 (6 r+s+3)}-2 z^{6 r+s+4}+2 z^{9 r+s+2}+4 z^{9 r+s+3}-2 z^{9 r+s+4}-4 z^{9 r+s+5}+2 z^{12 r+s+3}+4 z^{12 r+s+4}+4 z^{12 r+s+5}+2 z^{12 r+s+6}+z^{6 r+2 s+1}+3 z^{6 r+2 s+2}+3 z^{6 r+2 s+3}+2 z^{6 r+2 s+4}-2 z^{9 r+2 s+2}+2 z^{9 r+2 s+5}-2 z^{12 r+2 s+3}-3 z^{12 r+2 s+5}+2 (-(z-1) ((z (8 z-1)-1) z^s-(5 z+2) z+1) z^{3 r}+((z ((23-2 z) z-6)+3) z^s-(z (z+10)+1) z-z^{2 s} (z+1) (z^2+z+1)) z^{6 r+1}-(z-1) (((z-14) z+1) z^s+(z+1) (z+2) z^{2 s}+(2 z+3) z+1) z^{9 r+2}+((z (-3 (z-2) z-23)+2) z^s+(z (z+10)+1) z^{2 s}+(z (z+2)+2) z+1) z^{12 r+3}-(z-1) (((z-2) z-5) z^s-(z+1) z+8) z^{15 r+s+4}+(-3 (z+1) z^s+2 z+4) z^{18 r+s+5}+(-2 (2 z+1) z^s+3 z+3) z) z^t+(2 (z (-(z-1) (z+1) (z+2) z^{3 r}+(z (z+10)+1) z^{6 r+1}-(z-1) ((z-2) z-5) z^{9 r+2}-3 (z+1) z^{12 r+3}-(z+2) z-2)-1) z^s-((z+1) z^{3 r+1}+1) (z ((z+5) z^{3 r}+(5 z-2) z^{6 r+1}+(z-4) (z+1) z^{9 r+2}-2)-1) z^{2 s}+(2 (z^3-1) z^{3 r}-(z+2) (z^2+z+1) z^{6 r+1}+(2 z+3) z+3) z+1) z^{6 r+2 t+1}-4 z^2-7 z-2)+1)\).
12. \([2a;\; 2b ;\; 2b ;\; 2a ;\; c]\), para \(a = 2r\), \(b = 2s\) e \(c = 2t\), onde \(r, s, t \in \mathbb{N}\).
This is a particular case of the even family, and since the vertex is also a particular case of \([2a;\; 2b ;\; 2b ;\; 2a ;\; c]\), the formula obtained here is easier to apply.
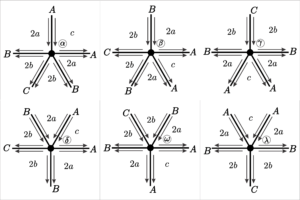
| Face | Start of the edge | Sinze | End of the edge | End of the vertex |
|---|---|---|---|---|
| \(T_1\) | between edge \(A\) and \(B\) | \(2a\) | between edge \(A\) and \(B\) | \(\delta\) |
| \(T_2\) | between edge \(B\) and \(C\) | \(2b\) | between edge \(B\) and \(C\) | \(\omega\) |
| \(T_3\) | between edge \(A\) and \(A\) | \(c\) | between edge \(A\) and \(A\) | \(\lambda\) |
| Vertex position | Generated positions | Started faces |
|---|---|---|
| \(\alpha\) | \(\alpha + 2\beta + \gamma\) | \(T_1 + 2T_2\) |
| \(\beta\) | \(2\alpha + \beta + \gamma\) | \(T_1 + T_2 + T_3\) |
| \(\gamma\) | \(2\alpha + 2\beta\) | \(2T_1 + T_3\) |
| \(\delta\) | \(\alpha + \beta + \gamma\) | \(T_1 + T_2\) |
| \(\omega\) | \(2\alpha + \beta\) | \(T_1 + T_3\) |
| \(\lambda\) | \(2\beta + \lambda\) | \(2T_2\) |
Thus, we conclude that the tiling vertices can be counted using the function below,
\(V(z) = (\left(1-z^{2r}\right) \left(1-z^{2s}\right) \left(1-z^t\right))/(1-4z+3z(z^t)+(2 z+1) \left(z^{2 r}+z^{2 s}\right)-(z+2) \left(z^{2 r+t}+z^{2 s+t}\right)-3(z^{2 r+2 s})+4 z^{2 r+2 s+t}-z^{r+s+t+1})\).
13. \([2a;\; 2b ;\; 2b ;\; 2a ;\; c]\), para \(a = 2r+2\), \(b = 2s + 1\) e \(c = 2t + 1\), onde \(r, s, t \in \mathbb{N}\).
Since there are odd parameters in this tiling, we have, in addition to the vertex positions shown in Figure 18, vertex positions containing fraternal edges. Such positions are shown in Figure 19.
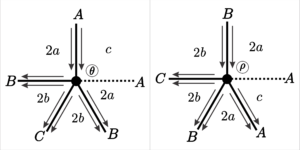
| Face | Start of the edge | Size | Edn of the edge | End of the vertex |
|---|---|---|---|---|
| \(T_1\) | between edges \(A\) and \(B\) | \(2a\) | between edges \(A\) and \(B\) | \(\delta\) |
| \(T_2\) | between edges \(B\) and \(C\) | \(2b\) | between edges \(B\) and \(C\) | \(\omega\) |
| \(T_3\) | between edges \(A\) and \(A\) | \(c\) | fraternal edge \(A\) | \(2\theta\) |
| \(T_4\) | fraternal edge \(A\) | \(2a\) | fraternal edge \(A\) | \(2\rho\) |
| \(T_5\) | fraternal edge \(A\) | \(c\) | between edges \(A\) and \(A\) | \(\lambda\) |
| Vertex position | Generated positions | Started faces |
|---|---|---|
| \(\omega\) | \(2\beta + \gamma\) | \(2T_2\) |
| \(\rho\) | \(\alpha + \beta + \gamma\) | \(T_1 + T_2\) |
Solving the system formed from the information contained in the tables, we add all the solutions, add \(1\) to this sum and obtain the function for general vertex count,
\(V(z)=((1+z)(1-z^a)(1-z^b)(1+z-2 z^{t+1}+2 z^{2 r+t+1}-z^{2 r+2 t+1}-z^{2 (r+t+1)}))/(1-3z-4 z^2+6 z^{t+2}+2 z^{2 r+t+1}-8 z^{2r+t+2}+(2 z^2+3 z+1) (z^a+z^b)-(3 z+3) (z^{a+b}-z^{a+2t}) -(2 z^2+4 z) (z^{a+t}+z^{b+t}) +(4 z^2+2 z) (z^{b+2r+t}+z^{4r+t+2})-(z^2+3 z+2) (z^{b+2r+c}+z^{4r+c+2})+8 z^{b+a+t+1}-2 z^{b+a+t+2}-6z^{b+4r+t+3}+4z^{b+4r+c+2}+3z^{b+2a+2t}-z^{b+2a+c})\).
14. \([2a;\; 2b ;\; 2b ;\; 2a ;\; c]\), for \(a = 2r + 1\), \(b = 2s+2\) and \(c = 2t + 1\), with \(r, s, t \in \mathbb{N}\).
Here we have two odd parameters, so the tiling has other types of vertex positions with fraternal edges, as shown in Figure 20.
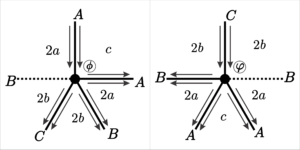
| Face | Start of the edge | Size | End of the edge | End of the vertex |
|---|---|---|---|---|
| \(T_1\) | between edges \(A\) and \(B\) | \(2a\) | between edges \(A\) and \(B\) | \(\delta\) |
| \(T_2\) | between edges \(B\) and \(C\) | \(2b\) | between edges \(B\) and \(C\) | \(\omega\) |
| \(T_3\) | between edges \(A\) and \(A\) | \(c\) | fraternal edge \(A\) | \(2\theta\) |
| \(T_4\) | fraternal edge \(A\) | \(2a\) | fraternal edge \(B\) | \(2\phi\) |
| \(T_5\) | fraternal edge \(B\) | \(2b\) | fraternal edge \(B\) | \(2\varphi\) |
| \(T_6\) | fraternal edge \(B\) | \(2a\) | fraternal edge \(A\) | \(2\rho\) |
| \(T_7\) | fraternal edge \(A\) | \(c\) | between edges \(A\) and \(A\) | \(\lambda\) |
| Vertex position | Generated positions | Started faces |
|---|---|---|
| \(\phi\) | \(\alpha + \beta + \gamma\) | \(T_1 + T_2\) |
| \(\varphi\) | \(2\alpha + \beta\) | \(T_1 + T_3\) |
Using generating functions, we obtain the following formula for the enumeration of vertices,
\(V(z) = ((1+z) (1-z^a) (1-z^b) (-z^{2 (2 r+s+t+1)}+2 z^{4 r+2 s+t+1}-z^{4 r+2 s+2 t+1}-2 z^{t+1}+z+1))/(1-3z-4 z^2+6 z^{t+2}+8 z^{a+b+t+1}-2 z^{a+b+t+2}+(2 z^2+3 z+1) (z^a+z^b)-(3 z+3) (z^{a+b}-z^{2 a+2 s+2 t}) -(2 z^2+4 z) (z^{a+t}+z^{b+t})-(z^2+3 z+2) (z^{2 a+c+4 s}+z^{b+6 r+2 t})+(4 z^2+2 z) (z^{6 r+2 s+t+1}+z^{4 r+4 s+t+2}) +2 z^{4 r+2 s+t+1}-8 z^{4 r+2 s+t+2}-6 z^{6 r+4 s+t+4}+4 z^{6 r+4 s+2 t+4}+3 z^{6 r+4 s+2 t+5}-z^{6 r+4 s+2 t+6})\).
15. \([2a;\; 2b ;\; 2b ;\; 2a ;\; c]\), com \(a = 2r +1\), \(b = 2s + 1\) e \(c = 2t + 1\), onde \(r, s, t \in \mathbb{N}\).
If all parameters are odd, the tiling has all vertex positions with fraternal edges. Thus, in addition to all the vertices already considered for tiling with this type of vertex, it is also necessary to consider the position shown in Figure 21.
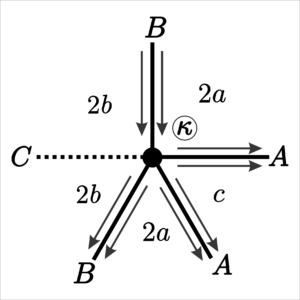
| Face | Start of the edge | Size | End of the edge | End of the vertex |
|---|---|---|---|---|
| \(T_1\) | between edges \(A\) and \(B\) | \(2a\) | between edges \(A\) and \(B\) | \(\delta\) |
| \(T_2\) | between edges \(B\) and \(C\) | \(2b\) | between edges \(B\) and \(C\) | \(\omega\) |
| \(T_3\) | between edges \(A\) and \(A\) | \(c\) | fraternal edge \(A\) | \(2\theta\) |
| \(T_4\) | fraternal edge \(A\) | \(2a\) | fraternal edge \(B\) | \(2\phi\) |
| \(T_5\) | fraternal edge \(B\) | \(2b\) | fraternal edge \(C\) | \(2\kappa\) |
| \(T_6\) | fraternal edge \(C\) | \(2b\) | fraternal edge \(B\) | \(2\varphi\) |
| \(T_7\) | fraternal edge \(B\) | \(2a\) | fraternal edge \(A\) | \(2\rho\) |
| \(T_8\) | fraternal edge \(A\) | \(c\) | between edges \(A\) and \(A\) | \(\lambda\) |
| Vertex position | Generated position | Started faces |
|---|---|---|
| \(\kappa\) | \(2\alpha + \beta\) | \(T_1 + T_3\) |
Thus, solving the system involving the generating functions of all vertex positions, it is enough to add the results found (plus the vertex of the origin) to obtain the function corresponding to the count of all vertices,
\(V(z) = ((1+z)(1-z^a)(1-z^b)(-z^{2 (2 r+2 s+t)}+2 z^{4 r+4 s+t}-z^{4 r+4 s+2 t+1}-2 z^{t+1}+z+1))/(1-3z-4 z^2+6 z^{t+2}+8 z^{a+b+t+1}-2 z^{a+b+t+2}+(2 z^2+3 z+1) (z^a+z^b)-(3 z+3) (z^{a+b}-z^{4 r+4 s+c})-(2 z^2+4 z) (z^{a+t}+z^{b+t})+(4 z^2+2 z) (z^{6 r+4 s+t}+z^{4 r+6 s+t})-(2+3z+z^2) (z^{6 r+4 s+c}+z^{4r+6 s+c})+2 z^{4 r+4 s+t}-8 z^{4 r+4 s+t+1}-6 z^{6 r+6 s+t+2}+4 z^{6 r+6 s+2 t+2}+3 z^{6 r+6 s+2 t+3}-z^{6 r+6 s+2 t+4})\).
16. \([4a;\;b;\;4a\;2c;\;2d]\), para \(a = 2r\),\(b = 2s\), \(c = 2t\) e \(d = 2p\), com \(r, s, t, p \in \mathbb{N}\).
The vertex has no symmetry and all parameters considered are even, so we only have \(5\) face formations: the faces that start and end in vertices. The vertex positions are shown in Figure 22.
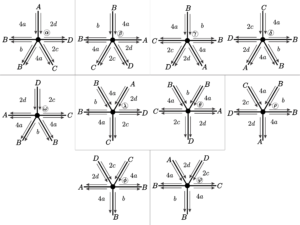
| Face | Starting of the edge | Size | End of the edge | End of the vertex |
|---|---|---|---|---|
| \(T_1\) | between edges \(A\) and \(B\) | \(4a\) | between edges \(A\) and \(B\) | \(\lambda\) |
| \(T_2\) | between edges \(B\) and \(B\) | \(b\) | between edges \(B\) and \(B\) | \(\theta\) |
| \(T_3\) | between edges \(B\) and \(C\) | \(4a\) | between edges \(B\) and \(C\) | \(\rho\) |
| \(T_4\) | between edges \(C\) and \(D\) | \(2c\) | between edges \(C\) and \(D\) | \(2\phi\) |
| \(T_5\) | between edges \(A\) and \(D\) | \(2d\) | between edges \(A\) and \(D\) | \(\varphi\) |
| Vertex position | Generated position | Started faces |
|---|---|---|
| \(\alpha\) | \(\beta + \gamma + \delta + \omega\) | \(T_2 + T_3 + T_4\) |
| \(\beta\) | \(\alpha + \beta + \delta + \omega\) | \(T_3 + T_4 + T_5\) |
| \(\gamma\) | \(\alpha + \gamma + \delta + \omega\) | \(T_1 T_4 + T_5\) |
| \(\delta\) | \(\alpha + \beta + \gamma + \omega\) | \(T_1 + T_2 + T_5\) |
| \(\omega\) | \(\alpha + \beta + \gamma + \delta\) | \(T_1 + T_2 + T_3\) |
| \(\lambda\) | \(\beta + \delta + \omega\) | \(T_3 + T_4\) |
| \(\theta\) | \(\alpha + \delta + \omega\) | \(T_4 + T_5\) |
| \(\rho\) | \(\alpha + \gamma + \omega\) | \(T_1 + T_5\) |
| \(\phi\) | \(\alpha + \beta + \gamma\) | \(T_1 + T_2\) |
| \(\varphi\) | \(\beta + \gamma + \delta\) | \(T_2 + T_3\) |
The information from Table 28 and 27, when used in the counting method, provides the following function for counting vertices,
\(V(z) = ((1+z)(1-z^{2a})(1-z^c)(1-z^d)(1-z^s))/(1-4z+3z(z^c+z^d+z^s)-(1+2z)(-z^{2a}+z^{c+d}+z^{c+s}+z^{d+s})-(2+z)(z^{2a+c}+z^{2a+d}+z^{2a+s}-z^{c+d+s})+3(z^{2a+c+d}+z^{2a+c+s}+z^{2a+d+s})-4z^{2a+c+d+s}+z^{2a+c+d+s+1})\).
17. \([4a;\; b;\; 4a;\; 2c;\; 2d]\), with \(a = 2r + 1\), \(b = 2s\), \(c = 2t\) and \(d = 2p\), where \(r, s, t, p \in \mathbb{N}\).
For such parameters, we have the same face positions as in item \(16\). The parity of \(a\) only affects the faces of size \(4a\), determining different final vertices according to the parity.
| Face | Star of the edge | Size | End of the edge | End of the vertex |
|---|---|---|---|---|
| \(T_1\) | between edges \(A\) and \(B\) | \(4a\) | between edges \(B\) and \(C\) | \(\rho\) |
| \(T_2\) | between edges \(B\) and \(B\) | \(b\) | between edges \(B\) and \(B\) | \(\theta\) |
| \(T_3\) | between edges \(B\) and \(C\) | \(4a\) | between edges \(A\) and \(B\) | \(\lambda\) |
| \(T_4\) | between edges \(C\) and \(D\) | \(2c\) | between edges \(C\) and \(D\) | \(\phi\) |
| \(T_5\) | between edges \(A\) and \(D\) | \(2d\) | between edges \(A\) and \(D\) | \(\varphi\) |
We apply the method and conclude that the function to count the vertices in this case is the same as the function used in item \(16\),
\(V(z) = ((1+z)(1-z^{2a})(1-z^c)(1-z^d)(1-z^s))/(1-4z+3z(z^c+z^d+z^s)-(1+2z)(-z^{2a}+z^{c+d}+z^{c+s}+z^{d+s})-(2+z)(z^{2a+c}+z^{2a+d}+z^{2a+s}-z^{c+d+s})+3(z^{2a+c+d}+z^{2a+c+s}+z^{2a+d+s})-4z^{2a+c+d+s}+z^{2a+c+d+s+1})\).
18. \([4a;\;b;\;4a\;2c;\;2d]\), for \(a = 2r+2\), \(b = 2s + 1\), \(c = 2t\) and \(d = 2p\), with \(r, s, t, p \in \mathbb{N}\).
If we change the parity of \(b\), we end up with faces on fraternal edges. Thus, it is necessary to add to our studies the positions of vertices shown in Figure 24.
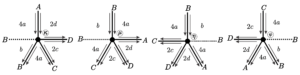
| Face | Start of the edge | Size | End of the edge | End of the vertex |
|---|---|---|---|---|
| \(T_1\) | between edges \(A\) and \(B\) | \(4a\) | between edges \(A\) and \(B\) | \(\lambda\) |
| \(T_2\) | between edges \(B\) and \(B\) | \(b\) | fraternal edge \(B\) | \(\mu + \eta\) |
| \(T_3\) | between edges \(B\) and \(C\) | \(4a\) | between edges \(B\) and \(C\) | \(\rho\) |
| \(T_4\) | between edges \(C\) and \(D\) | \(2c\) | between edges \(C\) and \(D\) | \(\phi\) |
| \(T_5\) | between edges \(A\) and \(D\) | \(2d\) | between edges \(A\) and \(D\) | \(\varphi\) |
| \(T_6\) | fraternal edge \(B\) | \(4a\) | fraternal edge \(B\) | \(\kappa + \psi\) |
| \(T_7\) | fraternal edge \(B\) | \(b\) | between edges \(B\) and \(B\) | \(\theta\) |
| Vertex position | Generated positions | started faces |
|---|---|---|
| \(\kappa\) | \(\beta + \delta + \omega\) | \(T_3 + T_4\) |
| \(\mu\) | \(\alpha + \delta + \omega\) | \(T_4 + T_5\) |
| \(\eta\) | \(\alpha + \delta + \omega\) | \(T_4 + T_5\) |
| \(\psi\) | \(\alpha + \gamma + \omega\) | \(T_1 + T_5\) |
We use the counting method with the information from the tables and simplify the function found. Here is the result obtained,
\(V(z)=((1+z)(1-z^c) (1-z^d) (1-z^{2a}) (1+z-2z^{s+1}+2z^{4r+s+3}-z^{4r+2s+3}-z^{4r+2s+4}))/(1-3z-4 z^2 +6 z^{s+2}+2 z^{4 r+s+3}-8 z^{4 r+s+4}+(3 z^2+3) (z^c+z^d) -(2 z^2+3 z+1) (-z^{2a}+z^{c+d}+z^{c+4r+2s+3}+z^{d+4r+2s+3})-(z^2+3 z+2) (z^{2a+c}+z^{2a+d}-z^{c+d+4 r+2 s+3}+z^{8 r+2 s+7})+(6 z+6) (z^{2a+c+s}+z^{2 a+d+s})+(3 z+3) (z^{c+8 r+2 s+7}+z^{d+8 r+2 s+7}+z^{4 r+2 s+4}+ z^{2 a+c+d})+(2 z^2+4 z) (z^{c+d+s}-z^{c+8 r+s+6}-z^{d+8 r+s+6}-z^{4 r+s+4})-(4 z^2+2 z) (z^{c+d+4 r+s+2}+z^{c+s}+z^{d+s}-z^{8 r+s+6})-8 z^{c+d+2a+s+1}+2 z^{c+d+2a+s+2}+6 z^{c+d+8 r+s+7}-4 z^{c+d+8 r+2 s+7}-3z^{4a+c+d+2s}+z^{4a+c+d+b})\).
19. \([4a;\; b;\; 4a;\; 2c;\; 2d]\), for \(a = 2r +1\), \(b = 2s + 1\), \(c = 2t\) and \(d = 2p\), with \(r, s, t, p \in \mathbb{N}\).
Changing the parity of \(a\) does not create new vertex positions, it just changes the final position of faces of size \(4a\).
| Face | Start of the edge | Size | End of the edge | End of the vertex |
|---|---|---|---|---|
| \(T_1\) | between edges \(A\) e \(B\) | \(4a\) | between edges \(B\) and \(C\) | \(\rho\) |
| \(T_2\) | between edges \(B\) and \(B\) | \(b\) | between edges \(B\) | \(\mu + \eta\) |
| \(T_3\) | between edges \(B\) and \(C\) | \(4a\) | between edges \(A\) and \(B\) | \(\lambda\) |
| \(T_4\) | between edges \(C\) and \(D\) | \(2c\) | between edges \(C\) and \(D\) | \(\phi\) |
| \(T_5\) | between edges \(A\) and \(D\) | \(2d\) | between edges \(A\) an \(D\) | \(\varphi\) |
| \(T_6\) | fraternal edge \(B\) | \(4a\) | fraternal edge \(B\) | \(\kappa + \psi\) |
| \(T_7\) | fraternal edge \(B\) | \(b\) | between edges \(B\) and \(B\) | \(\theta\) |
We calculate the generating functions and obtain a vertex count function equal to the one obtained in item \(18\),
\(V(z) = ((1+z)(1-z^{2a})(1-z^c)(1-z^d)(1+z-2z^{s+1}+2z^{4r+s+1}-z^{4r+2s+1}-z^{4r+2s+2}))/(1-3z-4 z^2+6 z^{s+2}+2 z^{4r+s+1}-8 z^{4r+s+2}+(3 z^2+3 z) (z^c+z^d)-(2 z^2+3 z+1) (-z^{2 a}+z^{c+d}+z^{c+4 r+2 s+1}+z^{d+4 r+2 s+1}) +(3 z+3) (z^{2 a+c+d}+z^{2 a+2 s}+z^{c+8 r+2 s+3}+z^{d+8 r+2 s+3})+(2 z^2+4 z) (-z^{2 a+s}+z^{c+d+s}-z^{c+8 r+s+2}-z^{d+8 r+s+2})-(z^2+3 z+2) (z^{2 a+c}+z^{2 a+d}-z^{c+d+4 r+2 s+1}+z^{8 r+2 s+3})+(6 z+6) (z^{2 a+c+s}+z^{2 a+d+s})-(4 z^2+2 z) (z^{c+d+4 r+s}+z^{c+s}+z^{d+s}-z^{8 r+s+2})-8 z^{2 a+c+d+s+1}+2 z^{2 a+c+d+s+2}+6 z^{c+d+8r+s+3}-4 z^{c+d+8 r+2 s+3}-3 z^{4 a+c+d+2 s}+z^{4 a+b+c+d})\).
20. \([2a;\; 2b;\; 2c;\;2d;\;2e]\).
In this kind of vertex we have that no face is symmetric to the other, around a vertex. This fact makes the tiling present a pattern for the equations involving the generating functions.
| Face | Start edge | Size | Ending edge | Ending vertex |
|---|---|---|---|---|
| \(T_1\) | \(A\) e \(B\) | \(2a\) | \(B\) e \(C\) | \(\lambda\) |
| \(T_2\) | \(B\) e \(C\) | \(2b\) | \(B\) e \(C\) | \(\theta\) |
| \(T_3\) | \(C\) e \(D\) | \(2c\) | \(C\) e \(D\) | \(\rho\) |
| \(T_4\) | \(D\) e \(E\) | \(2d\) | \(D\) e \(E\) | \(\phi\) |
| \(T_5\) | \(E\) e \(A\) | \(2e\) | \(E\) e \(A\) | \(\varphi\) |
| Vertex position | Generated position | Started faces |
|---|---|---|
| \(\alpha\) | \(\beta + \gamma + \delta + \omega\) | \(T_2 + T_3 + T_4\) |
| \(\beta\) | \(\alpha + \gamma + \delta + \omega\) | \(T_3 + T_4 + T_5\) |
| \(\gamma\) | \(\alpha + \beta + \delta + \omega\) | \(T_1 T_4 + T_5\) |
| \(\delta\) | \(\alpha + \beta + \gamma + \omega\) | \(T_1 + T_2 + T_5\) |
| \(\omega\) | \(\alpha + \beta + \gamma + \delta\) | \(T_1 + T_2 + T_3\) |
| \(\lambda\) | \(\beta + \delta + \omega\) | \(T_3 + T_4\) |
| \(\theta\) | \(\alpha + \delta + \omega\) | \(T_4 + T_5\) |
| \(\rho\) | \(\alpha + \beta + \omega\) | \(T_1 + T_5\) |
| \(\phi\) | \(\alpha + \beta + \gamma\) | \(T_1 + T_2\) |
| \(\varphi\) | \(\beta + \gamma + \delta\) | \(T_2 + T_3\) |
Summing the generating functions of all the face positions (plus the
origin), we find the formula for the sum of the tiling vertices:
\(V(z)=(1+z)(1-z^a)(1-z^b)(1-z^c)(1-z^d)(1-z^e)/(1-4z+3z(z^a+z^b+z^c+z^d+z^e)-(1+2z)(z^{a+b}+z^{a+c}+z^{a+d}+z^{a+e}+z^{b+c}+z^{b+d}+z^{b+e}+z^{c+d}+z^{c+e}+z^{d+e})+(2+z)(z^{a+b+c}+z^{a+b+d}+z^{a+c+d}+z^{a+c+e}+z^{a+d+e}+z^{a+b+e}+z^{b+c+d}+z^{b+c+e}+z^{b+d+e}+z^{c+d+e})-3(z^{a+b+c+d}+z^{a+b+c+e}+z^{a+b+d+e}+z^{a+c+d+e}+z^{b+c+d+e})+4
z^{a+b+c+d+e}-z^{a+b+c+d+e+1})\).
The functions for counting vertices of tilings with even parameters
showed a formation pattern, based on the sum of the coefficients in the
powers of \(z\). Note that this feature
may be a consequence of valence being an odd number, or even being a
prime number. Thus, in the next section, we study the formulas for
counting tilings of valence \(6\) with
even parameters, to verify if they present the same patterns found in
valence \(5\).
In this section, we present the formulas for counting vertices of uniform tilings of valence \(6\) with even parameters. We proceed similarly to the cases performed for valence \(5\). We emphasize that we will always be thinking of natural parameters that satisfy (1).
Note that all analyzed items are particular cases of the family \([2a;\; 2b;\; 2c;\; 2d;\; 2e;\; 2f]\), however, the formulas obtained for the even cases of other families are simpler to apply.
By means of the Lemma 1, we guarantee that, when constructing the tiling from a fixed vertex \(v\), no vertex has more than two arrival edges. Furthermore, using this result, we directly obtain the equivalent of Corollary 2 for tilings with valence \(n \geq 6\).
Corollary 3. Let \(\mathcal{T}\) be a uniform tiling of the hyperbolic plane with valence \(n\), with \(n \geq 6\). Consider the construction of the tiling from a fixed vertex \(v\) of \(\mathcal{T}\).
If \(w \in \mathcal{T}\) has only one arrival edge and two fraternal edges, then at least one of the faces enclosed by these fraternal edges is triangular;
If \(w \in \mathcal{T}\) has two arriving edges and has any fraternal edges, then the face formed by this fraternal edge is triangular.
Proof.
Let \(w \in \mathcal{T}\) be a vertex in the generation $m$ with only one arrival edge and two fraternal edges and consider $p$ as the vertex of the generation $m-1$ of the arrival edge of \(w\). Suppose that one of the faces enclosed by a fraternal edge is not triangular.
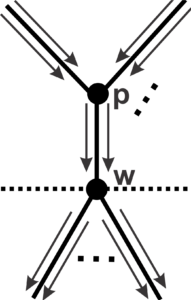
We insert a leading edge to \(p\) to construct such a face. By Lemma 1, there are at most two arrival edges in $p$ (and these are consecutive). Thus, we have at least $3$ edges that need to be inserted into \(p\) after the arrival edges and at most one can be a fraternal edge (this must be next to an arrival edge). We conclude that the other following edges are starting edges and, therefore, we form a triangle between two starting edges from \(p\) and a fraternal edge from $w$. Therefore, at least one of the faces ending in fraternal edges is triangular.
Let \(w \in \mathcal{T}\) be a vertex in the generation \(m\) with two arrival edges and a fraternal edge. We define by \(p\) the vertex of the generation \(m-1\) of the arrival edge of \(w\) next to the fraternal edge.
As \(w\) closes a face, we insert a leading edge to \(p\) to construct such a face, in the case where this face is not triangular. If \(w\) closes a triangle, then we insert a fraternal edge between the edge connecting \(w\) to \(p\) and the arriving edge at \(p\). By the Lemma 1, there are only two arrival edges in \(p\), which implies that we must add at least two edges (with at most one fraternal, and this one must be placed next to an arrival edge) on the side where we have the fraternal edge. Therefore, we form a triangle with two starting edges starting at \(p\) and the fraternal edge of \(w\).
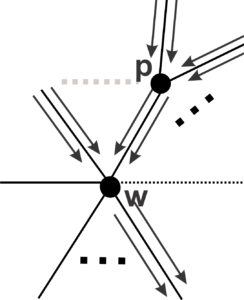
◻
Since we are considering even parameters, all faces of the worked tilings have size greater than \(3\). Thus, no vertex position has fraternal edges. We list below the formulas obtained for the cases studied.
\([m;\; n;\; m;\; n;\; m;\; n]\), for \(m = 2p\) and \(n = 2q\). \[V(z) = \frac{(1+z)(1-z^p)(1-z^q)}{1-5z-5z^{p+q}+(2z+2)(z^p+z^q)+z^{p+q+1}}.\]
\([2m;\; 2n;\; 2p;\; 2q;\; 2r;\;
2s]\).
\(V(z)
=((1+z)(1-z^m)(1-z^n)(1-z^p)(1-z^q)(1-z^r)(1-z^s))/
(1-5z+4z(z^m+z^n+z^p+z^q+z^r+z^s)-(3z+1)(z^{m+n}+z^{m+p}+z^{m+q}+z^{m+r}+z^{m+s}+z^{n+p}+z^{n+q}+z^{n+r}+z^{n+s}+z^{p+q}+z^{p+r}+z^{p+s}+z^{q+r}+z^{q+s}+z^{r+s})+(2z+2)(z^{m+n+p}+z^{m+n+q}+z^{m+n+r}+z^{m+n+s}+z^{m+p+q}+z^{m+p+r}+z^{m+p+s}+z^{m+q+r}+z^{m+q+s}+z^{m+r+s}+z^{n+p+q}+z^{n+p+r}+z^{n+p+s}+z^{n+q+r}+z^{n+q+s}+z^{n+r+s}+z^{p+q+r}+z^{p+q+s}+z^{p+r+s}+z^{q+r+s})-(z+3)(z^{m+n+p+q}+z^{m+n+p+r}+z^{m+n+p+s}+z^{m+n+q+r}+z^{m+n+q+s}+z^{m+n+r+s}+z^{m+p+q+r}+z^{m+p+q+s}+z^{m+p+r+s}+z^{m+q+r+s}+z^{n+p+q+r}+z^{n+p+q+s}+z^{n+p+r+s}+z^{n+q+r+s}+z^{p+q+r+s})+4(z^{m+n+p+q+r}+z^{m+n+p+q+s}+z^{m+n+p+r+s}+z^{m+n+q+r+s}+z^{m+p+q+r+s}+z^{n+p+q+r+s})-5z^{m+n+p+q+r+s}+z^{m+n+p+q+r+s+1}).\)
\([2m;\; 2n;\; p;\; 2n;\; 2m;\;
q]\), for \(m = 2a\), \(n = 2b\), \(p =
2c\) and \(q = 2d\).
\(V(z)
=((1+z)(1-z^{2a})(1-z^{2b})(1-z^c)(1-z^d))/
(1-5z+4z(z^d+z^c)-(3z+1)(z^{d+c}-z^{2a}-z^{2b})+(2z+2)(-z^{2a+c}-z^{2a+d}-z^{2b+c}-z^{2b+d})-(z+3)(-z^{c+d+2a}-z^{c+d+2b}+z^{2a+2b})+4(z^{2a+2b+c}+z^{2a+2b+d})-5z^{c+d+2a+2b}+z^{2a+2b+c+d+1}).\)
\([3m;\; 3m;\; 3n;\; 3m;\; 3n;\; 3n]\), for \(m = 3a\) and \(n= 3b\). \[V(z) = \frac{(1+z)(1-z^{3a})(1-z^{3b})}{1-5z+(2z+2)(z^{3a}+z^{3b})-5z^{3(a+b)}+z^{3a+3b+1}}.\]
\([6m;\; n;\; 6m;\; 6m;\; 2p;\;
2q]\), for \(n = 2b\), \(p = 2c\) and \(q
= 2d\).
\(V(z)
=((1+z)(1-z^{3m})(1-z^b)(1-z^p)(1-z^q))/
(1-5z+4z(z^b+z^p+z^q)-(3z+1)(z^{b+p}+z^{b+q}+z^{p+q})+(2z+2)(z^{b+p+q}+z^{3m})-(z+3)(z^{3m+b}+z^{3m+p}+z^{3m+q})+4(z^{3m+b+p}+z^{3m+b+q}+z^{3m+p+q})-5z^{3m+b+p+q}+z^{3m+b+p+q+1})\).
\([4m;\; n;\; 4m;\; 2p;\; 2q;\;
2r]\), for \(n = 2a\).
\(V(z)
=((1+z)(1-z^{2m})(1-z^a)(1-z^p)(1-z^q)(1-z^r))/
(1-5z+4z(z^a+z^p+z^q+z^r)-(3z+1)(z^{a+p}+z^{a+q}+z^{a+r}+z^{p+q}+z^{p+r}+z^{q+r}-z^{2m})+(2z+2)(z^{a+p+q}+z^{a+p+r}+z^{a+q+r}+z^{p+q+r}-z^{2m+a}-z^{2m+p}-z^{2m+r}-z^{2m+q})-(z+3)(-z^{2m+a+p}-z^{2m+a+q}-z^{2m+a+r}-z^{2m+p+q}-z^{2m+p+r}-z^{2m+q+r}+z^{a+p+q+r})+4(-z^{2m+a+p+q}-z^{2m+a+p+r}-z^{2m+a+q+r}-z^{2m+p+q+r})+5z^{2m+a+p+q+r}-z^{2m+a+p+q+r+1})\).
\([5m;\; 5m;\; 5m;\; 5m;\; 5m;\; n]\), for \(m = 2a\) e \(n = 2b\). \[V(z) = \frac{(z+1)(1-z^{5a})(1-z^b)}{1-5z+4z(z^{b})+4(z^{5a})-5z^{5a+b}+z^{5a+b+1}}.\]
\([4m;\; 4m;\; 4m;\; n;\; 4m;\;
p]\), for \(m = 2a\), \(n = 2b\) and \(p
= 2c\).
\(V(z)
=((1+z)(1-z^{4a})(1-z^b)(1-z^c))/(1-5z+4z(z^b+z^c)-(3z+1)(z^{b+c})-(z+3)(-z^{4a})+4(-z^{4a+b}-z^{4a+c})+5z^{4a+b+c}-z^{4a+b+c+1})\).
\([3m;\; 3m;\; 3m;\; 3n;\; 3n;\; 3n]\), for \(m = 2a\) and \(n = 2b\). \[V(z) = \frac{(1+z)(1-z^{3a})(1-z^{3b})}{1-5z+(2z+2)(z^{3a}+z^{3b})-5z^{3(a+b)}+z^{3a+3b+1}}.\]
\([3m;\; n;\; 3m;\; p;\; 3m;\;
q]\), for \(m = 2a\), \(n = 2b\), \(p =
2c\) and \(q = 2d\).
\(V(z)
=((1+z)(1-z^{3a})(1-z^b)(1-z^c)(1-z^d))/
(1-5z+4z(z^b+z^c+z^d)-(3z+1)(z^{b+c}+z^{b+d}+z^{c+d})+(2z+2)(z^{b+c+d}+z^{3a})-(z+3)(z^{3a+b}+z^{3a+c}+z^{3a+d})+4(z^{3a+b+c}+z^{3a+b+d}+z^{3a+c+d})-5z^{3a+b+c+d}+z^{3a+b+c+d+1})\).
\([3m;\; 3m;\; 3m;\; 2n;\; p;\;
2n]\), for \(m = 2a\), \(n = 2b\) and \(p
= 2c\).
\(V(z) =((1+z)(1-z^{3a})(1-z^{2b})(1-z^{c}))/
(1-5z+4z(z^c)-(3z+1)(-z^{2b})+(2z+2)(z^{3a}-z^{2b+c})-(z+3)(z^{3a+c})+4(-z^{3a+2b})+5z^{3a+2b+c}-z^{3a+2b+c+1})\).
\([4m;\; 4m;\; 4n;\; p;\; 4n;\;
2q]\), for \(p = 2c\).
\(V(z)
=((1+z)(1-z^{2m})(1-z^{2n})(1-z^c)(1-z^q))/
(1-5z+4z(z^q+z^c)-(3z+1)(z^{q+c}-z^{2m}-z^{2n})+(2z+2)(-z^{2m+c}-z^{2m+q}-z^{2n+c}-z^{2n+q})-(z+3)(-z^{c+q+2m}-z^{c+q+2n}+z^{2m+2n})+4(z^{2m+2n+c}+z^{2m+2n+q})-5z^{c+q+2m+2n}+z^{2m+2n+c+q+1})\).
We can determine the formulas for counting vertices using also odd parameters, as we did in the previous section. However, we chose to work only with even cases to understand the properties derived from this choice of parameters.
There is no conflict of interest related to this work.