In this paper we contribute to the literature of computational chemistry by providing exact expressions for the detour index of joins of Hamilton-connected (\(HC\)) graphs. This improves upon existing results by loosening the requirement of a molecular graph being Hamilton-connected and only requirement certain subgraphs to be Hamilton-connected.
Topological indices of graphs are real numbers that describe various aspects of the topology of a graph. In the field of chemical graph theory in which graphs represent the molecular structure of chemical compounds, topological indices encode information about chemical properties of compounds including chemical reactivity or biological activity. The study of topological indices in chemical graph theory was introduced in a 1947 work by Harold Wiener in which he investigated the relationship between molecular structure and the boiling point of paraffins [1]. He observed that there is a high degree of correlation (\(>0.9\)) between the boiling point and Wiener index. Application of topological indices have been widely studied, see e.g., [2-6], and have been extended to many other aspects of chemical graph theory and network theory.
One of the most critical aspects of network theory is network robustness. In order to agree whether a given network is robust, a way to quantitatively measure network robustness is needed. Naturally robustness is all about back-up possibilities, or alternative paths, but it is challenging to capture these concepts in a mathematical formula. During the past few decades many robustness measures have been proposed [7]. Scientists from different backgrounds like mathematics, chemistry, physics, network science and biology have contributed to the study of network robustness. As a result, there are many different methods designed to assess the robustness of a network. All of these approaches are based on the analysis of the underlying graph [7-12].
One such category of measures of network robustness is the distance-based topological indices. Let \(G=(V,E)\) be a connected simple graph. The distance between two vertices \(x\) and \(y\) in \(G\), denoted by \(d_{G}(x,y)\), is the length of a shortest path between \(x\) and \(y\) in \(G\). The degree of a vertex \(x\) is denoted by \(d(x)\) and defined as the number of edges incident with \(x\). An open neighborhood of \(x\) is the set of all vertices adjacent to \(x\) which is denoted by \(N_{G}(x)\). Similarly, a closed neighborhood of \(x\) is defined and denoted by \(N_{G}[x]=N_{G}(x)\cup\{x\}\).
The Wiener index of \(G\) is defined as [1] \[W(G) = \sum_{\{x,y\}\subseteq V(G)} d_{G}(x,y).\tag{1}\]
Other names for the Wiener index found in the literature are distance of a graph [13] and transmission of a graph [14]. Several mathematical papers deal with a closely related invariant called the average distance, defined as \(\mu(G)=2W(G)/n(n-1)\), where \(n = |V(G)|\) [15].
A graph \(G\) is Hamilton-connected (\(HC\)) if every two vertices of \(G\) are connected by a Hamiltonian path. While all \(HC\) graphs are Hamiltonian, it is not the case that all Hamiltonian graphs are Hamilton-connected (consider, for example, a Cycle \(C_{n}\)). All complete graphs are Hamilton-connected and thus Hamiltonian. Hamiltonicity and the Hamilton-connected property have played an important role in topological graph theory and have been widely studied both for their role in graph structures as well as for their potential applications in network theory [16-23].
In this paper we study Hamilton-connectedness in conjunction with a variant of the Wiener index, known as the detour index. In particular we study the detour index of joins of \(HC\) graphs and derive an explicit formula for the detour index of this family of graphs.
The detour index of a connected graph is defined as the sum of the lengths of the longest paths between each pair of vertices in the graph. The detour distance (also known as the elongation) between two vertices \(u\) and \(v\) of a graph \(G\) is the length of a longest path between \(u\) and \(v\), denoted by \(l(u,v)\) [24-27]. The detour index [24,27-29], the topological index studied throughout this paper, is defined as \[\omega(G)=\sum_{\{u,v\}\subseteq V(G)}l(u,v).\tag{2}\]
The detour index has application in quantitative structure activity relationship (QSAR) studies [30], and has even been compared favorably to the Wiener index for boiling point modelling in general [31] with success specifically when applied to cyclic and acyclic alkanes [29]. The detour index has also had great success in combination with the Wiener index in structure boiling point modelling of cyclic and acyclic saturated hydrocarbons. This success has led to the development of related indices such as the hyper-detour index [32] and the Cluj-detour index [33].
Lukovits and Razinger [34] proposed an algorithm for the detection of the longest path between any two vertices of a graph, which was used to derive analytical formulas for the detour index of fused bicyclic structures. Trinajsti\(\rm\acute{c}\) et al. [35] and R\(\rm\ddot{u}\)cker and R\(\rm \ddot{u}\)cker [29] proposed computer methods for computing the detour distances and hence for computing the detour index. It has been proved in [36], that the problem of finding the detour matrix is NP-complete. A method for constructing the detour matrix for graphs of moderate sizes were presented in [31].
Our primary contribution in this paper, an explicit derivation of the detour index for joins of \(HC\) graphs, relies on the use of a convenient topological property (Hamilton-connected) to allow for an efficient derivation of the detour index. This new result provides the exact value of the detour index for a new infinite family of graphs. This result is in addition to similar previous results which came in the form of bounds on the detour index of bipartite graphs and trees. These results are presented in the two following theorems.
Theorem 1. [37] Let \(G\) be a connected bipartite graph with \(n\geq2\) vertices. Then \[(n-1)^2\leq\omega(G)\leq\left\{ \begin{array}{ll} \frac{1}{2}(n-1)^3 & \hbox{if n is odd} \\ \frac{1}{4}n(2n^2-5n+4) & \hbox{if n is even.} \end{array} \right.\tag{3}\]
Theorem 2. [38] Let \(T\) be a \(n\)-vertex tree. Then \[(n-1)^2\leq W(T)\leq \frac{n^3-n}{6},\tag{4}\] with left equality if and only if \(G\cong S_n\) and with right equality if and only if \(G\cong P_n\).
The lower and upper bounds are tight with the graphs \(S_n\) and \(P_n\), respectively. Due to the fact that an acyclic graph has a unique path between every pair of vertices, we have that \(W(T)=\omega(T)\) for all acyclic graphs. Given the relationship between the Wiener index and the detour index for acyclic graphs, and given the expansive literature on the Wiener index, it is worth investigating the detour index of cyclic graphs. Since the detour index of unicyclic and bicyclic graphs were studied in [37] and [39], respectively, we decided to take the approach of studying graphs with possibly very many cycles, namely the \(HC\) graphs.
Results for general graphs are sparse in the literature. The following theorem does provide a very clean result bounding the detour index of connected graphs.
Theorem 3. [38]Let \(G\) be a connected graph with \(n\geq3\) vertices. Then \[(n-1)^2\leq \omega(G)\leq \frac{n(n-1)^2}{2}\tag{5}\] with left equality if and only if \(G\cong S_n\) and with right equality if and only if \(G\) is Hamilton-connected.
Since the upper bound holds if and only if \(G\) is Hamilton-connected, the importance of this class of graphs, the \(HC\) graphs, is demonstrated. To further this line of research, we study the join of \(HC\) graphs.
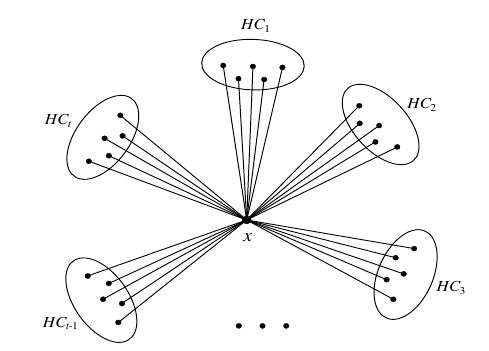
The join of two graphs \(G_{i}\) and \(G_{j}\), denoted by \(G_i+G_j\), is obtained by adding all edges between \(V(G_{i})\) and \(V(G_{j})\). For \(|V(G_{i})|=p\) and \(|V(G_{j})|=q\), the edge set of \(G_{i}+G_{j}\) is the union of disjoint edge sets of the graphs \(G_{i}\), \(G_{j}\) and the complete bipartite graph \(K_{p,q}\). Combinatorial problems involving the join of graphs is a longstanding problem in the literature of graph theory and network science. For more information on the join of graphs and related graph operations, the reader can refer to [40-42].
In this section, we focus on the join of \(t\) copies of Hamilton-connected graphs with a single vertex graph \(K_{1}\) and determine the Detour index of \(K_{1}+tHC\) explicitly in terms of the size of each of the Hamilton-connected components. This result is presented in the ensuing theorem. After stating and proving this theorem, we provide an important corollary which we will use to establish the detour index of windmill graphs later in this paper. Do notice that the join of \(t\) Hamilton-connected graphs with \(K_{1}\) is equivalent to a graph \(G\) which has a cut vertex \(x\) whose removal disconnects \(G\) into \(t\) Hamilton-connected components. The graph \(G\) is itself neither Hamilton-connected nor Hamiltonian.
Theorem 4. Let \(G\) be a graph with cut vertex \(x\) and removal of \(x\) disconnects the graph into \(t\) Hamilton-connected components \(G_1,G_2 \ldots G_t\) with cardinality \(n_1, n_2 \ldots n_t\) respectively, Then \[\omega(G)=\sum \limits_{i=1}^{t}\frac{n_i^{3}+n_i^{2}}{2}+\sum \limits_{1\leq i < j \leq t} {n_in_j(n_i+n_j)}.\tag{6}\]
Proof. \[\begin{aligned} \omega(G) & =\sum \limits_{\{u,v\}\subseteq V(G)}l(u,v)\\ & =\sum\limits_{i=1}^{t}\sum\limits_{\{u,v\}\subseteq V(G_i)}l(u,v)+ \sum\limits_{1\leq i < j \leq t}\sum\limits_{\small u\in V(G_i);\ v\in V(G_j)}l(u,v) +\sum\limits_{i=1}^{t}\sum\limits_{v\in V(G_i) }l(x,v)\\ & =\sum\limits_{i=1}^{t}\left( \begin{array}{c} n_i \\ 2 \end{array} \right){n_i}+ \sum\limits_{1\leq i < j \leq t}{\left(\begin{array}{c} n_i \\ 1 \end{array}\right)}{\left(\begin{array}{c} n_j \\ 1 \end{array}\right)}{(n_i + n_j)} +\sum\limits_{i=1}^{t}\left( \begin{array}{c} n_i \\ 1 \end{array} \right){n_i}\\ & =\sum\limits_{i=1}^{t} \frac{{n_i}({n_i}-1)}{2} {n_i}+ \sum\limits_{1\leq i < j \leq t}{n_i}{n_j}{(n_i + n_j)}+\sum\limits_{i=1}^{t}{n_i}{n_i}\\ & =\sum\limits_{i=1}^{t}\frac{n_i^{3}+n_i^{2}}{2}+\sum\limits_{1\leq i < j \leq t} {n_in_j(n_i+n_j).} \end{aligned}\] ◻
Corollary 1. Let \(G\) be a graph with cut vertex \(x\) and removal of \(x\) disconnects the graph into \(t\) Hamilton-connected components, \(G_1,G_2\ldots G_t\) with each of cardinality \(n_1 = n_2 =\ldots= n_t = k\) respectively. Then \[\omega(G)=\frac{k^2}{2}[2kt^2-(k-1)t].\tag{7}\]
Proof. \[\begin{aligned} \omega(G) & =\sum\limits_{\{u,v\}\subseteq V(G)}l(u,v)\\ & =\sum\limits_{i=1}^{t}\sum\limits_{\{u,v\}\subseteq V(G_i)}l(u,v)+ \sum\limits_{1\leq i < j \leq t}\sum\limits_{\small u\in V(G_i);\ v\in V(G_j)}l(u,v) +\sum\limits_{i=1}^{t}\sum\limits_{v\in V(G_i) }l(x,v)\\ & =\sum\limits_{i=1}^{t}\left( \begin{array}{c} k \\ 2 \end{array} \right){k}+ \sum\limits_{1\leq i < j \leq t}{\left( \begin{array}{c} k \\ 1 \end{array} \right)}{\left( \begin{array}{c} k \\ 1 \end{array} \right)}{(k + k)}+\sum\limits_{i=1}^{t}\left( \begin{array}{c} k \\ 1 \end{array} \right){k}\\ & =\sum\limits_{i=1}^{t} \frac{{k}({k}-1)}{2} {k}+ \sum\limits_{1\leq i < j \leq t}{k^{2}}{(2k)}+\sum\limits_{i=1}^{t}{(k)}{(k)}\\ & =\sum\limits_{i=1}^{t} \left(\frac{k^{3}-k^{2}}{2}+{k^{2}}\right)+2k^3\left( \begin{array}{c} t \\ 2 \end{array} \right)\\ & =\frac{k^2}{2}[2kt^2-(k-1)t]. \end{aligned}\] ◻
In this section, we apply Corollary 1 to determine the exact detour index of the family of windmill graphs \(K^{t}_{k}\). The windmill graph \(K^{t}_{k}\) for \(k>3\) consists of \(t\) copies of the complete graph \(K_{k}\) with a vertex in common [43]. The common vertex is a cut vertex whose removal disconnects the windmill graph into \(t\) connected components of \(K_{k-1}\). For a visual reference, see Figure 2. Various combinatorial problems pertaining to windmill graphs are studied in [44-48].
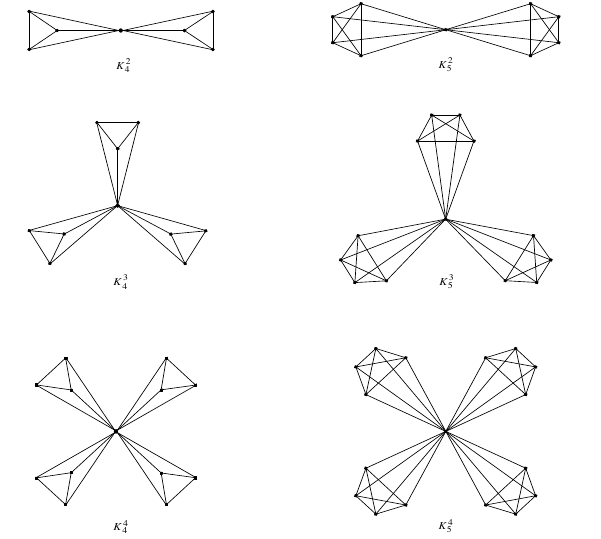
Theorem 5. For the windmill graph \(K_{k}^{t}\), \(\omega(K^{t}_k)=\frac{1}{2}\{2(k-1)^3t^2-(k-1)^2(k-2)t\}\).
Proof. By definition of windmill graph, the removal of a cut
vertex results \(t\) connected
components of \(K_{k-1}\). It is
evident that \(K_{k-1}\) is
Hamilton-connected. Hence we have by Corollary 1,
\(\omega(K^{t}_k)=\frac{1}{2}\{2(k-1)^3t^2-(k-1)^2(k-2)t\}\). ◻
In this section we give the exact expression for the detour index of the join of a Hamilton-connected graph with \(t\) pendent vertices.
Theorem 6. If \(G\) is Hamilton-connected with cardinality \(s\geq 2\) and for any positive integer \(t\), \(G+tK_1\) is Hamilton-connected if and only if \(t<s\).
Proof. To prove this, we consider two cases: when \(t<s\) and when \(t\geq s\).
Case 1: \(t<s\).
Let \(G\) be a Hamilton-connected graph with \(|V(G)|=s\), and let \(t<s\). Consider the graph \(G+tK_{1}\). Let \(S=\{v_{i}|v_{i}\in V(G)\}\) with the indexing defined by order in a Hamilton path between \(v_{1}\) and \(v_{s}\). and let \(T=\{u_{1},\dots,u_{t}\}\) be the set of pendant vertices. Let \(S_{T}=\{v_{i}|1\leq i\leq t\}\). By definition of the join operation, we may assign a bijection \(f\) between \(T\) and \(S_{T}\) by defining \(f(v_{i})=u_{i}\). In this way we may define a Hamilton path between any two vertices of \(S\) in \(G+tK_{1}\) by inserting the vertex \(f(v_{i})\) between \(v_{i}\) and \(v_{i+1}\) and hence we include \(T\) in any Hamilton path between vertices in \(S\).
Next we find a Hamilton path between any two vertices of \(T\), call them \(u_{1}\) and \(u_{t}\). To do this, choose any two vertices of \(S\) and call them \(v_{1}\) and \(v_{s}\). By definition of join, we can find a Hamilton path between \(v_{1}\) and \(v_{s}\) and include all of \(T^{\prime}=T\setminus\{u_{1},u_{t}\}\) via a bijection between \(T^{\prime}\) and \(S_{T^{\prime}}\) similar to the bijection between \(T\) and \(S_{T}\) defined earlier. Call this path \(P\). Then \(u_{1}Pu_{t}\) is our desired Hamilton path.
Lastly we find a Hamilton path between a vertex \(v_{1}\) in \(S\) and a vertex \(u_{t}\) in \(T\). Again we may define a similar
bijection between \(T^{\prime}=T\setminus{u_{t}}\) and \(S_{T^{\prime}}\). Since \(u_{t}\) is also adjacent to the vertex
\(v_{s}\) we may affix \(u_{t}\) to obtain the desired Hamilton
path. Since this is all possible cases, we conclude that if \(G\) is Hamilton-connected then \(G+tK_{1}\) is also
Hamilton-connected.
Case 2: \(t\geq
s\).
If \(t\geq s\) then the bijection defined in the previous case is no longer covers \(T\). Since there are no edges between vertices in \(T\), the pigeonhole principle implies that there can be no Hamilton path between vertices in \(T\), hence \(G+tK_{1}\) is not Hamilton-connected. ◻
Theorem 7. For an Hamilton-conneccted graph \(G\) with cardinality \(s\geq3\), and \(t\) be any positive integer
\(\omega(G+tK_1)=\left\{ \begin{array}{ll} \frac{1}{2}(s+t)(s+t-1)^{2} & \hbox{if $s>t$} \\ \frac{1}{2}[2s^3+4s^2(t-1)+2s(t-1)^2-t(t-1)] & \hbox{if $s\leq t$.} \end{array} \right.\)
Proof. Let \(G\) be an
Hamilton-connected graph such that \(|V(G)|=s\) and the graph \(G+tK_1\) is obtained by joining \(t\) pendent vertices to \(G\). \(V(G+tK_1)=S\cup T\) as defined in Theorem
6 and
we have the following cases.
Case 1. \(s>t\).
The proof follows from Theorems 3 and Theorem 6.
Case 2. \(s\leq
t\).
\[\begin{aligned} \omega(G+tK_1) & =\sum\limits_{\{u,v\}\subseteq V(G+tK_1)}l(u,v)\\ & =\sum\limits_{\{u,v\}\subseteq S}l(u,v)+\sum\limits_{\{u,v\}\subseteq T}l(u,v)+ \sum\limits_{u\in S;\ v\in T} l(u,v)\\ & =\left( \begin{array}{c} s \\ 2 \end{array} \right)(2s-2)+ \left( \begin{array}{c} t \\ 2 \end{array} \right)(2s-1)+\left( \begin{array}{c} s \\ 1 \end{array} \right) \left( \begin{array}{c} t \\ 1 \end{array} \right) (2s-1)\\ & =\frac{1}{2}[s(s-1)(2s-2)]+\frac{1}{2}[t(t-1)(2s-1)]+st(2s-1)\\ & = \frac{1}{2}[2s^3+4s^2(t-1)+2s(t-1)^2-t(t-1)]. \end{aligned}\] ◻
In this section we extend the results of this paper to the case of the join of a Hamilton-connected graph with several other Hamilton-connected graphs when all of the graphs have the same size vertex set. For reference, the reader may recall Figure 1 but replace the vertex \(x\) with a Hamilton-connected graph \(G\) satisfying \(|V(G)|=k\). Additionally, we assume that \(|V(HC_{i})|=k\) for each Hamilton-connected graph to be joined to \(G\).
Theorem 8. Let \(G\) be a Hamilton-connected graph with \(|V(G)|=k\) and let \(HC_{i}\) for \(1\leq i\leq t\) be Hamilton-connected graphs with \(|V(HC_{i})|=k\). Then \(\omega(G+tHC)= (\frac{3k-1}{2})[k^{2}(t^{2}+1)-k(t+1)]+2k^{2}\).
Proof. By a simple counting argument we have that the contribution to the detour number for each individual graph member of \(G+tHC\) is given by \(\frac{k(k-1)^{2}(t+1)}{2}\) (per Theorem 3). Similarly, we have that the total contribution from longest paths from \(G\) to \(HC_{i}\) is \(k^{2}(2k-1)t\). Lastly, the total contribution from longest paths originating and ending in distinct \(HC_{i}\) is given by \(\frac{k^{2}(3k-1)t(t-1)}{2}\). Combining these expressions and simplifying yields the desired result. ◻
In this paper we proved the detour index for several families of graph resulting from the join of Hamilton-connected graphs. In particular, we gave an exact expression for the windmill graph \(K_{k}^{t}\) in terms of only the parameters \(k\) and \(t\). This was generalized with the detour index of the join of a \(HC\) graph with several other vertex disjoint \(HC\) graphs when the order of each \(HC\) graph is fixed. These contributions not only extend on results on the detour index of Hamilton-connected graphs, but also demonstrate the usefulness of Hamilton-connected subgraphs and of connectivity in determining the detour index of various molecular graphs. Our results could be extended by further research which weakens our assumptions of Hamilton-connected subgraphs or which replaces cut vertices with cut vertex sets of size greater than one.
This work was supported by the National Natural Science Foundation of China (No. 11801135).
There is no conflict of interest related to this work.