Menu
Let \(\Gamma_{G}\) be the orbit graph of \(G\), with non-central orbits in the subset of order two commuting elements in \(G\), and the vertices of \(\Gamma_{G}\) connected if they are conjugate. The main objective of this study is to compute several topological indices for the orbit graph of a dihedral group, including the Wiener index, the Zagreb index, the Schultz index, and others. We also develop a relationship between the Wiener index and the other indices for the dihedral group’s orbit graph. Furthermore, their polynomial has been computed as well.
Graph theory has provided us with several useful tools, one of the
most studied and applicable tools is the topological index. Topological
indices (TIs) are the numerical parameters of a graph that can be
employed to characterize its topology. A topological index is also known
as a connectedness index in chemical graph theory, molecular topology,
and mathematical chemistry domains. A molecule can be represented as a
graph in the chemical graph theory, with atoms as vertices and bonds as
edges. Topological graph indices have been successfully utilized to
predict specific physicochemical properties as well as to determine the
structural properties of chemical compounds. Stankevich et al. [1] examined topological indices as
one way of identifying the relationship between the structure of the
chemical compound and its characteristics. Topological indices have also
assisted chemists, physicians, mathematicians, and others in solving
chemical and biological problems.
Diudea et al. [2] proposed a
unified approach to the Wiener topological index and its various
modifications, where they focus on the Schultz, Cluj, Szeged, Harary,
and Kirchhoff indices, as well as their numerous variants and
generalizations. They also obtained the relationship between these
indices and their correlations with the physicochemical properties of
molecules. Cancan et al. [3]
employed the findings obtained in [2] to investigate the generalized prism network.
Further, they have computed several degree-based indices such as the
Airthmetic-Geometric index, modified Randic, sum connectivity index, the
SK index, \(SK _{1}\) index, and \(SK _{2}\) index of generalised prism
network engineering.
The numerical representations of chemical structures with topological
indices are significant in medicinal chemistry and bioinformatics. In
the early 1990s, the invention and specification of the new TIs
increased consistently. Topological indices include degree-based,
distance-based, counting-related, and many other topological indices.
These indices are used to create quantitative structure-activity
relationships, in which a molecule’s biological activity, as well as
other properties like strain energy, stability, and boiling point, are
linked to its structure. To classify these indices, the structural
properties of the graphs are used to calculate the TIs. For example,
Zagreb indices are derived using the degrees of vertices and the wiener
index is obtained by using the distance between of vertices in the given
molecular graph. In 1947, [4]
the first graph-based molecular structure TI was discovered. Wiener has
provided only two important topological indices; the Wiener Index \(W(G)\), and the Wiener polarity index \(W_{p}\). These indices are used to obtain
the chemical and physical properties of chemical compounds. Some
formulas comprising terms of this kind were deduced a long time ago
while studying the dependence of total \(\pi\)-electron energy on molecule
structure. That is, \[\begin{eqnarray}
M_{1}= & \sum_{vertices}(d_{i})^{2} \\
M_{2}= & \sum_{edges}d_{i}.d_{j}
\end{eqnarray}\] with \(d_{i}\)
standing for the degree of the vertex \(v_{i}\) of the molecular graph [4]. In the chemical literature,
\(M_{1}\) and \(M_{2}\) are called the first Zagreb index
and the second Zagreb index respectively.
Many studies have been reported regarding the applications of
topological indices in the last four decades. Das et al. [5] introduced several significant
characteristics of the second Zagreb index. In their work, they have
declared and verified numerous findings for \(M _{2}\) identities and inequalities. The
M-polynomial for the graph has received a lot of attention since it
generates a lot of degree-based topological indices. Munir et al. [6] used this method to determine
M-polynomials of various nanostar dendrimers and subsequently retrieve a
large number of degree-based topological indices. Zhou et al. [7] derive several inequalities of
three previously investigated descriptors, namely the Zagreb, Wiener,
and Hyper-Wiener indices concerning the given molecular graph. Khalifeh
et al. [8] gave some exact
formulae for the first and second Zagreb indices of graph operations
containing the symmetric difference, composition, disjunction, join, and
cartesian product of graphs. For the nanostructure of bridge graphs,
Khalaf et al. [9] determine
the hyper-Zagreb index, first multiple Zagreb index, second multiple
index, Zagreb polynomials, and M-polynomials. Das et al. [10] compared the Wiener index and
the Zagreb indices, as well as the eccentric connectivity index for
trees. Bello et al. [11]
generalized the Wiener index, first and second Zagreb indices of the
ordered product prime graph on dihedral groups. Singh and Bhat [12] investigated the adjacency
matrix and various topological indices of the zero-divisor graph of
\(\mathbb{Z}_{n}\). Shahistha et al.
[13] calculate the Wiener index
of some significant chain graphs.
In the recent past, Poojary et al. [14] developed several topological indices and
polynomials for the Issac graph. Filipovski [15] established several relationships between the
Sombor index and degree-based topological indices such as the Zagreb
index, Forgotten index, and Randic index. Saleh et al. [16] introduced the first, second,
and forgotten downhill Zagreb indices of graphs. Saeed et al. [17] investigated degree-based
topological indices of Boron \(B_{12}\), such as the Randic index, the
first general Zagreb index, the hyper-Zagreb index, and others. Javaid
et al. [18] calculated novel
connection-based Zagreb indices for many wheel-related graphs such as
the wheel, gear, helm, flower, and sunflower graphs. Because of their
uses, entire versions of numerous indices have been introduced and
investigated. Naci et al. [19]
presented the Wiener index for trees and some graph families.
The above-mentioned applications motivate us to study topological
indices for the orbit graph of \(G\).
This study examines the Wiener index, the first, second, and third
Zagreb indices, Hyper first and second Zagreb indices, Modified first
Zagreb indices, Schultz and Modified Schultz indices, the Forgotten
index, Somber index, Randic and Reciprocal Randic indices for the orbit
graph of the dihedral group \(D_{t}\).
Furthermore, we also obtain the relationships between these indices with
the wiener index and the polynomials of indices for the orbit graphs of
\(D_{t}\).
The following definitions related to the group theory, graph theory and topological indices are stated as below.
Definition 1. Dihedral Group:
Let \(G\) be a dihedral group of order
\(2t\) and is represented as
\[D_{t}=\langle
a,b|a^{t}=b^{2}=e,bab=a^{-1}\rangle\] with \(t\) being a positive integer and \(t\geq 3\).
Definition 2. [20]The Set \(\Upsilon\): The set \(\Upsilon\) is the set of all pairs of
commuting elements of \(G\) and the
least common multiple of the elements having order two and is
represented as
\[\Upsilon=\{(a_{1},b_{1})\in G\times
G|a_{1}b_{1}=b_{1}a_{1},a_{1}\neq
b_{1},lcm(|a_{1}|,|b_{1}|)=2\}.\]
Definition 3. [20]Orbit: If a group \(G\) operates on a set \(\Upsilon\) and \(v_{1} \in \Upsilon\), then the subset \(R(v_{1})=\{gv_{1} \mid g \in G,v_{1} \in
\Upsilon\}\) is the orbit of \(v_{1}\) and is symbolized by \(R(v_{1})\). In this study, the conjugation
action is considered. Therefore, the orbit is written as
\[R(v_{1})=\{gv_{1} g^{-1}\mid g\in G,v_{1}
\in \Upsilon\}.\]
Definition 4. [20]Orbit Graph \(\Gamma_{G}^{\Upsilon}\): The orbit graph, \(\Gamma_{G}^{\Upsilon}\) is a graph whose vertices are non central orbits under group action on the set \(\Upsilon\) that is \(|V(\Gamma_{G}^{\Upsilon})|=|\Upsilon|-|B|\), where \(\Upsilon\) is a disjoint union of distinct orbits and \(B=\{v_{1} \in \Upsilon|v_{1} g=g v_{1},g\in G\}\). Two vertices \(v_{1}, v_{2}\) are adjacent if \(v_{1}, v_{2}\) are conjugate that is \(v_{1}=g^{v_{2}}\).
The following are some definitions that are used in computing the topological indices.
Definition 5. [21]Degree of a vertex: The number of incident edges \(|E(u)|\) on the vertex \(u\) is called degree of a vertex and is denoted by \(deg(u)\).
Definition 6. [21]Distance: The minimum number of edges between two vertices \(u_{i}\) and \(u_{j}\) of a graph is said to be a distance of two vertices and is denoted by \(d(u_{i},u_{j})\), where \(i\), \(j\) denotes the number of vertices.
Let \(u_{i}\) and \(u_{j}\) be two unique vertices with \(i\leq j\) and \(\Gamma_{G}^{\Upsilon}\) a connected graph
of \(t\) vertices, respectively. Then
there are the definitions of several indices that we utilise in this
work, which are listed in Table \(1\).
| Indices | Formulas | |
|---|---|---|
| \(W(\Gamma_{G}^{\Upsilon})\) | \(\frac{1}{2}\sum_{i=1}^{t}\sum_{j=1}^{t}d(u_{i},u_{j})\) | |
| \(M_{1}(\Gamma_{G}^{\Upsilon})\) | \(\sum_{u\in v(\Gamma_{G}^{\Upsilon})}(deg(u))^{2}\) | |
| \(M_{2}(\Gamma_{G}^{\Upsilon})\) | \(\sum_{u_{1},u_{2}\in E(\Gamma_{G}^{\Upsilon})}deg(u_{1})deg(u_{2})\) | |
| \(M_{3}(\Gamma_{G}^{\Upsilon})\) | \(\sum_{i,j=1}^{\frac{t(t-1)}{2}}(deg(u_{i})deg(u_{j}))(deg(u_{i})+deg(u_{j}))\) | |
| \(HM_{1}(\Gamma_{G}^{\Upsilon})\) | \(\sum_{i,j=1}^{\frac{t(t-1)}{2}}(deg(u_{i})+deg(u_{j}))^{2}\) | |
| \(HM_{2}(\Gamma_{G}^{\Upsilon})\) | \(\sum_{i,j=1}^{\frac{t(t-1)}{2}}(deg(u_{i})deg(u_{j}))^{2}\) | |
| \(ModM_{1}(\Gamma_{G}^{\Upsilon})\) | \(\sum_{i,j=1}^{t}\frac{1}{deg(u_{i})^{2}}\) | |
| \(S_{c}(\Gamma_{G}^{\Upsilon})\) | \(\frac{1}{2}\sum(deg(u_{i})+deg(u_{j}))d(u_{i},u_{j})\) | |
| \(S_{c}^{*}(\Gamma_{G}^{\Upsilon})\) | \(\frac{1}{2}\sum(deg(u_{i})deg(u_{j}))d(u_{i},u_{j})\) | |
| \(F(\Gamma_{G}^{\Upsilon})\) | \(\sum_{i,j=1}^{\frac{t(t-1)}{2}}deg(u_{i})^{2}+deg(u_{j})^{2}\) | |
| \(S_{o}(\Gamma_{G}^{\Upsilon})\) | \(\sum_{i,j=1}^{\frac{t(t-1)}{2}}(deg(u_{i})^{2}+deg(u_{j})^{2})^{\frac{1}{2}}\) | |
| \(R(\Gamma_{G}^{\Upsilon})\) | \(\sum_{i,j=1}^{\frac{t(t-1)}{2}}(deg(u_{i})deg(u_{j}))\frac{-1}{2}\) | |
| \(RR(\Gamma_{G}^{\Upsilon})\) | \(\sum_{i,j=1}^{\frac{t(t-1)}{2}}(deg(u_{i})deg(u_{j}))^{\frac{1}{2}}\) |
The orbit graph of all dihedral groups, \(D_{t}\), can be divided into three parts, according to Omer et al., [20], as stated in the following theorem. when \(t\) and \(\frac{t}{2}\) are even, \(|\Upsilon|=\frac{5t}{2}+1\) and \(|B|=1\), when \(t\) is even and \(\frac{t}{2}\) is odd, \(|\Upsilon|=\frac{5t}{2}+1\) and \(|B|=1\) and when \(t\) is odd, \(|\Upsilon|=t\) and \(|B|=0\). This fact will be utilised to support our primary findings.
Theorem 1. [20]Let \(G\) be a dihedral group of order \(2t\). If \(G\) acts on \(\Upsilon\) by conjugation. Then \[\Gamma_{G}^{\Upsilon}=\left\{ \begin{array}{ll} \bigcup_{i=1}^{5}K_{\frac{t}{2}i}, & \hbox{if}\;\hbox{ t is even and } \frac{t}{2} \hbox{ is odd },\\ (\bigcup_{i=1}^{4}K_{\frac{t}{2}i}) \bigcup (\bigcup_{i=1}^{2}K_{\frac{t}{4}}i), & \hbox{if}\;\hbox{ t and } \frac{t}{2} \hbox{ is odd },\\ K_{t}, & \hbox{if}\; \hbox{ t is odd }. \end{array} \right.\]
According to Theorem 1, only the third case involves a connected graph, while the other two cases involve disconnected graphs. As a result, we can only think about the case where \(t\) is odd. In this section, the Wiener index, the first, second and third Zagreb indices, Hyper first and second Zagreb indices, Modified first Zagreb indices, Schultz and Modified Schultz indices, Forgotten index, Somber index, Randic and Reciprocal Randic indices for the orbit graph of dihedral groups are calculated.
Theorem 2. Let \(G\) be a dihedral group \(D_{t}\) of order \(2t\). Then
\(W(\Gamma_{G}^{\Upsilon})\)
= \(\frac{1}{2}t(t-1)\)
\(M_{1}(\Gamma_{G}^{\Upsilon}\) = \(t(t-1)^{2}\)
\(M_{2}(\Gamma_{G}^{\Upsilon})\) = \(\frac{t(t-1)^{3}}{2}\)
\(M_{3}(\Gamma_{G}^{\Upsilon})\) = \(t(t-1)^{4}\)
\(HM_{1}(\Gamma_{G}^{\Upsilon})\) = \(2t(t-1)^{3}\)
\(HM_{2}(\Gamma_{G}^{\Upsilon})\) = \(\frac{t(t-1)^{5}}{2}\)
\(ModM_{1}(\Gamma_{G}^{\Upsilon})\) = \(\frac{t}{(t-1)^{2}}\)
\(S_{c}(\Gamma_{G}^{\Upsilon})\) = \(t(t-1)^{2}\)
\(S_{c}^{*}(\Gamma_{G}^{\Upsilon})\) = \(\frac{t(t-1)^{3}}{2}\)
\(F(\Gamma_{G}^{\Upsilon})\)
= \(t(t-1)^{3}\)
\(S_{o}(\Gamma_{G}^{\Upsilon})\) = \(t(t-1)^{2}\)
\(R(\Gamma_{G}^{\Upsilon})\)
= \(\frac{t}{2}\)
\(RR(\Gamma_{G}^{\Upsilon})\) = \(\frac{t(t-1)^{2}}{2}\)
Proof. In order to calculate the indices of a graph, we have
to determine the number of vertices of the graph. From the definition
\(2.4\), if the group action on the set
\(\Upsilon\) is applied then \(|\Upsilon|-|B|=t-0=t\) and the number of
vertices of the orbit graph is considered to be a non-central
orbit.
Since, we are considering the third case of the Theorem 1, where the graph is complete then the
number of edges of the orbit graph are \(\frac{t(t-1)}{2}\) and distance and degree
of the vertex is \((t-1)\) (All the
indices are determined on the basis of above predefined definitions).
Therefore, \[\begin{eqnarray}
W(\Gamma_{G}^{\Upsilon}) &=&
\frac{1}{2}\sum_{i=1}^{t}\sum_{j=1}^{t}d(u_{i},u_{j}) \\
&=&
\frac{1}{2}\sum_{i=1}^{t}[d(u_{i},u_{1})+d(u_{i},u_{2})+…+d(u_{i},u_{t})]
\\
&=&
\frac{1}{2}[d(u_{1},u_{1})+d(u_{2},u_{1})+…+d(u_{t},u_{1})+…+\\
& & d(u_{1},u_{t})+d(u_{2},u_{t})+…+d(u_{t},u_{t})] \\
&=& \frac{1}{2}[(t-1)+(t-1)+…+(t-1)] \\
&=& \frac{1}{2}[t(t-1)]
\end{eqnarray}\] \[\begin{eqnarray}
M_{1}(\Gamma_{G}^{\Upsilon}) &=&
\sum_{i=1}^{t}(deg(u_{i}))^{2} \\
&=& deg(u_{1})^{2}+deg(u_{2})^{2}+…+deg(u_{t})^{2} \\
&=& [(t-1)^{2}+(t-1)^{2}+…+(t-1)^{2}] \\
&=& t(t-1)^{2}
\end{eqnarray}\] \[\begin{eqnarray}
M_{2}(\Gamma_{G}^{\Upsilon})&=&
\sum_{i,j=1}^{\frac{t(t-1)}{2}}deg(u_{i})deg(u_{j}) \\
&=& (t-1)(t-1)+(t-1)(t-1)+…+(t-1)(t-1) \\
&=& (t-1)(t-1)(\frac{t(t-1)}{2})\\
&=& (t-1)^{3}\frac{t}{2}
\end{eqnarray}\] \[\begin{eqnarray}
M_{3}(\Gamma_{G}^{\Upsilon}) &=&
\sum_{i,j=1}^{\frac{t(t-1)}{2}}(deg(u_{i})deg(u_{j}))(deg(u_{i})+deg(u_{j}))
\\
&=& [((t-1)(t-1))((t-1)+(t-1))]+ \\
& & [((t-1)(t-1))((t-1)+(t-1))] +…+ \\
& & [((t-1)(t-1))((t-1)+(t-1))]\\
&=& (t-1)^{2}[2(t-1)]+(t-1)^{2}[2(t-1)]+…+ \\
& & (t-1)^{2}[2(t-1)]\\
&=& 2(t-1)^{3}+2(t-1)^{3}+…+2(t-1)^{3} \\
&=& \frac{t(t-1)}{2}[2(t-1)^{3}] \\
&=& t(t-1)^{4}
\end{eqnarray}\] \[\begin{eqnarray}
HM_{1}(\Gamma_{G}^{\Upsilon}) &=&
\sum_{i,j=1}^{\frac{t(t-1)}{2}}(deg(u_{i})+deg(u_{j}))^{2} \\
&=& ((t-1)+(t-1))^{2}+((t-1)+(t-1))^{2}+…+\\
& & ((t-1)+(t-1))^{2}\\
&=& (2(t-1))^{2}+(2(t-1))^{2}+…+(2(t-1))^{2}\\
&=& \frac{t(t-1)}{2}(2(t-1))^{2}\\
&=& \frac{t(t-1)}{2} [4(t-1)^{2}]\\
&=& 2t(t-1)^{3}
\end{eqnarray}\] \[\begin{eqnarray}
HM_{2}(\Gamma_{G}^{\Upsilon}) &=&
\sum_{i,j=1}^{\frac{t(t-1)}{2}}(deg(u_{i})deg(u_{j}))^{2} \\
&=& ((t-1)(t-1))^{2}+((t-1)(t-1))^{2}+…+\\
& & ((t-1)(t-1))^{2} \\
&=& ((t-1)^{2})^{2}+((t-1)^{2})^{2}+…+((t-1)^{2})^{2} \\
&=& (t-1)^{4}+(t-1)^{4}+…+(t-1)^{4} \\
&=& \frac{t(t-1)}{2}(t-1)^{4}\\
&=& \frac{t(t-1)^{5}}{2}
\end{eqnarray}\] \[\begin{eqnarray}
ModM_{1}(\Gamma_{G}^{\Upsilon}) &=&
\sum_{i,j=1}^{t}\frac{1}{deg(u_{i})^{2}}\\
&=&
\frac{1}{(t-1)^{2}}+\frac{1}{(t-1)^{2}}+…+\frac{1}{(t-1)^{2}}\\
&=& t[\frac{1}{(t-1)^{2}}]\\
&=& \frac{t}{(t-1)^{2}}
\end{eqnarray}\] \[\begin{eqnarray}
S_{c}(\Gamma_{G}^{\Upsilon})&=&
\frac{1}{2}\sum(deg(u_{i})+deg(u_{j}))d(u_{i},u_{j})\\
&=& \frac{1}{2}[((t-1)+(t-1))(t-1)+((t-1)+(t-1))\\
& & (t-1)+…+((t-1)+(t-1))(t-1)]\\
&=& \frac{1}{2}[2(t-1)^{2}+2(t-1)^{2}+…+2(t-1)^{2}]\\
&=& \frac{1}{2}t(2(t-1)^{2})\\
&=& t(t-1)^{2}
\end{eqnarray}\] \[\begin{eqnarray}
S_{c}^{*}(\Gamma_{G}^{\Upsilon}) &=&
\frac{1}{2}\sum(deg(u_{i})deg(u_{j}))d(u_{i},u_{j})\\
&=& \frac{1}{2}[((t-1)(t-1))(t-1)+((t-1)(t-1))(t-1)\\
& & +…+((t-1)(t-1))(t-1)]\\
&=& \frac{1}{2}[(t-1)^{3}+(t-1)^{3}+…+(t-1)^{3}]\\
&=& \frac{1}{2}t(t-1)^{3}
\end{eqnarray}\] \[\begin{eqnarray}
F(\Gamma_{G}^{\Upsilon})&=&
\sum_{i,j=1}^{\frac{t(t-1)}{2}}deg(u_{i})^{2}+deg(u_{j})^{2}\\
&=& ((t-1)^{2}+(t-1)^{2})+((t-1)^{2}+(t-1)^{2})\\
& & +…+((t-1)^{2}+(t-1)^{2})\\
&=& [2(t-1)^{2}+2(t-1)^{2}+…+2(t-1)^{2}]\\
&=& \frac{t(t-1)}{2}[2(t-1)^{2}]\\
&=& t(t-1)^{3}
\end{eqnarray}\] \[\begin{eqnarray}
S_{o}(\Gamma_{G}^{\Upsilon})&=&
\sum_{i,j=1}^{\frac{t(t-1)}{2}}(deg(u_{i})^{2}+deg(u_{j})^{2})^{\frac{1}{2}}\\
&=&
((t-1)^{2}+(t-1)^{2})^{\frac{1}{2}}+((t-1)^{2}+(t-1)^{2})^{\frac{1}{2}}\\
& & +…+((t-1)^{2}+(t-1)^{2})^{\frac{1}{2}}\\
&=&
(2(t-1)^{2})^{\frac{1}{2}}+(2(t-1)^{2})^{\frac{1}{2}}+…+(2(t-1)^{2})^{\frac{1}{2}}\\
&=& 2(t-1)+2(t-1)+…+2(t-1)\\
&=& \frac{t(t-1)}{2}(2(t-1))\\
&=& t(t-1)^{2}
\end{eqnarray}\] \[\begin{eqnarray}
R(\Gamma_{G}^{\Upsilon})&=&
\sum_{i,j=1}^{\frac{t(t-1)}{2}}(deg(u_{i})deg(u_{j}))\frac{-1}{2}\\
&=&
\sum_{i,j=1}^{\frac{t(t-1)}{2}}\frac{1}{\sqrt{deg(u_{i})deg(u_{j})}}\\
&=&
\frac{1}{((t-1)(t-1))^{\frac{1}{2}}}+\frac{1}{((t-1)(t-1))^{\frac{1}{2}}}+…+\\
& &
\frac{1}{((t-1)(t-1))^{\frac{1}{2}}}\\
&=&
\frac{1}{((t-1)^{2})^{\frac{1}{2}}}+\frac{1}{((t-1)^{2})^{\frac{1}{2}}}+…+\frac{1}{((t-1)^{2})^{\frac{1}{2}}}\\
&=& \frac{1}{(t-1)}+\frac{1}{(t-1)}+…+\frac{1}{(t-1)}
\end{eqnarray}\] \[\begin{eqnarray}
&=& \frac{t(t-1)}{2}(\frac{1}{(t-1)})\\
&=& \frac{t}{2}
\end{eqnarray}\] \[\begin{eqnarray}
RR(\Gamma_{G}^{\Upsilon})&=&
\sum_{i,j=1}^{\frac{t(t-1)}{2}}(deg(u_{i})deg(u_{j}))^{\frac{1}{2}}\\
&=&
((t-1)(t-1))^{\frac{1}{2}}+((t-1)(t-1))^{\frac{1}{2}}+…+\\
& & ((t-1)(t-1))^{\frac{1}{2}}\\
&=&
((t-1)^{2})^{\frac{1}{2}}+((t-1)^{2})^{\frac{1}{2}}+…+((t-1)^{2})^{\frac{1}{2}}\\
&=& \frac{t(t-1)}{2}[((t-1)^{2})\frac{1}{2}]\\
&=& \frac{t(t-1)^{2}}{2}
\end{eqnarray}\]
Example 1: Consider the orbit graph \(K_{15}\) (see Figure \(2\)).
Now, the graph \(K_{15}\) have \(|\Upsilon|-|B|=15-0=15\) vertices and \(\frac{15(15-1)}{2}=105\) edges,
respectively.
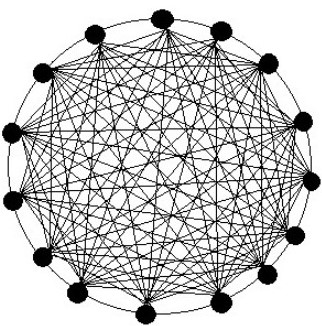
Also, the degree and distance of vertices are \((15-1)=14\). Then \[\begin{eqnarray} W(\Gamma_{G}^{\Upsilon}) & = & 105 \\ M_{1}(\Gamma_{G}^{\Upsilon})& = & 2940 \\ M_{2}(\Gamma_{G}^{\Upsilon})& = & 20580 \\ M_{3}(\Gamma_{G}^{\Upsilon})& = & 576240 \\ HM_{1}(\Gamma_{G}^{\Upsilon})& = & 82320 \\ HM_{2}(\Gamma_{G}^{\Upsilon})& = & 4033680 \\ ModM_{1}(\Gamma_{G}^{\Upsilon})& = & 0.00510 \\ S_{c}(\Gamma_{G}^{\Upsilon})& = & 2940 \\ S_{c}^{*}(\Gamma_{G}^{\Upsilon})& = & 20580 \\ F(\Gamma_{G}^{\Upsilon})& = & 41160 \\ S_{o}(\Gamma_{G}^{\Upsilon})& = & 2940\\ R(\Gamma_{G}^{\Upsilon})& = & 7.5 \\ RR(\Gamma_{G}^{\Upsilon})& = & 1470 \end{eqnarray}\]
In this section, we relate each of the indices with the Wiener index and also their relationship with each other.
Theorem 3. For orbit graph of dihedral
group,
\(S_{c}^{*}(\Gamma_{G}^{\Upsilon})=W(\Gamma_{G}^{\Upsilon})(t-1)^{2}=M_{2}(\Gamma_{G}^{\Upsilon})\)
Proof. As we obtain the modified schultz index for the orbit
graph of dihedral group in the above Theorem 2. Then we have
\[S_{c}^{*}(\Gamma_{G}^{\Upsilon}) =
\frac{t(t-1)^{3}}{2}\]
Since, \(W(\Gamma_{G}^{\Upsilon})\) =
\(\frac{1}{2}t(t-1)\) then by
substituting the value of \(W(\Gamma_{G}^{\Upsilon})\) in \(S_{c}^{*}(\Gamma_{G}^{\Upsilon})\),we get
\[\begin{eqnarray}
S_{c}^{*}(\Gamma_{G}^{\Upsilon})= & \frac{t(t-1)}{2}(t-1)^{2} \\
= & W(\Gamma_{G}^{\Upsilon})(t-1)^{2}
\end{eqnarray}\] This implies,
\(S_{c}^{*}(\Gamma_{G}^{\Upsilon})\)=\(W(\Gamma_{G}^{\Upsilon})(t-1)^{2}\).
and it is obvious from the above prove result that \(S_{c}^{*}(\Gamma_{G}^{\Upsilon})=M_{2}(\Gamma_{G}^{\Upsilon})\).
Theorem 4. \(M_{1}(\Gamma_{G}^{\Upsilon})= S_{c}(\Gamma_{G}^{\Upsilon})= S_{o}(\Gamma_{G}^{\Upsilon})= 2(t-1)W(\Gamma_{G}^{\Upsilon})\)
Proof. Since, \[\begin{eqnarray}
M_{1}(\Gamma_{G}^{\Upsilon})= & t(t-1)^{2}\\
S_{c}(\Gamma_{G}^{\Upsilon})= & t(t-1)^{2}\\
S_{o}(\Gamma_{G}^{\Upsilon})= & t(t-1)^{2}
\end{eqnarray}\] This implies, \[\begin{eqnarray}
W(\Gamma_{G}^{\Upsilon})= & \frac{1}{2}t(t-1)\\
2W(\Gamma_{G}^{\Upsilon})= & t(t-1)
\end{eqnarray}\] Therefore,
\(M_{1}(\Gamma_{G}^{\Upsilon})=
S_{c}(\Gamma_{G}^{\Upsilon})=S_{o}(\Gamma_{G}^{\Upsilon})=2(t-1)W(\Gamma_{G}^{\Upsilon})\)
Theorem 5. For orbit graph of dihedral group, the second Zagreb index is the product of Wiener index and the first Zagreb index. \[M_{2}(\Gamma_{G}^{\Upsilon})=\frac{1}{t}W(\Gamma_{G}^{\Upsilon})M_{1}(\Gamma_{G}^{\Upsilon})\]
Proof. we obtain \(M_{2}(\Gamma_{G}^{\Upsilon})\) of dihedral
group as
\[M_{2}(\Gamma_{G}^{\Upsilon})=\frac{t(t-1)^{3}}{2}\]
Then, \[\begin{eqnarray}
M_{2}(\Gamma_{G}^{\Upsilon})= & t(t-1)^{2}\frac{(t-1)}{2} \\
= & \frac{1}{2}(t-1)M_{1}(\Gamma_{G}^{\Upsilon})\\
= &
\frac{1}{t}W(\Gamma_{G}^{\Upsilon})M_{1}(\Gamma_{G}^{\Upsilon})
\end{eqnarray}\]
Theorem 6. \(M_{3}(\Gamma_{G}^{\Upsilon})=(t-1)^{2}M_{1}(\Gamma_{G}^{\Upsilon})=\frac{4}{t}W(\Gamma_{G}^{\Upsilon})M_{2}(\Gamma_{G}^{\Upsilon})\)
Proof. \[\begin{eqnarray} M_{3}(\Gamma_{G}^{\Upsilon})= & t(t-1)^{4} \\ = & t(t-1)^{2}(t-1)^{2}\\ = & (t-1)^{2}M_{1}(\Gamma_{G}^{\Upsilon}) \end{eqnarray}\] Again, \[\begin{eqnarray} M_{3}(\Gamma_{G}^{\Upsilon})= & t(t-1)^{4} \\ = & t(t-1)^{3}(t-1)\\ = & 2(t-1)M_{2}(\Gamma_{G}^{\Upsilon})\\ = & \frac{4}{t}W(\Gamma_{G}^{\Upsilon})M_{2}(\Gamma_{G}^{\Upsilon}) \end{eqnarray}\] where, \((t-1)=\frac{2}{t}W(\Gamma_{G}^{\Upsilon})\) and \(t(t-1)^{3}=2M_{2}(\Gamma_{G}^{\Upsilon})\).
Theorem 7. \(HM_{1}(\Gamma_{G}^{\Upsilon})=2(t-1)M_{1}(\Gamma_{G}^{\Upsilon})=\frac{4}{t}W(\Gamma_{G}^{\Upsilon})M_{1}(\Gamma_{G}^{\Upsilon})=4(t-1)^{2}W(\Gamma_{G}^{\Upsilon})\).
Proof. \[\begin{eqnarray}
HM_{1}(\Gamma_{G}^{\Upsilon})= & 2t(t-1)^{3}\\
= & 2(t-1)t(t-1)^{2}\\
= & 2(t-1)M_{1}(\Gamma_{G}^{\Upsilon})\\
= & \frac{4}{t}W(\Gamma_{G}^{\Upsilon})M_{1}(\Gamma_{G}^{\Upsilon})
\end{eqnarray}\] where, \((t-1)=\frac{2}{t}W(\Gamma_{G}^{\Upsilon})\).
Also, \[\begin{eqnarray}
HM_{1}(\Gamma_{G}^{\Upsilon})= & 2t(t-1)^{3}\\
= & 2t(t-1)(t-1)^{2}\\
= & 4(t-1)^{2}W(\Gamma_{G}^{\Upsilon})
\end{eqnarray}\] where, \(t(t-1)=2W(\Gamma_{G}^{\Upsilon})\).
Theorem 8. \(HM_{2}(\Gamma_{G}^{\Upsilon})=(t-1)^{4}W(\Gamma_{G}^{\Upsilon})=\frac{1}{2}(t-1)^{3}M_{1}(\Gamma_{G}^{\Upsilon})=(t-1)^{2}M_{2}(\Gamma_{G}^{\Upsilon})\).
Proof. By splitting the \(HM_{2}(\Gamma_{G}^{\Upsilon})=\frac{t(t-1)^{5}}{2}\), we obtain the result
Theorem 9. \(ModM_{1}(\Gamma_{G}^{\Upsilon})=\frac{2}{(t-1)^{2}}R(\Gamma_{G}^{\Upsilon})\)
Proof. From Theorem 2, we obtain \[\begin{eqnarray} ModM_{1}(\Gamma_{G}^{\Upsilon})= & \frac{t}{(t-1)^{2}} \end{eqnarray}\] and \[\begin{eqnarray} R(\Gamma_{G}^{\Upsilon})= & \frac{t}{2} \end{eqnarray}\] This implies, \[\begin{eqnarray} 2R(\Gamma_{G}^{\Upsilon})=& t \end{eqnarray}\] Substituting the value of \(t\) in \(ModM_{1}(\Gamma_{G}^{\Upsilon})\), we have \[\begin{eqnarray} ModM_{1}(\Gamma_{G}^{\Upsilon})= & \frac{2R(\Gamma_{G}^{\Upsilon})}{(t-1)^{2}} \end{eqnarray}\]
Theorem 10. For the orbit graph of dihedral group, Forgotten index is the twice of second Zagreb index and modified Schultz index \[\begin{eqnarray} F(\Gamma_{G}^{\Upsilon})&=&2M_{2}(\Gamma_{G}^{\Upsilon})=2S_{c}^{*}(\Gamma_{G}^{\Upsilon})\\ F(\Gamma_{G}^{\Upsilon})&=&2(t-1)^{2}W(\Gamma_{G}^{\Upsilon})=(t-1)M_{1}(\Gamma_{G}^{\Upsilon})=2(t-1)RR(\Gamma_{G}^{\Upsilon}). \end{eqnarray}\]
Proof. From Theorem 2, \(F(\Gamma_{G}^{\Upsilon})=2M_{2}(\Gamma_{G}^{\Upsilon})=2S_{c}^{*}(\Gamma_{G}^{\Upsilon})\).
Now,
\(F(\Gamma_{G}^{\Upsilon})=t(t-1)^{3}\)
by splitting the formula as \(t(t-1)^{2}(t-1)\), we have
\(F(\Gamma_{G}^{\Upsilon})=(t-1)M_{1}(\Gamma_{G}^{\Upsilon})\)
Since, \(W(\Gamma_{G}^{\Upsilon})=\frac{1}{2}t(t-1)\)
which gives \(F(\Gamma_{G}^{\Upsilon})=2(t-1)^{2}W(\Gamma_{G}^{\Upsilon})\)
Also, \[\begin{eqnarray}
F(\Gamma_{G}^{\Upsilon})= & t(t-1)^{3}\\
= & t(t-1)^{2}(t-1)\\
= & 2(t-1)RR(\Gamma_{G}^{\Upsilon})
\end{eqnarray}\] where, \(t(t-1)^{2}=2RR(\Gamma_{G}^{\Upsilon})\).
In this section, we obtain the polynomial of each index for the orbit graph of the dihedral group.
Theorem 11. Let \(\Gamma_{G}^{\Upsilon}\) be the orbit graph of the dihedral group. Then the polynomial of each index is
\(W(\Gamma_{G}^{\Upsilon}) = \sum
x^{\frac{1}{2}t(t-1)}\)
\(M_{1}(\Gamma_{G}^{\Upsilon}) =
\sum x^{t(t-1)^{2}}\)
\(M_{2}(\Gamma_{G}^{\Upsilon}) =
\sum x^{\frac{t(t-1)^{3}}{2}}\)
\(M_{3}(\Gamma_{G}^{\Upsilon}) =
\sum x^{t(t-1)^{4}}\)
\(HM_{1}(\Gamma_{G}^{\Upsilon}) =
\sum x^{2t(t-1)^{3}}\)
\(HM_{2}(\Gamma_{G}^{\Upsilon}) =
\sum x^{\frac{t(t-1)^{5}}{2}}\)
\(ModM_{1}(\Gamma_{G}^{\Upsilon}) =
\sum x^{\frac{t}{(t-1)^{2}}}\)
\(S_{c}(\Gamma_{G}^{\Upsilon}) =
\sum x^{t(t-1)^{2}}\)
\(S_{c}^{*}(\Gamma_{G}^{\Upsilon})
= \sum x^{\frac{t(t-1)^{3}}{2}}\)
\(F(\Gamma_{G}^{\Upsilon}) = \sum
x^{t(t-1)^{3}}\)
\(S_{o}(\Gamma_{G}^{\Upsilon}) =
\sum x^{t(t-1)^{2}}\)
\(R(\Gamma_{G}^{\Upsilon}) = \sum
x^{\frac{t}{2}}\)
\(RR(\Gamma_{G}^{\Upsilon}) = \sum x^{\frac{t(t-1)^{2}}{2}}\)
Proof. From Theorem 2, the result is obvious.
Example 2: Consider the orbit graph \(K_{9}\) (see Figure \(3\)).
Now, the graph \(K_{9}\) have \(|\Upsilon|-|B|=9-0=9\) vertices and \(\frac{9(9-1)}{2}=36\) edges,
respectively.
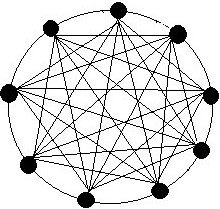
Also, the degree and distance of vertices are \((9-1)=8\). Then \[\begin{eqnarray} W(\Gamma_{G}^{\Upsilon})= & \sum x^{36} \\ M_{1}(\Gamma_{G}^{\Upsilon})= & \sum x^{576} \\ M_{2}(\Gamma_{G}^{\Upsilon})= & \sum x^{2304}\\ M_{3}(\Gamma_{G}^{\Upsilon})= & \sum x^{36864} \\ HM_{1}(\Gamma_{G}^{\Upsilon})= & \sum x^{9216} \\ HM_{2}(\Gamma_{G}^{\Upsilon})= & \sum x^{147456} \\ ModM_{1}(\Gamma_{G}^{\Upsilon})= & \sum x^{0.14} \\ S_{c}(\Gamma_{G}^{\Upsilon})= & \sum x^{576} \\ S_{c}^{*}(\Gamma_{G}^{\Upsilon})= & \sum x^{2304} \\ F(\Gamma_{G}^{\Upsilon})= & \sum x^{4608} \\ S_{o}(\Gamma_{G}^{\Upsilon})= & \sum x^{576}\\ R(\Gamma_{G}^{\Upsilon})= & \sum x^{4.5} \\ RR(\Gamma_{G}^{\Upsilon})= & \sum x^{288} \end{eqnarray}\]
Because topological indices can only be computed for connected graphs, we only consider the third case of the dihedral group’s orbit graph. Since the orbit graph of a dihedral group is complete, we obtain the indices by generalising the Wiener index, the first, second and third Zagreb indices, the Hyper first and second Zagreb indices, the Schultz and modified Schultz indices, the Somber index, the Forgotten index, and the Randic and Reciprocal Randic indices of a complete graph. We also learn how these indices relate to the Wiener index for the orbit graph of the dihedral group. Furthermore, the polynomial for the indices of the group’s orbit graph has been determined.
The authors would like to express their sincere thanks to referee(s) for comments and remarks.