Menu
Taekwondo behavior recognition has become a popular study issue in the past few decades due to its vast range of applications in the visual realm. The research of Taekwondo behavior recognition based on skeleton sequences has received increasing attention in recent years due to the widespread use of depth sensors and the development of real-time skeleton estimate methods based on depth images. In order to characterize the behavioral sequences, the majority of research work currently in existence extracts the spatial domain information of various skeleton joints within frames and the temporal domain information of the skeleton joints between frames. However, this research work ignores the fact that different joints and postures play different roles in determining the behavioral categories. Consequently, this paper presents a spatio-temporal weighted gesture Taekwondo features-based approach for Taekwondo recognition that employs a bilinear classifier to iteratively compute the weights of the static gestures and joint points relative to the action category in order to identify the joint points and gestures with high information content; concurrently, this paper introduces dynamic temporal regularization and Fourier time pyramid algorithms for temporal modeling in order to provide a better temporal analysis of the behavioural features, and ultimately employs support vector machines to complete the behavioural classification. According to experimental results on several datasets, this strategy outperforms certain other methods in terms of recognition accuracy and is highly competitive.
After a protracted developmental phase, Taekwondo and other related products fall into the same category of combat and fighting, which has attained a high degree worldwide, particularly in Japan, Europe, and other nations and regions [1, 2]. We can learn about the features of technique and tactic application in Taekwondo group hand-to-hand competitions and investigate the rules of victory through tracking analysis and research on the techniques and tactics of top Taekwondo players both domestically and internationally. This information can help Taekwondo players improve their skills and obtain scientific advice for both training and competition.
Sports tournaments heavily rely on tactical and technical analysis [3]. The traditional tactical analysis, which involves watching training and competition videos, examines the movement patterns of Taekwondo players, their technical attributes, and other data that helps to enhance the effectiveness and efficiency of Taekwondo players during training. It can also be utilized to develop strategies for competing against opponents based on their technical attributes and Taekwondo habits. The efficiency of technical and tactical intelligence analysis work is further limited by the traditional method, which requires manually watching a large number of training and competition videos. This method has several drawbacks, including high labor costs, significant data loss, lengthy delays, and low precision.
The ability to make a machine understand Taekwondo movements, or Taekwondo behavior recognition, is the key technology for the many computer vision-related human-computer interaction applications that have grown in popularity in recent years [4, 5]. These applications include behavioral monitoring, video games, healthcare, and more. Identifying Taekwondo behaviors accurately from RGB video sequences remains a challenging problem despite extensive research by experts and scholars. This is because of various factors that can interfere with the identification process, including changes in illumination, point-of-view, occlusion, and background clutter. Taekwondo behaviour recognition research has developed as a result of the growing prevalence of depth sensors and the suggestion of real-time skeleton estimate techniques based on depth photos [6]. In reality, Taekwondo tactics describe how players adapt to the rapidly evolving rules of the game and the circumstances in order to outmaneuver their opponent and use various strategies and techniques. The depth map sequence of the chosen sample action, tennis serve, is shown in Figure 1. From this, it is clear that the depth map sequence offers more depth information that is easily segmented from the complex scene of the desired target, drastically improving the background clutter and other issues and greatly simplifying the behavioural recognition model, which develops the Taekwondo behavioural recognition based on the three-dimensional skeleton sequence research.
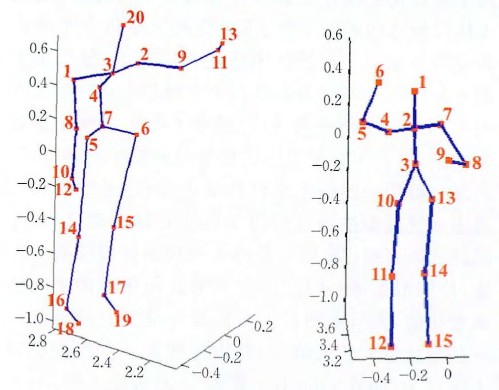
With the help of the skeleton estimation algorithm, which defines the skeleton as a graphical model made up of Taekwondo torso, head, and limb positions, it is possible to represent Taekwondo postures and behaviors using the positional parameters of the 3D skeleton and the Taekwondo, which has a better view invariance and also significantly reduces the model complexity and computational effort in the behavior recognition process [7, 8]. The algorithm can quickly and accurately estimate the 3D positional information of the skeleton’s joint points from the depth image, and it can even compute at a speed of 200 frames per second on the Xbox 360 GPU. The skeleton model with varying numbers of joint points is displayed in Figure 2, with the dots denoting the approximated Taekwondo joint points. Joint-point-based and body-part-based techniques are the two main categories into which existing skeleton-based behavior identification techniques can be divided.
In contrast, we present a behavior recognition approach in this study that uses spatiotemporal weighted gesture Taekwondo characteristics to address the aforementioned challenge. Because every 3D video sequence in the skeleton dataset can be thought of as a set made up of a number of arranged stationary postures, and sets can be thought of as point sets made up of a number of joint points. Based on this, this paper first addresses the joint point relationship of the corresponding point set of each stationary pose in order to obtain the video sequence’s spatial domain features; second, the Taekwondo vector of each joint point is obtained by examining the position relationship between the corresponding joint points in the neighboring moments; and finally, the dynamic change relationship model of the stationary poses over time is constructed in order to obtain the video sequences’ temporal domain features. Similar to this, different postures in the temporal video sequence play different roles in determining the behavioral category to which the video belongs, and important postures can aid in the more accurate determination of the behavioral category. In the stationary posture, on the other hand, different joints play different roles in identifying the posture, and distinguishable joints can help to identify the posture more accurately. In order to identify significant and recognizable joints and stationary poses, a bilinear classifier [9] is employed in this research to generate a weight matrix of joints and poses. This is expected to yield improved classification results.
Depth photos address issues like backdrop clutter and offer more depth information than conventional two-dimensional photographs. More accurate behavioural classification can be achieved with the recognition algorithm based on depth images [10]. The Taekwondo skeleton is extracted from depth images, which can simplify the behavioural recognition model, reduce computation, and have better view invariance while retaining the above information. Furthermore, the study focus of this paper is on how to build the behavioural feature model and obtain more accurate behavioural classification by utilising the joint point position parameters and Taekwondo information in the skeleton. There are two primary types of skeleton-based behavior recognition algorithms: those that rely on joint point features and those that rely on body component features.
Joint point feature based approach: the time domain hierarchical covariance feature approach presented in [11] establishes a time domain hierarchical covariance matrix descriptive sub-model to represent the Taekwondo trajectories of these joint points while also representing the Taekwondo skeleton using 3D joint point location information. A spatio-temporal graph model was proposed in study [12]. It represents video sequences using a spatio-temporal graph structure, with nodes representing multi-scale video clips and edges with directions representing the hierarchical spatio-temporal domain relationships between them. Ultimately, a graph model is learned from this and will be applied to classification. The Taekwondo skeleton is represented by the relative positional relationship between two by two joints in the behavioural set technique described in study [13], while the temporal sequence changes are represented by a multilayer Fourier factor model. Research [14] suggested intrinsic joint point features. To represent the Taekwondo skeleton features, they used the offset of the current moment frame from the initial frame, the amount of temporal displacement, and the relative position information of the joint points. They then classified them using the basic Bayesian nearest neighbor rule. A trajectory feature weighting method was proposed by Research [15]. It begins with the identification of points of interest from video sequences, followed by the extraction of particle and scale invariant feature transform (SIFT) trajectory features and weighting the two simultaneously. Finally, a support vector machine (SVM) is used to complete the behavioural classification. A viewpoint-invariant representation of the Taekwondo skeleton features was proposed by study [16]. They used a Hidden Markov Model to represent the time-varying relationship of the features and quantified these 3D point coordinates into orientation histograms by calculating the orientation of joint points in a fixed coordinate system. The deformable pose traversal convolution method described in study [17] traverses each joint point of the skeleton using a one-dimensional convolution operation, computes the optimal convolution kernel for each joint point to obtain the final pose features, and then uses the Long Short-Term Memory (LSTM) network to finish the classification.
Methods based on body part features: study [18] proposed a parametric modelling approach to divide Taekwondo into five parts, then Taekwondo behaviour is described by Taekwondo elemental features such as horizontal and vertical transformation relationships between Taekwondo parts and in-plane rotations, and finally Taekwondo behaviour is represented as a linear combination of a series of basic movements using principal component analysis. And study [19] proposed a bionic three-dimensional dynamic feature method, which splits the Taekwondo skeleton into smaller parts in multiple levels, and each part is represented by some bionic shape features, and finally the temporal change relationship of these bionic features is described by a linear dynamic system model.Additionally, study [20] proposed a new method for representing skeletons. Using the sequence of these joints, they represented Taekwondo behaviors. They did this by automatically selecting some informative joints based on the maximum angular velocity of the joints, the average or change value of the angle between joints, etc., in each time period. Additionally, in study [21], the Taekwondo skeleton sequences were described by the similarity of the angle trajectories of two and two joint sites, and the identification and classification of Taekwondo behaviors was accomplished through the use of a linear support vector machine. In contrast, study [22] advocated the use of a hierarchical recurrent neural network (HRNN) to segment the Taekwondo skeleton into five pieces, which include the torso, arms, and legs. These parts are then merged with a deep learning approach to simulate the interaction between them.
This paper’s primary contributions are as follows:
A new spatio-temporal postures Taekwondo feature extraction method is proposed, which extracts the intra-frame spatial domain information and inter-frame temporal domain information of the skeleton sequences;
A weight learning method is introduced to obtain the pattern features of 3D Taekwondo Taekwondo by using a bilinear classifier to compute the weight matrices of joints and postures during the training samples;
A spatio-temporal weighted postures behavior recognition algorithm is proposed, and the experimental results on multiple datasets show that the algorithm has a better recognition effect than the other methods.
Within the spatiotemporal dynamic change relationship of posture and weight learning, a behavior identification approach based on spatiotemporal weighted posture Taekwondo characteristics is proposed in this paper. Figure 3 illustrates the unique algorithmic framework. Initially, the data undergo normalization to establish a uniform scale feature for the various skeleton sequences. Subsequently, the intra- and inter-frame joint point features of the skeleton sequences are extracted to generate the spatio-temporal gesture Taekwondo feature representation of the skeleton sequences. The temporal modeling analysis is then conducted using the dynamic temporal regularisation and the Fourier time pyramid based on the extracted features. Meanwhile, during the training samples, the bilinear classifier is gradually calculated to obtain the weights of joints and postures in relation to the action types, leading to the identification of significant and identifiable joints and static postures; ultimately, a support vector machine is used to finish the behavior categorization by merging the feature model with the spatio-temporal weights of the static postures.
A Taekwondo stance, or point set made up of several joint points, can be associated with a frame at any given time in the Taekwondo skeleton dataset. These joint points and the relative positional relationship between them contain the spatial information of the Taekwondo stationary stance, which is physically expressed as the use of the vector between two points to measure the difference between two points. They also represent the intra-frame differences of the Taekwondo skeleton. In order to acquire the spatial domain properties of the video sequence, this work thus addresses the positional relationship between various joints in the corresponding point set of each stationary stance. This paper computes the coordinate difference between two different joints as a spatial domain feature of the Taekwondo static pose, assuming that the static pose consists of \(K\) joints, i.e., \(p=\left\{p_{1} ,p_{2} ,…,p_{k} \right\}\), and the coordinates of the \(i\)th joint, \(p_{i}\), are \(\left\{x_{i} ,y_{i} ,z_{i} \right\}\). This allows the description of the spatial positional relationship between the joints in the static pose at time \(t\).
$$f_{p} = \left\{ p_{i} – p_{j} \quad i,j = 1,2, \cdots , K; \, i \neq j \right\} \tag{1}$$
A video sequence consists of an ordered set of stationary postures; another challenge to be solved in this research is how to characterize the dynamic relationship of stationary postures over time. The position information of a single joint point at all times makes up the joint point’s Taekwondo trajectory, and the position vectors between adjacent moments roughly represent the joint point’s Taekwondo velocity, which is represented physically by the use of velocity vectors to indicate the point’s current Taekwondo direction and magnitude. Thus, in order to create the dynamic relationship between the poses over time and derive the time-domain characteristics of the video sequences, the Taekwondo vectors of every joint point in the stationary pose at the current moment and the corresponding joint points in the stationary pose at the neighboring moments are calculated in this paper. Using the Taekwondo postures at moments \(t\) and \(t+1\) as denoted by \(P_{t}\) and \(P_{t+1}\), respectively, this work computes the Taekwondo vectors of the identical joint points in the corresponding postures at times \(t\) and \(t+1\) to describe the temporal dynamic aspects of the stationary postures:
$$f_{m} = \left\{ p_{i}^{t+1} – p_{i}^{t} \,|\, p_{i}^{t} \in P_{t} ;\, p_{i}^{t+1} \in P_{t+1} ;\, i=1,2,\cdots ,K \right\} \tag{2}$$
Here, the normalization of the \(f_{p} ,f_{m} ,l_{2}\) norms causes each vector element to become extremely small, almost equal to zero but not quite, limiting each vector component to lie within the interval [-1, 1]. This reduces intraclass differences brought about by variations in the personal habits of various people carrying out the same action, and it also eliminates the impact of the presence of anomalous sample data, which accelerates the rate of convergence and enhances the stability of the model. It can enhance the model’s recognition stability and accelerate convergence. The effectiveness of the feature data processed by this normalisation method is demonstrated through experimental verification to be superior to that of the original feature data treated directly.Subsequently, this study establishes a direct link between the static posture features and the dynamic posture change over time, determining that the Taekwondo skeleton aspects are expressed as follows at moment \(t\). \[\label{GrindEQ__3_}\tag{3} f^{t} =\left\{f_{p} ,f_{m} \right\} .\]
In the end, the set of all Taekwondo skeletal characteristics at all \(t\) moments represents the spatiotemporal gestural Taekwondo features of a video sequence of \(N\) frames: \[\label{GrindEQ__4_}\tag{4} S=\left\{f^{t} |t=1,2,…,N\right\} .\]
The long short-term memory network (LSTM)-based feature extraction approaches from recent years are not as advantageous as the feature extraction method shown in this paper. In contrast to the black-box model of deep learning, the feature extraction method in this paper is more easily understood due to its first two advantages: it is computationally straightforward and intuitive, and it eliminates the need for a laborious iterative learning process and numerous updates and weighting parameter adjustments.
In this research, we train the SVM prediction using a one-versus-many classification technique. When training samples, we take into account that the position information of various joints in a static gesture influences the gesture’s category to varying degrees, and that the joints with a high degree of differentiation are better able to characterize the static gesture; similarly, the corresponding static gestures at various times also have varying effects on the behavioral sequence’s category. The stationary gesture; in a similar vein, the matching stationary gestures at various times have varying functions in classifying the behavioral sequence, with the key gestures frequently having a pivotal role. This paper presents a weight learning method based on this, wherein the contribution of various joint points and postures to the category of behavioural sequences is represented by joint point weight \(p_{s}\) and posture weight \(p_{m}\), respectively. A bilinear classifier is then adopted to obtain the weight matrices of various joint points and postures, and the feature model and support vector machine are finally combined to classify the behaviours.
The goal of a support vector machine in addressing a classification problem is to create a hyperplane that will correctly categorize all of the training vectors. This study begins by introducing some concepts and findings of SVM, as demonstrated by earlier research 23: \[\label{GrindEQ__5_}\tag{5} g(x)=w^{{\rm T}} x+w_{0} =0,\] \(w,w_{0}\) represents the hyperplane’s parameter, while \(x\) denotes the training set’s feature vector. Additionally, the best classification, i.e. \[\label{GrindEQ__6_}\tag{6} {\rm Minimisation}text{ } h(w)=\frac{1}{2} w^{2},\] \[\label{GrindEQ__7_}\tag{7} {\rm Restrictions}\text{ } y_{i} \left(w^{{\rm T}} w_{i} +w_{0} \right)\ge 1,i=1,2,\cdots ,n,\] where \(y_{i}\) might have a value of +1 or -1 and indicates the label of the associated category.
The process of learning weight is then demonstrated. First, this work introduces the joint point weight \(p_{s}\) and posture weight \(p_{m}\).Predicting a certain video behavioral sequence as a category \(v\) has a misclassification score of if the joint point weight and posture weight of the behavioral category \(v\) are \(p_{v}^{s}\) and \(p_{v}^{m}\), respectively. \[\label{GrindEQ__8_}\tag{8} c(v)=\left(p_{v}^{s} \right)^{{\rm T}} \frac{1}{2} w^{2} p_{v}^{m} .\]
Then, calculating the value of \(c^{*}\) is the best categorization method. \[\label{GrindEQ__9_}\tag{9} c^{*} ={\mathop{\arg \min }\limits_{v}c(v)} .\]
In temporal order, the aforementioned equation is enlarged and changed as \[\label{GrindEQ__10_}\tag{10} c^{*} ={\mathop{\arg \min }\limits_{v}} \sum _{i=1}^{N}p_{v}^{m} (i)\frac{1}{2} \left\| w^{{\rm T}} \sqrt{p_{v}^{s} } \right\| ^{2}.\]
To answer the aforementioned equation, we must first determine the values of \(p_{v}^{s}\) and \(p_{v}^{m}\). This paper defines the weight learning objective function as follows based on prior experience: \[\label{GrindEQ__11_}\tag{11} \begin{cases} {\min\limits_{{p_{v} ,p_{v}^{m} }}}_{s} {\frac{1}{2} \left\| p_{v}^{s} \left(p_{v}^{m} \right)^{{\rm T}} \right\| ^{2} +\lambda \sum _{i=1}^{M}\xi _{i} } \\ {{\rm \; s.t.\; }} {\sum\limits_{i=n}^{N}p_{v}^{m} (i)=N,p_{v}^{m} \ge 0} \\ {\xi _{i} \ge \max \left(0,1-l_{i} c\left(v_{i} \right)\right)^{2} } \\ {\xi _{i} \ge 0,i=1,2,\cdots ,M} \end{cases}\] where \(N\) is the number of frames in the video sequence, \(l_{i} \in \left\{-1,1\right\}\) is the label of the associated training samples, \(v_{i}\) is the \(i\)th training sample in category \(v\), \(M\) is the number of training samples, \(\lambda\) is the classification error penalty coefficient, and \(\xi _{i}\) is the classification error score. Additionally, by performing an iterative operation, the best solution to the aforementioned Eq. \ref{GrindEQ__10_} can be found. This particular iterative method consists of the following two steps:
Correct the \(p_{v}^{m}\) value and update the \(p_{v}^{s}\) value:
Eq. \ref{GrindEQ__11_} can be viewed as a support vector machine loss function problem meeting \(l_{2}\) regularisation when the \(p_{v}^{m}\)value is fixed, as demonstrated by Eq. \ref{GrindEQ__12_}: \[\label{GrindEQ__12_}\tag{12} \min _{p_{v}^{s} } \frac{1}{2} \beta _{1} \left\| p_{v}^{s} \right\| ^{2} +\lambda \sum _{i=1}^{K}\max \left(0,1-l_{i} c\left(v_{i} \right)\right)^{2},\] where \(\beta _{1} =\left\| p_{v}^{m} \right\| ^{2}\), and the optimization problem of this function is solved in this work using the LIBSVM library’s optimization method.
Where the initial value of \(p_{v}^{m}\) is set to 1, fix the value of \(p_{v}^{s}\) and update the value of \(p_{v}^{m}\) .
Eq. \ref{GrindEQ__11_} can be viewed as a convex optimization problem that satisfies the following linear constraints once the value of\(p_{v}^{s}\) has been determined. \[\label{GrindEQ__13_}\tag{13} \begin{cases}{\min\limits_{p_{v} }}_{m} \frac{1}{2} \beta _{2} \left\| p_{v}^{m} \right\| ^{2} +\lambda \sum _{i=1}^{K}\max \left(0,1-l_{i} c\left(v_{i} \right)\right)^{2} {\rm \; } \\ {{\rm s.\; t.\; }\sum _{i=1}^{N}p_{v}^{m} (i)=N,p_{v}^{m} \ge 0}. \end{cases}\]
In order to determine and update the value of \(p_{v}^{m}\), this work presents the convex optimization optimal solution approach [24]. Moreover, by initializing \(p_{v}^{m}\) to 1, that is, by presuming that the weights of all frames at all times are the same, and by iteratively updating the weights using Eqs. \ref{GrindEQ__12_} and \ref{GrindEQ__13_} until the objective function Eq. \ref{GrindEQ__11_} converges.
Three phases comprise the spatio-temporal weighted gesture behavior recognition algorithm: The particular approach is explained as follows: first, it extracts spatiotemporal gesture Taekwondo features; second, it learns weights during training; and third, it does temporal modeling and classification.
Algorithm: Weighted gesture behavior recognition with spatial and temporal dimensions.
/* Extracting Features */
FOR \(t=1\) TO \(t=N\)
\(p_{v}^{m} =1\)/*Greatly initialise the value of pose weight \(p_{v}^{m}\) */
Update(\(p_{v}^{s}\))/* fix the value of \(p_{v}^{m}\), calculate and update the value of joint weight \(p_{v}^{s}\) */
Update(\(p_{v}^{m}\))/* fix the value of \(p_{v}^{s}\), calculate and update the value of pose weight \(p_{v}^{m}\) */
END FOR
Using learnt weights and training for the best possible classification based on Eqs. \ref{GrindEQ__6_} to \ref{GrindEQ__9_}
/* Time-series modeling and classification */
FOR \(t=1\) TO \(t=N\)
dtw_modelling()/* To address behavioral traits and resolve the issue of inconsistent action rates, apply dynamic time-regularized DTW*/
ftp__modelling()/* A Fourier time pyramid FTP model [25] is introduced to address the issue of inconsistent action execution times, and high frequency signals are eliminated to lessen the influence of ambient noise*/
END FOR
Classify_with_SVM()/*SVM classification*/
RETURN
The aforementioned algorithmic process yields the following results: for a given skeleton with a constant \(K\) joints and a variable length of skeleton sequence \(N\), the feature extraction algorithm’s time complexity is \(O(N)\). This means that, in terms of operational efficiency, the feature extraction algorithm only needs to perform the addition operation \([k(k-1)/2+k]\) times during a pose frame, requiring a smaller amount of computational resources; in contrast, the weight learning algorithm’s time complexity is \(O(N)\), requiring it to update the pose weights \(p_{v}^{m}\) at that moment and the feature weights \(p_{v}^{s}\) of all the joints in the frame, respectively, and then perform \(2\times [k(k-1)/2+k]\) multiplication operations.
Information on the frequency of using technical movements, their success rate, their habit, the kind and application of tactics, and the movement trajectory are typically needed for tactical analysis of Taekwondo match films. The data of Taekwondo players’ frequency of using technical movements, as well as the recording and analysis of their movement trajectories, were completed with the help of the recently developed behavior recognition algorithm. In order to do this, the new topology’s performance in the graph convolution behavior recognition method was evaluated. By counting the frequency of technical moves using a homemade dataset, the efficacy of the developed method was further confirmed. It was also possible to analyze the movement trajectories of Taekwondo players intelligently.
A total of ten Taekwondo players from a domestic team were followed throughout the study, and their training and simulated match recordings were collected. These videos were then self-developed into a training and testing dataset. This dataset contains video recordings of three different motions: swinging, moving, and kicking. Eight orientations make up the camera angles, and the labels for Kicking, Punching, and Moving are Kicking, Hook Punch, and Moving, respectively. The 1,847 video clips in the dataset consist of 696 kicking, 625 swinging, and 526 moving footage. The duration of each video clip is approximately 10 seconds.
A total of 1,786 video clips—608 swinging, 499 moving, and 679 kicking clips—were used as the training set for this dataset. The test set consisted of an extra sixty-one video segments: seventeen kick clips, seventeen swing clips, and twenty-seven moving clips.
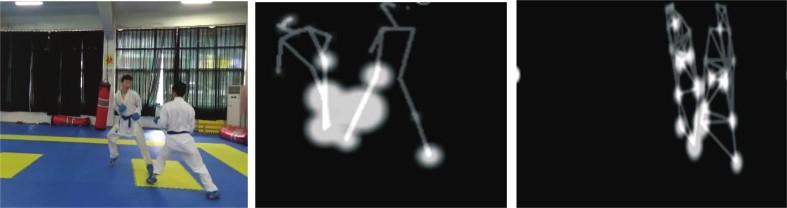
Figure 3 displays corresponding video frames from the kicking, swinging, and moving movies; Figure 4 displays corresponding video frames from three randomly selected perspectives in the test video.
Topological graphs based on Delaunay triangular dissection are constructed using an enhanced framework, which is based on the fundamental literature [25, 26]. As seen in Figure 5(Left), ST-GCN is merely the joints connected by themselves. As seen in Figure 5(Middle), AS-GCN is able to associate and connect joints that may be pertinent in a certain behavior. In this research, we present a graph construction approach using the Delaunay triangulation algorithm to derive the topology of video frames for various behaviors, as illustrated in Figure 2(Right).
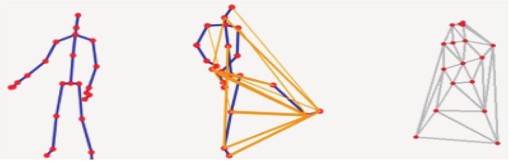
To enhance the precision of Taekwondo behavior classification in videos using skeleton points, the primary focus is on obtaining abundant and valuable feature data. Following multi-layer convolution through the features, the network learns by reducing the features or losing the information that represents the behavior. Thus, the goal of the study method is to enhance more valuable behavioral data.
A comparison of the features in this paper and the feature representation in ST-GCN is presented in Figure 6.
The white circles show how the attributes are correlated. More circles indicate the extraction of more correlated feature points from a given action. The wider the circle, the higher the correlation of a joint point for the feature representation of a certain behavior. Richer behavioral traits can be obtained by the created topological map, as depicted in Figure 6(Left), by obtaining more joint points with correlation.
The features of the right arm in the ST-GCN have been much diminished during the “kicking” behavior, as seen in Figures 3(Middle) and 3(Right), however the feature responsiveness in this paper is still there. There are more joints connected to the “kicking” action in comparison to the ST-GCN, which offers richer features for the behavior in terms of the matching feature responsiveness.
Table 1 illustrates the high accuracy rate that can be achieved by the method suggested in this work, which is trained on 1,786 video clips and tested on 61 test videos.
| Experiment | Top 1/% | Top 5/% |
|---|---|---|
| ST-GCN | 86.22 | 100 |
| AS-GCN | 87.17 | 100 |
| This work | 91.08 | 100 |
In order to analyze a particular Taekwondo player’s tactical habits and traits, their technical actions in a match film are recognized and categorized to determine how frequently they are used. For a visual video sequence consisting of \(T\) frames, based on the behavioural label sequences derived from the training model, for each frame \(t\), compute an integer divisible by 4 that corresponds to the label sequence derived from the model and show the associated category. Figure 7 displays the test video visualization.
The algorithmically generated frequency distribution of the Taekwondo players’ kicks and swings in the film is displayed in Figure 8. The number of “kicking” and “swinging” actions displayed by a Taekwondo practitioner in the test film is tallied. Additionally, after tallying the “kicking” and “swinging” actions of Taekwondo practitioners, the corresponding Taekwondo rules are obtained. These rules can then be modified during the training process, and training rules that correlate with them are provided. There are kicks and swings, respectively, as seen in Figures 8(a) and 8(b).
Ninety-seven kicks and seventeen swings were correctly counted out of the test set of footage. Our method counts the frequency of use of each sort of technical movement in a huge number of videos in order to analyze the strengths and weaknesses of a certain Taekwondo player’s technical moves.
To make observation easier, the coordinates of the lower right corner of the ground are converted to the coordinate origin based on the three-dimensional coordinates of the camera and the ground. This yields new three-dimensional spatial coordinates, which must be extracted from the joints (black joints) of the three-dimensional information coordinates, as illustrated in Figure 9. The trajectory map (black is the coordinate system) developed for a Taekwondo match is shown in Figure 10.
By designating the green dots of the red dots in the tactical picture, as seen in Figure 10, the system is able to count the Taekwondo trajectories of both Taekwondo players in the contest and distinguish and display them. The movement patterns of the Taekwondo players in attack and defense throughout the competition are examined by taking the movement trajectory of a single player from the extensive film, which truly meets the goal of technical and tactical study.
We present a new approach to behavior recognition with this study that combines the benefits of weight learning and temporal modeling. It is built on spatio-temporal weighted gesture Taekwondo characteristics. We emphasize important, discriminative features by effectively computing the weights of joint points and postures with respect to the action categories using a bilinear classifier. According to experimental results, the method performs better than existing methods on various datasets, suggesting that Taekwondo tactical analysis could benefit from its use. Better outcomes in fields like sports tactics training and performance analysis are anticipated as a result of this research’s fresh concepts for the field of sports behavior recognition.
No funding is available for this research.
The author declares no conflict of interests.