Graph theory is playing vital role in almost every field of our routine life. You make a conference call with your friends by using vertices (yourself and your friends) and edges (network connection). You construct a printed grid floor with different faces in your home by the help of graph theory. Authors in this study are using labelling of graphs and applying it in choosing best friends around you. The helping graphs in this article will be plane graphs which will be labelling under \(\Bbbk-\)labelling \(\mathrm{M}\) of kind \((\lambda,\mu,\nu)\). This study can be applied in many fields of everyday life.
Graph theory has wide applications in different fields of our routine life. For example, finding shortest route on Google maps, analyzing electrocardiogram (ECG)of a cardiac patient, managing security in housing societies, connecting people with Facebook and Whatsapp, handling transportation system etc. In this article, writers are focussing on applying the subtopic of graph theory, that is, face irregularity strength, to different daily routines of everyday life where six or more components (including people) will be attached. Mathematical graphs which are under consideration in this study are wheel graphs with six or more vertices. Writers have applied a similar application on a school with nine busses. After the successful application of this system, authors realized to publish it for the people around. All graphs \(G(V,E,F)\) in this article are simple, finite, plane and undirected. A wheel graph \(W_{n}\) with \(n\) vertices for \(n \geq 5\) can be constructed from a cycle graph. The edges of a wheel graph \(W_{n}\) can be calculated by \(2(n-1)\). In this article, we are assuming graphs with more than six vertices.
Reader should know some basic definitions which will be helpful in reading this paper. A simple graph is a graph which has no loop and multiple edges [1]. A connected graph is a graph where you can move from one vertex to another by an edge [2]. If all the vertices of a graph have same degree then such a graph is called regular graph. A graph will be \(t\)-regular if the degree of all its vertices is \(t\).
If the vertices of a graph do not have same degree then we call such graphs as irregular graphs [1]. If no two edges of a graph intersect each other then we say that graph is a planar graph [2]. Graph labelling is putting positive integers to vertices, edges and faces of the graph [3]. Weight of vertex of a graph can be calculated by adding the labels of the particular vertex and its surrounding edges, weight of an edge can be calculated by adding labels of two vertices surrounding that particular edge and the label of edge itself, weight of face can be calculated by adding the labels of surrounding vertices, edges and the label of that particular face itself. Let \(\mathrm{M}\) is a mapping from the graph elements \((V,E,F)\) into the set of positive integers \(\{1,2,3, \ldots, \Bbbk\}\) and consider the parameters \(\lambda, \mu, \nu\) which are either zero or one. A regular relation to calculate the face weight of any plane graph \(G(V,E,F)\) can be written as \(Wt_{\mathrm{M}_{(\lambda,\mu,\nu)}}(f) = \lambda\, \sum\limits_{v \sim f} \mathrm{M}(v) + \mu\, \sum\limits_{e \sim f} \mathrm{M}(e) + \nu\, \mathrm{M}(f)\) where \(Wt\) stands for weight and \(f\) stands for face of the graph. Suppose that \(\Bbbk\) is a positive integer then \(\Bbbk-\)labelling of graphs is a mapping \(\mathrm{M}\) from the graph elements into the set of positive integers. A \(\Bbbk-\)labelling \(\mathrm{M}\) of kind \((\lambda,\mu,\nu)\) is defined as the face irregular \(\Bbbk-\)labelling of kind \((\lambda,\mu,\nu)\) if for every two faces \(f_{1}\) and \(f_{2}\) of the plane graph, their weights are distinct, that is, \(Wt_{\mathrm{M}_{(\lambda,\mu,\nu)}}(f_{1}) \neq Wt_{\mathrm{M}_{(\lambda,\mu,\nu)}}(f_{2})\). The number \(\Bbbk\) should be the least positive integer among the set of integers and it should be the highest integer among the labelled integers in a plane graph.
The whole discussion will round over the domains \((1/0, 1/0, 1/0)\) where \((0,0,0)\) never exists. The \(\Bbbk-\)labelling will have different names which depend on domains. If the domain of labeling is the vertex set then we say it vertex \(\Bbbk-\)labelling of kind \((1,0,0)\), if the domain of labelling is edge set then we say it edge \(\Bbbk-\)labelling of kind \((0,1,0)\), if the domain of labelling is face set then we say it face \(\Bbbk-\)labelling of kind \((0,0,1)\), if the domain of labelling is vertex-edge set then we say it total \(\Bbbk-\)labelling of kind \((1,1,0)\), if the domain of labelling is edge-face set then we say it edge-face \(\Bbbk-\)labelling of kind \((0,1,1)\), if the domain of labelling is vertex-edge-face set then we say it entire \(\Bbbk-\)labelling of kind \((1,1,1)\). More details on \(\Bbbk-\)labelling and weights of graphs can be seen in [4, 5, 6, 7, 8].
The vertex set and edge set for wheel graphs can be written as \[\begin{aligned} V(W_{n}) &= \{v_{i} ; i=1,2,3, \ldots, n \}.\\ E(W_{n}) &= \{v_{1} v_{i} ; i=2,3, \ldots, n \} \cup \{v_{i} v_{i+1} ; i=2,3, \ldots, n-1 \} \cup \{v_{n} v_{2} \}. \end{aligned}\]
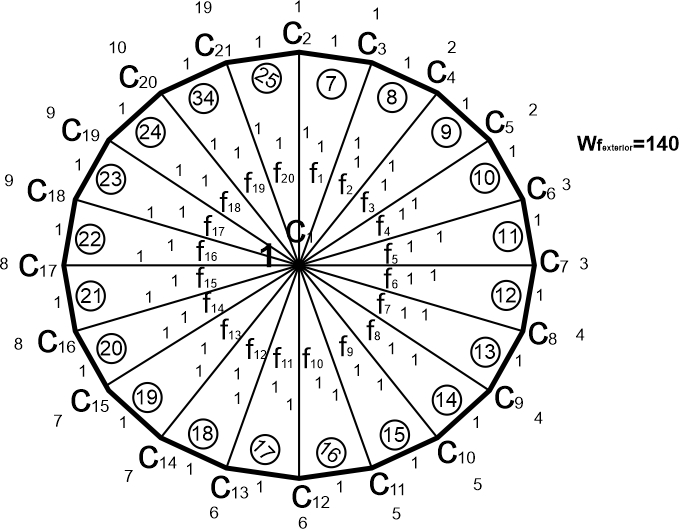
Graph theory is applicable on every field around us. Authors in this study are applying the subtopic of graph theory, that is, face irregularity strength, on some particular fields where one component may be attached with other components surrounding it. The Figure 1 represents a general diagram which can be fixed to any application of face irregularity strength. Mathematically, it represents a wheel graph with twenty-one vertices, forty edges and twenty-one faces including the external face. The labeling used in this diagram is \(\Bbbk-\)labelling \(\mathrm{M}\) of kind \((1,1,1)\) which is a labelling from the graph vertices, edges and faces into the set of positive integers. The numbers inside the faces, which are visible in circles, are the distinct weights of the faces. The parameters \(\{c_{1}, c_{2}, \ldots \}\) are the vertices in the graph, where the letter \(c\) stands for component. This component will vary from field to field. If we are applying this theory on computer networking system then components will be computers, if we are applying this theory on Facebook then components will be people and vice versa. Generally, for a wheel graph under entire \(\Bbbk-\)labelling \(\mathrm{M}\) of kind \((1,1,1)\), the labelling of vertices can be generalized as \(\mathrm{M}(c_{i}) = 1 \text{for} i=1\); \(\mathrm{M}(c_{i}) = \left\lceil \frac{i-1}{2} \right\rceil \text{for} i = 2,3,4, \ldots, n-1\); \(\mathrm{M}(c_{i}) = n-2 \text{for} i=n\), the labelling of edges can be generalized as \(\mathrm{M} \left(c_{1}c_{i}\right) = 1 \text{for} i = 2,3,4, \ldots, n\); \(\mathrm{M} \left(c_{i}c_{i+1}\right) = 1 \text{for} i = 2,3,4, \ldots, n-1\); \(\mathrm{M} \left(c_{i}c_{2}\right) = 1 \text{for} i = n\) and the labelling of faces can be generalized as \(\mathrm{M}\left(f_{i}\right) = 1 \text{for} i = 1,2,3,4, \ldots, n-1\) where \(Wt_{\mathrm{M} (1 ,1 ,1)}\left(f_{External}\right) > 6n\). The integers besides the vertices are the labels of vertices which are arranged in a sequence so that reader can easily understand them. The generalized formula is also elaborated so that you can construct any graph yourself. The labels of edges and faces are designed in the most easiest format, that is one for every edge and face. The weighs of faces are calculated by adding the labels of vertices, edges and the included face itself. For example, the weight of face 1 is equal to \(1+1+1+1+1+1+1=7\) and so on. The label of any edge, one, shows that there is one characteristic, behavior or trait between the two components. This label, one, can be designed in any format which depends on the category and its situation. In case of large numbers, they can be scaled down or can be compressed into smaller integers to maintain the existence of least positive integer \(\Bbbk\). Similar procedure can be analyzed with vertices and faces.
Theorem 1. Let \(G_{n}(V,E,F)\) be a wheel graph for \(n > 6\), then form an expression for the face irregularity strength of \(G\) under \(\Bbbk-\)labelling \(\mathrm{M}\) of kind \((\lambda, \mu, \nu)\).
Proof. Faces of the graph can be labeled under \(\Bbbk-\)labelling \(\mathrm{M}\) of kind \((\lambda, \mu, \nu)\) by the relation \(f_{i} = \{i; 1 \leq i \leq n-1 \}\). Since we are working only on face labelling of graphs. The labels of faces will be the only numbers to calculate weight. The weight of the graph faces would be calculated by adding only the face labels. So simply, the face labels will be the weights of the faces. The weights can be calculated as \(Wt_{\mathrm{M} (\lambda ,\mu ,\nu)}\left(f_{i}\right) = \{i; 1 \leq i \leq n-1\}\). Since a graph \(G\) has \(n\) faces including the external face. So the internal faces will be \(n-1\). The label of face 1 is 1 and similarly the label of face \(n-1\) will be \(n-1\). All the weights will be distinct. The maximum label that graph \(G\) can attain will be \(n-1\). Hence the expression for the face irregularity strength of graph \(G\) is \(n-1\). ◻
Theorem 2. Let \(G_{n}(V,E,F)\) be a wheel graph for \(n > 6\), then form an expression for the entire face irregularity strength of \(G\) under \(\Bbbk-\)labelling \(\mathrm{M}\) of kind \((\lambda, \mu, \nu)\).
Proof. We prove this theorem by mathematical induction. For
\(n=7\), vertices of the graph can be
demonstrated as \(\mathrm{M}(v_{i}) = 1
\text{for} i=1\); \(\mathrm{M}(v_{i}) = \left\lceil \frac{i-1}{2}
\right\rceil \text{for} i = 2,3,4,5,6\);
\(\mathrm{M}(v_{i}) = 5 \text{for}
i=7\), the edges can be demonstrated as \(\mathrm{M} \left(v_{1}v_{i}\right) = 1
\text{for} i = 2,3,4,5,6,7\); \(\mathrm{M} \left(v_{i}v_{i+1}\right) =
1 \text{for} i = 2,3,4,5,6\); \(\mathrm{M} \left(v_{i}v_{2}\right) = 1
\text{for} i = 7\). The faces will be labelled as
\(\mathrm{M}\left(f_{i}\right) = 1
\text{for} i = 1,2,3,4,5,6\). The face weights
according to the above mentioned labelling can be generalized as \(W_{\mathrm{M} (\lambda ,\mu
,\nu)}\left(f_{i}\right) = 8+i \text{for} i =
1,2,3, \ldots, n-3\); \(W_{\mathrm{M}
(\lambda ,\mu ,\nu)}\left(f_{i}\right) = 8+(n-3)+\left\lceil \frac{n}{2}
\right\rceil – 1 \text{for} i = n-2\) and
\(W_{\mathrm{M} (\lambda ,\mu
,\nu)}\left(f_{i}\right) = 8+(n-3)+1 \text{for}
i = n-1\) where \(W_{\mathrm{M}
(\lambda ,\mu ,\nu)}(f_{External}) \geq 2n\). Since all the face
weights are distinct so by the definition of face irregularity strength
of graphs, the results are true for \(n=7\).
Now suppose that the results are true for \(n=k\). Then vertices, edges and faces can
be labelled as \(\mathrm{M}(v_{i}) = 1
\text{for} i=1\); \(\mathrm{M}(v_{i}) = \left\lceil \frac{i-1}{2}
\right\rceil \text{for} i = 2,3,4, \ldots,
k-1\); \(\mathrm{M}(v_{i}) = k-2
\text{for} i=k\); \(\mathrm{M} \left(v_{1}v_{i}\right) = 1
\text{for} i = 2,3,4, \ldots, k\); \(\mathrm{M} \left(v_{i}v_{i+1}\right) =
1 \text{for} i = 2,3,4, \ldots, k-1\);
\(\mathrm{M} \left(v_{i}v_{2}\right) = 1
\text{for} i = k\); \(\mathrm{M}\left(f_{i}\right) = 1
\text{for} i = 1,2,3,4, \ldots, k-1\) respectively,
where \(W_{\mathrm{M} (\lambda ,\mu
,\nu)}\left(f_{External}\right) \geq 2k\). The face weights will
be written as \(W_{\mathrm{M} (\lambda ,\mu
,\nu)}\left(f_{i}\right) = 6+i \text{for} i =
1,2,3, \ldots, k-3\); \(W_{\mathrm{M}
(\lambda ,\mu ,\nu)}\left(f_{i}\right) = 6+(k-3)+\left\lceil \frac{k}{2}
\right\rceil – 1 \text{for} i = k-2\) and
\(W_{\mathrm{M} (\lambda ,\mu
,\nu)}\left(f_{i}\right) = 6+(k-3)+1 \text{for}
i = k-1\) where \(W_{\mathrm{M}
(\lambda ,\mu ,\nu)}(f_{External}) \geq 2k\). We have assumed
that the results are true for \(n=k\)
from the set \(\{7,8,9, \ldots, k-1, k, k+1,
\ldots, n\}\). Since the results are true for \(n=k\), so the results are obviously true
for \(n=k-1\). We observe that the face
\(f_{k-1}\) have one common edge with
the face \(f_{k}\) and the face weights
for \(f_{k-1}\) and \(f_{k}\) are distinct. Also, we know that
the labelling strategy is same for \(f_{k-1}\), \(f_{k}\) and \(f_{k+1}\). So, there is another common edge
between \(f_{k}\) and \(f_{k+1}\) and the face weights are also
distinct for \(f_{k}\) and \(f_{k+1}\). So labelling can be planned for
\(f_{k+1}\) with the same pattern which
is used for \(f_{k}\). Hence, we have
vertices as \(\mathrm{M}(v_{i}) = 1
\text{for} i=1\); \(\mathrm{M}(v_{i}) = \left\lceil \frac{i-1}{2}
\right\rceil \text{for} i = 2,3,4, \ldots,
(k+1)-1\); \(\mathrm{M}(v_{i}) = k-1
\text{for} i=(k+1)\), edges as \(\mathrm{M} \left(v_{1}v_{i}\right) = 1
\text{for} i = 2,3,4, \ldots, (k+1)\); \(\mathrm{M} \left(v_{i}v_{i+1}\right) =
1 \text{for} i = 2,3,4, \ldots,
(k+1)-1\); \(\mathrm{M}
\left(v_{i}v_{2}\right) = 1 \text{for} i =
(k+1)\) and faces as \(\mathrm{M}\left(f_{i}\right) = 1
\text{for} i = 1,2,3,4, \ldots, (k+1)-1\). The face
weights for \(n=k+1\) can be written as
\(W_{\mathrm{M} (\lambda ,\mu
,\nu)}\left(f_{i}\right) = 6+i \text{for} i =
1,2,3, \ldots, (k+1)-3\); \(W_{\mathrm{M} (\lambda ,\mu
,\nu)}\left(f_{i}\right) = 6+(k-2)+\left\lceil \frac{k+1}{2}
\right\rceil – 1 \text{for} i = (k+1)-2\)
and \(W_{\mathrm{M} (\lambda ,\mu
,\nu)}\left(f_{i}\right) = 6+(k-2)+1 \text{for}
i = (k+1)-1\) where \(W_{\mathrm{M}
(\lambda ,\mu ,\nu)}(f_{External}) \geq 2(k+1)\). Since the
weights are distinct so by the definition of irregularity strength of
graphs, the results are true for \(n=k+1\). Hence, we are done. ◻
import java.util.ArrayList;
import java.util.List;
public class WheelGraph {
public static void main(String[] args) {
int n = 21; // Number of vertices
List<List<Integer>> adjList = constructWheelGraph(n);
printGraph(adjList);
}
// Step 1: Function to construct a wheel graph with n vertices
public static List<List<Integer>> constructWheelGraph(int n) {
// Step 2: Initialize the adjacency list
List<List<Integer>> adjList = new ArrayList<>();
for (int i = 0; i < n; i++) {
adjList.add(new ArrayList<>());
}
// Step 3: Connect the outer cycle
for (int i = 0; i < n - 1; i++) {
adjList.get(i).add((i + 1) % (n - 1));
adjList.get((i + 1) % (n - 1)).add(i);
}
// Step 4: Connect the hub vertex to all outer vertices
for (int i = 0; i < n - 1; i++) {
adjList.get(n - 1).add(i);
adjList.get(i).add(n - 1);
}
return adjList;
}
// Step 5: Function to print the adjacency list representation
of the graph
public static void printGraph(List<List<Integer>> adjList) {
for (int i = 0; i < adjList.size(); i++) {
System.out.print("Vertex " + i + " is connected to: ");
for (int neighbor : adjList.get(i)) {
System.out.print(neighbor + " ");
}
System.out.println();
}
}
}Chao has a friends circle. He always face deceit from his friends. He is going to use face irregularity strength of graphs to find sincere friends in his circle. Chao has seven friends who are always close to him but he is confused to choose the best of them. He does not want to face deceit again. The Figure 2 shows that chao is using a popular graph in graph theory to choose his friends. This graph is a wheel graph, which is labelled under \(\Bbbk-\)labelling of kind \((1, 0, 1)\) because chao likes to solve his problems by the help of graph theory. If chao uses entire \(\Bbbk-\)labelling of kind \((1, 1, 1)\) of graphs then the additional feature in his friends will be the edge labelling which is always one for every edge so chao did not use the feature which is same in all his friends. You can see from diagram 2 that friends of chao are Lisha, Kexin, Dandan, Lihua, Jing, Fang, Ming. Fang and Lisha always try to be close to chao to get his full attraction towards them but chao does not know what is going on in their hearts, so chao uses graph theory to analyze the traits among his friends. Chao is looking for honest person because he never wants to face deceit again in his life. But he wants to compare their traits and then he will analyze by the help of face irregularity strength of this graph. The numbers, which are given to chao friends, are their number of traits, which are as follows. \(\text{Lisha} = \{\text{decent}\}\); \(\text{Kexin} = \{\text{honest}\}\); \(\text{Dandan} = \{\text{kind, beautiful}\}\); \(\text{Lihua} = \{\text{trustworthy, good listener}\}\); \(\text{Jing} = \{\text{kind, honest, beautiful}\}\) ; \(\text{Fang} = \{\text{forgiving, kind, soft hearted}\}\); \(\text{Ming} = \{\text{honest, beautiful, kind, soft hearted, good listener, decent}\}\).
Chao categorizes his friends into a wheel graph with six faces and every face contains three friends. His sixth sense works well now because he has faced many frauds in his life so he uses his sixth sense and gives numbering to every face of the graph. The condition behind these numbering is that the face weights should be distinct. Moving from top to clock wise, we see that numberings given by chao to the faces are, 1, 2, 3, 4, 5, 7 and 6. The condition of this k-numbering is that the face weights should be distinct which you can clearly see from the Figure 2. The face weights are shown in the circles inside each face, which are 4, 6, 8, 10, 12, 17 and 14 if we move in clock wise direction from Lisha.
Now the decision time comes here. Chao will first check the face irregularity strength of this graph. The face irregularity strength of a graph is the minimum integer (from the set of integers) in a graph for which the face weights are distinct. We can see clearly that the face irregularity strength of the Figure 2 is 7 which falls in the face containing Fang, Ming and Chao. So now chao has to choose Fang or Ming. Chao gave them number 7 because he was already interested in both of them because of their good traits. But chao has to choose one of them so he will go for Ming because Ming has much better traits as compare to Fang. So face irregularity strength in graph theory made it easy for chao to choose a best lifetime friend. Graph theory itself plays very important character in our everyday life problems but now the subtopics of graph theory need to apply on our routine life, which authors have done in this research.
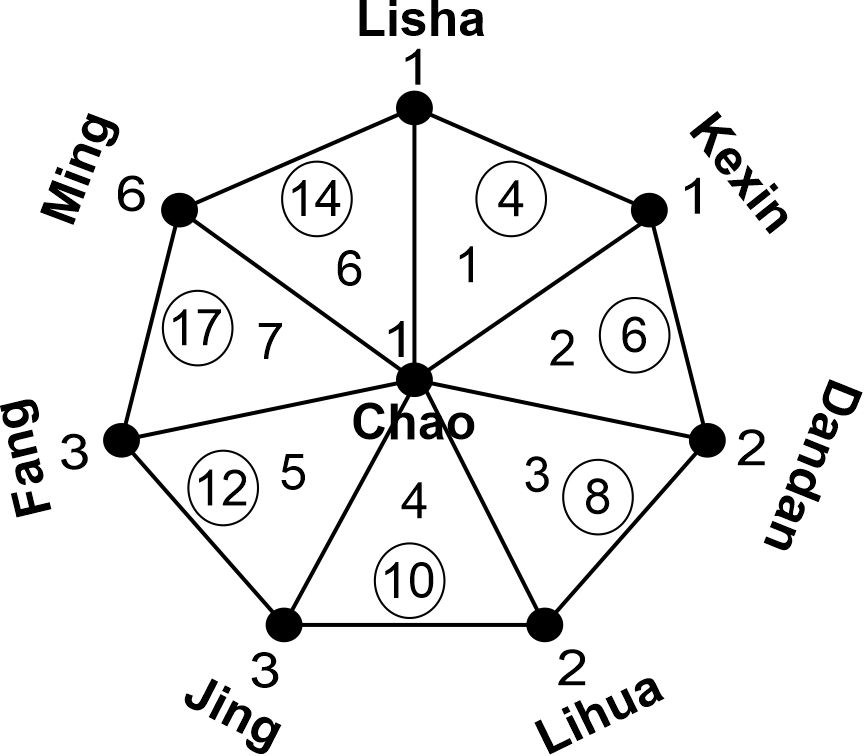
Remember that the numberings which chao used in his graph need not to be in order. You can assign integers according to your own wish but the face weight should be distinct and the least possible integers need to be used in your labelling. The numbers which are given to the edges and faces can also be others except one but you have to focus the whole graph, like, if you are giving a number 14 to the vertices then try to use a number less than 14 for the faces or edges. For larger number applications, you can use a scale to put them in a label form. For example, if you want to use the total number of engineering students of India in the graph then you can use scale, like, \(1000000\) equal to label \(1\) in the graph and vice versa.
Authors in this study made a user friendly system for the solution of our everyday routine life problems. They highlighted the environment for vertex, edge, face, total, edge-face, vertex-face and entire. This shows that almost every problem of everyday life can be dissolved according to this model. Writers applied this study on a local school which was successful in making cost effective transport system. In future, there is still much more space where applications of graph theory can be fixed.