Contents

Journal of Combinatorial Mathematics and Combinatorial Computing

  • Research article

On the Crossing Numbers of Cartesian Products of Small Graphs with Paths, Cycles and Stars

Kieran Clancy1, Michael Haythorpe1, Alex Newcombe1
11284 South Road, Tonsley 5042, Australia
  • Received: 12/12/2020
  • Accepted: 04/06/2021
  • Published: 31/03/2024

Abstract

There has been significant research dedicated towards computing the crossing numbers of families of graphs resulting from the Cartesian products of small graphs with arbitrarily large paths, cycles and stars. For graphs with four or fewer vertices, these have all been computed, but there are still various gaps for graphs with five or more vertices. We contribute to this field by determining the crossing numbers for fifteen such families.

Keywords: Crossing Number, Cartesian Product, Small Graphs, Path, Cycle, Star

1. Introduction

Consider a graph G comprising vertices V(G) and edges E(G). A drawing of G onto the plane is a mapping DG which maps vertices to distinct points and edges to continuous arcs. The image of an edge e = {u, v} is a continuous arc between the points associated with u and v such that the interior of the arc does not contain any points associated with vertices. without loss of generality, we call the points and arcs the ‘vertices’ and ‘edges’ of the drawing. The interiors of the edges are allowed to intersect at singleton points in such a way that each edge intersection is strictly a crossing between the edges, as opposed to the edges touching and then not crossing. For simplicity, we assume that no three edges intersect at the same point. These intersections form the crossings of the drawing and the number of crossings in D is denoted by crD(G). The crossing number of G, denoted cr(G), is the minimum number of crossings over all possible drawings. The crossing number problem (CNP) is the problem of determining the crossing number of a graph, and is known to be NP-hard [1]. The CNP is a notoriously difficult problem even for relatively small graphs; indeed, the crossing number of K13 has still not been determined [2].

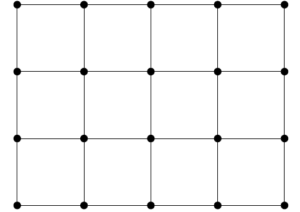
The Cartesian product of two graphs G and H, denoted by G□H, is a graph with vertex set V(G) × V(H), such that an edge exists between vertices (u, u′) and (v, v′) if and only if either u = v and {u′, v′} ∈ E(H), or u′ = v′ and {u, v} ∈ E(G). An example of the Cartesian product of two paths, P3□P4, is displayed in Figure 1. Note that Pn is the path on n + 1 vertices.

Figure 1: The Cartesian Product P3□P4.

One of the early results relating to crossing numbers is due to Beineke and Ringeisen [3] who, in 1980, considered families of graphs resulting from the Cartesian products of connected graphs on four vertices with arbitrarily large cycles. There are six connected graphs on four vertices, and with only one exception (the star S3), they were successful in determining the crossing numbers for each resulting family. The one unsolved case was subsequently handled by Jendrol and Šcerbová [4] in 1982. A decade later in 1994, Klešč [5] extended this result by determining the crossing numbers of families resulting from the Cartesian products of each of the connected graphs on four vertices with arbitrarily large paths and stars. In the ensuing years, significant effort has gone into extending these results to include graphs on more vertices; in particular five and six vertices. The pioneering work in this area was by Klešč and his various co-authors [5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27] who have spent the last three decades handling these cases, often on a graph-by-graph basis, requiring ad-hoc proofs that exploit the specific graph structure of the graphs in question. In the last fifteen years, a large number of other researchers have also contributed to this field. However, communication between the various researchers in this area has been poor, and it is has not been uncommon for multiple researchers to publish identical results.

To address this issue, a dynamic survey [28]on graphs with known crossing numbers was recently produced, which included tables of all known results of crossing numbers of families resulting from Cartesian products of small graphs with paths, cycles and stars. We reproduce the tables for crossing numbers of Cartesian products involving graphs on six vertices here. They are separated into Cartesian products involving paths (Table 1), cycles (Table 2) and stars (Table 3). In Tables 1–3, only those graphs for which results have been determined are included. The graph indices are taken from Harary [29], and an illustration of each graph on six vertices, as well as citations for each of the results in Tables 1–3 may be found in [28]. Note that, up to isomorphism, there are 156 graphs on six vertices, which includes 112 connected graphs.

For completeness, the tables include results determined in this paper and we highlight these indices in boldface. Additionally, note that some of the results are marked with asterisks. This indicates that the corresponding results appeared in journals which do not have adequate peer review processes. Hence, it would be valuable if these results could be re-proved in a journal which is fully peer reviewed. Indeed, in the present work, we provide a proof for one such asterisked result from [30], namely \(G^{6}_{120}\)□Pn.

Proving that a particular graph family has crossing number equal to a particular function is usually achieved as follows. First, an upper bound for the crossing number is determined by providing a drawing method for members of that family which realises the proposed number of crossings. This is then shown to coincide with a lower bound, which is usually determined by some form of inductive argument. The latter typically takes much more work than the former. However, in some cases, a lower bound can be easily determined. For instance, consider \(G^{6}_{46}\) and \(G^{6}_{60}\), which are displayed in Table 1. It is clear that the former is a subgraph of the latter. Then, for any graph H, it follows from the definition of the Cartesian product that \(G^{6}_{46}\)□H will be a subgraph of \(G^{6}_{60}\)□H. Thus, any lower bound for the crossing number of the former also provides a lower bound for the crossing number of the latter.

Furthermore, it is also clear that \(G^{6}_{46}\) contains a subgraph F consisting of a triangle with one pendant vertex attached. Then, any lower bound for cr(F□H) also serves as a lower bound for cr(\(G^{6}_{46}\)□H). Beineke and Ringeisen [3] proved that cr(F□Pn) = n − 1, and, thus, a corollary of the above arguments implies that cr(\(G^{6}_{60}\)□Pn) ≥ cr(\(G^{6}_{46}\)□Pn) ≥ n − 1. Hence, simply providing a drawing which establishes that cr(\(G^{6}_{60}\)□Pn) ≤ n − 1 is sufficient to decide the cases for both \(G^{6}_{46}\)□Pn and \(G^{6}_{60}\)□Pn; indeed, this exact argument was used in Klešč and Petrillová [24] to determine the crossing number of \(G^{6}_{46}\)□Pn. Of course, this kind of approach is only useful when the upper bound coincides with an established lower bound for a subgraph.

In what follows, we use approaches similar to the previous paragraph to determine the crossing number for fifteen additional families of graphs. Although the arguments are not complicated, the extensive research into filling in the gaps of Tables 1 – 3, which continues to this day, indicates the interest in this area; despite all of that research, these results have been hitherto undiscovered. We are in a unique position to present these simple arguments for two reasons. First, we are able to take advantage of the recently produced dynamic survey [28]] that gathers, for the first time, all known published results into one place, so that they can all be simultaneously drawn upon to provide good lower bounds. Second, we are also able to take advantage of the recently developed crossing minimisation heuristic, QuickCross [31], to aid us in finding good upper bounds.

2. New Results

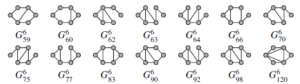
In this section we determine the crossing numbers of the Cartesian product of one of the graphs displayed in Figure 2, with various arbitrarily large paths, cycles and stars.

The upcoming proofs are laid out as follows. In Theorem 1 the crossing numbers of \(G^{6}_{90}\)□Pn and \(G^{6}_{120}\)□Pn are determined. In Theorems 2 and 3 the crossing numbers of the Cartesian products of various graphs in Figure 2 with cycles are determined. In Theorems 2 and 3, the results are only proved for sufficiently large cycles, and so the remaining cases involving small cycles are handled in Remark 1. Finally, in Theorem 4 the crossing number of \(G^{6}_{62}\)□Sn is determined. In all cases the lower bounds are obtained from previously published results. In Theorem 2 the upper bounds are also obtained from previously published results, and for the other theorems they are established by figures which show drawing methods for each Cartesian product considered.

Figure 2: We will Derive New Results for Cartesian Products Involving These Fourteen Graphs

Theorem 1. Consider the path graph Pn for n ≥ 1. Then, cr(\(G^{6}_{90}\)□Pn) = cr(\(G^{6}_{120}\)□Pn) = 3n − 3.

Proof. Consider the graph \(G^{6}_{51}\) which is displayed in Table 1. The crossing number cr(\(G^{6}_{51}\)□Pn) = 3n − 3 for n ≥ 1 was determined by Klešč et al [22]. It is clear that \(G^{6}_{51}\) is a subgraph of both \(G^{6}_{90}\) and \(G^{6}_{120}\). Hence, we have cr(\(G^{6}_{90}\)□Pn) ≥ 3n − 3 for n ≥ 1, and cr(\(G^{6}_{120}\)□Pn) ≥ 3n − 3 for n ≥ 1. It can be verified that the drawing methods for \(G^{6}_{90}\)□Pn displayed in Figure 3 and \(G^{6}_{120}\)□Pn displayed in Figure 4 each realise precisely 3n − 3 crossings, completing the proof. ◻

Theorem 2. Consider the cycle graph Cn for n ≥ 6. Then, cr(G596□Cn) = cr(\(G^{6}_{60}\)□Cn) = cr(G836□Cn) = cr(\(G^{6}_{90}\)□Cn) = 4n.

Proof. Consider graphs G406 and G1136, displayed in Table 2. The crossing number cr(G406□Cn) = 4n for n ≥ 6 was determined by Richter and Salazar [32], and the crossing number cr(G1136□Cn) = 4n for n ≥ 3 was determined by Klešč and Kravecová [20]. Then, consider graphs G596, \(G^{6}_{60}\), G836 and \(G^{6}_{90}\). It is clear that G406 is a subgraph of each of them, and G1136 is a supergraph of each of them. The result follows immediately. ◻

Figure 3: A Drawing of \(G^{6}_{90}\)□Pn with 3n − 3 Crossings. Each Circle of Vertices Is One Copy of \(G^{6}_{90}\)
Figure 4: A Drawing of \(G^{6}_{120}\)□Pn with 3n − 3 Crossings. Each Circle of Vertices Is One Copy of \(G^{6}_{120}\)

Theorem 3. Consider the cycle graph Cn. Then:

  1. cr(\(G^{6}_{63}\)□Cn) = 2n, for n ≥ 4

  2. cr(\(G^{6}_{64}\)□Cn) = 2n, for n ≥ 6.

  3. cr(\(G^{6}_{66}\)□Cn) = cr(\(G^{6}_{70}\)□Cn) = cr(\(G^{6}_{98}\)□Cn) = 3n, for n ≥ 5.

  4. cr(\(G^{6}_{75}\)□Cn) = 2n, for n ≥ 4.

  5. cr(\(G^{6}_{77}\)□Cn) = 2n, for n ≥ 6.

  6. cr(\(G^{6}_{92}\)□Cn) = 3n, for n ≥ 4.

Proof. Consider graphs \(G^{6}_{j}\) for j ∈ {41, 42, 47, 49, 53, 67}, all of which are displayed in Table 2, along with their crossing numbers, each of which were determined by Draženská and Klešč [8].

If we use ⊂ to denote subgraphs, then the following can be easily verified. First, \(G^{6}_{41}\) ⊂ \(G^{6}_{66}\) ⊂ \(G^{6}_{98}\), and \(G^{6}_{41}\) ⊂ \(G^{6}_{70}\) ⊂ \(G^{6}_{98}\). Second, \(G^{6}_{42}\) ⊂ \(G^{6}_{63}\). Third, \(G^{6}_{47}\) ⊂ \(G^{6}_{64}\). Fourth, \(G^{6}_{49}\) ⊂ \(G^{6}_{75}\). Fifth, \(G^{6}_{53}\) ⊂ \(G^{6}_{77}\). Finally, \(G^{6}_{67}\) ⊂ \(G^{6}_{92}\). It can be checked that these imply lower bounds for cr(\(G^{6}_{j}\)□Cn) that meet the proposed values for each of j ∈ {63, 64, 66, 70, 75, 77, 92, 98}. Then, all that remains is to provide upper bounds that also meet the proposed values. Drawing methods which realise the proposed values for j ∈ {63, 64, 75, 77, 92, 98} are displayed in Figures 5–10. Note that the drawing method for \(G^{6}_{98}\) also provides the corresponding drawing method for its subgraphs \(G^{6}_{66}\) and \(G^{6}_{70}\) if one removes the corresponding edges. ◻

Figure 5: A Drawing of \(G^{6}_{63}\)□Cn with 2n Crossings. The Solid Edges are the Copies of \(G^{6}_{63}\), While the Dotted Edges are those Introduced by the Cartesian Product
Figure 6: A Drawing of \(G^{6}_{64}\)□Cn with 2n Crossings. the Solid Edges are the Copies of \(G^{6}_{64}\), While the Dotted Edges are those Introduced by the Cartesian Product
Figure 7: A Drawing of \(G^{6}_{75}\)□Cn with 2n Crossings. the Solid Edges are the Copies of \(G^{6}_{75}\), While the Dotted Edges are those Introduced by the Cartesian Product
Figure 8: A Drawing of \(G^{6}_{77}\)□Cn with 2n Crossings. the Solid Edges are the Copies of \(G^{6}_{77}\), While the Dotted Edges are those Introduced by the Cartesian Product
Figure 9: A Drawing of \(G^{6}_{92}\)□Cn with 3n Crossings. the Solid Edges are the Copies of \(G^{6}_{92}\), While the Dotted Edges are those Introduced by the Cartesian Product
Figure 10: A Drawing of \(G^{6}_{98}\)□Cn with 3n Crossings. the Solid Edges are the Copies of \(G^{6}_{98}\), While the Dotted Edges are those Introduced by the Cartesian Product

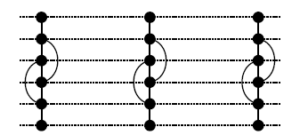
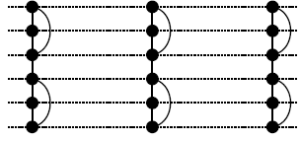
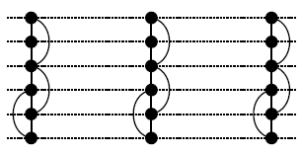
Each of the results in Theorems 2 and 3 is stated for the Cartesian product of a graph and a sufficiently large cycle. However, for small cycles, the results are not provided in those Theorems. We present them now in Table 4.

\(\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline {\bf i} & {\bf 59} & {\bf 60} & {\bf 63} & {\bf 64} & {\bf 66} & {\bf 70} & {\bf 75} & {\bf 77} & {\bf 83} & {\bf 90} & {\bf 92} & {\bf 98}\\ \hline {\bf cr(G^6_i \Box C_3)} & 8 & 8 & 6 & 6 & 7 & 7 & 6 & 6 & 10 & 11 & 9 & 9 \\ \hline {\bf cr(G^6_i \Box C_4)} & 16 & 16 & & 8 & 12 & 12 & & 8 & 16 & 16 & & 12\\ \hline {\bf cr(G^6_i \Box C_5)} & 20 & 20 & & 10 & & & & 10 & 20 & 20 & & \\ \hline\end{array}\)

Table 4: The Crossing Numbers for the Cartesian Products of Some Six-Vertex Graphs with Small Cycles. Only those Cases Not Already Handled in Theorems 2 and 3 are Displayed

Remark 1: To verify that the numbers provided in Table 4 are correct, we have submitted each graph to Crossing Number Web Compute [33, 34], an exact solver designed to handle sparse instances of small to moderate size. The proof files are available upon request from the corresponding author.

Theorem 4. Consider the star graph Sn for n ≥ 1. Then, \(cr(G^6_{62} \Box S_n) = 5[\frac{n}{2}][\frac{n-1}{2}]+2[\frac{n}{2}]\).

Proof. Consider the graph G276, which is displayed in Table 3. The crossing number \(cr(G^6_{27} \Box S_n) = 5[\frac{n}{2}][\frac{n-1}{2}]+2[\frac{n}{2}]\) for n ≥ 1 was determined by Klešč and Schrötter [27]. It is clear that G276 is a subgraph of \(G^{6}_{62}\). Hence, the lower bound is established. It can be verified that the drawing method for \(G^{6}_{62}\)□Sn, displayed in Figure 11, suffices to establish the upper bound. ◻

Figure 11: A Drawing of \(G^{6}_{62}\)□Sn with \(5[\frac{n}{2}][\frac{n-1}{2}]+2[\frac{n}{2}]\) Crossings. the Dotted Edges are the Copies of \(G^{6}_{62}\), While the Solid Edges are those Introduced by the Cartesian Product. There are \([\frac{n}{2}]\) Copies of \(G^{6}_{62}\) on the Left, and \([\frac{n}{2}]\) Copies of \(G^{6}_{62}\) on the Right

References:

  1. Garey, M.R. and Johnson, D.S., 1983. Crossing number is NP-complete. SIAM Journal on Algebraic Discrete Methods, 4(3), pp.312-316.
  2. McQuillan, D., Pan, S. and Richter, R.B., 2015. On the crossing number of K13. Journal of Combinatorial Theory, Series B, 115, pp.224-235.
  3. Beineke, L.W. and Ringeisen, R.D., 1980. On the crossing numbers of products of cycles and graphs of order four. Journal of Graph Theory, 4(2), pp.145-155.
  4. Jendroľ, S. and Ščerbová, M., 1982. On the crossing numbers of \(S_m \times P_n\) and \(S_m \times C_n\). Casopis pro pestovani matematiky, 107, 225-230.
  5. Klešč, M., 1994. The crossing numbers of products of paths and stars with 4-vertex graphs. Journal of Graph Theory, 18(6), pp.605-614.
  6. Drazenska, E., 2011. The crossing number of \(G \Box C_n\) for the graph \(G\) on six vertices. Mathematica Slovaca, 61(5), pp.675-686.
  7. Drazenska, E. and Klešč, M., 2008. The crossing numbers of products of the graph \(K_{2,2,2}\) with stars. Carpathian Journal of Mathematics, 24(3), pp.327-331.
  8. Drazenska, E. and Klešč, M., 2011. On the crossing numbers of \(G \Box C_n\) for graphs \(G\) on six vertices. Discrete Mathematics and Graph Theory, 31(2), pp.239-252.
  9. Klešč, M., 1991. On the crossing numbers of Cartesian products of stars and paths or cycles. Mathematica Slovaca, 41(2), pp.113-120.
  10. Klešč, M., 1995. The crossing numbers of certain Cartesian products. Discrete Mathematics and Graph Theory, 15(1), pp.5-10.
  11. Klešč, M., 1996. The crossing number of \(K_{2,3} \times P_n\) and \(K_{2,3} \times S_n\). Tatra Mountains Mathematical Publications, 9, pp.51-56.
  12. Klešč, M., 1999. The crossing number of \(K_5 \times P_n\). Tatra Mountains Mathematical Publications, 18, pp.63-68.
  13. Klešč, M., 1999. The crossing numbers of products of a 5-vertex graph with paths and cycles. Discrete Mathematics and Graph Theory, 19(1), pp.59-69.
  14. Klešč, M., 2001. On the crossing numbers of products of stars and graphs of order five. Graphs and Combinatorics, 17(2), pp.289-294.
  15. Klešč, M., 2001. The crossing numbers of Cartesian products of paths with 5-vertex graphs. Discrete Mathematics, 233(1-3), pp.353-359.
  16. Klešč, M., 2002. The crossing number of \(K_{2,3} \times C_3\). Discrete Mathematics, 251(1-3), pp.109-117.
  17. Klešč, M., 2005. Some crossing numbers of products of cycles. Discrete Mathematics and Graph Theory, 25(1-2), pp.197-210.
  18. Klešč, M., 2009. On the crossing numbers of Cartesian products of stars and graphs on five vertices. In J. Fiala, J. Kratochvíl, & M. Miller (Eds.), Combinatorial Algorithms. IWOCA 2009. Lecture Notes in Computer Science, 5874, pp.324-333. Springer.
  19. Klešč, M. and Kocúrová, A., 2007. The crossing numbers of products of 5-vertex graphs with cycles. Discrete Mathematics, 307(11-12), pp.1395-1403.
  20. Klešč, M. and Kravecová, D., 2008. The crossing number of \(P^2_5 \Box C_n\). Creativity in Mathematics and Informatics, 17(3), pp.431-438.
  21. Klešč, M. and Kravecová, D., 2012. The crossing number of $P^2_n \Box C_3$. Discrete Mathematics, 312(14), pp.2096-2101.
  22. Klešč, M., Kravecová, D. and Petrillová, J., 2014. On the crossing numbers of Cartesian products of paths with special graphs. Carpathian Journal of Mathematics, 30(3), pp.317-325.
  23. Klešč, M. and Petrillová, J., 2013. On the optimal drawings of products of paths with graphs. Acta Electrotechnica et Informatica, 13(3), pp.56-61.
  24. Klešč, M. and Petrillova, J., 2013. The crossing numbers of products of paths with graphs of order six. Disc. Math. Graph Th., 33(3), pp.571-582.
  25. Klešč, M., Petrillova, J. and Valo, M., 2017. On the crossing numbers of cartesian products of wheels and trees. Disc. Math. Graph Th., 37(2), pp.399-413.
  26. Klešč, M., Richter, R. B. and Stobert, I., 1996. The crossing number of \(C_5 \times C_n\). J. Graph Th., 22(3), pp.239-243.
  27. Klešč, M. and Schrotter, \v{S}., 2013. On the crossing numbers of cartesian products of stars and graphs of order six. Disc. Math. Graph Th., 33(3), pp.583-597.
  28. Clancy, K., Haythorpe, M. and Newcombe, A., 2020. A Survey of Graphs with Known or Bounded Crossing Numbers. Australasian Journal of Combinatorics, 78(2), pp.209-296.
  29. Harary, F., 1969. Graph Theory. Addison-Wesley.
  30. Su, Z. and Huang, Y., 2008. Crossing Numbers of Some Classes of Cartesian Product Graphic. J. Jishou Uni. Nat. Sci. Ed., 29(6), pp.25-28.
  31. Clancy, K., Haythorpe, M. and Newcombe, A., 2019. An effective crossing minimisation heuristic based on star insertion. Journal of Graph Algorithms and Applications, 23(2), pp.135-166.
  32. Richter, R. B. and Salazar, G., 2001. The crossing number of \(C_6 \times C_n\). Austral. J. Combin., 23, pp.135-143.
  33. Chimani, M. and Wiedera, T., 2016. An ILP-based proof system for the crossing number problem. In 24th Annual European Symposium on Algorithms (ESA 2016). Schloss-Dagstuhl-Leibniz Zentrum für Informatik.
  34. Chimani, M. and Wiedera, T., 2016. Crossing Number Web Compute. Retrieved from http://crossings.uos.de
Information
Guidelines
CP Initiatives
Follow CP
Facebook Twitter Linkedin
1970-2024 CP (Manitoba, Canada) unless otherwise stated.
Citation
Kieran Clancy, Michael Haythorpe, and Alex Newcombe. On the Crossing Numbers of Cartesian Products of Small Graphs with Paths, Cycles and Stars[J]. . Volume 119. 323-333. DOI: /10.61091/jcmcc119-31.