Menu
The gearbox gearbox transmission system, which is the foundation of a new energy vehicle, is responsible for the crucial duty of power transmission. In reality, the reducer gearbox system is the primary source of noise inside cars because of the design of the system, mistakes made during manufacturing and assembly, and gear engagement impulses. The research target is the second-stage retarder gearbox system of a new energy vehicle. A three-dimensional model of the retarder gearbox system is created using the Romax software.Static and dynamic analyses were carried out in Romax software based on the five typical conditions of start, acceleration, equal speed, deceleration, and stop in order to derive performance data such as maximum contact and bending stresses of the gears, single-position length load distribution, gearbox error, etc. In the NVH analysis, the system’s vibration acceleration was ascertained using the findings of the gearbox error analysis. In order to provide comparative data for vibration and noise reduction of gear modification, the comparative study analyses the data output results under various working conditions and analyses the relationship between gear engagement force and gear vibration.
On urban roadways, New Energy Vehicles (NEVs), which are powered entirely or in part by electric motors, are practically ubiquitous. NEVs, for all their great convenience, carry a certain risk to the safety of cyclists and pedestrians because of the relatively low noise they make when driving. This is especially evident at low speeds when EVs and HEVs, or hybrid electric vehicles, are operating [1, 2, 3]. National Highway Traffic Safety Administration (NHTSA) statistics on 8,387 HEVs and 559,703 ICEVs (internal combustion engine vehicles) show that collisions with bicyclists and pedestrians usually happen on the road, in low-speed zones, during the day, and in clear weather; HEVs are more likely than ICEVs to be involved in collisions with pedestrians; and HEVs are twice as likely to be involved in collisions with pedestrians when vehicles are slowing down or stopping, backing up, and entering or exiting parking spaces [4]. HEVs have a higher collision rate than ICEVs; in situations where cars are reversing, slowing down or stopping, or entering or leaving a parking space, HEVs are twice as likely to collide with pedestrians as ICEVs [5]. This implies that in order to alert pedestrians, EVs and HEVs must be retrofitted with audio alerts.
Three types of noise are found in hybrid cars: noise produced naturally (such as the noise produced by electric water and vacuum pumps, ventilators, rolling noise and ambient noise); noise produced accidentally; and noise produced by particular acoustic phenomena. When the internal combustion engine is turned off inside the car, there is nowhere to hide and noise from all other sources (fans, pumps, compressors, etc.) abruptly becomes very audible. Compared to conventional powertrains, hybrid powertrains include additional parts like high-voltage batteries, electronic control units, and electric motors. These parts interact differently and in novel ways, which produces new noises [6, 7].
Certain noises resulting from the combination of new parts and their novel interactions include the powertrain’s corrected moment of inertia and intrinsic frequency noise, as well as low-frequency vibration noise that occurs when the internal combustion engine is started or stopped during load changes. Electromagnetic noise [8] includes magnetic noise from the engine and generator during electric drive and regenerative braking; switching noise from the power control unit; and aerodynamic noise from the battery cooling system.
The majority of gear train studies currently in existence are based on simulated analyses of one particular condition, which means that the results cannot be applied to other conditions, and the evaluation of vibration noise is somewhat restricted [9, 10]. The operation of the gear flanks varies depending on the conditions under which the two-stage gearbox gearbox gearbox transmission system for new energy vehicles operates. For new energy vehicles, it is essential to analyse the two-stage gearbox gearbox gearbox transmission system under various circumstances, compare the variations in gear forces and vibration noises under various circumstances, and then carry out a more thorough and methodical investigation.
Therefore, the secondary gearbox gearbox transmission system of a new energy vehicle is the focus of this paper, which also builds a 3D parametric model of the gearbox gears using Romax software. Based on five typical conditions-start, acceleration, equal speed, deceleration, and stopping-the gearbox gears are then subjected to simulated contact force analysis and NVH analysis. In order to provide comparative data for a subsequent gear modification, the performance of each gear is assessed and compared, and the variations in gear stress and vibration noise under various conditions are analysed [11, 12].
The five standard operating conditions for new energy vehicles are basically acceleration, deceleration, stopping, and starting at the same speed. Table 1 displays the motor parameter values for the various operating conditions [13].
| Working conditions | Rated power/kW | Rated torque/(N · m) |
|---|---|---|
| Starting condition | 28 | 289 |
| Acceleration condition | 50 | 165 |
| Isokinetic condition | 26 | 43 |
| Deceleration condition | -45 | -90 |
| Parking conditions | -15 | -170 |
For evaluation comparison and simulation analysis, the isokinetic condition with the longest running time and the acceleration condition that contributes the most to vibration in the new energy vehicle were chosen. For Pinion Gear 1, for instance, the gear contact stress analyses, gear strength calibration, and root bending stress analyses were performed using Romax software, along with other static and contact analyses of the target drive train. Data comparison is offered for the gear wheel’s subsequent modelling following modification and noise reduction [14].
In actuality, the force manifestation of the energy transferring the gear train’s power is the flank contact forces that arise during gear engagement. The flank contact stresses of the gears, however, are an important component in the analysis of the entire gear train engagement since the forces act in concert and because excessive or unequally distributed flank contact forces can result in flank abrasion and other types of failure [13].
Furthermore, the service life and operational parameters of the entire multistage gearbox gearbox transmission system for new energy vehicles are directly impacted by the tooth contact stress of the gear wheels. Analysing the tooth contact stress of the gear wheels throughout the two-stage gearbox gearbox transmission system is therefore crucial.
Through the use of realistic working conditions simulation, the Romax software determines the tooth contact stresses. The instantaneous surface contact stress \({p_{{\rm{av}}}}\) is computed as follows using the contact hertz theory.
\[\label{e1}\tag{1} {p_{{\rm{av}}}} = {\pi \over 4}\sqrt {{{{F_{\rm{c}}}E} \over {2\pi {\rho _{{\rm{ec}}}}b\left( {1 – {\lambda ^2}} \right)}}} ,\] where \({\rho _{{\rm{ec}}}}\) is the equivalent curvature radius of the engaging gear, \(b\) is the gear’s tooth width, \(E\) is the gear’s modulus of elasticity, and \(\lambda\) is the gear’s Poisson’s ratio. \({F_{\rm{c}}}\) is the normal load applied to the gear wheel’s teeth. Eq. (2) gives the formula for \({F_{\rm{c}}}\):
\[\label{e2}\tag{2} {F_{\rm{c}}} = {{k{T_2}{{{Z_1}} \over {{Z_2}}}} \over {{r_c}\cos \alpha }},\] where \({Z_1}\) and \({Z_2}\) are the number of teeth on the driving and driven wheels, respectively; \(\alpha\) is the angle of pressure; \({r_c}\) is the radius of the contact point on the driving wheel; and \(k\) is the coefficient of load distribution between the teeth in the engaging area of the toothed wheel pair.
Eq. (3) provides the formula for \({\rho _{{\rm{ec}}}}\), where \({\rho _{{\rm{e1}}}}\) and \({\rho _{{\rm{e2}}}}\) stand for the driving and driven wheels’ respective curvature radii:
\[\label{e3}\tag{3} {\rho _{{\rm{ec}}}} = {{{\rho _{e1}}{\rho _{e2}}} \over {{\rho _{e1}} + {\rho _{e2}}}},{\rho _{e1}} = {1 \over 2}{d_1}\sin \alpha \pm {g_{\rm{c}}},{\rho _{e2}} = {1 \over 2}{d_2}\sin \alpha \pm {g_{\rm{c}}},\] where, as indicated by Eq. (4), \({g_{\rm{c}}}\) denotes the location of the contact point of the tooth flanks on the gearing’s line of engagement when the gearing system is engaged. \({d_1}\), \({d_2}\) represent the distances between the contact point and the node on the line of engagement, respectively [15]. \[\label{e4}\tag{4} {g_{\rm{c}}} = \mp {d_1}\sin \alpha \pm \sqrt {{{\left( {{1 \over 2}{d_1}\sin \alpha } \right)}^2} – {{\left( {{1 \over 2}{d_1}} \right)}^2} + {r_{\rm{c}}}} .\] In Eq. (4), the root contact of the driving wheel or the tooth apex contact of the driven wheel is represented by the lower symbol, and the tooth apex contact of the driving wheel is represented by the upper symbol.
The aforementioned formula for calculating contact stress, which serves as the theoretical foundation for the Romax software’s analysis of contact stress in the target gearbox, is used to determine the average contact stress when the gearing is engaged. The average contact stress of the gear wheel can only be determined by choosing the location of the selected variable’s contact point in relation to the gear wheel’s line of engagement in Eq. (1). The use of the Romax software allows simulation of the entire gearbox system to obtain a simulated analysis of the entire gearbox system, but because the engagement of the gear teeth of the gear wheel is a cyclic cycle, the impact of the gear wheels engaging and disengaging on the tooth surfaces results in an uneven distribution of the load on the contact surfaces of the gear wheels. Consequently, in order to determine the specific and dynamic load stresses on the entire gearbox system, Romax can be used to simulate and analyse the entire gearbox system.
In order to obtain the contact state and the variation of contact stresses during the meshing process of the gear unit, Romax software represents the dynamic meshing process of the entire gear unit, i.e., the distribution of equivalent stresses and contact pressures of the gear unit during a meshing cycle, using the tooth surface unit load distribution cloud and the gear contact stress wheel 3D diagram [16]. The load distribution cloud diagram per unit length (Figure 1) and the diagram of contact stress on the teeth (Figure 2) are obtained for the isokinetic condition and the accelerated condition, respectively, using the pinion 1 case as an example. The gears’ gearbox behaviour is influenced by the condition of contact between the gear units. The main source of vibration noise in the gearbox is high vibrations during the gearing process, which is caused by unusual contact between the gear wheels. This deformation of the components results in uneven load impacts on the engaged parts because of the engagement forces generated during the gearing process.
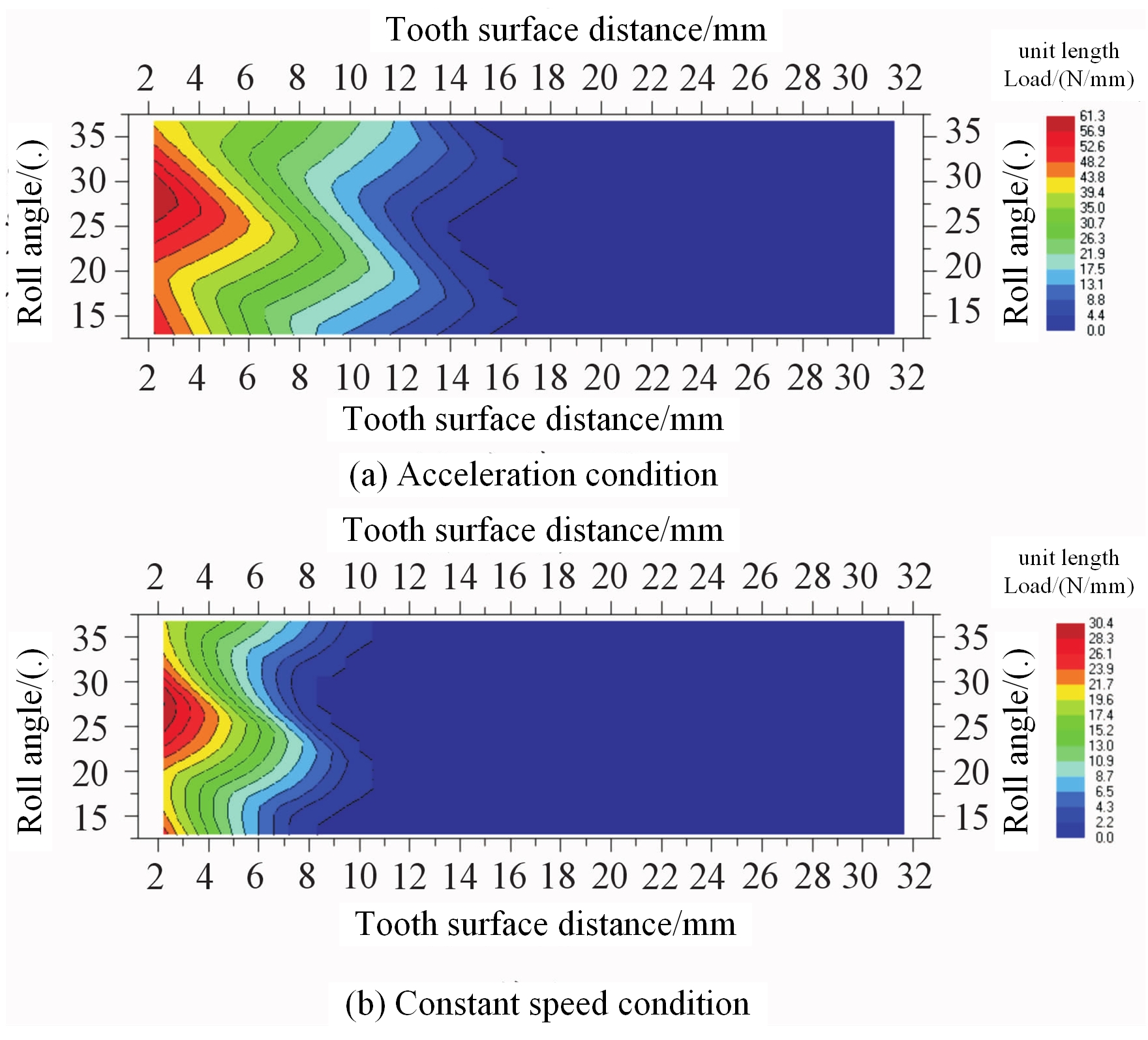
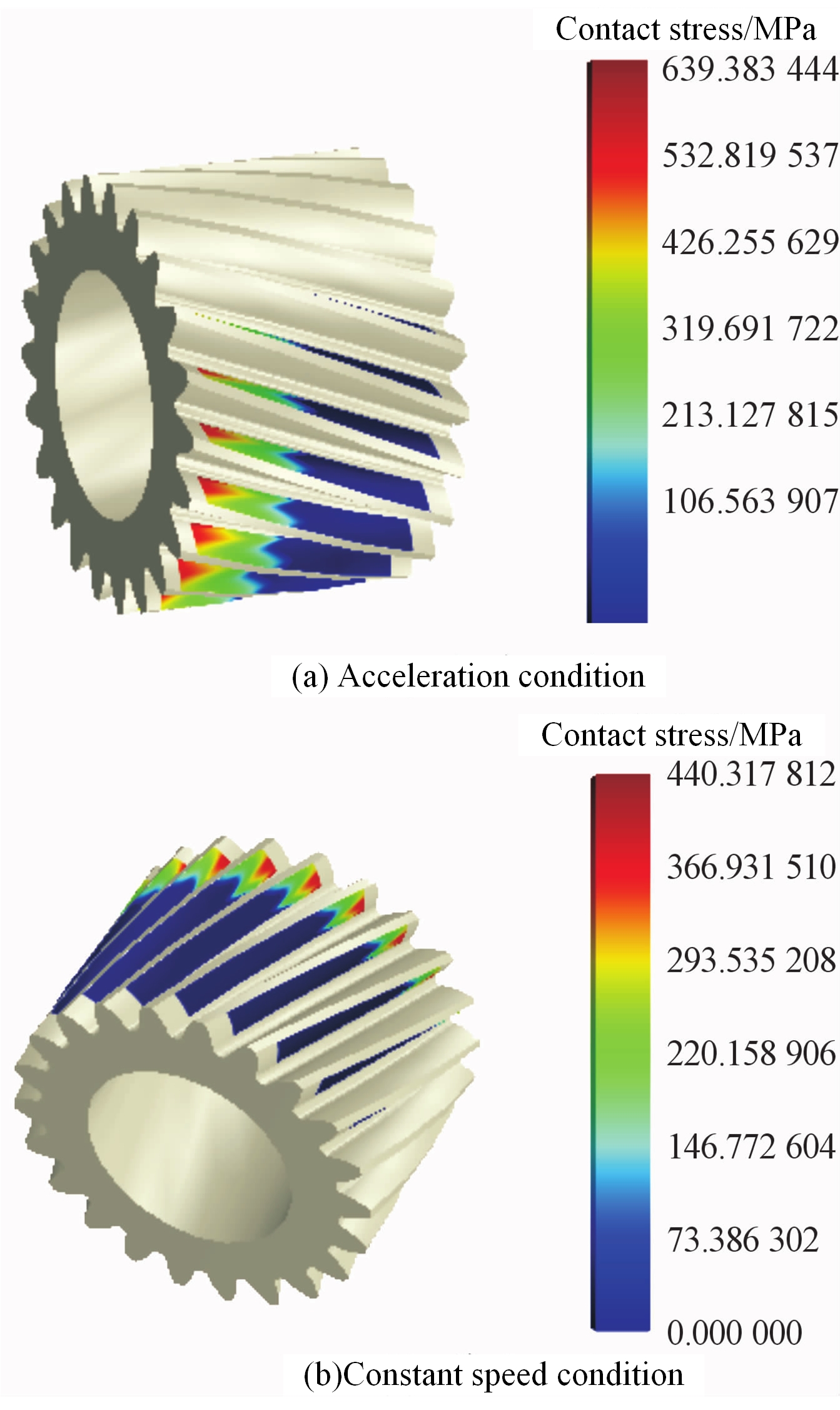
Under the two typical conditions, as shown in Figures 1 and 2, the left side of the pinion 1 experiences the highest stress load. A severe bias load condition is created when this stress load is concentrated at one end of the tooth surface and gradually decreases in the direction of the tooth width. The maximum contact stress value is 440.3 MPa for the equal speed condition and 639.38 MPa for the accelerated condition, according to a comparative study of the two condition diagrams. In the equal speed condition, the force load is lower than in the accelerated condition.
The tooth root bending stress analysis is an essential part of the contact analysis of the gear wheels in the entire new energy multi-stage gearbox gearbox gearbox transmission system. Excessive or uneven bending stresses at the root of the engaged gear wheels’ teeth negatively impact the gear wheel’s overall performance, which can even directly result in failures like broken gear teeth [16].
By computing the maximum value of the bending stress, the conventional bending stresses are compared with the strength of the most dangerous section, per the gearing stress analyses [12, 13, 14]. The Eq. (5) can be used to determine the maximum bending stress (\({\sigma _{\max }}\)) for the section that poses the greatest risk:
\[\label{e5}\tag{5} {\sigma _{\max }} = {{6{F_{{\rm{bn}}}}{h_{{\rm{Fa}}}}\left[ {1 + f\left( {1 + {{\Delta h} \over {{h_{{\rm{Fa}}}}}}} \right)\tan {\alpha _{{\rm{Fan}}}}} \right]\cos {\alpha _{{\rm{Fan}}}}{{\cos }^2}\beta } \over {bS_{{\rm{Fn}}}^2}},\] where \({F_{{\rm{bn}}}}\) represents the load normal to the gear wheel’s teeth along the line of engagement; \({h_{{\rm{Fa}}}}\) shows the distance between the gear wheel’s node and the dangerous section; \(f\) indicates the friction factor; \({{\alpha _{{\rm{Fan}}}}}\) shows the angle between the gear wheel’s apex and centre; \(\beta\) indicates the angle of rotation; \(S_{{\rm{Fn}}}^2\) indicates the thickness of the gear wheel’s teeth at the dangerous section; and \(\Delta h\) indicates the theoretical offset from the straight-line distance.
However, the actual bending stress calculation requires the consideration of several coefficients. The maximum bending stress \({\sigma _{\max }}\) at the dangerous cross-section can be found using the following formula:
\[\label{e6}\tag{6} {\sigma _{{\rm{max }}}} = {{2k{T_1}{Y_{{\rm{Fa}}}}{Y_{{\rm{sa}}}}{Y_\beta }{{\cos }^4}\beta \left[ {1 + f\left( {1 + {{\Delta h} \over {{h_{{\rm{Fa}}}}}}} \right)\tan {\alpha _{{\rm{Fan}}}}} \right]} \over {{\Psi _{\rm{d}}}{m^2}z_1^2\cos \beta \left( {1 + f\tan {\alpha _{{\rm{Fan}}}}} \right)}},\] where \({T_1}\) is the gear’s torque, \({Y_{{\rm{Fa}}}}\) is the toothing factor, and \({Y_{{\rm{sa}}}}\) is the gear’s stress correction factor. The gear is represented by the letters \({Y_\beta }\), which stands for screw angle factor, \(k\) for load factor, \({\Psi _{\rm{d}}}\) for tooth width factor, and m for gear module.
The bending stresses of the driving and driven wheels cannot be obtained in an intuitive and straightforward manner using the above conventional method, although it can be used to calibrate the root bending stresses of the gears. Consequently, in order to analyse the root stresses of the drive train’s gears-for instance, the large and small toothed wheel-the Romax software is used to perform a finite element analysis of the entire multistage gearbox drive train with engaging gear flanks.
The safety margins of the gearing operation are determined by using the safety coefficients that are computed based on the calibration results. Based on the default calculation standard ISO 6336:2006, which the software uses to determine the stress conditions and the safety coefficients of the gearbox under specified operating conditions, the strength of the gearing in the static analysis of the Romax software is calibrated. Eq. (7) is used to calculate the safety coefficients \([{\rm{e}}]\) in the Romax software:
\[\label{e7}\tag{7} [{\rm{e}}] = {e \over N},\] where \(N\) is the maximum stress that the drive gear material can withstand and e is the maximum stress.
The load spectrum reported by the gearing is exported, and the safety coefficients are derived using simulated analyses, as indicated in Table 2.
When using Romax software for static analyses, the safety factor is typically larger than 1 as long as the analyses’ outcomes satisfy the safety factor. It is feasible to run a simulation model to analyse the worst safety factor and simulate the drive train’s operation under specified operating conditions using the maximum contact and bending stresses.
The operational safety coefficient of the gearing is established to prevent excessive wear of the gearing surfaces or root breakage, and the maximum contact and bending load capacity of the gearing is determined by means of a strong calibration analysis. The coefficients of safety under maximum stress are still high and have a good margin of safety, as Table 2 illustrates.
| Working conditions | Gear | Contact stress/MPa | Bending stress/MPa | Contact safety factor | Bending safety factor |
| Starting condition | Large Gear 1 | 730 | 160 | 1.5 | 4.52 |
| Large Gear 2 | 575 | 110 | 2.3 | 7.5 | |
| Pinion 1 | 732 | 135 | 1.48 | 5.32 | |
| Pinion 2 | 570 | 0 | 2.01 | 8.45 | |
| Acceleration condition | Large Gear 1 | 635 | 125 | 1.72 | 5.62 |
| Large Gear 2 | 610 | 125 | 1.96 | 6.35 | |
| Pinion 1 | 630 | 104 | 1.70 | 6.56 | |
| Pinion 2 | 610 | 106 | 1.82 | 6.85 | |
| Isokinetic condition | Large Gear 1 | 442 | 82 | 2.15 | 8.44 |
| Large Gear 2 | 465 | 72 | 2.35 | 10.65 | |
| Pinion 1 | 445 | 75 | 2.10 | 9.86 | |
| Pinion 2 | 456 | 60 | 2.54 | 11.62 | |
| Deceleration condition | Large Gear 1 | 590 | 106 | 1.92 | 6.75 |
| Large Gear 2 | 530 | 95 | 2.24 | 8.15 | |
| Pinion 1 | 590 | 88 | 1.88 | 7.85 | |
| Pinion 2 | 530 | 80 | 2.15 | 8.85 | |
| Parking conditions | Large Gear 1 | 660 | 130 | 1.75 | 5.96 |
| Large Gear 2 | 500 | 85 | 2.54 | 10.25 | |
| Pinion 1 | 662 | 115 | 1.65 | 6.62 | |
| Pinion 2 | 500 | 74 | 2.28 | 11.06 |
The difference between the actual position and the theoretical position is known as the gearbox error, and it occurs when the driving and driven wheels in the gear train cannot work at the intended speed.
Gear noise issues are primarily caused by gearbox errors. Transmission errors cause the gears to engage, vibrating violently and making noise as they rub against the air. Reducing the transmission error is, therefore, the primary requirement for noise reduction. Eq. (8) illustrates how the theoretical formulae for the transmission error are typically expressed in two ways: first, in terms of angular error, and second, in terms of displacement along the gear flanks’ line of engagement. In this case, the angular error is expressed in micro radians.
\[\label{e8}\tag{8} TE = \left( {\theta – {\theta _{02}}} \right) – \left( {{\theta _2} – {\theta _{02}}} \right) = {{\left( {\theta – {\theta _{02}}} \right) – \left( {{\theta _1} – {\theta _{01}}} \right)} \over i},\] where, \(\theta\) represents the driven wheel’s actual angle of rotation; \({\theta _{01}}\) and \({\theta _{02}}\) are the driven and driving wheels’ starting angles; \({\theta _{1}}\) and \({\theta _{2}}\) are their theoretical angles of rotation; and i is the toothed wheel’s transmission ratio. It can be seen in Eq. (9) when expressed in terms of linear displacement.
\[\label{e9}\tag{9} TE = \left( {\theta – {{{\theta _1}} \over i}} \right){r_{b2}} = {r_{b2}}\theta – {r_{b1}}{\theta _1},\] where the base circle radii of the slave and master wheels are, respectively,\({r_{b1}}\) and \({r_{b2}}\).
The gearbox error analysis of the entire new energy vehicle multistage gearbox gear is based on two common scenarios, acceleration and equal speed, using the pinion gear as an example. The output results are displayed in Figure 3.
The transmission error of pinion 1 is estimated to be between 0.6 and 0.7 \(um\) under equal and accelerated speeds, based on the linear transmission error analysis in Figure 3. The gearbox error image produced by the Romax software only shows a portion of the gears’ entire engagement cycle. The peaks and valleys of the two values will be smaller to achieve the desired effect of the ensuing gear modification, which will lower the gearbox error of the two.
In the actual operating environment, the rotational speed of the NEM motor is not always fixed at a specific value. This suggests that the input shaft, to which the motor is connected, likewise has a variable rotational speed [17]. This is why the noise whistling analysis of the NEM multi-step retarder drive train cannot be done using the traditional method of noise spectrum analysis. Thus, the whole new energy vehicle multi-stage gearbox gearbox gearbox transmission system’s vibration state varies along with the vehicle motor’s shaft speed. When utilising the traditional method to measure the vibration state of the entire gearbox system, this results in noise overlap.
The order analysis method, which involves sampling and analysing the same kind of data for the drive train under various operating conditions under a specific modal condition, is employed in this work as a more accurate method of measuring the drive train vibration state of a multi-stage retarder for a new energy vehicle.
Both axial speed and frequency can be chosen on the x-axis of the displacement, speed, and acceleration report graphs that the Romax software noise analysis module generates. Below is a relationship between frequency and motor speed.
\[\label{e10}\tag{10} o = {{\omega \times 60} \over n},\] where \(n\) is the speed, \(\omega\) is the signal’s frequency value, and \(o\) is the order.
The motor’s output shaft is home to Bearing 1, which is the source of the most vibration. As a result, the node “7909CDTFY” on bearing 1 is chosen as the noise measurement node in the high-level whistle analysis interface, and the excitation source “Pinion 1 > Pinion 1” is chosen. The outcomes are displayed in Figure 11 for the two operating scenarios. Using the first order mode as an example, Figure 4 displays the output results under two distinct working conditions.
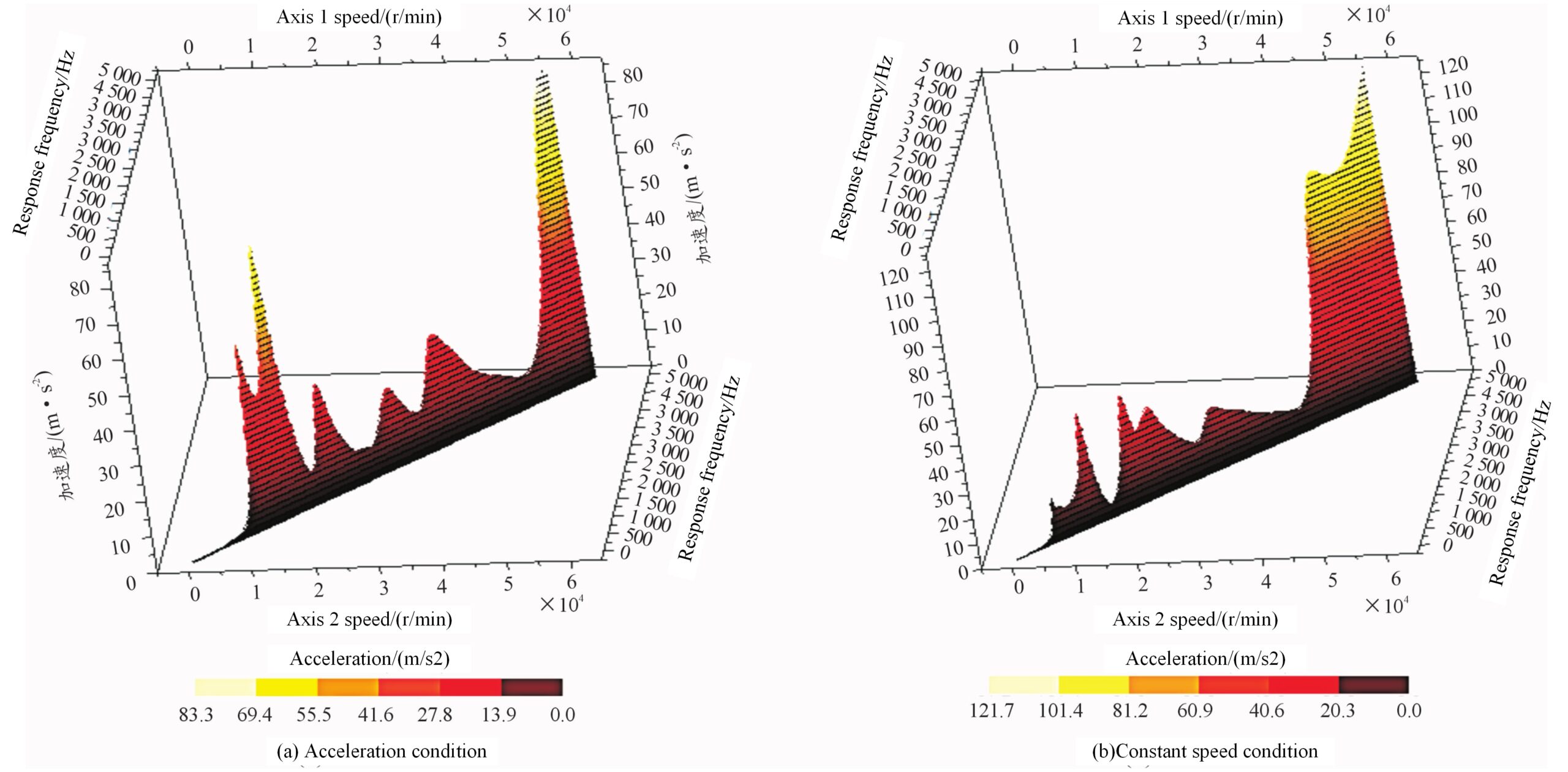
Figure 4 illustrates the highest effective values of the vibrational acceleration are 83.3 and 121.7 m.s-2 for the two different conditions of acceleration and isokinetic speed, respectively.
\[\label{e11}\tag{11} {V_{{\rm{AL}}}} = 20\log {\varepsilon \over {{\varepsilon _0}}},\] where \(\varepsilon\) is the effective value of the acceleration of vibration; \(\varepsilon _0\) is the initial acceleration of 10-6 m.s-2.
Table 3 displays the results of the noise calculation. Romax obtained the maximum effective values of vibration acceleration for each of the five conditions, which he then substituted into Eq. (11).
| Working conditions | Axis speed/r · min-1 | Effective value of acceleration/m · s-2 | Noise/dB |
|---|---|---|---|
| Starting condition | 856.5 | 32.10 | 150.12 |
| Acceleration condition | 2855.6 | 85.3 | 156.42 |
| Isokinetic condition | 5720.5 | 121.8 | 160.8 |
| Deceleration condition | 4860.2 | 59.80 | 156.48 |
| Parking conditions | 858.8 | 81.5 | 155.25 |
Table 3 illustrates that the gearbox system’s noise level can exceed 90 decibels in various operating scenarios. The noise level has surpassed the applicable noise quality standard, as per GB5076-1991 – Noise Evaluation of Toothed Gear Installations, and gear modification is required to reduce the noise.
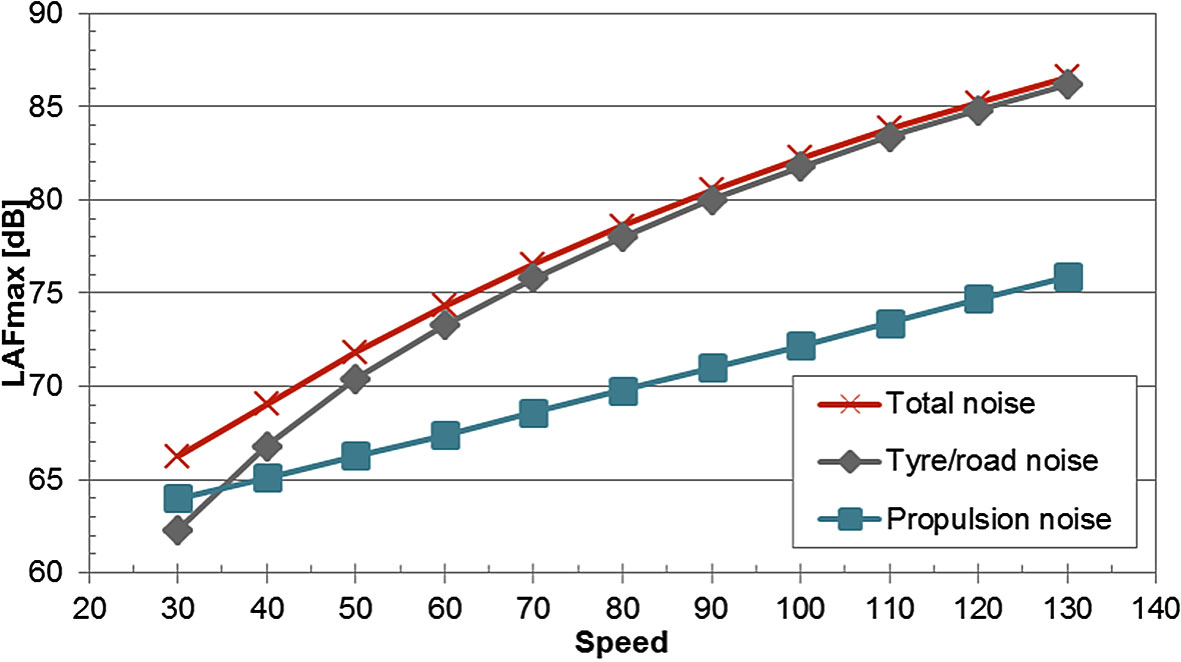
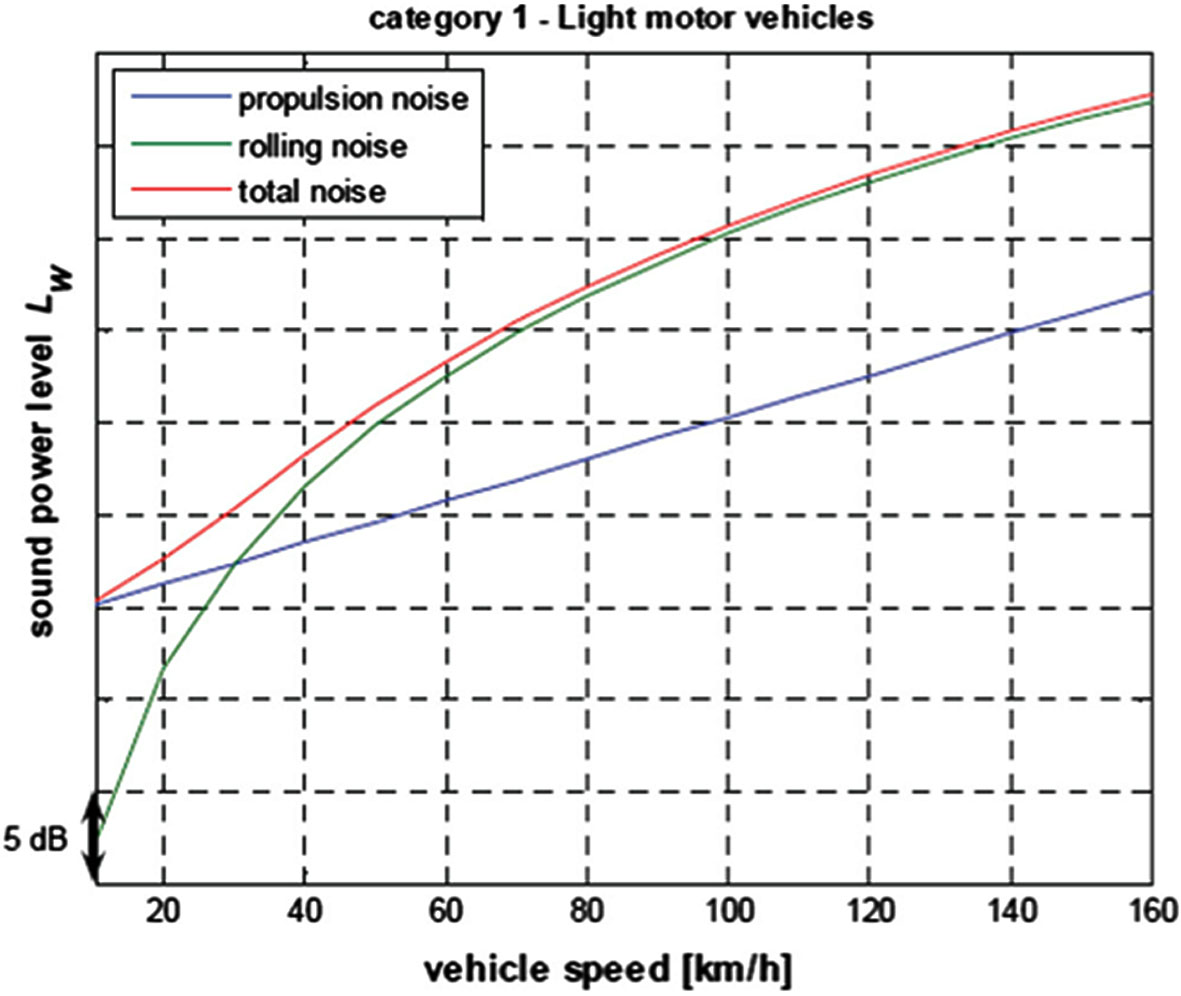
The noise produced by the tyres increases faster than the noise produced by the propulsion system. As illustrated in Figure 5, literature [18] used the Nord2000 model to compute the relationship between propulsive noise, tyre noise, and the overall noise of the vehicle and speed. According to the prediction model, tyre noise predominates at high speeds while propulsion noise does so at low ones.
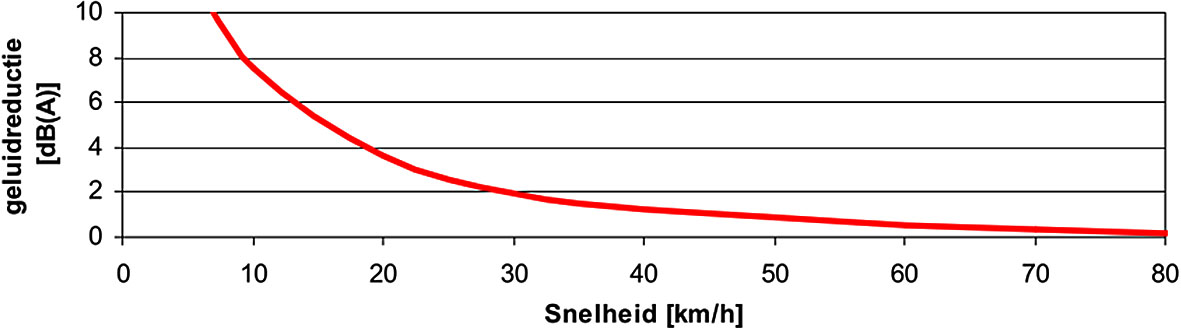
According to literature [18], the difference in noise emissions between combustion engine and hybrid vehicles increases with decreasing speed. Figure 6 illustrates this point by showing the total noise emissions from the hybrid vehicle’s engine and tyres. At 20 km/h, the reduction is more than 3 dB, drops to 1 dB at 50 km/h, and quickly to zero at 50 km/h and above, when tyre noise becomes the dominant factor and the difference in noise emissions between hybrid and non-hybrid cars almost vanishes [19, 20, 21].
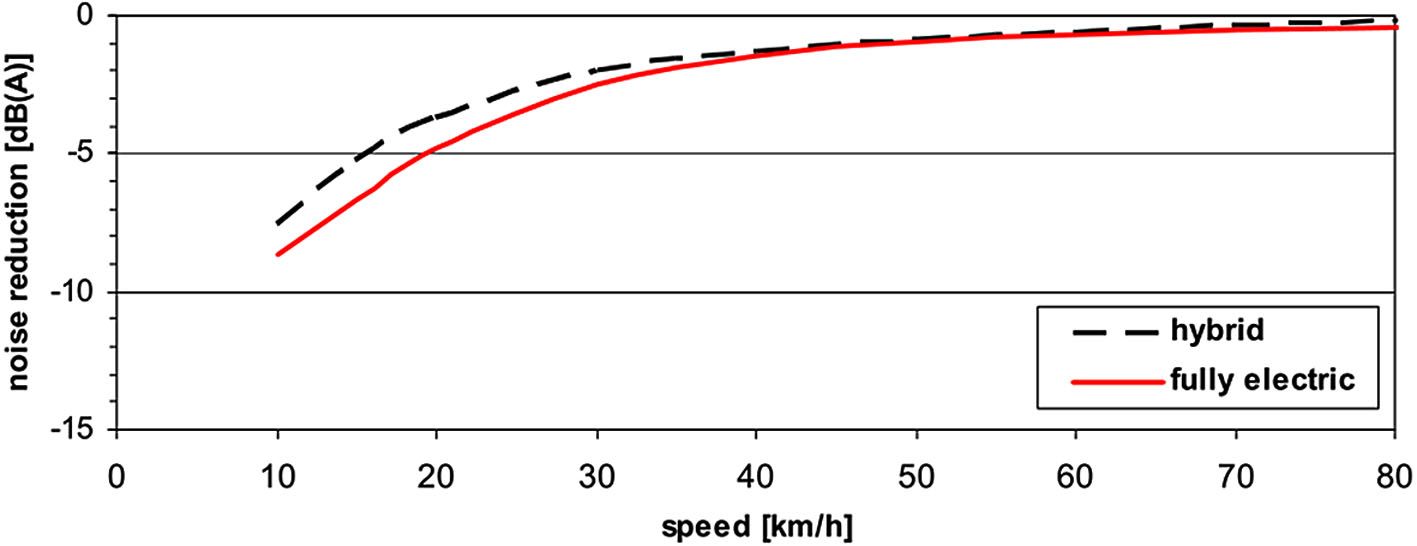
The reduction of overall noise emissions (engine and tyre road noise) for hybrid and electric vehicles is compared to that of internal combustion engine vehicles in the literature [22]. As illustrated in Figure 7, pure electric vehicles lack the noise produced by internal combustion engines and instead use an electric motor to replace it at speeds lower than 50 km/h. This means that the noise reduction level for electric vehicles is marginally higher than that of hybrid vehicles [19, 22, 23]. As a vehicle’s speed increases, the noise produced by its tyres and the road takes centre stage for both pure electric and hybrid vehicles. When a vehicle reaches a speed of more than fifty kilometres per hour, the noise produced by its tyres equals that of vehicles with internal combustion engines, and the tyre noise takes centre stage. Additionally, because the hybrid is activated in electric mode at low speeds, similar to an electric vehicle, electric and hybrid vehicles are quieter than combustion engine vehicles below 30 km/h. However, when a hybrid vehicle reaches a speed above 30 km/h, its noise reduction rapidly decreases relative to a combustion engine vehicle because at this point the vehicle has switched from electric mode to combustion engine mode.
The literature [23] has shown that, only when travelling at speeds under 20 km/h, there is a discernible difference in noise emissions between cars with internal combustion engines and hybrid cars (electric mode). As illustrated in Figure 8, the hybrid vehicle’s noise level difference with the fuel vehicle increases with decreasing speed in electric mode. At a standstill, the maximum noise level difference is approximately 20 dB, and at speeds of 20 km/h or higher, the noise level difference is even smaller [20].
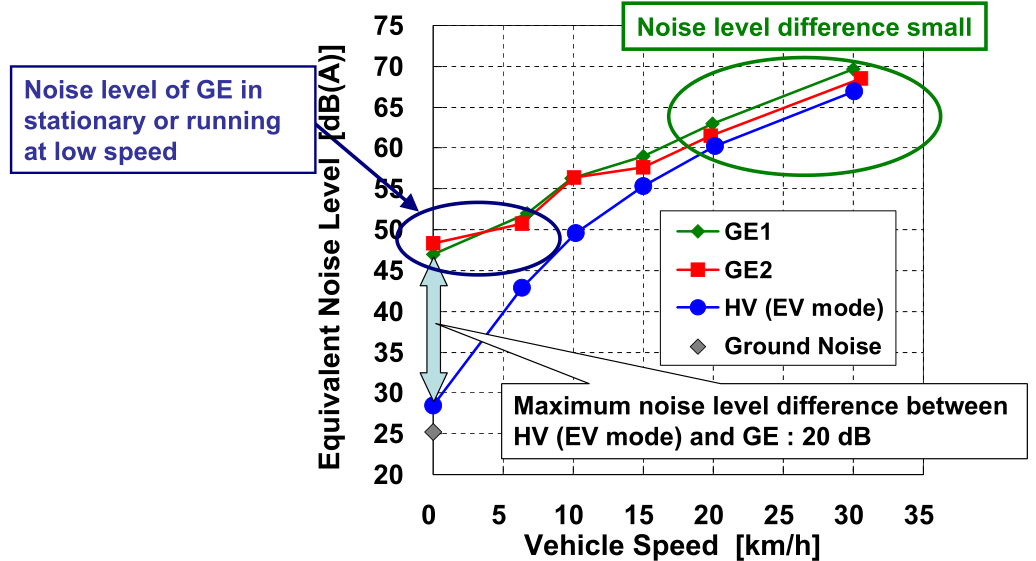
Figure 9 illustrates how tyre rolling noise starts to take centre stage in a fuel vehicle’s overall noise level at speeds higher than 30 km/h.
When internal and external noise characteristics of electric and internal combustion engine vehicles were compared, it was discovered that, at constant speed, the noise levels inside and outside the vehicle were remarkably similar.
Figure 10 compares the interior noise levels of an electric vehicle (Liiondrive) and a combustion engine vehicle (Fiat 500) at different constant speeds with the noise produced by the vehicle’s tyres rolling. It was found that the two cars’ interior noise levels were relatively similar at constant speeds, only 1 or 2 dB(A) higher than the rolling noise [21].
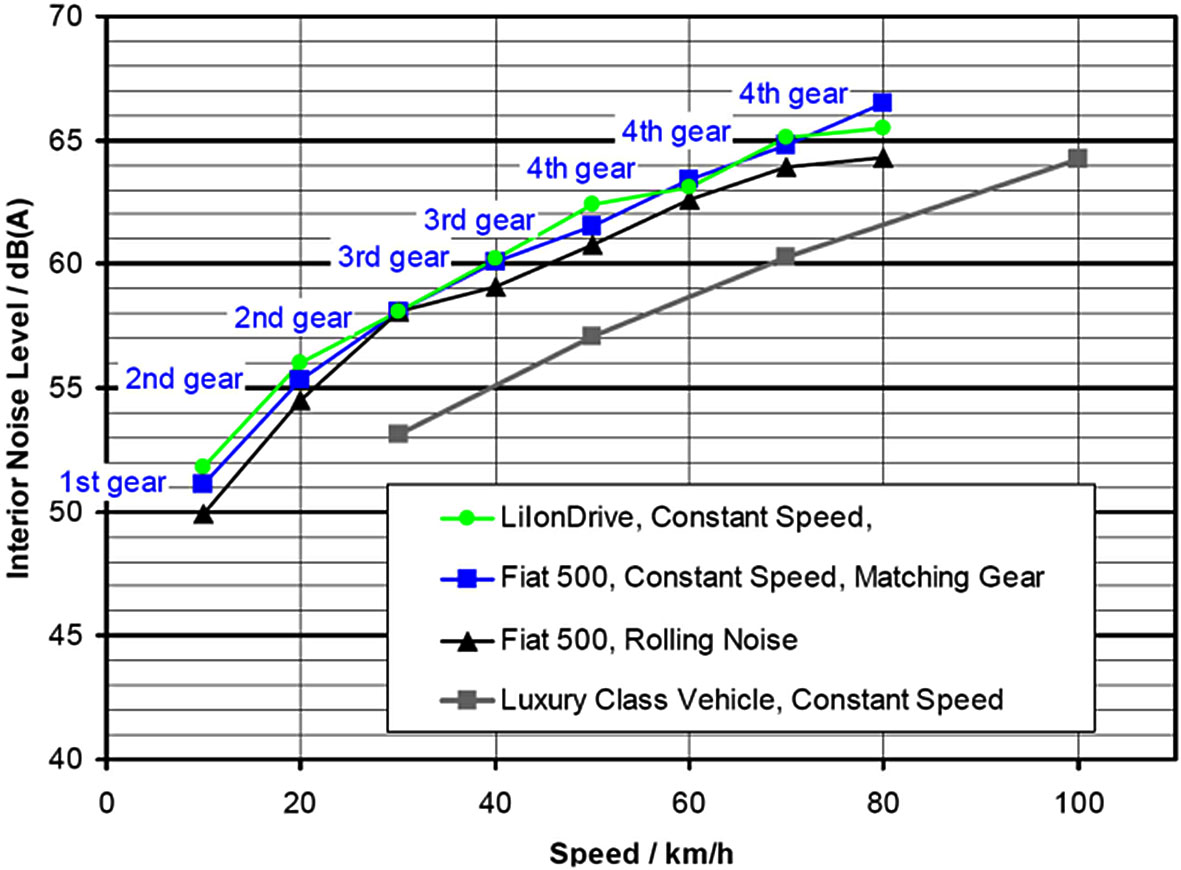
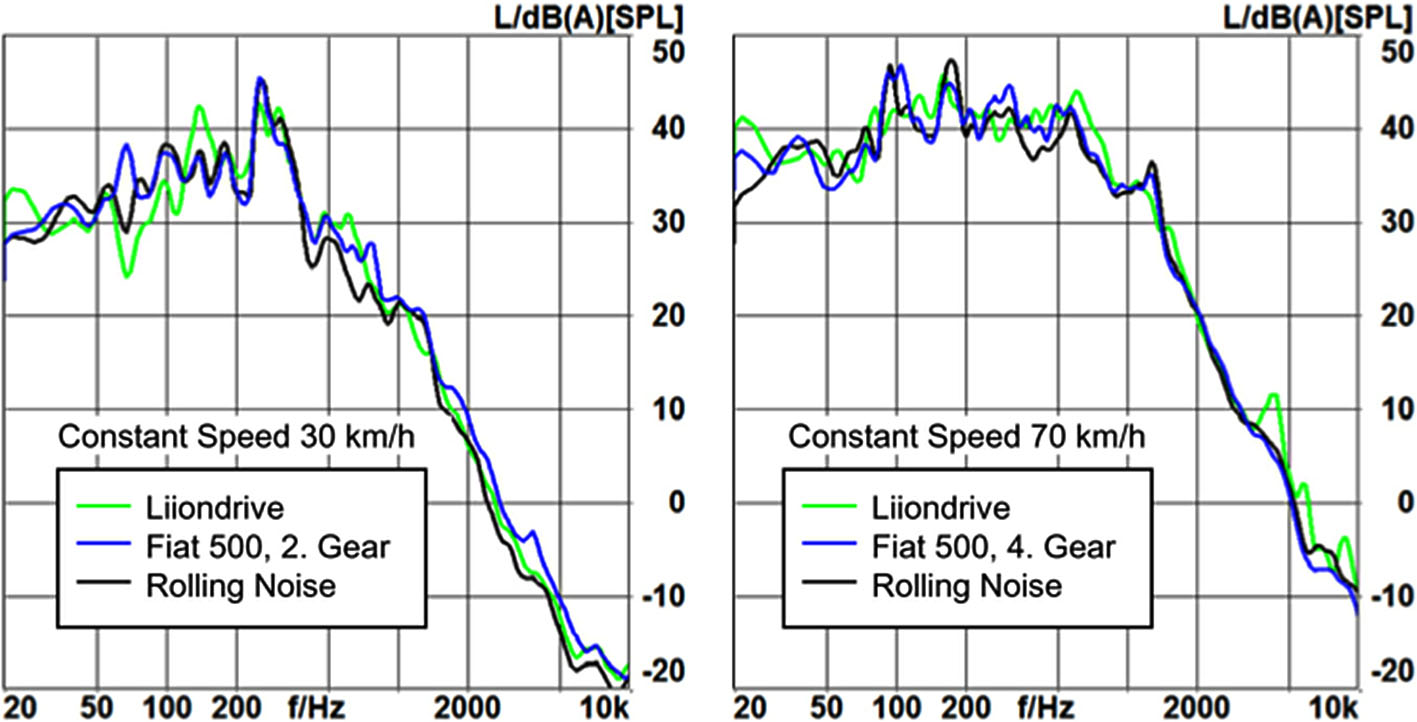
Figure 11 compares the noise spectra of the combustion engine vehicle (Fiat 500) and the electric vehicle (Liiondrive) at vehicle speeds of 30 and 70 km/h with the rolling noise of the combustion engine vehicle’s tyres. All three spectra are very similar at 30 km/h. The internal combustion engine car’s (Fiat 500) second stage engine produces mechanical noise, which is slightly higher at high frequency levels and exhibits a small peak in the spectrum at about 70 Hz. With the exception of a few high frequency resonance peaks in the electric vehicle’s (Liiondrive) spectrum, all three spectra are similar at 70 km/h [19].
Using Romax software, this article creates a three-dimensional model of the secondary reducer gearbox system of new energy vehicles. Static, dynamic, and NVH analyses are performed sequentially on the research object based on five typical working conditions: start, acceleration, constant speed, deceleration, and parking. We compare and analyse how different operating conditions affect noise and vibration. Create a data base so that the effects of gear modifications can be verified later. Static analysis of the gears in the gearbox system was done using software to create a model of the secondary reducer gearbox system of new energy vehicles. This made it possible to calculate the gearbox system’s maximum contact stress and maximum bending stress as well as the worst safety factor under different operating circumstances. Additionally, the gears underwent contact analysis, which produced the tooth root bending stress diagram and the tooth surface contact stress diagram. It is clear that, before modification, there was an uneven distribution of the bending and surface contact stresses in the teeth. Furthermore, there was a significant off-load caused by a relatively high level of stress on the gear’s edge.
This study is supported by National Key R&D Program:Creation and Application of Intelligent Low-carbon Field Management and Imitation Seedling Killing Technical Equipment(No.: SQ2023YFD2000030); National Natural Science Foundation of China (NSFC) Faceted Project:Research on bionic vibration deep-pine method for differentiated agronomic needs(No.: 52275288); Jilin Science and Technology Development Program:Development and demonstration of mid-frequency vibration deep-pine equipment for differentiated agronomy(No.: 20210202021NC).
The authors declare no conflict of interests.