Tunnels are essential infrastructure elements, and it is critical to maintain their stability for both operation and safety. Using engineering techniques, this study examines the correlation between rock mass motorized characteristics and tunnel surrounding rock stability. This study utilizes the multi-sensor monitoring data of the surrounding rock mechanical characteristics and tunnel support structure collected during tunnel boring machine construction as its research object. The integrated cuckoo search optimized Upgraded dynamic convolutional neural network (ICSO-UDCNN) has been utilized for predicting the tunnel parameters. In general, the surrounding rock’s hardness correlates with its level, which in turn determines how quickly tunnels are being excavated. There is a stronger correlation of 98\% between the field penetration index (FPI) variables of the rock’s characteristic slope along the conditions surrounding the tunnel. The most significant factor influencing its deformation is the surrounding rock’s mechanical characteristics. For engineers and other decision-makers engaged in tunnel design, building, and maintenance, the study’s findings add a greater understanding of the variables affecting tunnel stability. This research provides an establishment for enhancing security protocols, lowering hazards related to tunneling operation, and optimizing tunnel engineering techniques by quantitatively evaluating the influence of rock mass mechanical factors on solidity.
Tunnel is a fundamental constituent of urban subway systems, railroads, highways and other forms of subterranean space consumption [1,2]. However, since profound industrial is classically secreted, it can be complicated to establish, observe and control the structural protection of tunnel facilities in a diversity of convoluted situations [3]. The tunnel’s spatial form and functioning state are vulnerable to transformation due to the intricate environmental, climatic, and ecological circumstances which is located [4]. It is rather effortless for pathetic relations and injured nodes to start below the outcome of tunnel structure and durable procedure hidden terrorization such as twist, leakage, and crack, which can eventually result in shattering accidents [4]. One of the most fundamental steps in the immovability estimation of the neighbouring rock of an excavation is the valuation of the rock’s superiority [5,6]. The choice of structure invent parameter furthermore overall protection are closely linked to the irregular combination of various essentials in intricate rock classification which is personified in the rock mass [7,8]. Precise evaluation of the quality of the rock mass reflects it’s mechanical and physical characteristics provides a solid groundwork for architectural evaluation of stability and the avoidance, forecasting, and management of disasters [9]. The pressure serves as the basis for tunnel building and maintenance, which also happens to be the primary element influencing project costs [10]. Figure 1 depicts the diagrammatic representation of tunnel view.
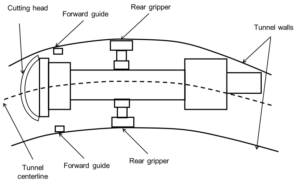
An essential area of research and one of the engineering community’s most pressing issues has been the examination of surrounding rock pressure in tunnel construction [11]. However, precisely estimating the strain of the rock around considerable because of the intricacy of geographical conditions, differences in building techniques, different supporting variables and spatiotemporal impacts [12]. Faults, fracture zones, internal joints and other factors are the main causes of the rock instability in the tunnel surrounding it. The bulk of tunnel instability is usually determined by the spatial distribution of the structural interfaces since the buried level of the roadway tunnels is modest and some of the mechanical features of the rock masses are insignificant. Block collapses during tunnel construction are caused by the growth of controllable surfaces, such as faults and weak interlayers, despite the great general stability of the rock mass and the high quality of the neighbouring rock . Furthermore, the likelihood of possible instability rises as the tunnel’s excavation area grows. This study utilizes the multi-sensor monitoring data for predicting and monitored data of the surrounding rock for evaluating the mechanical characteristics.
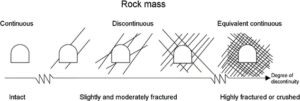
The assessment of rock quality plays a crucial role in analyzing the stability of a tunnel’s surrounding rock. Currently, the most commonly used method is the engineering analogy approach known as surrounding rock classification. This method utilizes systems such as Q, RMR (Rock Mass Rating), RMI (Rock Mass Index), and GSI (Geological Strength Index) for general classification. However, due to uncertainties in geotechnical parameters and variations caused by human errors and instrument mistakes during the evaluation process, different results can be obtained even when using the same evaluation system and classification standard. High-speed trains play a crucial role in offering convenient travel choices and boosting economic growth. In China, the high-speed railway tunnel network has surpassed 5,500 km in length as of the end of 2019. In Mathematical models, the strength of rock masses is described theoretically. The rock substance and the properties of the discontinuities can be modeled separately or together. A mathematical model requires determination of a large number of parameters and is often based on simplified assumptions. A Rock can be said to be continuous if it consists of either purely intact rock, or of individual rock pieces that are small in relation to the overall size of the construction element studied, see Figure 2.
The structure of the paper is follows: The formulation of theories and the presentation of relevant research are included in stage 2. The main characteristics of the sample and the method were presented in the third stage of the study. A result and discussion of the study are provided in Stage 4. Conclusions are established in stage 5.
Several investigations have been conducted to evaluate the grade of rock masses. Wu et al. [13]presented the most recent developments in ideas, practices, and engineering applications such as the efficient structuring of rock mass structures, the development of comprehensive stress-strain models, the shearing-induced dynamic characteristics of connected mass of rock, the three-dimensional manifestation of significant variables, and the active reinforcing of engineering rock masses. Kovačević et al. [14] discussed an approach for employing a neural network (NN) tool to implement Monte Carlo Simulation (MCS) to eliminate the requirement for a laborious statistical method for evaluating the effects of tunnel construction in a challenging karst setting. It was demonstrated that the generated NN could be utilized to determine the probabilistic distributions of tunnel design variables with accuracy, serving as a surrogate model. Additionally, it was demonstrated that in comparison to the NN-assisted MCS, approximation reliability evaluation methodologies typically minimize the chance of failures and overstate the dependability index. Finite element limit analysis (FELA) is utilized to construct computational lower and higher boundary methods for the problem of excavating rectangles in large rocks (Keawsawasvong et al. [15]) with the failure criterion. It developed an innovative machine learning-assisted forecast for the issue by utilizing the FELA databases including the analytical boundary estimates. Based on the HB failure criterion, the results demonstrated that the most effective rigidity of the rectangle tunnels is predicted by models for Artificial Neural Network (ANN) with extremely high accuracy. When geotechnical engineers are building rock tunnels, the solutions will give them a quick evaluation of the constancy of the tunnel in rock masses. Fan et al. [16] suggested a tunnel seismic prediction (TSP) and discrete element method (DEM)-based advanced analysis technique for integrated rock mass stability. A variety of traditional methods and analytical findings of linked rock mass stability are more trustworthy. The research’s conclusions offer useful guidance for building tunnels safely in interconnected rock masses. Based on TSP and DEM, which assess this technique’s precision and relevance, the outcome demonstrated that the dangerous block’s location is assumed to match the real-world exposure of the tunnel’s adjacent rocks.
Zhao et al. [17] utilized Bayesian inference to evaluate the mechanical variables’ uncertainty and identify them dynamically using the back testing structure. Bayesian estimation was used to take ambiguous and lacking information while excavating the tunnel. They spoke about how the surrounding rock mass behaved mechanically three models were utilized: an analytical model, a numerical model, and a surrogated model. The findings demonstrated that, in rock engineering, Bayesian inference offered a sensible technique for updating the exterior rock mass’s mechanics Lawongkerd et al. [18] facilitated the construction of shallow, untreated horseshoe tunnels in rock masses and developed new stability equations. The mathematical foundation of the upper- and lower-bound FELA is used to deduce the reliability of the resolutions of these problems utilizing the Hoek-Brown collapse criteria. A complex connection is produced by combining quantitative simulators with the relevance vector machine (RVM) (Zheng et al. [19]) between tunnel displacements and rock mass variables, preventing the need for several numerical simulations. It is found that the detected tunnel removals correspond to the ones anticipated by the RVM model. To assess the ambiguity of the attributes of the rock’s masses and the movement of the tunnel, they pushed out an innovative stochastic technique. Significant effects on the uncertainty results are caused by the parameter correlations it is assessed that there are more negative correlations between the rock mass factor, the uncertainty of the tunnel’s displacement decreases and its reliability raises. Huang et al. [20] investigated the stability assessment of clay tunnels. The strain and stress conditions of the rocks around it, that were the tunnel construction are predicted; These states provide an equation with multiple factors connected to the strain and stress state, as well as the physical-mechanical conditions of the surrounding rock. Together with the formulas and methods for calculating the tunnel structural reserves variable, it is necessary to develop a mathematical model of the non-linear degradation of the mechanical and physical characteristics of the rocks around it. Using the modelling of ceramic culverts, the outcomes of the suggested procedure were contrasted with those of the torque decrease methodology and the approach known as limit equilibrium.
Rock quality designation (RQD) is a standard technique in the mining industry for the qualitative and quantitative assessment of rock quality and degree of jointing, fracturing, and shearing in a rock mass. RQD is defined as the percentage of intact drill core pieces longer than 10 cm recovered during a single core run, and the general equation is expressed as:
\[\label{e1} R Q D \text { index }(\%)=100 \times \sum\frac{\text { Length of core pieces } \geq 0.10 \mathrm{~m}}{\text { Total length of core run }}. \tag{1}\]
It is used as a standard quality in drill core logging and its greatest value is perhaps its simplicity and quick determination, and also that it is inexpensive. RQD is to be seen as an index of rock quality where problematic rock, that is highly weathered, soft, fractured, sheared and jointed, is counted in complement to the rock mass. A number of indices and a range of definitions have been proposed, without much commonality. Recent International Standards have addressed this and provide unambiguous and clear definitions of which fractures should and should not be included in the quality assessment and of how the index should be measured. Although the RQD is only a crude indicator of rock quality, it is very widely used, on its own and correlated with other properties, in rock-mass classification systems (e.g. compressibility,diggability, tunnel stand-up time), see Table 1.
| RQD | Rock Quality |
| \( \geqslant \)90%–100% | Excellent |
| \( \geqslant \)75%–90% | good |
| \( \geqslant \)50%–75% | fair |
| \( \geqslant \)25%–50% | poor |
| \( \leqslant \)25% | Very poor |
The Rock Mass Rating (RMR) classification system divides the rock mass into distinct structural regions, with each region classified independently. This system utilizes six parameters, which are combined to compute the overall RMR value:
Uniaxial compressive strength of intact rock material
Rock Quality Designation (RQD)
Joint or discontinuity spacing
Joint condition
Groundwater conditions
Joint orientation
The first five parameters are combined to determine the basic RMR value, denoted as \(RMR_{\text{basic}}\). The sixth parameter, joint orientation, is treated separately due to its varying influence depending on the engineering application. The total RMR value is calculated by summing the ratings of the first five parameters and adjusting for joint and tunnel orientation using the sixth parameter, as expressed by the following equation:
\[\label{e2} RMR_{\text{basic}} = \sum \text{(parameters)}. \tag{2}\]
In the RMR classification, the rock mass along a tunnel is divided into structural regions where geological features are relatively uniform. The six parameters are determined for each region based on field measurements, typically reflecting the average rather than the worst conditions. It is important to note that the ratings for discontinuity spacing assume the presence of three discontinuity sets. In cases where only two sets are present, a conservative evaluation is applied.
The fundamental geotechnical parameters are represented by the following ratios:
Relative block size: \(\frac{RQD}{Jn}\)
Relative frictional strength (of the least favorable joint set or filled discontinuity): \(\frac{J_r}{J_a}\)
Active stress: \(\frac{J_w}{SRF}\)
Rock mass quality (Q-system): \(Q\)
The Q-system, a more comprehensive rock quality parameter, is defined as:
\[\label{e3} Q = \frac{RQD}{Jn} \times \frac{J_r}{J_a} \times \frac{J_w}{SRF}, \tag{3}\] where:
\(RQD\) is the Rock Quality Designation,
\(Jn\) refers to the number of joint sets,
\(Jr\) accounts for joint roughness,
\(Ja\) is based on the degree of joint alteration or clay filling,
\(Jw\) is influenced by water inflow or pressure, and
\(SRF\) represents the stress reduction factor due to geological faults or other conditions.
The Q-system can also be used to estimate the uniaxial compressive strength of a rock mass. The normalized Q-value, denoted by \(Q_C\), is given by:
\[\label{e4} Q_C = Q \times \frac{\sigma_c}{100}, \tag{4}\] where \(Q\) is the normalized Q-value, and \(\sigma_c\) is the uniaxial compressive strength in MPa, with 100 MPa used as the standard for hard rock.
In this model, elements may form or lose contact during any time step, allowing the simulation of failure modes such as vertical crack propagation, roof failure, floor heave, or subsidence. The stiffness matrix (\(k\)) relates nodal displacements to applied nodal forces. The equilibrium between the stiffness matrix, nodal displacement vector (\(q\)), and nodal force vector (\(Q\)) is expressed by:
\[\label{e5} (k)(q) = (Q). \tag{5}\]
The algorithm calculates the motion of each block due to unbalanced forces based on a force-displacement law. The normal force \(F_n\) between blocks is computed using the following linear force-displacement relationship:
\[\label{e6} F_n = K_n \delta_n, \tag{6}\] where \(K_n\) is the joint normal stiffness, and \(\delta_n\) represents the notional overlap at block boundaries.
The shear force at the contact is computed for an increment of shear displacement \(\delta_s\) by:
\[\label{e7} F_s = K_s \delta_s, \tag{7}\] where \(K_s\) is the joint shear stiffness. Shear failure or slip occurs when:
\[\label{e8} F_s = \mu F_n, \tag{8}\] where \(\mu\) is the coefficient of friction. When tension develops between blocks, both shear and normal forces are set to zero.
This study focuses on analyzing multi-sensor monitoring data related to the mechanical properties of surrounding rock and tunnel support structures during tunnel boring machine construction. The innovative ICSO-UDCNN optimization technique integrates this multi-sensor data to explore the independent fusion characteristics among field monitoring data and the mechanical properties of the structure. The primary variables assessed and predicted in this study include torque (\(Q\)), rotating speed (RS), thrust (\(T\)), and drivable coefficient (DC), all of which are crucial to the technical architecture of the equipment. A water transportation tunnel, characterized by geological features such as folds, faults, and groundwater variations, serves as the foundation for this investigation.
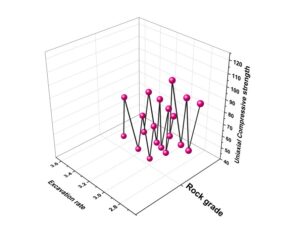
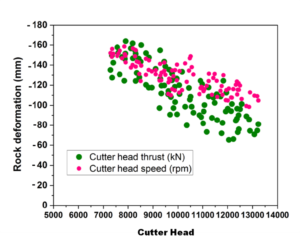
Challenges such as rock bursts, block falls, mud inflow, and water ingress frequently occur during tunnel construction. This research collects and evaluates field monitoring data to assess these issues. Machine tunneling speed, approximately 3 mm, is deemed to be in a state of “unable to dig,” primarily due to the surrounding rock’s excessive strength, the cutter head’s low penetration rate, and the difficulty of engaging the cutter head hob with the rock mass. In medium-strength rock, nearby stronger rocks cause potential issues such as edge collapse and eccentric wear on the hob. By precisely predicting rock deformation, engineers can optimize the cutter head’s thrust and rotating speed, thus expediting excavation. Figure 3 illustrates the statistical relationship between the excavation rate and geological displacement.
As excavation slows, neighboring rocks deteriorate. Predicting rock movement during tunnel excavation is critical to adjusting cutter head parameters in real-time to prevent emergencies.
In highway tunnel identification, isolated fractures are visually evaluated for structural components. Computer vision techniques are used to detect these fractures, while radar systems collect data as sensors move through the tunnel, gathering point clouds. The tunnel’s displacement is analyzed using optical systems, and the structural data of surrounding rocks are transmitted over long distances via optical fiber. By combining these data sets, conventional contours are reconstructed, and the tunnel’s structural integrity is evaluated.
The point clouds are flattened and rotated along the X-axis to generate discontinuous arc-shaped point clouds. The Delaunay triangulation method is then applied to create a mesh from the flattened data, allowing the reconstruction of the tunnel’s 3D representation. This technique, utilizing dimensional point cloud imagery, helps predict the tunnel’s mechanical properties and stability.
To improve tunneling efficiency, field-monitored sensor data is used to predict rock deformation and mechanical characteristics, assisting in the adjustment of tunneling parameters. This study employs the Integrated Cuckoo Search Optimized Upgraded Dynamic Convolutional Neural Network (ICSO-UDCNN) to address these predictions.
UDCNN extracts features from input data and comprises various layers for classification. The network was developed using advanced methods leveraging GPUs, allowing for optimized batch size and training parameters. UDCNN’s core layers include:
Convolution Layer: Two-dimensional filters, typically ranging from \(5 \times 5\) to \(1 \times 1\), transform input images to highlight important features.
Non-linearity Layer: Activation functions like ReLU, Tanh, or Sigmoid are applied to introduce non-linearity. ReLU is preferred for faster network training.
Pooling Layer: This layer reduces image size by grouping and sub-sampling pixels, calculating an average or maximum representative value for each group.
Classifier Layer: Using a fully connected layer, the network classifies images by treating each pixel as a separate neuron.
CSO is a global optimization algorithm that mimics the nesting behavior of cuckoos. Each cuckoo lays an egg in a random nest, and if detected, it is forced to build a new nest. The key step in CSO is Lévy flight, which governs the cuckoo’s search for optimal solutions. Lévy flight is described by:
\[\label{e9} w_j^{s+1} = w_j^s + \alpha_1 \otimes \text{Levy}(\alpha), \tag{9}\]
where \(\alpha_1\) is the step size, and Lévy distribution is given by:
\[\label{e10} \text{Levy} \sim s^{-\lambda}, \quad 1 < \lambda \leq 3. \tag{10}\]
The product \(\otimes\) denotes entry-wise multiplication. CSO optimizes the UDCNN by adjusting the neural network’s weights and biases during training, leading to faster convergence and improved performance.
The integration of CSO with UDCNN enhances predictive accuracy and efficiency in applications such as machine learning, data mining, and tunnel optimization.
The variables are examined and predicted using the mechanical and ICSO –UDCNN method. Important factors that affect the rock mass’s displacement and speed are the T, Q, RS, and compressive strength variables. The dynamic and complex nature of the rock throughout the tunnel excavation operation is seen in Figure 4.
The main cause is the additional tunnel displacement and cutter headwear there is the greater possibility of instrument blocks occurring when tunnel boring machine machinery excavates in weak rock with a high surrounding rock level. The drilling velocity is significantly impacted by this. In general, a faster tunnel-building rate, a lower surrounding rock level, and tougher bordering rock all contribute to an increased tunnel excavation rate. Figure 5 shows the connection between RS and the T of the stone displacement around the tunnel.
The most significant influence on the rock’s displacement throughout tunnelling is determined to be the mechanical properties of the rock. The stretching of the tunnel’s frame during the tunnelling operations is significantly connected to the physical and mechanical characteristics as well as the constructing variables of the tunnel drilling machinery. The Q and RS during the estimation equilibrium, as well as the T and DC factors’ accuracy alterations are displayed in Figure 6 and Figure 7.
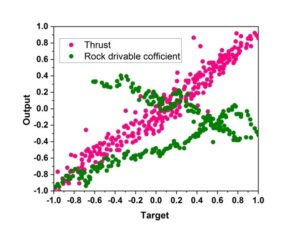
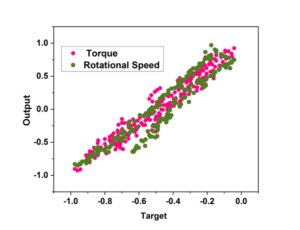
It illustrates the computation and fitting of the enhanced ICSO-UDCNN algorithm, for tunnel digging machines, surrounding material operable coefficients, Q, RS and T fitment correctness are better than 95% during physical construction. When the rock’s total strength is rather high, the hob’s ability to break through rock can be enhanced by a larger excavating force. This indicates that the equipment’s hydraulic push has a major influence on the digging of tunnels during the task. The enhanced ICSO-UDCNN algorithm incorporates the rock mass mechanical characteristics and the tunnel construction machinery performance variables that were derived from the model created in the tunnel stability section. Concurrently, the improved ICSO-UDCNN technique is employed to forecast the rock surround distortion in the tunnel excavating segment. The tunnel rock mass variables and the variables gathered by the sensors throughout the tunnel-building process are incorporated in the mathematical models. To confirm the precision and reasoning the adjusted ICSO-UDCNN method, we compared the results obtained from the algorithm with the monitoring findings during the tunnel construction process, as illustrated in Figure 8.
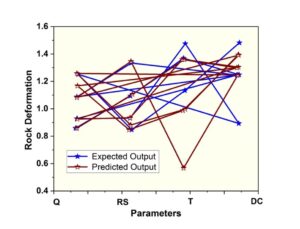
According to the establishing data, mechanical operate has a 98.9% fitting impact. Simultaneously, the tunnel excavation section’s surrounding rock deformation is predicted using the enhanced ICSO-UDCNN algorithm, and the variables gathered by the sensors during the tunnel constructing procedure and the tunnel rock mass variables are included into the calculation model. Every position has essentially the same deformation law of the surrounding rock, which is split into three stages: rapid growth, gradual development, and stable stage. Tunnel excavation causes settlement and deformation to first expand quickly, then move into a stage of moderate expansion and ultimately reach a relatively stable state.
This work explores independence and integration qualities between the mechanical attributes of the multi-sensor structures and the field tracking information to perform monitoring of the tunnel deformation and mechanical condition and security perceptions. This is accomplished throughout underground drilling equipment development by utilizing the underlying rock’s mechanics and the multi-sensor monitoring data of the tunnel support structure. The rate at which tunnels are excavated varies depending on the rock around its grade and the durability of the rock. In general, a quicker digging rate, a lower surrounding rock level, and tougher surrounding rock all contribute to an increased tunnel construction rate. The primary factor governing its motion is the mechanical composition of the adjacent rock. With a corresponding velocity of more than 85%, the RS, thrust, and Q of the machinery establish a good fitting relationship with the underlying rock displacement and its surrounding functioning index. With an acceptable outcome of 99.3%, the machine mechanics thrust has the highest correspondence among the parameter analysis fitting, suggesting that the machine’s thrust significantly affects the tunnel excavating in the tunnels excavating project.
All authors reviewed the results, approved the final version of the manuscript and agreed to publish it.
The experimental data used to support the findings of this study are available from the corresponding author upon request.
The authors declared that they have no conflicts of interest regarding this work.
Sulaiman, J.M. and Devi, M.G., 2020. Urban underground space development. International Research Journal of Engineering and Technology, 7(5), pp. 3095-3103.
McDonald, T., Robinson, M. and Tian, G.Y., 2022. Developments in 3D visualisation of the rail tunnel subsurface for inspection and monitoring. Applied Sciences, 12(22), p.11310.
Fruhwirt, D., Sturm, P., Steiner, H. and Borchiellini, R., 2023. Development of a methodology for studying tunnel climate in long railway tunnels and for optimizing the design process of cross-passage cooling systems. Tunnelling and Underground Space Technology, 138, p.105194.
Yang, Y., Wang, Y., Easa, S.M. and Yan, X., 2023. Risk factors influencing tunnel construction safety: Structural equation model approach. Heliyon, 9, p.e12924.
Su, Y., Su, Y., Zhao, M. and Vlachopoulos, N., 2021. Tunnel stability analysis in weak rocks using the convergence confinement method. Rock Mechanics and Rock Engineering, 54, pp.559-582.
Sari, M., 2021. Determination of representative elementary volume (REV) for jointed rock masses exhibiting scale-dependent behavior: a numerical investigation. International Journal of Geo-Engineering, 12(1), p.34.
Ma, T., Lin, D., Tang, C.A., Yadav, K.P., Feng, Z. and Ma, K., 2020. Microseismic monitoring, positioning principle, and sensor layout strategy of rock mass engineering. Geofluids, 2020(1), p.8810391.
Sousa, R.L. and Einstein, H.H., 2021. Lessons from accidents during tunnel construction. Tunnelling and Underground Space Technology, 113, p.103916.
Joshi, D.R., 2021. Assessment of Tunnel Stability and Evaluation of Rock Support in Headrace Tunnel of Super Madi Hydroelectric Project, Nepal (Doctoral dissertation, Pulchowk Campus).
Hu, B., Xiao, M., Fu, X., Yang, J., Xu, C., Wu, J. and Zhou, Y., 2023. FDEM numerical study of the influence law of geostress on state and pressure of tunnel surrounding rock. Frontiers in Ecology and Evolution, 11, p.1237250.
Chen, B., Gong, B., Wang, S. and Tang, C.A., 2022. Research on zonal disintegration characteristics and failure mechanisms of deep tunnel in jointed rock mass with strength reduction method. Mathematics, 10(6), p.922.
Yang, Y., Fang, Z., Ji, G., Zhao, B. and Wei, S., 2021. Study on mechanical properties and control technology of surrounding rock in the fracture zone of a roadway. Shock and Vibration, 2021(1), p.6628593.
Wu, F., Wu, J., Bao, H., Li, B., Shan, Z. and Kong, D., 2021. Advances in statistical mechanics of rock masses and its engineering applications. Journal of Rock Mechanics and Geotechnical Engineering, 13(1), pp.22-45.
Kovačević, M.S., Bačić, M. and Gavin, K., 2021. Application of neural networks for the reliability design of a tunnel in karst rock mass. Canadian geotechnical journal, 58(4), pp.455-467.
Keawsawasvong, S., Seehavong, S. and Ngamkhanong, C., 2022. Application of artificial neural networks for predicting the stability of rectangular tunnels in Hoek–Brown rock masses. Frontiers in Built Environment, 8, p.837745.
Fan, H., Li, L., Liu, H., Shi, S., Hu, J. and Zhou, S., 2021. Advanced stability analysis of the tunnels in jointed rock mass based on TSP and DEM. KSCE Journal of Civil Engineering, 25, pp.1491-1503.
Zhao, H., Chen, B., Li, S., Li, Z. and Zhu, C., 2021. Updating the models and uncertainty of mechanical parameters for rock tunnels using Bayesian inference. Geoscience Frontiers, 12(5), p.101198.
Lawongkerd, J., Shiau, J., Keawsawasvong, S., Seehavong, S. and Jamsawang, P., 2022. Design equations for predicting stability of unlined horseshoe tunnels in rock masses. Buildings, 12(11), p.1800.
Zheng, M., Li, S., Zhao, H., Huang, X. and Qiu, S., 2021. Probabilistic analysis of tunnel displacements based on correlative recognition of rock mass parameters. Geoscience Frontiers, 12(4), p.101136.
Huang, J., Liu, X., Ma, Z., Lv, G. and Dang, K., 2023. The stability evaluation of clay tunnels via the non-linear deterioration of physical and mechanical properties of surrounding rocks. Frontiers in Earth Science, 10, p.1112410.
1970-2025 CP (Manitoba, Canada) unless otherwise stated.