Let \( G = (V, E) \) be any graph. If there exists an injection \( f : V \rightarrow \mathbb{Z} \), such that \( |f(u) – f(v)| \) is prime for every \( uv \in E \), then we say \( G \) is a prime distance graph (PDG). The problem of characterizing the family of all prime distance graphs (PDGs) with chromatic number 3 or 4 is challenging. In the fourth part of this series of articles, we determined which fans are PDGs and which wheels are PDGs. In addition, we showed: (1) a chain of \( n \) mutually isomorphic PDGs is a PDG, and (2) the Cartesian product of a PDG and a path is a PDG. In this part of the series, we improve (1) by showing that there exists a chain of \( n \) arbitrary PDGs which is a PDG. We also show that the following graphs are PDGs: (a) any graph with at most three cycles, (b) the one-point union of cycles, and (c) a family of graphs consisting of paths with common end vertices.
By a graph \(G\) we mean a pair \(G = (V, E)\), where \(V \neq \emptyset\) is any arbitrary set and \(E\) is a subset of the set of all 2-element subsets of \(V\). The elements of \(V\) and \(E\) are called, respectively, the vertices and edges of \(G\). If \(\vert V(G) \vert < \infty\) then \(G\) is said to be finite. The graphs considered here are simple with finite or countably infinite vertex sets. By a distance graph \(Z(D)\), we mean a graph, whose vertex set is the set of integers \(Z,\) and two vertices \(u\) and \(v\) form an edge if and only if \(|u-v| \in D.\) If \(D=P\), the set of primes, then we call \(Z(P)\), the prime distance graph.
Given a graph \(G\) with vertex set \(V\) and edge set \(E\) and a set \(X\) of colors, an ordinary coloring is an assignment of elements of \(X\) to the elements of \(V\) in any order. A coloring \(f:V \rightarrow X\) is called proper if \(f\left(u\right)\neq f(v)\) for all \(uv \in E.\) Such a coloring is called a proper \(k\)-coloring if \(\left\vert \left\{f\left(u\right):u\in V(G)\right\}\right\vert = k\). The least \(k\) for which \(G\) has a proper \(k\)-coloring is called the chromatic number of \(G\) and is denoted by \(\chi\left(G\right)\). One can consult [1-15] for more on this topic.
Eggleton, Erdős, and Skilton attempted the task of finding the chromatic number of the prime distance graph \(Z(D)\) where \(D \subseteq P\). They found that \(\chi (Z(P))=4\) [9]. The problem of computing \(\chi(Z(D))\) where \(D\subset P\) is still open. Voigt and Walther in [16], Kemnitz and Kolberg in [2], and Yegnanarayanan et al. [17-21] have contributed more on this topic.
Observe that \(f:Z \rightarrow \frac{Z}{4Z}\) where \(f(v)=v\; \textbf{mod}\; 4\) is a 4-coloring of \(Z(D)\) for any \(D \subseteq P\). This is because if \(f\left(u\right) = f\left(v\right)\), then \(u\equiv v \pmod 4\) and \(\left\vert u-v\right\vert \equiv 0 \pmod 4\). Thus \(\left\vert u-v\right\vert \notin P\) and \(\chi(Z(D)) \leq 4\). As \(\chi\left(G\right)\) is a monotonic function, if \(D_{1} \subseteq D_{2}\) then \(\chi \left(D_{1}\right) \leq \chi \left(D_{2}\right)\). So, if \(D \subset P\) then the tough task is to classify \(Z(D)\) as per its chromatic number.
We say a graph \(G\) is of Class \(i\) if and only if \(\chi(G) = i\). It is obvious that \(Z(\emptyset)\) is the only distance graph that is Class 1, and \(Z(D)\) is Class 2 whenever \(D\) is a singleton set. It is already known from the results available in the literature that if \(\vert D \vert\) \(\geq\) 2 then \(Z(D)\) is Class 2 if and only if 2 \(\notin D\). Similarly, if 2 \(\in D\) and 3 \(\notin D\), then \(Z(D)\) is Class 3. If \(\left\vert D \right\vert = 3\) with \(\left\lbrace 2, 3, 5\right\rbrace\) \(\in D\) then \(Z(D)\) is Class 4 [6]. Also, if \(D=\left\lbrace 2, 3, p\right\rbrace\) with \(p \neq 5\), then \(Z(D)\) is Class 3. If \(2\) or \(3\) is contained in a subset \(D \subset P\), then \(\chi(D) =3\) or 4. It is an unsolved problem to classify these sets \(D\) whether they belong to Class 3 or 4 (see [6,9,22,23]).
Let \(G=(V,E)\) be any graph. If there exists an injection \(f:V \rightarrow Z,\) such that \(|f(u)-f(v)|\) is prime for every \(uv \in E,\) then we say \(f\) a prime distance labeling of \(G\) and \(G\) is a prime distance graph. The value of \(|f(u)-f(v)|\) is referred to as the induced label of the edge \(uv.\) For the sake of brevity, if this induced label is prime, we say the edge \(uv\) is prime.
It is known that a bipartite graph is a prime distance graph [24]. So every graph \(G\) with \(\chi(G)=2\) is a prime distance graph. In particular, trees are prime distance graphs. It is still open to find a characterization for graphs with \(\chi(G)=3\) or \(4\). In this paper we demonstrate the existence of several new collections of families of prime distance graphs with \(\chi(G)=3\) or \(4\).
Laison, Starr, and Walker showed that not only is every bipartite graph \(G\) a prime distance graph, but a prime distance labeling \(f\) can be found such that \(f(v)=0\) for any particular vertex \(v \in V(G)\) and \(f(u)\geq 0\) for all \(u \neq v\) [24]. They showed the same is true for cycles.
Theorem 1 (Laison, et al., [24]). Let \(G\) be a bipartite graph or a cycle and \(v \in V(G)\) be any vertex. There exists a prime distance labeling \(f:V(G) \to N\) such that \(f(v)=0\).
Next we share some observations that are used in the constructions throughout this paper. The following three observations are from [25].
Observation 2. Let \(G\) be any graph. An injection \(f:V(G) \rightarrow Z\) is a prime distance labeling of \(G\) if and only if \(-f\) is a prime distance labeling of \(G.\)
Observation 3. If \(G\) is a prime distance graph and \(H\) is a subgraph of \(G\), then \(H\) is also a prime distance graph.
Observation 4. Let \(G\) be any graph, \(f:V(G) \rightarrow Z\) an injection, and \(c\) any real number. The function \(f\) is a prime distance labeling of \(G\) if and only if \(f+c\) is a prime distance labeling of \(G\).
We call the operation from the previous observation lifting \(f\) by \(c.\)
Corollary 1. If \(G_1\) and \(G_2\) are both prime distance graphs, then the disjoint union \(G_1 \cup G_2\) is also a prime distance graph.
Proof. Let \(f\) and \(g\) be prime distance labelings of \(G_1\) and \(G_2\) respectively and \(c\) be the maximum label of \(f\). Label the vertices by \[\ell(v)= \begin{cases} f(v) & \text{if \;} v \in V(G_1) \\ g(v)+c & \text{if \;} v \in V(G_2) \end{cases}\] Since \(\ell\) is injective, it is a prime distance labeling of \(G_1 \cup G_2\) by Observation 4. ◻
Let \(P_n=u_1u_2u_3 \cdots u_n\) be the path on \(n\) vertices and \(C_n=u_1u_2u_3 \cdots u_nu_1\) be the cycle on \(n\) vertices.
Lemma 1. Let \(G\) be a prime distance graph. Then a graph \(G^+\) obtained from \(G\) by adding a pendant edge to \(G\) is also a prime distance graph.
Proof. Let \(V(G^+)=V(G) \cup \{u\}\) and \(uv\) be the pendant edge of \(G^+\) where \(v \in V(G).\) Suppose \(f\) is a prime distance labeling of \(G\) and \(p\) is the smallest prime such that \(p > \max \{f(x):x \in V(G)\}.\) Then a prime distance labeling of \(G^+\) is \[\ell(x)= \begin{cases} f(x) & \text{if \;} x \neq u \\ f(v) + p & \text{if \;} x=u \end{cases}\] since \(\ell\) is clearly an injection and the induced edge labels are prime. ◻
Notice that Lemma 1 can be repeatedly applied to make larger graphs from a given prime distance graph \(G_0.\) Let \(G\) be such a graph and \(v \in V(G)\) and \(v \not \in V(G_0)\) such that \(deg(v)=1\). Then it is possible to construct the prime distance labeling \(f\) from repeatedly applying Lemma 1 such that \(f(v)>f(u)\) for every \(u \in V(G).\) This will be important in the proof of Theorem 6.
A graph which contains no cycles is necessarily bipartite, and thus a prime distance graph by Theorem 1. A graph \(G\) is unicyclic if it contains exactly one cycle. If the cycle contained by \(G\) is even, then \(G\) belongs to Class \(2\). Otherwise, \(G\) belongs to Class \(3\). Our next result shows all unicyclic graphs are prime distance graphs.
Theorem 5. Every unicyclic graph \(G\) is a prime distance graph. Furthermore, for any vertex \(v\) lying on the cycle of \(G\), there exists a prime distance labeling \(f:V(G) \to N\) such that \(f(v)=0.\)
Proof. Let \(G\) be a unicyclic graph that contains \(t\) connected components. If \(t=1\), the vertices of \(G\) on the cycle may be labeled by Theorem 1. The result now follows by inductively applying Lemma 1.
On the other hand, if \(t\geq 2,\) label the connected component containing the cycle as in the previous case. The remaining components constitute a bipartite subgraph \(H\) of \(G.\) Therefore, \(H\) admits a distance prime labeling \(f:V(H) \to Z\) which may be suitably lifted by Observation 4 to obtain the result. ◻
A graph \(G\) is bicyclic if it contains exactly two cycles. If both cycles contained in \(G\) are even, then \(G\) belongs to Class \(2\). Otherwise, \(G\) belongs to Class \(3\).
Theorem 6. Every bicyclic graph is a prime distance graph.
Proof. Let \(G\) be a
bicyclic graph containing cycles \(C_m\) and \(C_n\). We establish two cases based on the
structure of \(G\).
\(C_m\) and \(C_n\) are not in the same connected
component.
In this case, \(G\) is the disjoint union of two unicyclic graphs. Therefore, the prime distance labeling exists by Theorem 5 and Corollary 1.
\(C_m\) and \(C_n\) belong to the same connected component.
We may assume \(G\) is the \(1\)-point intersection of two unicyclic subgraphs \(H_1\) and \(H_2\) with common vertex \(v\) such that \(C_m\) is contained in \(H_1\), \(C_n\) is contained in \(H_2\), \(deg_{H_1}(v)=1\), and \(v\) is contained in \(C_n\). By Theorem 5 and observation 4 a nonnegative prime distance labeling \(f\) of \(H_1\) exists such that \(f(v)=c > f(u)\) for all \(u \neq v.\) Lifting \(f\) by \(-c\) gives a prime distance labeling \(f'\) of \(H_1\) such that \(f'(v)=0\) and \(f'(u) \leq 0\) for all \(u \in V(H_1).\)
Let \(g\) be a nonnegative prime distance labeling of \(H_2\) such that \(g(v)=0.\) Such a labeling exists by Theorem 5. We combine the labelings \(f'\) and \(g\) to produce a labeling \(\ell\) as follows. Let \[\ell(u)= \begin{cases} f'(u) & \text{if \;} u \in V(H_1) \\ g(u) & \text{if \;} u \in V(H_2) \end{cases}\] It is clear that \(\ell\) is injective since \(f'(u) \leq 0\) for all \(u \in V(H_1)\), \(g(u) \geq 0\) for all \(u \in V(H_2)\), and \(V(H_1) \cap V(H_2)=\{v\}\) and \(f'(v)=g(v)=0.\) Further, every edge is prime since \(f'\) and \(g\) are prime distance labelings. ◻
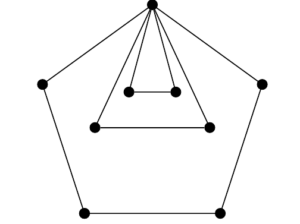
The graph of \(k\) edge-disjoint cycles \(C_{n_1},C_{n_2},\dots,C_{n_k}\) glued together at a common vertex is called a one point union of cycles. See Figure 1 for an example. Before investigating this family of graphs, we state a conjecture of de Polignac.
Conjecture 1 (de Polignac, 1849). For every positive integer \(n\), there are infinitely many primes that differ by \(2n\).
Notice that the famous Twin Prime Conjecture corresponds to the case \(n=1\) in de Polignac’s Conjecture. Laison, Starr, and Walker showed that the one point union of \(n\) \(3\)-cycles is a prime distance graph if and only if the Twin Prime Conjecture is true [24]. We prove some analogous but broader results using de Polignac’s Conjecture next.
Theorem 7. If de Polignac’s Conjecture is true, then the one point union of cycles \(C_{n_1},C_{n_2},\dots,C_{n_k}\) is a prime distance graph for any \(n_i \geq 3\) and \(k\geq 1.\)
Proof. Let \(p_i\) and \(p_i+2(n_i-2)\) be mutually distinct primes for \(i=1,2,\dots,k\) such that \(p_{i+1} \geq p_i+2(n_i-2)\). If de Polignac’s Conjecture is true, we may find such primes. Label the vertices of each cycle \(C_{n_i}\) by \(0,p_i,p_i+2,p_i+4,\dots,p_i+2(n_i-2),0\) consecutively around the cycle such that the vertex labeled \(0\) is common to all cycles.
The lengths of the edges in \(C_{n_i}\) form the set \(\{2,p_i,p_i+2(n_i-2)\}.\) Since every member of this set is prime and the labeling described is injective, we have completed the proof. ◻
A graph is tricyclic if it contains exactly \(3\) cycles. If a graph \(G\) is tricyclic, then the Class of \(G\) is \(2\) if all three of the cycles are even, and is \(3\) otherwise. For any \(n\geq 4\), a \(1\)-chorded \(n\)-cycle is a tricyclic graph with vertex set \(V=\{u_1,u_2,\dots,u_n\}\) and edge set \(E=\{u_1u_2,u_2u_3,\dots,u_nu_1\} \cup \{u_1u_{c}\}\) for some \(c \not \in \{2,n\}.\) The edge \(u_1u_c\) is called the chord.
For practical reasons, the next theorem only requires the truth of a much weaker version of Polignac’s conjecture: the existence of a prime gap of size \(2n\) for sufficiently large primes.
Theorem 8. If de Polignac’s Conjecture is true, then every \(1\)-chorded \(n\)-cycle is a prime distance graph.
Proof. Label the cycle \(u_1u_cu_{c+1}\dots u_nu_1\) using any prime distance labeling \(f\) of \(C_{n-c+2}\) such that \(f(u_1)=0\) and \(f(u_c)=2\) (see Theorem 3 in [24] for example). Let \(q=\max \{f(u_i):i=1,c,c+1,\dots,n\}\) and label the cycle \(u_1u_2\dots u_cu_1\) in order by \(0,p,p+2,p+4,\dots,p+2(c-3),2,0\) for any \(p>q\) such that both \(p\) and \(p+2(c-4)\) are both prime. Such a pair can be found if Conjecture 1 is true. Since \(f\) is a prime distance labeling, we need only check that the edges on the cycle \(u_1u_2\dots u_c u_1\) are all prime. Since these labels all belong to the set \(\{2,p,p+2(c-4)\},\) we have proven the theorem. ◻
Theorem 9. Every disconnected tricyclic graph is a prime distance graph.
Proof. If \(G\) is a disconnected tricyclic graph, then it is either the disjoint union of three unicyclic graphs or a bicyclic graph with a unicyclic graph. Therefore, the result follows from Theorems 5 and 6 and Corollary 1. ◻
Theorem 10. If de Polignac’s Conjecture is true, then every connected tricyclic graph is a prime distance graph.
Proof. Let \(G\) be a connected tricyclic graph. Then \(G\) either contains a \(1\)-chorded cycle or the one point union of three cycles. Therefore, the labeling can be carried out by Theorems 8 or 7, respectively. Labeling the remaining vertices in \(V(G)\) by Lemma 1 concludes the proof. ◻
For any set of graphs \(\mathcal G = \{G_1,G_2,\dots,G_n\}\) and integer \(n\geq 2\), we define an \(n\)-chain graph, \(G^*_n\) as any edge-disjoint union of \(G_1,G_2,\dots,G_n\) such that \(|V(G_i) \cap V(G_{i+1})|=1\) for every \(i=1,2,\dots,n-1\) and \(|V(G_i) \cap V(G_{j})|=0\) otherwise. Notice that two \(n\)-chains of the same set of \(n\) graphs are not necessarily isomorphic. The authors showed that if \(G_i \cong G\) for all \(i=1,2,\dots,n\) where \(G\) is a prime distance graph, then there exists a corresponding \(n\)-chain of \(G\) that is a prime distance graph [25]. Here, we prove a much stronger result.
Theorem 11. Let \(\mathcal{G}=\{G_1,G_2,\dots,G_n\}\) be any set of prime distance graphs. Then there exists an \(n\)-chain \(G^*_n\) that is a prime distance graph.
Proof. Let \(f_i: V(G_i) \rightarrow N\) be a prime distance labeling of \(G_i\) and \(u_i \in V(G_i)\) be a vertex such that \(f_i(u_i)=0\). We can make this assumption by Observation 4. Denote by \(v_i \in V(G_i)\) the vertex with the largest label, \(\rho_i.\) Form an \(n\)-chain \(G\) by gluing \(v_i\) to \(u_{i+1}\) for \(1 \leq i \leq n-1.\) Then it is easy to see that the labeling \[f(x) = \begin{cases} f_1(x) & \text{ if } x \in V(G_1) \\ f_i(x) + \rho_{i-1} & \text{ if } x \in V(G_i) \text{ and } 2\leq i \leq n \end{cases}\] is a prime distance labeling of \(G.\) ◻
One possible generalization of the \(1\)-chorded graphs can be defined as follows. Let \(\{n_1,n_2,\dots,n_k\}\) with \(0\leq n_1 \leq n_2 \leq \dots \leq n_k\) be any set of \(k\) non-decreasing integers. We define the rainbow graph \(R(n_1,n_2,\dots,n_k)\) as the union of \(k\) paths of the form \(ux^i_1x^i_2\dots x^i_{n_i}v\) for \(1 \leq i \leq k.\) Since we are only considering simple graphs, we require \(n_2 \geq 1.\) Simply put, \(R(n_1,n_2,\dots,n_k)\) is isomorphic to the graph obtained by gluing together the left endpoints and gluing together the right endpoints of \(k\) paths. The lengths of these paths may differ. We call the vertices \(u\) and \(v\) the rainbow ends. Notice that \(R(0,n_2,n_3)\) is isomorphic to a \(1\)-chorded \(C_{n_2+n_3+2}.\) See Figure 2 for an example of \(R(1,3,5).\)
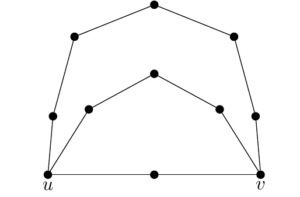
Theorem 12. If de Polignac’s Conjecture is true, then every rainbow graph \(R(n_1,n_2,\dots,n_k)\) is a prime distance graph.
Proof. For \(1\leq i \leq k\), let \(p_i\) be a prime such that \(p_i+2(n_i-2)\) is also prime. If de Polignac’s Conjecture is true, not only does such a set of primes exist, but we may further assume that the primes are all distinct (\(p_i\) may be chosen so that \(p_i > p_{i-1}+2(n_{i-1}-1)\)). For \(1\leq i \leq k\), label the path \(ux^i_1x^i_2\dots x^i_{n_i}v\) with \(0,p_i,p_i+2,\dots,p_i+2(n_i-1),2\) in order. It is easy to check that the induced edge labels comprise the set \(\{p_i,p_i+2(n_i-2):1\leq i \leq k\}\cup \{2\}.\) Since every member of this set is prime, the proof is complete. ◻
Let \(\mathcal{R}=\{R_1,R_2,\dots,R_n\}\) be a set of \(n\) rainbow graphs. We define the rainbow range \(RR(R_1,R_2,\dots,R_n)\) as the graph obtained by chaining together the rainbows \(R_1,R_2,\dots,R_n\) by gluing the \(v\) vertex of \(R_i\) to the \(u\) vertex of \(R_{i+1}\) for \(1\leq i \leq n-1.\) Notice that the next result does not necessarily follow from Theorem 11.
Theorem 13. If de Polignac’s Conjecture is true, then every rainbow range \(RR(R_1,R_2,\dots,R_n)\) is a prime distance graph for any \(n\geq 1\).
Proof. Let \(G \cong RR(R_1,R_2,\dots,R_n)\) and \(f_1:V(R_1) \rightarrow Z\) be a prime distance labeling of \(R_1\) as given in the proof of Theorem 12 with \(f_1(u)=0,f_1(v)=2,\) and maximum label \(\rho_1.\) Apply \(f_1\) in the natural way to the subgraph isomorphic to \(R_1\) in \(G.\)
Again, use the proof of Theorem 12 to find a prime distance labeling \(f_2\) of \(R_2\) such that \(f_2(u)=0, f_2(v)=2,\) and \(f_2(x)>\rho_1\) for all vertices \(x \not \in \{u,v\}.\) Then apply the labeling \(f_2+2\) to the subgraph \(R_2\) in \(G\). Continue in this way to label the subgraphs \(R_3,\dots, R_n\). Since lifting each labeling by 2 preserves the induced edge labels on each subgraph isomorphic to \(R_i\) for \(1 \leq i \leq n\), and introduces no conflicts in the labels of the ends of the rainbows, we see that \(G\) is a prime distance graph. ◻
We have provided many new families of graphs with chromatic number at least \(3\) which are prime distance graphs. One possible direction forward would be to prove Theorems 7,8,10,12 and 13 independently of de Polignac’s Conjecture (or show that the conjecture is necessary).
This research was funded by National Board of Higher Mathematics Department of Atomic Energy, Government of India, Mumbai, by their grant no. 02011/10/21NBHM- (R.P)/R&D/8007/Date: 13-07-2021. J George Barnabas and Yegnanarayanan Venkatraman gratefully acknowledges the same.
This work was supported by National Board of Higher Mathematics, Government of India.
The National Board of Higher Mathematics-NBHM, Department of Atomic Energy, Government of India has provided scholarship support for George Barnabas to complete his doctoral thesis work.
Chen, J. J., Huang, K. C. and Chang, G. J., 1997. Integral distance graphs. J. Graph Theory, 25, pp.287–294.
de Grey, A., 2018. The chromatic number of the plane is at least 5. Geocombinatorics, 28, pp.18–31.
Huele, M. J. H., 2018. Computing small unit-distance graphs with chromatic number 5. Geocombinatorics, 28, pp.32–50.
Holt, R., Rinehart, W. and Winston., 1964. Combinatorial Geometry in Plane. Geneva: University of Geneva.
Eggleton, R. B., 1988. New results on 3-chromatic prime distance graphs. Ars Combin., 26, pp.153–180.
Deuber, W. and Zhu, X., 1997. The chromatic number of distance graphs. J. Discrete Math., 25, pp.195–204.
Eggleton, R. B., Erdős, P. and Skilton, D. K., 1985. Coloring the real line. J. Combin. Theory Ser. B, 39, pp.86–100.
Eggleton, R. B., Erdős, P. and Skilton, D. K., 1986. Research problem 77. J. Discrete Math., 58, p.323.
Eggleton, R. B., Erdős, P. and Skilton, D. K., 1988. Update information on research problem 77. J. Discrete Math., 69, p.105.
Eggleton, R. B., Erdős, P. and Skilton, D. K., 1990. Coloring prime distance graphs. Graphs Combin., 32, pp.17–32.
Kemnitz, A. and Kolberg, H., 1998. Coloring of integer distance graphs. J. Discrete Math., 191, pp.113–123.
Voigt, M. and Walther, H., 1994. Chromatic number of prime distance graphs. J. Discrete Appl. Math., 51, pp.197–209.
Voigt, M., 1999. Coloring of distance graphs. Ars Combin., 52, pp.3–12.
Zhu, X., 1998. Pattern-periodic coloring of distance graphs. J. Combin. Theory Ser. B, 73, pp.195–206.
Voigt, M. and Walther, H., 1991. On the chromatic number of special distance graphs. Discrete Math., 97, pp.395–397.
Yegnanarayanan, V., 2014. Chromatic number of graphs with special distance sets I. Algebra Discrete Math., 17, pp.135–160.
Yegnanarayanan, V., 2002. On a question concerning prime distance graphs. J. Discrete Math., 245, pp.293–298.
Yegnanarayanan, V. and Barnabas, G., 2022. Chromatic coloring of distance graph III. Proyecciones, 42, pp.175–204.
Yegnanarayanan, V., Anitha, M., Rohatinovici, N. and Balas, E., 2021. Chromatic coloring of distance graph II. Journal of Tianjin University Science and Technology, 54(10), pp.56–67.
Yegnanarayanan, V., 2021. Chromatic coloring of distance graphs I. International Journal of Innovative Technology and Exploring Engineering, 10, pp.31–34.
Walther, H., 1990. Über eine spezielle Klasse unendlicher Graphen. In K. Wagner & R. Bodendiek (Eds.), Graphentheorie II (pp. 268–295). Mannheim: Bibliographisches Institut.
Eggleton, R. B., 1987. Three unsolved problems in graph theory. Ars Combin., 23, pp.105–121.
Laison, J. D., Starr, C. and Halker, A., 2013. Finite prime distance graphs and 2-odd graphs. Discrete Math., 313, pp.2281–2291. Yegnanarayanan, V., Barnabas, G. and Freyberg, B., 2024. Chromatic coloring of distance graphs IV. submitted.
1970-2025 CP (Manitoba, Canada) unless otherwise stated.