The multiplicative sum Zagreb index is a modified version of the well-known Zagreb indices. The multiplicative sum Zagreb index of a graph \(G\) is the product of the sums of the degrees of pairs of adjacent vertices. The mathematical properties of the multiplicative sum Zagreb index of graphs with given graph parameters deserve further study, as they can be used to detect chemical compounds and study network structures in mathematical chemistry. Therefore, in this paper, the maximal and minimal values of the multiplicative sum Zagreb indices of graphs with a given clique number are presented. Furthermore, the corresponding extremal graphs are characterized.
In this paper, we focus exclusively on undirected simple connected graphs. Let \(G=(V(G),E(G))\) denote a graph with vertex set \(V(G)\) and edge set \(E(G)\). The degree of a vertex \(u \in V(G)\) is denoted by \(d_{G}(u)\) (or \(d(u)\) for short). We denote \(G-uv\) as the graph obtained from \(G\) by deleting the edge \(uv \in E(G)\). Similarly, \(G+uv\) is the graph obtained from \(G\) by adding an edge \(uv \notin E(G)\), where \(u,v \in V(G)\). A tree is a connected graph with \(n\) vertices and \(n-1\) edges. The chromatic number of a graph is the minimum number of colors required to color the graph such that no two adjacent vertices share the same color. We use \(\chi(G)\) to denote the chromatic number of a graph \(G\). A clique of a graph \(G\) is a subset \(S\) of \(V(G)\) such that any two vertices in \(G[S]\) (the subgraph of \(G\) induced by \(S\)) are adjacent. The clique number of \(G\) is the maximum size of a clique in \(G\), denoted by \(\omega(G)\). As usual, we use \(P_{n}\) and \(K_{n}\) to denote the \(n\)-vertex path and the \(n\)-vertex complete graph, respectively.
Topological indices are numbers that reflect certain structural features of organic molecules derived from the molecular graph. They play an important role in chemistry, pharmacology, etc. (see [1-3]). One of the oldest topological indices is the well-known Zagreb index, first introduced in [4], where Gutman and Trinajsti\(\mathrm{\acute{c}}\) examined the dependence of total \(\pi\)-electron energy on molecular structure. For a (molecular) graph \(G\), the first Zagreb index \(M_{1}(G)\) and the second Zagreb index \(M_{2}(G)\) [4] are, respectively, defined as: \[\begin{aligned} M_{1}(G) &= \sum_{v \in V(G)} d_{G}(v)^{2}, \\ M_{2}(G) &= \sum_{uv \in E(G)} d_{G}(u)d_{G}(v). \end{aligned}\]
These two classical topological indices (\(M_{1}\) and \(M_{2}\)) and their modified versions have been used to study molecular complexity, chirality, ZE-isomerism, heterosystems, etc. Recently, Eliasi, Iranmanesh, and Gutman [5] introduced a variant of the Zagreb indices known as the multiplicative sum Zagreb index, defined as \[\begin{aligned} \Pi_{1}^{*}(G) = \prod_{uv \in E(G)} (d_{G}(u) + d_{G}(v)). \end{aligned}\] Eliasi, Iranmanesh, and Gutman [5] proved that the path has the minimal multiplicative sum Zagreb index among all connected graphs and determined the second minimal multiplicative sum Zagreb index of trees. In [6], Xu and Das characterized the trees, unicyclic, and bicyclic graphs with maximal and minimal multiplicative sum Zagreb indices. Božović et al. [7] provided a sharp upper bound for the multiplicative sum Zagreb index of chemical trees and characterized the corresponding extremal graphs. Azari and Iranmanesh [8] presented some lower bounds for the multiplicative sum Zagreb index of several graph operations such as union, join, corona product, and composition. The authors of this paper [9,10] presented the maximal \(\Pi_{1}^{*}\) with a given number of cut vertices, cut edges, vertex connectivity, and edge connectivity of graphs, and provided the maximal and minimal \(\Pi_{1}^{*}\) of trees with a fixed domination number. For other recent mathematical investigations of the multiplicative sum Zagreb index and its related indices, readers can refer to [11-18].
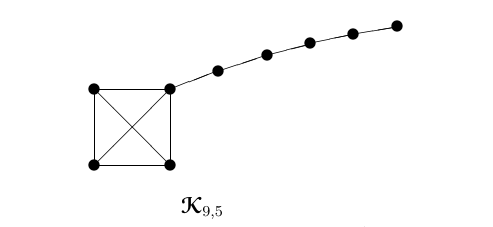
Let \({\mathcal{K}}_{n,n-k}\) be the graph obtained by identifying one vertex of \(K_{k}\) with a pendent vertex of the path \(P_{n-k+1}\). For example, \({\mathcal{K}}_{9,5}\) is shown in Figure 1. A complete \(k\)-partite graph whose partition sets differ in size by at most 1 is called a Turán graph, denoted by \(\textbf{{T}}_{n}(k)\). We denote by \({\chi}_{n,k}\) the set of \(n\)-vertex graphs with chromatic number \(k\), and \({\mathcal{W}}_{n,k}\) the set of \(n\)-vertex graphs with clique number \(k\), respectively. See [19] for other notations.
In recent years, many scholars have been interested in finding the extremal values of topological indices with a given clique number [20-25]. Hence, by using graph transformations and properties of the multiplicative sum Zagreb index, we show here that for the graphs in \({\mathcal{W}}_{n,k}\), the Turán graph \(\textbf{{T}}_{n}(k)\) has the maximal value of the multiplicative sum Zagreb index, while the minimal value of the multiplicative sum Zagreb index is attained only by the graph \({\mathcal{K}}_{n,n-k}\).
By the definition of the multiplicative sum Zagreb index, the following Lemma 2.1 is obvious and can be found in [6].
Lemma 1. [6] Let \(G=(V,E)\) be a simple connected graph. Then
If \(e=uv\notin E(G),\ u,v\in V(G)\), \(\Pi_{1}^{*}(G)<\Pi_{1}^{*}(G+e)\);
If \(e\in E(G)\), \(\Pi_{1}^{*}(G)>\Pi_{1}^{*}(G-e)\).

Definition 1 (Transformation \(A\)). Let \(G\) be a graph as shown in Figure 2, where \(G_{1}\ncong K_{1}\) and \(y\in V(G_{1})\). That is, we use \(G\) to denote the graph obtained from identifying \(y\) with the vertex \(x_{r}\) of a path \(x_{1}x_{2}\cdots x_{r-1}x_{r}\cdots x_{n}\), \(1<r<n\). Let \(G^{'}=G-x_{r-1}x_{r}+x_{n}x_{r-1}\), as shown in Figure 2.
Lemma 2. [6] Let \(G\) and \(G'\) be graphs in Figure 2. Then \(\Pi_{1}^{*}(G')<\Pi_{1}^{*}(G)\).

Corollary 1. [6] By repeating Transformation \(A\), any tree \(T\) attached to a graph \(G\) can be changed into a path as shown in Figure 3. Furthermore, during this process, the multiplicative sum Zagreb indices decrease.
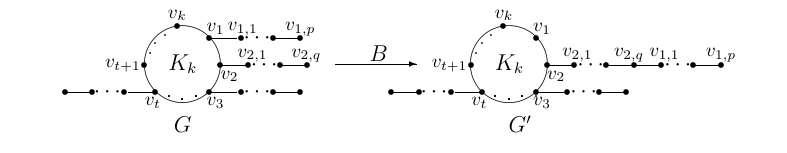
Definition 2 (Transformation \(B\)). Let \(G\) be a graph as shown in Figure 4, where \(V(K_{k})=\{v_{1},v_{2},\cdots,v_{k}\}\). That is, we use \(G\) to denote the graph obtained from identifying \(v_{i}\) with a pendant vertex of a path \(P_{i}\), \(1\leq i\leq t\), \(2\leq t\leq k\) and \(k\geq 3\), where \(v_{1}\) identifying the vertex \(v_{1,0}\) of a path \(v_{1,0}v_{1,1}\cdots v_{1,p}\) and \(v_{2}\) identifying the vertex \(v_{2,0}\) of a path \(v_{2,0}v_{2,1}\cdots v_{2,q}\). \(G'=G-v_{1}v_{1,1}+v_{2,q}v_{1,1}\), as shown in Figure 4.
Lemma 3. Let \(G\) and \(G'\) be graphs in Figure 4. Then \(\Pi_{1}^{*}(G')<\Pi_{1}^{*}(G)\).
Proof. We notice that \[\begin{aligned} \frac{\Pi_{1}^{*}(G)}{\Pi_{1}^{*}(G^{'})}&=\frac{\bigg(\prod\limits_{i=2}^{k}(d_{G}(v_{i})+d_{G}(v_{1}))\bigg)(d_{G}(v_{1})+d_{G}(v_{1,1})) (d_{G}(v_{2,q-1})+d_{G}(v_{2,q}))}{\bigg(\prod\limits_{i=2}^{k}(d_{G'}(v_{i})+d_{G'}(v_{1}))\bigg)(d_{G'}(v_{2,q-1})+d_{G'}(v_{2,q})) (d_{G'}(v_{2,q})+d_{G'}(v_{1,1}))}\\ &=\frac{\prod\limits_{i=2}^{k}(d_{G}(v_{i})+d_{G}(v_{1}))}{\prod\limits_{i=2}^{k}(d_{G}(v_{i})+d_{G}(v_{1})-1)}\cdot\frac{(d_{G}(v_{1})+d_{G}(v_{1,1})) (d_{G}(v_{2,q-1})+d_{G}(v_{2,q}))}{(d_{G'}(v_{2,q-1})+d_{G'}(v_{2,q})) (d_{G'}(v_{2,q})+d_{G'}(v_{1,1}))}. \end{aligned}\]
If \(p=q=1\), then \[\begin{aligned} \frac{\Pi_{1}^{*}(G)}{\Pi_{1}^{*}(G^{'})}>\frac{(k+1)(k+1)}{(k+2)(2+1)}>1, \end{aligned}\] since \((k+1)^{2}-3(k+2)=k^{2}-k-5>0\) for \(k\geq 3\).
If \(p=1\) and \(q>1\), then \[\begin{aligned} \frac{\Pi_{1}^{*}(G)}{\Pi_{1}^{*}(G^{'})}&=\frac{(k+1) (2+1)}{(2+2)(2+1)}>1. \end{aligned}\]
If \(p>1\) and \(q=1\), then \[\begin{aligned} \frac{\Pi_{1}^{*}(G)}{\Pi_{1}^{*}(G^{'})}>\frac{(k+2)(k+1)}{(k+2)(2+2)}=\frac{k+1}{4}\geq 1. \end{aligned}\]
If \(p,q>1\), then \[\begin{aligned} \frac{\Pi_{1}^{*}(G)}{\Pi_{1}^{*}(G^{'})}&=\frac{\prod\limits_{i=2}^{k}(d_{G}(v_{i})+d_{G}(v_{1}))}{\prod\limits_{i=2}^{k}(d_{G}(v_{i})+d_{G}(v_{1})-1)}\cdot\frac{(d_{G}(v_{1})+2) (2+1)}{(2+2)(2+2)}. \end{aligned}\] When \(k\geq 4\), \(\frac{\Pi_{1}^{*}(G)}{\Pi_{1}^{*}(G^{'})}>\frac{18}{16}>1\).
When \(k=3\), \[\begin{aligned} \frac{\Pi_{1}^{*}(G)}{\Pi_{1}^{*}(G^{'})}&>\frac{(d_{G}(v_{3})+3)(3+2) (2+1)}{(d_{G}(v_{3})+2)(2+2)(2+2)}\geq \frac{15\times(3+3)}{16\times (3+2)}>1, \end{aligned}\] since \(\frac{x+3}{x+2}=1+\frac{1}{x+2}\) is decreasing for \(2\leq x\leq 3\). ◻
Let \(G\in {\mathcal{W}}_{n,k}\). If \(k=1\), \(G\cong K_{1}\). If \(k=n\), \(G\cong K_{n}\). So, next, we always assume that \(1<k<n\).
Theorem 1. Let \(G\in {\mathcal{W}}_{n,k}\), where \(n\geq 3\), \(2\leq k\leq n-1\). Then \[\begin{aligned} \Pi_{1}^{*}(G)\geq \left\{\begin{array}{ll} 3^{2}4^{n-3},& \hbox{if}\ k=2,\\ 3(k+2)4^{n-k-2}(2k-1)^{k-1}(2k-2)^{\binom{k-1}{2}},& \hbox{if}\ 3\leq k\leq n-2,\\ n(2n-3)^{n-2}(2n-4)^{\binom{n-2}{2}},& \hbox{if} \ k=n-1, \end{array}\right. \end{aligned}\] with the equality holding if and only if \(G\cong {\mathcal{K}}_{n,n-k}\).
Proof. Choose a graph \(G\in {\mathcal{W}}_{n,k}\) such that \(G\) has the minimum multiplicative sum Zagreb index. By the definition of the set \({\mathcal{W}}_{n,k}\), \(G\) contains a clique \(K_{k}\) as a subgraph. From Lemma 1, \(G\) must be the graph that results from \(K_{k}\) by attaching some trees rooted at some vertices of \(K_{k}\). By Corollary 1, we conclude that, in \(G\), all the trees attached at some vertices of \(K_{k}\) must be paths.
If \(k=2\), then \(G\cong P_{n}\cong {\mathcal{K}}_{n,n-2}\) and the result hold obviously. If \(k\geq 3\), now we claim that \(G\cong {\mathcal{K}}_{n,n-k}\). Otherwise, suppose that there are two paths \(P_{1}\) and \(P_{2}\) attached at two vertices \(v_{1}\) and \(v_{2}\) of \(K_{k}\), respectively. From Lemma 3, \(G\) can be changed to \(G'\) by transformation \(B\) with a smaller multiplicative sum Zagreb index, which contradicts the choice of \(G\). Therefore \(G\cong {\mathcal{K}}_{n,n-k}\).
By the definition of multiplicative sum Zagreb index, we have \[\begin{aligned} \Pi_{1}^{*}({\mathcal{K}}_{n,n-k})=\left\{\begin{array}{ll} 3^{2}4^{n-3},& \hbox{if}\ k=2,\\ 3(k+2)4^{n-k-2}(2k-1)^{k-1}(2k-2)^{\binom{k-1}{2}},& \hbox{if}\ 3\leq k\leq n-2,\\ n(2n-3)^{n-2}(2n-4)^{\binom{n-2}{2}},& \hbox{if} \ k=n-1. \end{array}\right. \end{aligned}\] The proof is completed. ◻
Let \(K_{n_{1},n_{2},\cdots,n_{k}}\) denote the \(n\)-vertex complete \(k\)-partite graph whose partition sets size are \(n_{1},n_{2},\cdots,n_{k}\), respectively. Then \(n_{1}+n_{2}+\cdots + n_{k}=n\).
Lemma 4. Let \(G\in {\chi}_{n,k}\) be a graph with maximum multiplicative sum Zagreb index. Then \(G\cong K_{n_{1},n_{2},\cdots,n_{k}}\) for some \(n_{1},n_{2},\cdots,n_{k}\) that sum to \(n\).
Proof. By the definition of the set \({\chi}_{n,k}\) and Lemma 1, the lemma holds obviously. ◻
In order to get the maximum multiplicative sum Zagreb index, we first consider the multiplicative sum Zagreb indices of graphs \(G\in {\chi}_{n,k}\) in the following. Let \(n=ka+b\), where \(0\leq b <k\), i.e., \(a=\lfloor \frac{n}{k}\rfloor\).
Theorem 2. Let \(G\in {\chi}_{n,k}\), where \(2\leq k\leq n-1\). Then \[\begin{aligned} \Pi_{1}^{*}(G)\leq\ \Pi_{1}^{*}(\textbf{T}_{n}(k))=&\Big(2n-2\lfloor\frac{n}{k}\rfloor\Big)^{\binom{k-b}{2}\lfloor\frac{n}{k}\rfloor^{2}}\Big(2n-2\lfloor\frac{n}{k}\rfloor-2\Big)^{\binom{b}{2}(\lfloor\frac{n}{k}\rfloor+1)^{2}} \Big(2n-2\lfloor\frac{n}{k}\rfloor-1\Big)^{b(k-b)\lfloor\frac{n}{k}\rfloor(\lfloor\frac{n}{k}\rfloor+1)} \end{aligned}\] with the equality holding if and only if \(G\cong \textbf{T}_{n}(k)\).
Proof. In view of the definition of chromatic number, any graph \(G\in {\chi}_{n,k}\) has \(k\) color classes each of which is an independent set. Let the size of the \(k\) classes be \(n_{1},n_{2},\cdots,n_{k}\), respectively. By Lemma 4, the graph \(G\in {\chi}_{n,k}\) which reaches the maximum multiplicative sum Zagreb indices will be a complete \(k\)-partite graph \(K_{n_{1},n_{2},\cdots,n_{k}}\). Choose the graph \(G\in {\chi}_{n,k}\) such that \(G\) has the maximum multiplicative sum Zagreb indices.
Now we claim that \(G\in \textbf{{T}}_{n}(k)\). Otherwise, there exist two classes of size \(n_{r}\) and \(n_{s}\), respectively, satisfy \(n_{s}-n_{r}\geq 2\), that is, \(n_{s}-1\geq n_{r}+1\), without loss of generality, we assume that \(1\leq r<s\leq k\). We will find a contradiction.
By the definition of the multiplicative sum Zagreb index, we have \[\begin{aligned} \Pi_{1}^{*}(K_{n_{1},\cdots,n_{r},\cdots,n_{s},\cdots,n_{k}}) =&\Bigg(\prod_{\substack{1\leq i<j\leq k\\ i,j\neq r,s}}(2n-n_{i}-n_{j})^{n_{i}n_{j}}\Bigg) \Bigg(\prod_{\substack{i=1\\ i\neq r,s}}^{k}(2n-n_{i}-n_{r})^{n_{i}n_{r}}\Bigg)\\ &\cdot \Bigg(\prod_{\substack{i=1\\ i\neq r,s}}^{k}(2n-n_{i}-n_{s})^{n_{i}n_{s}}\Bigg) (2n-n_{r}-n_{s})^{n_{r}n_{s}}, \end{aligned}\] and \[\begin{aligned} \Pi_{1}^{*}(K_{n_{1},\cdots,n_{r}+1,\cdots,n_{s}-1,\cdots,n_{k}}) =&\Bigg(\prod_{\substack{1\leq i<j\leq k\\ i,j\neq r,s}}(2n-n_{i}-n_{j})^{n_{i}n_{j}}\Bigg) \Bigg(\prod_{\substack{i=1\\ i\neq r,s}}^{k}(2n-n_{i}-n_{r}-1)^{n_{i}(n_{r}+1)}\Bigg)\\ &\cdot \Bigg(\prod_{\substack{i=1\\ i\neq r,s}}^{k}(2n-n_{i}-n_{s}+1)^{n_{i}(n_{s}-1)}\Bigg) (2n-n_{r}-n_{s})^{(n_{r}+1)(n_{s}-1)}. \end{aligned}\] Since \((n_{r}+1)(n_{s}-1)-n_{r}n_{s}=n_{s}-n_{r}-1\geq 1\), \(2n-n_{i}-n_{r}-1\geq 2n-n_{i}-n_{s}+1\) and \((2n-n_{i}-n_{r}-1)(2n-n_{i}-n_{s}+1)-(2n-n_{i}-n_{r})(2n-n_{i}-n_{s})=n_{s}-n_{r}-1\geq 1\), where \(1\leq i\leq k\), \(i\neq r,s\), then \[\begin{aligned} \frac{\Pi_{1}^{*}(K_{n_{1},\cdots,n_{r}+1,\cdots,n_{s}-1,\cdots,n_{k}})}{\Pi_{1}^{*}(K_{n_{1},\cdots,n_{r},\cdots,n_{s},\cdots,n_{k}})} =&\Bigg(\prod_{\substack{i=1\\ i\neq r,s}}^{k}\frac{(2n-n_{i}-n_{r}-1)^{n_{i}(n_{r}+1)}(2n-n_{i}-n_{s}+1)^{n_{i}(n_{s}-1)}}{(2n-n_{i}-n_{r})^{n_{i}n_{r}}(2n-n_{i}-n_{s})^{n_{i}n_{s}}}\Bigg)\\ &\cdot (2n-n_{r}-n_{s})^{(n_{r}+1)(n_{s}-1)-n_{r}n_{s}}\\ >&\prod_{\substack{i=1\\ i\neq r,s}}^{k}\Bigg(\frac{(2n-n_{i}-n_{r}-1)^{n_{r}}(2n-n_{i}-n_{s}+1)^{n_{s}}}{(2n-n_{i}-n_{r})^{n_{r}}(2n-n_{i}-n_{s})^{n_{s}}}\cdot \frac{2n-n_{i}-n_{r}-1}{2n-n_{i}-n_{s}+1}\Bigg)^{n_{i}}\\ \geq &\prod_{\substack{i=1\\ i\neq r,s}}^{k}\Bigg(\bigg(\frac{(2n-n_{i}-n_{r}-1)(2n-n_{i}-n_{s}+1)}{(2n-n_{i}-n_{r})(2n-n_{i}-n_{s})}\bigg)^{n_{r}} \bigg(\frac{2n-n_{i}-n_{s}+1}{2n-n_{i}-n_{s}}\bigg)^{n_{s}-n_{r}}\Bigg)^{n_{i}}\\ >&1. \end{aligned}\] Thus, if \(G\notin \textbf{{T}}_{n}(k)\), we have \(\Pi_{1}^{*}(K_{n_{1},\cdots,n_{r}+1,\cdots,n_{s}-1,\cdots,n_{k}})>\Pi_{1}^{*}(K_{n_{1},\cdots,n_{r},\cdots,n_{s},\cdots,n_{k}})\), which contradicts the supposition that \(G\) has the maximum multiplicative sum Zagreb indices. So \(G\in \textbf{{T}}_{n}(k)\).
Recall that \(n=k\lfloor \frac{n}{k}\rfloor+b=(k-b)\lfloor \frac{n}{k}\rfloor+b(\lfloor\frac{n}{k}\rfloor+1)\). By the definition of the multiplicative sum Zagreb index, we obtain the value of \(\Pi_{1}^{*}(\textbf{{T}}_{n}(k))\) immediately.
Conversely, it is easy to see that the equality holds when \(G\cong \textbf{{T}}_{n}(k)\). The proof is completed. ◻
Lemma 5. [26] Let \(G=(V,E)\) be a graph with \(\omega (G)\leq k\). Then there is a \(k\)-partite graph \(G'=(V,E')\) such that for every vertex \(v\in V\), \(d_{G}(v)\leq d_{G'}(v)\).
Theorem 3. Let \(G\in {\mathcal{W}}_{n,k}\), where \(2\leq k\leq n-1\). Then \[\begin{aligned} \Pi_{1}^{*}(G)\leq \Pi_{1}^{*}(\textbf{{T}}_{n}(k))= &\Big(2n-2\lfloor\frac{n}{k}\rfloor\Big)^{\binom{k-b}{2}\lfloor\frac{n}{k}\rfloor^{2}}\Big(2n-2\lfloor\frac{n}{k}\rfloor-2\Big)^{\binom{b}{2}(\lfloor\frac{n}{k}\rfloor+1)^{2}} \Big(2n-2\lfloor\frac{n}{k}\rfloor-1\Big)^{b(k-b)\lfloor\frac{n}{k}\rfloor(\lfloor\frac{n}{k}\rfloor+1)} \end{aligned}\] with the equality holding if and only if \(G\cong \textbf{T}_{n}(k)\).
Proof. Choose a graph \(G\in {\mathcal{W}}_{n,k}\) such that \(G\) has the maximum multiplicative sum Zagreb indices. We claim that \(G\in {\chi}_{n,k}\). Otherwise, since \(\omega (G)= k\), by Lemma 5, we can get a \(k\)-partite graph \(H\) with \(V(H)=V(G)\) such that for every vertex \(v\in V(G)=V(H)\), \(d_{G}(v)\leq d_{H}(v)\), i.e., \(H\) is the extremal \(k\)-partite graph with \(V(H)=V(G)\) and \(\omega (H)=\omega (G)= k\) such that the degree of vertices in \(H\) is as large as possible. Obviously, \(H\in {\mathcal{W}}_{n,k}\). By the definition of multiplicative sum Zagreb index, we have \(\Pi_{1}^{*}(H)\geq\ \Pi_{1}^{*}(G)\).
By Theorem 2, considering the uniqueness of the extremal graph in the set \({\chi}_{n,k}\), the theorem holds immediately. ◻
Recently, the extremal values of the multiplicative Zagreb-related indices of graphs with given graph parameters have been widely explored. At present, we have obtained the maximum and minimum multiplicative sum Zagreb indices on the graphs of order \(n\) with given clique number \(k\), and we also identified the corresponding extremal graphs. Next we will consider the extremal multiplicative Zagreb indices of graphs with given other graph parameters as a near future work.
Sun is supported by the Natural Science Foundation of Shanxi Province of China (202303021211154).
Gutman, I. and Furtula (Eds.) B., 2010. Novel Molecular Structure Descriptors – Theory and Applications I. University of Kragujevac, Kragujevac.
Gutman, I. and Furtula (Eds.) B., 2010. Novel Molecular Structure Descriptors – Theory and Applications II. University of Kragujevac, Kragujevac.
Todeschini, R. and Consonni, V., 2000. Handbook of Molecular Descriptors. Wiley-VCH, Weinheim.
Gutman, I. and Trinajsti\(\mathrm{\acute{c}}\), N., 1972. Graph theory and molecular orbitals. III. Total \(\pi\)-electron energy of alternant hydrocarbons. Chemical Physics Letters, 17, pp.535-538.
Eliasi, M., Iranmanesh, A. and Gutman, I., 2012. Multiplicative versions of first Zagreb index. MATCH Communications in Mathematical and in Computer Chemistry, 68, pp.217-230.
Xu, K. and Das, K. Ch., 2012. Trees, unicyclic, and bicyclic graphs extremal with respect to multiplicative sum Zagreb index. MATCH Communications in Mathematical and in Computer Chemistry, 68, pp.257-272.
Bo\(\mathrm{\check{z}}\)ovi\(\mathrm{\acute{c}}\), V., Kovijani\(\mathrm{\acute{c}}\), \(\mathrm{\check{Z}}\). K. and Popivoda, G., 2016. Chemical trees with extreme values of a few types of multiplicative Zagreb indices. MATCH Communications in Mathematical and in Computer Chemistry, 76, pp.207-220.
Azari, M. and Iranmanesh, A., 2015. Some inequalities for the multiplicative sum Zagreb index of graph operations. Journal of Mathematical Inequalities, 9, pp.727-738.
Du, J. and Sun, X., 2020. On the multiplicative sum Zagreb index of graphs with some given parameters. Journal of Mathematical Inequalities, 14, pp.1165-1181.
Sun, X., Gao, Y. and Du, J., 2023. On multiplicative sum Zagreb index of trees with fixed domination number. Journal of Mathematical Inequalities, 17, pp.83-98.
Ali, A., Noureen, S., Moeed, A., Iqbal, N. and Hassan, T. S., 2024. Fixed-order chemical trees with given segments and their maximum multiplicative sum Zagreb index. Mathematics, 12, p.1259.
Dehgardi, N., Du, Z. and Shang, Y., 2024. Multiplicative Sombor index of trees. Notes on Number Theory and Discrete Mathematics, 30, pp.453-460.
Du, J. and Sun, X., 2023. Extremal quasi-unicyclic graphs with respect to the general multiplicative Zagreb indices. Discrete Applied Mathematics, 325, pp.200-211.
Du, J. and Sun, X., 2024. On bond incident degree index of chemical trees with a fixed order and a fixed number of leaves. Applied Mathematics and Computation, 464, p.128390.
Horoldagva, B., Xu, C., Buyantogtokh, L. and Dorjsembe, S., 2020. Extremal graphs with respect to the multiplicative sum Zagreb index. Match Communications in Mathematical and in Computer Chemistry, 84, pp.773-786.
Ismail, R., Azeem, M., Shang, Y., Imran, M. and Ahmad, A., 2023. A unified approach for extremal general exponential multiplicative Zagreb indices. Axioms, 12, p.675.
Noureen, S., Ali, A., Bhatti, A. A., Alanazi, A. M. and Shang, Y., 2024. Predicting enthalpy of formation of benzenoid hydrocarbons and ordering molecular trees using general multiplicative Zagreb indices. Heliyon, 10, p.e30913.
Xu, C., Horoldagva, B. and Buyantogtokh, L., 2021. Cactus graphs with maximal multiplicative sum Zagreb index. Symmetry, 13, p.913.
Bondy, J. A. and Murty, U. S. R., 1976. Graph Theory with Applications. Elsevier, New York.
Du, J., Shao, Y. and Sun, X., 2020. The zeroth-order general Randić index of graphs with a given clique number. Korean Journal of Mathematics, 28, pp.405-419.
Vetrík, T. and Balachandran, S., 2019. General multiplicative Zagreb indices of graphs with given clique number. Opuscula Mathematics, 39, pp.433-446.
Wali, M. and Guji, R., 2024. Extremal Sombor index of graphs with cut edges and clique number. Axioms, 13, p.66.
Xu, K., 2011. The Zagreb indices of graphs with a given clique number. Applied Mathematics Letters, 24, pp.1026-1030.
Xu, K., 2010. On the Hosoya index and the Merrifield-Simmons index of graphs with a given clique number. Applied Mathematics Letters, 23, pp.395-398.
Yang, J., Liu, H. and Wang, Y., 2024. Vertex-degree function index for concave functions of graphs with a given clique number. Journal of Applied Mathematics and Computing, 70, pp.2197-2208.
Erd\(\mathrm{\ddot{o}}\)s, P., 1970. On the graph theorem of Tur\(\mathrm{\acute{a}}\)n. Matematikai Lapok, 21, pp.249-251.
1970-2025 CP (Manitoba, Canada) unless otherwise stated.