In the era of intelligent education, technology is reshaping traditional music education by enhancing teaching quality, optimizing curriculum design, and improving teacher resources. However, its redistributive effects remain underexplored. This study examines how intelligent education technology impacts resource distribution in music education, focusing on the context of music teacher certification. The research highlights the reform needs of music teacher education, including student-centered goals, improved teaching methods, and optimized curricula. It introduces a music intelligence system based on a radial basis function (RBF) neural network and evaluates its potential in promoting equitable resource distribution through interactive teaching. Findings reveal that intelligent education technology enhances student learning outcomes and music skills by enabling personalized learning paths and strengthening practical teaching. Experimental results confirm the system’s effectiveness in significantly improving students’ music grades, demonstrating its value in transforming music education.
With the rapid development of information technology, intelligent education has garnered widespread attention and application worldwide, emerging as a transformative force in the field of education [17]. Music education, as an integral part of human cultural heritage and innovation, is undergoing significant changes, particularly under the influence of intelligent education [18]. This article aims to explore how intelligent education can optimize music education, particularly its redistributive effects on the music teacher education model, offering new perspectives and solutions to existing challenges in the current education framework.
Music education has always been a vital component of the education system, especially in music teacher training, which directly impacts the quality of basic education and students’ holistic development [16]. However, the traditional music education model faces several challenges: curricula are relatively rigid, lacking adaptability to meet students’ individual needs; teaching methods are often outdated, with insufficient emphasis on practical elements, which hampers the development of students’ creativity and self-learning abilities; and the unequal distribution of educational resources creates significant disparities in the quality of education across regions and schools [8]. These issues demand urgent solutions through innovative and transformative educational approaches.
The advent of intelligent education provides new opportunities for addressing these challenges. Technologies such as artificial intelligence and big data analysis enable personalized learning, cater to diverse student needs, optimize resource allocation, and enhance both the quality and efficiency of education [2]. In this context, studying how intelligent education redistributes educational resources in music teacher education holds significant theoretical and practical value. Such research not only fosters innovation in music education models but also supports the cultivation of high-quality music educators, thereby elevating the overall standard of basic education.
Recent studies on the application of intelligent education in music education have achieved notable progress. Research has explored the use of artificial intelligence in music creation, performance, and teaching [14]. For instance, interactive music learning systems powered by AI simulate human teaching methods, enabling intelligent and personalized music instruction [7]. These systems often utilize advanced algorithms, such as radial basis function (RBF) neural networks, to analyze student learning behaviors and dynamically adjust teaching strategies [9].
Despite these advancements, challenges remain in applying intelligent education to music education. Existing intelligent music education systems primarily focus on skill training, often neglecting broader aspects such as music theory and educational philosophy [20]. Furthermore, the integration of these systems into traditional music teacher education models is underexplored, and their effectiveness in practical teaching scenarios has not been fully validated [15]. Additionally, the redistributive effects of intelligent education on resource allocation and teaching quality evaluation remain insufficiently studied, limiting its widespread adoption in music education.
To address these challenges, this article proposes a research framework to explore the redistributive effects of intelligent education on music teacher education. First, it examines how intelligent education methods can optimize the training objectives of music teacher education, emphasizing student-centered teaching design, self-directed learning, and innovative thinking. Second, it investigates the use of intelligent education systems to improve teaching methodologies and curriculum design, aiming to enhance students’ comprehensive competencies and professional competitiveness through interactive and practical teaching approaches. Finally, it analyzes how intelligent education promotes educational equity and improves overall education quality by optimizing resource allocation.
The innovation of this study lies in its systematic exploration of the redistributive effects of intelligent education in music teacher education. Unlike prior research that primarily focuses on music skill training, this study encompasses broader dimensions, including music theory and educational philosophy. Furthermore, by integrating practical teaching cases, this research validates the effectiveness of intelligent education systems in enhancing education quality and fostering educational equity.
The RBF algorithm, an artificial intelligence algorithm, is incorporated into the fundamental algorithm model of the interactive teaching music intelligent system. This neural network algorithm, known as the radial basis function, consists of neurons with localized activation. Figure 1 illustrates the typical five-layer network model.
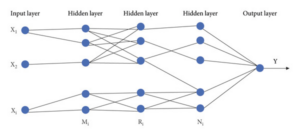
The first layer contains information factors relevant to the case, which can be classified into several music project indicators and fed into the neural network structure. The membership function for the second layer is defined in Eq. 1.
\[\label{e1} \mu_{ij}(x_i) = \exp\left[ -\frac{(x_i – c_{ij})^2}{\sigma_j^2} \right], \quad i = 1, 2, \ldots, r; \, j = 1, 2, \ldots, u. \tag{1}\]
The third layer describes the number of fuzzy rules, which minimizes and maximizes the rules learned through sample learning. The mathematical calculation for the output of the \(j\)th rule is shown in Eq. 2.
\[\label{e2} \phi_j = \exp\left[ -\frac{\sum_{i=1}^r (x_i – c_{ij})^2}{\sigma_j^2} \right] = \exp\left[ -\frac{\|X – C_j\|^2}{\sigma_j^2} \right], \quad j = 1, 2, \ldots, u. \tag{2}\]
Here, \(c_j = (c_{1j}, \ldots, c_{rj})\) represents the \(j\)th RBF unit’s center. The RBF neural network exhibits a property whereby neurons closer to the center exhibit higher activity, which aligns well with the interactive music learning style.
The normalization layer, the fourth layer, aligns the nodes with the fuzzy rule nodes. Its \(j\)th node’s output is given in Eq. 3.
\[\label{e3} \Psi_j = \frac{\phi_j}{\sum_{k=1}^N \phi_k}, \quad j = 1, 2, \ldots, u. \tag{3}\]
The output layer, the fifth layer, evaluates different musical performance qualities. The RBF algorithm, primarily based on the TS fuzzy model, produces the output in Eq. 4.
\[\label{e4} y(x) = \frac{\sum_{i=1}^u \left[ \left( a_{i0} + a_{i1}x_1 + \cdots + a_{ir}x_r \right) \exp\left( -\frac{\|x – c_i\|^2}{\sigma_i^2} \right) \right]}{\sum_{i=1}^u \exp\left( -\frac{\|x – c_i\|^2}{\sigma_i^2} \right)}. \tag{4}\]
The connection method for the \(k\)th rule is represented as the sum of the weight products of the output variables, as shown in Eq. 5.
\[\label{e5} y(x) = \sum_{k=1}^u w_k \cdot \Psi_k. \tag{5}\]
Based on the RBF algorithm, the interactive music learning mode successfully integrates algorithm principles into the platform’s architecture, providing a comprehensive explanation of the algorithm during the coding process and effectively connecting it to the platform’s interface functionalities. Here, \(X\) represents the proportion of learning time for 100 students who passed the music test and achieved excellent results; \({c_j}{\sigma_j}\) denotes the distribution of hidden layers in each music learning courseware corresponding to the students’ learning time \((X)\); and \(Y\) is the optimal music score corresponding to each input layer.
The second, third, and fourth layers can be reduced to hidden layers to expedite the RBF algorithm. The first and fifth layers act as input and output layers, respectively. An RBF model is built to help students learn music knowledge, with the initial training using the first \(m\) pieces of music data from a large dataset. The software platform undergoes continuous evaluation until a complete model is constructed. Figure 2 presents the program design diagram.

The educational effect of student classroom receptive music courses is called “listening method”, which adjusts the body and mind by listening to suitable music to achieve the purpose of course education effect [13]. Choose a fixed music course education effect room, requiring a quiet, spacious, soft lighting, suitable temperature, and unobstructed air environment. The room should be equipped with sofas and speakers, and the sofas should be placed in a large circle to facilitate communication between each other [1]. Intervene for 50 minutes each time, once on Saturday and Sunday evenings each week, for 8 weeks.
Select music based on the cultural background and appreciation level of classroom students, with beautiful, soothing, relaxed, quiet, active and cheerful music as the main melody [6]. The music muscle progressive relaxation training uses repertoire including Vivaldi’s “Four Seasons”, Haydn’s “Water Music”, Debussy’s orchestral suite “Sea”, Schumann’s “Fantasia”, etc; There are a total of 30 Chinese songs, including “Erquan Yingle”, “Happy Meeting”, “Spring Has Arrived”, “Jiangnan is Good”, “Night at the Military Port”, etc.
The guided music association mainly uses four themes, with one theme selected each week. Theme one: Grassland, using “On the Grasslands of Central and Western Asia” (Borodin) and “Symphony No. 6” (Beethoven); Theme 2: High Mountains, selected from the second movements of the Grand Canyon Suite (Grophy) and the Second Symphony (Brahms); Theme 3: Stream Water, selected from “The Voltava River” (Smetana) and “The Pine Trees of Rome” (Lespici); Theme four: The Sea, selected are “The Sea” (Debussy) and “Dancing with Wolves Theme” (John Barry). The optimal volume is 40-50 dB.
Intervention form: 1) Progressive relaxation training of music muscles (10-20 minutes). The music course education effect teacher guides members to relax their entire body muscles under the soothing melody of music [3]. The music curriculum education effect teacher guides individuals to freely associate in different types of music backgrounds, sets imaginative scenarios, and controls the entire process of music association [10].By guiding and triggering visual imagination of nature, evoking memories of the past, stimulating pleasant self experiences and positive things, enhancing members’ resilience, and strengthening their sense of security and relaxation [4].
Song discussion (about 20 minutes). After listening to different types of songs, discuss them. The discussion process not only reflects individuals’ preferences for music, but also reflects the deep needs and individual differences of members, which can serve as a breakthrough point for solving problems [5,11]. Group members expressing their emotional experiences towards the same song and listening to others’ experiences can not only promote emotional communication among group members, but also enable course educators to recognize members’ narrow thinking patterns and individual personality differences through sharing, thereby helping members correct incorrect thinking [12,19].
The best way to gauge the success of this teaching experiment is to look at the students’ grades, which also serve as a direct indicator of the caliber of instruction in the classroom. In order to determine whether the middle school music situational teaching activity based on the theory of multiple intelligences can raise students’ music grades, the author administered a music assessment and a semester-ending test to two selected classes: the experimental class and the control class. The data from the following students’ music score tests were processed and examined using SPSS23.0.
The same test paper was used to administer music assessments to every student in two classrooms prior to the experiment. The “2018-2019 Stage Exam of a Middle School – Seventh Grade First Volume Music Test Paper” was the instrument used for testing. The following test results are shown in Table 1:
| Class | N | M | SD | T | P | Significance | |
| Fraction | Experimental Class | 49 | 60.12 | 20.97 | 1.82 | 0.856 | × |
| Control class | 49 | 59.43 | 19.15 | 1.82 | 0.856 | × |
According to the data comparison in Table 1, before the start of the teaching experiment, the average music scores of the experimental class and the control class were 60.12 and 59.43 points, respectively, with only a difference of 0.69 points; Secondly, the music score of the experimental group was 60.12 ± 20.97 points, while the music score of the control group was 59.44 ± 19.15 points, with no significant difference. Based on the T-test results of the experiment’s first two sets of data, it was found that the music scores of these two classes were double tailed Sig. P=0.856 (P>0.05) was the significant probability for the two-tailed data.P>0.05, according to statistical analysis, denotes that there is not a statistically significant difference between the two samples before and after testing. The findings in Table 1 show that, prior to the experiment, there was no significant difference (P>0.05) in the music scores between the experimental and control groups, which was essentially equal and satisfied the criteria for comparison. Therefore, the many intelligences theory-based middle school music situational teaching experiment can make use of these two courses.
The “2019-2020 Stage Music Test of a Middle School” was used by the author as a post test (final exam) on the music scores of all pupils in the experimental and control classrooms following a year of experimental teaching. Table 2 displays the test results.
| Class | N | M | SD | T | P | Significance | |
| Fraction | Experimental Class | 49 | 67.60 | 17.58 | 2.037 | 0.046 | × |
| Control class | 49 | 60.45 | 17.17 | 2.037 | 0.046 | × |
The average music score of the 49 students in the experimental class was 67.60 points, while the average music score of the 49 students in the control class was 60.45 points, as shown by the data comparison in Table 2 following the middle school music situational teaching experiment based on the theory of multiple intelligences.There was a substantial difference in the music level between the experimental and control classes, with the experimental group scoring 17.17 points higher on average and having a much higher music level.Following the experiment, P=0.046 (0.01<P<0.05) was the significance probability of the two-tailed Sig (2-tailed) in the music scores of these two classes, according to the T-test results of the two sets of data. Based on statistical analysis, a difference between the two samples that is statistically significant before and after detection is displayed when 0.01<P<0.05.The experimental group and the control group had significantly different music scores following the training experiment (0.01<P<0.05), as indicated by the data in Table 2. Improvements in students’ music grades can be achieved with the use of music situational teaching, which was developed with the notion of multiple intelligences as a guide.
In order to determine whether there is a difference between the pre-test and post-test music scores of the students in the group, the author conducted statistical analysis on the music score data of 49 students in the control group before and after the experiment.A longitudinal comparative examination of the class’s music scores produced the following results (Table 3):
| Before and after the experiment | N | M | SD | T | P | Significance | |
| Fraction | Before the experiment | 49 | 59.43 | 19.15 | -0.373 | 0.713 | × |
| After the experiment | 49 | 60.45 | 17.17 | -0.373 | 0.713 | × |
Table 3 presents a comparison of the pre-test and post-test data of the music scores of the students in the control class after the teaching experiment. The average score and standard deviation of the control class’s pre-test were 59.43 and 19.15 points, respectively, while the control class’s post-test results were 60.43 and 17.17 points, respectively. Students in the control class now have better average music scores.The T-test results of the pre-test and post-test data showed that the significant probability of the two-tailed Sig (2-tailed) of the music scores of 49 students in the control group before and after the experiment was P=0.713 (P>0.05). Statistical analysis indicates that P>0.05 indicates that there is no statistically significant difference between the two samples pre- and post-testing. The data in Table 3 indicate that there was no significant change (P>0.05) in the music scores of the control group students before and after the experiment, indicating no actual improvement.
In order to determine whether there is a difference in the music test scores of the students before and after teaching, the author also conducted a longitudinal comparison study of the total scores of 49 students in the experimental class before and after the experiment. The following are the results (Table 4):
| Prior to and following the experiment | N | M | SD | T | P | Significance | |
| Fraction | Before the experiment | 49 | 60.12 | 20.97 | -2.599 | 0.011 | × |
| After the experiment | 49 | 67.59 | 17.62 | -2.599 | 0.011 | × |
Following the teaching experiment, the students in the experimental class had an average score of 60.12 and a standard deviation of 20.97 points on the pre- and post-tests for music, according to Table 4’s data comparison. The experimental class students’ post-test results showed an average score of 67.59 and a standard deviation of 17.62 points, respectively. The average music scores of the experimental class students have significantly improved.According to the t-test results of the pre-test and post test data, the significant probability of bilateral Sig (2-tailed) in the music scores of 49 students in the experimental class before and after the experiment was P=0.011 (0.01<P<0.05). Statistical analysis shows that when 0.01<P<0.05, there is a statistically significant difference between the two samples before and after testing. Table 4 shows that there is a significant difference (0.01<P<0.05) in the music scores of the experimental class students before and after the experiment. By applying the theory of multiple intelligences in experimental teaching to develop music scene programs, students’ music grades can be improved.
This study explores the potential of utilizing intelligent educational technology to achieve resource redistribution and personalized teaching in the field of music education. We have developed a new teaching model by combining a resource reallocation model with a personalized learning system based on RBF neural network, aiming to enhance the learning experience and teaching ability of music teacher education students. The research results indicate that intelligent education technology has significant advantages in resource optimization and personalized learning, which can effectively respond to the learning needs of different students and improve teaching effectiveness.In addition, the introduction of interactive music teaching mode not only improves students’ music skills and theoretical knowledge mastery, but also enhances their innovation ability and critical thinking to a certain extent. Future research should further explore the application of this teaching model in different educational backgrounds and majors to verify its broad applicability and long-term effects. In summary, this study provides theoretical basis and practical reference for the intelligent transformation in the field of music education, and has important educational and academic significance.
– Provincial Teaching Research Project of Higher Education Institutions in Hubei Province, China.
– Project name: Research on the Development Model of Theoretical Courses in Musicology Major of Higher Normal University under the Background of New Liberal Arts Project Number: 2020675.