We consider the generating function for increasingly labelled trees. By generalizing the proof through symbolic method, we are able to study various statistics regarding binary increasing trees with respect to height restrictions. We then apply our approach to special colorings of increasing trees in order to obtain their generating functions and, from there, derive the counting sequence for \((ak+a)\)-colored recursive trees. We also present some interesting bijections between colored and non-colored increasing trees.
The enumeration of trees has long been an interesting topic of study. It is a natural progression to assign some sort of labeling to the vertices of these trees, and from that, we have increasingly labeled trees. Formally speaking, an increasing tree is a tree which is labeled in a strictly increasing manner (where every vertex has a smaller label than any of its descendants) by \(\{1,\dots,n\}.\). One of the earliest results in increasing trees comes from Donaghey and his proof of a bijection between increasingly labeled binary trees and the alternating permutations [2].
This concept can also be expanded to trees with no restrictions on their down degrees (as opposed to the binary case, where all down degrees are 2 or 0), which are called recursive trees. Figure 1 shows an example. Recursive and random recursive trees have been extensively studied by Meir and Moon [5,6] and also by Szymański [10].
Interesting enumeration questions arise from these concepts. In the case of the recursive trees, it is well known that it is enumerated by \((n-1)!\). On the other hand, plane recursive trees are enumerated by \((2n-1)!!\) as seen in Prodinger’s paper [7]. A plane tree is a labeled tree in which the orderings between siblings matter, as illurstrated in Figure 2.
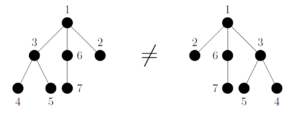
Based on the work of Bergeron, Flajolet, and Salvy in their landmark paper [1], one may consider various enumeration problems of colored increasingly labeled trees whose vertices have a number of color options based on their down degrees (the number of children of a vertex). In preparation for this, we first introduce some basic definitions and previous work on combinatorial classes and their generating functions in Section 2.
These essential ideas allow us to use generating functions to study increasing trees with restricted heights and study various interesting statistics in Section 3.
From there, we move on to consider colored increasing binary trees. Some of their counting sequences appear to coincide with some previously known sequences, with connections to a number of interesting concepts, including: alternating permutations, Euler and Bernoulli polynomials, zigzag numbers, trigonometric functions, Fourier transform of a square wave, quantum algebras, integrals over and in n-dimensional hypercubes and over Green functions [4,9], and generalized tangent numbers [8]. The counting sequences are justified through both generating functions and combinatorial arguments, and generalized for \(k\)-ary trees in Section 4.
We then shift our attention to colored recursive trees in Section 5, where similar analysis through generating functions is shown, followed by combinatorial arguments. In particular, the enumeration of \((k+1)\)-colored plane recursive trees (to be defined later) leads to \((3n-4)!!!\), closely related to the previous results of \((n-1)!;\) for standard recursive trees and \((2n-1)!!\) for plane recursive trees. A generalization is also discussed here.
Lastly, in Section 2, we briefly discuss the counting sequences introduced from this work. Some of the data is shown in the appendix.
The general definitions and techniques follow those developed in [1] and [3]. A combinatorial class is a finite set along with a size function where every object has a size that is a non-negative integer and the number of objects of any size is finite. The generating function of a combinatorial class \(B\) would be denoted by \(B(z)\). And we say two combinatorial classes \(A\) and \(B\) are isomorphic (or have a class isomorphism) if we have that \(A(z)=B(z)\) for their generating functions. The following definition is also crucial to our work that follows.
Plane: \[\phi(u)=\sum_{n\geq 0}s_{n}u^{n}.\]
Non-plane: \[\phi(u)=\sum_{n\geq 0}s_{n}\frac{u^{n}}{n!}.\]
The following theorem was given in [1]. Here, we provide details of the proof using symbolic notations developed in [3]. This approach is generalized to present some of the observations shown in this paper. With the given degree functions, the increasing trees are described by the combinatorial class \(\mathcal{I}=\mathcal{Z}^{\square}\star\phi(\mathcal{I})\) (where \(Z\) is the root of such a tree) with generating function \(I(z)\).
Proof. It is defined by Flajolet and Sedgewick in [3] that \(\mathcal{A}=\mathcal{B}\star \mathcal{C}\) is defined by \[A_{n}=\sum_{n_{1}+n_{2}}{n \choose n_{1},n_{2}}B_{n_{1}}C_{n_{2}}.\] It is then clear that by restricting our smallest element in to be in \(\mathcal{B},\) denoted by \(\mathcal{B}^{\square},\) we obtain \[A_{n}=\sum_{k=1}^{n}{n-1\choose k-1}B_{k}C_{n-k}=\frac{1}{n}\sum_{k=1}^{n}{n\choose k}kB_{k}C_{n-k}.\] So from the definition of an exponential generating function, \[A(z)=\sum_{n\geq 0} \frac{z^{n}}{n!}\frac{1}{n}\sum_{k=1}^{n}{n\choose k}kB_{k}C_{n-k}=\sum_{n\geq 0}\frac{z^{n}}{n}\sum_{k=1}^{n}\frac{k}{k!(n-k)!}B_{k}C_{n-k}.\] We then take the derivative, \[\begin{aligned} A'(z) &= \sum_{n\geq 0} z^{n-1}\sum_{k=1}^{n}\frac{k}{k!(n-k)!}B_{k}C_{n-k}\\ &= \sum_{n\geq 0}\sum_{k=1}^{n}\frac{z^{k-1}k}{k!}B_{k}\frac{z^{n-k}}{(n-k)!}C_{n-k}\\ &=B_{1}C_{0}+B_{1}C_{1}z+B_{2}C_{0}z+B_{1}C_{2}\frac{z^{2}}{2!}+B_{2}C_{1}z^{2}+\frac{z^{2}}{2}B_{3}C_{0}+\dots\\ &= (B_{1}+zB_{2}+\frac{z^{2}}{2}B_{3}+\dots)(C_{0}+zC_{1}+\frac{z^{2}}{2}C_{2}+\dots)\\ &=\partial_{z}B(z)\cdot C(z). \end{aligned}\]
We now apply this to \(\mathcal{I}=\mathcal{Z}^{\square}\star\phi(\mathcal{I}),\) \[I'(z)=\partial_{z}z\cdot \phi(I(z))=\phi(I(z)).\] Therefore, \[\begin{aligned} \frac{I'(z)}{\phi(I(z))} &= 1\\ \int_{0}^{z}\frac{I'(z)}{\phi(I(z))}\:dz &= z\\ \int_{0}^{I(z)} \frac{1}{\phi(u)}\:du &= z, \end{aligned}\] where \(u=I(z).\) ◻
As an example, applying Theorem 2.2 to the degree function \[\phi(u)=\sum_{n=0}^{\infty}\frac{u^{n}}{n!} = e^{u},\] we have \[\int_{0}^{R(z)}e^{-u}\:du = z,\] Therefore, we obtain \(R(z)=\ln\left(\frac{1}{1-z}\right)\) and \(\{ (n-1)! \}\) as the counting sequence for non-plane increasingly labeled recursive trees. This can also be seen through simple recursive combinatorial argument where the vertex with label \(n\) can be a child to any of the vertices labeled 1 through \(n-1\).
We may apply the developed approach to increasing trees with restricted heights. We will denote the class of all increasing trees with height less than or equla to \(h\) by \(\mathcal{I}_{h}\). Then, \[\mathcal{I}_{h} = \mathcal{Z}^{\square}\star \phi(\mathcal{I}_{h-1})\] as the height of the subtree formed by the children of the root is one less than that of the original tree. Following similar arguments to the proof of Theorem 2.2, we have the following based on the fact that \(I_{h}'(z)=\phi(I_{h-1}(z))\).
As an example, Proposition 3.1 can be used to calculate the generating function for plane binary increasing trees whose height is less than or equal to three.
\[\begin{aligned} B_{3}(z) &= \int_{0}^{z} B_{2}^{2}(t) + 1 \:dt\\ &= \int_{0}^{z} \left[1 + \left(\int_{0}^{t} B_{1}^{2}(u)+1\: du\right)^{2} \right]\:dt\\ &= \int_{0}^{z} \left[1 + \left(\int_{0}^{t}1 + \left(\int_{0}^{u} B_{0}^{2}(x)+1\: dx\right)^{2}\: du\right)^{2} \right]\:dt\\ &= \int_{0}^{z} \left[ 1 + \left(\int_{0}^{t}1 + \left(\int_{0}^{u} 2\: dx\right)^{2}\: du\right)^{2} \right]\:dt\\ &= \int_{0}^{z} \left[ 1 + \left(\int_{0}^{t}1 + 4u^{2}\: du\right)^{2} \right]\:dt\\ &= \int_{0}^{z}\left[ 1 + \left(t+\frac{4}{3}t^{3}\right)^{2} \right]\:dt\\ &= \int_{0}^{z} \left[ 1 + t^{2} + \frac{8}{3}t^{4} + \frac{16}{9} t^{6} \right]\:dt\\ &= \frac{16}{63}z^{7} + \frac{8}{15}z^{5} + \frac{1}{3}z^{3} + z. \end{aligned}\]
In general, we may apply Proposition 3.1 to obtain various statistics related to binary increasing trees. In Figure 3, we plot the probability of trees of a given order has restricted height \(\leq h\). From left to right each curve corresponds to a particular bound from zero to eleven.
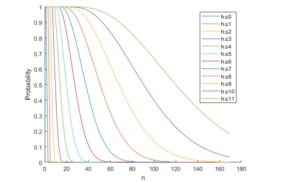
We may also use our data to identify three thresholds where the percentage of non-plane binary increasing trees of restricted height passes or achieves \(25\%,\) \(50\%,\) and \(75\%\) of the total number of non-plane binary increasing trees. We give this information in Table 1.
| height | order | probability |
| \(h\leq 6\) | \(17\) | \(28.3\%\) |
| \(h\leq 7\) | \(24\) | \(25.2\%\) |
| \(h\leq 8\) | \(32\) | \(27\%\) |
| \(h\leq 9\) | \(44\) | \(25\%\) |
| \(h\leq 10\) | \(58\) | \(26.3\%\) |
| \(h\leq 11\) | \(78\) | \(25.3\%\) |
| \(h\leq 6\) | \(14\) | \(52.1\%\) |
| \(h\leq 7\) | \(19\) | \(51.6\%\) |
| \(h\leq 8\) | \(25\) | \(53.7\%\) |
| \(h\leq 9\) | \(34\) | \(51.5\%\) |
| \(h\leq 10\) | \(45\) | \(51.6\%\) |
| \(h\leq 11\) | \(60\) | \(50.6\%\) |
| \(h\leq 6\) | \(11\) | \(79\%\) |
| \(h\leq 7\) | \(15\) | \(76.4\%\) |
| \(h\leq 8\) | \(20\) | \(75.6\%\) |
| \(h\leq 9\) | \(26\) | \(76.5\%\) |
| \(h\leq 10\) | \(34\) | \(76.6\%\) |
| \(h\leq 11\) | \(45\) | \(75.7\%\) |
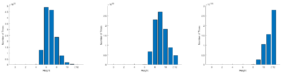
Given the order of the increasing binary trees, we may also study the distribution of them according to different values. As examples, we consider trees of order 31, 61, and 121 respectively in Figure 4. Note that the final column represents trees with height \(\geq 12\).
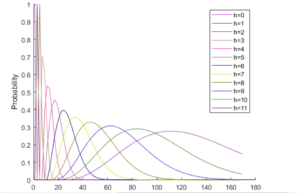
Lastly, in Figure 5, we present the probability of a non-plane binary increasing tree of order \(n\) having height exactly \(h\).
We move on to study general theories and specific combinatorial argument related to colored increasing trees.
First of all, We say an increasing binary tree is \((a;b)\)-colored if there exist \(a\) colors for vertices of down degree \(0\) and \(b\) colors for nodes of down degree \(2\). We begin by presenting the generating functions for \((a;b)\)-colored increasing binary trees.
\[B_{p}(z)=\frac{\sqrt{a}}{\sqrt{b}}\tan\left(z\sqrt{ab}\right).\]
Proof. From Definition 2.1 we obtain the degree function \[\phi(u)=\sum_{n}s_{n}u^{n}.\] With \(n=\{0,2\}\) and \(s_{0}=a,s_{2}=b\), we have \[\phi(u)=\sum_{n}s_{n}u^{n}=a+bu^{2}.\]
By Theorem 2.2, we have \[\begin{aligned} \int_{0}^{B_{p}(z)}\frac{1}{a+bu^{2}} \text{ du }&=z\\ \frac{1}{\sqrt{ab}}\arctan\left(\frac{\sqrt{b}}{\sqrt{a}}B_{p}(z)\right) &= z\\ \arctan\left(\frac{\sqrt{b}}{\sqrt{a}}B_{p}(z)\right) &= z\sqrt{ab}\\ \frac{\sqrt{b}}{\sqrt{a}}B_{p}(z) &= \tan\left(z\sqrt{ab}\right)\\ B_{p}(z) &= \frac{\sqrt{a}}{\sqrt{b}}\tan\left(z\sqrt{ab}\right).\\ \end{aligned}\] ◻
Similarly, for non-plane trees we have the following.
\[B_{np}(z)=\frac{\sqrt{2a}}{\sqrt{b}}\tan\left(z\frac{\sqrt{ab}}{\sqrt{2}}\right).\]
Proof. We obtain the degree function in a similar way,
\[\phi(u)=\sum_{n}s_{n}\frac{u^{n}}{n!}=a+\frac{b}{2}u^{2}.\]
The proof proceeds from Theorem 2.2 giving us,
\[\begin{aligned} \int_{0}^{B_{p}(z)}\frac{1}{a+\frac{b}{2}u^{2}} \text{ du }&=z\\ \frac{\sqrt{2}}{\sqrt{ab}}\arctan\left(\frac{\sqrt{b}}{\sqrt{2a}}B_{np}(z)\right) &= z\\ \arctan\left(\frac{\sqrt{b}}{\sqrt{2a}}B_{np}(z)\right) &= z\frac{\sqrt{ab}}{\sqrt{2}}\\ \frac{\sqrt{b}}{\sqrt{2a}}B_{np}(z) &= \tan\left(z\frac{\sqrt{ab}}{\sqrt{2}}\right)\\ B_{np}(z) &=\frac{\sqrt{2a}}{\sqrt{b}}\tan\left(z\frac{\sqrt{ab}}{\sqrt{2}}\right).\\ \end{aligned}\] ◻
From the above proofs, it is easy to see that the generating functions for \((a;2b)\)-colored non-plane increasing binary trees is \[\frac{\sqrt{2a}}{\sqrt{2b}}\tan\left(z\frac{\sqrt{2ab}}{\sqrt{2}}\right) = \frac{\sqrt{a}}{\sqrt{b}}\tan\left(z\sqrt{ab}\right),\] exactly that of the \((a;b)\)-colored plane increasing binary trees, leading us to the following result as an immediate consequence. We will provide a combinatorial proof for this connection.
Proof. We start with the simple case of \(a=b=1\). For any increasing binary tree, we know that we can determine the number of trees on \(n\) vertices by the ways in which we can rearrange the labelings and the number of children for each vertex. If this tree is plane then we also must consider the number of ways in which we can rearrange the branches. This of course only applies to vertices with a down degree of \(2\), where each vertex has \(2\) possible ways in which we can rearrange the branches. In a non-plane binary tree, we have no such consideration though. However, if we are to color the vertices of down degree \(2\) with \(2\) possible colors, then we now have the same consideration, except instead of rearranging the branches we must consider the ways in which we could color the vertex. This establishes the bijection between the plane increasing binary tree and the \((1;2)\)-colored non-plane increasing binary tree.
Similarly, in the more general case: in the plane tree we have \(b\) colors for each node with \(2\) children (hence 2 ways to arrange them) and in the non-plane case \(2b\) colors. Once again though we can arrange the branches in the plane case in \(2\) possible ways for each node of down degree \(2\) this combined with the \(b\) colors gives \(2b\) possible considerations for each node with children. While in the non-plane case, we have \(2b\) considerations from the coloring and no considerations due to arranging the branches, which gives us just \(2b\) total. Thus we have an equal number of trees. ◻
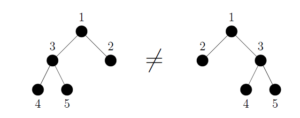
However, in the case of the non-plane binary tree we see that same can not be said which we illustrate in Figure 7.
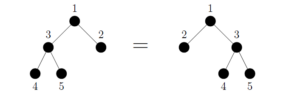
If we instead color the non-plane binary tree though we see that they are no longer equivalent as in Figure 8.
This allows us to map them like in Figure 9 and Figure 10.
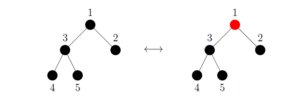
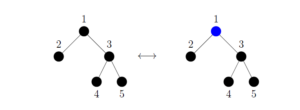
We can take this a step further, while no generating functions can be explicitly shown for \(k\)-ary trees with \(k>2\), the above combinatorial arguments apply to show the following more general statement. The proof, which we omit, follows exactly the same logic but noting that there are \(k!\) ways to arrange the pending branches of each nonleaf vertex.
We now move on to consider general trees with all possible down degrees allowed. First, we define a \(f(k)\)-colored recursive tree to be a recursive tree where each vertex of down degree \(k\) has \(f(k)\) possible colors. Throughout this section we’ll consider different type of trees from different \(f(k)\) functions. Recall the following important result from [1].
Let \(R_{p}\) denote the class of plane recursive trees. Then,
\[R_{p}(z)=1-\sqrt{1-2z}.\]
For \(k!\)-colored non-plane recursive trees, we have the following.
\[N_{np}(z)=R_{p}(z).\]
Proof. It is clear that degree function given by the \(k!\)-colored non-plane recursive tree is,
\[\phi(u)=\sum_{n\geq 0}n!\frac{u^{n}}{n!}=\sum_{n\geq 0}u^{n}.\]
The rest follows from the fact that this is the same degree function as that of the (non-colored) plane recursive trees. ◻
It is not difficult to apply combinatorial arguments similar to the last section to justify that the plane recursive trees and \(k!\)-colored non-plane recursive trees are equinumerous. We make a more general statement as follows.
Proof. Starting from the set of non-plane trees we can generate the plane trees by multiplying by the number of ways in which we can arrange the branches of each vertex. This is the same as multiplying by \(k!\), the number of ways to permute \(k\) children, for each vertex of down degree \(k\).
On the other hand, this is the same to let each vertex in the non-plane tree with down degree \(k\) to have \(k!\) possible colors. ◻
First we consider the case \(a=1\), the degree function is given by \[\phi(u)=\sum_{n=0}^{\infty}(n+1)u^{n}=\frac{1}{(u-1)^{2}}.\]
Letting \(R\) be the combinatorial class for the \((k+1)\)-colored plane recursive trees. Then, \[\begin{aligned} \int_{0}^{R(z)}(u-1)^{2}\text{ du } &= z,\\ \frac{R(z)^{3}}{3}-R(z)^{2}+R(z) &= z,\\ \frac{R(z)^{3}}{3}-R(z)^{2}+R(z) -z &= 0. \end{aligned}\] Solving for \(R(z)\), we have \[R(z)=(3z-1)^{\frac{1}{3}}+1.\]
This generating function coincides with that of the sequence A008544 in the Online Encyclopedia of Integer Sequences, where simple application of the general binomial coefficients yields \[(3n-4)!!! := (3n-4)\cdot (3n-7) \cdots 5 \cdot 2,\] as the counting sequence, below we provide a combinatorial proof for this fact.
Proof. Let \(A_n\) be the number of such trees on \(n\) vertices. Let \(T\) be such a tree with \(n-1\) vertices and let \(v\in T\) be an arbitrary vertex with down degree \(k\). It follows from our definition that \(v\) has \((k+1)\) different colors. We now append a new vertex \(w\) to this one \(v\) will now have \(k+2\) different colors and we may also place \(w\) in \((k+1)\) positions to generate a distinct tree with \(n\) vertices, this is because changing the position of \(w\) rearranges the branch which \(w\) forms. So far we have that appending \(w\) to \(v\) generates \((k+1)(k+2)\) new trees of size \(n\). Dividing by \((k+1)\), the original number of color choices for \(v\), this gives us \((k+2)\) new trees generated by appending \(w\) to \(v\).
In order to consider all possible cases, we must sum \((k+2)\) over all \(k_{i}\) corresponding to each \(v_{i}\in T\) as we could append \(w\) to any vertex in \(T\). Since there are only \((n-1)\) vertices in \(T\) this gives \(\sum_{i=1}^{n-1}k_{i}+2,\) and it follows that \(\sum_{i=1}^{n-1}k_{i}+2=2n-2+\sum_{i=1}^{n-1}k_{i}\). Note that the sum of down degrees is the same as the total number of children, \(n-2\).
Thus, \(2n-2+\sum_{i=1}^{n-1}k_{i}=2n-2+n-2=3n-4,\) new trees generated by appending \(w\) to \(T\). Hence \(A_n=(3n-4)A_{n-1}=(3n-4)!!!\). ◻
The above argument is illustrated in Figure 11.
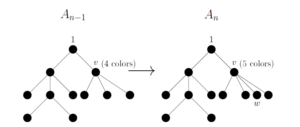
Should one apply similar generating functions and/or combinatorial arguments to \((ak+a)\)-colored plane recursive trees, we have the followings.
Let \(\{A_{n}\}\) be the counting sequence corresponding to the \((ak+a)\)-colored plane recursive trees, then \(A_{n}=(3n-4)!!!a^{n}\)
Indeed, if the number of color choices for each vertex is multiplied by a fixed value \(a\), then the total number of possible trees is multiplied by \(a^n\) as there are \(n\) vertices.
Applying the symbolic approach, we studied the generating functions corresponding to various classes of colored increasingly labelled trees. This approach allows us to study various statistics related to such trees with restricted heights, as well as colored analogues. Both computational data and combinatorial observations are presented.
1970-2025 CP (Manitoba, Canada) unless otherwise stated.