For a set \( S \) of vertices in a connected graph \( G \), the multiplicative distance of a vertex \( v \) with respect to \( S \) is defined by \(d_{S}^{*}(v) = \prod\limits_{x \in S, x \neq v} d(v,x).\) If \( d_{S}^{*}(u) \neq d_{S}^{*}(v) \) for each pair \( u,v \) of distinct vertices of \( G \), then \( S \) is called a multiplicative distance-locating set of \( G \). The minimum cardinality of a multiplicative distance-locating set of \( G \) is called its multiplicative distance-location number \( loc_{d}^{*}(G) \). If \( d_{S}^{*}(u) \neq d_{S}^{*}(v) \) for each pair \( u,v \) of distinct vertices of \( G-S \), then \( S \) is called an external multiplicative distance-locating set of \( G \). The minimum cardinality of an external multiplicative distance-locating set of \( G \) is called its external multiplicative location number \( loc_{e}^{*}(G) \). We prove the existence or non-existence of multiplicative distance-locating sets in some well-known classes of connected graphs. Also, we introduce a family of connected graphs such that \( loc_{d}^{*}(G) \) exists. Moreover, there are infinite classes of connected graphs \( G \) for which \( loc_{d}^{*}(G) \) exists as well as infinite classes of connected graphs \( G \) for which \( loc_{d}^{*}(G) \) does not exist. A lower bound for the multiplicative distance-location number of a connected graph is established in terms of its order and diameter.
Let \(G\) be a connected graph and let \(W=\{w_1,w_2,\cdots,w_k\}\) be an ordered set of vertices in \(G\). If \(v \in V(G)\), the \(k\)-vector \(C_W(v)\) of \(v\) with respect to \(W\) is defined by \(C_W(v) = (d(v,w_1),d(v,w_2),\cdots,d(v,w_k))\) where \(d(v,w_i)\) is the distance between \(v\) and \(w_i\) \((1 \leq i \leq k)\). The set \(W\) is called a locating set if for every pair of distinct vertices \(u,v \in V(G)\), \(C_W(u)\neq C_W(v)\). It is also called a resolving set. The \(k\)-vector \(C_W(v)\) is called the locating code of \(v\) with respect to \(W\). The cardinality of a minimum locating set in \(G\) is called the location number of \(G\) and it is denoted by \(loc(G)\). In 1975 and later in 1988, Slater [1,2] introduced the concept of “Locating Set” of a graph G. Independently, in 1976, Harary and Melter [3] discovered these concepts as well but used the term Metric Dimension, rather than location number. Let \(S\) be a subset of \(V(G)\). The distance of a vertex \(v\) with respect to \(S\) is defined by \(d_S(v) = \sum\limits_{\substack{x \in s \\ x \neq v}} d(v,x)\).
If \(d_S(u) \neq d_S(v)\) for each pair \(u,v\) of distinct vertices of \(G\), then \(S\) is called a distance-locating set of \(G\). In 2003, Chartrand et al. [4] defined the concept “Distance-Locating Set” of a graph G and the minimum cardinality of a distance-locating set of G is the distance-location number \(loc_{d}(G)\). They found the relationship between \(loc(G)\) and \(loc_{d}(G)\). Further, they found the existence of distance-locating sets in some well-known classes of connected graphs and proved that no distance-locating set in a connected graph G has cardinality 2 or 3.
Moreover, there are infinite classes of connected graphs G for which \(loc_{d}(G)\) exists as well as infinite classes of connected graphs G for which \(loc_{d}(G)\) doest not exist. Also, they found the lower bound for the distance-location number of a connected graph in terms of its order and diameter.
Motivated by the concept Distance-Locating Set of a graph \(G,\) we introduce the new concept “Multiplicative Distance-Locating Set” of a graph G and we define the cardinality of a minimum multiplicative distance-locating set of G as the multiplicative distance-location number \(loc_{d}^{*}(G)\). Then we find the relationship between \(loc(G)\) and \(loc_{d}^{*}(G).\) Also, we find the existence of multiplicative distance-locating sets in some well-known classes of connected graphs and we prove that no multiplicative distance-locating set in a connected graph G has cardinality 2. Moreover, we find an infinite classes of connected graphs such as complete graph and star graph for which \(loc_{d}^{*}(G)\) does not exist. Also, we find that the path \(P_{3}\) is the only connected graph G of diameter 2 such that \(loc_{d}^{*}(G)\) exists. We define the new class of connected graph \(P_{n} \divideontimes C_{m}\), obtained by identifying any two consecutive vertices of \(C_{m}\) with the \((n-2)^{th}\) and \((n-1)^{th}\) vertices of \(P_{n}\), for which \(loc_{d}^{*}(G)\) exists. Also, we find the lower bound for the multiplicative distance-location number of a connected graph in terms of its order and diameter.
Chartrand et al. [4] defined the concept External Distance-Locating Set of G and the cardinality of a minimum external distance-locating set of G is the external location number \(loc_{e}(G)\). Further, they found the relationship between \(loc(G), loc_{d}(G)\) and \(loc_{d}(G)\) and studied the external location number of some well-known classes of connected graphs.
Motivated by the concept External Distance-Locating Set of a graph G, we introduce the new concept “External Multiplicative Distance-Locating Set” of a graph G and the cardinality of a minimum external multiplicative distance-locating set of G is the external multiplicative location number \(loc_{e}^{*}(G)\). Further, we find the external multiplicative location number of some well-known classes of connected graphs. Also, we introduce the new concept “Magic Locating Set” of a graph G and we determine the magic location number of some well-known classes of connected graphs.
For a set \(S\) of vertices in a connected graph \(G,\) the multiplicative distance of a vertex \(v\) in \(V\) with respect to \(S\) is defined by \[d_{S}^{*}(v) = \prod _{x \in S, x \neq v} d(v,x).\] If \(S = \{v\}\), then we assign \(0\) to \(d_S^*(v)\). If \(d_{S}^{*}(u) \neq d_{S}^{*}(v)\) for each pair \(u,v\) of distinct vertices of \(G,\) then \(S\) is called a multiplicative distance-locating set of \(G\). A minimum multiplicative distance-locating set of \(G\) is a multiplicative distance-locating set of minimum cardinality and this cardinality is the multiplicative distance-location number \(loc_{d}^{*}(G)\). The following results describe a relationship between \(loc_{d}^{*}(G)\) and \(loc(G)\).
Proposition 1. Every multiplicative distance-locating set of a graph is a locating set.
Proof. On the contrary, assume that the multiplicative distance-locating set \(S = \{w_1,w_2,\cdots,w_k\}\) is not a locating set. Then there exists two distinct vertices \(u,v \in V(G)\) such that \(C_S(u) = C_S(v)\). That is, \((d(u,w_1), d(u,w_2),\) \(\cdots,d(u,w_k)) = (d(v,w_1, d(v,w_2),\cdots, d(v,w_k))\). Then \(\prod_{w_i \in S} d(u,w_i) = \prod_{w_i \in S} d(v,w_i)\). Therefore \(d_S^*(u) = d_S^*(v)\), which is a contradiction to the fact that \(S\) is a multiplicative distance-locating set of \(G\). ◻
Corollary 1. If \(G\) is a connected graph such that \(loc_{d}^{*}(G)\) exists, then \(loc(G) \leq loc_{d}^{*}(G)\).
The following Theorem 1 shows that the path \(P_{n}\) is the only connected graph of order \(n\) with \(loc_{d}^{*}(G)=1\).
Theorem 1. Let \(G\) be a connected graph of order \(n \geq 2\). Then \(loc_{d}^{*}(G)=1\) if and only if \(G=P_{n}\).
Proof. Let \(G=P_{n}: v_{1}, v_{2},… , v_{n}\) be a path on \(n\) vertices. Since \(d(v_{i}, v_{1})=i-1\) for \(1 \leq i \leq n\), \(\lbrace v_{1} \rbrace\) is a minimum multiplicative distance-locating set of \(P_{n}\). Therefore, \(loc_{d}^{*}(G)=1\). Conversely, suppose \(loc_{d}^{*}(G)=1\). Let \(S=\lbrace w \rbrace\) be a minimum multiplicative distance-locating set for G. Then \(d_{S}^{*}(v)=d(v,w)\) for each vertex \(v\) of G is a non-negative integer less than \(n\). Since \(d_{S}^{*}(v)\), \(v \in V(G)\) are distinct, there exists a vertex \(u\) in G such that \(d(u,w)=n-1\). Consequently the diameter of G is \(n-1\). Hence \(G=P_{n}\). ◻
Proposition 2. No multiplicative distance-locating set in a connected graph G consists of two vertices of \(G.\)
Proof. Suppose \(S= \lbrace u,v \rbrace\) is a multiplicative distance-locating set for \(G.\) Then \(d_{S}^{*}(u)=d(u,v)=d_{S}^{*}(v)\), which is a contradiction. ◻
In the case of distance-locating set of a graph \(G,\) there is no distance-locating set with exactly three vertices of \(G\) for any graph \(G.\) However, multiplicative distance-locating set of a graph may consists of three vertices of \(G.\) For example, for the following graph \(G\),
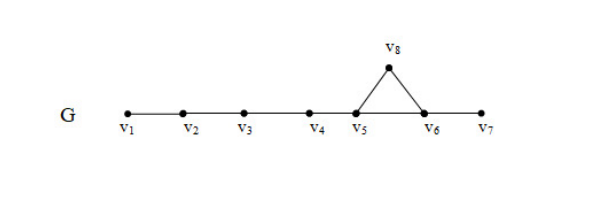
\(S = \{v_1,v_2,v_7\}\) is a minimum multiplicative distance locating set and hence \(loc_d^*(G) = 3\). In order to give examples of other graphs G for which \(loc_{d}^{*}(G)\) does not exist, we now make some observations. In a graph \(G\), the nieghbourhood of a vertex \(v\) in \(G\) is the set \(N(v)\) consisting of all vertices which are adjacent to \(v\). The closed neighbourhood is \(N[v] = N(v) \cup \{v\}\)
Proposition 3. If \(u\) and \(v\) are distinct vertices of a connected graph G such that either \(N(u) = N(v)\) or \(N[u] = N[v]\), then every multiplicative distance-locating set of G contains exactly one of \(u\) and \(v\).
Proof. Let \(u,v \in G\)
and \(u \neq v\). Suppose S is a
multiplicative distance-locating set for \(G.\)
Case 1. Suppose \(N(u) =
N(v)\).
If \(u,v \in S\), then \(u\) and \(v\) are having the same distance apart from
each vertex of G. Therefore,\(d_{S}^{*}(u)=d_{S}^{*}(v)\) , which is a
contradiction to the fact that S is a multiplicative distance-locating
set. Similar proof holds when \(u,v \notin
S\).
Case 2. Suppose \(N[u] =
N[v]\).
The proof is similar to the case 1. ◻
Corollary 2. If \(G\) is a connected graph containing three distinct vertices \(u\), \(v\) and \(w\) such that either \(N(u) = N(v) = N(w)\) or \(N[u] = N[v] = N[w]\), then \(loc_{d}^{*}(G)\) does not exist.
In a graph \(G\), if \(deg v = 1\), then \(v\) is called an end-vertex.
Corollary 3. If \(G\) is a connected graph such that \(loc_{d}^{*}(G)\) exists, then every vertex of G is adjacent to at most two end-vertices.
The converse of Corollary 3 does not necessarily hold. For example, in the following graph \(G\) every vertex of \(G\) is adjacent to at most two end vertices, but \(loc_{d}^{*}(G)\) does not exist.
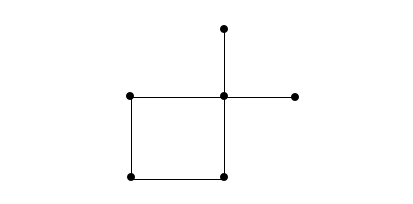
We have verified this fact by considering all possible cases.
Corollary 4. If \(n \geq 3\), then \(loc_{d}^{*}(K_{n})\) and \(loc_{d}^{*}(K_{1,n})\) do not exist.
Proof. Immediately follows from Corollaries 2 and 3. ◻
Next we show that the path \(P_{3}\) is the only connected graph \(G\) of diameter 2 such that \(loc_{d}^{*}(G)\) exists.
Theorem 2. If \(G\) is a connected graph of diameter 2 for which \(loc_{d}^{*}(G)\) exists, then \(G = P_{3}\).
Proof. Let \(S\) be a minimum multiplicative distance-locating set for G and let \(\vert S \vert =k\). Suppose \(k = 1\). Since diameter of G is 2 and \(\vert S \vert =1\), by Theorem 1, \(G = P_{3}\). By Proposition 2, \(k \neq 2\). Suppose \(k = 3\). Let \(S = \lbrace u,v,w \rbrace\). Then \(d_{S}^{*}(u) = d(u,v) \times d(u,w)\), \(d_{S}^{*}(v) = d(u,v) \times d(v,w)\) and \(d_{S}^{*}(w) = d(u,w) \times d(v,w)\). Since \(S\) is a multiplicative distance-locating set, \(d_{S}^{*}(u) \neq d_{S}^{*}(v)\) and hence \(d(u,w) \neq d(v,w)\). Since diameter of \(G\) is 2, without loss of generality, we may assume that \(d(u,w)=1\), \(d(v,w)=2\). Then \(d_{S}^{*}(u)=d(u,v)\), \(d_{S}^{*}(v)=2d(u,v)\) and \(d_{S}^{*}(w)=2\) Since \(G\) has diameter 2, either \(d(u,v)=1\) or \(d(u,v)=2\). If \(d(u,v)=1\), then \(d_{S}^{*}(v)=2\). Therefore, \(d_{S}^{*}(v)=d_{S}^{*}(w)\), which is a contradiction. If \(d(u,v)=2\), then \(d_{S}^{*}(u)=2\). Therefore, \(d_{S}^{*}(u)=d_{S}^{*}(w)\), which is a contradiction. Thus, \(S\) is not a multiplicative distance-locating set for \(G.\) Hence assume that \(k \geq 4\). Let \(H = \langle S \rangle\) be the subgraph of \(G\) induced by \(S.\) Since \(G\) has diameter 2, for each \(v \in V(H)=S\), it follows that \(d_{S}^{*}(v)\) is uniquely determined by \(k-deg_H(v)\) vertices of \(S\) since \(d_H(u,v) = 1\) for the vertices \(u\) which are adjacent to \(v\). Since \(H\) is nontrivial and diameter of \(G\) is \(2\), \(H\) contains at least two vertices \(x\) and \(y\) such that \(deg_{H}(x)=deg_{H}(y)\). Suppose \(deg_{H}(x)=deg_{H}(y)=a\). Since \(G\) has diameter 2, \(d_{S}^{*}(x)=2^{k-a-1}\) and \(d_{S}^{*}(y)=2^{k-a-1}\). Hence \(S\) is not a multiplicative distance-locating set for \(k \geq 4\). ◻
A graph \(G\) is a \(k\)-partite graph if \(V(G)\) can be partitioned into \(k\) subsets \(V_1,V_2,\cdots, V_k\) such that \(uv\) is an edge of \(G\) if \(u\) and \(v\) are belong to different partite sets. If, in addition, every two vertices in different partite sets are joined by an edge, then \(G\) is a complete \(k\)-partite graph. If \(|V_i| = n_i\) for \(1 \leq i \leq k\), then we denote this complete \(k\)-partite graph by \(K_{n_1,n_2,\cdots,n_k}\). The complete \(k\)-partite graphs are aslo referred to as complete multiplartite graphs.
The following result provides another well-known class of graphs for which \(loc_{d}^{*}(G)\) does not exist.
Corollary 5. If \(G\) is a complete multipartite graph of order at least 4 that is not complete, then \(loc_{d}^{*}(G)\) does not exist.
Now, we define a family of connected graph \(P_{n} \divideontimes C_{m}\) such that \(loc_{d}^{*}(G)\) exists.
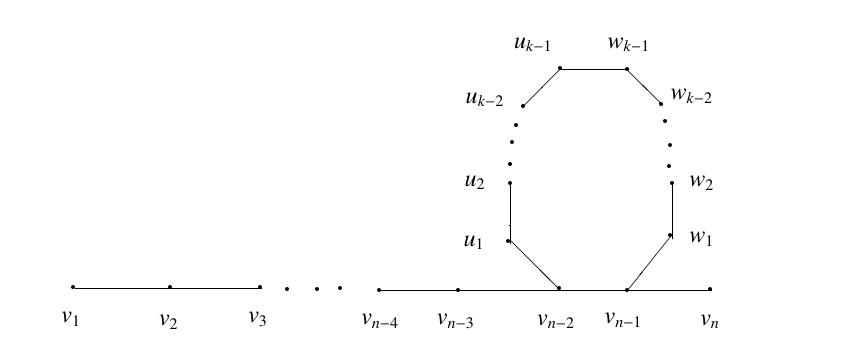
Definition 1. Let \(P_{n}\) be a path on \(n\) vertices and let \(C_{m}\) be a cycle on \(m\) vertices. The graph \(P_{n} \divideontimes C_{m}\) is obtained by identifying any two consecutive vertices of \(C_{m}\) with the \((n-2)^{th}\) and \((n-1)^{th}\) vertices of \(P_{n}\) as shown in the following Figure 1,
Theorem 3. For \(n > 4\), \(m \geq 3\), \(loc_{d}^{*}(P_{n} \divideontimes C_{m}) \leq 4\).
Proof. Case 1. Suppose \(m\) is even, \(m = 2k\). Let \(\lbrace v_{1},v_{2}, \ldots ,v_{n},u_{1},u_{2}, \ldots ,u_{k-1},w_{1},w_{2}, \ldots w_{k-1} \rbrace\) be the vertices of \(P_{n} \divideontimes C_{m}\) as shown in the above Figure 1.
Let \(S= \lbrace v_{n},v_{n-2},v_{n-3},v_{n-4} \rbrace\) be a subset of the vertex set of \(P_{n} \divideontimes C_{m}\). Then \[\begin{aligned} d_{S}^{*}(v_{i})&=d(v_{i},v_{n}) \times d(v_{i},v_{n-2}) \times d(v_{i},v_{n-3}) \times d(v_{i},v_{n-4} ),\; \text{for}\;1 \leq i \leq n-5\\ &=(n-i)(n-i-2)(n-i-3)(n-i-4).\\ d_{S}^{*}(u_{i})&=d(u_{i},v_{n}) \times d(u_{i},v_{n-2}) \times d(u_{i},v_{n-3}) \times d(u_{i},v_{n-4} ),\; \text{for}\; 1 \leq i \leq k-1\\ &=i(i+1)(i+2)^{2}.\\ d_{S}^{*}(w_{i})&=d(w_{i},v_{n}) \times d(w_{i},v_{n-2}) \times d(w_{i},v_{n-3}) \times d(w_{i},v_{n-4} ),\; \text{for} \;1 \leq i \leq k-1\\ &=(i+1)^{2}(i+2)(i+3).\\ d_{S}^{*}(v_{n-4})&=d(v_{n-4},v_{n}) \times d(v_{n-4},v_{n-2}) \times d(v_{n-4},v_{n-3}) =4 \times 2 \times 1=8.\\ d_{S}^{*}(v_{n-3})&=d(v_{n-3},v_{n}) \times d(v_{n-3},v_{n-2}) \times d(v_{n-3},v_{n-4}) =3 \times 1 \times 1=3.\\ d_{S}^{*}(v_{n-2})&=d(v_{n-2},v_{n}) \times d(v_{n-2},v_{n-3}) \times d(v_{n-2},v_{n-4}) =2 \times 1 \times 2=4.\\ d_{S}^{*}(v_{n-1})&=d(v_{n-1},v_{n}) \times d(v_{n-1},v_{n-2}) \times d(v_{n-1},v_{n-3}) \times d(v_{n-1},v_{n-4}) =1 \times 1 \times 2 \times 3=6.\\ d_{S}^{*}(v_{n})&=d(v_{n},v_{n-2}) \times d(v_{n},v_{n-3}) \times d(v_{n},v_{n-4}) =2 \times 3 \times 4=24. \end{aligned}\] Certainly, \(d_{S}^{*}(v_{i}) \neq d_{S}^{*}(v_{j})\) for each pair \(i\), \(j\) of distinct integers \(1 \leq i, j \leq n-5\) and \(d_{S}^{*}(u_{i}) \neq d_{S}^{*}(u_{j})\) and \(d_{S}^{*}(w_{i}) \neq d_{S}^{*}(w_{j})\) for each pair \(i,j\) of distinct integers \(1 \leq i,j \leq k-1\). Since \(\min\{ d_{S}^{*}(v_{i}):1 \leq i \leq n-5, n > 5 \} =30\) and \(\max \{ d_{S}^{*}(v_{i}):n-4 \leq i \leq n \} =24\), \(d_{S}^{*}(v_{i}) \neq d_{S}^{*}(v_{j})\) for each pair \(i\), \(j\) of distinct integers \(1 \leq i,j \leq n\). The factors of \(d_{S}^{*}(v_{i})\), \(d_{S}^{*}(u_{i})\) and \(d_{S}^{*}(w_{i})\) are: \(d_{S}^{*}(v_{i})=x(x+1)(x+2)(x+4)\) where \(x=n-i-4\), \(d_{S}^{*}(u_{i})=y(y+1)(y+2)^{2}\) where \(y=i\) and \(d_{S}^{*}(w_{i})=z^{2}(z+1)(z+2)\) where \(z=i+1\).
We claim that \(d_{S}^{*}(v_{i}) \neq d_{S}^{*}(u_{j})\) for every two integers \(1 \leq i \leq n\), \(1 \leq j \leq k-1\). First we discuss when \(i\) varies from 1 to \(n-5\) and \(j\) varies from 1 to \(k-1\). If \(y < x-2\) or \(y > x+4\),then \(d_{S}^{*}(v_{i}) \neq d_{S}^{*}(u_{j})\). We consider the following cases:
Suppose \(d_{S}^{*}(v_{i})=d_{S}^{*}(u_{j})\). Then \(x(x+1)(x+2)(x+4)=y(y+1)(y+2)^{2}\)
(a) Suppose \(y = x-2\). Then \(x(x+1)(x+2)(x+4)=(x-2)(x-1)x^{2}\). This implies \((x+1)(x+2)(x+4)=x(x-1)(x-2)\), which is a contradiction.
(b) Suppose \(y = x-1\). Then \(x(x+1)(x+2)(x+4)=(x-1)x(x+1)^{2}\). This implies \(x^{2}+6x+8=x^{2}-1\). Therefore, \(x= -3/2\), which is a contradiction to the fact that \(x\) is a positive integer.
(c) Suppose \(y = x\). Then \(x(x+1)(x+2)(x+4)=x(x+1)(x+2)^{2}\). This implies that 4=2, which is a contradiction.
(d) Suppose \(y = x+1\). Then \(x(x+1)(x+2)(x+4)=(x+1)(x+2)(x+3)^{2}\). Hence \(x= -9/2\), which is a contradiction.
(e) Suppose \(y = x+2\). Then \(x(x+1)(x+2)(x+4)=(x+2)(x+3)(x+4)^{2}\). Thus, \(x = -2\), which is a contradiction.
(f) Suppose \(y = x+3\). Then \(x(x+1)(x+2)(x+4)=(x+3)(x+4)(x+5)^{2}\). This implies \(10x^{2}+53x+75=0\). Since \(b^{2}-4ac=-191<0\), it has no real solution, which is a contradiction.
(g) Suppose \(y = x+4\). Then \(x(x+1)(x+2)(x+4)=(x+4)(x+5)(x+6)^{2}\). This implies \(14x^{2}+94x+180=0\). Since \(b^{2}-4ac=-1244<0\), it has no real solution, which is a contradiction.
Thus, \(d_{S}^{*}(v_{i}) \neq d_{S}^{*}(u_{j})\) for every two integers \(1 \leq i \leq n-5\), \(1 \leq j \leq k-1\). Since \(\max \{ d_{S}^{*}(v_{i}) : n-4 \leq i \leq n \} = 24\) and \(\lbrace d_{S}^{*}(u_{j}): 1 \leq j \leq k-1 \rbrace = \lbrace 18,96, \ldots \rbrace\), \(d_{S}^{*}(v_{i}) \neq d_{S}^{*}(u_{j})\) for every two integers \(1 \leq i \leq n\), \(1 \leq j \leq k-1\). Next we claim that \(d_{S}^{*}(v_{i}) \neq d_{S}^{*}(w_{j})\) for every two integers \(1 \leq i \leq n\), \(1 \leq j \leq k-1\). First we discuss when \(i\) varies from 1 to \(n-5\) and \(j\) varies from 1 to \(k-1\). If \(z < x-2\) or \(z > x+4\), then \(x(x+1)(x+2)(x+4) \neq z^{2}(z+1)(z+2)\). Therefore, \(d_{S}^{*}(v_{i}) \neq d_{S}^{*}(w_{j})\).
Suppose \(d_{S}^{*}(v_{i})=d_{S}^{*}(w_{j})\). Then \(x(x+1)(x+2)(x+4)=z^{2}(z+1)(z+2)\). If \(x-2 \leq z \leq x+4\), then the proof is similar to the above case. Thus, \(d_{S}^{*}(v_{i}) \neq d_{S}^{*}(w_{j})\) for every two integers \(1 \leq i \leq n-5\), \(1 \leq j \leq k-1\). Since \(\max \{ d_{S}^{*}(v_{i}) : n-4 \leq i \leq n \} = 24\) and \(min \lbrace d_{S}^{*}(w_{j}):1 \leq j \leq k-1 \rbrace =48\), \(d_{S}^{*}(v_{i}) \neq d_{S}^{*}(w_{j})\) for every two integers \(1 \leq i \leq n\), \(1 \leq j \leq k-1\). Next we claim that \(d_{S}^{*}(u_{i}) \neq d_{S}^{*}(w_{j})\) for every two integers \(1 \leq i,j \leq k-1\). If \(z < y-3\) or \(z > y+2\), then \(d_{S}^{*}(u_{i}) \neq d_{S}^{*}(w_{j})\).
Suppose \(d_{S}^{*}(u_{i})=d_{S}^{*}(w_{j})\). Then \(y(y+1)(y+2)^{2}=z^{2}(z+1)(z+2)\). If \(y-3 \leq z \leq y+2\), then the proof is similar to the first case. Thus, \(d_{S}^{*}(u_{i}) \neq d_{S}^{*}(w_{j})\) for every two integers \(1 \leq i,j \leq k-1\). From the above three cases, \(d_{S}^{*}(u) \neq d_{S}^{*}(v)\) for any two pair of distinct vertices \(u,v\) of \(P_{n} \divideontimes C_{m}\). Therefore, S is a multiplicative distance-locating set for \(P_{n} \divideontimes C_{m}\). Hence, \(loc_d^{*}(P_{n} \divideontimes C_{m}) \leq 4\) when \(m\) is even.
Case 2. Suppose \(m\) is odd, \(m=2k+1\).
Let \(\lbrace v_{1},v_{2}, \ldots ,v_{n},u_{1},u_{2}, \ldots ,u_{k-1},w_{1},w_{2}, \ldots ,w_{k-1},w_{k} \rbrace\) be the vertices of \(P_{n} \divideontimes C_{m}\) as shown in the Figure 2.
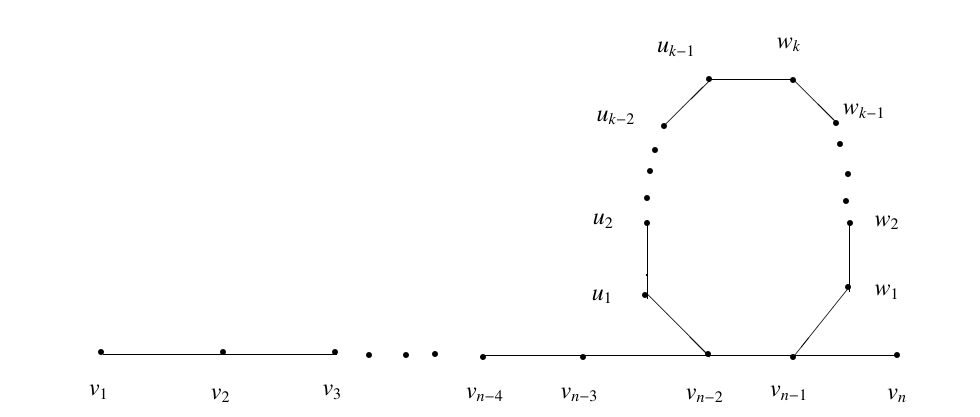
Let \(S= \lbrace v_{n},v_{n-2},v_{n-3},v_{n-4} \rbrace\) be a subset of the vertex set of \(P_{n} \divideontimes C_{m}\). Then \[\begin{aligned} d_{S}^{*}(v_{i})&=d(v_{i},v_{n}) \times d(v_{i},v_{n-2}) \times d(v_{i},v_{n-3}) \times (v_{i},v_{n-4}),\; \text{for}\;1 \leq i \leq n-5\\ &=(n-i)(n-i-2)(n-i-3)(n-i-4).\\ d_{S}^{*}(u_{i})&=d(u_{i},v_{n}) \times d(u_{i},v_{n-2}) \times d(u_{i},v_{n-3}) \times d(u_{i},v_{n-4} ),\; \text{for}\; 1 \leq i \leq k-1\\ &=i(i+1)(i+2)^{2}.\\ d_{S}^{*}(w_{i})&=d(w_{i},v_{n}) \times d(w_{i},v_{n-2}) \times d(w_{i},v_{n-3}) \times d(w_{i},v_{n-4} ),\; \text{for}\; 1 \leq i \leq k-1\\ &=(i+1)^{2}(i+2)(i+3).\\ d_{S}^{*}(w_{k})&=d(w_{i},v_{n}) \times d(w_{i},v_{n-2}) \times d(w_{i},v_{n-3}) \times d(w_{i},v_{n-4}) =k(k+1)^{2}(k+2).\\ d_{S}^{*}(v_{n-4})&=d(v_{n-4},v_{n}) \times d(v_{n-4},v_{n-2}) \times d(v_{n-4},v_{n-3}) =4 \times 2 \times 1=8.\\ d_{S}^{*}(v_{n-3})&=d(v_{n-3},v_{n}) \times d(v_{n-3},v_{n-2}) \times d(v_{n-3},v_{n-4}) =3 \times 1 \times 1=3.\\ d_{S}^{*}(v_{n-2})&=d(v_{n-2},v_{n}) \times d(v_{n-2},v_{n-3}) \times d(v_{n-2},v_{n-4}) =2 \times 1 \times 2=4.\\ d_{S}^{*}(v_{n-1})&=d(v_{n-1},v_{n}) \times d(v_{n-1},v_{n-2}) \times d(v_{n-1},v_{n-3}) \times d(v_{n-1},v_{n-4}) =1 \times 1 \times 2 \times 3=6.\\ d_{S}^{*}(v_{n})&=d(v_{n},v_{n-2}) \times d(v_{n},v_{n-3}) \times d(v_{n},v_{n-4}) =2 \times 3 \times 4=24. \end{aligned}\] By case 1, \(d_{S}^{*}(u) \neq d_{S}^{*}(v)\) for any two pair of distinct vertices \(u,v\) of \(P_{n} \divideontimes C_{m}\). Therefore, \(S\) is a multiplicative distance-locating set for \(P_{n} \divideontimes C_{m}\). Thus, \(loc_{d}^{*}(P_{n} \divideontimes C_{m}) \leq 4\) for \(m\) is odd. Hence \(loc_{d}^{*}(P_{n} \divideontimes C_{m}) \leq 4\). ◻
Corollary 6. The multiplicative distance location number of \(P_{n} \divideontimes C_{m}\) is either 3 or 4.
Proof. Since \(P_{n} \divideontimes C_{m}\) is not a path, the proof follows from Theorem 1 and Proposition 2 ◻
Now we establish a lower bound for the multiplicative distance-location number of a connected graph in terms of its order and diameter. Let \(G\) be a connected graph of order \(n\). For a subset \(S\) of \(V(G)\), define
\(D_{min}^{*}(S) = \min \{ d_{S}^{*}(v) : v
\in V(G) \},\)
\(D_{max}^{*}(S) = \max \{ d_{S}^{*}(v) : v
\in V(G) \}.\)
Observation 4. Let \(G\) be a connected graph of order \(n \geq 2\) and diameter \(d \geq 2\). If \(S\) is a multiplicative distance-locating set for G with \(\vert S \vert =k\), then \(n-1 \leq D_{max}^{*}(S)-D_{min}^{*}(S) \leq d^{k}\).
Proof. Suppose \(S\) is a multiplicative distance-locating set for \(G.\) Then the numbers \(d_{S}^{*}(v),v \in V(G)\) are distinct. The set \(\lbrace d_{S}^{*}(v):v \in V(G) \rbrace\) contains \(n\) distinct numbers. Therefore, \[\label{a1} D_{max}^{*}(S)-D_{min}^{*}(S) \geq n-1\ldots.\tag{1}\] Since \(S\) is a multiplicative distance-locating set, \(diam G=d\) and \(\vert S \vert =k\), \(D_{min}^{*}(S) \geq 0\) and \(D_{max}^{*}(S) \leq d^{k}\). Thus, \[\label{a2} D_{max}^{*}(S)-D_{min}^{*}(S) \leq d^{k} \ldots.\tag{2}\] Combining (1) and (2), we get, \(n-1 \leq D_{max}^{*}(S)-D_{min}^{*}(S) \leq d^{k}\). ◻
Observation 5. If \(G\) is a connected graph of order n\(\geq\)2 and diameter d\(\geq\)2 for which \(loc_{d}^{*}(G)\) exists, then \(loc_{d}^{*}(G) \geq \left\lceil \frac {log(n-1)}{logd} \right\rceil\).
Proof. Let \(S\) be a multiplicative distance-locating set for G and let \(\vert S \vert = k\). By Observation 4, \(n-1 \leq D_{max}^{*}(S)-D_{min}^{*}(S) \leq d^{k}\). Therefore, \(n-1 \leq d^{k}\). Thus \(loc_{d}^{*}(G) \geq \left\lceil \frac {log(n-1}{logd} \right\rceil\). ◻
We shown in Section 2, for many graphs G, \(loc_{d}^{*}(G)\) does not exist. However, there is a closely related parameter that is defined for every graph. For a set \(S\) of vertices in a connected graph \(G,\) the multiplicative distance of a vertex \(v\) with respect to \(S\) is defined by \[d_{S}^{*}(v) = \prod\limits_{x \in S, x \neq v} d(v,x).\] If \(d_{S}^{*}(u) \neq d_{S}^{*}(v)\) for each pair \(u,v\) of distinct vertices of \(G-S\), then \(S\) is called an external multiplicative distance-locating set of \(G.\) The cardinality of a minimum external multiplicative distance-locating set of \(G\) is called the external multiplicative location number of \(G.\) It is denoted by \(loc_{e}^{*}(G)\).
Proposition 4. Every external multiplicative distance-locating set is a locating set.
Proof. Let \(S\) be an external multiplicative distance-locating set for \(G.\) Then the numbers \(d_{S}^{*}(v), v \in V(G)-S\) are distinct. Let \(u,v\) be any two distinct vertices of \(G.\)
If \(u,v \in S\), then \(C_{S}(u) \neq C_{S}(v)\).
Suppose \(u,v \in V(G)-S\). If \(C_{S}(u)=C_{S}(v)\), then \(d_{S}^{*}(u)=d_{S}^{*}(v)\), which is a contradiction. Therefore, \(C_{S}(u) \neq C_{S}(v)\).
Suppose \(u \in S\) and \(v \in V(G)-S\). Then the locating code of the vertex \(u\) with respect to S, \(C_{S}(u)\) contains the zero vector. Since \(v \in V(G)-S\), \(C_{S}(v)\) does not contain the zero vector. Therefore, \(C_{S}(u) \neq C_{S}(v)\). Thus, from the above three cases, \(S\) is a locating set.
◻
Since the vertex set of \(G\) is an external multiplicative distance-locating set, \(loc_{e}^{*}(G)\) exists for every graph \(G.\) Since every multiplicative distance-locating set is an external multiplicative distance-locating set and since every external multiplicative distance-locating set is a locating set, we have the following.
Theorem 6. For every connected graph \(G,\) \(loc(G) \leq loc_{e}^{*}(G)\). Moreover, if \(G\) is a connected graph G of order \(n \geq 2\) for which \(loc_{d}^{*}(G)\) exists, then \(1 \leq loc(G) \leq loc_{e}^{*}(G) \leq loc_{d}^{*}(G)\).
In Theorem 1 the path \(P_{n}\) of order \(n \geq 2\) is the only connected graph with \(loc_{d}^{*}(G)=1\). It is straight forward to show that the path \(P_{n}\) is also the only connected graph of order \(n\) with \(loc_{e}^{*}(G)=1\).
Theorem 7. Let \(G\) be a connected graph G of order \(n \geq 2\). Then \(loc_{e}^{*}(G)=1\) if and only if \(G=P_{n}\).
It is shown that the complete graph \(K_{n}\) of order \(n \geq 2\) is the only connected graph of order \(n\) with \(loc(G)=n-1\), while \(loc_{d}^{*}(K_{n})\) does not exist by Corollary 6. Certainly \(loc_{e}^{*}(K_{n})=n-1\) for all n\(\geq\)2 as well. On the other hand, \(K_{n}\) is not the only connected graph of order \(n\) with external multiplicative location number \(n-1\).
Theorem 8. If \(G\) is an \(r-\)regular connected graph of order \(n\) and diameter \(2,\) then \(loc_{e}^{*}(G)=n-1\).
Proof. Suppose \(G\) is an \(r-\)regular connected graph of order \(n\) and diameter \(2.\) Because of Theorem 7, it suffices to show that for each integer \(k\) with \(2 \leq k \leq n-2\), there is no external multiplicative distance-locating set of \(G\) consisting of \(k\) vertices. Assume to the contrary, that there is an external multiplicative distance-locating set of order \(k\) in \(G.\) Let \(S= \lbrace w_{1},w_{2}, \ldots ,w_{k} \rbrace\) be an external multiplicative distance-locating set for \(G,\) where \(2 \leq k \leq n-2\). Let \(V(G)-S= \lbrace v_{1},v_{2}, \ldots ,v_{n-k} \rbrace\). For each \(v_{i} \in V(G)-S\), where \(1 \leq i \leq n-k\), let \(s_{i}\) be the number of vertices of \(S\) that are adjacent to \(v_{i}\), and let \(t_{i}\) be the number of vertices of \(S\) that are not adjacent to \(v_{i}\). Thus, \(s_{i} + t_{i} = k\), \(0 \leq s_{i} \leq \min \{ r, k \}\), and \(0 \leq t_{i} \leq \min \{ n-1-r, k \}\), for all \(i\) with \(1 \leq i \leq n-k\). Since \(diam G=2\), \(d_{S}^{*}(v_{i})=2t_{i}\) for all \(i\) with \(1 \leq i \leq n-k\). Since \(S\) is an external multiplicative distance-locating set for \(G\), all \(n-k\) numbers \(d_{S}^{*}(v_{i})\) are distinct. Therefore, \(t_{i} \neq t_{j}\). Since \(s_{i}+t_{i}=k\), all \(n-k\) numbers \(s_{i}\) are distinct and all \(n-k\) numbers \(t_{i}\) are distinct. Let \(H= \langle V(G)-S \rangle\) be the subgraph induced by \(V(G)-S\). Then \(deg_{H}(v_{i})=r-s_{i}\) for all \(i\) with \(1 \leq i \leq n-k\). Since the \(n-k\) numbers \(s_{i}\) are distinct, \(deg_{H}(v_{i})\) are distinct, \(1 \leq i \leq n-k\). Therefore, no two vertices of \(H\) have the same degree, which is impossible. Hence \(loc_{e}^{*}(G)=n-1\). ◻
As an immediate consequence of Theorem 8 we obtain the external location number of the Petersen graph.
Corollary 7. The Petersen graph has external location number 9.
Next we determine the external location number of the complete bipartite graphs.
Theorem 9. For integers \(r,s \geq 1\) with \(r+s \geq 4\),
\[loc_{e}^{*}(K_{r,s})= \Bigg \lbrace \begin{array}{cc} r+s-2 & \text{if}\; r \neq s, \\ r+s-1 & \text{if}\; r=s. \end{array}\]
Proof. Assume that \(r \leq s\). Let \(V_{1}= \lbrace u_{1},u_{2}, \ldots ,u_{r} \rbrace\) and \(V_{2}= \lbrace v_{1},v_{2}, \ldots ,v_{s} \rbrace\) be the partite sets of \(K_{r,s}\). If \(r=s,\) then by Theorem 8 \(loc_{e}^{*}(K_{r,s})=r+s-1\). So we may assume that \(r<s\). Every external multiplicative distance-locating set of \(K_{r,s}\) contains at least \(r-1\) vertices from \(V_{1}\) and at least \(s-1\) vertices from \(V_{2}\). Thus, \(loc_{e}^{*}(K_{r,s}) \geq r+s-2\). Let \(W=(V_{1}- \lbrace u_{r} \rbrace ) \cup (V_{2}- \lbrace v_{s} \rbrace )\). Then \(d_{W}^{*}(u_{r})=2^{(r-1)}\) and \(d_{W}^{*}(v_{s})=2^{(s-1)}\). Suppose \(d_{W}^{*}(u_{r})=d_{W}^{*}(v_{s})\). Then \(r=s,\) which is a contradiction. Therefore, \(d_{W}^{*}(u_{r}) \neq d_{W}^{*}(v_{s})\). Thus, \(W\) is an external multiplicative distance-locating set for \(K_{r,s}\). Since \(loc_{e}^{*}(K_{r,s}) \geq r+s-2\), \(W\) is the minimum external multiplicative distance-locating set for \(K_{r,s}\). Therefore, \(loc_{e}^{*}(K_{r,s} )=r+s-2\). ◻
Let \(G\) be a connected graph with vertex set \(V(G).\) Let \(S\) be a subset of \(V(G).\) We define the distance of a vertex \(v\) with respect to \(S\) by \[d_{S}^{*}(v) = \sum _{x \in S, x \neq v} d(v,x).\] If \(d_{S}(u)=d_{S}(v)\) for each pair \(u,v\) of distinct vertices of \(G-S\), then \(S\) is called a magic locating set of \(G.\) The cardinality of a minimum magic locating set of \(G\) is called the magic location number of \(G.\) It is denoted by \(loc_{M}(G)\). Every distance-locating set is not a magic locating set and every external distance-locating set is not a magic locating set.
The following Theorem 10 characterizes graph \(G\) with \(loc_{M}(G)=1.\)
Theorem 10. Let \(G\) be a connected graph of order \(n \geq 2\). Then \(\text{loc}_{M}(G)=1\) if and only if \(G\) contains a vertex of degree \(n-1\).
Proof. Suppose \(\text{loc}_{M}(G)=1\). Let \(S= \lbrace w \rbrace\) be a minimum magic locating set for \(G\). Then \(d(u,w)=d(v,w)\) for each pair \(u,v\) of distinct vertices of \(V(G)-S\). Assume that \(d(u,w)=l>1\) for some \(u \in V(G)-S\), where \(2 \leq l \leq n-1\). Then there exists a path \(P: u=u_{0},u_{1},u_{2}, \ldots, u_{l-1},u_{l}=w\) in \(G\). Therefore, \(d(u,w)=l\) and \(d(u_{l-1},w)=1\), which is a contradiction. Thus, \(d(u,w)=1\) for all \(u \in V(G)-S\). Hence, \(w\) is adjacent to all the vertices of \(G-S\). Therefore, \(\deg(w)=n-1\).
Conversely, assume that \(G\) contains a vertex of degree \(n-1\). Let \(w\) be a vertex of \(G\) such that \(\deg(w)=n-1\). Let \(S= \lbrace w \rbrace\). Then \(d_{S}(u)=1\) for all \(u \in V(G)-S\). Therefore, \(S\) is a minimum magic locating set for \(G\). Hence, \(\text{loc}_{M}(G)=1\). ◻
Corollary 8. The magic location number of the graphs \(K_{n},K_{1,n},W_{n},F_{n}\) is 1.
In Theorem 11 and Theorem 12 we determine the magic location number of an even cycle and the complete bipartite graphs.
Theorem 11. If \(C_{n}\) is an even cycle, then \(loc_{M}(C_{n})=2\).
Proof. Let \(C_{n}: v_{1},v_{2}, \ldots ,v_{k}, \ldots ,v_{2k}\) be an even cycle. Let \(S= \lbrace v_{k},v_{2k} \rbrace\) be a subset of \(V(C_{n})\). Then \(d_{S}(v_{i})=k\) for \(1 \leq i < k\) and \(d_{S}(v_{i})=k\) for \(k < i < 2k\). Hence \(S\) is a magic locating set for \(C_{n}\). Therefore, \(loc_{M}(C_{n}) \leq 2\). By Theorem 10 \(loc_{M}(C_{n})=2\). ◻
Theorem 12. For \(m,n \geq 2\), \(loc_{M}(K_{m,n})=2\).
Proof. Let \(G\) be a complete bipartite graph with vertex set \(V = V_{1} \cup V_{2}\) where \(V_{1}= \lbrace v_{1},v_{2}, \ldots ,v_{m} \rbrace\) and \(V_{2}= \lbrace u_{1},u_{2}, \ldots ,u_{n} \rbrace\). Let \(S= \lbrace v_{1},u_{1} \rbrace\) be a subset of \(V(G).\) Then \(d_{S}(v_{i})=3\) for \(1 \leq i \leq m\) and \(d_{S}(v_{i})=3\) for \(1 \leq i \leq n\). Hence \(S\) is a magic locating set for \(G.\) Therefore, \(loc_{M}(K_{m,n}) \leq 2\). By Theorem 10 \(loc_{M}(K_{m,n})=2\). ◻
Theorem 13 shows that the magic location number of a path \(P_{n}\) of order \(n \geq 2\) is less than or equal to \(n-2\).
Theorem 13. If \(P_{n}\) is a path on \(n\) vertices, then \(loc_{M}(P_{n}) \leq n-2\).
Proof. Let \(P_{n}: v_{1},v_{2}, \ldots ,v_{k}, \ldots ,v_{n}\) be a path on \(n\) vertices. Let \(S= \lbrace v_2,v_3, \ldots ,v_{n-1} \rbrace\) be a subset of the vertex set of \(P_{n}\). Then \(d_{S}(v_{1})=1+2+ \ldots +(n-2)= \dfrac{(n-2)(n-1)}{2}\) and \(d_{S}(v_{n})=(n-2)+(n-3)+ \ldots +2+1= \dfrac{(n-2)(n-1)}{2}\). Thus, \(S\) is a magic locating set for \(P_{n}\). Therefore, \(loc_{M}(P_{n}) \leq n-2\). ◻
We have defined some new concepts Multiplicative Distance-locating set, multiplicative distance location number, External Multiplicative location number and magic location number of graphs. We have discussed the existence or non-existence of these numbers for some well known classes of connected graphs. For future study we would like to propose the following open problems.
If \(G\) is a connected graph of diameter 3 for which \(loc_{d}^{*}(G)\) exists, then what about \(G?\)
For what values of \(n\) and \(m,\) \(loc_{d}^{*}(P_{n} \divideontimes C_{m})=4\).
For what values of \(n\) and \(m\), \(loc_{d}^{*}(P_{n} \divideontimes C_{m})=3\).
Does equality holds in Theorem 13. Based on our experience we believe that equality holds.
The authors would like to thank the two referees for their useful suggestions and comments.
1970-2025 CP (Manitoba, Canada) unless otherwise stated.