Let \(G=(V(G),E(G))\) be a graph with \(p\) vertices and \(q\) edges. A graph \(G\) of size \(q\) is said to be odd graceful if there exists an injection \(\lambda: V(G) \to {0,1,2,\ldots,2q-1}\) such that assigning each edge \(xy\) the label or weight \(|\lambda(x) – \lambda(y)|\) results in the set of edge labels being \({1,3,5,\ldots,2q-1}\). This concept was introduced in 1991 by Gananajothi. In this paper, we examine the odd graceful labeling of the \(W\)-tree, denoted as \(WT(n,k)\).
The graph considered in this study is finite, connected, and simple. The symbols \(V(G)\) and \(E(G)\) denote the vertex set and edge set of the graph \(G\), respectively. Additionally, \(p\) and \(q\) represent the number of vertices and edges in \(G\), respectively.
Definition 1. [1] Rosa defined a \(\beta\)-valuation of a graph \(G\) with \(q\) edges as an injection from the vertices of \(G\) to the set \(\{1,2,\ldots,q\}\). This valuation is such that when each edge \(xy\) is assigned the label \(|f(x) – f(y)|\), the resulting edge labels are distinct.
Definition 2. A graceful labeling \(f\) possesses the property that there exists an integer \(\lambda\) such that for each edge \(xy\), either \[f(x) \leq \lambda < f(y) \quad \text{or} \quad f(y) \leq \lambda < f(x).\] If \(f\) satisfies this condition, it is referred to as an \(\alpha\)-labeling.
Definition 3. [2] A graph \(G\) of size \(q\) is odd graceful if there exists an injection \(f\) from \(V(G)\) to \(\{0,1,2,\ldots,2q-1\}\). When each edge is assigned the label or weight \(|f(x) – f(y)|\), the resulting edge labels are \(\{1,3,\ldots,2q-1\}\).
Many types of labeling exist, such as magic, total, antimagic, harmonious, graceful, and odd-graceful. This work focuses on formulating odd-graceful labeling for some new graphs. The study of graceful graphs and graceful labeling was introduced by Rosa. \(\beta\)-valuations are functions that produce graceful labeling. The term ’graceful labeling’ became widely used after Golomb’s study of such labeling several years later [3]. Graceful labeling and \(\alpha\)-labeling are among the most popular classes of graph labeling [4]. It is known that not every graph is graceful. The Ringel-Kotzig conjecture [5], which posits that all trees are graceful, remains a well-known open problem.
The concept of odd graceful labeling was introduced by Gnanajothi [2]. Gnanajothi proposed the conjecture that all trees are odd-graceful and provided evidence for this conjecture in trees of order up to 10. Barrientos extended this conjecture to trees of order up to 12, proving that certain graphs are odd graceful, such as:
Subdividing each edge exactly once,
Every forest whose components are caterpillars,
Every tree with a diameter of at most five,
All disjoint unions of caterpillars.
Barrientos also conjectured that every bipartite graph is odd graceful.
Eldergill generalized Gnanajothi’s results on stars, demonstrating that a graph obtained by joining one endpoint from each of an odd number of paths of equal length is odd graceful [6]. Gao worked on the union of graphs and proved that unions of paths, stars, cycles \(C_m \cup P_n\), \(C_m \cup C_n\), and unions of cycles of order divisible by 4 are odd or both types of graceful.
S.K. Vaidya and L.Bijukumar investigated odd graceful labeling, focusing on combining two copies of \(C_n\) with a path \(P_n\) and two copies of a cycle \(C_n\) sharing a common edge, leading to various results.
Graph labeling has become an increasingly useful mathematical model for a wide range of applications, including ambiguities in X-Ray crystallography, communication network labeling, and circuit layout optimization. Most graph labeling problems involve three elements:
A set of numbers \(S\) from which the labels are chosen,
A rule assigning a value to each edge,
A condition that these values must satisfy.
Motivated by Gananajothi’s research, many other graphs have been studied since then, which are odd graceful, leading to many new results. However, there still exist many interesting open problems. Inspired by the research in [2, 7], we began investigating the odd graceful labeling of the \(W\)-tree and its disjoint union with other graph families.
In this work, we demonstrate that a subclass, namely the \(W\)-tree \(WT(n,k)\), admits odd graceful labeling. We also prove that the graph obtained by the disjoint union of a \(W\)-tree \(WT(n,k)\) with a path \(P_m\), a star \(K_{1,m}\), a bistar \(B_{m,l}\), and a ladder \(L_h\) are odd graceful graphs.
Firstly, we define some terms that will aid in understanding the subsequent work.
Definition 4. [4] A path is a tree \(P_n\) with vertex set \(V(P_n) = \{x_i : 1 \leq i \leq n\}\) and edge set \(E(G) = \{x_i x_{i+1} : 1 \leq i \leq n-1\}\).
Definition 5. [4] Let \(x_0\) define the central vertex of star \(S_n\), \(1 \leq n\) and let \(x_i\), \(1 \leq i\leq n\) be its leaves.
Definition 6. A bistar is a graph obtain by joining the central vertices of two star graphs.
Definition 7. [4] Let \(L_n= P_n \times P_2\) be a lader with \(V(L_n)=\{u_i v_i : 1 \leq i \leq n\}\) and \(E(L_n)=\{u_i u_i+1,v_i vi+1: 1 \leq i \leq n\} \cup \{u_i v_i : 1 \leq i \leq n\}\)
Definition 8. Let G be a graph with the set of vertices and edges as \[V(G)=\{(c_1,c_2,b,w,d) \cup (x^1,x^2,…,x^n) \cup(y^1,y^2,…y^n)\}\] \[E(G)= \{(c_1x^1,c_1x^2,…,c_1x^n) \cup (c_2y^1,c_2y^2,…,c_2y^n) \cup (c_1b,c_1w) \cup (c_2w,c_2d)\}\] we call it \(w\)-graph and it shall be denoted by W(n).
Definition 9. Suppose that we have k isomorphic copies of w-graphs W(n). A w-tree WT(n,k) is a tree obtain by taking a new vertex a and joining it with \(\{d_i: 1\leq i \leq k \}\), where \(n\geq2 \ \ and \ \ k\geq3\).
In this section, we will define the odd graceful labeling of W-tree.
Theorem 1. For \(k\geq 3\), \(G \cong WT(n,k)\) admits odd graceful labeling if \(n\geq 2k-2\).
Proof. Let G be a graph , we denote the vertex and edge set of G as follows:
\[\textbf{V(G)}=\{a\} \cup \{b_i: 1\leq i \leq n\} \cup \{W_i: 1\leq i \leq n\}\] \[U \{d_i:1\leq i \leq n\} \cup \{C_{i1}:1\leq i \leq n\} \cup \{C_{i2}:1\leq i \leq n\}\] \[\cup \{x^p_i:1\leq i \leq n, 1\leq p \leq k\} \cup \{y^p_i:1\leq i \leq n, 1\leq p \leq k \}\] \[\textbf{E(G)}=\{b_i c_{i1} : 1 \leq i \leq n \} \cup \{w_i c_{i1} : \leq i \leq n \}\] \[\cup \{w_i c_{i2} : 1 \leq i \leq n \} \cup \{d_i c_{i2} : 1\leq i \leq n \}\] \[\cup \{c_{i1} x^p_i : 1\leq i \leq n, 1\leq p \leq k\} \cup \{c_{i2} y^p_i : 1\leq i \leq n, 1\leq p \leq k\}\]
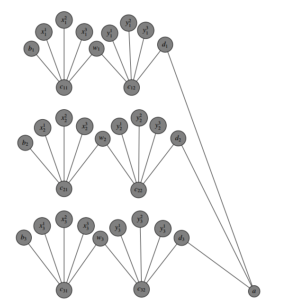
\[|V(G)|=(2n+3)k+2k+1\] and \[|E(G)|=(2n+5)k\] where \(v=|V(G)|\) and \(q=|E(G)|\).
Now, we define the labeling as follows \[\lambda: V(G)\longrightarrow
\{0,1,2,…,2q-1\}\] where \(1\leq
i\leq k\) \[\lambda (c_{i1})=
\begin{cases}2q-1-4(i-1)\end{cases}\] \[\lambda (c_{i2})=\begin{cases}
2q-3-4(i-1)\end{cases}\] \[\lambda
(b_i)=\begin{cases}(2n+3)(2i-2)\ \ \ for \ \ 1\leq i\leq k
\end{cases}\] \[\lambda
(w_i)=\begin{cases}(2n+2)(2i-1)+2(i-1)\ \ \ for \ \ 1\leq i\leq k
\end{cases}\] \[\lambda
(d_i)=\begin{cases}\lambda (w_i)+ 4i-2\ \ \ for \ \ 1\leq i\leq k
\end{cases}\] For \(1\leq i\leq
k\) and \(1\leq p\leq n\) \[\lambda (x_i^p)=
\begin{cases}2p+(4n+6)(i-1)\end{cases}\] \[\lambda (y_i^p)=\begin{cases}
\lambda (w_i)+2p& \text{if $1\leq p\leq 2i-2$} \\
\lambda (w_i)+2(p+1)& \text{if $2i-2\leq p\leq n$}
\end{cases}\] \[\lambda
(a)=\begin{cases}\lambda (d_k)+1\end{cases}\]
The odd graceful labeling of disjoint union of two isomorphic copies of w-tree will presented in this section.
Theorem 2. Let \(G\cong2WT(n,k)\) be an odd graceful graph for \(n\geq4k-2\).
Proof. Let \(G\) be a graph, we denote the vertex and edge set of \(G\) as follows:
\[\textbf{V(G)}=\{a\} \cup \{b_i: 1\leq i\leq k\} \cup \{w_i: 1\leq i \leq k\}\] \[\cup \{d_i: 1\leq i\leq k\} \cup \{c_{i1}: 1\leq i\leq k\} \cup \{c_{i2}: 1\leq i\leq k\}\] \[\cup \{x_{i}^p: 1\leq i\leq k, 1\leq p\leq n\} \cup \{y_{i}^p: 1\leq i\leq k, 1\leq p\leq n\}\] \[\cup \{a\} \cup \{b'_i: 1\leq i\leq k\} \cup \{w'_i: 1\leq i \leq k\}\] \[\cup \{d'_i: 1\leq i\leq k\} \cup \{c'_{i1}: 1\leq i\leq k\} \cup \{c'_{i2}: 1\leq i\leq k\}\] \[\cup \{x_i^{p}: 1\leq i\leq k, 1\leq p\leq n\} \cup \{y'_i: 1\leq i\leq k, 1\leq p\leq n\}\]
\[\textbf{E(G)}= \{b_ic_{i1}: 1\leq i\leq k\} \cup \{w_ic_{i1}: 1\leq i\leq k\}\] \[\cup \{w_ic_{i2}: 1\leq i\leq k\} \cup \{d_ic_{i2}: 1\leq i\leq k\}\] \[\cup \{c_{i1} x_i^p: 1\leq i\leq k,1\leq p\leq n\} \cup \{c_{i2} y_i^p: 1\leq i\leq k,1\leq p\leq n\}\] \[\cup \{ad_{i}: 1\leq i\leq k\} \cup \{ a'd'_{i}: 1\leq i\leq k\}\] \[\cup \{b'_ic'_{i1}: 1\leq i\leq k\} \cup \{w'_ic'_{i1}: 1\leq i\leq k\}\] \[\cup \{w'_ic'_{i2}: 1\leq i\leq k\} \cup \{d'_ic'_{i2}: 1\leq i\leq k\}\] \[\cup \{c'_{i1} x_i^p: 1\leq i\leq k,1\leq p\leq n\} \cup \{c'_{i2} y_i^p: 1\leq i\leq k,1\leq p\leq n\}\] then \[|V(G)|=2(2n+3)k+2k+1\] and \[|E(G)|=2(2n+5)k\] Now we define the labeling as follows. \[\lambda: V(G)\longrightarrow \{0,1,2,…,2q-1\}\] where \(1\leq i\leq k/2\) \[\lambda (c_{i1})= \begin{cases}2q-1-4(i-1)\end{cases}\] \[\lambda (c_{i2})=\begin{cases} 2q-3-4(i-1)\end{cases}\]
\[\lambda (c'_{i1})= \begin{cases}2q-1-4(i-1)-2k\end{cases}\] \[\lambda (c'_{i2})=\begin{cases} 2q-3-4(i-1)-2k\end{cases}\]
\[\lambda (b_i)=\begin{cases}(2n+3)(2i-2)\ \ \ for \ \ 1\leq i\leq k/2 \end{cases}\] \[\lambda (b'_i)=\begin{cases}(2n+3)(2i-2+2k)\ \ \ for \ \ 1\leq i\leq k/2 \end{cases}\]
\[\lambda (w_i)=\begin{cases}(2n+2)(2i-1)+2(i-1)\ \ \ for \ \ 1\leq i\leq k/2 \end{cases}\] \[\lambda (w'_i)=\begin{cases}(2n+2)(k+2i-1)+2(k/2+i-1)\ \ \ for \ \ 1\leq i\leq k/2 \end{cases}\]
\[\lambda (d_i)=\begin{cases}\lambda (w_i)+ 4i-2\ \ \ for \ \ 1\leq i\leq k/2 \end{cases}\] \[\lambda (d'_i)=\begin{cases}\lambda (w'_i)+2k+4(i-1)\ \ \ for \ \ 1\leq i\leq k/2 \end{cases}\]
For \(1\leq i\leq k/2\) and \(1\leq p\leq n\) \[\lambda (x_i^p)= \begin{cases}2p+(4n+6)(i-1)\end{cases}\] \[\lambda (x_i^p)= \begin{cases}\lambda (b'_i)+2p+(4n+6)(i-1)\end{cases}\]
\[\lambda (y_i^p)=\begin{cases} \lambda (w_i)+2p& \text{if $1\leq p\leq 2i-2$} \\ \lambda (w_i)+2(p+1)& \text{if $2i-2\leq p\leq n$} \end{cases}\] \[\lambda (y_i^p)=\begin{cases} \lambda (w'_i)+2p& \text{if $1\leq p\leq 2i+3$} \\ \lambda (w'_i)+2(p+1)& \text{if $2i+4\leq p\leq n$} \end{cases}\] Now for the apex vertex \(a\) and \(a'\), we have: \[\lambda (a)=\begin{cases}\lambda (c'_{(k/2)2}-2(n-9)\end{cases}\] \[\lambda (a)=\begin{cases}\lambda (d'_{k/2})+1\end{cases}\]
The odd graceful labeling of w-tree with some other known families of graphs like path, star, bistar, lader has been formulated in this section.
Theorem 3. A graph \(G\cong WT(n,k) \cup P_m\) admits the odd graceful labeling if \(n\geq2k-2\).
Proof. Let \(G\) be a graph, where \(q\) represents the total number of edges of path \(P_m\) and \(WT(n,k)\) and \(q'\) represents the total number of edges of path \(p_m\) and \(m\) represents the total number of vertices of path \(P_m\). The vertex and the edge set of \(G\) can be represented as follows: \[V(G)=V(P_m) \cup V(WT(n,k))\] \[\textbf{V(G)}=\{a\} \cup \{v_{i'}: 1\leq i'\leq m\} \cup \{b_i: 1\leq i \leq k\}\cup \{w_i: 1\leq i \leq k\}\] \[\cup \{d_i: 1\leq i\leq k\} \cup \{c_{i1}: 1\leq i\leq k\} \cup \{c_{i2}: 1\leq i\leq k\}\] \[\cup \{x_{i}^p: 1\leq i\leq k, 1\leq p\leq n\} \cup \{y_{i}^p: 1\leq i\leq k, 1\leq p\leq n\}\] and
\[E(G)=E(P_m) \cup E(WT(n,k))\]
\[\textbf{E(G)}= \{v_{i'}v_{i'+1}:
1\leq i'\leq m\} \cup \{ad_i: 1\leq i \leq k\}\cup \{w_ic_{i1}:
1\leq i \leq k\}\] \[\cup \{d_ic_{i2}:
1\leq i \leq k\}\cup \{w_ic_{i2}: 1\leq i \leq k\}\cup \{b_ic_{i1}:
1\leq i \leq k\}\] \[\cup \{c_{i1}
x_i^p: 1\leq i\leq k,1\leq p\leq n\} \cup \{c_{i2} y_i^p: 1\leq i\leq
k,1\leq p\leq n\}\] then \[|V(G)|=(2n+3)k+2k+m+1\] and \[|E(G)|=(2n+5)k+m-1\] Now we define the
labeling as follows. \[\lambda:
V(G)\longrightarrow \{0,1,2,…,2q-1\}\] We have different
schemes for both path and w-tree,
where \(1\leq i'\leq m\) \[\lambda (v_{i'})=\begin{cases}
2q-i'& \text{if $i\equiv 1(mod 2)$} \\
i'-2& \text{if $i\equiv 0(mod 2)$}
\end{cases}\] Now for the w-tree, we have the following scheme
where \(1\leq i\leq k\) \[\lambda (c_{i1})=
\begin{cases}2q-q'-1-4(i-1)\end{cases}\] \[\lambda (c_{i2})=\begin{cases}
2q-q'-3-4(i-1)\end{cases}\] \[\lambda (b_i)=\begin{cases}q'+(4n+6)(i-1)\ \
\ for \ \ 1\leq i\leq k \end{cases}\] \[\lambda (w_i)=\begin{cases}\lambda (b_i)+2n+2\ \
\ for \ \ 1\leq i\leq k \end{cases}\] \[\lambda (d_i)=\begin{cases}\lambda (w_i)+ 4i-2\ \
\ for \ \ 1\leq i\leq k \end{cases}\] For \(1\leq i\leq k\) and \(1\leq p\leq n\) \[\lambda (x_i^p)= \begin{cases}\lambda
(b_i)+2p\end{cases}\] \[\lambda
(y_i^p)=\begin{cases}
\lambda (w_i)+2p& \text{if $1\leq p\leq 2i-2$} \\
\lambda (w_i)+2(p+1)& \text{if $2i-2\leq p\leq n$}
\end{cases}\] \[\lambda
(a)=\begin{cases}\lambda (d_k)+1\end{cases}\]
Theorem 4. Let \(G\cong WT(n,k) \cup K_{(1,m)}\) admits the odd graceful labeling if \(n\geq2k-2\).
Proof. Let \(G\) ba a graph and \(q\) is the total number of edges of star \(K_{(1,m)}\) and w-tree \(WT(n,k)\) and \(q'\) represents the total number of edges of star \(K_{(1,m)}\) and \(m\) represents the total number of vertices. The vertex and edge set of graph \(G\) is follows: \[V(G)=V(K_{(1,m)}) \cup V(WT(n,k))\]
\[\textbf{V(G)}=\{v_o\} \cup \{v_{i'}: 1\leq i'\leq m\} \cup \{a\} \cup \{b_i: 1\leq i \leq k\}\cup \{w_i: 1\leq i \leq k\}\] \[\cup \{d_i: 1\leq i\leq k\} \cup \{c_{i1}: 1\leq i\leq k\} \cup \{c_{i2}: 1\leq i\leq k\}\] \[\cup \{x_{i}^p: 1\leq i\leq k, 1\leq p\leq n\} \cup \{y_{i}^p: 1\leq i\leq k, 1\leq p\leq n\}\] and
\[E(G)=E(K_{(1,m)}) \cup
E(WT(n,k))\] \[\textbf{E(G)}=
\{v_{0}v_{i'}: 1\leq i'\leq m\} \cup \{ad_i: 1\leq i \leq
k\}\cup \{w_ic_{i1}: 1\leq i \leq k\}\] \[\cup \{d_ic_{i2}: 1\leq i \leq k\}\cup
\{w_ic_{i2}: 1\leq i \leq k\}\cup \{b_ic_{i1}: 1\leq i \leq k\}\]
\[\cup \{c_{i1} x_i^p: 1\leq i\leq k,1\leq
p\leq n\} \cup \{c_{i2} y_i^p: 1\leq i\leq k,1\leq p\leq n\}\]
then \[|V(G)|=(2n+3)k+2k+m+1\] and
\[|E(G)|=(2n+5)k+m-1\] Now we define
the labeling as follows. \[\lambda:
V(G)\longrightarrow \{0,1,2,…,2q-1\}\] Now we have different
schemes for both star and w-tree.
For star \(K_{(1,m)}\), we have the
following scheme:
where \(1\leq i'\leq m\), \[\lambda (v_i)=\begin{cases}
0& \text{if $i=0$} \\
2q-1-2(i'-1)& \text{if $i\equiv 1(mod2)$}\\
2q-3-2(i'-1)& \text{if $i\equiv 0(mod2)$}
\end{cases}\] Now for the w-tree, we have the following scheme
where \(1\leq i\leq k\) \[\lambda (c_{i1})=
\begin{cases}2q-q'-1-4(i-1)\end{cases}\] \[\lambda (c_{i2})=\begin{cases}
2q-2q'-2-4(i-1)\end{cases}\] \[\lambda (b_i)=\begin{cases}(4n+6)(i-1)+1\ \ \ for
\ \ 1\leq i\leq k \end{cases}\] \[\lambda (w_i)=\begin{cases}\lambda (b_i)+2(n+1)\
\ \ for \ \ 1\leq i\leq k \end{cases}\] \[\lambda (d_i)=\begin{cases}\lambda (w_i)+ 4i-2\ \
\ for \ \ 1\leq i\leq k \end{cases}\] For \(1\leq i\leq k\) and \(1\leq p\leq n\) \[\lambda (x_i^p)= \begin{cases}\lambda
(b_i)+2p\end{cases}\] \[\lambda
(y_i^p)=\begin{cases}
\lambda (w_i)+2p& \text{if $1\leq p\leq 2i-2$} \\
\lambda (w_i)+2(p+1)& \text{if $2i-2\leq p\leq n$}
\end{cases}\] \[\lambda
(a)=\begin{cases}\lambda (d_k)+1\end{cases}\]
Theorem 5. Let \(G\cong WT(n,k) \cup B_{(m,l)}\) admits odd graceful labeling if \(n\geq 2k-2\).
Proof. Let \(G\) ba a graph and \(q\) is the total number of edges of bistar \(B_{(m,l)}\) and w-tree \(WT(n,k)\) and \(q'\) represents the total number of edges of bistar \(B_{(m,n)}\) and \(m\) represents the total number of vertices. The vertex and edge set of graph \(G\) is follows: \[V(G)=V(B_{(m,l)}) \cup V(WT(n,k))\]
\[\textbf{V(G)}=\{a\} \cup \{u,v,u_{i'}v_{i'}: 1\leq i'\leq m\} \cup \{b_i: 1\leq i \leq k\}\cup \{w_i: 1\leq i \leq k\}\] \[\cup \{d_i: 1\leq i\leq k\} \cup \{c_{i1}: 1\leq i\leq k\} \cup \{c_{i2}: 1\leq i\leq k\}\] \[\cup \{x_{i}^p: 1\leq i\leq k, 1\leq p\leq n\} \cup \{y_{i}^p: 1\leq i\leq k, 1\leq p\leq n\}\] and
\[E(G)=E(B_{(m,l)}) \cup E(WT(n,k))\] \[\textbf{E(G)}= \{v v_{i'}: 1\leq i'\leq m\} \cup\{uv\} \cup \{uu_{i'}: 1\leq i \leq k\}\cup \{w_ic_{i1}: 1\leq i \leq k\}\] \[\cup \{d_ic_{i2}: 1\leq i \leq k\}\cup \{w_ic_{i2}: 1\leq i \leq k\}\cup \{b_ic_{i1}: 1\leq i \leq k\}\] \[\cup \{c_{i1} x_i^p: 1\leq i\leq k,1\leq p\leq n\} \cup \{c_{i2} y_i^p: 1\leq i\leq k,1\leq p\leq n\}\] then \[|V(G)|=(2n+3)k+2k+2m+1\] and \[|E(G)|=(2n+5)k+2m\]
Now we define the labeling as follows. \[\lambda: V(G)\longrightarrow
\{0,1,2,…,2q-1\}\] Now we have different schemes for both
bistar and w-tree. As we know that a bistar consist of two isomorphic
copies of a star, so we discuss each star separately.
Now for the first star. we have the following scheme:
where \(1\leq i'\leq m\), \[\lambda (v_i)=\begin{cases}
0& \text{if $i'=0$} \\
2q-1-2(i'-1)& \text{if $i'\equiv 1(mod2)$}\\
2q-3-2(i'-1)& \text{if $i'\equiv 0(mod2)$}
\end{cases}\] Now for the second star. we have the following
scheme:
where \(1\leq i'\leq l\), \[\lambda (v_i)=\begin{cases}
1& \text{if $i'=0$} \\
\lambda (v_i)-1-2(i'-1)& \text{if $i'\equiv 1(mod2)$}\\
\lambda (v_i)-3-2(i'-1))& \text{if $i'\equiv 0(mod2)$}
\end{cases}\]
Now for the w-tree, we have the following scheme where \(1\leq i\leq k\) \[\lambda (c_{i1})= \begin{cases}2q-q'-1-4(i-1)\end{cases}\] \[\lambda (c_{i2})=\begin{cases} 2q-2q'-2-4(i-1)\end{cases}\] \[\lambda (b_i)=\begin{cases}q'-1+(4n+6)(i-1)\ \ \ for \ \ 1\leq i\leq k \end{cases}\] \[\lambda (w_i)=\begin{cases}\lambda (b_i)+2(n+1)\ \ \ for \ \ 1\leq i\leq k \end{cases}\] \[\lambda (d_i)=\begin{cases}\lambda (w_i)+ 4i-2\ \ \ for \ \ 1\leq i\leq k \end{cases}\] For \(1\leq i\leq k\) and \(1\leq p\leq n\) \[\lambda (x_i^p)= \begin{cases}\lambda (b_i)+2p\end{cases}\] \[\lambda (y_i^p)=\begin{cases} \lambda (w_i)+2p& \text{if $1\leq p\leq 2i-2$} \\ \lambda (w_i)+2(p+1)& \text{if $2i-2\leq p\leq n$} \end{cases}\] \[\lambda (a)=\begin{cases}\lambda (d_k)+3\end{cases}\]
Theorem 6. Let \(G\cong WT(n,k) \cup L_h\) admits odd graceful labeling if \(n\geq 2k-2\).
Proof. Let \(G\) ba a graph and \(q\) is the total number of edges of ladder \(L_h=\) and w-tree \(WT(n,k)\) and \(q'\) represents the total number of edges of ladder \(L_h=\) and \(m\) represents the total number of vertices of path \(P_m\). The vertex and edge set of graph \(G\) is follows: \[V(G)=V(L_h) \cup V(WT(n,k))\]
\[\textbf{V(G)}=\{a\} \cup \{u_{i'}v_{i'}: 1\leq i'\leq m\} \cup \{b_i: 1\leq i \leq k\}\cup \{w_i: 1\leq i \leq k\}\] \[\cup \{d_i: 1\leq i\leq k\} \cup \{c_{i1}: 1\leq i\leq k\} \cup \{c_{i2}: 1\leq i\leq k\}\] \[\cup \{x_{i}^p: 1\leq i\leq k, 1\leq p\leq n\} \cup \{y_{i}^p: 1\leq i\leq k, 1\leq p\leq n\}\] and
\[E(G)=E(L_h) \cup E(WT(n,k))\] \[\textbf{E(G)}= \{u_{i'} u_{i'+1} v_{i'} v_{i'+1}: 1\leq i'\leq m\} \cup \{u_{i'}v_{i'}: 1\leq i \leq k\}\cup \{w_ic_{i1}: 1\leq i \leq k\}\] \[\cup \{d_ic_{i2}: 1\leq i \leq k\}\cup \{w_ic_{i2}: 1\leq i \leq k\}\cup \{b_ic_{i1}: 1\leq i \leq k\}\] \[\cup \{c_{i1} x_i^p: 1\leq i\leq k,1\leq p\leq n\} \cup \{c_{i2} y_i^p: 1\leq i\leq k,1\leq p\leq n\}\cup \{ad_{i}: 1\leq i \leq k\}\] then \[|V(G)|=(2n+3)k+2k+3m+2\] and \[|E(G)|=(2n+5)k+3m\] Now we define the labeling as follows. \[\lambda: V(G)\longrightarrow \{0,1,2,…,2q-1\}\]
Now we have different schemes for both lader and w-tree.
where \(1\leq i'\leq m\), \[\lambda (x_{1i'})=\begin{cases}
2q'-1& \text{if $i'=1$} \\
2q'-2i'& \text{if $i'\equiv 1(mod2)\ \ \ i'\neq
1$}\\
i'+[6(i'-2)/2]& \text{if $i'\equiv 0(mod2)$}
\end{cases}\]
\[\lambda (x_{2i'})=\begin{cases}
0& \text{if $i'=1$} \\
2q'-2i'+1& \text{if $i'\equiv 1(mod2)\ \ \ i'\neq
1$}\\
4i'-2& \text{if $i'\equiv 0(mod2)$}
\end{cases}\] Now for w-tree we have following scheme, where
\(s\) is the least edge weight in the
ladder graph.
where \(1\leq i\leq k\) \[\lambda (c_{i1})=
\begin{cases}s-1-4(i-1)\end{cases}\] \[\lambda (c_{i2})=\begin{cases}
s-3-4(i-1)\end{cases}\] \[\lambda
(b_i)=\begin{cases}1+(4n+6)(i-1)\ \ \ for \ \ 1\leq i\leq k
\end{cases}\] \[\lambda
(w_i)=\begin{cases}\lambda (b_i)+2(n+1)\ \ \ for \ \ 1\leq i\leq k
\end{cases}\] \[\lambda
(d_i)=\begin{cases}\lambda (w_i)+ 4i-2\ \ \ for \ \ 1\leq i\leq k
\end{cases}\] For \(1\leq i\leq
k\) and \(1\leq p\leq n\) \[\lambda (x_i^p)= \begin{cases}\lambda
(b_i)+2p\end{cases}\] \[\lambda
(y_i^p)=\begin{cases}
\lambda (w_i)+2p& \text{if $1\leq p\leq 2i-2$} \\
\lambda (w_i)+2(p+1)& \text{if $2i-2\leq p\leq n$}
\end{cases}\] \[\lambda
(a)=\begin{cases}\lambda (d_k)+1\end{cases}\]
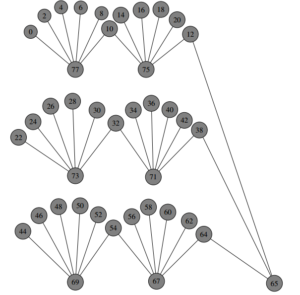
In this paper, we have demonstrated that a specific subclass, the W-tree denoted by \(WT(n,k)\), admits an odd graceful labeling. Additionally, we prove that graphs obtained through the union of a W-tree \(WT(n,k)\) with various other graphs-namely, a path \(P_m\), a star \(K_{1,m}\), a bistar \(B_{m,m}\), and a ladder \(L_n = P_n \times P_n\)-are also odd graceful graphs. However, a more comprehensive understanding of the odd graceful labeling of W-trees requires further investigation.
The authors declare no conflict of interest.
1970-2025 CP (Manitoba, Canada) unless otherwise stated.