Chemical applicability of GQ and QG indices of a graph and their bounds

1. Introduction

Degree-based indices have grown since topological invariants were first developed and used in Chemical Graph Theory (CGT). Nowadays, research on chemical applications and mathematical properties of degree-based topological invariants are significantly active, see [4, 13]. The reason behind the sudden increase in the introduction of these indices could be attributed to their straightforward definitions, computationally easy techniques and unexpectedly good performance in predicting the physico-chemical properties of molecules. The study of degree-based topological indices is applied mathematically to irregularity measures and metrics of graph branching [1].

Throughout this article, we consider a simple, connected and undirected graph ${\rm Y}=(V({\rm Y}),E({\rm Y}))$, with $V({\rm Y})$ and $E({\rm Y})$ as its vertex and edge set, respectively. The degree ${\mathrm{\Im }}_u$ of a vertex $u\in V({\rm Y})$ is the total number of edges associated with that vertex. Also, $|V({\rm Y})|=n$ and $|E({\rm Y})|=m$ are the order and size of the graph, respectively. We use $\delta$ and $\mathrm{\Delta }$ to denote the minimum degree and maximum degree of the graph ${\rm Y}$, respectively [41].

Since when the idea of topological molecular descriptors is employed, several notable degree-based topological descriptors have been introduced. Below we state some standard topological descriptors which will be utilized in the rest of this article.

One of the oldest degree-dependent topological indices is the Zagreb indices [19]. Gutman and Trinajstic introduced them in 1972 and defined them as follows: $$\begin{array}{}\text{(1)}& M_1({\rm Y})=\sum _{uv\in E({\rm Y})}({\mathrm{\Im }}_u+{\mathrm{\Im }}_v),\end{array}$$ and $$\begin{array}{}\text{(2)}& M_2({\rm Y})=\sum _{uv\in E({\rm Y})}{\mathrm{\Im }}_u\cdot {\mathrm{\Im }}_v.\end{array}$$

Despite their age, they are appropriate and significant even today and several publications on Zagreb indices are appearing [14, 20, 42].

The forgotten index was seen in the same article as the Zagreb indices [19], but it was sitting in the shadow for almost 40 years. Later, B. Furtula and I. Gutman reintroduced it in [16] and defined as follows:

$$\begin{array}{}\text{(3)}& F({\rm Y})=\sum _{uv\in E({\rm Y})}({\mathrm{\Im }}_u^2+{\mathrm{\Im }}_v^2).\end{array}$$

Recently in [21, 32], the forgotten topological index of a graph and its some new inequalities are investigated.

Randić index [35] is a widely employed well-known degree-based topological index. It is defined as follows: $$\begin{array}{}\text{(4)}& R({\rm Y})=\sum _{uv\in E({\rm Y})}\frac{1}{\sqrt{{\mathrm{\Im }}_u\cdot {\mathrm{\Im }}_v}}.\end{array}$$

For more than 40 years, the Randić index has been studied, resulting in hundreds of publications and numerous books [3,5, 31,33]. Several improvements to this index have been put forward in order to improve its predictive potential [33]. One of such improvements is the reciprocal Randić index which is defined as $$\begin{array}{}\text{(5)}& \mathit{\text{RR}}({\rm Y})=\sum _{uv\in E({\rm Y})}\sqrt{{\mathrm{\Im }}_u\cdot {\mathrm{\Im }}_v}.\end{array}$$

In 2013, the idea of the first and second hyper-Zagreb indices are proposed in [37] and they are defined as follows: $$\begin{array}{}\text{(6)}& {\mathit{\text{HM}}}_1({\rm Y})=\sum _{uv\in E({\rm Y})}({\mathrm{\Im }}_u+{\mathrm{\Im }}_v{)}^2,\end{array}$$ and $$\begin{array}{}\text{(7)}& {\mathit{\text{HM}}}_2({\rm Y})=\sum _{uv\in E({\rm Y})}({\mathrm{\Im }}_u\cdot {\mathrm{\Im }}_v{)}^2.\end{array}$$

Later, these indices were also studied for several classes of graphs in [6, 17].

More than one decades ago, the idea of symmetric division deg index of a graph ${\rm Y}$ is proposed in [38]. We denote it as $\mathit{\text{SDD}}({\rm Y})$ and it is defined as $$\begin{array}{}\text{(8)}& \mathit{\text{SDD}}({\rm Y})=\sum _{uv\in E({\rm Y})}(\frac{{\mathrm{\Im }}_u}{{\mathrm{\Im }}_v}+\frac{{\mathrm{\Im }}_v}{{\mathrm{\Im }}_u}).\end{array}$$

Moreover, it has just lately gained a lot of interest because of its some reasonable predictive capability [2,15].

Recently, I. Gutman proposed three novel topological indices one of them was Sombor index [18], and defined as follows: $$\begin{array}{}\text{(9)}& \mathit{\text{SO}}({\rm Y})=\sum _{uv\in E({\rm Y})}\sqrt{{\mathrm{\Im }}_u^2+{\mathrm{\Im }}_v^2}.\end{array}$$

Geometrically, the Sombor index is a measure of the distance of the point $({\mathrm{\Im }}_u,{\mathrm{\Im }}_v)$ from the origin in the $2D$ Cartesian coordinate system. A new method to compute the different ombor-type indices via -polynomial was proposed in [29].

Inspired by the work on Sombor index, V.R. Kulli proposed Nirmala index [23] of the graph ${\rm Y}$ and defined as follows: $$\begin{array}{}\text{(10)}& N({\rm Y})=\sum _{uv\in E({\rm Y})}\sqrt{{\mathrm{\Im }}_u+{\mathrm{\Im }}_v}.\end{array}$$

Further, the first inverse Nirmala index (denoted as ${\mathit{\text{IN}}}_1({\rm Y})$) and second inverse Nirmala index (denoted as ${\mathit{\text{IN}}}_2({\rm Y})$) of a molecular graph ${\rm Y}$ are established by Kulli et al. [25] in $2021$ which are defined as follows: $$\begin{array}{}\text{(11)}& {\mathit{\text{IN}}}_1({\rm Y})=\sum _{uv\in E({\rm Y})}\sqrt{\frac{1}{{\mathrm{\Im }}_u}+\frac{1}{{\mathrm{\Im }}_v}}=\sum _{uv\in E({\rm Y})}\sqrt{\frac{{\mathrm{\Im }}_u+{\mathrm{\Im }}_v}{{\mathrm{\Im }}_u{\mathrm{\Im }}_v}},\end{array}$$

$$\begin{array}{}\text{(12)}& {\mathit{\text{IN}}}_2({\rm Y})=\sum _{uv\in E({\rm Y})}\frac{1}{\sqrt{\frac{1}{{\mathrm{\Im }}_u}+\frac{1}{{\mathrm{\Im }}_v}}}=\sum _{uv\in E({\rm Y})}\sqrt{\frac{{\mathrm{\Im }}_u{\mathrm{\Im }}_v}{{\mathrm{\Im }}_u+{\mathrm{\Im }}_v}}.\end{array}$$

Lately, the derivation formulas of Nirmala indices and its generalized version (($a,b$)-Nirmala index) based on M-polynomials were suggested in [10,11]. Comparative study between irmala and ombor indices based on their applicability, degeneracy and smoothness was presented in [28,26]. The ordhaus-addum-type inequalities for the irmala Indices were obtained in the article [30].

In the year 2022, V.R. Kulli proposed two novel topological indices based on the geometric and quadratic mean of degrees of end vertices of an edge $uv\in E({\rm Y})$. They are named as geometric-quadratic (GQ) and quadratic-geometric (QG) indices [24]. The mathematical definitions of the GQ and QG indices are:

$$\begin{array}{}\text{(13)}& \mathit{\text{GQ}}({\rm Y})=\sum _{uv\in E({\rm Y})}\frac{\sqrt{2{\mathrm{\Im }}_u{\mathrm{\Im }}_v}}{\sqrt{{\mathrm{\Im }}_u^2+{\mathrm{\Im }}_v^2}},\end{array}$$ and $$\begin{array}{}\text{(14)}& \mathit{\text{QG}}({\rm Y})=\sum _{uv\in E({\rm Y})}\frac{\sqrt{{\mathrm{\Im }}_u^2+{\mathrm{\Im }}_v^2}}{\sqrt{2{\mathrm{\Im }}_u{\mathrm{\Im }}_v}}.\end{array}$$

The computation of the GQ and QG indices for some standard graphs and jagged-rectangle benzenoid system was reported in [24,8]. The GQ and QG indices-based entropy measures of some silicon carbide networks were computed in [9].

Apart from the above mathematical developments on GQ and QG indices, one can find the evidence of usability of the indices in the article [12].

In this article, the authors performed the Quantitative Structure-Property Relationship (QSPR) analysis to predict the physico-chemical properties of certain well-known COVID-19 drugs, where the GQ and QG indices have shown a good correlation with some of the physico-chemical properties of the drugs. The cubic regression models corresponding to the indices with the squared correlation coefficients $0.9910$ and $0.9872$, respectively (determined in Table 8 of [12]), depict that the indices predict the mass (M) of the drugs significantly. For more details, readers can see Tables 8 and 9, Figure 18(b) and point number (vi) in the conclusion section of the recently published article [12]. Moreover, very recently, the authors of [27] examined the newly defined GQ–QG indices’ chemical applicability and compare their prediction power, degeneracy, and structural sensitivity to those of existing notable degree-based topological indices.

Hence, the study of the mathematical properties and bounds of the GQ and QG indices is worthy of investigation in the field of chemical graph theory.

The rest of the manuscript is built as follows. The chemical applicability of the considered GQ and QG indices is investigated over the physico-chemical properties of 22 benzenoid hydrocarbons in Section 2. In Section 3, some tight upper and lower bounds for the GQ and QG indices in terms of size, degree sequence of a graph and the above-mentioned degree-based topological indices are established. Section 4 is reserved for the conclusion.

2. Chemical applicability of GQ and QG indices

The novel topological indices should correlate well with one of the physico-chemical properties of a molecular compound. The ability to discriminate between isomers, predictive power and smoothness of the GQ and QG indices have been investigated in article [27]. Here, we focus our attention to test the chemical applicability of the concerned indices over the physico-chemical properties of $22$ benzenoid hydrocarbons. Benzenoid hydrocarbons are a specific type of organic compound with a condensed polycyclic structure made up only of hexagonal rings. It has been utilized by numerous researchers to evaluate the strength and quality of different molecular descriptors and structural invariants for QSPR/QSAR analysis [34]. These chemical graphs have notable variance, shape, non-polarity, and branching because of the diversity of their structures. Many researchers have conducted a variety of studies on benzenoid hydrocarbons, see [22, 7, 36,39]. The physico-chemical properties such as boiling point (BP), standard heat of formation (DHFORM), molecular weight (MW), $logP$ and $\pi$-electron energy ($E_{\pi }$) of benzenoid hydrocarbons are comprised from the article [7, 39]. These properties together with the computed values of GQ–QG indices of benzenoid hydrocarbons are cataloged in Table 1 to perform the linear regression analysis.

2.1. Linear regression model ($LRM$)

$$\begin{array}{}\text{(15)}& P=p_1\times TI+p_2,\end{array}$$ is performed for regression analysis. In Eq. (15), $P$ denotes the physico-chemical property, $\mathit{\text{TI}}$ symbolizes the topological index and $p_i$ where $i=1,2$ represent the fitting coefficients.

The linear regression models are performed using MATLAB R2019a software and fitting coefficients $p_1$ and $p_2$ are taken with $95\mathrm{\%}$ confidence bounds. The statistical parameters obtained from linear regression analysis are $R^2$, $Adj$–$R^2$, root mean square error (RMSE) and sum of square error (SSE).

The squared of correlation-coefficient ($R^2$) closer to $1$ and RMSE near to $0$ represent the goodness of a linear regression model. The linear regression models for GQ and QG indices with different physico-chemical properties of benzenoid hydrocarbons are detailed below.

(i) Boiling point (BP):

LRM for GQ index: $BP=p_1\times \mathit{\text{GQ}}+p_2$, where coefficients (with $95\mathrm{\%}$ confidence bounds) $p_1=21.3200(20.3600,22.2800)\text{and}{p}_2=-13.9000(-36.0600,8.2670).$

Goodness of fit:$R^2=0.9908,\mathit{\text{Adj-}}{R}^2=0.9903,\mathit{\text{SSE}}=3227\text{and}\mathit{\text{RMSE}}=12.7000$

LRM for QG index: $BP=p_1\times \mathit{\text{QG}}+p_2$, where coefficients (with $95\mathrm{\%}$ confidence bounds) $p_1=20.5900(19.7300,21.4500),p_2=-12.6900(-33.1700,7.7920)$.

Goodness of fit:$R^2=0.9921,\mathit{\text{Adj-}}{R}^{=}0.9917\mathit{\text{SSE}}=2772\text{and}\mathit{\text{RMSE}}=11.7700.$

(ii) Standard enthalpy of formation (DHFORM):

LRM for GQ index: $DHFORM=p_1\times \mathit{\text{GQ}}+p_2$, where coefficients (with $95\mathrm{\%}$ confidence bounds) $p_1=11.9400(10.0000,13.8800)p_2=20.3600(-24.4500,65.1700).$

Goodness of fit: $R^2=0.8917,\mathit{\text{Adj-}}{R}^2=0.8863,\mathit{\text{SSE}}=1.319e+04\text{and}\mathit{\text{RMSE}}=25.6800.$

LRM for QG index: $DHFORM=p_1\times \mathit{\text{QG}}+p_2$, where coefficients (with $95\mathrm{\%}$ confidence bounds): $p1=11.5500(9.6980,13.4000),p2=20.7900(-23.2900,64.8700).$

Goodness of fit: $R^2=0.8946,\mathit{\text{Adj-}}{R}^2=0.8893,\mathit{\text{SSE}}=1.284e+04\text{and}\mathit{\text{RMSE}}=25.3400.$

(iii) Molecular weight (MW):

LRM for molecular weight (MW): $MW=p_1\times \mathit{\text{GQ}}+p_2$, where coefficients (with $95\mathrm{\%}$ confidence bounds): $p_1=9.7450(9.3830,10.1100),p_2=23.8700(15.5000,32.2400).$

Goodness of fit: $R^2=0.9937,\mathit{\text{Adj-}}R=0.9934,\mathit{\text{SSE}}=460\text{and}\mathit{\text{RMSE}}=4.7960.$

LRM for molecular weight (MW): $MW=p_1\times \mathit{\text{QG}}+p_2$, where coefficients (with $95\mathrm{\%}$ confidence bounds): $p_1=9.4110(9.0820,9.740),p_2=24.4900(16.6400,32.3400).$

Goodness of fit: $R^2=0.9944,\mathit{\text{Adj-}}{R}^2=0.9941,\mathit{\text{SSE}}=407.1000\text{and}\mathit{\text{RMSE}}=4.5120.$

(iv)

LRM for GQ index: $logP=p_1\times GQ+p_2$, where coefficients (with $95\mathrm{\%}$ confidence bounds): $p_1=0.2262(0.2090,0.2435),p_2=0.8776(0.4793,1.2760).$

Goodness of fit: $R^2=0.9740,\mathit{\text{Adj-}}{R}^2=0.9727,\mathit{\text{SSE}}=1.0420\text{and}\mathit{\text{RMSE}}=0.2282.$

LRM for QG index: $logP=p_1\times QG+p_2$, where coefficients (with $95\mathrm{\%}$ confidence bounds): $p_1=0.2185(0.2022,0.2348),p_2=0.8908(0.5024,1.2790).$

Goodness of fit: $R^2=0.9751,\mathit{\text{Adj-}}{R}^2=0.9739,\mathit{\text{SSE}}=0.9967\text{and}\mathit{\text{RMSE}}=0.2232.$

(v) $\pi$-electron energy ($E_{\pi }$):

LRM for GQ index: $E_{\pi }=p_1\times GQ+p_2$, where coefficients (with $95\mathrm{\%}$ confidence bounds): $p_1=1.1380(1.1190,1.1580),p_2=1.4400(0.9862,1.8930).$

Goodness of fit: $R^2=0.9986,\mathit{\text{Adj-}}{R}^2=0.9986,\mathit{\text{SSE}}=1.3520\text{and}\mathit{\text{RMSE}}=0.2600.$

LRM for QG index: $E_{\pi }=p_1\times QG+p_2$, where coefficients (with $95\mathrm{\%}$ confidence bounds): $p_1=1.0990(1.0810,1.1170),p_2=1.5200(1.0820,1.9580).$

Goodness of fit: $R^2=0.9987,\mathit{\text{Adj-}}{R}^2=0.9987,\mathit{\text{SSE}}=1.2700\text{and}\mathit{\text{RMSE}}=0.2519.$

We extract the following observations from the above-performed QSPR models:

(i) GQ and QG indices predict the boiling point (BP) with the $R^{2}0.9908$ and $0.9921$, respectively.

(ii) GQ and QG indices obtain the square correlation coefficient $R^2$ $0.8917$ and $0.8946$, respectively with the standard heat of formation (DHFORM).

(iii) GQ and QG indices forecast the molecular weight (MW) with the $R^{2}0.9937$ and $0.9944$, respectively.

(iv) GQ and QG indices report the $R^2$-values $0.9740$ and $0.9751$, respectively, with $\log P$ property of benzenoid hydrocarbons.

(v) GQ and QG indices predict the $\pi$-electron energy ($E_{\pi }$) with the $R^{2}0.9986$ and $0.9987$, respectively.

Figure 1 illustrates the linear regression model between the $\mathit{\text{GQ}}$–$\mathit{\text{QG}}$ indices and the boiling point (BP) of benzenoid hydrocarbons. Figure 2 demonstrates the regression model between the $\mathit{\text{GQ}}$–$\mathit{\text{QG}}$ indices and the standard heat of formation ($\mathrm{\Delta }{H}_{\text{form}}$). Figure 3 depicts the relationship between the $\mathit{\text{GQ}}$–$\mathit{\text{QG}}$ indices and molecular weight (MW). Figure 4 presents the linear regression plot between the $\mathit{\text{GQ}}$–$\mathit{\text{QG}}$ indices and logP values of benzenoid hydrocarbons. Finally, Figure 5 shows the regression analysis between the $\mathit{\text{GQ}}$–$\mathit{\text{QG}}$ indices and the $\pi$-electron energy ($\pi$-E).

3. Bounds of GQ and QG indices for general graph

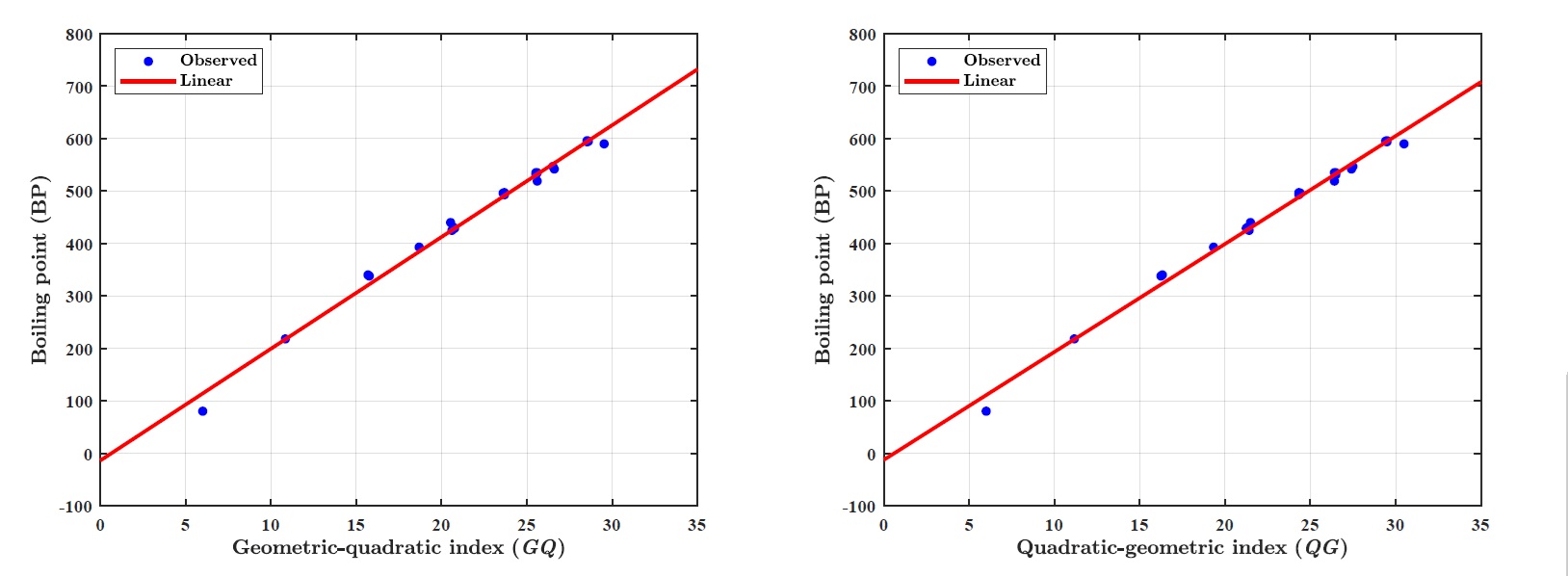
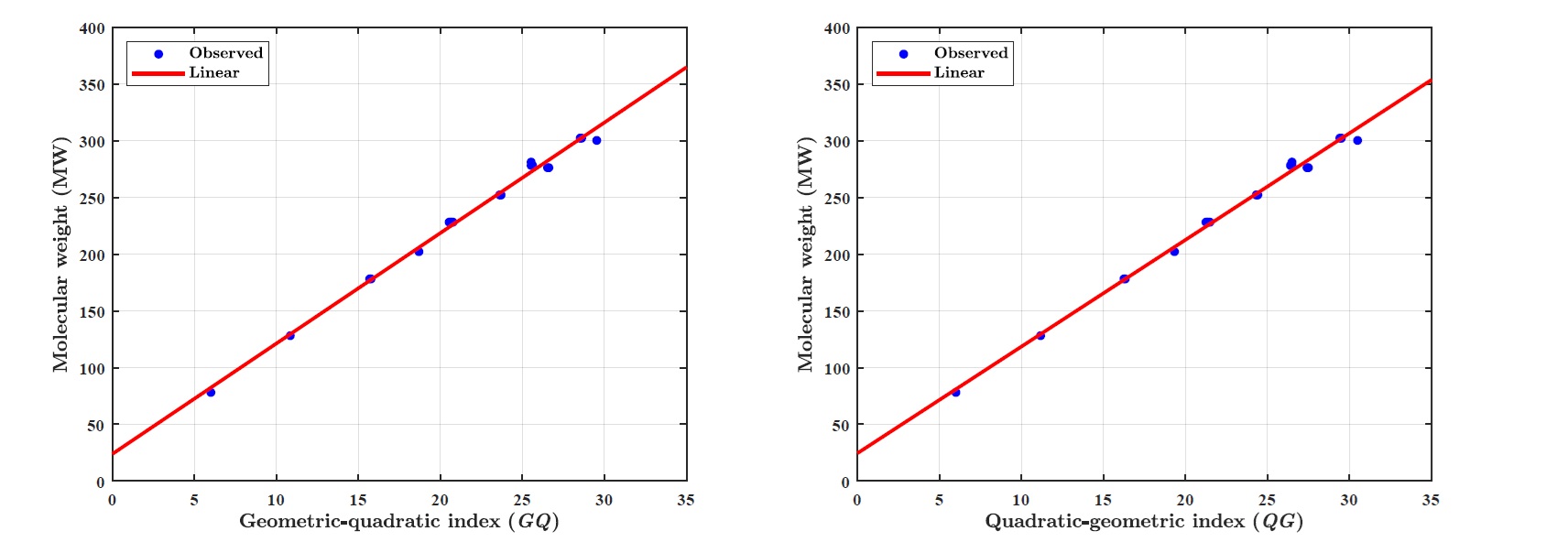
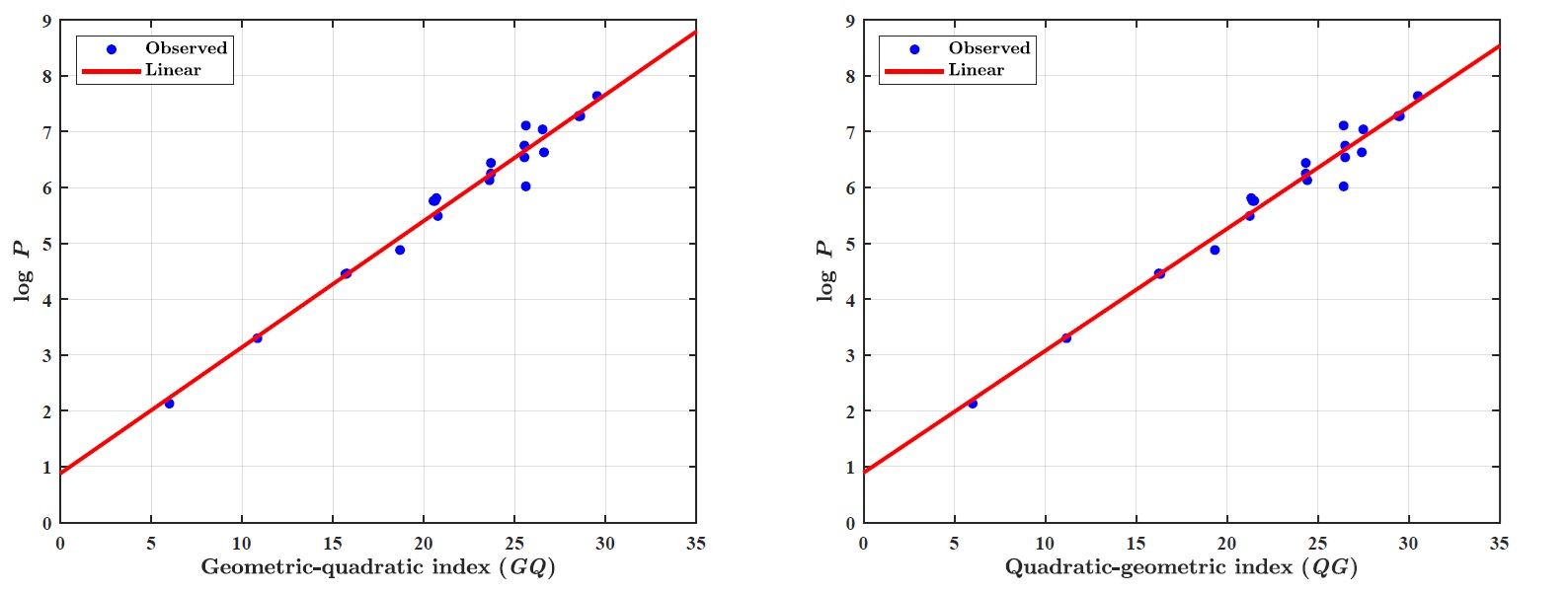
Here, we establish some tight upper and lower bounds for the GQ and QG indices of a graph ${\rm Y}$ in terms of its size, degree sequence and some notable degree-based topological descriptors. Before moving further, let us recall a small relation between GQ and QG indices as stated in Theorem 3.1.

3.1. In terms of size and degree

Here, we discuss the bounds of GQ and QG indices in terms of the size and degree of a graph.

The following corollary is straightaway from the above theorem.

3.2. In terms of degree sequence and size

In this part, we discuss the bounds of GQ and QG indices in terms of degree sequence and size of a graph.

Next, we present another version of Theorem 3.4.

We take the following example to see the tightness of the lower and upper bounds for non-regular graphs.

Keeping in mind the idea of Example 3.6, the above result can be generalized as follows:

3.3. In terms of the first Zagreb index

This section deals with the upper and lower bounds of GQ and QG indices in terms of the first Zagreb index, size, maximum and minimum degrees of graph ${\rm Y}$. The following lemma is required in order to prove the upper bound of GQ and QG indices in Theorems 3.9 and 3.15.

3.4. In terms of the second Zagreb index

This section includes the upper and lower bounds of GQ and QG indices in terms of the second Zagreb index, size, and the maximum and minimum degree of graph ${\rm Y}$.

3.5. In terms of the forgotten topological index

In this segment, we present the mathematical relation of GQ and QG indices in terms of the forgotten index, size, and the maximum and minimum degree of graph ${\rm Y}$.

3.6. In terms of the Randić index

Here, we establish the lower and upper bounds of GQ and QG indices mainly in terms of Randić index.

3.7. In terms of the reciprocal Randić index

In this section, we prove the lower and upper bound of GQ and QG indices in terms of reciprocal Randić index, maximum and minimum degree of graph ${\rm Y}$.

3.8. In terms of the first Hyper-Zagreb index

This portion deals with the lower and upper bounds of GQ and QG indices mainly in terms of the first hyper-Zagreb index of graph ${\rm Y}$.

3.9. In terms of the second Hyper-Zagreb index

This section discusses about the lower and upper bound of GQ and QG indices in terms of the second hyper-Zagreb index, maximum and minimum degree of graph ${\rm Y}$.

3.10. In terms of the symmetric division deg index

The bounds of GQ and QG indices in terms of the symmetric division deg index, maximum degree and minimum degree of graph ${\rm Y}$ are discussed below.

3.11. In terms of the Sombor index

In this section, we provide bounds of GQ and QG indices in terms of Sombor index, maximum degree and minimum degree of graph ${\rm Y}$.

3.12. In terms of the Nirmala indices

In this section, we establish the lower and upper bounds of GQ and QG indices mainly in terms of Nirmala indices, namely, the Nirmala index, first and second inverse Nirmala index of a graph ${\rm Y}$.

4. Conclusion

In this article, the chemical applicability and bounds of the novel degree-based GQ and QG indices are investigated. More precisely, a QSPR analysis is performed between the GQ–QG indices and physico-chemical properties of $22$ benzenoid hydrocarbons to check the applicability of the indices. The obtained results depict that both the GQ and QG indices predict the physico-chemical properties of benzenoid hydrocarbons with the correlation coefficients $R>0.9$. Furthermore, we have put forward our interest to develop the mathematical relations of each of the GQ and QG indices with some well-known degree-based topological indices and some graph invariants, such as, degree sequence, size, maximum degree and minimum degree of a graph. Our performed results associated to QSPR analysis demonstrate that both the GQ and QG indices may be considered as a strong contender in the future experimentation of the chemical drugs and molecular compounds.

Acknowledgment

The authors are grateful to the reviewers for the thorough reviews of our manuscript. The valuable comments and suggestions have helped us to improve the quality of the article. Moreover, The first author (Shibsankar Das) is obliged to the Development Cell, Banaras Hindu University for financially supporting this work through the Faculty “Incentive Grant” under the Institute of Eminence (IoE) Scheme for the year 2024-25 (Project sanction order number: R/Dev/D/IoE/Incentive (Phase-IV)/2024-25/82483, dated 7 January 2025) and the second author (Virendra Kumar) is grateful to the UNIVERSITY GRANTS COMMISSION, Ministry of Human Resource Development, India for awarding the Senior Research Fellowship (SRF) with reference to UGC-Ref. No.: 1127/(CSIR-UGC NET JUNE 2019) dated 11-December-2019.