In this paper, we introduce the edge version of doubly resolving set of a graph which is based on the edge distances of the graph. As a main result, we computed the minimum cardinality \(\psi_E\) of edge version of doubly resolving sets of family of \(n\)-sunlet graph \(S_n\) and prism graph \(Y_n\).
Let us take a graph \(G=(V(G), E(G)),\) which is simple, connected and undirected, where its vertex set is \(V(G)\) and edge set is \(E(G)\). The order of a graph \(G\) is \(|V(G)|\) and the size of a graph \(G\) is \(|E(G)|\). The distance \(d(a, b)\) between the vertices \(a\), \(b\in V(G)\) is the length of a shortest path between them. If \(d(c, a)\neq d(c, b)\), then the vertex \(c\in V(G)\) is said to resolve two vertices \(a\) and \(b\) of \(V(G)\). Suppose that \(N=\{n_{1}, n_{2},\ldots,n_{k}\}\subseteq V(G)\) is an ordered set and \(m\) is a vertex of \(V(G)\), then the representation \(r(m, N)\) of \(m\) with respect to \(N\) is the k-tuple \(\big(d(m, n_{1}), d(m, n_{2}),\ldots,d(m, n_{k})\big)\). If different vertices of \(G\) have different representations with respect to \(N\), then the set \(N\) is said to be a resolving set of \(G\). The metric basis of \(G\) is basically a resolving set having minimum cardinality. The cardinality of metric basis is represented by \(\dim (G)\), and is called metric dimension of \(G.\)
In [1], Slater introduced the idea of resolving sets and also in [2], Harary and Melter introduced this concept individually. Different applications of this idea has been introduced in the fields like network discovery and verification [3], robot navigation [4] and chemistry.
The introduction of doubly resolving sets is given by Caceres et al. (see [5]) by presenting its connection with metric dimension of the cartesian product \(G\Box G\) of the graph \(G\). The doubly resolving sets create a valuable means for finding upper bounds on the metric dimension of graphs. The vertices \(a\) and \(b\) of the graph \(G\) with order \(|V(G)|\geq 2\) are supposed to doubly resolve vertices \(u_{1}\) and \(v_{1}\) of the graph \(G\) if \(d(u_{1}, a)-d(u_{1}, b)\neq d(v_{1}, a)-d(v_{1}, b).\) A subset \(D\) of vertices doubly resolves \(G\) if every two vertices in \(G\) are doubly resolved by some two vertices of \(D\). Precisely, in \(G\) there do not exist any two different vertices having the same difference between their corresponding metric coordinates with respect to \(D.\) A doubly resolving set with minimum cardinality is called the minimal doubly resolving set. The minimum cardinality of a doubly resolving set for \(G\) is represented by \(\psi(G).\) In case of some convex polytopes, hamming and prism graphs, the minimal doubly resolving sets has been obtained in [6], [7] and [8] respectively.
Clearly, if \(a\) and \(b\) doubly resolve \(u_{1}\) and \(v_{1},\) then \(d(u_{1}, a)-d(v_{1}, a)\neq 0\) or \(d(u_{1}, b)-d(v_{1}, b)\neq 0,\) and thus \(a\) or \(b\) resolve \(u_{1}\) and \(v_{1},\) this shows that a doubly resolving set is also a resolving set, which implies \(\dim(G)\leq \psi(G)\) for all graphs \(G\). Finding \(\psi(G)\) and \(\dim(G)\) are NP-hard problems proved in [9, 10].
The line graph \(L(G)\) of a graph \(G\) is defined as the graph whose vertices are the edges of \(G\), with two adjacent vertices if the corresponding edges have one vertex common in \(G\). In mathematics, the metric properties of line graphs have been studied to a great extent (see [11, 12, 13, 14, 15, 16]) and in chemistry literature, its significant applications have been proved (see [17, 18, 19, 20, 21, 22, 23]). In [24], the edge version of metric dimension has been introduced, which is defined as:
Definition 1.
The edge distance \(d_E(f, g)\) between two edges \(f, g \in E(G)\) is the length of a shortest path between vertices \(f\) and \(g\) in the line graph \(L(G).\)
If \(d_E(e, f)\neq d_E(e, g)\), then the edge \(e\in E(G)\) is said to edge resolve two edges \(f\) and \(g\) of \(E(G)\).
Suppose that \(N_E=\{f_{1}, f_{2},\ldots, f_{k}\}\subseteq E(G)\) is an ordered set and \(e\) is an edge of \(E(G)\). Then the edge version of representation \(r_E(e, N_E)\) of \(e\) with respect to \(N_E\) is the k-tuple \(\big(d_E(e, f_{1}), d_E(e, f_{2}),\ldots,d_E(e, f_{k})\big)\).
If different edges of \(G\) have different edge version of representations with respect to \(N_E\), then the set \(N_E\) is said to be an edge version of resolving set of \(G\).
The edge version of metric basis of \(G\) is basically an edge version of resolving set having minimum cardinality. The cardinality of edge version of metric basis is represented by \(\dim_E (G)\), and is called edge version of metric dimension of \(G.\)
The following theorems in [24] are important for us.
Theorem 1. Let \(S_n\) be the family of \(n\)-sunlet graph then \[\,\,\ \dim_E(S_{n})= \left\{ \begin{array}{ll} 2, & {\rm if}\ n\text{ is even}; \\[2mm] 3 , & {\rm if}\ n \text{ is odd.} \\[2mm] \end{array} \right.\]
Theorem 2. Let \(Y_n\) be the family of prism graph then \(\dim_E(Y_n)=3\) for \(n\ge3.\)
In this article, we proposed minimal edge version of doubly resolving sets of a graph \(G\), based on edge distances of graph \(G\) as follows:
Definition 2.
The edges \(f\) and \(g\) of the graph \(G\) with size \(|E(G)|\geq 2\) are supposed to edge doubly resolve edges \(f_{1}\) and \(f_{2}\) of the graph \(G\) if \(d_E(f_{1}, f)-d_E(f_{1}, g)\neq d_E(f_{2}, f)-d_E(f_{2}, g)\).
Let \(D_E = \{f_1, f_2,\ldots, f_k\}\) be an ordered set of the edges of \(G\). Then if any two edges \(e\neq f\in E(G)\) are edge doubly resolved by some two edges of set \(D_E\) then the set \(D_E\subseteq E(G)\) is said to be an edge version of doubly resolving set of \(G\). The minimum cardinality of an edge version of doubly resolving set of \(G\) is represented by \(\psi_E (G).\)
Note that every edge version of a doubly resolving set is an edge version of a resolving set, which implies \(\dim_E(G)\leq \psi_E(G)\) for all graphs \(G\).
The family of \(n\)-sunlet graph \(S_{n}\) is obtained by joining \(n\) pendant edges to a cycle graph \(C_n\) (see Figure 1).
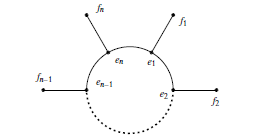
For our purpose, we label the inner edges of \(S_{n}\) by {\(e_i\) : \(\forall\) \(0\leq i\leq n-1\)} and the pendent edges by {\(f_i\) : \(\forall\) \(0\leq i\leq n-1\)} as shown in Figure 1.
As motivated by Theorem 1, we obtain \[\,\,\ \psi_E (S_{n})\geq \left\{ \begin{array}{ll} 2, & {\rm if}\ n\text{ is even}; \\[2mm] 3 , & {\rm if}\ n \text{ is odd.} \\[2mm] \end{array}\right.\]
Furthermore, we will show that \(\psi_E
(S_{n})=3\) for \(n\geq4.\)
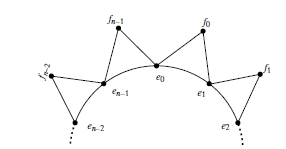
In order to calculate the edge distances for family of \(n\)-sunlet graphs \(S_n\), consider the line graph \(L(S_n)\) as shown in Figure 2.
| \(n\) | \(i\) | \(S_{i}(e_{0})\) |
|---|---|---|
| \(1 \leq i\leq k\) | {\(f_{i-1}\), \(e_{i}\), \(f_{n-i}\), \(e_{n-i}\)} | |
| \(2k (k\geq 2)\) | \(k\) | \(\{f_{k-1}, f_{k}, e_{k}\}\) |
| \(2k+1 (k\geq 2)\) | \(k\) | \(\{f_{k-1}, e_{k}, f_{k+1}, e_{k+1}\}\) |
| \(k+1\) | \(\{f_{k}\}\) |
The symmetry in Figure 2 shows that \(d_E(e_{i}, e_{j})= d_E(e_{0}, e_{|j-i|})\) for \(0 \leq |j-i|\leq n-1.\) If \(n= 2k\), where \(k\geq 2,\) we have
\[\,\,\ d_E(f_{i}, f_{j})= \left\{ \begin{array}{ll} d_E(e_{0}, f_{|j-i|})-1, & {\rm if}\ |j-i|= 0; \\[2mm] d_E(e_{0}, f_{|j-i|}), & {\rm if}\ 1\leq |j-i|< k; \\[2mm] d_E(e_{0}, f_{|j-i|})+1, & {\rm if}\ k\leq |j-i|\leq n-1, \\[2mm] \end{array} \right.\]
\[\,\,\ d_E(e_{i}, f_{j})= \left\{ \begin{array}{ll} d_E(e_{0}, f_{|j-i|}), & {\rm if}\ 0\leq |j-i|\leq n-1 \text{ for } i\leq j; \\[2mm] d_E(e_{0}, f_{|j-i|})-1, & {\rm if}\ 1\leq |j-i|< k \text{ for } i> j ; \\[2mm] d_E(e_{0}, f_{|j-i|}), & {\rm if}\ |j-i|= k \text{ for } i> j ; \\[2mm] d_E(e_{0}, f_{|j-i|})+1, & {\rm if}\ k < |j-i|\leq n-1 \text{ for } i> j. \\[2mm] \end{array} \right.\]
If \(n=2k+1\) where \(k\geq 2,\) we have
\[\,\,\ d_E(f_{i}, f_{j})= \left\{ \begin{array}{ll} d_E(e_{0}, f_{|j-i|})-1, & {\rm if}\ |j-i|=0; \\[2mm] d_E(e_{0}, f_{|j-i|}), & {\rm if}\ 1\leq |j-i|\leq k; \\[2mm] d_E(e_{0}, f_{|j-i|})+1, & {\rm if}\ k< |j-i|\leq n-1, \\[2mm] \end{array} \right.\]
\[\,\,\ d_E(e_{i}, f_{j})= \left\{ \begin{array}{ll} d_E(e_{0}, f_{|j-i|}), & {\rm if}\ 0\leq |j-i|\leq n-1 \text{ for } i\leq j; \\[2mm] d_E(e_{0}, f_{|j-i|})-1, & {\rm if}\ 1\leq |j-i|\leq k \text{ for } i> j ; \\[2mm] d_E(e_{0}, f_{|j-i|})+1, & {\rm if}\ k < |j-i|\leq n-1 \text{ for } i> j. \\[2mm] \end{array} \right.\]
As a result, if we know the edge distance \(d_E(e_{0},e)\) for any \(e\in E(S_{n})\), then one can recreate the edge distances between any two edges from \(E(S_n).\)
Lemma 1. \(\psi_E(S_{n})> 2\), for \(n=2k\), \(k\geq 2.\)
Proof. As we know that for \(n =2k\), \(\psi_E(S_{n})\geq 2.\) So it is necessary to prove that each of the subset \(D_E\) of edge set \(E(S_{n})\) such that \(|D_E|=2\) is not an edge version of doubly resolving set for \(S_{n}.\) In Table 2, seven possible types of the set \(D_E\) are presented and for each of them the resultant non-edge doubly resolved pair of edges from edge set \(E(S_{n})\) is found. To verify, let us take an example, the edges \(e_{k}, e_{k+1}\) are not edge doubly resolved by any two edges of the set \(\{e_{0}, e_{i}; k< i \leq n-1\}\). Obviously, for \(k< i\leq n-1\), we have \(d_E(e_{0}, e_{k})= d_E(e_{0}, e_{|k-0|})= k\), \(d_E(e_{0}, e_{k+1})= d_E(e_{0}, e_{|k+1-0|})= k-1\), \(d_E(e_{i}, e_{k})= d_E(e_{0}, e_{|k-i|})= i-k\) and \(d_E(e_{i}, e_{k+1})=d_E(e_{0}, e_{|k+1-i|})=i-k-1\). So, \(d_E(e_{0}, e_{k})- d_E(e_{0}, e_{k+1})= d_E(e_{i}, e_{k})- d_E(e_{i}, e_{k+1})= 1,\) that is, \(\{e_{0}, e_{i}; k< i \leq n-1\}\) is not an edge version of doubly resolving set of \(S_{n}\). Using this procedure we can verify all other non-edge doubly resolved pairs of edges for all other possible types of \(D_E\) from Table 2.
| \(D_E\) | Non-edge doubly resolved pairs |
|---|---|
| \(\{e_{0}, e_{i}\}\), \(0 < i < k\) | \(\{e_{0}, e_{n-1}\}\) |
| \(\{e_{0}, e_{i}\}\), \(k < i \leq n-1\) | \(\{e_{k}, e_{k+1}\}\) |
| \(\{e_{0}, f_{i}\}\), \(0 \leq i < k\) | \(\{e_{0}, f_{n-1}\}\) |
| \(\{e_{0}, f_{i}\}\), \(k \leq i \leq n-1\) | \(\{e_{0}, f_{0}\}\) |
| \(\{f_{0}, f_{i}\}\), \(1 \leq i < k\) | \(\{e_{k}, f_{k}\}\) |
| \(\{f_{0}, f_{k}\}\) | \(\{e_{0}, e_{1}\}\) |
| \(\{f_{0}, f_{i}\}\), \(k < i \leq n-1\) | \(\{e_{1}, f_{1}\}\) |
◻
Lemma 2. \(\psi_E(S_{n})=3,\) for \(n=2k\), \(k\geq 2.\)
Proof. The Table 3 demonstrate that edge version of representations of \(S_{n}\) in relation to the set \(D_E^{\ast} = \{e_{0}, e_{1}, e_{k}\}\) in a different manner.
| \(i\) | \(S_{i}(e_{0})\) | \(D_E^{\ast}= \{{e_{0}, e_{1}, e_{k}}\}\) |
|---|---|---|
| \(0\) | \(e_{0}\) | \((0, 1, k)\) |
| \(1\leq i< k\) | \(f_{i-1}\) | \((i, i-1, k+1-i)\) |
| \(e_{i}\) | \((i, i-1, k-i)\) | |
| \(f_{n-i}\) | \((i, i+1, k+1-i)\) | |
| \(e_{n-i}\) | \((i, i+1, k-i)\) | |
| \(i=k\) | \(f_{k-1}\) | \((k, k-1, 1)\) |
| \(f_{k}\) | \((k, k, 1)\) | |
| \(e_{k}\) | \((k, k-1, 0)\) |
Now from Table 3, as \(e_{0} \in D_E^{\ast}\), so the first edge version of metric coordinate of the vector of \(e_{0}\in S_{i}(e_{0})\) is equal to \(0\). For each \(i\in \{1,2,3,\ldots,k\}\), one can easily check that there are no two edges \(h_1, h_2 \in S_{i}(e_{0})\) such that \(r_E(h_1, D_E^{\ast})- r_E(h_2, D_E^{\ast})=0\). Also, for each \(i, j\in \{1,2,3,\ldots,k\}, i\neq j\), there are no two edges \(h_1 \in S_{i}(e_{0})\) and \(h_2 \in S_{j}(e_{0})\) such that \(r_E(h_1,D_E^{\ast})- r_E(h_2,D_E^{\ast})=i- j\). In this manner, the set \(D_E^{\ast}= \{{e_{0}, e_{1}, e_{k}}\}\) is the minimal edge version of doubly resolving set for \(S_{n}\) with \(n=2k\), \(k\geq 2\) and hence Lemma 2 holds. ◻
Lemma 3. \(\psi_E(S_{n})=3\), for \(n=2k+1\), \(k\geq 2.\)
Proof. The Table 4 demonstrate that the edge version of representations of \(S_{n}\) in relation to the set \(D_E^{\ast} = \{e_{0}, e_{1}, e_{k+1}\}\) in a different way.
| \(i\) | \(S_{i}(e_{0})\) | \(D_E^{\ast}= \{{e_{0}, e_{1}, e_{k+1}}\}\) |
|---|---|---|
| \(0\) | \(e_{0}\) | \((o, 1, k)\) |
| \(1\leq i< k\) | \(f_{i-1}\) | \((i, i-1, k+2-i)\) |
| \(e_{i}\) | \((i, i-1, k+1-i)\) | |
| \(f_{n-i}\) | \((i, i+1, k+1-i)\) | |
| \(e_{n-1}\) | \((i, i+1, k-i)\) | |
| \(i=k\) | \(f_{k-1}\) | \((k, k-1, 2)\) |
| \(e_{k}\) | \((k, k-1, 1)\) | |
| \(f_{k+1}\) | \((k, k+1, 1)\) | |
| \(e_{k+1}\) | \((k, k, 0)\) | |
| \(i=k+1\) | \(f_{k}\) | \((k+1, k, 1)\) |
Now from Table 4, as \(e_{0} \in D_E^{\ast}\), so the first edge version of metric coordinate of the vector of \(e_{0}\in S_{i}(e_{0})\) is equal to \(0\). Similarly for each \(i\in \{1,2,3,\ldots,k+1\}\), one can easily find that there are no two edges \(h_1, h_2 \in S_{i}(e_{0})\) such that \(r_E(h_1,D_E^{\ast})- r_E(h_2,D_E^{\ast})=0\). Likewise, for every \(i, j\in \{1,2,3,\ldots,k+1\}, i\neq j\), there are no two edges \(h_1 \in S_{i}(e_{0})\) and \(h_2 \in S_{j}(e_{0})\) such that \(r_E(h_1,D_E^{\ast})- r_E(h_2,D_E^{\ast})=i- j\). Like so, the set \(D_E^{\ast}= \{{e_{0}, e_{1}, e_{k+1}}\}\) is the minimal edge version of doubly resolving set for \(S_{n}\) with \(n=2k+1\), \(k\geq 2\) and consequently Lemma 3 holds. ◻
It is displayed from the whole technique that \(\psi_E(S_{n})=3\), for \(n\geq 4\). We state the resulting main theorem by using Lemma 2 and Lemma 3 as mentioned below;
Theorem 3. Let \(S_{n}\) be the \(n\)-sunlet graph for \(n\geq 4.\) Then \(\psi_E(S_{n})=3.\)
A family of prism graph \(Y_n\) is a cartesian product graph \(C_n\times P_2\), where \(C_n\) is a cycle graph of order \(n\) and \(P_2\) is a path of order \(2\) (see Figure 3).
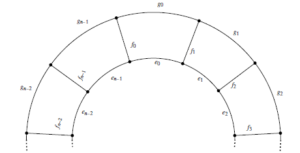
The family of prism graph \(Y_{n}\) consists of \(4\)-sided faces and \(n\)-sided faces. For our purpose, we label the inner cycle edges of \(Y_{n}\) by {\(e_i\) : \(0\leq i\leq n-1\)}, middle edges by {\(f_i\) : \(0\leq i\leq n-1\)} and the outer cycle edges by {\(g_i\) : \(1\leq i\leq n-1\)} as shown in Figure 3.
As motivated by Theorem 1, we obtain \(\psi_E (Y_{n})\geq 3\). Furthermore, we will show that \(\psi_E (Y_{n})=3\) for \(n\geq6.\)
In order to calculate the edge distances for family of prism graphs \(Y_n\), consider the line graph \(L(Y_n)\) as shown in Figure 4.
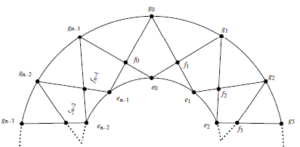
Define \(S_{i}(f_{0})=\{f\in E(Y_{n}):d_E(f_{0}, f)= i\}\). For \(\psi_E (Y_{n})\) with \(n\geq 6,\) we can locate the sets \(S_{i}(f_{0})\) that are represented in the Table 5. It is clearly observed from Figure 4 that \(S_{i}(f_{0})= \emptyset\) for \(i\geq k+2.\) From the above mentioned sets \(S_{i}(f_{0}),\) it is clear that they can be utilized to define the edge distance between two arbitrary edges of \(E(Y_{n})\) in the subsequent way.
| \(n\) | \(i\) | \(S_{i}(f_{0})\) |
|---|---|---|
| 1 | \(\{e_{0}, g_{0}, e_{n-1}, g_{n-1}\}\) | |
| 2 \(\leq i\leq k\) | \(\{f_{i-1}, e_{i-1}, g_{i-1}, f_{n+1-i}, e_{n-i}, g_{n-i}\)} | |
| \(2k(k\geq 3)\) | \(k+1\) | \(\{f_{k}\}\) |
| \(2k+1(k\geq 3)\) | \(k+1\) | \(\{f_{k}, e_{k}, g_{k}, f_{k+1}\}\) |
The symmetry in Figure 4 shows that \(d_E(f_{i}, f_{j})= d_E(f_{0}, f_{|j-i|})\)
for \(0 \leq |j-i|\leq n-1.\) If \(n= 2k\), where \(k\geq 3,\) we have
\[\,\,\ d_E(e_{i}, e_{j})= d_E(g_{i}, g_{j})= \left\{ \begin{array}{ll} d_E(f_{0}, e_{|j-i|})-1, & {\rm if}\ 0\leq |j-i|< k; \\[2mm] d_E(f_{0}, e_{|j-i|}), & {\rm if}\ k\leq |j-i|\leq n-1, \\[2mm] \end{array} \right.\]
\[\,\,\ d_E(f_{i}, e_{j})= d_E(f_{i}, g_{j})= \left\{ \begin{array}{ll} d_E(f_{0}, e_{|j-i|}), & {\rm if}\ 0\leq |j-i|\leq n-1, \text{ for } i\leq j; \\[2mm] d_E(f_{0}, e_{|j-i|})-1, & {\rm if}\ 1\leq |j-i|< k, \text{ for } i> j; \\[2mm] d_E(f_{0}, e_{|j-i|}), & {\rm if}\ |j-i|=k, \text{ for } i> j; \\[2mm] d_E(f_{0}, e_{|j-i|})+1, & {\rm if}\ k < |j-i|\leq n-1, \text{ for } i> j, \\[2mm] \end{array} \right.\] \[\,\,\, d_E(e_{i}, g_{j})= \left\{ \begin{array}{ll} d_E(f_{0}, e_{|j-i|})+1, & {\rm if}\ |j-i|=0; \\[2mm] d_E(f_{0}, e_{|j-i|}), & {\rm if}\ 1\leq |j-i|< k; \\[2mm] d_E(f_{0}, e_{|j-i|})+1, & {\rm if}\ k \leq |j-i|\leq n-1. \\[2mm] \end{array} \right.\] If \(n= 2k+1\) where \(k\geq 3,\) we have \[\,\,\ d_E(e_{i}, e_{j})= d_E(g_{i}, g_{j})= \left\{ \begin{array}{ll} d_E(f_{0}, e_{|j-i|})-1, & {\rm if}\ 0\leq |j-i|\leq k; \\[2mm] d_E(f_{0}, e_{|j-i|}), & {\rm if}\ k< |j-i|\leq n-1, \\[2mm] \end{array} \right.\] \[\,\,\ d_E(f_{i}, e_{j})= d_E(f_{i}, g_{j})= \left\{ \begin{array}{ll} d_E(f_{0}, e_{|j-i|}), & {\rm if}\ 0\leq |j-i|\leq n-1 \text{ for } i\leq j; \\[2mm] d_E(f_{0}, e_{|j-i|})-1, & {\rm if}\ 1\leq |j-i|\leq k \text{ for } i> j ; \\[2mm] d_E(f_{0}, e_{|j-i|})+1, & {\rm if}\ k < |j-i|\leq n-1 \text{ for } i> j, \\[2mm] \end{array} \right.\] \[\,\,\, d_E(e_{i}, g_{j})= \left\{ \begin{array}{ll} d_E(f_{0}, e_{|j-i|})+1, & {\rm if}\ |j-i|=0; \\[2mm] d_E(f_{0}, e_{|j-i|}), & {\rm if}\ 1\leq |j-i|\leq k; \\[2mm] d_E(f_{0}, e_{|j-i|})+1, & {\rm if}\ k < |j-i|\leq n-1. \\[2mm] \end{array} \right.\] As a result, if we know the edge distance \(d_E(f_{0},f)\) for any \(f\in E(Y_n)\) then one can recreate the edge distances between any two edges from \(E(Y_n).\)
Lemma 4. \(\psi_E (Y_{n})=3,\) for \(n=2k\), \(k\geq 3.\)
Proof. The Table 6 demonstrate that edge version of representations of \(Y_{n}\) in relation to the set \(D_E^{\ast} = \{e_{0}, e_{k-1}, f_{k+1}\}\) in a different manner.
Now from Table 6, as \(e_{0} \in D_E^{\ast}\), so the first edge version of metric coordinate of the vector of \(f_{0}\in S_{i}(f_{0})\) is equal to \(1\). For each \(i\in \{1,2,3,\ldots,k+1\}\), one can easily check that there are no two edges \(h_1, h_2 \in S_{i}(f_{0})\) such that \(r_E(h_1, D_E^{\ast})- r_E(h_2, D_E^{\ast})=0\). Also, for each \(i, j\in \{1,2,3,\ldots,k+1\}, i\neq j\), there are no two edges \(h_1 \in S_{i}(f_{0})\) and \(h_2 \in S_{j}(f_{0})\) such that \(r_E(h_1,D_E^{\ast})- r_E(h_2,D_E^{\ast})=i- j\). In this manner, the set \(D_E^{\ast}= \{{e_{0}, e_{k-1}, f_{k+1}}\}\) is the minimal edge version of doubly resolving set for \(Y_{n}\) with \(n=2k\), \(k\geq 3\) and hence Lemma 4 holds. ◻
Lemma 5. \(\psi_E (Y_{n})=3\), for \(n=2k+1\), \(k\geq 3.\)
Proof. The Table 7 demonstrate that the edge version of
representations of \(Y_{n}\) in
relation to the set \(D_E^{\ast} = \{e_{0},
e_{k}, g_{k+2}\}\) in a different way.
| \(i\) | \(S_{i}(f_{0})\) | \(D_E^{\ast}= \{{e_{0}, e_{k}, g_{k+2}}\}\) |
|---|---|---|
| \(0\) | \(f_{0}\) | \((1, k+1, k-1)\) |
| \(1\) | \(e_{0}\) | \((0, k, k)\) |
| \(g_{0}\) | \((2, k+1, k-1)\) | |
| \(e_{n-1}\) | \((1, k, k-1)\) | |
| \(g_{n-1}\) | \((2, k+1, k-2)\) | |
| \(2\) | \(f_{1}\) | \((1, k, k)\) |
| \(e_{1}\) | \((1, k-1, k+1)\) | |
| \(g_{1}\) | \((2, k, k)\) | |
| \(f_{n-1}\) | \((2, k, k-2)\) | |
| \(e_{n-2}\) | \(\,\,\ = \left\{ \begin{array}{ll} (2, 2, 2), & {\rm if}\ k=3; \\[2mm] (2, k-i, k-2), & {\rm if}\ k< 3. \end{array} \right.\) | |
| \(g_{n-2}\) | \((3, k, k-3)\) | |
| \(3\leq i \leq k\) | \(f_{i-1}\) | \((i-1, k+2-i, k+4-i)\) |
| \(e_{i-1}\) | \((i-1, k+1-i, k+4-i)\) | |
| \(g_{i-1}\) | \((i, k+2-i, k+3-i)\) | |
| \(f_{n+1-i}\) | \(\,\,\ = \left\{ \begin{array}{ll} (k, 2, 1), & {\rm if}\ i=k; \\[2mm] (i, k+2-i, k-i), & {\rm if}\ i+1 \leq k \end{array} \right.\) | |
| \(e_{n-i}\) | \(\,\,\ = \left\{ \begin{array}{ll} (k, 1, 2), & {\rm if}\ i=k; \\[2mm] (i,2, 2), & {\rm if}\ i+1=k; \\[2mm] (i, k+1-i, k-i), & {\rm if}\ i+1 < k \end{array} \right.\) | |
| \(g_{n-i}\) | \(\,\,\ = \left\{ \begin{array}{ll} (k+1, 2, 1), & {\rm if}\ i=k; \\[2mm] (i+1, k+2-i, k-1-i), & {\rm if}\ i+1 \leq k \end{array} \right.\) | |
| \(i=k+1\) | \(f_{k}\) | \((k, 1, 3)\) |
| \(e_{k}\) | \((k, 0, 3)\) | |
| \(g_{k}\) | \((k+1, 2, 2)\) | |
| \(f_{k+1}\) | \((k+1, 1, 2)\) |
Now from Table 7, as \(e_{0} \in
D_E^{\ast}\), so the first edge version of metric coordinate of
the vector of \(f_{0}\in S_{i}(f_{0})\)
is equal to \(1\). Similarly for each
\(i\in \{1,2,3,\ldots,k+1\}\), one can
easily find that here are no two edges \(h_1,
h_2 \in S_{i}(f_{0})\) such that \(r_E(h_1,D_E^{\ast})-
r_E(h_2,D_E^{\ast})=0\). Likewise, for every \(i, j\in \{1,2,3,\ldots,k+1\}, i\neq j\),
there are no two edges \(h_1 \in
S_{i}(f_{0})\) and \(h_2 \in
S_{j}(f_{0})\) such that \(r_E(h_1,D_E^{\ast})- r_E(h_2,D_E^{\ast})=i-
j\). Like so, the set \(D_E^{\ast}=
\{{e_{0}, e_{k}, g_{k+2}}\}\) is the minimal edge version of
doubly resolving set for \(Y_{n}\) with
\(n= 2k+1\), \(k\geq 3\) and consequently Lemma 5
holds.
◻
It is displayed from the whole technique that \(\psi_E(Y_{n})=3\), for \(n\geq 6\). We state the resulting main
theorem by using Lemma 4 and Lemma 5 as mentioned
below;
Theorem 4. Let \(Y_{n}\) be the prism graph for \(n\geq 6.\) Then \(\psi_E (Y_{n})=3.\)
In this article, we computed the minimal edge version of doubly resolving sets and its cardinality \(\psi_E(G)\) by considering \(G\) as a family of \(n\)-sunlet graph \(S_{n}\) and prism graph \(Y_{n}\). In case of \(n\)-sunlet graphs, the graph is interesting to consider in the sense that its edge version of metric dimension \(\dim_E(S_{n})\) is dependent on the parity of \(n\) for both even and odd cases. The cardinality \(\psi_E(S_{n})\) of minimal edge version of doubly resolving set of \(n\)-sunlet graph \(S_{n}\) is independent from the parity of \(n\). In the case of prism graph \(Y_{n}\), the edge version of metric dimension \(\dim_E (Y_{n})\) and the cardinality \(\psi_E(Y_{n})\) of its minimal edge version of doubly resolving set are same for every \(n\geq 6.\)
Problem 1. Compute edge version of doubly resolving sets for some generalized petersen graphs.
The authors would like to express their honest appreciation to the referees for their valuable comments, which led to a improved manuscript.