Given a connected simple undirected graph
The theory of abstract convexity spaces was originally developed to
generalize classical convexity invariants such as Helly, Carathéodory,
and Radon numbers in
Graph convexity spaces have been a topic of much interest among the
several structures of abstract convexity spaces. Many researchers have
studied graph convexities from different perspectives. The most
prominent types of graph convexities are defined in terms of paths in
the graph, such as geodesic, induced path, and all-paths convexity [6-10]. An interesting
type of path convexity in graphs is defined using the paths
The Carathéodory number is a classical convexity invariant whose
relationship with two other classical convexity invariants, namely, the
Helly and Radon numbers of abstract convexities, has been extensively
studied in [5, 16]. Parker et
al. studied the Carathéodory number of the
We restrict our attention to finite, simple, and undirected graphs.
We denote a graph by
, and
is closed under arbitrary intersections.
A convexity space is a pair
Proposition 1. Let
If
If
No proper subset
The convex hull
In this section, we settle the Conjecture 4 on the upper bound of
Carathéodory number of claw-free graphs from [13]. We state it as a theorem (Theorem 1).
To establish the theorem, we commence by introducing relevant notations
and subsequently derive a lemma that specifically addresses a single
case of the theorem. Let
By definition of
Lemma 1. Let
Proof. Let
Now consider
Both
One of the
Case (1): If
Case (2): If one of the vertices
Subcase (2.1):
Since
If
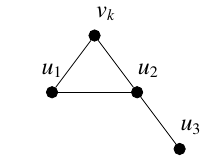
Suppose
If
If
Subsubcase 2.1.1:
If either
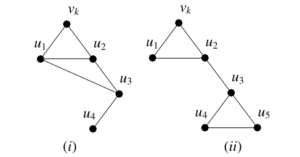
Subsubcase 2.1.2:
Let
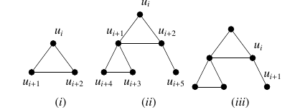
Sub-subcase 2.1.3: If both neighbours are same (Figure 5).
Then change
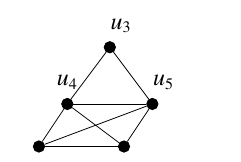
In general, if
Now continue the process with
Subcase 2.2:
We change
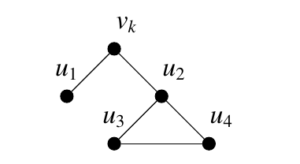
We obtain a sequence of vertices
Theorem 1. Let
Proof. Let
If
Case 1:
If
If
If
If
If
Subcase 2.2: If
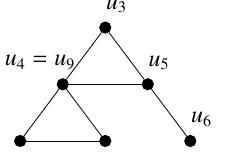
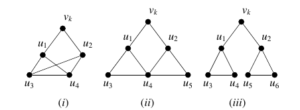
Case 3: If all neighbours are distinct(as given in
Figure 7
By following the procedure mentioned above, we eventually obtain a
finite sequence of vertices
Next, our goal is to identify all claw-free graphs that attain the
upper bound of the Carathéodory number for
Now, we will construct a collection of possible graphs from
More generally, if
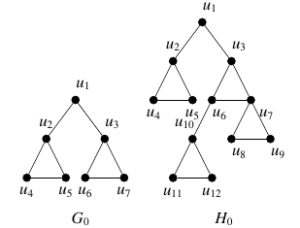
Theorem 2. Let
Proof. We can verify that
Now, we will prove that if
It should be noted that
Theorem 3. Let
Proof. The sufficiency of the statement is proven by the
theorem mentioned above. To prove the converse part of the theorem,
suppose
For
For subcases (a) and (b) of case 3, we have
Now, as in the proof, let
If they are not in
We continue by considering the vertices
Now, as in the proof, let
Note that if any of these five vertices has already been considered,
then we would have
Assume that there exists an edge between a vertex
Then
Now there are two cases: (1)
Case (1): If
Case (2):
Thus, If
Definition 1. Let
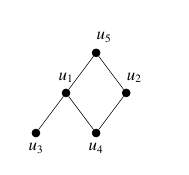
Theorem 4. If
Proof. Let
We now describe a procedure that adjusts the values
Case 1: If
Case 2: If only one of them belongs to
Subcase 2.1: If
If
If
If
Now, in general, if
Since
Since
If both of them belong to
If
If
If
If
If
If
Similarly, if
If
Subcase 2.2:
Case 3: Both
Continuing like this, we get a sequence that contains
1970-2025 CP (Manitoba, Canada) unless otherwise stated.