Two colorings have been introduced recently where an unrestricted coloring \(c\) assigns nonempty subsets of \([k]=\{1,\ldots,k\}\) to the edges of a (connected) graph \(G\) and gives rise to a vertex-distinguishing vertex coloring by means of set operations. If each vertex color is obtained from the union of the incident edge colors, then \(c\) is referred to as a strong royal coloring. If each vertex color is obtained from the intersection of the incident edge colors, then \(c\) is referred to as a strong regal coloring. The minimum values of \(k\) for which a graph \(G\) has such colorings are referred to as the strong royal index of \(G\) and the strong regal index of \(G\) respectively. If the induced vertex coloring is neighbor distinguishing, then we refer to such edge colorings as royal and regal colorings. The royal chromatic number of a graph involves minimizing the number of vertex colors in an induced vertex coloring obtained from a royal coloring. In this paper, we provide new results related to these two coloring concepts and establish a connection between the corresponding chromatic parameters. In addition, we establish the royal chromatic number for paths and cycles.
For a positive integer \(k\), let \({\cal P}^*([k])\) denote the set of nonempty subsets of \([k]=\{1, 2, \ldots, k\}\). For a connected graph \(G\), let \(c: E(G) \to {\cal P}^*([k])\) be an edge coloring of \(G\) where adjacent edges may be colored the same. An induced vertex coloring \(c': V(G) \to {\cal P}^*([k])\) can defined by either
(1) \(\displaystyle c'(v)=\bigcup_{e \in E_v} c(e)\) or (2) \(\displaystyle c'(v)=\bigcap_{e \in E_v} c(e)\),
where \(E_v\) is the set of edges incident with \(v\). In the case of (1), if \(c'\) is a proper vertex coloring of \(G\), that is, \(c'\) assigns adjacent vertices different colors, then \(c\) is called a royal \(k\)-edge coloring of \(G\). The minimum positive integer \(k\) for which a graph \(G\) has a royal \(k\)-edge coloring is the royal index \(\mathop{\rm roy}(G)\) of \(G\). If \(c'\) is vertex-distinguishing, that is, \(c'\) assigns a unique color to each vertex, then \(c\) is a strong royal \(k\)-edge coloring of \(G\). The minimum positive integer \(k\) for which a graph \(G\) has a strong royal \(k\)-edge coloring is the strong royal index \(\mathop{\rm sroy}(G)\) of \(G\). In the case of (2), if \(c'\) is a proper vertex coloring of \(G\), then \(c\) is called a regal \(k\)-edge coloring of \(G\). The minimum positive integer \(k\) for which a graph \(G\) has a regal \(k\)-edge coloring is the regal index \(\mathop{\rm reg}(G)\) of \(G\). If \(c'\) is vertex-distinguishing, then \(c\) is a strong regal \(k\)-edge coloring of \(G\). The minimum positive integer \(k\) for which a graph \(G\) has a strong regal \(k\)-edge coloring is the strong regal index \(\mathop{\rm sreg}(G)\) of \(G\). In this paper, we focus on the strong royal and strong regal indexes of graphs.
The concept of royal colorings was introduced in [1] in 2017 by Bousquet et al and independently studied in [2]. Regal colorings were introduced and studied in [3] in 2018. It was shown that these parameters exist for any connected graph of order at least \(3\) and have been established for many well-known classes of graphs.
Theorem 1. [1-3]For each integer \(n \ge 4\),
\(\mathop{\rm sreg}(K_n) = 1 + \lfloor{\log_2 n}\rfloor\) and \(\mathop{\rm sroy}(K_{n}) = 1+ \left\lceil{\log_2 n}\right\rceil\).
Here we can see that these indexes can take different values for an infinite class of graphs. Similarly, these indexes take on distinct values for a path of order \(7\), namely \(\mathop{\rm sreg}(P_7)=4\) while \(\mathop{\rm sroy}(P_7)=3\). However, these indexes agree for all of order \(n\) at least \(4\) with \(n\not=7\) and for all cycles of order \(n\) at least \(4\).
Theorem 2. [1-3] If \(n \ge 4\) is an integer with \(n\ne 7\), then
\(\mathop{\rm sreg}(P_n) = \mathop{\rm sroy}(P_n) = 1 + \lfloor{\log_2 n}\rfloor\).
Theorem 3. [1,3,4] For each integer \(n \ge 4\), \[\mathop{\rm sreg}(C_n)=\mathop{\rm sroy}(C_n) =\left\{\begin{array}{cl} 1+ \left\lceil{\log_2 (n+1)}\right\rceil & \mbox{ if $n = 7$}\\ 1 + \lfloor{\log_2 n}\rfloor & \mbox{ if $n \ne 7$.} \end{array}\right.\]
For these classes of graphs, the strong regal index and the strong royal index differ by at most one. This phenomenon, in fact, is generally true for all connected graphs with order at least \(3\).
Theorem 4. If \(G\) is a connected graph of order at least \(3\), then \[|\mathop{\rm sroy}(G)-\mathop{\rm sreg}(G)|\leq 1.\]
Proof. First, we show that \(\mathop{\rm sroy}(G)\leq \mathop{\rm sreg}(G)+1\). Let \(\mathop{\rm sreg}(G)=k\) and suppose that \(c:E(G)\to {\cal P}^*([k])\) is a strong regal \(k\)-edge coloring of \(G\) where the vertex coloring \(c':V(G)\to {\cal P}^*([k])\) is a vertex-distinguishing vertex coloring induced by \(c\). Define a complementary coloring \(\overline{c}:E(G)\to {\cal P}^*([k+1])\) by \(\overline{c}(e)=[k+1]-c(e)\). Then \(\overline{c}':V(G)\to {\cal P}^*([k+1])\) is a strong royal \((k+1)\)-edge coloring of \(G\). Indeed, observe that \[\overline{c}'(v)=\bigcup_{e\in E_v}\overline{c}(e)=\bigcup_{e\in E_v}\left([k+1]-c(e)\right)=[k+1]-c'(v)\] where \(E_v\) is the set of edges incident to \(v\). Note that \(\overline{c}'(v)\) is nonempty since \(c'(v)\subseteq [k]\). Since \(c'\) is vertex-distinguishing, it follows that \(\overline{c}'\) is also vertex-distinguishing. Hence, \(\mathop{\rm sroy}(G)\leq k+1=\mathop{\rm sreg}(G)+1\).
Next, we show that \(\mathop{\rm sreg}(G)\leq \mathop{\rm sroy}(G)+1\). Let \(\mathop{\rm sroy}(G)=k\) and suppose that \(c:E(G)\to {\cal P}^*([k])\) is a strong royal \(k\)-edge coloring of \(G\) where the vertex coloring \(c':V(G)\to {\cal P}^*([k])\) is a vertex-distinguishing vertex coloring induced by \(c\). Define a complementary coloring \(\overline{c}:E(G)\to {\cal P}^*([k+1])\) by \(\overline{c}(e)=[k+1]-c(e)\). Then \(\overline{c}':V(G)\to {\cal P}^*([k+1])\) is a strong regal \((k+1)\)-edge coloring of \(G\). Indeed, observe that \[\overline{c}'(v)=\bigcap_{e\in E_v}\overline{c}(e)=\bigcap_{e\in E_v}\left([k+1]-c(e)\right)=[k+1]-c'(v)\] where \(E_v\) is the set of edges incident to \(v\). Note that \(\overline{c}'(v)\) is nonempty since \(c'(v)\subseteq [k]\). Since \(c'\) is vertex-distinguishing, it follows that \(\overline{c}'\) is also vertex-distinguishing. Hence, \(\mathop{\rm sreg}(G)\leq k+1=\mathop{\rm sroy}(G)+1\). Consequently, \(\mathop{\rm sroy}(G)\geq \mathop{\rm sreg}(G)-1\) and so
\(\mathop{\rm sreg}(G)-1\leq \mathop{\rm sroy}(G)\leq \mathop{\rm sreg}(G)+1\).
Therefore, \[|\mathop{\rm sroy}(G)-\mathop{\rm sreg}(G)|\leq 1.\] ◻
It is possible for either \(\mathop{\rm sreg}(G)<\mathop{\rm sroy}(G)\) or \(\mathop{\rm sroy}(G)<\mathop{\rm sreg}(G)\) for a connected graph \(G\). For example, we saw that \(\mathop{\rm sreg}(K_5)=3\) while \(\mathop{\rm sroy}(K_5)=4\). On the other hand, \(\mathop{\rm sroy}(P_7)=3\) while \(\mathop{\rm sreg}(P_7)=4\).
In addition, a common lower bound has been established for these parameters for a given a graph in terms of its order and upper bounds on these parameters relating to subgraph structure are known.
Proposition 1. [2,3] If \(G\) is a connected graph of order \(n \ge 4\), then
\(\mathop{\rm sroy}(G) \ge 1 + \lfloor{\log_2 n}\rfloor\) and \(\mathop{\rm sroy}(G) \ge 1 + \lfloor{\log_2 n}\rfloor\).
Proposition 2. [2,3] For a connected graph \(G\) of order \(4\) or more, let \({\cal H}\) be the set of connected spanning subgraphs of \(G\). Then
\(\mathop{\rm sreg}(G) \le \min\{\mathop{\rm sreg}(H): \ H \in {\cal H}\}\)
and
\(\mathop{\rm sroy}(G) \le 1+ \min\{\mathop{\rm sroy}(H): \ H \in {\cal H}\}\).
For a graph \(G\) of order \(n\geq 3\), let \(k\) be the unique positive integer such that \(2^{k-1}\leq n \leq 2^{k}-1\). In [2,3], corresponding versions of the following conjecture were stated.
Conjecture 1. If \(G\) is a connected graph of order \(n\) at least \(3\) where \(2^{k-1}\leq n \leq 2^{k}-1\), then
\(\mathop{\rm sroy}(G) \in \{k,k+1\}\) and \(\mathop{\rm sreg}(G)\in \{k,k+1\}.\)
A connected graph \(G\) of order \(n \ge 3\) where \(2^{k-1} \le n \le 2^k-1\) is a royal-zero graph if \(\mathop{\rm sroy}(G)=k\) and is a royal-one graph if \(\mathop{\rm sroy}(G)=k+1\). Similarly, \(G\) is a regal-zero graph if \(\mathop{\rm sreg}(G)=k\) and is a regal-one graph if \(\mathop{\rm sreg}(G)=k+1\). As a consequence of Proposition 4, we have the following result.
Corollary 1.If \(G\) is royal-zero or regal-zero, then
\(\mathop{\rm sroy}(G) \in \{k,k+1\}\) and \(\mathop{\rm sreg}(G)\in \{k,k+1\}\).
The corona \(\mathop{\rm cor}(G)\) of a graph \(G\) is the graph obtained from \(G\) by adding a pendant edge at each vertex of \(G\). Thus, if the order of \(G\) is \(n\), then the order of \(\mathop{\rm cor}(G)\) is \(2n\). It was shown in [4] that the strong royal index of \(\mathop{\rm cor}(G)\) never exceeds \(\mathop{\rm sroy}(G)\) by more than 1. We prove a similar result for the strong regal index of \(\mathop{\rm cor}(G)\).
Proposition 3. If \(G\) is a connected graph of order \(n \ge 4\), then
\(\mathop{\rm sreg}(\mathop{\rm cor}(G)) \le \mathop{\rm sreg}(G) + 1\).
Furthermore, if \(G\) is regal-zero, then \(\mathop{\rm cor}(G)\) is regal-zero.
Proof. Let \(V(G)=\{v_1, v_2, \ldots, v_n\}\) and let \(H = \mathop{\rm cor}(G)\) be obtained from \(G\) by adding the pendant edge \(u_iv_i\) at \(v_i\) for \(1 \le i \le n\). Let \(c_G: E(G) \to {\cal P}^*([k])\) be a strong regal \(k\)-edge coloring of \(G\). Define an edge coloring \(c_H: E(H) \to {\cal P}^*([k+1])\) by \[c_H(e)=\left\{ \begin{array}{ll} c_G(e) & \mbox{ if $e \in E(G)$}\\ c'_G(v_i) \cup \{k+1\} & \mbox{ if $e= u_iv_i$ for $1 \le i \le n$.} \end{array}\right.\] Then the induced vertex coloring \(c'\) is given by
\(c_H'(u_i) = c'_G(v_i)\cup \{k+1\}\) and \(c'_H(v_i) = c_G'(v_i)\) for \(1 \le i \le n\).
Since \(c'_H\) is vertex-distinguishing, it follows that \(c_H\) is a strong regal \((k+1)\)-edge coloring of \(\mathop{\rm cor}(G)\) and so \(\mathop{\rm sreg}(H) \le \mathop{\rm sreg}(G) + 1\).
If \(G\) is a connected graph of
order \(n \ge 4\) where \(2^{k-1} \le n \le 2^k-1\), then \(\mathop{\rm cor}(G)\) is a connected graph
of order \(2n \ge 8\) where \(2^{k} \le 2n \le 2^{k+1}-2\). Since \(\mathop{\rm sreg}(\mathop{\rm cor}(G)) \ge
k+1\) by Proposition 1 and there is a strong
regal \((k+1)\)-edge coloring of \(\mathop{\rm cor}(G)\), it follows that
\(\mathop{\rm sreg}(\mathop{\rm cor}(G))=
k+1\) and so \(\mathop{\rm
cor}(G)\) is regal-zero. 0◻
Though thus far we consider only connected graphs of order at least
\(3\), any graph whose connected
components have order at least \(3\)
also have strong royal and strong regal colorings and, consequently, the
associated chromatic parameters. Let \(F\) and \(H\) be two graphs with disjoint vertex
sets. The union \(G =
F+ H\) of \(F\) and \(H\) has vertex set \(V(G) = V(F) \cup V(H)\) and edge set \(E(G) = E(F) \cup E(H)\). The union \(H+H\) of two disjoint copies of \(H\) is denoted by \(2H\). If a graph \(G\) consists of \(k\) (\(\ge
2\)) disjoint copies of a graph \(H\), then we write \(G = kH\). ◻
Proposition 4. If \(F\) and \(H\) are connected graphs of order at least \(3\), then
\(\max\{\mathop{\rm sroy}(F), \ \mathop{\rm sroy}(H)\} \le \mathop{\rm sroy}(F+ H)\leq \max\{\mathop{\rm sroy}(F), \ \mathop{\rm sroy}(H)\}+1\)
and
\(\max\{\mathop{\rm sreg}(F), \ \mathop{\rm sreg}(H)\} \le \mathop{\rm sreg}(F+ H)\leq \max\{\mathop{\rm sreg}(F), \ \mathop{\rm sreg}(H)\}+1\).
Proof. Since the argument for both the royal and regal cases are similar, we prove the result for only the regal case. Suppose that \(\mathop{\rm sreg}(F) = k_F\) and \(\mathop{\rm sreg}(H)= k_H\), where say \(k_F \le k_H\). Since the restriction of a strong regal coloring of \(F + H\) to \(H\) is also a strong regal coloring of \(H\), it follows that
\(\mathop{\rm sreg}(H) = \max\{\mathop{\rm sreg}(F), \ \mathop{\rm sreg}(H)\} \le \mathop{\rm sreg}(F+ H)\).
Thus, the lower bound holds. For the upper bound, we show that there is a strong regal \(k_H\)-edge coloring of \(F + H\). Let \(c_F\) be a strong regal \(k_F\)-edge coloring of \(F\) and let \(c_H\) be a strong regal \(k_H\)-edge coloring of \(H\). Define an edge coloring \(c: E(F + H ) \to {\cal P}^*([k_H+1])\) by \[c(e) =\left\{ \begin{array}{ll} c_F(e) & \mbox{ if $e\in E(F)$}\\ c_H(e)\cup \{k_H+1\} & \mbox{ if $e\in E(H)$.} \end{array} \right.\] Then the induced coloring \(c': V(F + H ) \to {\cal P}^*([k_H+1])\) is given by \[c'(v) =\left\{ \begin{array}{ll} c'_F(v) & \mbox{ if $v\in V(F)$}\\ c'_H(v)\cup \{k_H+1\} & \mbox{ if $v\in V(H)$.} \end{array} \right.\] Since \(c'_F\) and \(c'_H\) are vertex-distinguishing and \(c'(x) \ne c'(y)\) if \(x \in V(F)\) and \(y \in V(H)\), it follows that \(c'\) is a vertex-distinguishing vertex coloring of \(F + H\). Therefore, \(c\) is a strong regal \(k_H\)-edge coloring of \(F + H\). 0◻ Note that Proposition 4 cannot be improved. For example, we saw that \(\mathop{\rm sreg}(P_3)=\mathop{\rm sreg}(K_3) = \mathop{\rm sreg}(P_3+K_3) =3\), but \(\mathop{\rm sreg}(P_3) =\mathop{\rm sreg}(P_7) = 3\) and \(\mathop{\rm sreg}(P_3 + P_7) =4\).
Let \(F\) and \(H\) be two graphs with disjoint vertex sets. The join \(G = F\vee H\) of \(F\) and \(H\) has vertex set \(V(G) = V(F) \cup V(H)\) and edge set
\(E(G) = E(F) \cup E(H) \cup\{uv: u \in V(F), v\in V(H)\}\).
◻
Proposition 5. If \(F\) and \(H\) are connected graphs of order at least \(3\), then
\(\mathop{\rm sreg}(F\vee H)\leq \max\{\mathop{\rm sreg}(F), \ \mathop{\rm sreg}(H)\}+1\)
and
\(\mathop{\rm sroy}(F\vee H)\leq \max\{\mathop{\rm sroy}(F), \ \mathop{\rm sroy}(H)\}+2\).
Proof. Let \(G=F\vee H\). It suffices to show that a strong regal \(s\)-edge coloring and a strong royal \(t\)-edge coloring of \(G\) exist for values of \(s\) and \(t\) corresponding to each desired upper bound.
First, we consider \(\mathop{\rm sreg}(F\vee H)\). We may assume that
\(\mathop{\rm sreg}(F)\leq \mathop{\rm sreg}(H)=k\)
and so \(\max\{\mathop{\rm sreg}(F), \ \mathop{\rm sreg}(H)\}+1=k+1\). Then there are strong regal \(k\)-edge colorings \(c_F:E(F) \to {\cal P}^*([k])\) and \(c_H:E(H) \to {\cal P}^*([k])\) of \(F\) and \(H\) with vertex-distinguishing induced vertex colorings \(c_F'\) and \(c_H'\) respectively. Define an edge coloring \(c: E(G) \to {\cal P}^*([k+1])\) by
\[c(e) =\left\{ \begin{array}{ll} c_F(e) & \mbox{ if $e\in E(F)$}\\ c_H(e)\cup \{k+1\} & \mbox{ if $e\in E(H)$}\\ \{k+1\} & \mbox{ otherwise.} \end{array} \right.\] Then the induced coloring \(c': V(G ) \to {\cal P}^*([k+1])\) is given by \[c'(v) =\left\{ \begin{array}{ll} c'_F(v) & \mbox{ if $v\in V(F)$}\\ c'_H(v)\cup \{k+1\} & \mbox{ if $v\in V(H)$.} \end{array} \right.\] Since \(c'_F\) and \(c'_H\) are vertex-distinguishing and \(c'(x) \ne c'(y)\) if \(x \in V(F)\) and \(y \in V(H)\), it follows that \(c'\) is a vertex-distinguishing vertex coloring of \(G\). Therefore, \(c\) is a strong regal \((k+1)\)-edge coloring of \(G=F\vee H\).
Next, we consider \(\mathop{\rm sroy}(F \vee H)\). We may assume that
\(\mathop{\rm sroy}(F)\leq \mathop{\rm sroy}(H)=k\)
and so \(\max\{\mathop{\rm sroy}(F), \ \mathop{\rm sroy}(H)\}+2=k+2\). Then there are strong royal \(k\)-edge colorings \(c_F:E(F) \to {\cal P}^*([k])\) and \(c_H:E(H) \to {\cal P}^*([k])\) of \(F\) and \(H\) with vertex-distinguishing induced vertex colorings \(c_F'\) and \(c_H'\) respectively. Define an edge coloring \(c: E(G) \to {\cal P}^*([k+2])\) by
\[c(e) =\left\{ \begin{array}{ll} c_F(e) & \mbox{ if $e\in E(F)$}\\ c_H(e)\cup \{k+1\} & \mbox{ if $e\in E(H)$}\\ \{k+2\} & \mbox{ otherwise.} \end{array} \right.\] Then the induced coloring \(c': V(G) \to {\cal P}^*([k+2])\) is given by \[c'(v) =\left\{ \begin{array}{ll} c'_F(v)\cup \{k+2\} & \mbox{ if $v\in V(F)$}\\ c'_H(v)\cup \{k+1,k+2\} & \mbox{ if $v\in V(H)$.} \end{array} \right.\]
Since \(c'_F\) and \(c'_H\) are vertex-distinguishing and
\(c'(x) \ne c'(y)\) if \(x \in V(F)\) and \(y \in V(H)\), it follows that \(c'\) is a vertex-distinguishing vertex
coloring of \(G\). Therefore, \(c\) is a strong royal \((k+2)\)-edge coloring of \(G=F\vee H\). 0◻
Equality can be obtained for both bounds. Note that \(\mathop{\rm sreg}(P_3)=3\) and \(\mathop{\rm sroy}(P_3\vee P_3)=4\) while
\(\mathop{\rm sroy}(P_3)=2\) and \(\mathop{\rm sroy}(P_3\vee P_3)=4\).
Let \(F\) and \(H\) be two graphs with disjoint vertex sets. The Cartesian product \(G = F \ \Box \ H\) of \(F\) and \(H\) has vertex set \(V(G) = V(F) \times V(H)\), where two distinct vertices \((u, v)\) and \((x, y)\) of \(F \ \Box \ H\) are adjacent if either \(u = x\) and \(vy \in E(H)\) or \(v = y\) and \(ux \in E(F)\). In particular, the graph \(G\ \Box \ K_2\) consists of two copies \(G_1\) and \(G_2\) of \(G\). If \(V(G_1)=\{u_1,u_2,\dots u_n\}\) where \(u_i\) is labeled \(v_i\) in \(G_2\), then \(V(G_2) = \{v_1,v_2,\dots, v_n\}\) and
\(E(H)= E(G_1)\cup E(G_2) \cup \{u_iv_i: 1 \le i \le n\}\).
If \(G\) is a connected graph of order \(n \ge 4\) where \(2^{k-1} \le n \le 2^k-1\) for some integer \(k\), then \(G\ \Box \ K_2\) is a connected graph of order \(2n \ge 8\) where \(2^{k} \le 2n \le 2^{k+1}-2\). Therefore, \(\mathop{\rm sreg}(G\ \Box \ K_2) \ge k+1\) by Proposition 1. A bound was given for \(\mathop{\rm sroy}(G\ \Box \ K_2)\) in terms of \(\mathop{\rm sroy}(G)\) in [4]. ◻
Proposition 6.[4] If \(G\) is a connected graph of order at least \(3\), then
\(\mathop{\rm sroy}(G\ \Box \ K_2)\leq \mathop{\rm sroy}(G)+1\).
Here we extend this result to the strong regal indexes of graphs.
Proposition 7. If \(G\) is a connected graph of order at least \(3\), then
\(\mathop{\rm sreg}(G\ \Box \ K_2)\leq \mathop{\rm sreg}(G)+1\).
Proof. Suppose that \(\mathop{\rm sreg}(G)=k\). Then it suffices to show that there exists a strong regal \((k+1)\)-edge coloring of \(G\ \Box \ K_2\). By definition, \(G\ \Box \ K_2\) consists of two copies of \(G\), say \(G_1\) and \(G_2\) as describe previously. There exist strong regal \(k\)-edge colorings \(c_1:E(G_1) \to {\cal P}^*([k])\) and \(c_2:E(G_2) \to {\cal P}^*([k])\) with vertex-distinguishing induced vertex colorings \(c_1'\) and \(c_2'\) respectively.
Define an edge coloring \(c: E(G\ \Box \ K_2) \to {\cal P}^*([k+1])\) by
\[c(e) =\left\{ \begin{array}{ll} c_1(e) & \mbox{ if $e\in E(G_1)$}\\ c_2(e)\cup \{k+1\} & \mbox{ if $e\in E(G_2)$}\\ \{k+1\} & \mbox{ otherwise.} \end{array} \right.\] Then the induced coloring \(c': V(G\ \Box \ K_2) \to {\cal P}^*([k+1])\) is given by \[c'(v) =\left\{ \begin{array}{ll} c'_1(v) & \mbox{ if $v\in V(G_1)$}\\ c'_2(v)\cup \{k+1\} & \mbox{ if $v\in V(G_2)$.} \end{array} \right.\] Since \(c'_1\) and \(c'_2\) are vertex-distinguishing and \(c'(x) \ne c'(y)\) if \(x \in V(G_1)\) and \(y \in V(G_2)\), it follows that \(c'\) is a vertex-distinguishing vertex coloring of \(G\ \Box \ K_2\). Therefore, \(c\) is a strong regal \((k+1)\)-edge coloring of \(G\ \Box \ K_2\). 0◻ ◻
Since every connected graph contains a spanning tree, Proposition 2 suggests that studying these indexes for common classes of trees can aid in verifying Conjecture 1 for many graphs. For this reason, we consider a well-known class of trees. A caterpillar is a tree \(T\) of order 3 or more, the removal of whose leaves produces a path and a tree \(T\) is called cubic if every vertex of \(T\) that is not an end-vertex has degree 3. The strong royal index of cubic caterpillars has been determined.
Proposition 8. [4] If \(T\) is a cubic caterpillar of order at least \(4\), then \(T\) is royal-zero.
Here we determine the strong regal index for cubic caterpillars. We begin with a lemma. For integers \(a\) and \(b\) with \(a < b\), let
\([a, b] = \{a, a+1, \ldots, b\}\).
Lemma 1. For every integer \(n\geq 4\) with \(n\ne 7\) and \(k = 1 + \lfloor{\log_2 n}\rfloor\), there exist a strong regal \(k\)-coloring \(c\) of \(P_n\) such that if \(c'(u)=[k]\) for some vertex \(u\in V(P_n)\), then \(u\) is a leaf of \(P_n\).
Proof. Let \(k = 1 + \lfloor{\log_2 n}\rfloor\), where \(n \ge 4\) and \(n \ne 7\). Figure 1 shows that \(P_n\) has such a coloring for \(n \in [4, 6]\cup [12, 15]\). Notice in each case that if \([k]\) is an induced color, it is induced on an end vertex. Observe that the induced vertex coloring of each path \(P_n\) in Figure 1 for \(n \in [4, 5]\cup [12, 15]\) contains two adjacent vertices whose colors are disjoint. For an integer \(n \in [4, 5]\cup [12, 15]\), let
\(H =(v_1, v_2, \ldots, v_n)\)
be the path \(P_n\) of order \(n\) and let
\(H^{\star}=(v_n, v_{n-1}, \ldots, v_1)\)
be the path \(P_n\) in reverse order. Let \(c_H\) be the edge coloring of \(H\) shown in Figure 1. Notice that for the colorings of \(P_4\) and \(P_{13}\) of Figure 1, since \([k]\) (where \(k = 3\) for \(P_4\) and \(k = 4\) for \(P_{13}\)) is not the induced vertex color of any vertex in each of these two colorings, it follows that both colorings satisfy the conditions in the statement vacuously.
\[ \mathcal{S}_c(P_{3}) = (12, 23)\\ \mathcal{S}_{c'}(P_{3}) = {\bf (12, 2, 23, )}\\ \mathcal{S}_c(P_{4}) = (12, 23, 13)\\ \mathcal{S}_{c'}(P_{4}) = {\bf (12, \underline{2, 3}, 13)}\\ \mathcal{S}_c(P_{5}) = ([3], 12, 23, 13)\\ \mathcal{S}_{c'}(P_{5}) = {\bf ([3], 12, \underline{2, 3}, 13)}\\ \mathcal{S}_c(P_{6}) = ([3], 23, 13, 13, 12)\\ \mathcal{S}_{c'}(P_{6}) = {\bf ([3], 23, 3, 13, 1, 12)}\\ \mathcal{S}_c(P_{12}) = ([4], 123, 124, 34, 134, [4], 23, 13, 134, 12, 24)\\ \mathcal{S}_{c'}(P_{12}) = {\bf ([4], 123, \underline{12, 4}, 34, 134, 23, 3, 13, 1, 2, 24)}\\ \mathcal{S}_c(P_{13}) = (123, 13, 124, 12, 234, 124, [4], 234, 23, 134, 14, 34)\\ \mathcal{S}_{c'}(P_{13}) = {\bf (123, 13, 1, 12, 2, 24, 124, 234, 23, \underline{3, 14}, 4, 34)}\\ \mathcal{S}_c(P_{14}) = (123, 13, 124, 12, 234, 124, [4], 234, 23, 134, 14, 34, 134)\\ \mathcal{S}_{c'}(P_{14}) = {\bf (123, 13, 1, 12, 2, 24, 124, 234, 23, \underline{3, 14}, 4, 34, 134)}\\ \mathcal{S}_c(P_{15}) = ([4], 123, 13, 124, 12, 234, 124, [4], 234, 23, 134, 14, 34, 134)\\ \mathcal{S}_{c'}(P_{15}) = {\bf ([4], 123, 13, 1, 12, 2, 24, 124, 234, 23, \underline{3, 14}, 4, 34, 134).} \]
We now define a strong regal \((k+1)\)-coloring \(c_{H^{\star}}: E(H^{\star})\to {\cal P}^*([k+1])\) of \(H^{\star}\) by
\(c_{H^{\star}}(v_{i+1}v_{i}) = c_H(v_{i}v_{i+1}) \cup\{k+1\}\) for \(1 \le i \le n-1\).
Let \(G\) be the path of order \(2n\) obtained from \(H\) and \(H^{\star}\) by joining the two vertices \(v_n\) in \(H\) and \(H^{\star}\) by the edge \(f\). The edge coloring \(c_{G}: E(G)\to {\cal P}^*([k+1])\) is defined by \[c_G(e)=\left\{ \begin{array}{ll} c_H(e) & \mbox{ if $e \in E(H)$}\\ c_{H^{\star}}(e) & \mbox{ if $e \in E(H^{\star})$}\\ c_{H^{\star}}(v_nv_{n-1}) & \mbox{ if $e = f.$} \end{array}\right.\] The coloring \(c_G\) is illustrated in Figure 2 for \(G=P_{10}\) when \(n = 5\). Note that, in order for \([k+1]\) to be an induced color of a vertex in \(G\), \([k]\) had to be an induced color of a vertex in \(H\). By Figure 1, if such a vertex exists, it must be \(v_1\), in which case \(c_{H^{\star}}(v_1)=[k+1]\), which implies that \([k+1]\) is assigned to an end vertex of \(G\). Since this edge coloring is a strong regal \((k+1)\)-coloring of the path \(G\) of order \(2n\), it follows that the desired result holds for order \(n=2\ell\), with \(\ell\ge 2\).

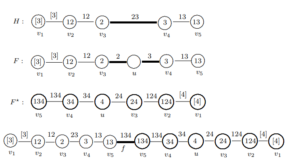
Next, for each \(n \in [4, 5]\cup [12, 15]\), let \(F\) be the path of \(n+1\) obtained from \(H\) by subdividing an edge \(v_jv_{j+1}\) of \(H\) where \(c'_H(v_j) \cap c'_H(v_{j+1}) = \emptyset\), obtaining the subpath \((v_j, u, v_{j+1})\). Define an edge coloring \(c_F\) of \(F\) by \[c_F(e)=\left\{ \begin{array}{ll} c'_H(v_j) & \mbox{ if $e= v_ju$}\\ c'_H(v_{j+1}) & \mbox{ if $e= uv_{j+1}$}\\ c_{H}(e) & \mbox{ if $e \ne v_ju, uv_{j+1}$.} \end{array}\right.\] (The edge coloring \(c_F\) is not a regal edge coloring since \(c'_F(u)= \emptyset\).) Let
\(F^{\star}\) \(=\) (\(v_n\), \(v_{n-1}\), \(\ldots\), \(v_{j+1}\), \(u\), \(v_j\), \(\ldots\), \(v_1\))
be the path \(F\) in reverse order. Define the edge coloring \(c_{F^{\star}}: E(F^{\star})\to {\cal P}^*([k+1])\) of \(F^{\star}\) by
\(c_{F^{\star}}(e)= c_F(e)\cup \{k+1\}\) for each \(e \in E(F^{\star})\).
Then \(c'_{F^{\star}}(v_i) = c'_H(v_i) \cup \{k+1\}\) for \(1 \le i \le n\) and \(c'_{F^{\star}}(u) =\{k+1\}\). In particular, \(c'_{F^{\star}}(v_1)=[k+1]\). Since \(c'_{F^{\star}}\) is vertex-distinguishing, it follows that \(c_{F^{\star}}\) is a strong regal \((k+1)\)-coloring of \(F^{\star}\). The graphs \(H\), \(F\) and \(F^{\star}\) are shown in Figure 3 as well as the corresponding edge colorings.
Let \(G\) be the path of order \(2n+1\) obtained from \(H\) and \(F^{\star}\) by joining the vertex \(v_n\) in \(H\) and \(F^{\star}\) by the edge \(f\). The edge coloring \(c_{G}: E(G)\to {\cal P}^*([k+1])\) is defined by \[c_G(e)=\left\{ \begin{array}{ll} c_H(e) & \mbox{ if $e \in E(H)$}\\ c_{F^{\star}}(e) & \mbox{ if $e \in E(F^{\star})$}\\ c_{F^{\star}}(v_nv_{n-1}) & \mbox{ if $e = f.$} \end{array}\right.\] The coloring \(c_G\) is illustrated in Figure 3 for \(G=P_{11}\) when \(n = 5\). This edge coloring is a strong regal \((k+1)\)-coloring of the path \(G\) of order \(2n+1\), where if \([k+1]\) appears as an induced color, it is induced on an end vertex.
The colorings defined above show, in particular, that if \(n \in [4, 31]\) where \(n \ne 7\), then \(P_n\) has a strong regal \(k\)– coloring with \(k=1 + \lfloor{\log_2 n}\rfloor\) such that if \([k]\) appears as an induced color, it is induced on an end vertex. Furthermore, the induced vertex coloring of each such path \(P_n\) where \(n \in [16, 31]\) has the property that there exist two adjacent vertices whose colors are disjoint and \([5]\) is induced on an end vertex if it appears in the induced coloring. By proceeding as above, we see that if \(n \in [32, 63]\), then there is a strong regal \(1 + \lfloor{\log_2 n}\rfloor\) coloring of \(P_n\) such that the induced vertex coloring of each such path has the property that there exist two adjacent vertices whose colors are disjoint and \([6]\) is induced on an end vertex if it appears in the induced coloring. Consequently, for each integer \(\ell\ge 2\) and each integer \(n \in [2^{\ell}, 2^{\ell+1}-1]\) except \(n = 7\) the result holds. That is, for each integer \(n \ge 4\) and \(n\ne 7\), there exist a strong regal \(k\)-coloring of \(P_n\), say \(c\), with such that if \(c'(u)=[k]\) for some vertex \(u\in V(P_n)\), then \(u\) is a leaf of \(P_n\) . 0◻ ◻
Proposition 9.If \(T\) is a cubic caterpillar of order \(n\geq 4\), then \(T\) is regal-zero, that is, \(\mathop{\rm sreg}(T)=1 + \lfloor{\log_2 n}\rfloor\).
Proof. By Proposition 1, it suffices to show that a strong regal \(k\)-coloring exists, where \(k=1 + \lfloor{\log_2 n}\rfloor\). If \(n=4\), then \(T\) is a star and the result holds. Since every vertex in a cubic caterpillar has odd degree, \(n\) must be even. Assume \(n=2\ell\) where \(\ell\geq 3\) . Let \(P_s=(v_1,v_2,v_3,\ldots, v_s)\) be the shortest path in \(T\) such that every vertex in \(T\) has distance at most one from a vertex in \(P_s\). This implies that \(v_1\) and \(v_s\) are each adjacent to at least one other vertex not in \(P_s\), say \(v_0\) and \(v_{s+1}\) respectively, for otherwise \(P_s\) would not be a minimum path with the designated property. Since each vertex \(v\in V(P_s)\) has \(\deg_T(v)\geq 2\), each vertex in \(P_s\) must have exactly \(3\) neighbors, so each vertex \(v_i\) in \(P_s\) is adjacent to another vertex \(u_i\) not in \(P_s\), for \(1\leq i\leq s\). Note that since \(T\) is a caterpillar, \(\deg(u_i)=1\) for \(1\leq i\leq s\). This implies the order of \(T\) is \(2s+2\). Let \(P=(v_0,v_1,v_2,\dots,v_s)\). Since the order of \(T\) is even, \(2^{k-1}\leq n\leq 2^k-2\). If follows that \(2^{k-2}\leq \frac{n}{2}\leq 2^{k-1}-1\). Observe that the order of \(P\) is \(s+1=\frac{n}{2}\). Then, by Lemma 1 it follows that \(P\) has a strong regal \(k-1\)-coloring, say \(c_P\), and we may assume that
\(c_P'(v_0)=\{1,2,\dots, k-1\}\).
Define a coloring \(c:E(T)\to{\cal P}^*([k])\) by \[c(e)=\left\{ \begin{array}{ll} c_P(e) & \mbox{ if $e \in E(P)$}\\ c'_P(v_i)\cup \{k\} & \mbox{ if $e=u_iv_i$, $1\le i\le s$}\\ $[k]$ & \mbox{ if \(e = v_s v_{s+1}\).} \end{array}\right.\] Then, the induced coloring \(c':V(T)\to{\cal P}^*([k])\) is given by \[c'(v)=\left\{ \begin{array}{ll} c'_P(v) & \mbox{ if $v \in V(P)$}\\ c'_P(v_i)\cup \{k\} & \mbox{ if $v=u_i$, $1\le i\le s$}\\ $[k]$ & \mbox{ if $v = v_{s+1}$.} \end{array}\right.\] It follows that \(c'\) is neighbor distinguishing since no neighbor of a vertex \(u_i\) is assigned the color \(\{1,2,\dots,k-1\}\) by \(c_P'\). Thus, \(c\) is a strong regal \(k\) coloring of \(T\) and so \(\mathop{\rm sreg}(T)=1 + \lfloor{\log_2 n}\rfloor\). ◻
For a connected graph \(G\) of order \(3\) or more with \(\mathop{\rm roy}(G)=k\), let \(c\) be a royal \(k\)-edge coloring of \(G\). Recall that this means we only require the induced vertex coloring \(c'\) to be proper. If the induce vertex coloring \(c'\) is rainbow, then the number of vertex colors used in maximum; while if the vertex coloring \(c'\) is proper, the number of vertex colors used may not be minimum. Define the royal chromatic number of a connected graph \(G\) of order \(3\) or more with royal index \(k\) to be the minimum possible number of vertex colors used in a royal \(k\)-edge coloring \(G\). This parameter is denoted by \(\chi_{\mathop{\rm sroy}}(G)\). A majestic \(k\)-edge coloring is a royal \(k\)-edge coloring with the added restriction that each edge color is a singleton. The majestic index \(maj(G)\) of a graph \(G\) is the minimum value of \(k\) such that \(G\) has a majestic \(k\)-edge coloring. Similarly, the majestic chromatic number of a connected graph \(G\) of order \(3\) or more with majestic index \(k\) is the minimum possible number of vertex colors used in a majestic \(k\)-edge coloring \(G\). This value is denoted by \(\chi_{\mathop{\rm maj}}(G)\). Majestic colorings were introduced by Györi et al. in [5] and the majestic chromatic number was introduced in [6].
Proposition 10.] If \(G\) is a connected graph of order \(n\geq 3\) with \(\mathop{\rm roy}(G)=k\), then
\(\displaystyle\max\{3, \chi(G)\}\leq\chi_{\mathop{\rm roy}}(G)\leq n,\)
\(\displaystyle\mathop{\rm roy}(G)\geq \lceil\log_2(\chi_{\mathop{\rm roy}}(G)+1)\rceil,\)
If \(\mathop{\rm maj}(G)=\mathop{\rm roy}(G)=k\), then \(\chi_{\mathop{\rm roy}}(G)\leq \chi_{\mathop{\rm maj}}(G)\).
Proof. Consider a royal coloring \(c\) of \(G\). Since the induced vertex coloring \(c'\) must be proper, it must use at least \(\chi(G)\) colors, however no vertex coloring can use more colors than the number of vertices in the graph. Consequently, \(\chi(G)\leq\chi_{\mathop{\rm roy}}(G)\leq n\). Next, we obtain that \(\chi_{\mathop{\rm roy}}(G)\geq 3\). Since \(G\) is nonempty, \(\chi(G)\geq 2\), so \(\chi_{\mathop{\rm roy}}(G)\geq 2\). It suffices to show that \(\chi_{\mathop{\rm roy}}(G)\not= 2\). Assume, to the contrary, that \(\chi_{\mathop{\rm roy}}(G)=2\). Then, there exists a royal \(k\)-edge coloring \(c\) of \(G\) such that the induced vertex coloring \(c'\) uses exactly two distinct vertex colors, say sets \(A\) and \(B\). Let \(u\) be a vertex in \(G\) such that \(c'(u)=A\). Then, for any vertex \(w\in N(u)\), \(c'(w)=B\), since \(c'\) is proper. It follows that \(c(e)\subseteq B\) for every edge incident to \(u\), since \(e\) is incident to a neighbor of \(u\). This implies that \(A\subseteq B\). Considering a symmetric argument, \(B\subseteq A\), which demonstrates that \(A=B\), which is impossible because of our assumption that \(A\) and \(B\) were distinct colors. Next, a royal \(k\)-edge coloring of \(G\) can use at most \(2^k-1\) vertex colors, given \(|{\cal P}^*([k])|=2^k-1\), which implies that \(\chi_{\mathop{\rm roy}}\mathop{\rm roy}(G)\leq 2^k-1\) for any graph \(G\) with \(\mathop{\rm roy}(G)=k\). It follows that \(\displaystyle\mathop{\rm roy}(G)\geq \lceil\log_2(\chi_{\mathop{\rm roy}}(G)+1)\rceil\). Lastly, suppose that \(\mathop{\rm maj}(G)=\mathop{\rm roy}(G)=k\) and let \(\chi_{\mathop{\rm maj}}(G)=\ell\). Then, there exists a majestic \(k\)-edge coloring of \(G\) that uses exactly \(\ell\) distinct vertex colors. However, every majestic coloring is also a royal coloring. Thus, \(\chi_{\mathop{\rm roy}}(G)\leq \ell\). 0◻ Note that \(\chi_{\mathop{\rm roy}}(K_n)=n\), which demonstrates that the upper bound on the royal chromatic number given in Proposition 10 is sharp. Recall an observation involving the majestic chromatic number. ◻
Observation 5. If \(G\) is a connected graph with \(\mathop{\rm maj}(G)=2\), then \[\chi_{\mathop{\rm maj}}(G)=3.\]
The connection between majestic and royal colorings leads to the following result.
Proposition 11. If \(\mathop{\rm roy}(G)=2\) for a connected graph \(G\) with order \(n\geq 3\), then \(\mathop{\rm maj}(G)=\mathop{\rm roy}(G)=2\) and \(\chi_{\mathop{\rm roy}}(G)=\chi_{\mathop{\rm maj}}(G)= 3\).
Proof. Let \(G\) be a graph with \(\mathop{\rm roy}(G)=2\). Let \(c:E(G)\to {\cal P}^*([2])\) be a royal \(2\)-edge coloring of \(G\). Then, \(c\) induces a proper vertex coloring \(c':V(G)\to {\cal P}^*([2])\). Observe that \(c(e)\) must be a singleton set for all \(e\in E(G)\). If there was an edge \(e=uv\), such that \(c(e)=\{1,2\}\), then it would follow that \(c'(u)=c'(v)\), which is impossible since \(c'\) is proper. Since \(c\) assigns only singleton sets to the edges of \(G\), it can also be viewed as a majestic \(2\)-edge coloring of \(G\), which implies \(\mathop{\rm maj}(G)=2\). By Observation 5, \(\chi_{\mathop{\rm maj}}(G)=3\). Applying Proposition 10 yields the following string of inequalities: \[3\leq \chi_{\mathop{\rm roy}}(G)\leq \chi_{\mathop{\rm maj}}(G)=3.\] Hence \(\chi_{\mathop{\rm roy}}(G)=3\). 0◻ ◻
Next, we determine the royal chromatic number of paths and cycles. The majestic chromatic number of odd length paths of order \(n\not=6\) is \(4\). The royal chromatic number for paths has been determined and differs from the majestic chromatic number for paths of even order.
Proposition 12.If \(n=4\), then \(\chi_{\mathop{\rm roy}}(P_n)=4\).
Proof. First note that in [6], it is shown that \(\mathop{\rm maj}(P_4)=3\). Also, \(\mathop{\rm roy}(G)\leq \mathop{\rm maj}(G)\). By Proposition 5, it follows that \(\mathop{\rm roy}(P_4)=3\). Since \(\chi_{\mathop{\rm roy}}(P_4)\geq 3\) and \(\mathop{\rm roy}(P_4)=3\), we must show no royal \(3\)-edge coloring exists that uses only \(3\) induced vertex colors. Assume, to the contrary, that there is a royal \(3\)-edge coloring \(c:E(P_4)\to {\cal P}^*([3])\) such that the induced vertex coloring \(c':V(P_4)\to {\cal P}^*([3])\) uses only \(3\) colors. Let \(P_4=(u_1,u_2,u_3,u_4)\). In order to properly color \(P_4\) using less than \(4\) colors, two vertices must be assigned the same color by \(c'\). If \(c'(u_1)=c'(u_4)=A\), then \(c(u_1u_2)=A\) and \(c(u_3u_4)=A\). Thus, for any set \(c(u_2u_3)\), \(c'(u_2)=c'(u_3)\), a contradiction. We may assume \(c'(u_1)=c'(u_3)=A\), with \(A\subseteq[3]\). Since \(c'\) is proper, we must have that \(c'(u_2)=B\), with \(B\subseteq[3]\) and \(A\not=B\). It follows that \(c(u_1u_2)=A\), \(c(u_1u_2)\subseteq B\) and \(c(u_2u_3)\subseteq A\), so \(c'(u_2)=B\subseteq A\) and \(c'(u_1)=A\subseteq B\). However, this implies that \(A=B\), which is impossible, since \(c'\) is proper. Define a royal \(3\)-edge coloring \(c\) of \(P_4\) by the sequence \(s=(\{1\},\{2\},\{3\})\). Then, the induced vertex coloring \(c'\) is given by the color sequence \(s'=(\{1\},\{1,2\},\{2,3\},\{3\})\), which is a proper vertex coloring of \(C_5\) using exactly 4 colors. 0◻ ◻
Theorem 6.
If \(P_n\) is a path of order \(n\geq 3\) with \(n\not=4\), then
\(\chi_{\mathop{\rm roy}}(P_n)=3\).
Proof. By Proposition 10, \(\chi_{\mathop{\rm roy}}(P_n)\geq 3\). It suffices to show that a royal \(k\)-edge coloring of \(P_n\) exists using exactly \(3\) vertex colors, where \(k=\mathop{\rm roy}(P_n)\). We consider two cases Case \(1\). \(n\) is odd. If \(n\) is odd, then \(\mathop{\rm roy}(P_n)=2\), since \(\mathop{\rm maj}(P_n)=2\) when \(n\) is odd (see [6]. The desired result follows from Proposition 11. Case \(2\). \(n\) is even. Since \(\mathop{\rm maj}(P_n)=3\) for even \(n\) (see [6], it follows that \(\mathop{\rm roy}(P_n)=3\) by Proposition 11. Let \(P_n=(u_1,u_2,\dots, u_n)\). Define a royal \(3\)-edge coloring \(c:E(G)\to {\cal P}^*([3])\) of \(P_n\) by \[c(u_iu_{i+1}) = \left\{ \begin{array}{ll} 1 & \mbox{ if $i=3$}\\ 2 & \mbox{ if $i=4$}\\ 3 & \mbox{ if $i= 2$}\\ \{1,2\} & \mbox{ if $i=1$ or $i\equiv 0,3\ (\mathrm{mod}\ {4}$ for $7\leq i\leq n-1$}\\ \{1,3\} & \mbox{ if $i\equiv 1,2\ (\mathrm{mod}\ {4}$ for $5\leq i\leq n-1$.} \end{array}\right.\] Then, the induced coloring \(c':V(P_n)\to {\cal P}^*([3])\) is given by \[c'(u_i) = \left\{ \begin{array}{ll} \{1,2\} & \mbox{ if $i=1$ or $i\equiv 0\ (\mathrm{mod}\ {4}$ for $4\leq i\leq n$}\\ \{1,3\} & \mbox{ if $i=3$ or $i\equiv 2\ (\mathrm{mod}\ {4}$ for $6\leq i\leq n$}\\ \{3\}& \mbox{ if $i=2$ or $i\equiv 1,3\ (\mathrm{mod}\ {4}$ for $5\leq i\leq n-1$.} \end{array}\right.\] Since \(c'\) is a proper \(3\)-coloring of \(G\), it follows that \(\chi_{\mathop{\rm roy}}(P_n)=3\) for \(n\geq 3\), with \(n\not=4\). 0◻ For a cycle \(C_n\) of order \(n\geq 3\), \(\chi_{\mathop{\rm maj}}(C_n)=3\) if and only if \(n\equiv 0 \ (\mathrm{mod}\ {4}\) or \(n\equiv 0\ \ (\mathrm{mod}\ {3}\) by results in [6]. Otherwise \(\chi_{\mathop{\rm maj}}(C_n)\geq 4\). As with paths, the royal chromatic number of cycles contrasts that of the majestic chromatic number by achieving the lower bound given in Proposition 11 in all but one case. ◻
Proposition 13.If \(n=5\), then \(\chi_{\mathop{\rm roy}}(C_n)=4\).
Proof. First, \(\mathop{\rm maj}(C_5)=3\) (see [6]. By Proposition 11, it follows that \(\mathop{\rm roy}(C_5)=3\). Since \(\chi_{\mathop{\rm roy}}(C_5)\geq 3\) and \(\mathop{\rm roy}(C_5)=3\), we must show no royal \(3\)-edge coloring exists that uses only \(3\) induced vertex colors and exhibit a royal \(3\)-edge coloring that uses exactly \(4\) induced vertex colors. First, assume to the contrary that a royal \(3\)-edge coloring \(c:E(C_5)\to {\cal P}^*([3])\) exists such that the induced vertex coloring \(c':V(C_5)\to {\cal P}^*([3])\) uses only \(3\) colors. Let \(C_5=(u_0,u_1,u_2,u_3,u_4,u_5=u_0)\). Observe that a proper coloring of \(C_5\) may assign the same color to at most two vertices in \(C_5\). It follows that two pairs of vertices in \(C_5\) must be assigned the same color by \(c'\). We may assume that \(c'(u_0)=c'(u_2)=A\), for some \(A\subseteq [3]\). Since \(c'\) is proper \(c'(u_3)\not=c'(u_4)\), so either \(c'(u_1)=c'(u_3)\) or \(c'(u_1)=c'(u_4)\). Without loss of generality, let \(c'(u_1)=c'(u_3)=B\), with \(B\subseteq [3]\). Then, \(A\not=B\). However, since \(u_0u_1\) and \(u_1u_2\) are both incident to a vertex colored \(A\), \(c(u_0u_1)\subseteq A\) and \(c(u_1u_2)\subseteq A\). These are the only edges incident to \(u_1\), hence \(c'(u_1)=B\subseteq A\). Similarly, since \(u_1u_2\) and \(u_2u_3\) are both incident to a vertex colored \(B\), \(c(u_1u_2)\subseteq B\) and \(c(u_2u_3)\subseteq B\). These are the only edges incident to \(u_2\), hence \(c'(u_2)=A\subseteq B\). This implies that \(A=B\), which is impossible since \(c'\) must be proper.
Now, define a royal \(3\)-edge coloring \(c\) of \(C_5\) by the sequence \[s=(\{1\},\{1\},\{1,2\},\{3\},\{2\}).\] Then, the induced vertex coloring \(c'\) is given by the color sequence \[s'=(\{1,2\},\{1\},\{1,2\},[3],\{2,3\}),\] which is a proper vertex coloring of \(C_5\) using exactly 4 colors. ◻
Theorem 7.
If \(C_n\) is a cycle of order \(n\geq 3\) with \(n\not=5\), then \[\chi_{\mathop{\rm roy}}(C_n)=3.\]
Proof. By Proposition 10, \(\chi_{\mathop{\rm roy}}(C_n)\geq 3\). It suffices to show that there exists a royal \(k\)-edge coloring \(C_n\) using exactly \(3\) vertex colors, where \(k=\mathop{\rm roy}(C_n)\). Let \(C_n=(u_0,u_2,\dots, u_n=u_0)\). We consider four cases. Case \(1\). \(n\equiv 0 \ (\mathrm{mod}\ {4}\). Recall that if \(n\equiv 0 \ (\mathrm{mod}\ {4}\), then \(\mathop{\rm maj}(G)=2\) and so \(\mathop{\rm roy}(G)=2\) by Proposition 11 (see [6]. It follows that from Proposition 5 that \(\chi_{\mathop{\rm roy}}(C_n)=3\) for \(n\equiv 0 \\ (\mathrm{mod}\ {4}\). Case \(2\). \(n\equiv 1 \ (\mathrm{mod}\ {4}\). Then \(\mathop{\rm maj}(C_n)=3\) and so \(\mathop{\rm roy}(C_n)=3\) by Proposition 11 (see [6]. For the case of \(n=9\), let a royal \(3\)-edge coloring be given by the color sequence \[s=(\{1\},\{3\},\{1,2\},\{1\},\{3\},\{1,2\},\{1\},\{3\},\{1,2\}).\] The vertex color sequence induced by \(s\) is given by \[s'=(\{1,2\},\{1,3\},[3],\{1,2\},\{1,3\},[3],\{1,2\},\{1,3\},[3]),\] as desired. We may assume \(n\geq 13\). Define a royal \(3\)-edge coloring \(c:E(C_n)\to {\cal P}^*([3])\) of \(C_n\) by \[c(u_iu_{i+1}) = \left\{ \begin{array}{ll} \{1\} & \mbox{ if $i\in\{0,3,6\}$}\\ \{3\} & \mbox{ if $i\in \{1,4,7\}$}\\ \{1,2\} & \mbox{ if $i\in \{2,5\}$ or $i\equiv 0,1\ (\mathrm{mod}\ {4}$ for $8\leq i\leq n-1$}\\ \{1,3\} & \mbox{ if $i\equiv 3,4\ (\mathrm{mod}\ {4}$ for $10\leq i\leq n-2$.} \end{array}\right.\]
Then, the induced coloring \(c':V(C_n)\to {\cal P}^*([3])\) is given by \[c'(u_i) = \left\{ \begin{array}{ll} \{1,2\} & \mbox{ if $i\in \{0,3,6\}$ or $i \equiv 1\ (\mathrm{mod}\ {4}$ for $9\leq i\leq n-4$}\\ \{1,3\} & \mbox{ if $i\in \{1,4\}$ or $i\equiv 3\ (\mathrm{mod}\ {4}$ for $7\leq i\leq n-2$}\\ \{3\}& \mbox{ if $i\in \{2,5\}$ or $i\equiv 0,2\ (\mathrm{mod}\ {4}$ for $8\leq i\leq n-1$.} \end{array}\right.\] Since \(c'\) is a proper \(3\)-coloring of \(C_n\), it follows that \(\chi_{\mathop{\rm roy}}(P_n)=3\) for \(n\equiv 1 \ (\mathrm{mod}\ {4}\), with \(n\geq 9\). Case \(3\). \(n\equiv 2 \ (\mathrm{mod}\ {4}\). Then \(\mathop{\rm maj}(C_n)=3\) and so \(\mathop{\rm roy}(C_n)=3\) by Proposition 11 (see [6]. We may assume \(n\geq 6\). Define a royal \(3\)-edge coloring \(c:E(C_n)\to {\cal P}^*([3])\) of \(C_n\) by \[c(u_iu_{i+1}) = \left\{ \begin{array}{ll} \{1\} & \mbox{ if $i\in\{0,3\}$}\\ \{3\} & \mbox{ if $i= 1$}\\ \{1,2\} & \mbox{ if $i=2$ or $i\equiv 1,2\ (\mathrm{mod}\ {4}$ for $5\leq i\leq n-1$}\\ \{1,3\} & \mbox{ if $i\equiv 0,3\ (\mathrm{mod}\ {4}$ for $4\leq i\leq n-2$.} \end{array}\right.\] Then, the induced coloring \(c':V(C_n)\to {\cal P}^*([3])\) is given by \[c'(u_i) = \left\{ \begin{array}{ll} \{1,2\} & \mbox{ if $i\in \{0,3\}$ or $i \equiv 2\ (\mathrm{mod}\ {4}$ for $6\leq i\leq n-4$}\\ \{1,3\} & \mbox{ if $i=1$ or $i\equiv 0\ (\mathrm{mod}\ {4}$ for $4\leq i\leq n-2$}\\ \{3\}& \mbox{ if $i\in \{2,5\}$ or $i\equiv 0,2\ (\mathrm{mod}\ {4}$ for $5\leq i\leq n-1$.} \end{array}\right.\] Since \(c'\) is a proper \(3\)-coloring of \(C_n\), it follows that \(\chi_{\mathop{\rm roy}}(C_n)=3\) for \(n\equiv 2 \ (\mathrm{mod}\ {4}\), with \(n\geq 6\). Case \(4\). \(n\equiv 3 \ (\mathrm{mod}\ {4}\). Then \(\mathop{\rm maj}(C_n)=3\) and so \(\mathop{\rm roy}(C_n)=3\) by Proposition 11 (see [6]. For the case of \(n=3\), let a royal \(3\)-edge coloring be given by the color sequence \(s=(\{1\},\{3\},\{1,2\})\). The vertex color sequence induced by \(s\) is given by \(s'=(\{1,2\},\{1,3\},[3])\), as desired. We may assume \(n\geq 7\). Define a royal \(3\)-edge coloring \(c:E(C_n)\to {\cal P}^*([3])\) of \(C_n\) by \[c(u_iu_{i+1}) = \left\{ \begin{array}{ll} \{1\} & \mbox{ if $i=0$}\\ \{3\} & \mbox{ if $i= 1$}\\ \{1,2\} & \mbox{ if $i\equiv 2,3\ (\mathrm{mod}\ {4}$ for $2\leq i\leq n-1$}\\ \{1,3\} & \mbox{ if $i\equiv 0,1\ (\mathrm{mod}\ {4}{4}$ for $4\leq i\leq n-2$.} \end{array}\right.\] Then the induced coloring \(c':V(C_n)\to {\cal P}^*([3])\) is given by \[c'(u_i) = \left\{ \begin{array}{ll} \{1,2\} & \mbox{ if $i=0$ or $i \equiv 3\ (\mathrm{mod}\ {4}$ for $3\leq i\leq n-4$}\\ \{1,3\} & \mbox{ if or $i\equiv 1\ (\mathrm{mod}\ {4}$ for $1\leq i\leq n-2$}\\ \{3\}& \mbox{ if $i\equiv 0,2\ (\mathrm{mod}\ {4}$ for $2\leq i\leq n-1$.} \end{array}\right.\] Since \(c'\) is a proper \(3\)-coloring of \(C_n\), it follows that \(\chi_{\mathop{\rm roy}}(C_n)=3\) for \(n\equiv 3 \ (\mathrm{mod}\ {4}\). ◻
We have seen in Theorem 4 that if \(G\) is a connected graph of order at least \(3\), then \(|\mathop{\rm sroy}(G)-\mathop{\rm sreg}(G)|\leq 1.\) This gives rise to the following question.
Problem 1. Let \(G\) be a connected graph of order at least \(3\). What conditions must \(G\) possess to guarantee that \(\mathop{\rm sroy}(G) =\mathop{\rm sreg}(G)\)?
By Conjecture 1, if \(G\) is a connected graph of order \(n\ge 3\) where \(2^{k-1}\leq n \leq 2^{k}-1\), then \(\mathop{\rm sroy}(G) \in \{k,k+1\}\) and \(\mathop{\rm sreg}(G)\in \{k,k+1\}.\) There is another natural question here.
Problem 2. Let \(G\) be a connected graph of order \(n \ge 3\) where \(2^{k-1}\leq n \leq 2^{k}-1\). Is there a necessary and sufficient condition for which \(\mathop{\rm sroy}(G) = k\)? Similarly, is there a necessary and sufficient condition for which \(\mathop{\rm sreg}(G) = k\)?
We saw that if \(G\) is a connected graph of order \(n \ge 4\), then \(\mathop{\rm sroy}(\mathop{\rm cor}(G)) \le \mathop{\rm sroy}(G) + 1\) and \(\mathop{\rm sreg}(\mathop{\rm cor}(G)) \le \mathop{\rm sreg}(G) + 1\). There is a related question here.
Problem 3. If \(G\) be a connected graph of order at least \(4\), is it true that \(\mathop{\rm sroy}(\mathop{\rm cor}(G)) \ge \mathop{\rm sroy}(G)\) and \(\mathop{\rm sreg}(\mathop{\rm cor}(G)) \ge \mathop{\rm sreg}(G)\)?
By Propositions 6 and 7, if \(G\) is a connected graph of order at least \(3\), then \(\mathop{\rm sroy}(G\ \Box \ K_2)\leq \mathop{\rm sroy}(G)+1\) and \(\mathop{\rm sreg}(G\ \Box \ K_2)\leq \mathop{\rm sreg}(G)+1\). There is also a related question here.
Problem 4. If \(G\) be a connected graph of order at least \(3\), is it true that \(\mathop{\rm sroy}(G\ \Box \ K_2)\geq \mathop{\rm sroy}(G)\) and \(\mathop{\rm sreg}(G\ \Box \ K_2)\geq \mathop{\rm sreg}(G)\)?
We are grateful to the anonymous referee whose valuable suggestions resulted in an improved paper.
The authors declare no conflict of interest.