The dominating set of a graph \(G\) is a set of vertices \(D\) such that for every \(v \in V(G)\) either \(v \in D\) or \(v\) is adjacent to a vertex in \(D\). The domination number, denoted \(\gamma(G)\), is the minimum number of vertices in a dominating set. In 1998, Haynes and Slater [1] introduced paired-domination. Building on paired-domination, we introduce 3-path domination. We define a 3-path dominating set of \(G\) to be \(D = \{ Q_1,Q_2,\dots , Q_k\, |\:Q_i \text{ is a 3-path}\}\) such that the vertex set \(V(D) = V(Q_1) \cup V(Q_2) \cup \dots \cup V(Q_k)\) is a dominating set. We define the 3-path domination number, denoted by \(\gamma_{P_3}(G)\), to be the minimum number of 3-paths needed to dominate \(G\). We show that the 3-path domination problem is NP-complete. We also prove bounds on \(\gamma_{P_3}(G)\) and improve those bounds for particular families of graphs such as Harary graphs, Hamiltonian graphs, and subclasses of trees. In general, we prove \(\gamma_{P_3}(G) \leq \frac{n}{3}\).
In this paper, assume any graph \(G=(V,E)\) is finite and simple with vertex set \(V\) and edge set \(E\). A dominating set \(D \subseteq V\) of \(G\) is a set such that every vertex \(v \in V\) is either in \(D\) or adjacent to a vertex in \(D\). The domination number of \(G\), denoted \(\gamma(G)\), is defined as the minimum cardinality of a dominating set of \(G\). An application of domination theory considers the task of assigning guards to rooms in a museum. In this application vertices represent the exhibit rooms and edges represent hallways joining them. Thus a dominating set of the representative graph is a set of vertices whose corresponding rooms could hold guards with the result that the entire museum would be under surveillance with guards monitoring adjacent rooms via the hallways.
Many variations on domination have been studied. See Haynes and Slater [2] for an introduction to many of these areas. In 1998, Haynes and Slater introduced paired-domination [1] in which the induced subgraph on a dominating set of vertices contains a perfect matching. In this version of the application, we say that every guard has another guard watching their back. The paired-domination number, denoted \(\gamma_{pr}(G)\), is the minimum cardinality of a paired-dominating set of \(G\). We introduce a natural extension of paired-domination, namely 3-path domination. We say \(Q_i\) is a 3-path if it is isomorphic to \(P_3\). We define a 3-path dominating set of \(G\) to be a set \(D=\{ Q_1,Q_2,\dots , Q_k\}\) of 3-paths such that the vertex set \(V(D) = V(Q_1) \cup V(Q_2) \cup \dots \cup V(Q_k)\) is a dominating set of \(G\). Here we continue our application analogy by allowing stationed guards to walk between 3 rooms and look down hallways extending from those 3 rooms. Note that while in paired domination every vertex of the perfect matching represents the position of a guard, in 3-path domination, not every vertex in \(V(D)\) necessarily will represent a position of a guard; only one guard is placed per 3-path. The 3-path domination number, denoted \(\gamma_{P_3}(G)\), is the minimum cardinality of a 3-path dominating set. We will use the abbreviation \(\gamma_{P_3}\)-set for a minimum 3-path dominating set. The study of the guard analogy and its variations was introduce in 1997 as the Watchman’s Walk Problem by Hartnell, Rall and Whitehead, see [3]. In 2003, Davies et al. [4] studied the Watchman’s Walk Problem on trees. The Watchman’s Walk Problem asks how many watchman are required such that each vertex is visited or observed by a watchman on a walk in a given time interval. The walks need not be uniform in length.
In this paper we prove that determining \(\gamma_{P_3}\) is NP-complete and then establish bounds on \(\gamma_{P_3}\) for all graphs, specifically \[\gamma_{P_3}(G) \leq\frac{n}{3}.\] Tighter bounds and formulas for \(\gamma_{P_3}\) for specific families of graphs such as caterpillars, Harary graphs, banana trees, paths, and cycles are also shown
In 1998, Haynes and Slater proved that the paired domination problem was NP-complete [1]. We generalize this result to show the 3-path domination problem is also NP-complete.
Theorem 1. Deciding for a given graph H and positive integer k such that \(3k \le {\lvert}{\rvert}{V(H)}\), ”Is \(\gamma_{P_3}(H) \le\) k?” is NP-complete.
Proof. We will use the known NP-complete domination problem,“For a given graph \(G\) and a positive integer \(k\), is \(\gamma(G) \le k\)?” [5]. Let \(V(G)=\{v_1,v_2,…,v_n\}\). Construct graph \(H\) by letting \(V(G_i)= \{v_1^i,v_2^i,…,v_n^i\}\) for \(1\le i\le 6\) and letting \(v_h^iv_j^i\in E(G_i)\) if and only if \(v_hv_j \in E(G)\). Let \(H\) be the graph created by these six disjoint copies of \(G\) and by adding the following edges. Let \(v_h^1v_j^2\), \(v_h^3v_j^4\), and \(v_h^5v_j^6\) be in \(E(H)\) if and only if either \(h=j\) or \(v_hv_j \in E(G)\). Add the edges \(v_h^1v_h^3\) and \(v_h^3v_h^5\) for \(1 \le h \le n\) to \(H\). Thus the graph \(H\) has \(6n\) vertices and can be constructed from \(G\) in polynomial time.
We claim that \(\gamma(G) \le k\) if and only if \(\gamma_{P_3}(H) \le k\).
Assume \(D\subset V(G)\) is a dominating set of \(G\) with \({\lvert}{\rvert}{D} \le k\). Let \(R\) be a set of 3-paths with \(R=\{\{v_h^1, v_h^3, v_h^5\}\,|\: v_h \in D \}\). Thus R is a 3-path dominating set of H with \({\lvert}{\rvert}{R} \le k\), so \(\gamma_{P_3}(H) \le k\).
Now, assume \(R\) is a 3-path dominating set of \(G\) with \({\lvert}{\rvert}{R} \le k\). Let \(T=\bigcup_{Q_i \in R} V(Q_{i})\). Since 3-paths are not necessarily disjoint and have 3 vertices each, \({\lvert}{\rvert}{T} \le 3k\). Thus since \(G_1\cup G_2 \cong G_3\cup G_4 \cong G_5\cup G_6\), we can assume that \({\lvert}{\rvert}{T_{1,2}} = {\lvert}{\rvert}{T \cap (V(G_1)\cup V(G_2))}\le k\). Let \(T^*= \{v_h^2\,|\:v_h^1\in T_{1,2}\} \cup (T \cap V(G_2))\). Then \({\lvert}{\rvert}{T^*} \le {\lvert}{\rvert}{T_{1,2}}\le k\) and \(T^*\) dominates \(V(G_2)\). Hence, \(\gamma (G) \le k\). ◻
Having shown that the 3-path domination problem is NP-complete, we find general bounds on \(\gamma_{P_3}\) and formulas and improved bounds for the 3-path domination number of specific families of graphs.
In this section, we prove bounds based on parameters of a graph \(G\), namely \(\gamma(G)\), \(\gamma_{pr}(G)\), and \(\Delta(G)\). Note that 3-path domination requires any component of a graph to have at least three vertices.
Theorem 2. For a graph \(G\) on \(n\geq 3\) vertices, \(\gamma_{P_3}(G) \geq \frac{\gamma(G)}{3}\).
Proof. Let \(D\) be a \(\gamma_{P_3}\)-set of \(G\) and \(V(D)\) be the set of vertices in \(D\). Then \(|V(D)| \leq 3|D| = 3\gamma_{P_3}(G)\) since some 3-paths may share vertices. Furthermore, \(|V(D)| \geq \gamma(G)\) as \(V(D)\) forms a dominating set of \(G\). So we have \[3\gamma_{P_3}(G)\geq |V(D)| \geq \gamma(G) ,\] and solving yields \(\gamma_{P_3}(G) \geq \frac{\gamma(G)}{3}\). ◻
For the next lower bound, we generalize an argument from Haynes and Slater involving \(\Delta(G)\) [1].
Theorem 3. For a connected graph \(G\) on \(n\geq 3\) vertices, \(\gamma_{P_3}(G) \geq \frac{n}{3\Delta(G)}\).
Proof. Let \(D\) be a \(\gamma_{P_3}\)-set of a graph \(G\) on \(n\) vertices, and let \(T\) be the set of edges in \(G\) having one vertex in \(V(D)\) and the other in \(V(G) \setminus V(D)\). Since \(\Delta(G) \geq \deg(v)\) for all \(v \in V(D)\) and each vertex in \(V(D)\) has at least one neighbor in \(V(D)\), \[ |T|=t \leq (\Delta(G)-1)|V(D)|\leq (\Delta(G)-1)3\gamma_{P_3}(G). \] In addition, \(t \geq |V(G) \setminus V(D)|\) since there is at least one edge of \(T\) incident to every vertex in \(G\) that is not in \(V(D)\). So, \[t \geq |V(G) \setminus V(D)|= n – |V(D)|\geq n-3\gamma_{P_3}(G). \]
So we have \(n-3\gamma_{P_3}(G) \leq t \leq (\Delta(G)-1)3\gamma_{P_3}(G)\), and solving yields \(\gamma_{P_3}(G) \geq \frac{n}{3\Delta(G)}\). ◻
Having established some lower bounds on \(\gamma_{P_3}\), we explore some upper bounds.
Theorem 4. For a connected graph \(G\) on \(n \geq 3\) vertices, \(\gamma_{P_3}(G) \leq \frac{\gamma_{pr}(G)}{2}\).
Proof. Let \(G\) be a graph with \(|V(G)| \geq 3\) and \(D\) be a \(\gamma_{pr}\)-set of \(G\). Since there are \(\frac{\gamma_{pr}(G)}{2}\) pairs of vertices in \(D\) and \(n \geq 3\), for each pair we can create a 3-path using the pair and a neighbor. This forms a 3-path dominating set with cardinality \(\frac{\gamma_{pr}(G)}{2}\). ◻
Notice that since the induced subgraph on a \(\gamma_{pr}\)-set is a perfect matching, the edges in the induced subgraph are vertex disjoint. This is not always the case for 3-path domination, as shown in Figure 1.
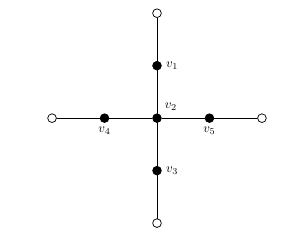
For the following theorem, we note that a private neighbor of a 3-path \(Q\) is a vertex that is dominated by \(Q\) and no other 3-path of the 3-path dominating set. It is possible for the private neighbor to be a vertex of \(Q\).
Theorem 5. For a graph \(G\) with \(n \geq 3\), there exists a minimal 3-path dominating set that is edge-disjoint.
Proof. Let \(G\) be a graph and \(D\) be a minimal 3-path dominating set on \(G\). Suppose there are two 3-paths in \(D\) that share an edge, \(Q_1 = \{v_1,v_2,v_3\}\) and \(Q_2= \{v_2,v_3,v_4\}\). Consider the following two possibilities:
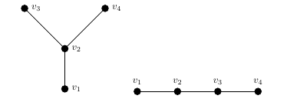
Referring to Figure 2, \(Q_1\) and \(Q_2\) each have at least one private neighbor. If \(Q_1\) or \(Q_2\) do not have any private neighbors, then \(D\) is not minimal as \(G\) would still be dominated if we remove one path without private neighbors. Let \(p_1\) be a private neighbor of \(Q_1\) and \(p_2\) be a private neighbor of \(Q_2\). Note, \(p_1\) must be adjacent to \(v_1\), and \(p_2\) must be adjacent to \(v_4\), otherwise they would be dominated by both \(Q_1\) and \(Q_2\). Without loss of generality, we set \(Q'_1 = \{v_2,v_1,p_1\}\), making \(Q'_1\) and \(Q_2\) edge-disjoint. Let \(C=D-{Q_1}+{Q_1'}\). Now \(C\) is not guaranteed to be minimal. If \(C\) is not minimal, it must be the case that \(Q'_1\) dominates what were the private neighbors of some other 3-path in \(D\). Remove 3-paths from \(C\) that do not have any private neighbors in \(G\) with respect to \(C\) to obtain a new minimal 3-path dominating set \(D'\). Repeat this process until \(D'\) is edge-disjoint and minimal. ◻
Corollary 1. For a connected graph \(G\) on \(n \geq 3\) vertices, \(\gamma_{P_3}(G) \leq \lfloor{\frac{|E(G)|}{2}}\rfloor\).
Proof. Let \(G\) be a graph with \(|V(G)| \geq 3\). By Theorem 5, there exists a minimal, edge-disjoint 3-path dominating set of \(G\), call it \(D\). Since no two 3-paths share an edge, and each 3-path contains two edges, \(|D| \leq \lfloor {\frac{|E(G)|}{2}}\rfloor\). ◻
Having an upper bound in terms of the number of edges of \(G\) is useful when dealing with classes of graphs whose number of edges directly relate to the number of vertices. For example, if we consider a tree \(T\) on \(n\) vertices, \(|E(T)|=n-1\), and so \(\gamma_{P_3}(T)\leq \lfloor{\frac{n-1}{2}}\rfloor\). We can improve this upper bound for trees. Recall a leaf of a tree is a vertex of degree 1, and the diameter of a graph \(G\) is the length of a longest path between a pair of vertices in \(G\), denoted \({diam}(G)\). We will call a vertex adjacent to a leaf a support vertex. Note that if \({diam}(T)=2\), then \(T\) is a star with \(n-1\) leaves, and \(n-(n-1)-1=0\) while clearly \(\gamma_{P_3}(T)\geq1\) for all trees on at least three vertices. Thus for the following corollary we must assume that the diameter of the tree is at least three, so that \(n-L-1\geq 1\), where \(L\) is the number of leaves of \(T\).
Corollary 2. For a tree \(T\) on \(n\) vertices with \({diam}(T) \geq 3\), \(\gamma_{P_3}(T) \leq \lceil{\frac{n-L-1}{2}}\rceil\) where \(L\) is the number leaves of \(T\).
Proof. Let \(T\) be a tree with \({diam}(T)\geq 3\). Obtain a new graph \(T'\) by deleting all the leaves of \(T\). Now \(T'\) has \(n-L\) vertices. Using Corollary 1, we have \(\gamma_{P_3}(T') \leq \lfloor{\frac{n-L-1}{2}}\rfloor\). Let \(D'\) be a 3-path dominating set of size \(\lfloor{\frac{n-L-1}{2}}\rfloor\). Note that if \(T'\) has an even number of edges, this would be as if all the edges of \(T'\) were paired into disjoint 3-paths in \(D'\). Hence, if we added the \(L\) vertices of \(T\) back, all the support vertices of \(T\) would be in one of the 3-paths of \(D'\) so \(D'\) would form a 3-path dominating set in \(T\) as well. However, if \(T'\) has an odd number of edges, \(|E(D')|=n-L-2\), that is, there would be an edge of \(T'\), call it \(e\), not included in the edge set of \(D'\). In \(T\), it is possible that \(e\) is incident to a support vertex. Hence we may need one more 3-path in \(T\) than we needed in \(T'\). Therefore \(\gamma_{P_3}(T) \leq \lceil {\frac{n-L-1}{2}}\rceil\). ◻
Increasing adjacencies in a graph, can only decrease the 3-path domination number. Thus we have the following observation.
Observation 6. If an edge is added to a graph \(G\) to form a new graph \(G^*\), then \(\gamma_{P_3}(G^*) \leq \gamma_{P_3}(G)\).
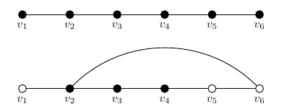
Thus the 3-path domination number of any spanning subgraph of \(G\) is an upper bound on the 3-path domination number of \(G\). Refer to Figure 3 for an example. A spanning tree \(T\) of a graph \(G\) is a tree such that \(V(T) = V(G)\) and \(E(T) \subseteq E(G)\). We now use Observation 6 and spanning trees to establish a bound for general graphs.
Theorem 7. For any connected graph \(G\) on \(n\geq 3\) vertices, \(\gamma_{P_3}(G) \leq \lceil{\frac{n-3}{2}}\rceil\).
Proof. Let \(G\) be a graph on \(n\) vertices and let \(T_G\) be a spanning tree of \(G\). Notice, since \(V(T_G) = V(G)\) and \(E(T_G) \subseteq E(G)\), we can construct \(G\) from \(T_G\) by adding the edges in \(E(G) \setminus E(T_G)\). By Observation 6, \(\gamma_{P_3}(G) \leq \gamma_{P_3}(T_G)\). Since \(T_G\) is a tree on \(n\) vertices, \(\gamma_{P_3}(T_G) \leq \lceil{\frac{n-L-1}{2}}\rceil\) by Corollary 2. Since \(L\geq2\) for all trees with \(n\geq 3\), \(\gamma_{P_3}(G) \leq \lceil{\frac{n-3}{2}}\rceil\). ◻
The next observation will be useful in this section and the following.
Observation 8. If a vertex \(u\) is a support vertex in \(V(G)\), then \(u\) must be part of a dominating 3-path.
Haynes and Slater [1] proved the following upper bound for paired-domination number.
Theorem 9. [1] If a connected graph \(G\) has \(n \geq 6\) and \(\delta(G) \geq 2\), then \[\gamma_{pr}(G) \leq \frac{2n}{3}.\]
The following result follows readily from Theorem 1 and Theorem 1.
Corollary 3. If a connected graph \(G\) has \(n \geq 6\) and \(\delta(G) \geq 2\), then \[\gamma_{P_3}(G) \leq \frac{n}{3}.\]
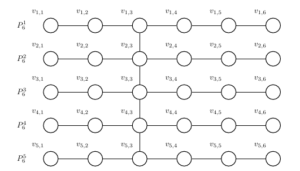
We show that this bound actually holds for all graphs. While this may seem obvious since each 3-path uses three vertices, the paths in 3-path dominating sets are not necessarily vertex disjoint. Note that this bound is sharp. Consider \(P_6\) (graph \(H\) in Figure 3). This requires two 3-paths to dominate. We can generalize \(P_6\) with an infinite family of graphs, \(F\), where each graph \(G_k\) in \(F\) is formed from \(k\) disjoint copies of \(P_6\) with vertices of each \(P_6^i\) labeled in order: \(v_{i,1}, v_{i, 2},\dots, v_{i,6}\), and the additional edges \(v_{1,3} v_{2,3}, v_{2,3} v_{3,3},\dots, v_{k-1,3}v_{k,3}\). See Figure 4 for an example of \(G_k\). Each \(G_k\) has \(6k\) vertices, and by Observation 8, we must have \(2k\) 3-paths in the dominating set. Therefore \(\gamma_{P_3}(G_k)=\frac{n}{3}\).
Theorem 10. For any tree \(T\) on \(n \geq 3\) vertices, \(\gamma_{P_3}(T) \leq\frac{n}{3}\).
Proof. Let \(T\) be a tree of order \(n\ge 3\). We will proceed by induction on \(n\). For \(n=3\) we have \(T=P_3\), and \(\gamma_{P_3} (P_3) = 1 = \frac{3}{3}\).
Let \(n>3\). Either there exists a longest path \(P\) in \(T\) such that one of the vertices on \(P\) adjacent to its endvertices has degree greater than two, or the vertices adjacent the endvertices of every longest path have degree two. Note the endvertices of a longest path are leaves, and therefore the vertices adjacent to the endvertices on the path are support vertices. Refer to Figure 5 for an illustration of an example of a support vertex, \(v\), of degree greater than two for Case 1, and of support vertices, labeled \(m_i\), all of degree two for Case 2.

In Case 1, let \(P\) be a longest path with a support vertex, \(v\), adjacent to \(k \ge 2\) leaves in \(T\). Let \(e\) be the edge of \(P\) incident to \(v\), but not to an endvertex of \(P\). Then \(T-e\) is a forest with components \(T'\) on \(n-(k+1)\) vertices and \(K_{1,k}\). If \(n-(k+1)\leq2\), then \(T\) is a star or a double star and we only need one \(P_3\) to dominate \(T\), which is less than \(\frac{n}{3}\). If \(n-(k+1) \ge 3\), the induction hypothesis gives \(\gamma_{P_3}(T') \le \frac{n-(k+1)}{3}\). Let \(D'\) be a 3-path dominating set of \(T'\) with \(|D'|\le \frac{n-(k+1)}{3}\). Note that we only require one 3-path, say \(Q\), to dominate \(K_{1,k}\). Thus \(D = D' \cup Q\) is a 3-path dominating set of \(T\) with \(|D|\le \gamma_{P_3}(T')+1 = \frac{n-(k+1)+3}{3} \le \frac{n}{3}\), since \(k+1 \ge 3\).
In Case 2, all the support vertices of the endvertices of the longest paths have degree two. Let \(P\) be a longest path and let \(v\) be a vertex on \(P\) that is not a leaf and is adjacent to the support vertex of an endvertex of \(P\), that is, a vertex that is distance \(2\) away from an endvertex of \(P\). Consider the neighbors of \(v\) including neighbors not on \(P\) and the support vertex of the endvertex of \(P\). Label these \(i\) neighbors \(m_i\). Note that each \(m_i\) is either degree two or degree one otherwise we contradict the assumption of Case 2. For any \(m_i\) that has degree two, label its leaf neighbor \(\ell_i\). Let \(e\) be the edge of \(P\) incident to \(v\), but not to an endvertex of \(P\). Then \(T-e\) is a forest with components \(H\) (containing \(v\) and all the \(m_i\) and \(\ell_i\)) and \(T'\).
If \(|V(T')|\leq 2\), then \(T\) is either \(P_4\), \(P_5\), or a spider with center vertex \(v\) and legs of length one or two. Note that if \(T\) is one of the two paths, we need only one \(P_3\) to dominate it, which is less than \(\frac{n}{3}\). Suppose \(T\) is a spider with \(k\) legs of length two, and \(j\) legs of length one. If \(k\) is even, then we create 3-paths between pairs of support vertices of the legs of length two to obtain a \(\gamma_{P_3}\)-set of size \(\frac{k}{2}\). If \(k\) is odd, we create pairs of support vertices using \(k-1\) of the legs of length two, and add one 3-path from \(v\) to the leaf of the unpaired leg of length two to obtain a \(\gamma_{P_3}\)-set of size \(\frac{k+1}{2}\). (We use this method again when we look at banana trees in Theorem 4.5.) Note that in both cases, \(n=2k+j+1\), and \(\frac{k}{2}\) and \(\frac{k+1}{2}\) are both less than \(\frac{n}{3}\).
Suppose \(|V(T')| \ge 3\). Then \(H\) is a spider. Let \(k\) be the number of paths of the form \(\{v,m_i,\ell_i\}\), i.e. legs of length two. If \(k\) is even, then we dominate \(H\) using \(\frac{k}{2}\) many 3-paths and by the induction hypothesis \(\gamma_{P_3}(T') \le \frac{n-(2k+1)}{3} = \frac{n}{3} – \frac{2k+1}{3}\) (\(H\) contains \(v\), \(2k\) vertices for each leg of length two, and possibly more vertices if \(v\) has leaves as neighbors.) So \[ \gamma_{P_3}(T) \leq \gamma_{P_3}(T')+ \gamma_{P_3}(H) \le \frac{n}{3} – \frac{2k+1}{3} + \frac{k}{2}= \frac{n}{3} – \frac{k+2}{6}\le \frac{n}{3}. \] If \(k\) is odd, then \(k\geq 1\) and we need \(\frac{k+1}{2}\) many 3-paths to dominate \(H\), so similarly \[ \gamma_{P_3}(T) \leq \gamma_{P_3}(T')+ \gamma_{P_3}(H) \le \frac{n}{3} – \frac{2k+1}{3} + \frac{k+1}{2}= \frac{n}{3} – \frac{k-1}{6}\le \frac{n}{3}. \]
By induction, we have shown that \(\gamma_{P_3}(T)\le \frac{n}{3}\). ◻
The following result follows readily from Theorem 10 by considering a spanning tree of \(G\).
Corollary 4. For any connected graph \(G\) on \(n \geq 3\) vertices, \(\gamma_{P_3}(G) \leq \frac{n}{3}\).
While bounds for general graphs are desirable, it is useful to restrict ourselves to families of graphs to obtain formulas or tighter upper bounds for those families. We begin by looking at path and cycle graphs.
Theorem 11. For \(n \geq 3\), \(\gamma_{P_3}(P_n) = \gamma_{P_3}(C_n) = \lceil{\frac{n}{5}}\rceil\).
Proof. Consider \(P_n\) for \(n \geq 3\). Suppose \(n = 5q+k\) for nonnegative integers \(q\) and \(k\), where \(k < 5\). We can partition \(P_n\) into \(q\) vertex-disjoint segments \(S_i\), where \(|V(S_i)| = 5\), and one segment \(S_{q+1}\) with \(k\) vertices. (Refer to Figure 6.) We can dominate at most five vertices with a 3-path in \(P_n\), specifically the three in the 3-path and potentially two others adjacent to the ends. Thus we need one 3-path for each \(S_i\). Hence if \(k=0\) we need \(q\) 3-paths and if \(k>0\) we need \(q+1\) 3-paths. Hence \(\gamma_{P_3}(P_n) \lceil{\frac{n}{5}}\rceil\).
The same argument holds for \(C_n\), from which we can obtain \(P_n\) by deleting one edge. ◻

Corollary 5. If \(G\) is a connected graph on \(n\geq 3\) vertices that has a Hamiltonian path, then \(\gamma_{P_3}(G) \leq \lceil{\frac{n}{5}}\rceil\).
Proof. Suppose \(P\) is a Hamiltonian path of \(G\). Then \(P\cong P_n\) and since \(\gamma_{P_3}(P_n) = \lceil{\frac{n}{5}}\rceil\) and \(G\) is obtained from \(P\) by adding edges, by Observation 6, we find that \(\gamma_{P_3}(G) \leq \lceil{\frac{n}{5}}\rceil\). ◻
Introducing even the slightest complexity to a graph can hinder our ability to find a formula for \(\gamma_{P_3}(G)\). One such example is the caterpillar tree. A caterpillar is a tree in which every leaf is adjacent to a central path, or stalk. See Figure 7 for an example.

We will use the following observation in the proof of the next theorem.
Observation 12. If a new vertex is connected by a single edge to a graph \(G\) to form a new graph \(G^*\), then \(\gamma_{P_3} (G) \leq \gamma_{P_3} (G^*)\).
Theorem 13. Let \(A\) be a caterpillar with stalk \(S\) and \(m = {\lvert}{\rvert}{V(S)}\). Then \(\lceil{\frac{m+2}{5}}\rceil \leq \gamma_{P_3}(A) \leq \lceil{\frac{m}{3}}\rceil\).
Proof. Let \(A\) be a caterpillar with stalk \(S\) and \(m=|V(S)|\). Then there exists a longest path, \(P\), in \(A\) of length \(m+2\), such that \(V(S) \subseteq V(P)\). Any vertex in \(V(A\setminus P)\) must be a leaf that is adjacent to a vertex of \(P\) that is not a leaf. Thus \(\gamma_{P_3}(A) \geq \gamma_{P_3}(P)\) by Observation 12. By Theorem 11, \(\gamma_{P_3}(P) \geq \lceil{\frac{m+2}{5}}\rceil\).
By Observation 8, a caterpillar in which every vertex of the stalk is a support vertex has a 3-path domination number at least as large as any caterpillar with in which at least one stalk vertex is not a support vertex. Thus we consider the case where every \(v_i \in V(S)\) is a support vertex Then, each of the \(v_i\) must be part of a 3-path by Observation 8. Furthermore, \(V(S)\) is a dominating set of \(A\). Thus a minimum 3-path dominating set would require that the 3-paths be as vertex disjoint as possible. At most two of the 3-paths would need to share vertices. Thus at most \(\lceil{\frac{m}{3}}\rceil\) 3-paths are needed. ◻

A banana tree, denoted \(B_{n,k}\) for \(n, k\geq 1\), is a tree composed of \(n\) copies of a \(K_{1,k-1}\) graph in which one leaf from each copy is joined by an edge to a vertex called the root vertex (See Figures 9 and 10 for examples).
Theorem 14. For \(n+k\geq 3\), the following formulas hold for \(\gamma_{P_3}(B_{n,k}):\)
\(\gamma_{P_3}(B_{n,1})=1\).
\(\gamma_{P_3}(B_{n,2}) = \lceil{\frac{n}{2}}\rceil\).
For \(k \geq 3\), \(\gamma_{P_3}(B_{n,k}) = n\).
Proof.
Note that \(B_{n,1}\) is a star, \(K_{1,n}\). Any 3-path in a star will contain the center vertex and thus dominate all vertices. Hence, \(\gamma_{P_3}(B_{n,1})=1\).
For \(k=2\), we pick our 3-paths with the following process. In \(B_{n,2}\), the support vertices are the vertices adjacent to the root vertex. We make unique pairs of support vertices, and choose the unique 3-path between each pair to be in our dominating set. If \(n\) is odd, then one support vertex is not in a pair and the last 3-path will include the leaf adjacent to the lone support vertex. See Figure [fig:banana1]. By Observation 1, every support vertex must be in a 3-path, so this is best possible.
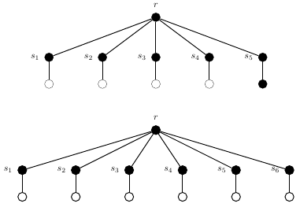
For \(k \geq 3\), by Observation 8, the center vertex of every copy of \(K_{1,k-1}\) must be part of a 3-path. It is impossible to include any two centers in the same 3-path. So we must have a 3-path for each copy of \(K_{1,k-1}\). We can insure that at least one of these 3-paths contains or is adjacent to the root vertex. Then one 3-path for each \(K_{1,k-1}\) is best possible. Since we have \(n\) copies, \(\gamma_{P_3}(B_{n,k})=n\). See Figure 10.
◻

A Harary graph, denoted \(H_{k,n}\), is a \(k\)-regular graph of order \(n\) with \(k \leq n-1\), \(V(G) = \{v_1,v_2,\dots,v_n\}\) and adjacencies as follows. If \(k\) is even, then \(k=2j\) for some integer \(j\) and we join \(v_i\) to \(\{v_{i-j},v_{i-j+1},\dots , v_{i-1},v_{i+1}, \dots ,v_{i-1+j}, v_{i+j}\}\). If \(k\) is odd, then \(k= 2j+1\) for some \(j\) and \(n = 2\ell\) for some \(\ell\), and we join \(v_i\) to \(\{v_{i-j},v_{i-j+1},\dots v_{i-1},v_{i+1},\dots , v_{i-1+j}, v_{i+j}\}\) and \(v_{i+\ell}\). See Figure 11 for an example.
Theorem 15. For \(k\) even, we have \(\gamma_{P_3}(H_{k,n}) =\lceil{\frac{n}{2k+1}}\rceil\).
Proof. Suppose we have \(G = H_{k,n}\) where \(k=2j\) for some integer \(j\). Note that a Hamiltonian cycle exists in each Harary graph and we can assume the vertices around this cycle are labeled \(v_1,\dots, v_n\). To construct a 3-path dominating set of \(G\), we create 3-paths as follows. Define a 3-path, \(Q\), by choosing any vertex \(v_m\) to be the middle vertex and then choose neighbors \(v_{m-j}\) and \(v_{m+j}\) to be the end vertices such that there is a path of length \(\frac{k}{2}\) from \(v_m\) to \(v_{m-j}\) and \(v_{m+j}\). Notice, \(v_m\) dominates \(k+1\) vertices, and each of \(v_{m-j}\) and \(v_{m+j}\) has an additional \(\frac{k}{2}\) private neighbors with respect to \(Q\) so long as \(n\) is sufficiently large. So, \(Q\) dominates \(k+1 + \frac{k}{2} + \frac{k}{2} = 2k+1\) vertices. Note, \(Q\) dominates the largest number of vertices possible by a 3-path in \(G\). In addition, all the dominated vertices lie on a single path (Figure 11). Suppose \(n=(2k+1)q+r\) where \(0\leq r\leq 2k\). Then we can partition the labeled Hamiltonian cycle of \(G\) into \(q\) segments of \(2k+1\) vertices and one segment with \(r\) vertices. We choose a 3-path \(Q\) for each of those segments, and thus we can dominate \(G\) with \(\lceil{\frac{n}{2k+1}}\rceil\) 3-paths and this is best possible. ◻
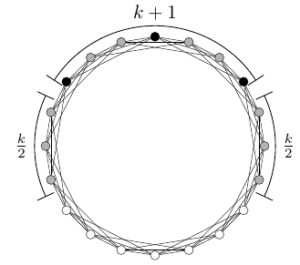
The case when \(k\) is odd is more complicated because the neighbors of a vertex are not confined to a sequential path along a Hamiltonian cycle. Ignoring the neighbors not along a sequential path, we can use the proof of Theorem 15 to obtain the following upper bound on the 3-path domination number of Harary graphs of odd degree.
Corollary 6. For \(k\) odd, we have \(\gamma_{P_3}(H_{k,n}) \leq \lceil\frac{n}{2k-1}\rceil\).
The authors wish to thank Bert Hartnell of Saint Mary’s University in Halifax for his suggestions and support. The authors also wish to thank Kevin O’Bryant of CUNY – Staten Island and Daniel Cranston of Virginia Commonwealth University for their feedback and suggestions.
This article is based on the research completed at the NSF HWS-REU (grant no. DMS 1757616) in the summer of 2018. At the time, Rayan Ibrahim was a student at the College of Staten Island, and Rebecca Jackson was a student at Charleston Southern University. As of January 2020, Ibrahim is a graduate student at Virginia Commonwealth University and Jackson is a graduate student at the University of Arkansas.
The authors declare no conflict of interest.