In this paper we introduce the concept of independent fixed connected geodetic number and investigate its behaviours on some standard graphs. Lower and upper bounds are found for the above number and we characterize the suitable graphs achieving these bounds. We also define two new parameters connected geo-independent number and upper connected geo-independent number of a graph. Few characterization and realization results are formulated for the new parameters. Finally an open problem is posed.
The introduction of Graph Theory is a revolution in the field of Mathematics. Various concepts were made easily understandable by its simple expression through graphical models. By a graph \(G\) we mean \(V\), the set of vertices; \(E\), the set of edges together with a binary operation of association. We refer to [1,2, 3 ] for basic graph theoretic terms. In \(G\), a shortest \(x-y\) path is also known as \(x-y\) geodesic. The distance \(d(x,y)\) is defined as the number of edges of an \(x-y\) geodesic in \(G\). For any two vertices \(x\) and \(y\) in \(G\), the closed interval \(I[x, y]\) is the collection of vertices on an \(x-y\) geodesic. The closed interval \(I[S,S']\), where \(S, S'\subseteq V(G)\), is defined as the union of subintervals \(I[x, y]\) for some \(x\in S\) and \(y\in S'\). i.e., \(I[S, S'] = \bigcup_{x\in S, y\in S'} I[x, y]\). A vertex \(v\) in \(G\) is called an extreme vertex or simplicial vertex if the subgraph induced by its adjacent vertices is complete.
A set \(S\subseteq V(G)\) is called a geodetic set or geodomination set if every vertex of \(G\) is on some \(x-y\) geodesic where \(x, y\in S\). The minimum cardinality of a geodetic set of \(G\) is called as the geodetic number of \(G\), denoted by \(g(G)\) [4, 5, 6, 7, 8]. If \(S\) is a geodetic set of \(G\) and \(\left\langle S \right\rangle\) is connected, then \(S\) is called the connected geodetic set of \(G\). Its minimum order is named as the connected geodetic number of \(G\), denoted by \(cg(G)\). A connected geodetic set of cardinality \(cg(G)\) is called a \(cg\)-set of \(G\) [9]. Again parameters upper connected geodetic number and forcing connected geodetic number were defined and investigated in [10]. Santhakumaran and Titus first introduced the vertex geodomination number in [11] and further studied in [12, 13]. For any vertex \(x\) in \(G\), a set \(S \subseteq V(G)\) is called an \(x\)-geodominating set of \(G\) if every vertex \(v\) in \(G\) is on an \(x-y\) geodesic for some \(y\) in \(S\). The minimum cardinality of an \(x\)-geodominating set of \(G\) is defined as the \(x\)-geodomination number of \(G\), denoted by \(g_x(G)\). An \(x\)-geodominating set of cardinality \(g_x(G)\) is called a \(g_x\)-set of \(G\). A connected \(x\)-geodominating set of \(G\) is an \(x\)-geodominating set \(S\) such that \(\left\langle S \right\rangle\) is connected. The minimum cardinality of a connected \(x\)-geodominating set of \(G\) is the connected \(x\)-geodomination number of \(G\) and is denoted by \(cg_x(G)\). A connected \(x\)-geodominating set of cardinality \(cg_x(G)\) is called a \(cg_x\)-set of \(G\) [14].
Let \(e=xy\) be any edge of a connected graph \(G\) of order atleast 3. A set \(S\) of vertices of \(G\) is an \(e\)-geodominating set of \(G\) if every vertex of \(G\) is either on an \(x-u\) geodesic or on an \(y-u\) geodesic for some element \(u\) in \(S\). The minimum cardinality of an \(e\)-geodominating set of \(G\) is defined as the \(e\)-geodomination number of \(G\) and is denoted by \(g_e(G)\) or \(g_{xy}(G)\). An \(e\)-geodominating set of cardinality \(g_e(G)\) is called a \(g_e\)-set of \(G\) [15].
It is clear that \(x\)-geodominating set of \(G\) is obtained by fixing a vertex \(x\) in \(G\) and \(e\)-geodominating set of \(G\) is obtained by fixing an edge \(e = xy\) in \(G\). Based on these concepts we defined a new parameter called independent fixed geodomination number (or independent fixed geodetic number) in [16]. Let \(S\) be an independent set of a connected graph \(G\) of order atleast \(2\). Let \(S'\) be a subset of \(V(G)\). If each vertex \(v\) in \(G\) is on an \(x-y\) geodesic for some \(x\in S\) and \(y\in S'\), then \(S'\) is an \(S\)-fixed geodetic set of \(G\) . The \(S\)–fixed geodetic number \(g_s(G)\) of \(G\) is the minimum cardinality of an \(S\)-fixed geodetic set of \(G\). The independent fixed geodetic number of \(G\) is \(g_{if}(G) = min \left\{g_s(G)\right\}\), where the minimum is taken over all independent sets \(S\) in \(G\). An independent fixed geodetic set of cardinality \(g_{if}(G)\) is described as \(g_{if}\)-set of \(G\). We too further proceed to infer about connectedness of an \(S\)-fixed geodetic set of \(G\), where \(S\) is an independent set in a connected graph \(G\). In the computation of independent fixed connected geodetic number, the succeeding theorems will be employed.
Theorem 1. [16] For any connected graph \(G\), \(1\leq g_{if}(G) \leq {p-1}\).
Theorem 2. [16] Let \(G\) be a connected graph. Then \(g_{if}(G) = 1\) if and only if there is an independent set \(S\) and its eccentric vertex \(y\) such that every vertex of \(G\) is on an \(x-y\) geodesic for some \(x\in S\).
Theorem 3. [16] For any complete graph \(K_p\), \(g_{if}(K_p)={p-1}\).
Definition 1. Let \(S\) be an independent set of a connected graph \(G\) of order atleast 2. An \(S\)-fixed connected geodetic set of \(G\) is an \(S\)-fixed geodetic set \(S'\) such that \(\left\langle S'\right\rangle\) is connected. The \(S\)-fixed connected geodetic number \(cg_s(G)\) of \(G\) is the minimum cardinality of an \(S\)-fixed connected geodetic set of \(G\). The independent fixed connected geodetic number \(cg_{if}(G)\) of \(G\) is defined as \(cg_{if}(G) = min \left\{cg_s(G)\right\}\), where the minimum is taken over all independent sets \(S\) in \(G\). An independent fixed connected geodetic set of cardinality \(cg_{if}(G)\) is called a \(cg_{if}\)-set of G.
Example 1. Consider a graph \(G\) as shown in Figure 1. The Table 1 gives the independent sets \(S\), their corresponding minimum \(S\)-fixed geodetic sets and minimum \(S\)-fixed connected geodetic sets, the \(S\)-fixed geodetic numbers \(g_s(G)\) and the \(S\)-fixed connected geodetic numbers \(cg_s(G)\). Then the independent fixed geodetic number of \(G\) is \(g_{if}(G) = min\left\{g_s(G)\right\} = 2\) and the independent fixed connected geodetic number of \(G\) is \(cg_{if}(G) = min\left\{cg_s(G)\right\} = 3\).
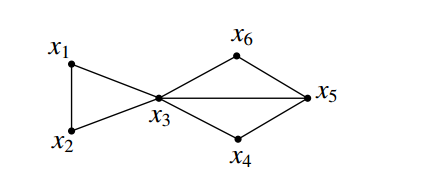
| Independent | Minimum \(S\)-fixed | \(S\)-fixed | Minimum \(S\)-fixed | \(S\)-fixed |
| set \(S\) | geodetic set | geodetic | connected geodetic set | connected |
| number \(g_s{G}\) | geodetic | |||
| number \(cg_s{G}\) | ||||
| \(\{x_1\}\) | \(\{x_2, x_4, x_5, x_6\}\) | \(4\) | \(\{x_2, x_3, x_4, x_5, x_6\}\) | \(5\) |
| \(\{x_2\}\) | \(\{x_1, x_4, x_5, x_6\}\) | \(4\) | \(\{x_1, x_3, x_4, x_5, x_6\}\) | \(5\) |
| \(\{x_3\}\) | \(\{x_1, x_2, x_4, x_5, x_6\}\) | \(5\) | \(\{x_1, x_2, x_3, x_4, x_5, x_6\}\) | \(6\) |
| \(\{x_4\}\) | \(\{x_1, x_2, x_6\}\) | \(3\) | \(\{x_1, x_2, x_3, x_6\}\) | \(4\) |
| \(\{x_5\}\) | \(\{x_1, x_2, x_4, x_6\}\) | \(4\) | \(\{x_1, x_2, x_3, x_4, x_6\}\) | \(5\) |
| \(\{x_6\}\) | \(\{x_1, x_2, x_4\}\) | \(3\) | \(\{x_1, x_2, x_3, x_4\}\) | \(4\) |
| \(\{x_1, x_4\}\) | \(\{x_2, x_6\}\) | \(2\) | \(\{x_2, x_3, x_6\}\) | \(3\) |
| \(\{x_1, x_5\}\) | \(\{x_2, x_4, x_6\}\) | \(3\) | \(\{x_2, x_3, x_4, x_6\}\) | \(4\) |
| \(\{x_1, x_6\}\) | \(\{x_2, x_4\}\) | \(2\) | \(\{x_2, x_3, x_4\}\) | \(3\) |
| \(\{x_2, x_4\}\) | \(\{x_1, x_6\}\) | \(2\) | \(\{x_1, x_3, x_6\}\) | \(3\) |
| \(\{x_2, x_5\}\) | \(\{x_1, x_4, x_6\}\) | \(3\) | \(\{x_1, x_3, x_4, x_6\}\) | \(4\) |
| \(\{x_2, x_6\}\) | \(\{x_1, x_4\}\) | \(2\) | \(\{x_1, x_3, x_4\}\) | \(3\) |
| \(\{x_4, x_6\}\) | \(\{x_1, x_2, x_5\}\) | \(3\) | \(\{x_1, x_2, x_3, x_5\}\) | \(4\) |
| \(\{x_1, x_4, x_6\}\) | \(\{x_2, x_5\}\) | \(2\) | \(\{x_2, x_3, x_5\}\) | \(3\) |
| \(\{x_2, x_4, x_6\}\) | \(\{x_1, x_5\}\) | \(2\) | \(\{x_1, x_3, x_5\}\) | \(3\) |
Theorem 4. In a connected graph \(G\), \(1\leq g_{if}(G)\leq cg_{if}(G)\leq {p-1}\).
Proof. For any independent set \(S\) in a connected graph \(G\), every \(S\)-fixed connected geodetic set is an \(S\)-fixed geodetic set of \(G\), we have \(g_{if}(G)\leq cg_{if}(G)\). Then by Theorem 1, we have \(1\leq g_{if}(G)\leq cg_{if}(G)\leq {p-1}\).
We intend to characterize the graphs that realize the bounds in Theorem 4. For that we use the following definition.
Definition 2. [16] Let \(G\) be a connected graph of order atleast 2. Let \(S\subset V(G)\) and \(y\in V(G)-S\). The distance between the set \(S\) and the vertex \(y\) is \(d(S, y) = min \{d(x, y): x\in S\}\). The eccentricity of the set \(S\) is \(e(S) = max \{d(S,y): y\in {V(G)-S}\}\). An eccentric vertex of \(S\) is a vertex \(v\) of \(G\) with \(d(S, v) = e(S)\).
Theorem 5. Let \(G\) be a connected graph of order atleast 2. Then \(cg_{if}(G) = 1\) if and only if there is an independent set \(S\) and its eccentric vertex \(y\) such that every vertex of \(G\) is on an \(x-y\) geodesic for some \(x\in S\).
The following theorem gives \(cg_{if}(G)\) for some standard graphs.
Theorem 6.
If \(G = T\) or \(K_{m,n}\), then \(cg_{if}(G)=1\).
If \(G = C_p\), then \(cg_{if}(G)\) is 1 or 2 according as \(p\) is even or odd.
If \(G = K_1 + \cup m_jK_j\) with \(G\) is neither a complete graph nor a star, then \(cg_{if}(G) = j-1\) or \(\sum m_j(j-1)+1\) according as \(\sum_{j\geq2}m_j=1\) or \(\sum_{j\geq2}m_j\geq2\).
In view of Theorem 4, we proceed to characterize graphs \(G\) with \(cg_{if}(G) = {p-1}\).
Theorem 7. Let \(G\) be a connected graph of order \(p\geq 2\). Then \(cg_{if}(G) = {p-1}\) if and only if \(G = K_p\).
Proof. Let \(cg_{if}(G) = p-1\). Claim that \(G = K_p\). If not, then \(G\) has a diametral path \(P: u_0, u_1, \ldots, u_d\) of length \(d\geq 2\). It is clear that \(u_0\) and \(u_d\) are non-cut vertices of \(G\). If \(u_0\) or \(u_d\) is an end vertex of \(G\), then \(S=\{u_0,u_d\}\) is an independent set of \(G\) and \(S'=V(G)-S\) is an \(S\)-fixed connected geodetic set of \(G\). Hence \(cg_{if}(G) \leq {p-2}\), but this leads to a contradiction. If both \(u_0\) and \(u_d\) are non-end vertices of \(G\), then there exist atleast two \(u_0-u_d\) paths in \(G\). If atleast one vertex other than \(u_0\) and \(u_d\) is common for any two \(u_0-u_d\) paths in \(G\), then \(S=\{u_0,u_d\}\) is an independent set of \(G\) and \(S'=V(G)-S\) is an \(S\)-fixed connected geodetic set of \(G\). Hence \(cg_{if}(G) \leq {p-2}\), but this leads to a contradiction. Suppose that there exist two \(u_0-u_d\) paths, say \(P_1\) and \(P_2\), has no common vertices other than \(u_0\) and \(u_d\). Let \(z\) be an adjacent vertex of \(u_0\) in \(P_1\). If \(z\) is a cut vertex of \(G\), then let \(H\) be a component of \(G-z\) with \(u_0\) not in \(H\). Let \(z_1\) be a vertex farthest away from \(z\) in \(H\). Then it is clear that \(S=\{z_1,u_d\}\) is an independent set of \(G\) and \(S'=V(G)-S\) is an \(S\)-fixed connected geodetic set of \(G\). Hence \(cg_{if}(G) \leq {p-2}\), but this leads to a contradiction. If \(z\) is not a cut vertex and \(\{u_o,z\}\) is not a vertex-cut of \(G\), then \(S=\{u_0\}\) is an independent set of \(G\) and \(S'=V(G)-\{u_0,z\}\) is an \(S\)-fixed connected geodetic set of \(G\). Hence \(cg_{if}(G) \leq {p-2}\), but this leads to a contradiction. If \(z\) is not a cut vertex and \(\{u_0,z\}\) is a vertex-cut of \(G\), then there exists another \(u_0-z\) path, say \(Q\), of length atleast 2. Let \(w\) be an adjacent vertex of \(u_0\) on \(Q\). If \(w\) is a cut vertex of \(G\), then let \(H_1\) be a component of \(G-w\) with \(u_0\) not in \(H_1\). Let \(w_1\) be a vertex farthest away from \(w\) in \(H_1\). Then it is clear that \(S=\{w_1,u_d\}\) is an independent set of \(G\) and \(S'=V(G)-S\) is an \(S\)-fixed connected geodetic set of \(G\). Hence \(cg_{if}(G) \leq {p-2}\), but this leads to a contradiction. If \(w\) is not a cut vertex and \(\{w,u_d\}\) is not a vertex-cut of \(G\), then \(S=\{w,u_d\}\) is an independent set of \(G\) and \(S'=V(G)-S\) is an \(S\)-fixed connected geodetic set of \(G\). Hence \(cg_{if}(G) \leq {p-2}\), but this leads to a contradiction. If \(w\) is not a cut vertex and \(\{w,u_d\}\) is a vertex-cut of \(G\), then \(S=\{w\}\) is an independent set of \(G\) and \(S'=V(G)-\{w,u_0\}\) is an \(S\)-fixed connected geodetic set of \(G\). Hence \(cg_{if}(G) \leq {p-2}\), but this leads to a contradiction. Converse is clear from Theorems 3 and 4.
Now we proceed to characterize graphs \(G\) with \(cg_{if}(G) = p-2\). For that we require the definition of a special graph \(K_m\leftarrow P_r\rightarrow K_n\).
Definition 3. The graph \(G=K_m\leftarrow P_r\rightarrow K_n\) is obtained from two complete graphs \(K_m, K_n\) and a path \(P_r\) by joining every vertex in \(K_m\) with an end vertex of \(P_r\) and joining every vertex in \(K_n\) with the other end vertex of \(P_r\).
The graph \(G = K_m\leftarrow P_r\rightarrow K_n\) is shown in Figure 2.
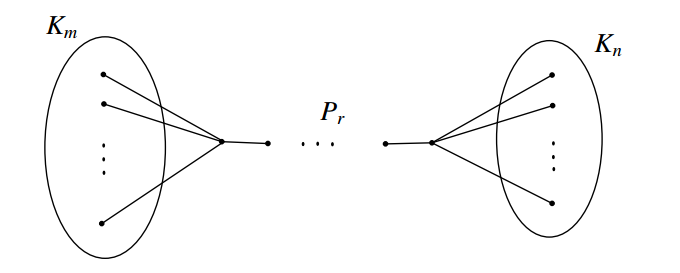
Theorem 8. Let \(G\) be a connected graph of order \(p\geq 3\). Then \(cg_{if}(G) = p-2\) if and only if \(G\) is either \(P_3\) or \(K_m\leftarrow P_r\rightarrow K_n\) (\(m, n\geq 2\) and \(r\geq 1\)).
Proof. Let \(cg_{if}(G) =
p-2\). If \(p = 3\), then by
Theorems 7 and 6\((i)\) we
conclude that \(G = P_3\). If \(p = 4\), then \(G\) is either \(K_4, K_2+\bar{K_2}, K_1 +(K_1\cup K_2), K_{1,3},
P_4\) or \(C_4\). If \(G = K_4\), then by Theorem 7, \(cg_{if}(G) =3= p-1\), but this leads to a
contradiction. If \(G =
K_2+\bar{K_2}\), then \(G\) has
two simplicial vertices, say \(x\) and
\(y\). It is obvious that \(S = \{x\}\) is an independent set of \(G\) and \(S'
= \{y\}\) is the minimum \(S\)-fixed connected geodetic set of \(G\). Hence \(cg_{if}(G) = 1 = p-3\), but this leads to a
contradiction. If \(G = K_1 +(K_1\cup K_2),
K_{1,3}, P_4\) or \(C_4\), then
by Theorem 6, \(cg_{if}(G) =1 =
p-3\), but this leads to a contradiction.
Now, let \(p\geq 5\). Since \(cg_{if}(G) = p-2\), by Theorem 7, we
have \(G \neq K_p\). First, we show
that every vertex of \(G\) is either a
cut vertex or a simplicial vertex. Incase there exists a vertex, say
\(x\), in \(G\) which is neither a cut vertex nor a
simplicial vertex, then \(x\) lies on a
cycle in \(G\). Let \(C\) be a largest chordless cycle containing
the vertex \(x\) in \(G\). We consider three cases.
Case (1) Length of the cycle \(C\) is more than 3 and degree of \(x\) is 2.
Let \(y\) and \(z\) be the adjacent vertices of \(x\) on \(C\). Since \(C\) is a chordless cycle, \(y\) and \(z\) are non-simplicial vertices of \(G\).
Subcase (1) \(deg~y=deg~z=2\). Let \(S = \{x\}\) be an independent set of \(G\). If \(C\) is an even cycle, then \(y\) and \(z\) is on an \(x-x_1\) geodesic, where \(x_1\) is an eccentric vertex of \(x\) on \(C\); and if \(C\) is an odd cycle, then \(y\) is on an \(x-x_1\) geodesic and \(z\) is on an \(x-x_2\) geodesic, where \(x_1\) and \(x_2\) are the eccentric vertices of \(x\) on \(C\). Then it is clear that \(S' = V(G)-\{x,y,z\}\) is an \(S\)-fixed geodetic set of \(G\). Since \(deg~y=deg~z=deg~x=2\), \(\left\langle S' \right\rangle\) is
connected. Hence \(S'\) is an \(S\)-fixed connected geodetic set of \(G\) and so \(cg_{if}(G)\leq {p-3}\), but this leads to a
contradiction.
Subcase (2) \(deg~y \geq
3\) and \(deg~z \geq 3\). Since
\(deg~x=2\), \(G-x\) is a connected graph. If \(y\) and \(z\) are cut vertices of \(G\), then let \(G_1\) and \(G_2\) be the components of \(G-y\) and \(G-z\), respectively, with the vertex \(x\) not in both \(G_1\) and \(G_2\). Let \(y_1\) be a vertex farthest away from \(y\) in \(G_1\) and let \(z_1\) be a vertex farthest away from \(z\) in \(G_2\). Then it is vivid that \(S = \{x, y_1, z_1\}\) is an independent set
of \(G\) and \(S' = V(G)-S\) is an \(S\)-fixed connected geodetic set of \(G\). Hence \(cg_{if}(G)\leq {p-3}\), but this leads to a
contradiction.
If \(y\) and \(z\) are non-cut vertices of \(G\) and \(\{y,
z\}\) is a vertex-cut of \(G-x\), then \(y,x\) and \(z\) are the consecutive vertices of another
chordless cycle, say \(C'\), in
\(G\). Let \(z'\neq x\) be an adjacent vertex of
\(z\) on \(C'\). If \(z'\) is a non-cut vertex of \(G\), then \(S =
\{x, z'\}\) is an independent set of \(G\) and \(S'
= V(G)-\{x,z,z'\}\) is an \(S\)-fixed connected geodetic set of \(G\). Hence \(cg_{if}(G)\leq p-3\), but this leads to a
contradiction. If \(z'\) is a cut
vertex of \(G\), then let \(G_3\) be a component of \(G-z'\) with the vertex \(z\) not in \(G_3\). Let \(z''\) be a vertex farthest away
from \(z'\) in \(G_3\). Then \(S_1
= \{x, z''\}\) is an independent set of \(G\) and \(S_1' = V(G)-\{x, z, z''\}\) is
an \(S\)-fixed connected geodetic set
of \(G\). Hence \(cg_{if}(G)\leq {p-3}\), but this leads to a
contradiction.
If \(y\) and \(z\) are non-cut vertices of \(G\) and \(\{y,
z\}\) is not a vertex-cut of \(G-x\). It is clear that \(S=\{x\}\) is an independent set of \(G\) and \(S'
= V(G)-\{x, y, z\}\) is an \(S\)-fixed connected geodetic set of \(G\) and so \(cg_{if}(G)\leq {p-3}\), but this leads to a
contradiction. If either \(y\) or \(z\) is a cut vertex of \(G\), then by the arguments similar to the
above, we get a contradiction.
Subcase (3) \(deg~y=2\) and \(deg~z \geq 3\) ((or) \(deg~y \geq 3\) and \(deg~z=2\)). If \(z\) is a cut vertex of \(G\), then let \(G_1\) be a component of \(G-z\) with the vertex \(x\) not in \(G_1\). Let \(z'\) be a vertex farthest away from
\(z\) in \(G_1\). Then \(S=\{x, z'\}\) is an independent set of
\(G\) and \(S'=V(G)-\{x,y,z'\}\) is an \(S\)-fixed connected geodetic set of \(G\) and so \(cg_{if}(G)\leq {p-3}\), but this leads to a
contradiction.
If \(z\) is not a cut vertex of \(G\), then clearly \(S=\{x\}\) is an independent set of \(G\) and \(S'=V(G)-\{x,y,z\}\) is an \(S\)-fixed connected geodetic set of \(G\). Hence \(cg_{if}(G)\leq {p-3}\), but this leads to a
contradiction.
Case (2) Length of the cycle \(C\) is more than 3 and degree of \(x\) is more than 2.
Subcase (1) \(\{x,y\}\) and \(\{x,z\}\) are non vertex-cuts of \(G\). Then it is clear that \(S=\{x\}\) is an independent set of \(G\) and \(S'=V(G)-\{x,y,z\}\) is an \(S\)-fixed connected geodetic set of \(G\). Hence \(cg_{if}(G)\leq {p-3}\), but this leads to a
contradiction.
Subcase (2) \(\{x,y\}\) and \(\{x,z\}\) are vertex-cuts of \(G\). Then \(G\) has two more cycles, say \(C_1\) and \(C_2\), with \(xy\) an edge of \(C_1\) and \(xz\) an edge of \(C_2\). Let \(x'\neq y\) be an adjacent vertex of
\(x\) on \(C_1\) and let \(x''\neq z\) be an adjacent vertex
of \(x\) on \(C_2\). If \(x'\) is a cut vertex of \(G\), then take \(a = x_1'\), where \(x_1'\) is a vertex farthest away from
\(x'\) in a component \(H\) of \(G-x'\) with \(x\) not a vertex of \(H\). Otherwise, take \(a =x'\). Similarly, if \(x''\) is a cut vertex of \(G\), then take \(b = x_1''\), where \(x_1''\) is a vertex farthest away
from \(x''\) in a component
\(H_1\) of \(G-x''\) with \(x\) not a vertex of \(H_1\). Otherwise, take \(b =x''\). It is clear that \(S=\{a,b\}\) is an independent set of \(G\) and \(S'=V(G)-\{x,a,b\}\) is an \(S\)-fixed connected geodetic set of \(G\). It implies \(cg_{if}(G)\leq {p-3}\), but this leads to a
contradiction.
Subcase (3) \(\{x,y\}\) is a vertex-cut and \(\{x,z\}\) is not a vertex-cut of \(G\) ((or) \(\{x,y\}\) is not a vertex-cut and \(\{x,z\}\) is a vertex-cut of \(G\)). Then \(G\) has one more chordless cycle, say \(C_1\), with \(xy\) an edge of \(C_1\). Let \(x'\neq y\) be an adjacent vertex of
\(x\) on \(C_1\). If \(x'\) is adjacent to \(y\) in \(G\) and \(x'\) is not a cut vertex of \(G\), then \(S=\{x'\}\) is an independent set of
\(G\) and \(S'=V(G)-\{x,x',z\}\) is an \(S\)-fixed connected geodetic set of \(G\) and so \(cg_{if}(G)\leq {p-3}\), but this leads to a
contradiction. If \(x'\) is
adjacent to \(y\) in \(G\) and \(x'\) is a cut vertex of \(G\), then by an argument similar to Subcase
(3) of Case (1), \(S=\{x,x''\}\) is an independent set
of \(G\) and \(S'=V(G)-\{x,x'',z\}\) is an
\(S\)-fixed connected geodetic set of
\(G\). Hence \(cg_{if}(G)\leq {p-3}\), but this leads to a
contradiction.
Similarly, if \(x'\) is a
non-adjacent vertex of \(y\) on \(C_1\) and \(x'\) is a non-cut vertex of \(G\), then \(S=\{x\}\) and \(S'=V(G)-\{x,x',z\}\). If \(x'\) is a non-adjacent vertex of \(y\) and \(x'\) is a cut vertex of \(G\), then \(S=\{x,x''\}\) and \(S'=V(G)-\{x,x'',z\}\), where
\(x''\) is a vertex farthest
away from \(x'\) in a component
\(H\) of \(G-x'\) with \(x\) not a vertex of \(H\). In both cases, \(S\) is an independent set of \(G\) and \(S'\) is an \(S\)-fixed connected geodetic set of \(G\) and hence \(cg_{if}(G)\leq {p-3}\), but this leads to a
contradiction.
Case (3) Length of the cycle \(C\) is 3.
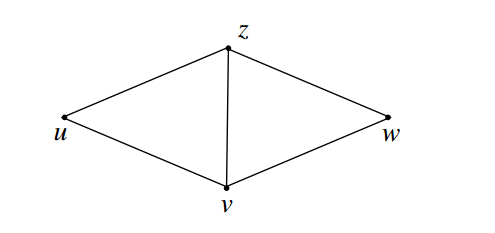
Then the graph \(H\) given in Figure 2.3 is a subgraph of \(G\). If not, every block of \(G\) is either \(K_2\) or \(K_3\) and so every vertex of \(G\) is either a cut vertex or a simplicial vertex, which is a contradiction to our assumption. Here we take the vertex \(u\) as \(x\) and the cycle \(u,v,w,z,u\) in \(H\) as \(C\) and continue the procedure exactly similar to Case (1) and Case (2), we get \(cg_{if}(G)\leq {p-3}\), but this leads to a contradiction.
Hence in all the three cases we get a contradiction and so every
vertex in \(G\) is either a cut vertex
or a simplicial vertex. Since \(cg_{if}(G)={p-2}\), by Theorem 7, \(G\) is a non-complete graph. Hence \(G\) has atleast one cut vertex. Let \(Q=\{u_1,u_2,\ldots,u_a\}\) be the set of
all cut vertices of \(G\). We consider
two cases.
Case (1) \(G\) has
exactly one cut vertex, say \(u_1\).
Let \(G_1,G_2,\ldots,G_t(t\geq2)\)
be the components of \(G-u_1\). If
\(t\geq3\), then \(S=\{x_1,x_2,\ldots,x_t\}\), where \(x_i\in G_i (1\leq i\leq t)\), is an
independent set of \(G\) and \(S'=V(G)-S\) is an \(S\)-fixed connected geodetic set of \(G\) and so \(cg_{if}(G)\leq {p-3}\), but this leads to a
contradiction. Hence \(t=2\). Now claim
that each component \(G_i (1\leq i\leq
2)\) has atleast two vertices. If \(G_1\) has exactly one vertex, say \(v\), then \(S=\{v,z\}\), where \(z\in G_2\), is an independent set of \(G\). It is clear that \(S'=V(G)-\{v,z,u_1\}\) is an \(S\)-fixed connected geodetic set of \(G\) and so \(cg_{if}(G)\leq {p-3}\), but this leads to a
contradiction. Hence \(G\) has exactly
one cut vertex and two components with each component having atleast two
vertices. Hence \(G=K_m\leftarrow
P_r\rightarrow K_n\) (\(m,n\geq
2\) and \(r=1\)).
Case (2) \(G\) has two
or more cut vertices.
Let \(R=\{z_1,z_2,\ldots,z_l\} (l\geq 0)\) be the set of all cut vertices of degree \(\geq 3\) in \(G\). If \(l=0\), then \(G\) is a path and so by Theorem 6(i), \(cg_{if}(G)=1<{p-3}\), but this leads to a contradiction. Now, let \(l\geq 1\) and let \(S=\{x_1,x_2,\ldots,x_b\}\) \((b\geq max\{2,l\})\), where \(x_i\) is a simplicial vertex of \(G\) in the \(i^{th}\) component of \(G-R\). If \(l\geq 3\), then clearly \(S\) is an independent set of \(G\) and \(S'=V(G)-S\) is an \(S\)-fixed connected geodetic set of \(G\) and so \(cg_{if}(G)\leq {p-3}\), but this leads to a contradiction. If \(l=1\), then clearly \(S\) is an independent set of \(G\) and \(S'=V(G)-\{S\cup(Q-R)\}\) is an \(S\)-fixed connected geodetic set of \(G\). Hence \(cg_{if}(G)\leq {p-3}\), but this leads to a contradiction. Hence \(l=2\). If \(G-R\) has 3 or more components, then \(S\) is an independent set of \(G\) and \(S'=V(G)-S\) is an \(S\)-fixed connected geodetic set of \(G\) and so \(cg_{if}(G)\leq {p-3}\), but this leads to a contradiction. Hence \(G-R\) has exactly 2 components. Since every vertex of \(G\) is either a cut vertex or a simplicial vertex, the components of \(G-R\) are complete graphs. Since \(l=2\), the two components of \(G-R\) are complete graphs with atleast two vertices and \(\left\langle R\right\rangle\) is a path. Hence \(G=K_m\leftarrow P_r\rightarrow K_n\) (\(m,n\geq2\) and \(r\geq1\)).
Conversely, let \(G=P_3\) or \(K_m\leftarrow P_r\rightarrow K_n\) \((m,n\geq 2\) and \(r\geq 1)\). If \(G=P_3\), then by Theorem 6(i), \(cg_{if}(G)=1={p-2}\). If \(G=K_m\leftarrow P_r\rightarrow K_n\), then every vertex in \(K_m\cup K_n\) is a simplicial vertex of \(G\). It is clear that any independent set \(S\) of \(G\) contains atmost one vertex from each \(K_m\) and \(K_n\). Also, every \(S\)-fixed connected geodetic set of \(G\) contains atleast \(m-1\) vertices from \(K_m\) and atleast \(n-1\) vertices from \(K_n\). Since \(m\geq 2\), \(n\geq 2\) and \(r\geq 1\), every vertex of \(P_r\) is an element of any \(S\)-fixed connected geodetic set of \(G\). Hence \(S'=V(G)-S\) is an \(S\)-fixed connected geodetic set of \(G\) and so \(cg_{if}(G)\geq {p-2}\). Let \(S_1=\{x,y\}\), where \(x\in V(K_m)\) and \(y\in V(K_n)\), and let \(S_1'=V(G)-S_1\). It is clear that \(S_1\) is an independent set of \(G\) and \(S_1'\) is an \(S_1\)-fixed connected geodetic set of \(G\) and so \(cg_{if}(G)={p-2}\).
Based on Theorem 4, we have the following realization result.
Theorem 9. For any three positive integers \(a,b\) and \(p\) with \(2\leq a\leq b\leq {p-3}\), it is possible to identify a connected graph \(G\) of order \(p\) with \(g_{if}(G)=a\) and \(cg_{if}(G)=b\).
Proof. We consider two cases.
Case (1) \(2\leq a=b\leq
{p-3}\). Let \(P_{p-a-1}:
v_1,v_2,\ldots,v_{p-a-1}\) be a path of order \(p-a-1\) and let \(K_{a+1}\) be the complete graph of order
\(a+1\). Let \(G\) be the graph obtained from \(P_{p-a-1}\) and \(K_{a+1}\) by joining an end vertex \(v_{p-a-1}\) of \(P_{p-a-1}\) with every vertex of \(K_{a+1}\). The resultant graph \(G\) is shown in Figure 4 and its order is
\(p\).
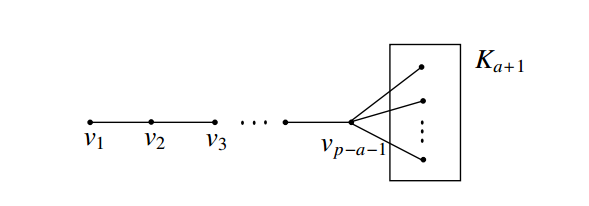
It is clear that any independent set of \(G\) contains atmost one vertex from the
complete graph \(K_{a+1}\). Also,
atleast \(a\) vertices in \(K_{a+1}\) lie in every \(S\)-fixed geodetic set of \(G\), where \(S\) is an independent set of \(G\). Hence \(g_{if}(G)\geq a\). Let \(S=\{v_1,x\}\) and \(S'=V(K_{a+1})-\{x\}\), where \(x\in V(K_{a+1})\). Since \(a\leq {p-3}\), \(S\) is an independent set of \(G\) and it is clear that every vertex of
\(V(G)-S\) is on a \(v_1-y\) geodesic for any \(y\in S'\). Hence \(S'\) is an \(S\)-fixed geodesic set of \(G\) and so \(g_{if}(G)=\left|S'\right|=a\). Also,
since \(\left\langle
S'\right\rangle\) is connected, we have \(cg_{if}(G)=g_{if}(G)=a\).
Case (2) \(2\leq a<b\leq
{p-3}\). Let \(P_{p-a-2}:
v_1,v_2,\ldots,v_{p-b-2},\ldots,v_{p-a-2}\) be a path of order
\(p-a-2\). Let \(K_2\) and \(K_a\) be two complete graphs of orders
\(2\) and \(a\), respectively. Let \(G\) be the graph obtained from \(P_{p-a-2}\), \(K_2\) and \(K_a\), by joining the vertex \(v_{p-b-1}\) of \(P_{p-a-2}\) with every vertex of \(K_2\) and joining the end vertex \(v_{p-a-2}\) of \(P_{p-a-2}\) with every vertex of \(K_a\). The resultant graph \(G\) is shown in Figure 5 and its order is
\(p\).
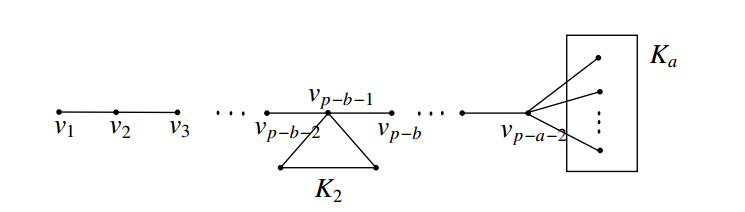
It is clear that any independent set of \(G\) contains atmost one vertex from each complete graphs \(K_2\) and \(K_a\). Also, atleast one vertex in \(K_2\) and atleast \(a-1\) vertices in \(K_a\) lie in every \(S\)-fixed geodetic set of \(G\), where \(S\) is any independent set of \(G\). Hence \(g_{if}(G)\geq a\). Let \(S=\{v_1,x,y\}\) and let \(S'=(V(K_2)-\{x\}) \cup (V(K_a)-\{y\})\), where \(x\in V(K_2)\) and \(y\in V(K_a)\). Since \(a< b\leq {p-3}\), \(S\) is an independent set of \(G\) and it is clear that every vertex of \(V(G)-S\) lies on a \(u- v\) geodesic for some \(u\) in \(S\) and \(v\) in \(S'\). Hence \(S'\) is an \(S\)-fixed geodetic set of \(G\) and so \(g_{if}(G)=\left|S'\right|=a\). But \(\left\langle S'\right\rangle\) is not connected and so \(cg_{if}(G)> a\). Since every \(S\)-fixed geodetic set of \(G\) contains atleast one vertex from each complete graphs \(K_2\) and \(K_a\), every \(S\)-fixed connected geodetic set of \(G\) contains the cut vertices \(\{v_{p-b-1},v_{p-b},\ldots,v_{p-a-2}\}\). Let \(S''=S'\cup \{v_{p-b-1},v_{p-b},\ldots,v_{p-a-2}\}\). It is clear that \(S''\) is a minimum \(S\)-fixed connected geodetic set of \(G\) and so \(cg_{if}(G)=\left|S''\right|=b\).
We know that the diameter of any connected graph lies between its radius and two times of its radius. For that Ostrand [17] has given a realization result. Ostrand’s theorem can be extended so that \(cg_{if}(G)\) can also be prescribed.
Theorem 10. For any three positive integers \(r, d\) and \(n\) with \(r\leq d\leq 2r\), a connected graph \(G\) can be identified with radius \(r\), diameter \(d\) and the independent fixed connected geodetic number \(n\).
Proof. If \(r=1\), then \(d=1\) or \(2\). If \(d=1\), then by Theorem 7, \(G=K_{n+1}\) has the desired property. Now, let \(d=2\). Let \(G\) be the graph obtained from the complete graphs \(K_2\) and \(K_{n+2}\) by merging a vertex of \(K_2\), say \(y\), and a vertex of \(K_{n+2}\). Then \(G\) has radius 1, diameter 2 and is shown in Figure 6.
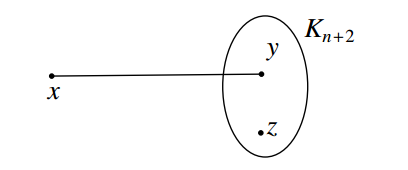
Let \(T=V(K_{n+2})-\{y\}\). If \(S\) is any independent set of \(G\), then atleast \(n\) vertices in \(T\) lie in every \(S\)-fixed connected geodetic set of \(G\) and so \(cg_{if}(G)\geq n\). Let \(S=\{x,z\}\), where \(z\neq y\) in \(K_{n+2}\), and let \(S'=T-\{z\}\). Clearly, \(S\) is an independent set of \(G\) and \(S'\) is the minimum \(S\)-fixed connected geodetic set of \(G\) and so \(cg_{if}(G)=n\).
Now, let \(r\geq 2\). We construct a
graph \(G\) which meets our
requirement.
Case (1) \(r=d\). Let
\(K_{n+2}\) be the complete graph with
vertex set \(V(K_{n+2})=\{u_1,u_2,\ldots,\\
u_{n+2}\}\) and let \(C_{2r}\)
be the even cycle with vertex set \(V(C_{2r})=\{v_1,v_2,\ldots,v_{2r}\}\). Let
\(G\) be the graph obtained from \(K_{n+2}\) and \(C_{2r}\) by merging the edge \(u_1u_2\) in \(K_{n+2}\) and \(v_rv_{r+1}\) in \(C_{2r}\). The resultant graph \(G\) is shown in Figure 7.
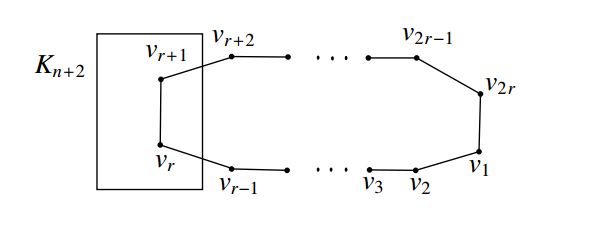
It can be easily verified that \(e(v)=r\) for any vertex \(v\in G\) and so \(rad~G=diam~G=r\). Also, \(T=V(K_{n+2})-\{u_1,u_2\}\) is the set of
all simplicial vertices of \(G\) and
any independent set of \(G\) contains
atmost one element in \(T\). If \(S\) is any independent set of \(G\), then atleast \({n-1}\) vertices in \(T\) lie in every \(S\)-fixed connected geodetic set of \(G\) and so \(cg_{if}(G)\geq {n-1}\). Also, it is clear
that all the vertices of \(C_{2r}\) are
not on any \(x-y\) geodesic for some
\(x\in V(C_{2r})\) and \(y\in T\). Hence \(cg_{if}(G)>{n-1}\). Let \(S=\{v_1,u_3\}\) and let \(S'=(T-\{u_3\})\cup \{v_{r+1}\}\).
Clearly, every vertex of \(C_{2r}\) is
on a \(v_1-v_{r+1}\) geodesic and so
\(S'\) is an \(S\)-fixed geodetic set of \(G\). Also, \(\left\langle S'\right\rangle\) is
connected and so \(cg_{if}(G)=n\).
Case (2) \(r<d\leq
2r\). Let \(K_{n+1}\) be the
complete graph with the vertex set \(V(K_{n+1})=\{u_1,u_2,\cdots,u_{n+1}\}\),
let \(P_{d-r}\) be a path with the
vertex set \(V(P_{d-r})=\{v_1,v_2,\ldots,v_{d-r}\}\) and
let \(C_{2r}\) be the cycle with the
vertex set \(V(C_{2r})=\{w_1,w_2,\ldots,w_{2r}\}\). Let
\(G\) be the graph obtained from \(K_{n+1}, P_{d-r}\) and \(C_{2r}\) by joining every vertex of \(K_{n+1}\) with the vertex \(v_1\) in \(P_{d-r}\), and joining the vertex \(v_{d-r}\) of \(P_{d-r}\) with the vertex \(w_1\) in \(C_{2r}\). The graph \(G\) is shown in Figure 8.
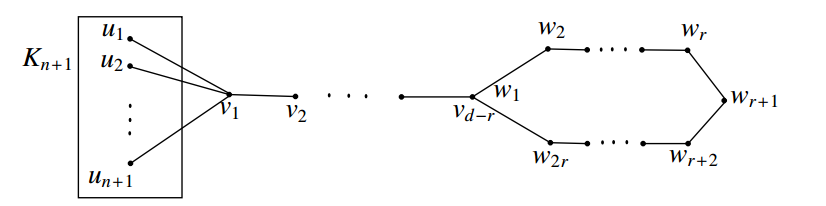
It can be easily verified that \(r\leq e(x)\leq d\), \(e(w_1)=r\) and \(e(w_{r+1})=d\). Hence \(rad~G=r\) and \(diam~G=d\). It is clear that \(T=V(K_{n+1})\) is the set of all simplicial vertices of \(G\). Then by an argument similar to Case (1) of Theorem 2.10, we have \(S=\{u_1,w_{r+1}\}\) is an independent set of \(G\) and \(S'=T-\{u_1\}\) is a minimum \(S\)-fixed connected geodetic set of \(G\). Hence \(cg_{if}(G)=n\).
Definition 4. The minimum (maximum) independent set required to form a \(cg_{if}\)-set of \(G\) is called a connected geo-independent set (upper connected geo-independent set) of \(G\). The cardinality of a connected geo-independent set (upper connected geo-independent set) of \(G\) is called the connected geo-independent number (upper connected geo-independent number) of \(G\) and is denoted by \(cgin(G)\) (\(cgin^+(G)\)).
Example 2. For the graph \(G\) given in Figure 2.1, we have \(cg_{if}(G)=3\). From Table 1, it can be easily seen that \(S_1=\{x_1, x_4\}, S_2=\{x_1,x_6\}\), \(S_3=\{x_2,x_4\}\) and \(S_4=\{x_2,x_6\}\) are the connected geo-independent sets of \(G\), \(S_5=\{x_1,x_4,x_6\}\) and \(S_6=\{x_2,x_4,x_6\}\) are the upper connected geo-independent sets of \(G\). Hence \(cgin(G)=2\) and \(cgin^+(G)=3\).
The following result gives the connected geo-independent numbers and the upper connected geo-independent numbers of certain special classes of graphs.
Result 11.
If \(G=P_p\), then \(cgin(G)=1\) and \(cgin^+(G)=\left\lceil \frac{p}{2}\right\rceil\).
If \(G=K_{1, p-1}(p\geq3)\), then \(cgin(G)= p-2\) and \(cgin^+(G)=p-1\).
If \(G=K_p\), then \(cgin(G)=cgin^+(G)=1\).
If \(G=C_p\), then \(cgin(G)= 1\) and \(cgin^+(G)=\left\lfloor \frac{p}{2}\right\rfloor\) or \(\left\lfloor \frac{p}{2}\right\rfloor-1\) according as \(\left\lfloor \frac{p}{2}\right\rfloor\) is odd or even.
If \(G=K_{m,n}\) \((2\leq m\leq n)\), then \(cgin(G)=m-1\) and \(cgin^+(G)=n-1\).
If \(G=Q_n\) \((n\geq 3)\), then \(cgin(G)=1\) and \(cgin^+(G)=2^{n-1}\).
The following observation is an easy consequence of some of the previous results.
Observation 12. For any connected graph \(G\) of order \(p\geq 2\),
\(1\leq cgin(G)\leq cgin^+(G)\leq \beta(G)\leq {p-1}\), where \(\beta(G)\) is the independence number of \(G\).
\(2\leq cgin(G)+cg_{if}(G)\leq p\) and \(2\leq cgin^+(G)+cg_{if}(G)\leq p\).
Theorem 13. Let \(G\) be a connected graph of order \(p\geq 2\). Then
\(cgin(G)=1\) if and only if \(cg_x(G)=cg_{if}(G)\) for some vertex \(x\) in \(G\).
\(cgin(G)={p-1}\) if and only if \(G=K_2\).
\(cgin^+(G)={p-1}\) if and only if \(G=K_{1,p-1}\).
Proof. (i) Let \(cgin(G)=1\). Then there exists a vertex,
say \(x\), in \(G\) with \(S=\{x\}\) and \(S'\), a minimum \(S\)-fixed connected geodetic set of \(G\). Hence every vertex of \(G\) is on an \(x-y\) geodesic for some \(y\in S'\) and \(\left\langle S'\right\rangle\) is
connected, and so \(S'\) is a
minimum connected \(x\)-geodominating
set of \(G\). Hence \(cg_x(G)=\left|S'\right|=cg_{if}(G)\).
Converse is clear from the respective definitions.
(ii) Let \(cgin(G)={p-1}\). If \(p=2\), then we get the required result. So,
let \(p\geq 3\). Since the connected
graph \(G\) has \({p-1}\) independent vertices, all the
independent vertices are end vertices of \(G\). Hence \(G\) is a star. Then by Result 11(ii),
\(cgin(G)={p-2}\), but this leads to a
contradiction. Conversely, let \(G=K_2\). Then by Result 11(iii), \(cgin(G)=1={p-1}\).
(iii) The result follows from the proof of (ii) and Result 1(ii).
Problem 14. Characterize graphs \(G\) for which \(cgin^+(G)=1\).
The following theorem gives a realization result.
Theorem 15. For any four positive integers \(a,b,c\) and \(n\) with \(2\leq a\leq b\leq c\), a connected graph \(G\) can be identified with \(cgin(G)=a\), \(cgin^+(G)=b\), \(\beta(G)=c\) and \(cg_{if}(G)=n\).
Proof. Case (1) \(a=b\). Let \(H_1, H_2, H_3\) and \(H_4\) be the complete graphs with vertex sets \(V(H_1)=\{x,y\}, V(H_2)=\{u_1, u_2,\ldots, u_{c-a+1}\}, V(H_3)=\{v_1, v_2, \ldots, v_{a-2}\}\) and \(V(H_4)=\{w_1, w_2,\ldots,w_{n+1}\}\) respectively. Let the graph \(G\) be constructed using \(\bar{H_1},\bar{H_2},\bar{H_3}\) and \(H_4\) by (i) joining the vertices \(x\) and \(y\) in \(\bar{H_1}\) with every vertex of \(\bar{H_2}\) and (ii) joining the vertex \(y\) in \(\bar{H_1}\) with every vertex of \(\bar{H_3}\cup H_4\). The resultant graph \(G\) is shown in Figure 9.
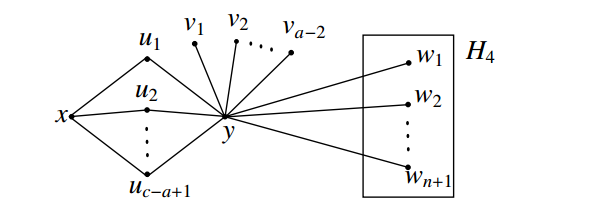
Every independent set of \(G\) contains atmost one vertex from \(H_4\). Then atleast \(n\) vertices in the complete graph \(H_4\) lie on every \(S\)-fixed geodetic set of \(G\), where \(S\) is an independent set of \(G\). Hence \(cg_{if}(G)\geq n\). Let \(S=\{x,v_1,v_2,\ldots,v_{a-2},w_i\}\) and let \(S'=V(H_4)-\{w_i\}\) for any \(i (1\leq i\leq {n+1})\). Clearly \(S\) is an independent set of \(G\) and every vertex of \(V(G)-S\) is on an \(x-s\) geodesic for any \(s\in S'\) and \(\left\langle S'\right\rangle\) is connected. Hence \(S'\) is an \(S\)-fixed connected geodetic set of \(G\) and so \(cg_{if}(G)=\left|S'\right|=n\). Also, it is clear that, for any independent set \(S\) of \(G\), every minimum \(S\)-fixed connected geodetic set contains \(n\) vertices from \(H_4\).
Let \(T\) be any independent set of
\(G\) with \(T'\), a \(T\)-fixed connected geodetic set of \(G\) and \(\left|T'\right|=cg_{if}(G)=n\). Hence
\(T'\subset V(H_4)\). Now claim
that \(V(\bar{H_3})\subseteq T\). If
not, let \(z\in V(\bar{H_3})\) and
\(z\notin T\). Since \(z\) is an end vertex of \(G\), \(z\)
is not an internal vertex of any geodesic and so \(z\in T'\), which is a contradiction to
\(T'\subset V(H_4)\). Hence \(V(\bar{H_3})\subseteq T\). Also, since
\(cg_{if}(G)=n\) and \(T'\subset V(H_4)\), exactly one vertex
in \(H_4\), say \(w_1\), belongs to \(T\). Since \(w_1\) is adjacent to \(y\), \(y\notin
T\). Then either \(x\) or \(u_i (1\leq i\leq {c-a+1})\) but not both
belongs to \(T\).
Subcase (1) \(x\in
T\). Then every vertex of \(G-\bar{H_3}\) is on an \(x-w\) geodesic for any \(w\in T'\) and so \(T=V(\bar{H_3})\cup \{x,w_1\}\) is an
independent set of \(G\) with \(T'\), a \(T\)-fixed connected geodetic set of \(G\) and \(\left|
T'\right|=n\).
Subcase (2) \(u_i\in T (1\leq
i\leq {c-a+1})\). If all the vertices \(u_i\in T\), then \(x\) is not an internal vertex of any \(s-t\) geodesic for any \(s\in T\) and \(t\in T'\). Hence \(x\in T'\), which is a contradiction to
\(T'\subset V(H_4)\). If atleast
one vertex \(u_i\notin T\), then \(u_i\) is not an internal vertex of any
\(s-t\) geodesic for any \(s\in T\) and \(t\in T'\). Hence \(u_i\in T'\), which is a contradiction
to \(T'\subset V(H_4)\). Thus \(T_i=V(\bar{H_3})\cup \{x,w_i\}\), where
\(w_i\in V(H_4)\) \((1\leq i\leq {n+1})\), is the independent
set of \(G\) with \(T_i'=V(H_4)-\{w_i\}\), the \(T_i\)-fixed connected geodetic set of \(G\) and \(\left|T_i'\right|=n\). Hence \(cgin(G)=cgin^+(G)=a\).
Claim \(\beta(G)=c\). It can be easily
verified that \(W_i=V(\bar{H_2}\cup
\bar{H_3})\cup \{w_i\}\), where \(1\leq
i\leq {n+1}\), is a maximum independent set of \(G\) and so \(\beta(G)=c\).
Case (2) \(a<b\).
Let \(H_1,H_2,H_3,H_4\) and \(H_5\) be the complete graphs with vertex
sets \(V(H_1)=\{x,y,z\},
V(H_2)=\{u_1,u_2,\ldots,u_{c-b+1}\}, V(H_3)=\{v_1,v_2,\ldots,v_{a-2}\},
V(H_4)=\{w_1,w_2,\ldots,w_{b-a}\}\) and \(V(H_5)=\{t_1,t_2,\ldots,t_{n+1}\}\),
respectively. Let \(G\) be the graph
obtained from \(\bar{H_1},\bar{H_2},\bar{H_3},\bar{H_4}\)
and \(H_5\) by (i) joining the vertices
\(x\) and \(y\) in \(\bar{H_1}\) with every vertex of \(\bar{H_2}\), (ii) joining the vertex \(y\) in \(\bar{H_1}\) with every vertex of \(\bar{H_3}\), (iii) joining the vertices
\(y\) and \(z\) in \(\bar{H_1}\) with every vertex of \(\bar{H_4}\), and (iv) joining the vertex
\(z\) in \(\bar{H_1}\) with every vertex of \(H_5\). The resultant graph \(G\) is shown in Figure 10.
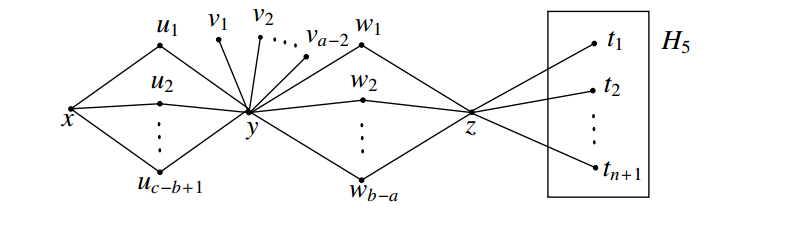
By an argument similar to Case (1), for any independent set \(S\) of \(G\), every minimum \(S\)-fixed connected geodetic set contains atleast \(n\) vertices from \(H_5\). Let \(S=V(\bar{H_3})\cup \{x,t_1\}\) and let \(S'=V(H_5)-\{t_1\}\). Then clearly \(S\) is an independent set of \(G\) and \(S'\) is an \(S\)-fixed connected geodetic set of \(G\) and so \(cg_{if}(G)=\left|S'\right|=n\).
Next, prove that \(cgin(G)=a\). By an argument similar to Case (1), to form an \(S\)-fixed connected geodetic set \(S'\) with \(\left|S'\right|=n\), we need all the vertices in \(\bar{H_3}\), the vertex \(x\) in \(\bar{H_1}\) and exactly one vertex in \(H_5\) for \(S\). Hence \(cgin(G)\geq a\). As in the above paragraph, \(S=V(\bar{H_3})\cup \{x,t_1\}\) is an independent set of \(G\) and \(S'=V(H_5)-\{t_1\}\) is the \(S\)-fixed connected geodetic set with \(\left|S'\right|=n\). Hence \(S\) is a connected geo-independent set of \(G\) and so \(cgin(G)=\left|S\right|=a\).
Claim that \(cgin^+(G)=b\). Let \(T\) be any independent set of \(G\) with \(T'\), a \(T\)-fixed connected geodetic set of \(G\) and \(\left|T'\right|=cg_{if}(G)=n\). Then by an argument similar to Case (1), \(V(\bar{H_3})\cup \{x,t_i\}\subseteq T_i, V(H_5)-\{t_i\}=T_i'\) for any \(i\) \((1\leq i\leq {n+1})\), and \(s\notin T_i\), where \(s\in V(\bar{H_2})\cup\{y,z\}\). Let \(S_i=V(\bar{H_3}\cup\bar{H_4})\cup\{x,t_i\}\). Then clearly \(S_i\) is a maximum independent set of \(G\) with \(S_i'=V(H_5)-\{t_i\}\), the \(S_i\)-fixed connected geodetic set of \(G\) and \(\left|S_i'\right|=n\). Hence \(cgin^+(G)=\left|S_i\right|=b\).
It can be easily verified that \(W_i=V(\bar{H_2}\cup \bar{H_3}\cup \bar{H_4})\cup\{t_i\}\), where \(1\leq i\leq {n+1}\), is a maximum independent set of \(G\) and so \(\beta(G)=c\).
The authors declare no conflict of interests.