Consider a total labeling \(\xi\) of a graph \(G\). For every two different edges \(e\) and \(f\) of \(G\), let \(wt(e) \neq wt(f)\) where weight of \(e = xy\) is defined as \(wt(e)=|\xi(e) – \xi(x) – \xi(y)|\). Then \(\xi\) is called edge irregular total absolute difference \(k\)-labeling of \(G\). Let \(k\) be the minimum integer for which there is a graph \(G\) with edge irregular total absolute difference labeling. This \(k\) is called the total absolute difference edge irregularity strength of the graph \(G\), denoted \(tades(G)\). We compute \(tades\) of \(SC_{n}\), disjoint union of grid and zigzag graph.
Chartrand et al. [1] introduced irregularity strength and irregular assignments of a graph in 1988. The other kind of total labeling the total edge irregularity strength of a graph was studied by Baca et al. [2]: Consider a graph \(G=(V,E)\). A labeling \(\xi : V \bigcup E \rightarrow \{1,2,\cdots,k\}\) is called an edge irregular total \(k\)-labeling if for every pair of distinct edges \(uv\) and \(xy\), \(\xi(u)+\xi(v)+\xi(uv) \neq \xi(x)+\xi(y)+\xi(xy)\). If a graph \(G\) admits an edge irregular total \(k\)-labeling and \(k\) is minimum then \(G\) is said to have a total edge irrgularity strength denoted by \(tes(G)\). The results about the \(tes(G)\) can be found in [3,4,5,6,7,8,9,10].
Ramalakshmi and Kathiresan introduced the total absolute difference edge irregularity strength of graphs to lower edge weights, using \(tes(G)\) and graceful labeling. Consider a total labeling \(\xi\) of a graph \(G\). For every two different edges \(e\) and \(f\) of \(G\), let \(wt(e) \neq wt(f)\) where weight of \(e = xy\) is defined as \(wt(e)=|\xi(e) – \xi(x) – \xi(y)|\). Then \(\xi\) is called edge irregular total absolute difference \(k\)-labeling of \(G\). Let \(k\) be the minimum integer for which there is a graph \(G\) with edge irregular total absolute difference labeling. This \(k\) is called the total absolute difference edge irregularity strength of the graph \(G\), denoted \(tades(G)\).
Lourdusamy et al. [11] determined the total absolute difference edge irregular strength for snake related graphs, wheel related graphs, lotus inside the circle and double fan graph. Also, they obtained the \(tades\) of \(T_{p}\)-tree related graphs [12]. Lourdusamy et al. [13] discussed the \(tades\) of super subdivision of certain families of graphs and corona graphs. Also, they obtained the \(tades\) of transformed tree and path related graphs [14]. Here, we discuss the \(tades\) of staircase graph, disjoint union of zigzag and grid graphs.
Theorem 1. [15] For a graph \(G=(V,E)\), we have \(\left\lceil \frac{|E|}{2} \right\rceil \leq tades(G) \leq |E|+1\).
In this section, we compute the exact value of total absolute difference edge irregularity strength of staircase graph.
Theorem 2. For \(SC_{n}\), the total absolute difference edge irregularity strength is \(tades(SC_{n}) = \left\lceil\frac{n(n+3)}{2} \right\rceil\).
Proof. Let \(k= \left\lceil\frac{n(n+3)}{2} \right\rceil\). Let \(V(SC_{n}) = \{a_{r,s}: r=0,1 , 0 \leq s \leq n \} \cup \{a_{r,s}: 2 \leq r \leq n , r-1 \leq s \leq n \}\) and \(E(SC_{n}) = \{a_{r,s}a_{r+1,s} : r=0 , 0 \leq s \leq n\} \cup \{a_{r,s}a_{r+1,s} : 1 \leq r \leq n-1, r \leq s \leq n\} \cup \{a_{r,s}a_{r,s+1} : r=0,1 , 0 \leq s \leq n-1\} \cup \{a_{r,s}a_{r,s+1} : 2 \leq r \leq n, r-1 \leq s \leq n-1\}\). Note that \(\left|V(SC_{n})\right|= \frac{1}{2} (n+1)(n+2)+n\) and \(\left|E(SC_{n})\right|= n(n+3)\).
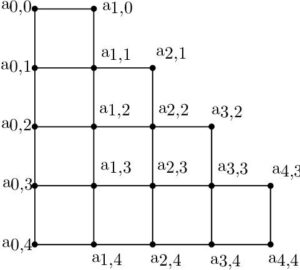
From Theorem 1, \(tades(SC_{n}) \geq
k\). To complete the proof we show that \(tades(SC_{n}) \leq k\). We define a, \(k\)-labeling \(\xi:V(SC_{n}) \cup E(SC_{n}) \rightarrow
\{1,2,\cdots k\}\) as follows:
\(\xi(a_{r,0})= 1, r=0,1;\)
For \(1 \leq s \leq n\)
\(\xi(a_{0,s})= \left\lceil \frac{s^{2}+3s}{2}
\right\rceil-\left\lfloor \frac{s}{2} \right\rfloor;\)
Case 1. \(s\) is odd
Let \(1 \leq s \leq n\) and \(s\) is odd .
Fix \(\xi(a_{1,s})= \left\lceil
\frac{s^{2}+3s}{2} \right\rceil – \left\lfloor
\frac{s}{2}\right\rfloor.\)
Let \(2 \leq r \leq n, \ r-1 \leq s \leq
n\) and \(s\) is odd.
Fix \(\xi(a_{r,s})=\begin{cases} \left\lceil
\frac{s^{2}+3s}{2} \right\rceil – \left\lfloor \frac{s}{2}\right\rfloor+
\frac{r-1}{2} & \text{ if } \ r \ \text{is odd}\\ \left\lceil
\frac{s^{2}+3s}{2} \right\rceil – \left\lfloor \frac{s}{2}\right\rfloor
+ \frac{r}{2} & \text{if} \ r \ \text{is even} \ ;
\end{cases}\)
Case 2. \(s\) is even
Let \(1 \leq s \leq n\) and \(s\) is even.
Fix \(\xi(a_{1,s})= \left\lceil
\frac{s^{2}+3s}{2} \right\rceil – \left\lfloor
\frac{s}{2}\right\rfloor+1.\)
Let \(2 \leq r \leq n, \ r-1 \leq s \leq
n\) and \(s\) is even.
Fix \(\xi(a_{r,s})=\begin{cases} \left\lceil
\frac{s^{2}+3s}{2} \right\rceil – \left\lfloor \frac{s}{2}\right\rfloor+
\frac{r+1}{2} & \text{if} \ r \ \text{is odd}\\ \left\lceil
\frac{s^{2}+3s}{2} \right\rceil – \left\lfloor \frac{s}{2}\right\rfloor
+ \frac{r}{2} & \text{if} \ r \ \text{is even} \ .
\end{cases}\)
We fix the edge labels as follows:
\(\xi(a_{0,0}a_{1,0})=2\);
\(\xi(a_{0,0}a_{0,1})=2\);
\(\xi(a_{1,0}a_{1,1})=1\);
\(\xi(a_{0,s}a_{1,s})=1\) , for \(1 \leq s \leq n\);
\(\xi(a_{r,s}a_{r+1,s})=1\), for \(1 \leq r \leq n-1\) and \(r \leq s \leq n\);
\(\xi(a_{r,s}a_{r,s+1})=1\), for \(r=0,1\) and \(1
\leq s \leq n-1\);
\(\xi(a_{r,s}a_{r,s+1})=1\), for \(2 \leq r \leq n\) and \(r-1 \leq s \leq n-1\).
We then have the weight of the edges as follows:
\(wt(a_{0,0}a_{1,0})=0\);
\(wt(a_{0,0}a_{0,1})=1\);
\(wt(a_{1,0}a_{1,1})=2\);
\(wt(a_{0,s}a_{1,s})=s^{2}+2s\) for
\(1 \leq s \leq n\);
\(wt(a_{r,s}a_{r+1,s})=s^{2}+2s+r\),
for \(1 \leq r \leq n-1\) and \(r \leq s \leq n\);
\(wt(a_{r,s}a_{r,s+1})=s^{2}+3s+1\),
for \(r=0,1\) and \(1 \leq s \leq n-1\);
\(wt(a_{r,s}a_{r,s+1})=s^{2}+3s+r+1\),
for \(2 \leq r \leq n\) and \(r-1 \leq s \leq n-1\).
Hence \(\xi\) is total absolute
difference edge irregular \(k\)-labeling with \(k=\left\lceil\frac{n(n+3)}{2}
\right\rceil\) as the weights for the edges are different.
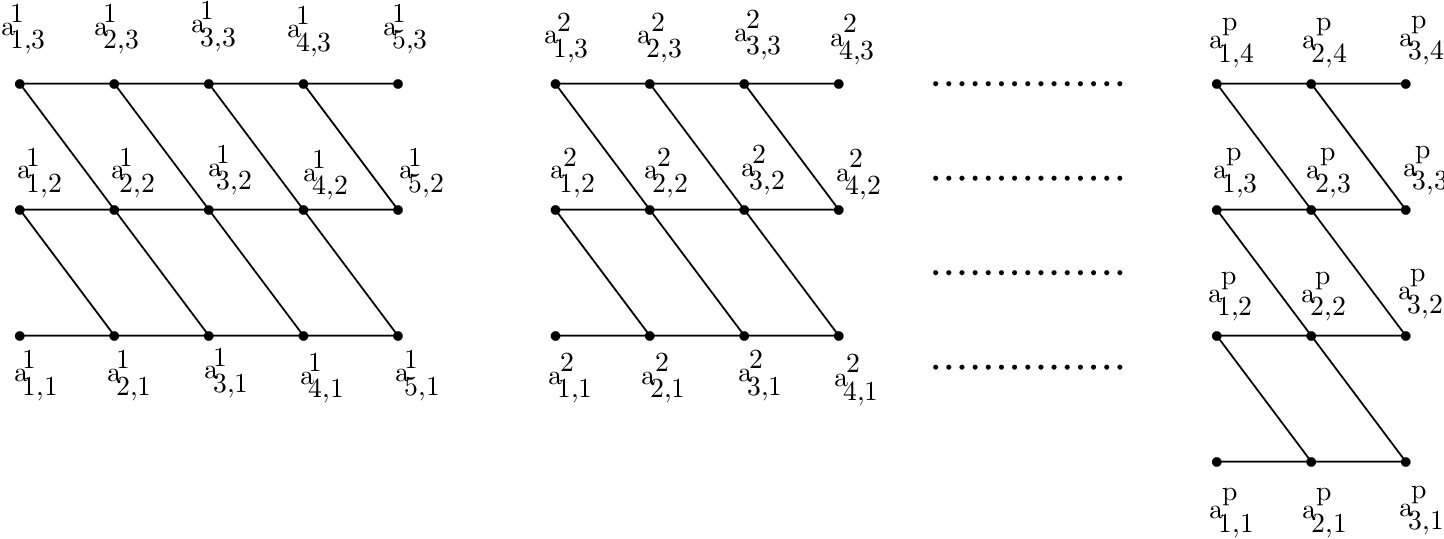
In this section, we compute the exact value of total absolute difference edge irregularity strength of disjoint union of zigzag graphs \(\bigcup_{j=1}^{p} Z_{n_{j}}^{m_{j}}\) with \(n_{j} \geq 2\) and \(m_{j} \geq 2\).
Theorem 3. For any integer \(n_{j} \geq 2\), \(m_{j} \geq 2\), \(tades(\bigcup_{j=1}^{p} Z_{n_{j}}^{m_{j}}) = \left\lceil\frac{\sum _{j=1}^{p}(n_{j}-1)(2m_{j}-1)}{2} \right\rceil\).
Proof. Let \(k=\left\lceil\frac{\sum
_{j=1}^{p}(n_{j}-1)(2m_{j}-1)}{2} \right\rceil\). The disjoint
union \(\bigcup_{j=1}^{p}
Z_{n_{j}}^{m_{j}}\) of zigzag graphs \(Z_{n}^{m}\) is defined to be a graph with
vertex set \(V(\bigcup_{j=1}^{p}
Z_{n_{j}}^{m_{j}}) =\{a_{i,s}^{j}:1 \leq i \leq n_{j}, 1 \leq s \leq
m_{j}, 1 \leq j \leq p\}\) and the edge set \(E(\bigcup_{j=1}^{p}
Z_{n_{j}}^{m_{j}})=\{a_{i,s}^{j}a_{i+1,s}^{j}:1 \leq i \leq n_{j}-1, 1
\leq s \leq m_{j}, 1 \leq j \leq p\}
\bigcup\{a_{i,s}^{j}a_{i-1,s+1}^{j}:1 \leq i \leq n_{j}, 1 \leq s \leq
m_{j}-1, 1 \leq j \leq p\}\). The disjoint union of zigzag graphs
\(\bigcup_{j=1}^{p} Z_{n_{j}}^{m_{j}}\)
has \(\sum_{j=1}^{p} n_{j}m_{j}\)
vertices and \(\sum_{j=1}^{p}(n_{j}-1)(2m_{j}-1)\) edges.
Based on Theorem 1, we have \(tades(\bigcup_{j=1}^{p} Z_{n_{j}}^{m_{j}}) \geq
\left\lceil\frac{\sum _{j=1}^{p}(n_{j}-1)(2m_{j}-1)}{2}
\right\rceil\).
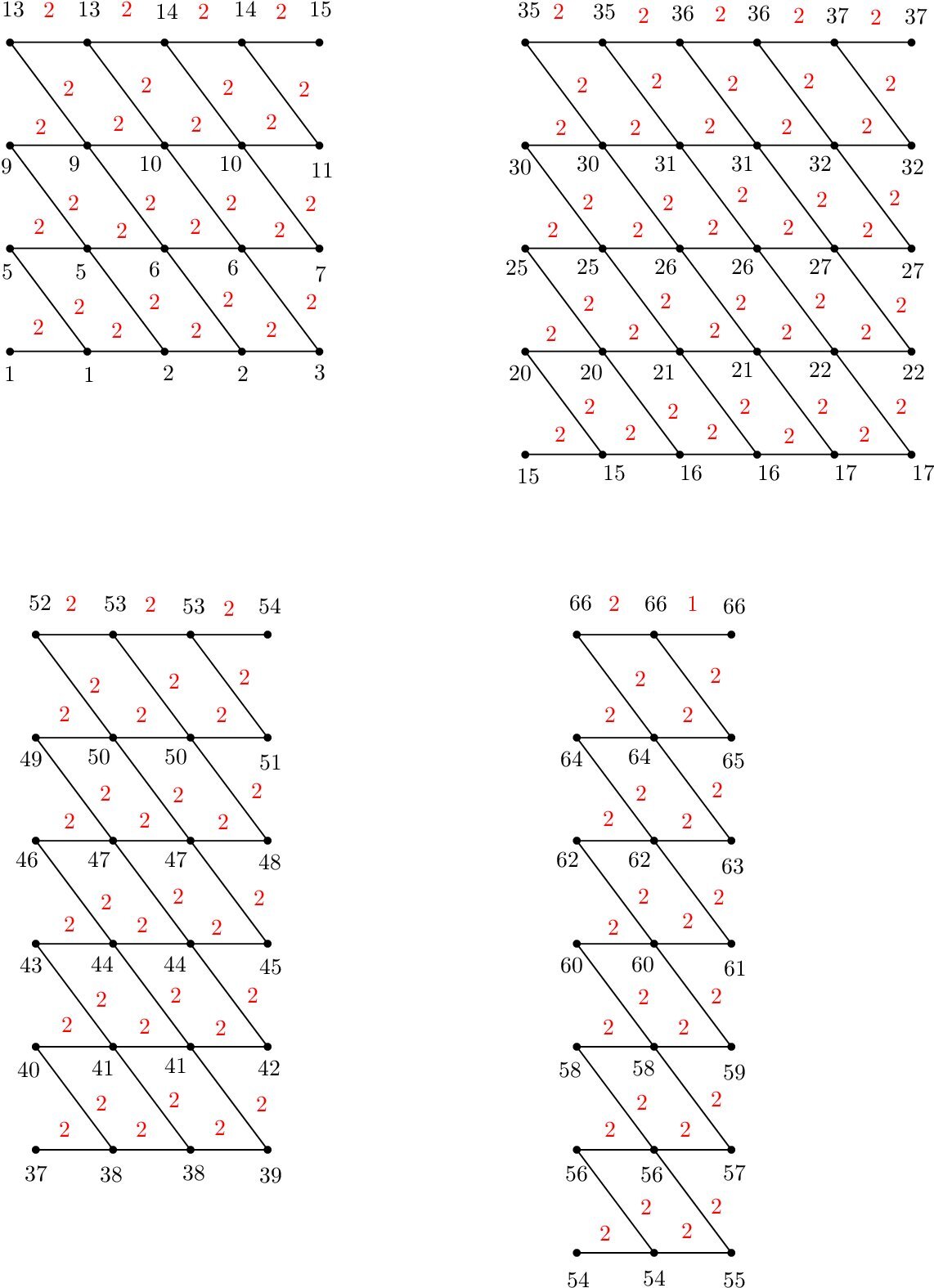
We define \(\xi\) as follows:
for \(1 \leq i \leq n_{j}\), \(1 \leq s \leq m_{j}\) and \(1 \leq j \leq p-1\),
\(\xi(a_{i,s}^{j})= \left\lceil
\frac{r}{2}\right\rceil+(s-1)(n_{j}-1)+\left\lfloor
\frac{i+\frac{1}{2}((-1)^{r}+1)}{2}\right\rfloor\) where \(r =
\sum_{q=1}^{j-1}(n_{q}-1)(2m_{q}-1)\);
for \(1 \leq i \leq n_{p}\), \(1 \leq s \leq m_{p}-1\) and \(r =
\sum_{q=1}^{p-1}(n_{q}-1)(2m_{q}-1)\),
\(\xi(a_{i,s}^{p})= \left\lceil
\frac{r}{2}\right\rceil+(s-1)(n_{p}-1)+\left\lfloor
\frac{i+\frac{1}{2}((-1)^{r}+1)}{2}\right\rfloor\) ;
\(\xi(a_{i,m_{p}}^{p})= \begin{cases}
\left\lceil \frac{r}{2} \right\rceil +(m_{p}-1)(n_{p}-1)+\left\lfloor
\frac{i+\frac{1}{2}((-1)^{r}+1)}{2}\right\rfloor & \text{if} \ 1
\leq i \leq n_{p}-1 \\ k & \text{ if } \ i=n_{p} \ ;
\end{cases}\)
\(\xi(a_{i,s}^{j}a_{i+1,s}^{j}) =
2\), for \(1 \leq i \leq
n_{j}-1\), \(1 \leq s \leq
m_{j}\) and \(1 \leq j \leq
p-1\);
\(\xi(a_{i,s}^{p}a_{i+1,s}^{p} =
2\), for \(1 \leq i \leq
n_{p}-1\), \(1 \leq s \leq
m_{p}-1\);
\(\xi(a_{i,m_{p}}^{p}a_{i+1,m_{p}}^{p}) =
2\), for \(1 \leq i \leq
n_{p}-2\);
\(\xi(a_{n_{p-1},m_{p}}^{p}a_{n_{p},m_{p}}^{p}) =
\begin{cases}
1 & \text{if} \ |E(\bigcup_{j=1}^{p} Z_{n_{j}}^{m_{j}})| \ \text{is
even} \\ 2 & \text{if} \ |E(\bigcup_{j=1}^{p} Z_{n_{j}}^{m_{j}})| \
\text{is odd}\end{cases};\)
\(\xi(a_{i-1,s+1}^{j}a_{i,s}^{j})=2\),
for \(2 \leq i \leq n_{j}\), \(1 \leq s \leq m_{j}-1\) and \(1 \leq j \leq p.\)
We now arrive at the weight of the edges:
for \(1 \leq i \leq n_{j}-1\), \(1 \leq s \leq m_{j}\), \(1 \leq j \leq p\) and \(r =
\sum_{q=1}^{j-1}(n_{q}-1)(2m_{q}-1)\),
\(wt(a_{i,s}^{j}a_{i+1,s}^{j})= 2\left\lceil
\frac{r}{2}\right\rceil+2(s-1)(n_{j}-1)+i+\frac{1}{2}((-1)^{r}+1)-2;\)
for \(1 \leq i \leq n_{j}\), \(1 \leq s \leq m_{j}-1\), \(1 \leq j \leq p\) and \(r =
\sum_{q=1}^{j-1}(n_{q}-1)(2m_{q}-1)\),
\(wt(a_{i,s}^{j}a_{i-1,s+1}^{j})= 2\left\lceil
\frac{r}{2}\right\rceil+(2s-1)(n_{j}-1)+i+\frac{1}{2}((-1)^{r}-1)-3.\)
It is clear that, the labels for vertices and edges receive values are
not more than \(k\). Also we see that
the weights for the edges are all distinct. Hence \(tades(\bigcup_{j=1}^{p} Z_{n_{j}}^{m_{j}}) =
\left\lceil\frac{\sum _{j=1}^{p}(n_{j}-1)(2m_{j}-1)}{2}
\right\rceil\).
Illustration for \(tades\) of \(Z_{5}^{4} \bigcup Z_{6}^{5} \bigcup Z_{4}^{6} \bigcup Z_{3}^{7}\) is shown in Figure 3.
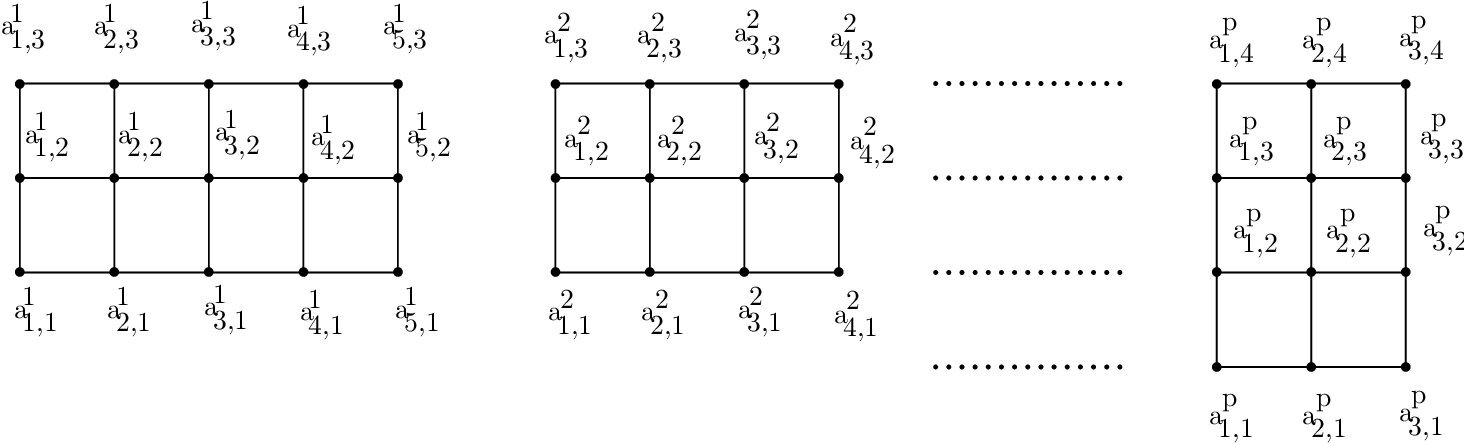
In this section, we compute the exact value of total absolute difference edge irregularity strength of disjoint union of grid graphs \(\bigcup_{j=1}^{p} Z_{n_{j}}^{m_{j}}\) with \(n_{j},m_{j} \geq 2\).
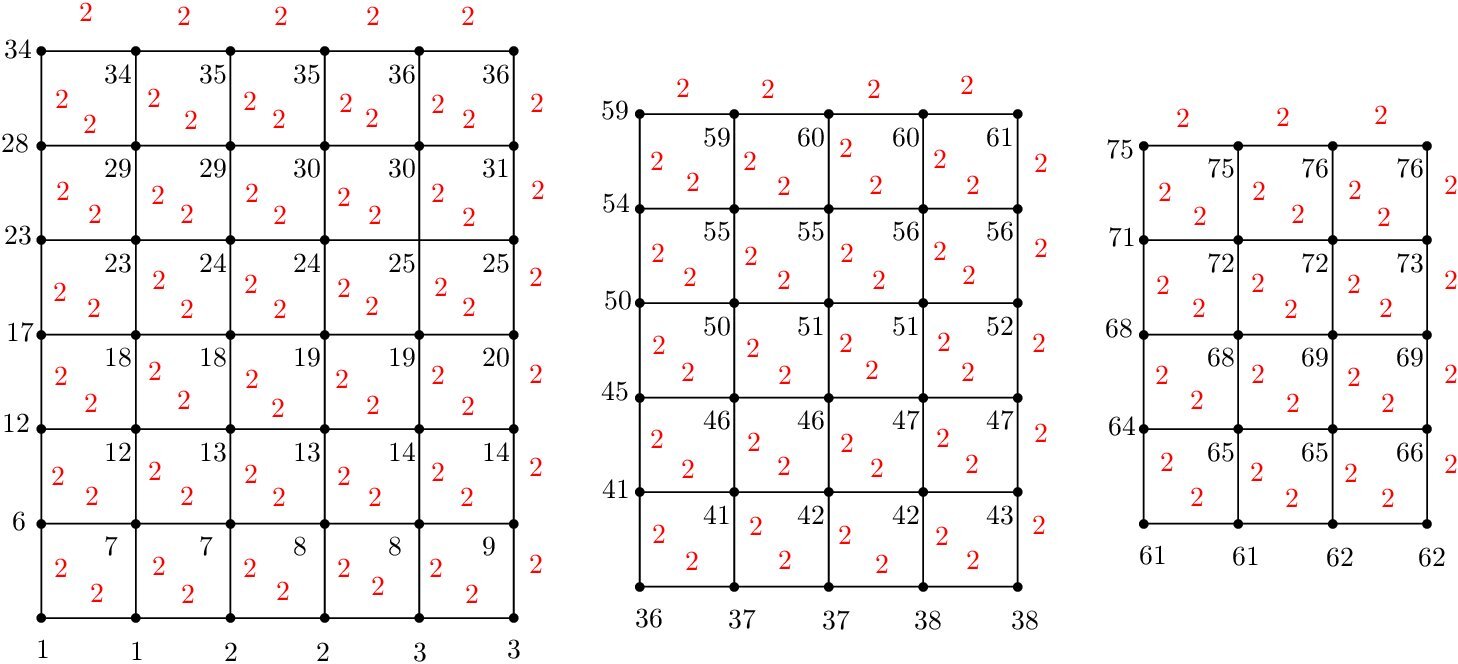
Theorem 4. For any integer \(n_{j},m_{j} \geq 2\) and \(1 \leq j \leq p\), \(tades(\bigcup_{j=1}^{p} G_{n_{j},m_{j}})=\left\lceil \frac{\sum _{j=1}^{p} (2n_{j}m_{j}-m_{j}-n_{j})} {2}\right\rceil\).
Proof. Let \(k=\left\lceil
\frac{\sum _{j=1}^{p} (2n_{j}m_{j}-m_{j}-n_{j})}
{2}\right\rceil\). We define disjoint union \(\bigcup_{j=1}^{p} G_{n_{j},m_{j}}\) of grid
graphs \(G_{n,m}\) as follows:
Let \(V(\bigcup_{j=1}^{p}
G_{n_{j},m_{j}})=\{a_{i,s}^{j}: 1 \leq i \leq n_{j}, 1 \leq s \leq
m_{j}, 1 \leq j \leq p \}\). Let \(E(\bigcup_{j=1}^{p}
G_{n_{j},m_{j}})=\{a_{i,s}^{j},a_{i+1,s}^{j}: 1 \leq i \leq n_{j}-1, 1
\leq s \leq m_{j}, 1 \leq j \leq p \} \bigcup \{a_{i,s}^{j},
a_{i,s+1}^{j}: 1 \leq i \leq n_{j}, 1 \leq s \leq m_{j-1}, 1 \leq j
\leq p \}\). From Theorem 1, \(tades(\bigcup_{j=1}^{p} G_{n_{j},m_{j}}) \geq
\left\lceil \sum _{j=1}^{p} \frac {(2n_{j}m_{j}-m_{j}-n_{j})}
{2}\right\rceil\). Now we prove the converse part.
Let us define \(\xi : V(\bigcup_{j=1}^{p}
G_{n_{j},m_{j}}) \cup E(\bigcup_{j=1}^{p} G_{n_{j},m_{j}})\rightarrow
\{1,2, \cdots ,\left\lceil \frac{\sum _{j=1}^{p}
(2n_{j}m_{j}-m_{j}-n_{j})} {2}\right\rceil\}\) as follows:
for \(1 \leq i \leq n_{j}\), \(1 \leq s \leq m_{j}\) and \(1 \leq j \leq p-1\),
\(\xi(a_{i,s}^{j})=\begin{cases}\left\lceil
\frac{t}{2}\right\rceil +\frac{s-1}{2}(2n_{j}-1)+\left\lfloor
\frac{i+\frac{1}{2}((-1)^t+1)}{2}\right\rfloor & \ \text{if} \ s \
\text{is odd} \\ \left\lceil
\frac{t}{2}\right\rceil+n_{j}(s-1)-\frac{s}{2}+\left\lceil
\frac{i+\frac{1}{2}((-1)^t+1)}{2}\right\rceil & \ \text{if}
\ s \ \text{is even} \ ; \end{cases}\)
where \(t= \sum_{q=1}^{j-1}
2n_{q}m_{q}-m_{q}-n_{q}\)
for \(1 \leq i \leq n_{p}, 1 \leq s \leq
m_{p}-1\) and \(t= \sum_{q=1}^{p-1}
2n_{q}m_{q}-m_{q}-n_{q}\)
\(\xi(a_{i,s}^{p})=\begin{cases}\left\lceil
\frac{t}{2}\right\rceil +\frac{s-1}{2}(2n_{p}-1)+\left\lfloor
\frac{i+\frac{1}{2}((-1)^t+1)}{2}\right\rfloor & \ \text{if} \ s \
\text{is odd} \\ \left\lceil
\frac{t}{2}\right\rceil+n_{p}(s-1)-\frac{s}{2}+\left\lceil
\frac{i+\frac{1}{2}((-1)^t+1)}{2}\right\rceil & \ \text{if} \ s \
\text{is even} \ ; \end{cases}\)
for \(1 \leq i \leq n_{p}-1\),
\(\xi(a_{i,m_{p}}^{p})=\begin{cases}\left\lceil
\frac{t}{2}\right\rceil +\frac{m_{p}-1}{2}(2n_{p}-1)+\left\lfloor
\frac{i+\frac{1}{2}((-1)^t+1)}{2}\right\rfloor & \ \text{if} \ s \
\text{is odd} \\ \left\lceil
\frac{t}{2}\right\rceil+n_{p}(m_{p}-1)-\frac{m_{p}}{2}+\left\lceil
\frac{i+\frac{1}{2}((-1)^t+1)}{2}\right\rceil & \ \text{if} \ s \
\text{is even} \ ; \end{cases}\)
\(\xi(a_{n_{p},m_{p}}^{p})=k\);
\(\xi(a_{i,s}^{j}a_{i+1,s}^{j}) =
2\), for \(1 \leq i \leq
n_{j}-1\), \(1 \leq s \leq
m_{j}\) and \(1 \leq j \leq
p-1\);
\(\xi(a_{i,s}^{p}a_{i+1,s}^{p}) =
2\), for \(1 \leq i \leq
n_{p}-1\), \(1 \leq s \leq
m_{p}-1\);
\(\xi(a_{i,m_{p}}^{p}a_{i+1,m_{p}}^{p}) =
2\), for \(1 \leq i \leq
n_{p}-2\);
\(\xi(a_{n_{p-1},a_{p}}^{p}a_{n_{p},m_{p}}^{p}) =
\begin{cases}
1 & \text{if} \ |E(\bigcup_{j=1}^{p} G_{n_{j},m_{j}})| \ \text{is
even} \\ 2 & \text{if} \ |E(\bigcup_{j=1}^{p} G_{n_{j},m_{j}})| \
\text{is odd}\end{cases};\)
\(\xi(a_{i,s}^{j}a_{i,s+1}^{j})=2\),
for \(2 \leq i \leq n_{j}\), \(1 \leq s \leq m_{j}-1\) and \(1 \leq j \leq p.\)
Below we arrive at the weight of the edges. for \(1 \leq i \leq n_{j}-1\), \(1 \leq s \leq m_{j}\), \(1 \leq j \leq p\) and \(t= \sum_{q=1}^{j-1}
2n_{q}m_{q}-m_{q}-n_{q}\),
\(wt(a_{i,s}^{j}a_{i+1,s}^{j})= \begin{cases}
2 \left\lceil
\frac{t}{2}\right\rceil+(s-1)(2n_{j}-1)+i+\frac{1}{2}((-1)^{t}+1)-2
& \ s \ \text{is odd}\\ 2 \left\lceil
\frac{t}{2}\right\rceil+(s-1)2n_{j}-s+i+1+\frac{1}{2}((-1)^{t}+1)-2
& \ s \ \text{is even};\end{cases}\)
for \(1 \leq i \leq n_{j}\), \(1 \leq s \leq m_{j}-1\), \(1 \leq j \leq p\) and \(t= \sum_{k=1}^{j-1}
2n_{j}m_{j}-m_{j}-n_{j}\),
\(wt(a_{i,s}^{j}a_{i,s+1}^{j})= 2 \left\lceil
\frac{t}{2}\right\rceil+(2s-1)n_{j}-s+i+\frac{1}{2}((-1)^{t}+1)-2.\)
It is clear that, the labels for vertices and edges receive values are
not more than \(k\). Also we see that
the weights for the edges are all distinct. Hence \(tades(\bigcup_{j=1}^{p}
G_{n_{j},m_{j}})=\left\lceil \frac{\sum _{j=1}^{p}
(2n_{j}m_{j}-m_{j}-n_{j})} {2}\right\rceil.\)
Illustration for \(tades\) of \(G_{6,7} \bigcup G_{5,6} \bigcup G_{4,5}\) is shown in Figure 5.
The authors declare no conflict of interests.
1970-2025 CP (Manitoba, Canada) unless otherwise stated.