A total dominator coloring of \(G\) without isolated vertex is a proper coloring of the vertices of \(G\) in which each vertex of \(G\) is adjacent to every vertex of some color class. The total dominator chromatic number \(\chi^t_d(G)\) of \(G\) is the minimum number of colors among all total dominator coloring of \(G\). In this paper, we will give the polynomial time algorithms to computing the total dominator coloring number for \(P_4\)-reducible and \(P_4\)-tidy graphs.
Let \(G =(V,~E)\) be a graph with the vertex set \(V\) of order \(n\) and the edge set \(E\) of size \(m\). The open neighborhood and the closed neighborhood of a vertex \(v \in V\) are \(N(v) = \{u \in V | uv \in E\}\) and \(N[v] = N_G(v) \cup \{v\}\), respectively. The degree of a vertex \(v\) is \(deg_G(v) =|N_G(v)|\). The minimum and maximum degree of \(G\) are denoted by \(\delta=\delta(G)\) and \(\Delta=\Delta(G)\), respectively. A dominating set of a graph \(G\) is a vertex subset \(S\) in \(G\) such that \(N_G[S] = V\). The domination number \(\gamma(G)\) of \(G\) is the cardinality of a minimum dominating set. As a generalization of the dominating set, the total dominating set \(TS\) of a graph \(G\) is a subset of the vertices in \(G\) such that \(N_G(TS)= V\). The total domination number \(\gamma_t(G)\) of G is the cardinality of a minimum total dominating set. The literature on total domination has been surveyed and detailed in the book [1].
A total dominator coloring of a graph \(G\) without isolated vertex is a proper coloring of \(G\) in which each vertex of the graph is adjacent to every vertex of some (other) color class. For convenience, we abbreviated write TD-coloring for total dominator coloring. The total dominator chromatic number \(\chi^t_d(G)\) of \(G\) is the minimum number of color classes in a \(TD\)-coloring of \(G\). It was introduced by Kazemi in [2] and studied further, the more details can refer to [3, 4.]
A similarly concept has been given by Gera, Horton and Rasmussen [5], which is called dominator coloring. A dominator coloring, briefly \(DC\), of a graph \(G\) is a proper coloring of \(G\) such that every vertex of \(V(G)\) dominates all vertices of at least one color class (possibly its own class). The dominator chromatic number \(\chi_d(G)\) of G is the minimum number of color classes in a dominator coloring of \(G\). As a consequence result, we have \(\chi(G) \leq \chi_d(G) \leq \chi^t_d(G)\) for \(G\) without isolate vertex. Since then, many researchers studied on it, the details refer to [6,7,8,9,10].
An induced path on \(k\) vertices shall be denoted by \(P_k\). Vertices of degree one (resp. two) in \(P_k\) will be called endpoints (resp. midpoints). An induced subgraph of \(G\) isomorphic to \(P_k\) is simply said to be a \(P_k\) in \(G\). A chordless cycle on \(k\) vertices is denoted by \(C_k\). A cograph is a graph that does not contain \(P_4\) as an induced subgraph [11]. Several generalizations of cographs have been defined in the literature, such as \(P_4\)-sparse [12], \(P_4\)-lite [13], \(P_4\)-extendible [14] and \(P_4\)-reducible graphs [15]. A graph class generalizing all of them is the class of \(P_4\)-tidy graphs [16].
The practical applications (to computational semantics, examination scheduling, clustering analysis, group-based cooperation) of these classes of graphs, have certainly motivated the theoretical and algorithmical study. For some \(NP\)-hard problem, these classes of graphs have polynomial time algorithms. Bagan et al. [17] proved that determining \(\chi^t_d\) is \(NP\)-hard for general graphs, but polynomial-time solvable for some special graphs, such as cographs and \(P_4\)-sparse graphs.
In this paper, we consider the total dominator coloring of graphs. In the next section, we give a polynomial time to compute the total dominator chromatic number of \(P_4\)-reducible graphs. In the last section, the algorithm of the total dominator coloring of \(P_4\)-tidy graphs is given, which is also a polynomial time algorithm.
In this section, we first give some basic lemmas, which will be used in the following section. And then we give a polynomial time algorithm to compute the value of the total dominator chromatic number of the \(P_4\)-reducible graph. Lerchs el at. [18] proved that the cographs are precisely the graphs obtained from single-vertex graphs by a finite sequence of \(\cup\) and \(\vee\) operations defined as follows.
Let \(G_{1}=(V_{1},E_{1})\) and \(G_{2}=(V_{2},E_{2})\) be arbitrary graphs with \(V_{1}\cap V_{2}=\emptyset\). Now,
– \(G_{1} \cup G_{2}\) is the union of \(G_{1}\) and \(G_{2}\).
– \(G_{1} \vee G_{2}\) is the join of \(G_{1}\) and \(G_{2}\).
For the purpose of constructing the \(P_{4}\)-reducible graphs, Jamison el at. [15] defined yet another graph operation, denoted by \(\oplus\), as follows. Let the graphs \(G_{1}=(V_{1},E_{1})\) and \(G_{2}=(V_{2},E_{2}) (V_{1}\cap V_{2}=\emptyset)\) be such that \(V_{1}=\{a,d\}, E_{1}=\emptyset\), and some adjacent vertices \(b,c\) in \(V_{2}\) are adjacent to all the remaining vertices in \(V_{2}\).
– \(G_{1} \oplus G_{2}=(V_{1}\cup V_{2},\{ab,cd\}\cup E_{2})\).
A graph \(G\) is \(B-P_{4}\) if there exists a unique \(P_{4}= abcd\) in \(G\) such that every vertex of \(G\) outside \(\{a,b,c,d\}\) is adjacent to both \(b\) and \(c\) and nonadjacent to both \(a\) and \(d\).
Proposition 1. [15] A graph \(G\) is \(P_{4}\)-reducible if and only if, \(G\) is obtained from single-vertex graphs by a finite sequence of operations \(\cup,~\vee\) and \(\oplus\).
In the same paper, Jamison el at. also gave the following characterization of the \(P_{4}\)-reducible graphs.
Theorem 1. [15]A graph \(G\) is \(P_{4}\)-reducible if, and only if, for every induced subgraph \(H\) of \(G\) exactly one of the following conditions are satisfied
(\(i\)) \(H\) is disconnected;
(\(ii\)) \(\overline{H}\) is disconnected;
(\(iii\)) \(H\) is a \(B-P_{4}\) graph.
Before giving the main result, we need a new notation as follows.Given a graph \(G\) with a \(TD\)-coloring \(f\). Let \(q_{f}\) to be the number of colors used by \(f\). Since \(f\) is a \(TD\)-coloring, there exists a set of color classes of \(f\) such that every vertex of \(G\) total dominates at least one color class in that set; and we denote by \(p_{f}\) the size of a smallest such set. Obviously, \(p_{f} < q_{f}\).
In a graph \(G\), a complete bipartite graph \(G[X,Y]\) is called universal if every vertex in \(V(G)\setminus\{X,Y\}\) is adjacent to every vertex of at least one set of \(X\) and \(Y\).
Lemma 1. Let \(G\) be a connected graph,Then
(i) The following are equivalent.
— \(G\) has a \(TDC\) \(f\) with \(p_{f}=2\);
— \(G\) has a universal complete bipartite graph;
— Every proper coloring of \(G\) is a \(TD\)-coloring with \(p_{f}=2\).
(ii) If \(\overline{G}\) is not connected, then every proper coloring of \(G\) is a \(TDC\) and \(\chi^{t}_{d}=\chi(G)\). Moreover, \(G\) must has a universal complete bipartite graph with \(p_{f}=2\).
Proof. (i) Suppose that \(G\) has a \(TDC\) \(f\) with \(p_{f}=2\). So there are two color classes \(X\) and \(Y\) such that every vertex of \(G\) total dominates at least one of \(X\) and \(Y\). In particular, every vertex of \(X\) must dominate every vertex of \(Y\), every vertex of \(Y\) must dominate every vertex of \(X\), Thus \(G[X,Y]\) is a universal complete bipartite graph. Conversely, if \(G\) has a universal complete bipartite graph, then every proper coloring \(f\) is obviously a \(TDC\) with \(p_{f}=2\).
(ii) Since \(\overline{G}\) is not connected, there is a partition of \(V(G)\) into two non-empty sets \(V_{1}\) and \(V_{2}\) such that every vertex of \(V_{1}\) is adjacent in \(G\) to every vertex of \(V_{2}\). Let \(f\) be any proper coloring of \(G\). Then some color \(\alpha\) appears only in \(V_{1}\) and some color \(\beta\) appears only in \(V_{2}\). So every vertex of \(V_{1}\) totally dominates color \(\beta\),and every vertex of \(V_{2}\) totally dominates color \(\alpha\), Thus \(f\) is a \(TDC\). and \(\chi^{t}_{d}=\chi(G)\). Moreover, the same argument shows that \(p_{f}\leq2\), and every \(TDC\) \(f\) of \(G\) satisfies \(p_{f}\geq2\), then \(G\) must has a universal complete bipartite graph with \(p_{f}=2\).
Lemma 2. Let \(G\) be a non-connected graph with components \(G_{1},\ldots,G_{k}\), \(k\geq2\). Then \[\chi^{t}_{d}=min\left\{\sum\limits_{i=1}^{k}p_{f_{i}}+\max\limits_{1\leq i \leq k}\{q_{f_{i}}-p_{f_{i}}\}\right\},\] where the minimum is over all choices of a \(TD\)-coloring \(f_{i}\) for each \(G_{i}\).
Proof. Let \(f\) be any \(TD\)-coloring of \(G\). For \(i=1,\ldots,k\), any color class whose vertices are all in \(G_{i}\) will be called a private color of \(G_{i}\). Let \(p_{i}\) be the number of private colors in \(G_{i}\). Let \(f_{i}\) be the coloring induced by \(f\) on \(G_{i}\). Consider any vertex \(v\) of \(G_{i}\). Since \(f\) is a \(TD\)-coloring, \(v\) totally dominates a color class, which must therefore be a private color of \(G_{i}\). By the same argument , \(f_{i}\) is a \(TD\)-coloring of \(G_{i}\). Then \(p_{i}\geq p_{f_{i}}\). Moreover, if \(R_{i}\) denotes the set of vertices of all private colors of \(G_{i}\), then \(f\) uses \(q_{f_{i}}-p_{i}\) colors on the vertices of \(G_{i}\setminus R_{i}\). Such colors can be used on several components. So \(f\) uses at least \[\sum\limits_{i=1}^{k}p_{i}+\max\limits_{1\leq i \leq k}\{q_{f_{i}}-p_{i}\}\] colors. This value is larger than or equal to \[\sum\limits_{i=1}^{k}p_{f_{i}}+\max\limits_{1\leq i \leq k}\{q_{f_{i}}-p_{f_{i}}\}.\]
Because replacing \(p_{i}\) by \(p_{f_{i}}\) can only decrease the sum, and if it increases the max then it decreases the sum correspondingly. On the other hand, we can turn \(f\) into a \(TD\)-coloring \(f'\) with a number of colors equal to the second displayed value. Indeed, let \(q=\max\limits_{1\leq i \leq k}\{q_{f_{i}}-p_{f_{i}}\}\). It suffices to use in each \(G_{i}\) precisely \(p_{c_{i}}\) private colors and to rename \(1,\ldots, q_{f_{i}}-p_{f_{i}}\) the other colors of \(f_{i}\). Since \(f\) is any \(TD\)-coloring, it follows that \(\chi^{t}_{d}\) is equal to the minimum of this value.
If the graph \(G\) is constructed by operation \(\oplus\), then we give the following lemma.
Lemma 3. Let \(G\) be a connected \(B-P_{4}\) graph, and let \(G^{*}\) be the vertex-induced subgraph by the outside of \(\{a,b,c,d\}\). Then \[\chi^{t}_{d}(G)=2+\chi(G^{*}).\]
Moreover, every \(TD\)-coloring of \(G\) has a universal bipartite graph with \(p_{f}=2\).
Proof. Color \(G^*\) using \(\chi(G^{*})\) such that \(G^*\) is proper coloring and color \(a,~b\) with the two colors in \(\chi(G^*)\), and then color \(b\) and \(c\) with two different new colors, respectively. For any vertex \(v \in V(G)\), \(v\) must be adjacent to one of \(\{b,c\}\), since \(G\) is a \(B-P_4\) graph. This is to say, every vertex in \(G\) total dominates a color set. Then \(\chi^{t}_{d}(G)\leq2+\chi(G^{*})\). Suppose that \(\chi^{t}_{d}(G)\leq 1+\chi(G^{*})\). Then there must be two adjacent vertices \(b,~c\) in \(G\) have the same color by pigeonhole principle, a contradiction. So the lemma holds.
Combining the above lemmas, we give the following theorem.
Theorem 2. Let \(G\) be a \(P_{4}\)-reducible graph.
(i) If \(G\) is \(B-{P_{4}}\) graph and \(G^{*}\) defined as Lemma 3, then \(\chi^{t}_{d}(G)=2+\chi(G^{*})\);
(ii) If \(G\) is connected and not a \(B-{P_{4}}\) graph, then \(\chi^{t}_{d}=\chi(G)\);
(iii) If \(G\) is not connected, and let \(k ~(\geq 2)\) be the number of components in \(G\), then \[\chi^{t}_{d}(G)=\chi(G)+2k-2.\]
Proof. (i) From the Lemma 3, we have \(\chi^{t}_{d}(G)=2+\chi(G^{*})\).
(ii) Let \(G\) be a connected graph and not a \(B-P_4\) graph. Then \(\overline{G}\) is not connected by Theorem 1. From Lemma 1 (ii), we have \(\chi^{t}_{d}(G)=\chi(G)\).
(iii) Suppose that \(G\) is not connected. Let \(G_{1},\ldots,G_{k}\) be the components of \(G\). By Lemma 2, we have \[\chi^{t}_{d}=min\left\{\sum\limits_{i=1}^{k}p_{f_{i}}+\max\limits_{1\leq i \leq k}\{q_{f_{i}}-p_{f_{i}}\}\right\},\] for some appropriate choice of a \(TD\)-coloring \(f_{i}\) for each \(G_{i}\). Consider any component \(G_{i}\) of \(G\). If \(G_{i}\) has a universal bipartite graph, then we have \(p_{f_{i}}=2\) (whatever the choice of \(f_{i}\)) since Lemma 1. If \(G_{i}\) has no universal bipartite graph, then \(\overline{G_{i}}\) is not connected from the Lemma 1. And further we have \(p_{f_{i}}=2\) (whatever the choice of \(f_i\) again) by Lemma 1. It follows that in the formula above, the sum term is equal to \(2k\). Moreover, we may assume that \(q_{f_{i}}=\chi(G_{i})\) for each \(i\) since this is the best way to minimize the value in the formula. More precisely, if some component \(G_{i}\) of \(G\) has a universal bipartite graph and satisfies \(\chi(G_{i})=\chi(G)\), then the max term in the formula is equal to \(\chi(G)-2\), so we obtain the conclusion.
In this section, we mainly study on the total dominator coloring of the \(P_4\)-tidy graphs. Now, we begin with some preliminaries. Let \(G=(V,E)\) be a graph. Set \(F=\{e \in E|e \text{~belongs ~to ~an ~ induced} ~P_{4} ~\text{of}~ G\}\) and \(G_{p}=(V,F)\). A connected component of \(G_{p}\) having exactly one vertex is called a weak vertex. Any connected component of \(G_{p}\) distinct from a weak vertex is called a \(p\)-component of \(G\). A graph \(G\) is \(p\)-connected if it has only one \(p\)-component and no weak vertices.
An \(p\)-connected graph \(G=(V,E)\) is \(p\)-separable if \(V\) can be partitioned into two sets (\(C,S\)) such that each \(P_{4}\) that contains vertices from \(C\) and from \(S\) has its midpoints in \(C\) and its endpoints in \(S\). we will call it a \(p\)-partition. An urchin (resp. starfish) of size \(k\) (\(\geq2\)), is a \(p\)-separable graph with \(p\)-partition (\(C,S\)), where \(C=\{c_{1},\ldots,c_{k}\}\) is a clique; \(S=\{s_{1},\ldots,s_{k}\}\) is a stable set; \(s_{i}\) is adjacent to \(c_{i}\) if and only if \(i=j\)(resp. \(i\neq j\)). A quasi-urchin (resp. starfish) of size \(k\) is a graph obtained from an urchin (resp.starfish) of size \(k\) by replacing at most one vertex by \(K_{2}\) or \(S_{2}\). Note that the new vertices result in true or false twins, respectively, and they are in the same set of the new \(p\)-partiton (\(C^{*},S^{*}\)). The elements of \(S^{*}\) are called legs and \(C^{*}\) is called the body of the quasi-starfish or quasi-urchin.
Note that there are five possible quasi-starfishes of size two, and they are also the five possible quasi-urchins of size two: \(P_4, ~P,~ \bar{P}\), fork and kite (see Figure 1). To avoid ambiguity, we will consider these five graphs as quasi-starfishes, while quasi-urchins will be always of size at least three.
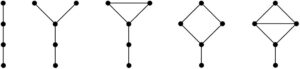
When considering quasi-urchins and quasi-starfishes, we have ten kinds of them. We will call Type \(1\) (resp. Type \(2\)) the urchins (resp. starfish); Type \(3\) (resp. Type \(4\)) the urchins (resp. starfish), where a vertex in the body was replaced by \(K_{2}\); Type \(5\) (resp. Type \(6\)) the urchins (resp. starfish), where a vertex in the body was replaced by \(S_{2}\); Type \(7\) (resp. Type \(8\)) the urchins (resp. starfish), where a leg was replaced by \(K_{2}\); and Type \(9\) (resp. Type \(10\)) the urchins (resp. starfish), where a leg was replaced by \(S_{2}\). To avoid ambiguity, we will let the graph of odd type have size at least three.
Let \(G_{1}=(V_{1},E_{1})\) and \(G_{2}=(V_{2},E_{2})\) be two graphs with \(V_{1}\cap V_{2}=\emptyset\), such that \(G_{1}\) is \(p\)-separable with partition \((V_{1}^{1},V_{1}^{2})\). Consider the graph with vertex set \(V_{1}\cup V_{2}\) and edge set \(E_{1}\cup E_{2} \cup \{xy|x\in V_{1}^{1},y\in V_{2}\}\). we shall denote this graph by \(G_{1}\underline{\vee}G_{2}\).
Proposition 2. [16]A graph \(G\) is \(P_{4}\)-tidy if and only if every p-component is isomorphic to either \(P_{5}\) or \(\overline{P_{5}}\) or \(C_{5}\) or a quasi-starfish or a quasi-urchin. Quasi-starfishes or quasi-urchins are the p-separable p-components of \(G\).
Lemma 4. Let \(G\) be a quasi-starfish or quasi-urchin of size \(k\). Then
(1) If \(G\) is type \(1, 2, 5, 6, 7, 9\) or \(10\), then \(\chi(G)=k\).
(2) If \(G\) is type \(3, 4\) or \(8\), then \(\chi(G)=k+1\).
Proof. Since a proper coloring of the maximum clique in \(G\) can be extended to \(G\) without adding other colors, then the results are hold.
In [19], Corneil el at. gave the chromatic number of the union and join graph operations.
Theorem 3. [19]If \(G\) is the trivial graph, then \(\chi(G)=1\). Let \(G_1 = (V_1, E_1)\) and \(G_2 = (V_2, E_2)\) be two graphs such that \(V_1 \cap V_2 = \emptyset\). Then,
i. \(\chi(G_1 \cup G_2) = \text{max}\{\chi(G_1),\chi(G_2)\}\);
ii. \(\chi(G_1 \vee G_2) = \chi(G_1)+\chi(G_2)\).
Lemma 5. Let \(G\) be a quasi-starfish or quasi-urchin of size \(k\). Then
(1) If \(G\) is type \(1, 2, 5, 6, 9\) or \(10\), then \(\chi_{d}^{t}(G)=k+1\);
(2) If \(G\) is type \(3, 4, 7\) or \(8\), then \(\chi_{d}^{t}(G)=k+2\).
Proof. (1) By the configuration of \(G\), let (\(C^{*},S^{*}\)) be the \(p\)-partition of \(G\). Now we give a coloring \(f\) of \(G\) as follows. If \(G\) is in type \(1\) (resp. type \(2\), type \(9\) or type \(10\)), then color every vertex of \(C^{*}\) a new color and color all vertices of \(S^{*}\) another new color. Then \(f\) is a \(TD\)-coloring in \(G\) since every vertex is total dominator a color set, and \(\chi^t_d(G) \leq k+1\). If \(G\) is in type \(5\) (resp. type \(6\)), then color each \(S_2\) with a different colors and color all the vertices in \(S^*\) another new colors. Then \(f\) is a \(TD\)-coloring of \(G\) and \(\chi_{d}^{t}(G)\leq k+1\).
Suppose \(\chi_{d}^{t}(G)=k\). We obtain \(\chi_{d}^{t}(C^{*})=k\), since \(C^*\) is a clique. Then there must be two vertices \(c_{i}(\in C^{*})\), \(s_{j}(\in S^{*})\) such that they have been colored by the same color and they are not adjacent. Let \(s_{i}(\in S^{*})\) is adjacent to \(c_i\), we can get \(c_i\) is not adjacent to all the vertices in any color, a contradiction. Then \(\chi^t_d(G) = k+1\).
(2) Since the proof of type \(3\) and type \(4\) are similar to type \(1\), we limit them. Now assume that \(G\) is in type \(7\) (resp. type \(8\)). Let \(s_{1},s'_{1}\) be two adjacent vertices in \(S^*\). We give the following coloring \(f\) of \(G\). Color each vertex in \(C^*\) a new color; color the vertices \(s_{1},s'_{1}\) two new colors and color the remained vertex in \(S^*\) by the same color of \(s_{1}\) or \(s'_{1}\). Then \(f\) is a \(TD\)-coloring of \(G\) with \(|f|=k+2\). Then \(\chi^t_d(G) \leq k+2\).
Suppose \(\chi^t_d(G) =k+1\). Since \(C^*\) is a clique of size \(k\), then color \(C^*\) must use \(k\) colors. All vertices of \(S^{*}\) do not color the same color, since \(s_{1}\) or \(s'_{1}\) is adjacent. Then either \(s_{1}\) or \(s'_{1}\) must have been colored by the same color of a vertex \(c_{i}\) in \(C^{*}\). Then there are must be a vertex in \(S^{*} \setminus \{s_{1},s'_{1}\}\) that not dominate the color class which contains \(s_{1}\), a contradiction. Then \(\chi^t_d(G) = k+2\).
A redundant color of \(G\) is a color in a total dominating coloring of \(G\) that no vertex in \(G\) total dominating the vertices in this color. Let \(r(G)\) be the number of redundant colors in a total dominating coloring of \(G\). Now, we give the lemmas as follows.
Lemma 6. (1) Let \(G=G_1\cup G_2\). Then \[\chi^{t}_d(G)=\chi^{t}_d(G_1)+\chi^{t}_d(G_2)-\text{min}\{r(G_1),r(G_2)\}.\]
(2) Let \(G=G_{1}\vee G_{2}\). Then \[\chi_{d}^{t}(G)=\chi(G)=\chi(G_{1})+\chi(G_{2}).\]
Proof. (1)Let \(f_i\) be a total dominator coloring of \(G_i\) with \(r(G_i)\) redundant colors, where \(i \in \{1,~2\}\). Without loss of generality, we assume that \(r(G_1) \leq r(G_2)\). Now, we define the coloring \(f\) in \(G\) as follows. Color \(G_i\) as \(f_i\) and then using \(r(G_1)\) redundant colors to repeat some redundant colors in \(G_2\). Because \(f_1\) and \(f_2\) are total dominator coloring of \(G_1\) and \(G_2\), respective. Then \(f\) is total dominator coloring of \(G\) and then \(\chi^{t}_d(G)=\chi^{t}_d(G_1)+\chi^{t}_d(G_2)-r(G_1)\). On the other hand, suppose that \(\chi^{t}_d(G)\leq \chi^{t}_d(G_1)+\chi^{t}_d(G_2)-\text{min}\{r(G_1),r(G_2)\}-1\). By Pigeonhole Principle, there are some vertex which is not total dominating. Then the result holds.
(2) By Theorem 3 (ii), \(\chi(G)=\chi(G_1)+\chi(G_2)\). Let \(f\) be a proper coloring of \(G\) using \(\chi(G)\) colors. Since \(G=G_{1}\vee G_{2}\) contains a complete bipartite graph as a induced subgraph, then \(f\) is a total dominator coloring and \(\chi^t_d(G) \leq \chi(G)\). So \(\chi_{d}^{t}(G)=\chi(G)=\chi(G_{1})+\chi(G_{2})\), since \(\chi^t_d(G) \geq \chi(G)\).
Note that we can compute the number of redundant color in a total dominator coloring in polynomial time.
Lemma 7. Let \(G_{1}=(V_{1},E_{1})\) be a \(p\)-separable \(p_{4}\)-tidy graph, and \(G_{2}=(V_{2},E_{2})\) a graph such that \(V_{1}\cap V_{2}=\emptyset\). Then,
(1) If \(G\) is not type \(7\), then \(\chi_{d}^{t}(G_{1}\underline{\vee}G_{2})=\chi(G_{1})+\chi(G_{2})+1\);
(2) If \(G\) is type \(7\), then \(\chi_{d}^{t}(G_{1}\underline{\vee}G_{2})=\chi(G_{1})+\chi(G_{2})+2\).
Proof. Let \(G=G_{1}\underline{\vee}G_{2}\). By Proposition 2, \(G_{1}\) is a quasi-urchin or a quasi-starfish and set (\(C^{*},S^{*}\)) be its \(p\)-partition. Then \(G\) contains \(G_{1}[C^{*}]\vee G_{2}\) as an induced subgraph. Thus \(\chi_{d}^{t}(G)\geq \chi_{d}^{t}(G_{1}[C^{*}]\vee G_{2})\). On the other hand, if \(G\) is type \(7\) or type \(8\), a \(TDC\) of \(G_{1}[C^{*}]\vee G_{2}\) can be extended to \(G\) by adding two new colors. Hence \(\chi_{d}^{t}(G)= \chi_{d}^{t}(G_{1}[C^{*}]\vee G_{2})+2\); if \(G\) is not type \(7\) or type \(8\), a \(TDC\) of \(G_{1}[C^{*}]\vee G_{2}\) can be extended to \(G\) by adding one new colors. Hence \(\chi_{d}^{t}(G)= \chi_{d}^{t}(G_{1}[C^{*}]\vee G_{2})+1\). By Lemma 6, we get \(\chi_{d}^{t}(G_{1}\vee G_{2})=\chi(G_{1})+\chi(G_{2})\), so by Lemma 4, we can know if \(G_{1}\) is type \(8\), then \(\chi(G_{1}[C^{*}])=\chi(G_{1})-1\); otherwise, \(\chi(G_{1}[C^{*}])=\chi(G_{1})\).
Combining the above, we can get that if \(G\) is type \(7\), then \(\chi_{d}^{t}(G)=\chi(G_{1})+\chi(G_{2})+2\); otherwise, \(\chi_{d}^{t}(G)=\chi(G_{1})+\chi(G_{2})+1\).
Theorem 4. [20] Every graph \(G\) either is \(p\)-connected or can be obtained uniquely from its \(p\)-components and weak vertices by a finite sequence of \(\cup\), \(\vee\), \(\underline{\vee}\) operations.
Combining the above lemmas and theorems, we get the following theorem.
Theorem 5. Total dominator chromatic number of \(P_4\)-tidy can be computed in polynomial time on \(P_4\)-tidy graphs.
The authors would like to thank the anonymous referee for many helpful comments and suggestions.
The authors declares no conflict of interests.