A tremendous amount of drug experiments revealed that there exists a strong inherent relation between the molecular structures of drugs and their biomedical and pharmacology characteristics. Due to the effectiveness for pharmaceutical and medical scientists of their ability to grasp the biological and chemical characteristics of new drugs, analysis of the bond incident degree (BID) indices is significant of testing the chemical and pharmacological characteristics of drug molecular structures that can make up the defects of chemical and medicine experiments and can provide the theoretical basis for the manufacturing of drugs in pharmaceutical engineering. Such tricks are widely welcomed in developing areas where enough money is lacked to afford sufficient equipment, relevant chemical reagents, and human resources which are required to investigate the performance and the side effects of existing new drugs. This work is devoted to establishing a general expression for calculating the bond incident degree (BID) indices of the line graphs of various well-known chemical structures in drugs, based on the drug molecular structure analysis and edge dividing technique, which is quite common in drug molecular graphs.
The frontier of biomedical science has rarely been as exciting and as full of spectacular innovations as it is today. The last decade has seen rapid technological progress and developments in medicine manufacturing, chemical and pharmaceutical techniques. A large number of new nano-materials, crystalline materials and efficacious drugs emerge every year. Enormous amount of chemical experiments and work is required to determine the chemical properties of new compounds and drugs to test their physical features, chemical reactivity, and biological activity. Advanced equipment, sufficient reagents and human resources are required to investigate the performance and the reaction of these new drugs.
Medicinal chemistry is a problem-solving discipline concerned with the discovery, design, and use of drugs. Medicinal chemists are now increasingly involved in the drug discovery and development process; they have become tremendously important in the innovation and discovery of drugs. The main paradigm of medicinal chemistry is that biological activity, as well as physical and chemical properties of organic compounds such as melting point, boiling point, and toxicity of drugs, is inherent in their molecular structures.
Mathematical chemistry had a tremendous growth spurt in the second half of the twentieth century and the same trend is continuing now. Mathematical chemistry focuses on mathematical ideas and concepts which are adapted or developed for being used in chemistry. Nonempirical parameters of chemical structures derived from graph-theoretic formalisms are being widely used by many researchers in studies and pertaining to molecular design, pharmaceutical drug-design, and environmental hazard assessment of chemicals. Graph theory applied in the study of molecular structures represents an interdisciplinary science, called chemical graph theory or molecular topology. It is used to mathematically model molecules in order to gain insight into the physical properties of the chemical compounds. Some physical properties, such as the boiling point, are related to the geometric structure of the compound. In theoretical chemistry, the physico-chemical properties of chemical compounds are often modeled by topological indices. Topological indices are numerical quantities of a molecular graph, which are invariant under graph isomorphism and reflect certain structural features of the corresponding molecule. During recent decades, topological indices have been widely used in quantitative structure-property relationship and quantitative structure-activity relationship studies.
For the convenience of our discussion about the medicine mathematical model, we first recall some relevant terminologies and notations, which can be found in [1] with a clear explanation. Conventionally the structure of a drug is considered as an undirected (chemical) graph where each vertex expresses an atom and each edge represents a chemical bond between these atoms. We consider \(G\) as a simple graph corresponding to a drug structure with an atom (vertex) set as \(V(G)\) and a chemical bond (edge) set as \(E(G)\). The Topological index of a molecule structure can be considered as a non-empirical numerical quantity which quantitates the molecular structure and its branching pattern. In this point of view, it is used as a descriptor of the molecule under testing. A topological index defined on the molecule structure \(G\) can be regarded as a real-valued function \(f:G\rightarrow\mathbb{R^{+}}\) which maps each drug molecular structure to certain real numbers. Scientists have established significant indices decades ago that have broad applications in the correlation and prediction of several molecular properties and also in tests of similarity and isomorphism of the drug molecules [2]. Several reports help to determine the topological indices of special molecular graphs in chemical, nanomaterials, and pharmaceutical engineering which help researchers to understand the physical features, chemical reactivity, and biological activity of their corresponding molecular structures.
A large number of such indices depend only on vertex degree of the molecular graph. A considerable amount of these degree-based topological indices can be represented as the sum of edge contributions of a graph. These kinds of degree-based topological indices (TI) are known as bond incident degree (BID) indices whose general form is \[\label{e:WeakBase}\tag{1} TI(G) = \displaystyle\sum_{\delta(G)\leq a\leq b\leq \triangle(G)}x_{a,b}(G).\theta_{a,b},\] where \(\theta_{a,b}\) is a nonnegative real valued function that depends on \(a\) and \(b\), \(\delta(G)\) is the minimum degree in the graph \(G\), \(\triangle(G)\) is the maximum degree in the graph \(G\), and \(x_{a,b}(G)\) is the number of edges in \(G\) connecting the vertices of degrees \(a\) and \(b\) (Ali, Raza, and Bhatti [3]). For instance, we mention here some special cases of eq. 1 in which the function \(\theta_{a,b}\) is defined in the following manner (second equation, third equation, fourth equation, fifth equation, sixth equation, seventh equation, eighth equation, ninth equation and tenth equation):
\[\theta_{a,b} = a+b,\,\,\,\,\,\,\,\,\,\,\,\text{First Zagreb index},\tag{2}\] \[\theta_{a,b} = ab,\,\,\,\,\,\,\,\,\,\,\,\text{Second Zagreb index},\tag{3}\] \[\theta_{a,b} = \frac{1}{\sqrt{ab}},\,\,\,\,\,\,\,\,\,\,\,\text{Randi\'c index},\tag{4}\] \[\theta_{a,b} = \frac{2}{\sqrt{a+b}},\,\,\,\,\,\,\,\,\,\,\,\text{Harmonic index},\tag{5}\] \[\theta_{a,b} = \sqrt{\frac{a+b-2}{ab}},\,\,\,\,\,\,\,\,\,\,\,\text{Atom-bond connectivity index},\tag{6}\] \[\theta_{a,b} = \frac{1}{\sqrt{a+b}},\,\,\,\,\,\,\,\,\,\,\,\text{Sum-connectivity index},\tag{7}\] \[\theta_{a,b} = \frac{\sqrt{ab}}{\frac{1}{2}(a+b)},\,\,\,\,\,\,\,\,\,\,\,\text{First geometric-arithmetic index},\tag{8}\] \[\theta_{a,b} = \left(\frac{ab}{a+b-2}\right)^{3},\,\,\,\,\,\,\,\,\,\,\,\text{Augmented Zagreb index},\tag{9}\] \[\theta_{a,b} = \sqrt{(a-1)(b-1)},\,\,\,\,\,\,\,\,\,\,\,\text{Reduced reciprocal Randi\'c index}.\tag{10}\]
Besides, there are many other BID indices in the literature. Details about BID indices can be found in the papers by Vukičević and Gašperov [4]; Gutman, Furtula and Elphick [5]; Deng, Yang and Xia [6]; Furtula, Gutman and Dehmerc [7]; Goubko and Gutman [8]; Gutman and Tošović [9]; Ali, Iqbal and Iqbal [10] and related references cited therein.
In order to control and prevent diseases, efficient anti-cancer and anti-HIV drugs are required. The development and analysis of drugs for treatment of cancer and HIV has become a major research objective in the past decade. The joint effort of mathematicians, chemists and clinicians is required for efficient drug design. Recently, bond incident degree indices has proved to be highly useful for analysis of anti-cancer and anti-HIV drug activity.
Let \(\delta(G)\) and \(\Delta(G)\) be the minimum and maximum degree of \(G\), respectively. The vertex set \(V(G)\) can be divided into several partitions such that \(V_{i}\) represents a vertex having degree \(i\) is also addressed as an \(i-degree\,vertex\) and \(v_{i} = |V_{i}|\). Line graph \(L(G)\) of a graph \(G\) has the vertex set \(V(L(G)) = E(G)\) where the two distinct vertices of \(L(G)\) are adjacent if the corresponding edges of \(G\) are adjacent.
With continued work on Gao et al. [11] we obtained the bond incident degree (BID) indices of line graphs of various essential chemical structures in drugs.
Graphene is one of the most promising nanomaterials as it is
extraordinarily strong and electrically super-conductive. It is a
one-atom thick and single tightly packed sheet of hexagonally arranged
carbon atoms. It is a two dimensional layer of honeycomb lattice, in
which carbon atoms are bonded together in a repeating pattern of
hexagons, with each carbon atom covalently bonded to three other carbon
atoms. Graphene, unlike a buckyball or nanotube, has no inside because
it is flat. It enables both disease detection and drug delivery.
Graphene has great potential for the detection and treatment of cancer.
It is the main element of certain carbon allotropes including charcoal,
fullerenes and graphite etc. See Shigehalli and Kanabur [12] for more details.
Theorem 1. The bond incident degree (BID) indices of line graph of \(G(m,n)\) are
where \(G(m,n)\) is a molecular graph of graphene with \(n\) rows and \(m\) columns.
Proof. By analyzing the molecular structure of the line graph of graphene \(G(m,n)\), for \(n=1\) and \(m=1\), we infer \(n_{22}=6\). Therefore, using the definition of bond incident degree indices, we obtain \[\begin{aligned} TI(L(G(m,n))) =\displaystyle\sum_{2\leq a\leq b\leq 2}x_{a,b}(L(G(m,n))).\theta_{a,b}=\sum_{uv\in E_{22}}x_{2,2}(L(G(m,n))).\theta_{2,2}=6(\theta_{2,2}). \end{aligned}\] For \(n=1\) and \(m\geq2\): we infer \(n_{22}=4\), \(n_{23}=4\), \(n_{33}=4m-6\) and \(n_{34}=4m-4\). Therefore, by using the definition of bond incident degree indices, we obtain
\[\begin{aligned} TI(L(G(m,n)))& =\displaystyle\sum_{2\leq a\leq b\leq 4}x_{a,b}(L(G(m,n))).\theta_{a,b}\\ &=\sum_{uv\in E_{22}}x_{2,2}(L(G(m,n))).\theta_{2,2}+\sum_{uv\in E_{23}}x_{2,3}(L(G(m,n))).\theta_{2,3}\\&\quad+\sum_{uv\in E_{33}}x_{3,3}(L(G(m,n))).\theta_{3,3}+\sum_{uv\in E_{34}}x_{3,4}(L(G(m,n))).\theta_{3,4}\\ &=(4).\theta_{2,2}+(4).\theta_{2,3}+(4m-6).\theta_{3,3}+(4m-4).\theta_{3,4}\\ &=4(\theta_{3,3}+\theta_{3,4})m+2[2(\theta_{2,2})+2(\theta_{2,3})-3(\theta_{3,3})-2(\theta_{3,4})]. \end{aligned}\] For \(n\geq2\) and \(m=1\): we infer \(n_{22}=4\), \(n_{23}=2n\), \(n_{33}=2\), \(n_{34}=4n-4\) and \(n_{44}=2n-4\). Therefore, by using the definition of bond incident degree indices, we obtain \[\begin{aligned} TI(L(G(m,n)))& =\displaystyle\sum_{2\leq a\leq b\leq 4}x_{a,b}(L(G(m,n))).\theta_{a,b}\\ &=\sum_{uv\in E_{22}}x_{2,2}(L(G(m,n))).\theta_{2,2}+\sum_{uv\in E_{23}}x_{2,3}(L(G(m,n))).\theta_{2,3}+ \sum_{uv\in E_{33}}x_{3,3}(L(G(m,n))).\theta_{3,3}\\ &\quad+\sum_{uv\in E_{34}}x_{3,4}(L(G(m,n))).\theta_{3,4}+\sum_{uv\in E_{44}}x_{4,4}(L(G(m,n))).\theta_{4,4}\\ &=(4).\theta_{2,2}+(2n).\theta_{2,3}+(2).\theta_{3,3}+(4n-4).\theta_{3,4}+(2n-4).\theta_{4,4}\\ &=2[\theta_{2,3}+2(\theta_{3,4})+\theta_{4,4}]n+2[2(\theta_{2,2})+\theta_{3,3}-2(\theta_{3,4})-2(\theta_{4,4})]. \end{aligned}\] For \(n\geq2\) and \(m\geq2\): we infer \(n_{22}=2\), \(n_{23}=2n+4\), \(n_{33}=4m-4\), \(n_{34}=4m+4n-8\) and \(n_{44}=6mn-6m-4n+2\). Similarly, by using the definition of bond incident degree indices, we obtain \[\begin{aligned} TI(L(G(m,n)))& =\displaystyle\sum_{2\leq a\leq b\leq 4}x_{a,b}(L(G(m,n))).\theta_{a,b}\\ &=\sum_{uv\in E_{22}}x_{2,2}(L(G(m,n))).\theta_{2,2}+\sum_{uv\in E_{23}}x_{2,3}(L(G(m,n))).\theta_{2,3}+ \sum_{uv\in E_{33}}x_{3,3}(L(G(m,n))).\theta_{3,3}\\&\quad+\sum_{uv\in E_{34}}x_{3,4}(L(G(m,n))).\theta_{3,4}+ +\sum_{uv\in E_{44}}x_{4,4}(L(G(m,n))).\theta_{4,4}\\ &=(2).\theta_{2,2}+(2n+4).\theta_{2,3}+(4m-4).\theta_{3,3}+(4m+4n-8).\theta_{3,4}+(6mn-6m-4n +2).\theta_{4,4}\\ &=6(\theta_{4,4})mn+2[2(\theta_{3,3})+2(\theta_{3,4})-3(\theta_{4,4})]m+2[\theta_{2,3}+2(\theta_{3,4})-2(\theta_{4,4})]n\\ &+2[\theta_{2,2}+2(\theta_{2,3})-2(\theta_{3,3})-4(\theta_{3,4})+\theta_{4,4}]. \end{aligned}\] ◻
Dendrimers are large and complex molecules with very well-defined chemical structures. They are produced in an iterative sequence of reaction steps. The nanostar dendrimers are part of a new group of macromolecules with a precise tailored architecture. These are hyper-branched nanostructures that can be synthesized by divergent or convergent methods, and they are built up from branched units called monomers using a nanoscale fabrication process. In this section, we determine the bond incident degree (BID) indices of line graphs of three famous infinite classes \(NS_{1}[n]\), \(NS_{2}[n]\) and \(NS_{3}[n]\) of dendrimer stars which widely appear in the drug structures. For detailed structure, see Ashrafi and Nikzad [13].
Theorem 2. The bond incident degree (BID) indices of line graphs of three infinite classes \(NS_{1}[n]\), \(NS_{2}[n]\) and \(NS_{3}[n]\) of dendrimer stars are
where \(n\) is the number of steps of growth of these three classes of dendrimer stars.
Proof. By observing the structures of the line graphs of these three infinite classes of dendrimer stars, we deduce its edge partition as follows;
For \(L(NS_{1}[n])\): \(n_{22}=\frac{9}{2}(2^{n})\), \(n_{23}=9(2^{n})+6\), \(n_{33}=\frac{45}{2}(2^{n})-24\), \(n_{35}=9\) and \(n_{55}=3\).
For \(L(NS_{2}[n])\): \(n_{22}=6(2^{n})\), \(n_{23}=12(2^{n})+4\), \(n_{33}=30(2^{n})-16\) and \(n_{34}=4\).
For \(L(NS_{3}[n])\): \(n_{22}=8(2^{n})-4\), \(n_{23}=28(2^{n})-6\), \(n_{24}=4(2^{n})\), \(n_{33}=22(2^{n})-6\), \(n_{34}=12(2^{n})\) and \(n_{44}=4(2^{n})\).
Therefore, according to the definition of bond incident degree indices, we check
For \(L(NS_{1}[n])\):-
\[\begin{aligned} TI(L(NS_{1}[n]))& =\displaystyle\sum_{2\leq a\leq b\leq 5}x_{a,b}(L(NS_{1}[n])).\theta_{a,b}\\ &=\sum_{uv\in E_{22}}x_{2,2}(L(NS_{1}[n])).\theta_{2,2}+\sum_{uv\in E_{23}}x_{2,3}(L(NS_{1}[n])).\theta_{2,3}+\sum_{uv\in E_{33}}x_{3,3}(L(NS_{1}[n])).\theta_{3,3}\\ &\quad+\sum_{uv\in E_{35}}x_{3,5}(L(NS_{1}[n])).\theta_{3,5}+\sum_{uv\in E_{55}}x_{5,5}(L(NS_{1}[n])).\theta_{5,5}\\ &=\left[\frac{9}{2}(2^{n})\right].\theta_{2,2}+\left[9(2^{n})+6\right].\theta_{2,3}+\left[\frac{45}{2}(2^{n})-24\right].\theta_{3,3}+(9).\theta_{3,5}+(3).\theta_{5,5}\\ &=9\left[\frac{1}{2}(\theta_{2,2})+\theta_{2,3}+\frac{5}{2}(\theta_{3,3})\right](2^{n})+3\left[2(\theta_{2,3})-8(\theta_{3,3})+3(\theta_{3,5})+\theta_{5,5}\right]. \end{aligned}\]
For \(L(NS_{2}[n])\):-
\[\begin{aligned} TI(L(NS_{2}[n]))& =\displaystyle\sum_{2\leq a\leq b\leq 4}x_{a,b}(L(NS_{2}[n])).\theta_{a,b}\\ &=\sum_{uv\in E_{22}}x_{2,2}(L(NS_{2}[n])).\theta_{2,2}+\sum_{uv\in E_{23}}x_{2,3}(L(NS_{2}[n])).\theta_{2,3}+\sum_{uv\in E_{33}}x_{3,3}(L(NS_{2}[n])).\theta_{3,3}\\ &\quad+\sum_{uv\in E_{34}}x_{3,4}(L(NS_{2}[n])).\theta_{3,4}\\ &=\left[6(2^{n})\right].\theta_{2,2}+\left[12(2^{n})+4\right].\theta_{2,3}+\left[30(2^{n})-16\right].\theta_{3,3}+(4).\theta_{3,4}\\ &=6\left[\theta_{2,2}+2(\theta_{2,3})+5(\theta_{3,3})\right](2^{n})+4\left[\theta_{2,3}-4(\theta_{3,3})+\theta_{3,4}\right]. \end{aligned}\]
For \(L(NS_{3}[n])\):-
\[\begin{aligned} TI&(L(NS_{3}[n])) =\displaystyle\sum_{2\leq a\leq b\leq 4}x_{a,b}(L(NS_{3}[n])).\theta_{a,b}\\ &=\sum_{uv\in E_{22}}x_{2,2}(L(NS_{3}[n])).\theta_{2,2}+\sum_{uv\in E_{23}}x_{2,3}(L(NS_{3}[n])).\theta_{2,3}+ \sum_{uv\in E_{24}}x_{2,4}(L(NS_{3}[n])).\theta_{2,4}\\ &\quad+\sum_{uv\in E_{33}}x_{3,3}(L(NS_{3}[n])).\theta_{3,3}+ \sum_{uv\in E_{34}}x_{3,4}(L(NS_{3}[n])).\theta_{3,4}+\sum_{uv\in E_{44}}x_{4,4}(L(NS_{3}[n])).\theta_{4,4}\\ &=[8(2^{n})-4].\theta_{2,2}+[28(2^{n})-6].\theta_{2,3}+[4(2^{n})].\theta_{2,4}+[22(2^{n})-6].\theta_{3,3}+[12(2^{n})].\theta_{3,4}+[4(2^{n})].\theta_{4,4}\\ &=2[4(\theta_{2,2})+14(\theta_{2,3})+2(\theta_{2,4})+11(\theta_{3,3})+6(\theta_{3,4})+2(\theta_{4,4})].(2^{n})-2[2(\theta_{2,2})+3(\theta_{2,3})+3(\theta_{3,3})]. \end{aligned}\] ◻
Dendrimers are nano-sized, radially symmetric molecules with well-defined chemical structure consisting of tree-like arms or branches. The structure of dendrimer molecules begins with a central atom or group of atoms labeled as the core. From this central structure, the branches of other atoms called dendrons grow through a variety of chemical reactions. In this section, we analyze an essential chemical structure \(D_{3}[n]\) which denoted the \(n\)-th growth of star dendrimer for \(\forall\)\(n\) \(\in\) \(\mathbb{N}\) \(\cup\) \(\{0\}\). For more details on the structure of this chemical molecular graph which is quite common in drug structures see Farahani [14].
Theorem 3. The bond incident degree (BID) index of line graph of \(D_{3}[n]\) is \[TI(L(D_{3}[n]))=3[10(\theta_{2,3})+4(\theta_{3,3})+6(\theta_{3,4})+3(\theta_{4,4})](2^{n})-6[2(\theta_{2,3})+\theta_{3,3}+2(\theta_{3,4})+\theta_{4,4}],\] where \(D_{3}[n]\) is a molecular graph of the dendrimer stars having \(n\)th growth.
Proof. By observing the structure of line graph of dendrimer stars \(D_{3}[n]\), we deduce its edge partition as, \(n_{23}=30(2^{n})-12\), \(n_{33}=12(2^{n})-6\), \(n_{34}=18(2^{n})-12\) and \(n_{44}=9(2^{n})-6\). Therefore, according to the definition of bond incident degree indices, we check \[\begin{aligned} TI(L(D_{3}[n]))& =\displaystyle\sum_{2\leq a\leq b\leq 4}x_{a,b}(L(D_{3}[n])).\theta_{a,b}\\ &=\sum_{uv\in E_{23}}x_{2,3}(L(D_{3}[n])).\theta_{2,3}+\sum_{uv\in E_{33}}x_{3,3}(L(D_{3}[n])).\theta_{3,3}\\&\quad+\sum_{uv\in E_{34}}x_{3,4}(L(D_{3}[n])).\theta_{3,4}+\sum_{uv\in E_{44}}x_{4,4}(L(D_{3}[n])).\theta_{4,4}\\ &=[30(2^{n})-12].\theta_{2,3}+[12(2^{n})-6].\theta_{3,3}+[18(2^{n})-12].\theta_{3,4}+[9(2^{n})-6].\theta_{4,4}\\ &=3[10(\theta_{2,3})+4(\theta_{3,3})+6(\theta_{3,4})+3(\theta_{4,4})](2^{n})-6[2(\theta_{2,3})+\theta_{3,3}+2(\theta_{3,4})+\theta_{4,4}]. \end{aligned}\] ◻
A \(k\)-polyomino system is a finite 2-connected plane graph such that each interior face (also called cell) is surrounded by a regular \(4k\)-cycle (\(C_{4k}\)) of length one. In other words, it is an edge-connected union of cells in the planar square lattice. This polyomino system divides the plane into one infinite external region and a number of finite internal regions where all internal regions must be squares. For the origin of polyominoes and more details can be found in Klarner and Polyominoes [15], Ghorbani and Ghazi [16] and Mansour and Schork [17].
Theorem 4. The bond incident degree (BID) indices of line graph of polyomino chain of 8-cycles is: \[TI(L(G))=8[\theta_{2,2}+\theta_{2,3}+2(\theta_{3,4})+\theta_{4,4}]n+2[2(\theta_{2,2})+\theta_{3,3}-2(\theta_{3,4})-2(\theta_{4,4})].\] where \(G\) is a molecular graph of the zig-zag chain of 8-cycles and \(n\) is the number of steps.
Proof. By means of structure analysis of line graph of the zig-zag chain of 8-cycles, we infer \(n_{22}=8n+4\), \(n_{23}=8n\), \(n_{33}=2\), \(n_{34}=16n-4\) and \(n_{44}=8n-4\). Therefore, using the definition of bond incident degree indices, we obtain \[\begin{aligned} TI(L(G))& =\displaystyle\sum_{2\leq a\leq b\leq 4}x_{a,b}(L(G)).\theta_{a,b}\\ & =\sum_{uv\in E_{22}}x_{2,2}(L(G)).\theta_{2,2}+\sum_{uv\in E_{23}}x_{2,3}(L(G)).\theta_{2,3}+\\ &\sum_{uv\in E_{33}}x_{3,3}(L(G)).\theta_{3,3}+\sum_{uv\in E_{34}}x_{3,4}(L(G)).\theta_{3,4}+\sum_{uv\in E_{44}}x_{4,4}(L(G)).\theta_{4,4}\\ &=(8n+4).\theta_{2,2}+(8n).\theta_{2,3}+(2).\theta_{3,3}+(16n-4).\theta_{3,4}+(8n-4).\theta_{4,4}\\ &=8[\theta_{2,2}+\theta_{2,3}+2(\theta_{3,4})+\theta_{4,4}]n+2[2(\theta_{2,2})+\theta_{3,3}-2(\theta_{3,4})-2(\theta_{4,4}). \end{aligned}\] ◻
The benzene molecule is a usual molecule in chemistry, physics and nano-sciences and is very useful to synthesize aromatic compounds. Triangular benzenoid denoted by \(T(n)\) is a family of benzenoid molecular graphs, which is the generalization of benzene molecule \(C_{6}H_{6}\) in which benzene rings form a triangular shape. Triangular benzenoid consists of hexagons arranged in rows and in each row one hexagon increases. Details related to its structure can be found in Ghorbani and Ghazi [16].
Theorem 5. The bond incident degree (BID) indices of line graph of \(T(n)\) are
where \(T(n)\) is a molecular graph of triangular benzenoid and \(n\) represents the \(n\)-steps of its growth.
Proof. Using the edge dividing technique for the line graph of triangular benzenoid \(T(n)\), for \(n=1\), we derive \(n_{22}=6\). Hence, by means of the definition of bond incident degree indices, we get \[\begin{aligned} TI(L(T(n)))& =\displaystyle\sum_{2\leq a\leq b\leq 2}x_{a,b}(L(T(n))).\theta_{a,b}\\ &=\sum_{uv\in E_{22}}x_{2,2}(L(T(n))).\theta_{2,2}\\&=6(\theta_{2,2}). \end{aligned}\] For \(n\geq2\), we derive \(n_{22}=3\), \(n_{23}=6\), \(n_{33}=6n-9\), \(n_{34}=6n-6\) and \(n_{44}=3n^{2}-6n+3\). Similarly, by means of the definition of bond incident degree indices, we get \[\begin{aligned} TI(L(T(n)))& =\displaystyle\sum_{2\leq a\leq b\leq 4}x_{a,b}(L(T(n))).\theta_{a,b}\\ &=\sum_{uv\in E_{22}}x_{2,2}(L(T(n))).\theta_{2,2}+\sum_{uv\in E_{23}}x_{2,3}(L(T(n))).\theta_{2,3}+\sum_{uv\in E_{33}}x_{3,3}(L(T(n))).\theta_{3,3}\\ &\quad+\sum_{uv\in E_{34}}x_{3,4}(L(T(n))).\theta_{3,4}+\sum_{uv\in E_{44}}x_{4,4}(L(T(n))).\theta_{4,4}\\ &=(3).\theta_{2,2}+(6).\theta_{2,3}+(6n-9).\theta_{3,3}+(6n-6).\theta_{3,4}+(3n^{2}-6n+3).\theta_{4,4}\\ &=3(\theta_{4,4})n^{2}+6[\theta_{3,3}+\theta_{3,4}-\theta_{4,4}]n+3[\theta_{2,2}+2(\theta_{2,3})-3(\theta_{3,3})-2(\theta_{3,4})+\theta_{4,4}]. \end{aligned}\] ◻
Carbon nanotubes are allotropes of carbon with a cylindrical nanostructure. Their name is derived from their long, hollow structure. They have many structures differing in length, thickness, and number of layers. The properties of nanotubes can be different depending on how the graphene sheet has rolled up to form the tube causing it to act either metallic or as a semiconductor.
Consider the \(m\)\(\times\)\(n\) quadrilateral section \(P^{n}_{m}\) with \(m\geq2\) hexagons on the top and bottom sides and \(n\geq2\) hexagons on the lateral sides cut from the regular hexagonal lattice. See Bača et al. [18] for more details.
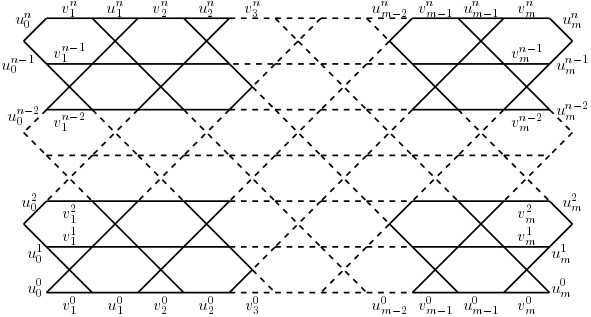
If we identify two lateral sides of \(P^{n}_{m}\) such that we identify the vertices \(u^{j}_{0}\) and \(u^{j}_{m}\) for \(j = 0, 1, 2, …, n\), then we obtain the nanotube \(NA^{n}_{m}\).
Theorem 6. The bond incident degree (BID) index of line graph of \(NA^{n}_{m}\) is \[TI(L(NA^{n}_{m}))=6(\theta_{4,4})mn+2[2(\theta_{3,3})+2(\theta_{3,4})-3(\theta_{4,4})]m,\] where \(NA^{n}_{m}\) is a molecular graph of carbon nanotube for \(m, n\geq2\).
Proof. For the line graph of tube \(NA^{n}_{m}\), we derive \(n_{33}=4m\), \(n_{34}=4m\) and \(n_{44}=6mn-6m\). Hence, by means of the definition of bond incident degree indices, we get \[\begin{aligned} TI(L(NA^{n}_{m}))& =\displaystyle\sum_{3\leq a\leq b\leq 4}x_{a,b}(L(NA^{n}_{m})).\theta_{a,b}\\ &=\sum_{uv\in E_{33}}x_{3,3}(L(NA^{n}_{m})).\theta_{3,3}+\sum_{uv\in E_{34}}x_{3,4}(L(NA^{n}_{m})).\theta_{3,4}+\sum_{uv\in E_{44}}x_{4,4}(L(NA^{n}_{m})).\theta_{4,4}\\ &=(4m).\theta_{3,3}+(4m).\theta_{3,4}+(6mn-6m).\theta_{4,4}\\ &=6(\theta_{4,4})mn+2[2(\theta_{3,3})+2(\theta_{3,4})-3(\theta_{4,4})]m. \end{aligned}\] ◻
Let \(n\) be even, \(n\geq2\), and \(m\geq2\). If we identify the top and bottom sides of the quadrilateral section \(P^{n}_{m}\) in such a way that we identify the vertices \(u^{0}_{i}\) and \(u^{n}_{i}\) for \(i = 0, 1, 2, …, m\), and the vertices \(v^{0}_{i}\) and \(v^{n}_{i}\) for \(i = 1, 2, 3, …, m\), then we obtain the carbon nanotube \(NC^{n}_{m}\).
Theorem 7. The bond incident degree (BID) indices of line graph of \(NC^{n}_{m}\) are
where \(NC^{n}_{m}\) is a molecular graph of carbon nanotube for \(n\geq2\) even and \(m\geq2\).
Proof. For \(n\geq2\) and \(n\) is even, by means of structure analysis of the line graph of tube \(NC^{n}_{m}\), we derive \(n_{23}=2n\), \(n_{34}=4n\) and \(n_{44}=6mn-7n\). Hence, by using the definition of bond incident degree indices, we get \[\begin{aligned} TI(L(NC^{n}_{m}))& =\displaystyle\sum_{2\leq a\leq b\leq 4}x_{a,b}(L(NC^{n}_{m})).\theta_{a,b}\\ &=\sum_{uv\in E_{23}}x_{2,3}(L(NC^{n}_{m})).\theta_{2,3}+\sum_{uv\in E_{34}}x_{3,4}(L(NC^{n}_{m})).\theta_{3,4}+\sum_{uv\in E_{44}}x_{4,4}(L(NC^{n}_{m})).\theta_{4,4}\\ &=(2n).\theta_{2,3}+(4n).\theta_{3,4}+(6mn-7n).\theta_{4,4}\\ &=6(\theta_{4,4})mn+[2(\theta_{2,3})+4(\theta_{3,4})-7(\theta_{4,4})]n. \end{aligned}\] For \(n\geq2\) and \(n\) is odd: By means of structure analysis of line graph of tube \(NC^{n}_{m}\), we derive \(n_{23}=2n-2\), \(n_{34}=4n+2\) and \(n_{44}=6mn-7n\). Hence, by using the definition of bond incident degree indices, we get \[\begin{aligned} TI(L(NC^{n}_{m}))& =\displaystyle\sum_{2\leq a\leq b\leq 4}x_{a,b}(L(NC^{n}_{m})).\theta_{a,b}\\ &=\sum_{uv\in E_{23}}x_{2,3}(L(NC^{n}_{m})).\theta_{2,3}+\sum_{uv\in E_{34}}x_{3,4}(L(NC^{n}_{m})).\theta_{3,4}+\sum_{uv\in E_{44}}x_{4,4}(L(NC^{n}_{m})).\theta_{4,4}\\ &=(2n-2).\theta_{2,3}+(4n+2).\theta_{3,4}+(6mn-7n).\theta_{4,4}\\ &=6(\theta_{4,4})mn+[2(\theta_{2,3})+4(\theta_{3,4})-7(\theta_{4,4})]n+2(\theta_{3,4}-\theta_{2,3}). \end{aligned}\] ◻
A benzenoid system is a connected collection of congruent regular hexagons arranged in a plane in such a way that two hexagons are either completely disjoint or have one common edge. The Circumcoronene Homologous Series of Benzenoid is a connected family of molecular graphs and has remarkable structure. This family generates from several copies of benzene \(C_{6}\). We denote the \(k\)-th terms of this series by \(H_{k}\) for \(k\geq1\). The first terms of this series are \(H_{1}\) = benzene, \(H_{2}\) = coronene, \(H_{3}\) = circumcoronene, \(H_{4}\) = circumcircumcoronene. See Farahani [19] for more structural details.
Theorem 8. The bond incident degree (BID) indices of line graph of \(H_{k}\) are
where \(H_{k}\) is a molecular graph of the circumcoronene series of benzenoid and \(k\) represents the growth of this series for \(k\geq1\).
Proof. Consider the line graph of circumcoronene series of benzenoid \(H_{k}\) for \(k\geq1\), for \(k=1\), we deduce \(n_{22}=6\). Thus, using the definition of bond incident degree indices, we infer \[\begin{aligned} TI(L(H_{k}))& =\displaystyle\sum_{2\leq a\leq b\leq 2}x_{a,b}(L(H_{k})).\theta_{a,b}\\ &=\sum_{uv\in E_{22}}x_{2,2}(L(H_{k})).\theta_{2,2}\\ &=6(\theta_{2,2}). \end{aligned}\] For \(k\geq2\), we deduce \(n_{23}=12\), \(n_{33}=12k-18\), \(n_{34}=12k-12\) and \(n_{44}=18k^{2}-36k+18\). Similarly, using the definition of bond incident degree indices, we infer \[\begin{aligned} TI(L(H_{k}))& =\displaystyle\sum_{2\leq a\leq b\leq 4}x_{a,b}(L(H_{k})).\theta_{a,b}\\ &=\sum_{uv\in E_{23}}x_{2,3}(L(H_{k})).\theta_{2,3}+\sum_{uv\in E_{33}}x_{3,3}(L(H_{k})).\theta_{3,3}\\ &\quad+\sum_{uv\in E_{34}}x_{3,4}(L(H_{k})).\theta_{3,4}+\sum_{uv\in E_{44}}x_{4,4}(L(H_{k})).\theta_{4,4}\\ &=(12).\theta_{2,3}+(12k-18).\theta_{3,3}+(12k-12).\theta_{3,4}+(18k^{2}-36k+18).\theta_{4,4}\\ &=18(\theta_{4,4})k^{2}+12[\theta_{3,3}+\theta_{3,4}-3(\theta_{4,4})]k+6[2(\theta_{2,3})-3(\theta_{3,3})-2(\theta_{3,4})+3(\theta_{4,4})]. \end{aligned}\] ◻
Capra-designed planar benzenoid has symmetric structure. Capra \(Ca\) map operation enables one to build a new structure of a planar graph \(G\). It is a method of drawing and modifying the covering of a polyhedral structure. Capra-operation of arbitrary graph \(G\) is \(Ca(G)\), iteration of Capra will be denoted by \(CaCa(G)\) (or we denote \(Ca_{2}(G)\)). By iterating the Capra-operation on the hexagon (i.e. benzene graph \(C_{6}\)) and its \(Ca\)-transforms, a benzenoid series can be designed. The first members of this series are denoted as \(Ca(C_{6})\), \(Ca_{2}(C_{6})\) and \(Ca_{3}(C_{6})\). For more details regarding to the definition of Capra-transform and the structure of capra-designed planar benzenoid series see Farahani and Vlad [20] and [21].
Theorem 9. The bond incident degree (BID) index of line graph of \(Ca_{k}(C_{6})\) is \[\begin{aligned} TI(L(Ca_{k}(C_{6})))=&6(\theta_{4,4})(7^{k})+[2(\theta_{3,3})+6(\theta_{3,4})-5(\theta_{4,4})](3^{k})+12[\theta_{2,3}\\ &-\theta_{4,4}]k^{2}+24[\theta_{4,4}-\theta_{2,3}]k+3[8(\theta_{2,3})-2(\theta_{3,4})-7(\theta_{4,4})], \end{aligned}\] where \(Ca_{k}(C_{6})\) is a molecular graph of the capra-designed planar benzenoid series and \(k\) represents the number of steps of this series.
Proof. By analyzing the molecular structure of line graph of \(Ca_{k}(C_{6})\), we check that the edge set of line graph of \(Ca_{k}(C_{6})\) can be divided into four partitions, \(n_{23}=12(k^{2}-2k+2)\), \(n_{33}=2(3^{k})\), \(n_{34}=6(3^{k})-6\) and \(n_{44}=6(7^{k})-5(3^{k})-12k^{2}+24k-21\). Thus, using the definition of bond incident degree indices, we infer \[\begin{aligned} TI(L(Ca_{k}(C_{6})))& =\displaystyle\sum_{2\leq a\leq b\leq 4}x_{a,b}(L(Ca_{k}(C_{6}))).\theta_{a,b}\\ & =\sum_{uv\in E_{23}}x_{2,3}(L(Ca_{k}(C_{6}))).\theta_{2,3}+\sum_{uv\in E_{33}}x_{3,3}(L(Ca_{k}(C_{6}))).\theta_{3,3}\\ &\quad+\sum_{uv\in E_{34}}x_{3,4}(L(Ca_{k}(C_{6}))).\theta_{3,4}+\sum_{uv\in E_{44}}x_{4,4}(L(Ca_{k}(C_{6}))).\theta_{4,4}\\&=[12(k^{2}-2k+2)].\theta_{2,3}+[2(3^{k})].\theta_{3,3}+[6(3^{k})-6].\theta_{3,4}+[6(7^{k})\\ &\quad-5(3^{k})-12k^{2}+24k-21].\theta_{4,4}\\ &=6(\theta_{4,4})(7^{k})+[2(\theta_{3,3})+6(\theta_{3,4})-5(\theta_{4,4})](3^{k})+12[\theta_{2,3}-\theta_{4,4}]k^{2}+24[\theta_{4,4}-\theta_{2,3}]k\\ &\quad+3[8(\theta_{2,3})-2(\theta_{3,4})-7(\theta_{4,4})]. \end{aligned}\] ◻
Let’s consider \(\{G_{i}\}^{d}_{i=1}\) be a set of finite pairwise disjoint molecular graphs with \(v_{i}\) \(\in\) \(V(G_{i})\). The bridge molecular graph \(B(G_{1},…,G_{d}) = B(G_{1},…,G_{d};\) \(v_{1},…,v_{d})\) of \(\{G_{i}\}^{d}_{i=1}\) with regard to the vertices \(\{v_{i}\}^{d}_{i=1}\) is acquired from the molecular graphs \(G_{1},…,G_{d}\) in which the vertices \(v_{i}\) and \(v_{i+1}\) are attached through an edge from \(i = 1, 2, …, d-1\). In this section we determine the formulas of some degree based indices for the line graphs of infinite family of drug structures of the bridge molecular graph with \(G_{1},…,G_{d}\). Then we determine \(L(G_{d}(H,v)) = L(B(H,…,H,v,…,v))\) for special situations of the bridge molecular graphs.
We analyze the line graphs of bridge molecular graphs as follows and the main parts of the graphs are path, cycle and complete molecular graph, respectively. See Gao et al. [11] and [22] for more structural details.
Theorem 10. The bond incident degree (BID) indices of line graph of \(G_{d}(P_{n},v)\) are
where \(G_{d}(P_{n},v)\) is a bridge molecular graph of path graph \(P_{n}\) with \(n\) vertices.
We can prove this theorem in the similar way by using the definition of bond incident degree indices. The edge counting of the molecular structure of the line graph of bridge molecular graph \(G_{d}(P_{n},v)\) of path graph \(P_{n}\) with \(n\) vertices is,
For \(n\geq2\) and \(d=2\), we infer \(n_{12}=2\) and \(n_{22}=2n-4\).
For \(n=2\) and \(d=3\), we infer \(n_{13}=2\), \(n_{23}=2\) and \(n_{33}=1\).
For \(n=2\) and \(d\geq4\), we infer \(n_{13}=n_{23}=n_{34}=2\), \(n_{24}=2d-6\) and \(n_{44}=d-4\).
For \(n=3\) and \(d=3\), we infer \(n_{12}=2\), \(n_{13}=1\), \(n_{23}=2\) and \(n_{33}=3\).
For \(n=3\) and \(d\geq4\), we infer \(n_{12}=2\), \(n_{13}=d-2\), \(n_{23}=2\), \(n_{33}=2\), \(n_{34}=2d-4\) and \(n_{44}=d-4\).
For \(n\geq4\) and \(d=3\), we infer \(n_{12}=3\), \(n_{22}=3n-10\), \(n_{23}=3\) and \(n_{33}=3\).
For \(n\geq4\) and \(=4\), we infer \(n_{12}=4\), \(n_{22}=4n-14\), \(n_{23}=4\), \(n_{33}=2\) and \(n_{34}=4\).
For \(n\geq4\) and \(d\geq5\), we infer \(n_{12}=n_{23}=d\), \(n_{22}=dn-4d+2\), \(n_{33}=2\), \(n_{34}=2d-4\) and \(n_{44}=d-4\).
Theorem 11. The bond incident degree (BID) indices of line graph of \(G_{d}(C_{n},v)\) are
where \(G_{d}(C_{n},v)\) is a bridge molecular graph of cyclic graph \(C_{n}\) with \(n\) vertices.
We can prove this theorem in the similar way by using the definition of bond incident degree indices. The edge counting of the molecular structure of the line graph of bridge molecular graph \(G_{d}(C_{n},v)\) of cyclic graph \(C_{n}\) with \(n\) vertices is,
For \(n\geq3\) and \(d=2\), we infer \(n_{22}=2n-6\), \(n_{23}=4\), \(n_{33}=2\) and \(n_{34}=4\).
For \(n\geq3\) and \(d=3\), we infer \(n_{22}=3n-9\), \(n_{23}=4\), \(n_{24}=2\), \(n_{33}=2\), \(n_{35}=4\), \(n_{44}=1\), \(n_{45}=4\) and \(n_{55}=1\).
For \(n\geq3\) and \(d=4\), we infer \(n_{22}=4n-12\), \(n_{23}=n_{24}=n_{35}=n_{45}=n_{46}=4\) and \(n_{33}=n_{44}=n_{56}=2\).
For \(n\geq3\) and \(d\geq5\), we infer \(n_{22}=dn-3d\), \(n_{23}=n_{35}=n_{45}=4\), \(n_{24}=2d-4\), \(n_{33}=n_{56}=2\), \(n_{44}=d-2\), \(n_{46}=4d-12\) and \(n_{66}=d-4\).
Theorem 12. The bond incident degree (BID) indices of line graph of \(G_{d}(K_{n},v)\) are
where \(G_{d}(K_{n},v)\) is a bridge molecular graph of complete graph \(K_{n}\) with \(n\) vertices.
Theorem 13. The bond incident degree (BID) index of line graph of \(G_{d}(K_{n},v)\) is for \(n\geq4\) and \(d=3\) is \(TI(L(G_{d}(K_{n},v)))=9\left[2n-8+2^{(n-4)}\right] \theta_{(2n-4),(2n-4)}+4\left[2^{(n-3)}+ 2^{(\frac{n^{2}-7n+12}{2})}\right].\theta_{(2n-4),(2n-3)}+2\left[2^{(n-3)}+ 2^{(\frac{n^{2}-7n+12}{2})}\right].\theta_{(2n-4),(2n-2)}+\left[n^{3}-3n^{2}-10n+ 48-3\{2^{(n-3)}\}-2^{(n-1)}-4\left\{2^{(\frac{n^{2}-7n+12}{2})}\right\}\right]. \theta_{(2n-3),(2n-3)}+(2n-2).\theta_{(2n-3),(2n-1)}+\left[\frac{1}{2}n^{3}- \frac{3}{2}n^{2}-5n+24-9\{2^{(n-4)}\}-3\{2^{(n-3)}\}+2^{(n-1)}- 2\left\{2^{(\frac{n^{2}-7n+12}{2})}\right\}\right].\theta_{(2n-2),(2n-2)}+(2n-2).\theta_{(2n-2),(2n-1)}+ \theta_{(2n-1),(2n-1)},\) where \(G_{d}(K_{n},v)\) is a bridge molecular graph of complete graph \(K_{n}\) with \(n\) vertices.
\(\blacksquare\)
Theorem 14. The bond incident degree (BID) index of line graph of \(G_{d}(K_{n},v)\) is for \(n\geq4\) and \(d\geq4\,\) is \(TI(L(G_{d}(K_{n},v)))=3d\left[2n-8+2^{(n-4)}\right]. \theta_{(2n-4),(2n-4)}+4\left[2^{(n-3)}+ 2^{(\frac{n^{2}-7n+12}{2})}\right].\theta_{(2n-4),(2n-3)}+2(d-2)\left[2^{(n-3)}+2^{(\frac{n^{2}-7n+12}{2})}\right].\theta_{(2n-4),(2n-2)}+\left[n^{3}-3n^{2}-10n+ 48-3\{2^{(n-3)}\}-2^{(n-1)}-4\left\{2^{(\frac{n^{2}-7n+12}{2})}\right\}\right].\theta_{(2n-3),(2n-3)}+(2n-2).\theta_{(2n-3),(2n-1)}+(d-2)\left[\frac{1}{2}n^{3}-\frac{3}{2}n^{2}-5n+24-9\{2^{(n-4)}\}- 3\{2^{(n-3)}\}+2^{(n-1)}-2\left\{2^{(\frac{n^{2}-7n+12}{2})}\right\}\right]. \theta_{(2n-2),(2n-2)}+(2n-2).\theta_{(2n-2),(2n-1)}+2(dn-d-3n+3).\theta_{(2n-2)(2n)}+(2).\theta_{(2n-1),(2n)}+(d-4).\theta_{(2n)(2n)}\), where \(G_{d}(K_{n},v)\) is a bridge molecular graph of complete graph \(K_{n}\) with \(n\) vertices.
We can prove these theorems in the similar way by using the definition of bond incident degree indices. The edge counting of the molecular structure of the line graph of bridge molecular graph \(G_{d}(K_{n},v)\) of complete graph \(K_{n}\) with \(n\) vertices is
For \(n=2\) and \(d\geq2\), we infer \(n_{12}=2\) and \(n_{22}=2d-4\).
For \(n=3\) and \(d=2\), we infer \(n_{23}=4\), \(n_{33}=2\) and \(n_{34}=4\).
For \(n=3\) and \(d=3\), we infer \(n_{23}=n_{35}=n_{45}=4\), \(n_{24}=n_{33}=2\) and \(n_{44}=n_{55}=1\).
For \(n\geq4\) and \(d=2\), we infer \(n_{(2n-4)(2n-4)}=6\left[2n-8+2^{(n-4)}\right]\), \(n_{(2n-4)(2n-3)}=4\left[2^{(n-3)}+2^{(\frac{n^{2}-7n+12}{2})}\right]\), \(n_{(2n-3)(2n-3)}=n^{3}-3n^{2}-10n+48-3\left\{2^{(n-3)}\right\}-2^{(n-1)}-4\left\{2^{(\frac{n^{2}-7n+12}{2})}\right\}\) and \(n_{(2n-3)(2n-2)}=2n-2\).
For \(n\geq4\) and \(d=3\), we infer \(n_{(2n-4)(2n-4)}=9\left[2n-8+2^{(n-4)}\right]\), \(n_{(2n-4)(2n-3)}=4\left[2^{(n-3)}+2^{(\frac{n^{2}-7n+12}{2})}\right]\), \(n_{(2n-4)(2n-2)}=2\left[2^{(n-3)}+2^{(\frac{n^{2}-7n+12}{2})}\right]\), \(n_{(2n-3)(2n-3)}=n^{3}-3n^{2}-10n+48-3\left\{2^{(n-3)}\right\}-2^{(n-1)}-4\left\{2^{(\frac{n^{2}-7n+12}{2})}\right\}\), \(n_{(2n-3)(2n-1)}=2n-2\), \(n_{(2n-2)(2n-2)}=\frac{1}{2}n^{3}-\frac{3}{2}n^{2}-5n+24-9\left\{2^{(n-4)}\right\}-3\left\{2^{(n-3)}\right\}+2^{(n-1)}-2\left\{2^{(\frac{n^{2}-7n+12}{2})}\right\}\), \(n_{(2n-2)(2n-1)}=2n-2\) and \(n_{(2n-1)(2n-1)}=1\).
For \(n\geq4\) and \(d\geq4\), we infer \(n_{(2n-4)(2n-4)}=3d\left[2n-8+2^{(n-4)}\right]\), \(n_{(2n-4)(2n-3)}=4\left[2^{(n-3)}+2^{(\frac{n^{2}-7n+12}{2})}\right]\), \(n_{(2n-4)(2n-2)}=2(d-2)\left[2^{(n-3)}+2^{(\frac{n^{2}-7n+12}{2})}\right]\), \(n_{(2n-3)(2n-3)}=n^{3}-3n^{2}-10n+48-3\left\{2^{(n-3)}\right\}-2^{(n-1)}-4\left\{2^{(\frac{n^{2}-7n+12}{2})}\right\}\), \(n_{(2n-3)(2n-1)}=2n-2\), \(n_{(2n-2)(2n-2)}=(d-2)\frac{1}{2}n^{3}-\frac{3}{2}n^{2}-5n+24-9\left\{2^{(n-4)}\right\}-3\left\{2^{(n-3)}\right\}+2^{(n-1)}-2\left\{2^{(\frac{n^{2}-7n+12}{2})}\right\}\), \(n_{(2n-2)(2n-1)}=2n-2\), \(n_{(2n-2)(2n)}=2(dn-d-3n+3)\), \(n_{(2n-1)(2n)}=2\) and \(n_{(2n)(2n)}=d-4\).
We live in an age in which technology is moving at a rapid pace, creating new fields and disrupting existing models and processes. Numerous studies discovered that a large number of new diseases are originated in the world every year, which are caused by contentiously emerging viruses at a high speed. Some of these viruses are such harmful that they can even cause several deaths. Recent endeavors in field of molecular topology shed light on unprecedented use of topological indices in rectifying the viral diseases that is valuable for pharmaceutical and medical scientists to comprehend the biological and chemical characteristics of new drugs. The method of computing bond incident degree (BID) indices is very suitable and serviceable for developing countries in which they can obtain the medical and biological information of new drugs without chemical experiment conditions. In this paper, we established the bond incident degree indices of line graphs of some molecular graphs of drug structures, in terms of vertex dividing technique with respect to their degrees and drug structure analysis. These results can be utilized by many scientists to theoretically identify the chemical characteristics of the drug molecular structures, which illustrate the promising prospects of the applications for pharmaceutical engineering.
The authors are indebted to the referee for his/her useful suggestions critical comments.
The authors declare no conflict of interests.
1970-2025 CP (Manitoba, Canada) unless otherwise stated.