In this paper, we investigate the \((d,1)\)-total labelling of generalized Petersen graphs \(P(n,k)\) for \(d\geq 3\). We find that the \((d,1)\)-total number of \(P(n,k)\) with \(d\geq 3\) is \(d+3\) for even \(n\) and odd \(k\) or even \(n\) and \(k=\frac{n}{2}\), and \(d+4\) for all other cases.
We consider only finite undirected graphs without loops or multiple edges. Let \(G=(V(G),E(G))\) be a graph with vertex set \(V(G)\) and edge set \(E(G)\). A \((d, 1)\)-total labelling of a graph \(G\) is an assignment of integers to \(V(G)\cup E(G)\) such that:
any two adjacent vertices of \(G\) receive distinct integers,
any two adjacent edges of \(G\) receive distinct integers, and
a vertex and its incident edge receive the integers that differ by at least \(d\) in absolute value.
The span of a \((d, 1)\)-total labelling is the maximum difference between two labels. The minimum span of labels required for such a \((d, 1)\)-total labelling of \(G\) is called the \((d, 1)\)-total number and is denoted by \(\lambda^{\small{\mbox{T}}}_{d}(G)\). It reduces to the traditional total coloring when d is taken as 1.
The notion of \((d, 1)\)-total labelling of a graph \(G\) was first introduced by Havet and Yu [1, 2]. They conjectured that \(\lambda^{\small{\mbox{T}}}_{d}(G)\leq \Delta(G)+2d – 1\) for every graph \(G\) [1, 2], where \(\Delta(G)\) is the maximum degree of \(G\). The validity of conjecture has been verified for complete graphs [3, 4], complete bipartite graphs [5], planar graphs [6, 7, 8, 9, 10, 11] and graphs with a given maximum average degree [12]. The exact values of \(\lambda^{\small{\mbox{T}}}_{d}(G)\) were determined for some graphs, such as \((d,1)\)-total labelings of flower snarks and quasi flower snarks [13] and the (2,1)-total number of joins of paths and cycles [14].
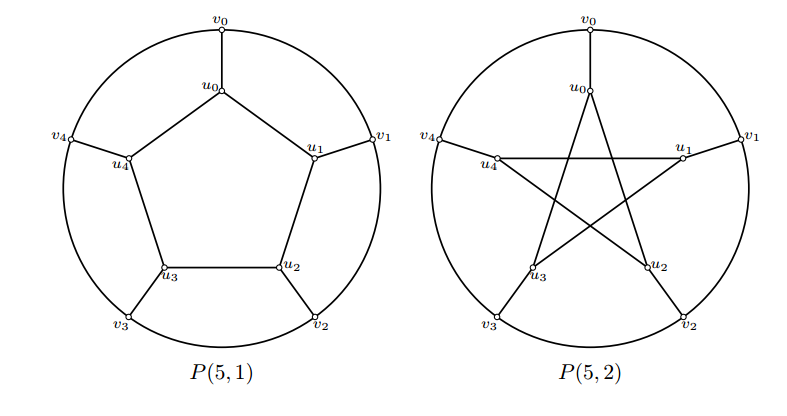
A well-known class of graphs is the generalized Petersen graphs \(P(n,k)\). By definnition [15], \(P(n,k)\) is a graph on \(2n\) \((n\geq 3)\) vertices with \(V(P(n,k))\) = \(\{u_i,v_{i}:0 \leq i \leq n-1\}\) and \(E(P(n,k)) = \{u_{i}u_{i+k},u_{i}v_{i},v_iv_{i+1}:0 \leq i \leq n-1\}\), where subscripts are to be read modulo \(n\) and \(1\leq k \leq n-1\). For example, \(P(5,1)\) and \(P(5,2)\) are shown in Figure 1.
A number of articles has been devoted to the study of the labeling and coloring of \(P(n,k)\), in particular, to the study of L(2,1)-labeling and total coloring [16, 17, 18, 19, 20, 21]. However, the \((d,1)\)-total labeling of generalized Petersen graphs still remains open. To fill the gap, in this paper, we study the \((d,1)\)-total numbers of generalized Petersen graphs. We aim to determine the \((d,1)\)-total numbers of \(P(n,k)\) for \(d\geq 3\). This paper is organized as follows. We first prove that the \((d,1)\)-total number of \(P(n,k)\) for \(k=\frac{n}{2}\) is \(d+3\) in Section 2, and we then discuss the \((d,1)\)-total number of \(P(n,k)\) for \(k\neq \frac{n}{2}\) in Section 3.
For a graph \(G\) with \(\Delta(G) \leq d\), there is always \(\lambda^{\mbox{T}}_{d}(G)\geq d+\Delta(G)\) [4]. Since \(\Delta(P(n,k))=3\), we have Lemma 1.
Lemma 1. \(\lambda^{\mbox{T}}_{d}(P(n,k))\geq d+3\) for \(d\geq 3\).
To obtain the exact value of \(\lambda^{\mbox{T}}_{d}(P(n,k))\), we prove Lemma 2.
Lemma 2. \(\lambda^{\mbox{T}}_{d}(P(n,k))\leq d+3\) if \(k=\frac{n}{2}\).
Proof. We use \(f\) to represent the assignment of integers to \(V(G)\cup E(G)\). In the case of \(k=\frac{n}{2}\), we can define the assignment as follows, \[\begin{array}{llll} f(u_i)=\left\{\begin{array}{lll} \frac{1+(-1)^{i}}{2},& 0\leq i\leq \frac{n}{2}-1,\hspace{220pt} \\ {-1pt} 2,& \frac{n}{2}\leq i\leq n-1.\\ \end{array}\right.\\ f(u_{i}u_{i+k})=d+2, \hspace{4pt}0\leq i\leq \frac{n}{2}-1.\\ f(u_{i}v_{i})=d+3, \hspace{4pt} 0\leq i\leq n-1.\\ f(v_i)=\frac{1-(-1)^{i}}{2},\hspace{4pt} 0\leq i\leq n-1.\\ f(v_iv_{i+1})=d+1+\frac{1-(-1)^{i}}{2}, \hspace{4pt}0\leq i\leq n-1. \end{array}\]
Clearly, the assignment \(f\), defined above, gives a \((d,1)\)-total labelling. Indeed, it is easy to verify that \(f\) fulfills all the three conditions, i.e.,
any two adjacent vertices receive distinct integers,
any two adjacent edges receive distinct integers, and
a vertex and its incident edge receive the integers that differ by at least \(d\).
We then have \(\lambda^{\mbox{T}}_{d}(P(n,k))\leq d+3\) for \(k=\frac{n}{2}\). This completes the proof of Lemma 2.
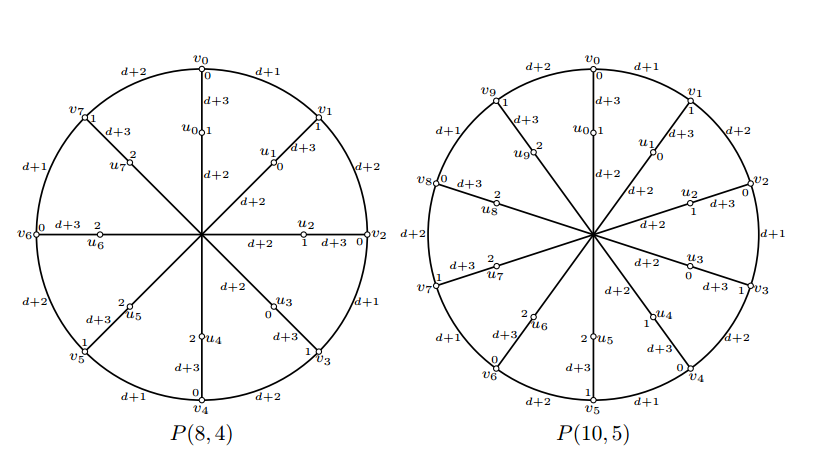
Figure 2 shows (d,1)-total labelings of \(P(8,4)\mbox{ and } P(10,5)\).
Lemma 2 determines the upper bound of \(\lambda^{\mbox{T}}_{d}(P(n,k))\) for \(k=\frac{n}{2}\) while Lemma 1 gives the lower bound of \(\lambda^{\mbox{T}}_{d}(P(n,k))\). Hence, we have Theorem 1.
Theorem 1. \(\lambda^{\mbox{T}}_{d}(P(n,k))= d+3\) for \(d\geq 3\) if \(k=\frac{n}{2}\).
Since \(P(n,k)\cong P(n,n-k)\), we need only to consider the labeling of \(P(n,k)\) for \(1\leq k<\frac{n}{2}\). Therefore, we assume \(1\leq k<\frac{n}{2}\) in the following discussion.
We first consider \(P(n,k)\) for even \(n\) and odd \(k\). In this case, \(P(n,k)\) is \(3\)-regular bipartite graphs, and by borrowing the result obtained in Ref. [4], which indicates that \(\lambda^{\mbox{T}}_{d}(G)=d+r\) if \(G\) is an \(r\)-regular bipartite graph, we immediately obtain the \((d,1)\)-total number of \(P(n,k)\) for even \(n\) and odd \(k\). We state it as Theorem 2.
Theorem 2. \(\lambda^{T}_{d}(P(n,k))\) = \(d+3\) if \(n\) is even and \(k\) is odd.
We now consider \(P(n,k)\) for odd \(n\) or even \(n\) and even \(k\) (\(k\neq \frac{n}{2}\)). In this case, \(P(n,k)\) is \(3\)-regular nonbipartite graph, and by borrowing the result obtained in Ref. [13], which indicates \(\lambda^{\mbox{T}}_{d}(G) \geq d + r +1\) if \(G\) is an \(r\)-regular nonbipartite graph and \(d\geq r\geq 3\), we have Lemma 3.
Lemma3. \(\lambda^{\mbox{T}}_{d}(P(n,k))\geq d+4\) for \(d\geq 3\) if \(n\) is odd or both \(n\) and \(k\) are even (\(k\neq \frac{n}{2}\)).
To determine the exact value of \(\lambda^{\mbox{T}}_{d}(P(n,k))\), we prove the following lemma.
Lemma 4. \(\lambda^{\mbox{T}}_{d}(P(n,k))\leq d+4\) if \(n\) is odd or both \(n\) and \(k\) are even.
Proof. Let \(g=\gcd(n,k)\) and \(l=n/g\). We refer to cycle \(u_{i}u_{i+k}u_{i+2k}\cdots\) \(u_{i+(l-1)k}u_{i}\) \((0\leq i\leq g-1)\) as an inner cycle, cycle \(v_{0}v_{1}\cdots v_{n-1}v_{0}\) as an outer cycle, and \(u_iv_{i}\) \((0\leq i\leq n-1)\) as a spoke. Obviously, \(P(n,k)\) contains \(g\) non-intersecting inner cycles with length \(l\). With these notions, we can divide our proof of Lemma 4 into the following two cases.
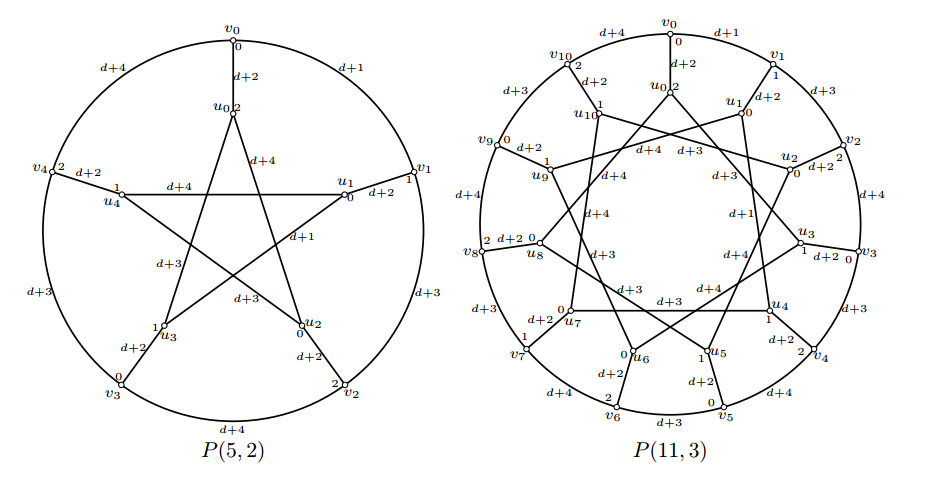
Case 1. \(g=1\). In this case, \(l\) and \(n\) are odd. It follows that both the inner cycle and the outer cycle are odd cycles. We define the assignment \(f\) as follows, \[\begin{array}{llll} f(u_{ik})=\left\{\begin{array}{lll} {-1pt} 2, & i=0,\\ {-1pt} \frac{1-(-1)^{i+j}}{2},& 1\leq i,j\leq n-1\mbox{ and } j\mbox{ is~defined~by }jk\mbox{ (mod~n)}=1. \hspace{14pt}\\ %{-1pt} \frac{1+(-1)^{j}}{2},& 1\leq i,j\leq n-1\mbox{ and } i \mbox{ (mod } 2)=1 \mbox{ where }jk \mbox{ (mod } n)=1.\\ \end{array}\right.\\ f(u_{1+ik}u_{1+(i+1)k})=\left\{\begin{array}{lll} {-1pt} d+1,& i=0,\\ {-1pt} d+3+\frac{1+(-1)^{i}}{2},& 1\leq i\leq n-1.\hspace{400pt} \\ \end{array}\right.\\ f(u_{i}v_{i})=d+2, \hspace{4pt} 0\leq i\leq n-1.\\ f(v_i)=\left\{\begin{array}{lll} {-1pt} \frac{1-(-1)^{i}}{2},& 0\leq i\leq1,\\ {-1pt} 2,& 2\leq i\leq n-1\mbox{ and } i \mbox{ (mod } 2)=0,\\ {-1pt} 1-f(u_i),& 2\leq i\leq n-2\mbox{ and } i \mbox{ (mod } 2)=1.\hspace{400pt} \\ \end{array}\right.\\ f(v_iv_{i+1})=\left\{\begin{array}{lll} {-1pt} d+1,& i=0,\\ {-1pt} d+3+\frac{1+(-1)^{i}}{2},& 1\leq i\leq n-1.\hspace{400pt} \\ \end{array}\right.\\ \end{array}\] Figure 3 shows (d,1)-total labelings of \(P(5,2) \mbox{ and } P(11,3)\).
Case 2. \(g\geq2\). We further divide this case into the following two subcases.
Case 2.1. \(l\) is even. In this case, \(n\) must be even. It follows that both the outer cycle and the inner cycles are even cycles. We define the assignment \(f\) as follows, \[\begin{array}{llll} f(u_{ik+j})=\frac{1-(-1)^{i}}{2}, \hspace{7pt} 0\leq i\leq l-1,\mbox{ }0\leq j\leq g-1.\\ f(u_{ik+j}u_{(i+1)k+j})=d+3+ \frac{1-(-1)^{i}}{2}, \hspace{7pt} 0\leq i\leq l-1,\mbox{ }0\leq j\leq g-1.\\ f(u_{i}v_{i})=d+2,\hspace{7pt} 0\leq i\leq n-1.\\ f(v_i)=\left\{\begin{array}{lll} {-1pt} f(u_{n-1}),& i=0,\\ {-1pt}\min(\{0,1,2\}-\{ f(v_{i-1}),f(u_i)\}),& 1\leq i\leq n-1.\hspace{400pt} \\ \end{array}\right.\\ f(v_iv_{i+1})=d+3+\frac{1-(-1)^{i}}{2}, 0\leq i\leq n-1.\\ \end{array}\]
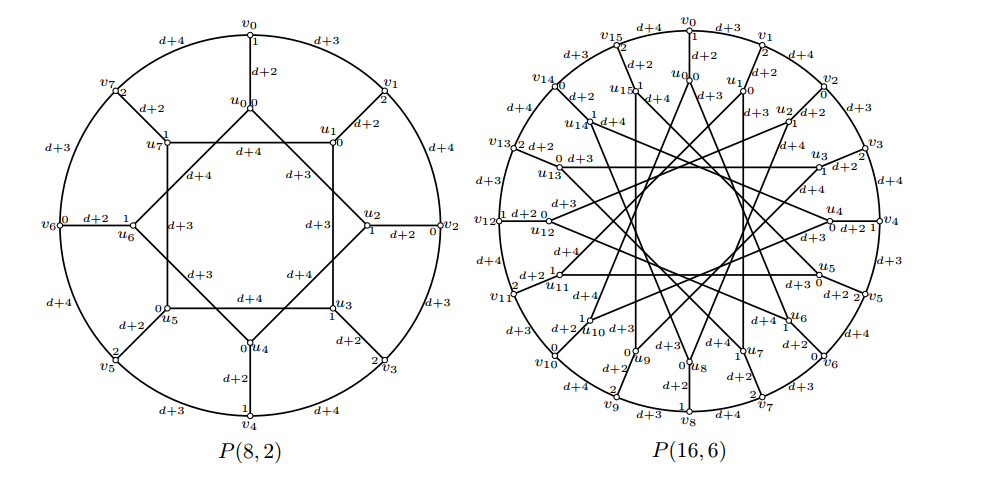
Figure 4 shows (d,1)-total labelings of \(P(8,2) \mbox{ and } P(16,6)\).
Case 2.2. \(l\) is odd. In this case, the inner cycles are odd cycles. We define the assignment \(f\) as follows, \[\begin{array}{llll} f(u_{ik+j})=\left\{\begin{array}{lll} {-1pt} 2,& i=0, \mbox{ }0\leq j\leq g-1,\\ {-1pt} \frac{1+(-1)^{i}}{2},& 1\leq i\leq l-1,\mbox{ }0\leq j\leq g-1.\hspace{400pt} \\ \end{array}\right.\\ f(u_{(1+i)k+j}u_{(1+i+1)k+j})=\left\{\begin{array}{lll} {-1pt} d+1,& i=0,\mbox{ }0\leq j\leq g-1,\\ {-1pt} d+3+ \frac{1+(-1)^{i}}{2},& 1\leq i\leq l-1,\mbox{ }0\leq j\leq g-1.\hspace{400pt} \\ \end{array}\right.\\ f(u_{i}v_{i})=d+2, \hspace{4pt} 0\leq i\leq n-1.\\ f(v_i)=\left\{\begin{array}{lll} {-1pt} f(u_{n-1}),& i=0,\\ {-1pt}\min(\{0,1,2\}-\{ f(v_{i-1}),f(u_i)\}),& 1\leq i\leq n-1.\hspace{400pt} \\ \end{array}\right.\\ f(v_iv_{i+1})=\left\{\begin{array}{lll} d+2+(-1)^{n},& \hspace{4pt} i=0 ,\\ {0pt} d+3+\frac{1-(-1)^{i+n}}{2},&\hspace{4pt} 1\leq i\leq n-1.\\ \end{array}\right.\\ \end{array}\] Figure 5 shows (d,1)-total labelings of \(P(9,3)\) and \(P(10,4)\).
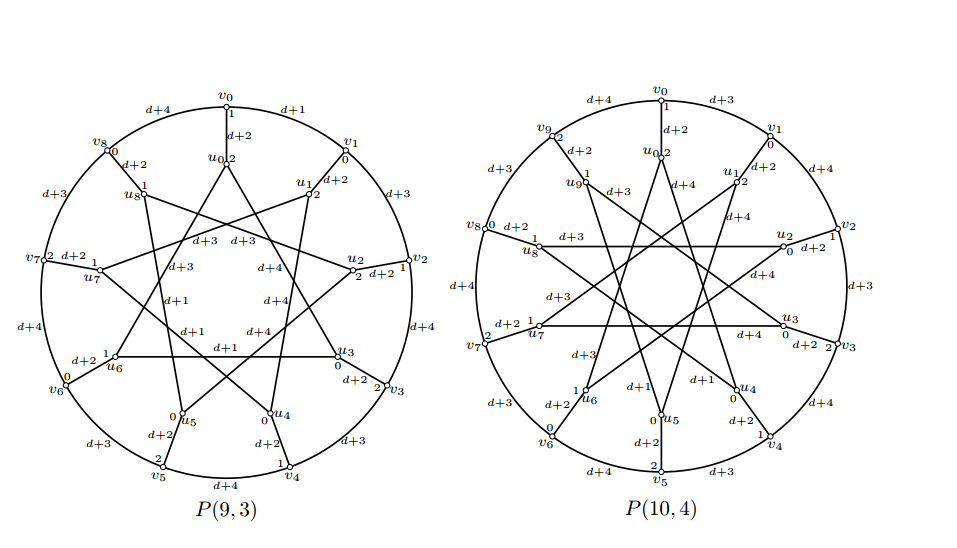
It is obvious that in the above labeling scheme, any two adjacent edges receive distinct integers, and each vertex and its incident edges receive the integers that differ by at least \(d\). Besides, it is also obvious that any two adjacent vertices of inner cycles receive distinct integers. To complete our proof, we need further to verify that each vertex of outer cycle and its adjacent vertices receive distinct integers. We examine the labeling in each case. In case 1, according to the assignment of \(f(u_{ik})\) and \(f(v_i)\), we can easily find that \(f(v_i)\neq f(v_{i+1})\) for \(0\leq i\leq n-1\) and \(f(v_i)\neq f(u_i)\) for \(i=0\) and \(2\leq i\leq n-1\). Furthermore, since \(jk\) (mod \(n\))=1 and \(ik\) (mod \(n\))=1 for \(f(u_1)\), we have \(f(u_1)=0 \neq f(v_1)\). In case 2, since \(f(v_i)=\min(\{0,1,2\}-\{f(v_{i-1}),f(u_i)\})\) for \(1\leq i\leq n-1\), we then have \(f(v_{i})\neq f(v_{i-1})\) and \(f(v_{i})\neq f(u_{i})\) for \(1\leq i\leq n-1\). Furthermore, since \(f(v_0)= f(u_{n-1})\), we have \(f(v_{n-1})\neq f(v_0)\) and \(f(v_0)=1\neq f(u_0)\). That is, our labeling scheme presented above fulfills all the three conditions (i) (ii) and (iii), being a \((d,1)\)-total labeling. This concludes the proof of Lemma 4. ◻
By Lemmas 3 and 4, we have Theorem 3.
Theorem 3. \(\lambda^{\mbox{T}}_{d}(P(n,k))= d+4\) for \(d\geq 3\) if \(n\) is odd or both \(n\) and \(k\) are even (\(k\neq \frac{n}{2}\)).
In summary, we have presented a \((d,1)\)-total labelling of generalized Petersen graphs \(P(n,k)\) for \(d\geq 3\), and given the exact values of \(\lambda^{\mbox{T}}_{d}(P(n,k))\). By combing Theorems 1, 2 and 3, we have the following conclusion.
The \((d,1)\)-total number of \(P(n,k)\) with \(d\geq 3\) is \(d+3\) for even \(n\) and odd \(k\) or even \(n\) and \(k=\frac{n}{2}\), and \(d+4\) for all other cases.
This work was supported by Chinese Natural Science Foundation NO. 61562066 and Shandong Province Higher Educational Science and Technology Project NO. J17KA073
The authors declares no conflict of interests.
1970-2025 CP (Manitoba, Canada) unless otherwise stated.