Coded caching technology can better alleviate network traffic congestion. Since many of the centralized coded caching schemes now in use have high subpacketization, which makes scheme implementation more challenging, coded caching schemes with low subpacketization offer a wider range of practical applications. It has been demonstrated that the coded caching scheme can be achieved by creating a combinatorial structure named placement delivery array (PDA). In this work, we employ vector space over a finite field to obtain a class of PDA, calculate its parameters, and consequently achieve a coded caching scheme with low subpacketization. Subsequently, we acquire a new MN scheme and compare it with the new scheme developed in this study. The subpacketization \(F\) of the new scheme has significant advantages. Lastly, the number of users \(K\), cache fraction \(\frac{M}{N}\), and subpacketization \(F\) have advantages to some extent at the expense of partial transmission rate \(R\) when compared to the coded caching scheme in other articles.
As mobile networks continue to develop, the rapid growth in users and their rising need for video content has a compounding effect on data traffic during peak hours [1], which causes network congestion. Simultaneously, caching serves as an effective tool to alleviate traffic congestion. Caching technology consists of two phases: placement and delivery [2]. During the placement phase, users cache a part of contents from the server. In the delivery phase, upon receiving all user’s requests, the server transmits signals enabling users to retrieve requested files using these signals along with cached contents.
Previous research concentrated on either content placement or delivery design. In [2], Maddah-Ali and Niesen first proposed the need for the joint design of placement and delivery phases in a caching system. Compared to conventional uncoded caching schemes, significant gains can be obtained by coding in the delivery phase. There are several recent works on coded caching schemes [3-10].
Yan et al. [11] proposed a new structure to characterize the caching system, i.e., Placement Delivery Array(PDA). Based on a PDA of size \(F\times K\), the caching scheme can support \(K\) users by dividing each file into \(F\) equal packets. This work uses PDA structures to identify coded caching schemes. Yan et al. [12] proved PDA is equivalent to the set of color classes of an \(S\)–\(strong\)–\(edge\)–\(coloring\) of a bipartite graph and through ideas of coloring construct two types of PDA. A caching scheme based on grouping users, through sacrificing part of the transmission rate, attained lower subpacketization than the MN scheme [13]. In [14], Shang-guan, Zhang, and Ge discerned an important connection between PDAs and 3-uniform, 3-partite hypergraphs with the \((6,3)\)-free property as well as constructed PDAs for which \(F\) increases subexponentially with \(K\). In [3], constructing two new coded caching schemes, using the bipartite graph framework and utilizing some basic ideas from the projective geometries over finite fields. It is worth noting that all current deterministic centralized coding caching schemes can be represented as PDAs.
In this paper, we construct a PDA via vector space over finite field, then we obtain a new coded caching scheme with low subpacketization. Through asymptotic analysis, we find that the subpacketization in our new scheme increases sub-exponentially with the growth in the number of users. Via numerical comparisons, it is evident that our new scheme has advantages on the number of users \(K\) and subpacketization \(F\).
\(\bullet\) Calligraphic capital letters are used to represent sets, such as \(\cal A\).
\(\bullet\) For a positive integer \(a\), the set \(\{0, 1,\dots, a-1\}\) is denoted as \([0,a)\).
\(\bullet\) Binomial coefficients are denoted by \(\binom{n}{k}\) where \(\binom{n}{k}=\frac{n!}{k!(n-k)!}\), and \(\binom{n}{k}=0\) for \(n<k\).
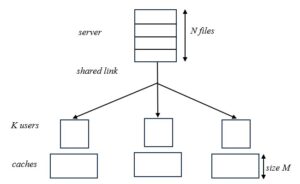
Let us consider a caching system as illustrated in figure 1. The caching system consisting of one server containing \(N\) files \(\cal W\) = \(\{W_i:i\in[0,N)\}\) and \(K\) users \(\cal K\)=\([0,K)\). The server is connected to the users through a shared error-free link. The files in \(\cal W\) are of equal size, we assume each file is of unit size. Additionally, each user has a cache of size \(M\) units.
An \(F\)–\((K, M, N)\) coded caching scheme operates in two phases [2]:
1) Placement Phase: A file is subdivided into \(F\) equal packets (we will often refer to \(F\) as the subpacketization), i.e., \(W_i\) = \(\{W_{i,j}:j\in [0,F)\}\), and denote \(\cal F\)=\([0,F)\). Each packet is of size \(1/F\). Each user is accessible to the files set \(\cal W\). Each packet is placed in different user caches determinately. Denote \(Z_k\) to represent the cache contents of user \(k\).
2) Delivery Phase: Each user independently requests a file from \(\cal W\) at random, the request is denoted by \(d=(d_0,d_1,\dots,d_{K-1})\), i.e., user \(k\) requests file \(W_{d_k}\), where \(k\in \cal K\), \(d_k\in [0, N)\). Once the server receives the request \(d\), it broadcasts a signal to users. Each user can attain its requested file from the signal received in the delivery phase with the help of the contents within its cache.
In this subsection, we quickly review PDAs and see the correspondence between PDA and coded caching scheme.
Definition 1. [11] For positive integers \(K, F, Z\) and \(S\), an \(F\times K\) array \(P=(p_{j,k}),j\in [0, F),k\in [0, K)\), composed of a specific symbol \(“*"\) and \(S\) nonnegative integers, namely \(0,1,\dots, S-1\), is called a \((K, F, Z, S)\) placement delivery array (PDA) if it satisfies the following conditions:
C1. The symbol \(“*"\) appers \(Z\) times in each column;
C2. Each integer occurs at least once in the array;
C3. For any two distinct entries \(p_{{j_1},{k_1}}\) and \(p_{{j_2},{k_2}}\), \(p_{{j_1},{k_1}}=p_{{j_2},{k_2}}=s\) is an integer only if
a. \({j_1}\neq {j_2},{k_1}\neq {k_2}\), i.e., they lie in distinct rows and distinct columns;
b. \(p_{{j_1},{k_2}}=p_{{j_2},{k_1}}=*\), i.e., the corresponding \(2\times 2\) sub-array formed by rows \(j_1,j_2\) and columns
\(k_1,k_2\) must be of the following form \[\begin{pmatrix} s & * \\ * & s \end{pmatrix}\ or\ \begin{pmatrix} * & s \\ s & * \end{pmatrix}.\]
Placement Phase: After the server separates each file, each user has access to the set of files \(\cal W\), and the packets cached by user \(k\in \cal K\) are recorded as \[Z_k = \{W_{i,j}|p_{j,k}=*,i\in [0, N)\},\] clearly, each user’s cache of size \(M=Z\cdot\frac{1}{F}\cdot N\).
Delivery Phase: When the server receives the request \(d\), at the moment \(s\in S\), the server sends the following signal \[\bigoplus _{p_{j,k}=s,j\in {\cal F},k\in {\cal K}}W_{d_k,j},\] in a \((K,F,Z,S)\)-PDA P=\((p_{j,k}),j\in [0,F),k\in [0,K)\), each column represents a user, if \(p_{j,k}=*\), i.e., user \(k\) has cached the \(j\)–\(th\) packet of all the files. For user \(k\), if \(p_{j,k}=s\), then user \(k\) does not cache the \(j\)–\(th\) packet of \(W_{d_k}\), but in the moment \(s\), the signal sent by server are all in the user’s cache except \(W_{d_k,j}\), so the user \(k\) can get the requested packet.
Example 1. Given a (3,3,1,3) PDA corresponding to a (3,1,3) coded caching scheme. \[P=\left( \begin{array}{ccc} 0 & 2 & *\\ 1 & * & 2\\ * & 1 & 0 \end{array} \right). \nonumber\]
In the placement phase: We have \(W_0 = \{W_{0,0},W_{0,1},W_{0,2}\}\), \(W_1 = \{W_{1,0},W_{1,1},W_{1,2}\}\), \(W_2 = \{W_{2,0},W_{2,1},W_{2,2}\}\), and \(Z_0=\{W_{0,2},W_{1,2},W_{2,2}\}\), \(Z_1=\{W_{0,1},W_{1,1},W_{2,1}\}\), \(Z_2=\{W_{0,0},W_{1,0},W_{2,0}\}\).
In the delivery phase: Assume that the request vector is \(d=(0,1,2)\), and the server sends the following coded signals: \(W_{0,0}\bigoplus W_{2,2}, W_{0,1}\bigoplus W_{1,2}, W_{1,0}\bigoplus W_{2,1}\). User 0 needs file \(W_0\) and solves \(W_{0,0}\) and \(W_{0,1}\) through \(W_{0,0}\bigoplus W_{2,2}\) and \(W_{0,1}\bigoplus W_{1,2}\). User 1 needs file \(W_1\) and solves \(W_{1,2}\) and \(W_{1,0}\) through \(W_{0,1}\bigoplus W_{1,2}\) and \(W_{1,0}\bigoplus W_{2,1}\). User 2 requires file \(W_2\) and solves \(W_{2,2}\) and \(W_{2,1}\) through \(W_{0,0}\bigoplus W_{2,2}\) and \(W_{1,0}\bigoplus W_{2,1}\).
Lemma 1. [11] In an \(F\)–\((K,M,N)\) coded caching scheme, by a \((K, F,Z,S)\)-PDA, using Algorithm 1, with the cache fraction \(\frac{M}{N}\)=\(\frac{Z}{F}\) and transmission rate \(R\)=\(\frac{S}{F}\).
| Algorithm 1 Coded Caching scheme based on PDA on [2] |
|---|
| 1: procedure PLACEMENT(P,\(W\)) |
| 2: Split each file \(W_i \in \)\(W\) into \(F\) packets: \(W_i=\{W_{i,j} : j \in [0,F)\}\) |
| 3: for \(k \in [0,K)\) do |
| 4: \(Z_k \gets \{W_{i,j} \mid p_{j,k}=*,i \in [0,N)\}\) |
| 5: end for |
| 6: end procedure |
| 7: procedure DELIVERY(P,\(W\),d) |
| 8: for \(;s=0,1,\dots,S-1\); do |
| 9: Server sends \(\bigoplus _{p_{j,k}=s,j \in {\cal F},k \in {\cal K}}W_{d_k,j}\); |
| 10: end for |
| 11: end procedure |
Let \(\mathbb F_q\) be the finite field with \(q\) elements, where \(q\) is a prime power, and \(n\) is a positive integer, we use \[\mathbb F_q^n=\{(x_1,x_2,\dots,x_n)|x_i\in \mathbb F_q,i=1,2,\dots,n\}\] to denote the \(n\)-dim row vector space over \(\mathbb{F}_{q}\) formed by the set of all \(n\)-dim row vectors. Clearly, \(\mathbb F_q^n\) has altogether \(q^n\) vectors.
Assume \(P\) be an \(m\)-dimensional vector subspace of \(\mathbb{F}_{q}^{n}\), we use the same letter \(P\) to denote a matrix representation of the vector subspace \(P\), i.e., \(P\) is an \(m\times n\) matrix of rank \(m\) whose rows form a basis of \(P\).
Let \(0< m\leq n\), and \(q\) is a power of a prime, \(N(m,n)\) be the number of \(m\)-dim vector subspaces in \(\mathbb F_q^n\). It is known that \(N(m,n)\) is equal to the Gaussian coefficient \({\left[ \begin{array}{l}n\\m\end{array} \right]_q}\), \[{\left[ \begin{array}{l} n\\ m \end{array} \right]_q} = \frac{{\prod\limits_{i = n – m + 1}^n {\left( {{q^{i}} – 1} \right)}} } {{\prod\limits_{i = 1}^m {\left( {{q^i} – 1} \right)} }},\] by convention \({\left[ \begin{array}{l}n\\0\end{array} \right]_q}=1\) for all integer \(n\).
The following known results are used to serve our construction.
Lemma 2. Let \(0\leq k\leq m\leq n\) and \(N(k,m,n)\) be the number of \(k\)-dim vector subspaces contained in a given \(m\)-dim vector subspaces of \(\mathbb F_q^n\), then \[N(k,m,n)=N(k,m)={\left[ \begin{array}{l}m\\k\end{array} \right]_q}.\]
Lemma 3. Let \(0\leq k\leq m\leq n\). Then the number \(N'(k,m,n)\) of \(m\)-dim vector subspaces containing a given \(k\)-dim vector subspace of \(\mathbb F_q^n\) is equal to \({\left[ \begin{array}{l}n-k\\m-k\end{array} \right]_q}\).
Lemma 4. Consider a \(m\)-dim subspaces of \(\mathbb F_q^n\). Let \(1 \leq m < n\), then \[{\left[ \begin{array}{l}n\\m\end{array} \right]_q}={\left[ \begin{array}{l}\quad n\\n-m\end{array} \right]_q}.\]
Construct a type of PDA based on the knowledge of vector space, where the set of the \(v\)-dim subspace of the \(\mathbb{F}_{q}^n\) is \(\mathbb V\) and the set of the \((v+h)\)-dim subspace of the \(\mathbb{F}_{q}^n\) is \(\mathbb U\). Let \(\mathbb V= \cal K\) and \(\mathbb U=\cal F\), then an \(F \times K\) array P=\((p_{U,V}),U\in \mathbb U,V\in \mathbb V\) is obtained according to the following rules:
\[p_{U,V}=\begin{cases} H & H\bigoplus V=U,\\ * \quad &else.\end{cases}\]
Remark 1. Each row does not have the same non-\(*\) element in array P. On the one hand, the non-\(*\) elements in each row are \(h\)-dim subspace \(H\) and have the quantity \({{\left[ \begin{array}{l}v+h\\\quad h\end{array} \right]_q}}.\) On the other hand, given an \((v+h)\)-dim subspace \(U\), if the \(v\)-dim subspace \(V\) is contained in \(U\), then there is element \(H\), and the number of \(V\) is \({{\left[ \begin{array}{l}v+h\\\quad v\end{array} \right]_q}},\) i.e., \({{\left[ \begin{array}{l}v+h\\\quad h\end{array} \right]_q}}={{\left[ \begin{array}{l}v+h\\\quad v\end{array} \right]_q}}\). Clearly, Each column does not have the same non-\(*\) element in array P.
Example 2. Consider the 3-dim vector space over \(\mathbb F_2\) and the 1-dim subspace of \(\mathbb F_2^3\) which are listed as follows, \[V_1=span\{(1,0,0)\}, V_2=span\{(0,1,0)\}, V_3=span\{(0,0,1)\}, V_4=span\{(1,1,0)\},\] \(\quad\quad\;\;\;\;\;\; V_5=span\{(1,0,1)\}, V_6=span\{(0,1,1)\}, V_7=span\{(1,1,1)\}.\\\)
Let \(\mathbb V=\{V_1,V_2,V_3,V_4,V_5,V_6,V_7\}\). Consider the 2-dim subspace of \(\mathbb F_2^3\) which are listed as follows, \[U_1=span\{(1,0,0),(0,1,0),(1,1,0),(0,0,0)\}, U_2=span\{(1,0,0),(0,0,1),(1,0,1),(0,0,0)\},\] \[U_3=span\{(1,0,0),(0,1,1),(1,1,1),(0,0,0)\}, U_4=span\{(0,1,0),(0,0,1),(0,1,1),(0,0,0)\},\] \[U_5=span\{(0,1,0),(1,0,1),(1,1,1),(0,0,0)\}, U_6=span\{(0,0,1),(1,1,0),(1,1,1),(0,0,0)\},\] \(\quad\;\; U_7=span\{(1,1,0),(1,0,1),(0,1,1),(0,0,0)\}.\\\)
Let \(\mathbb U=\{U_1,U_2,U_3,U_4,U_5,U_6,U_7\}\). Use the elements in \(\mathbb U\) as row index and the elements in \(\mathbb V\) as column index, then the elements in the array are represented as 1-dim subspace. By construction, we can attain the following \(7\times 7\) array, actually, \(H_i=V_i, i\in\{1,2,3,4,5,6,7\}\). It is easily apparent that this refers to \((7,7,4,7)\)-PDA.
| \(V_1\) | \(V_2\) | \(V_3\) | \(V_4\) | \(V_5\) | \(V_6\) | \(V_7\) | |
|---|---|---|---|---|---|---|---|
| \(U_1\) | \(H_2\) | \(H_4\) | \(*\) | \(H_1\) | \(*\) | \(*\) | \(*\) |
| \(U_2\) | \(H_3\) | \(*\) | \(H_5\) | \(*\) | \(H_1\) | \(*\) | \(*\) |
| \(U_3\) | \(H_6\) | \(*\) | \(*\) | \(*\) | \(*\) | \(H_7\) | \(H_1\) |
| \(U_4\) | \(*\) | \(H_3\) | \(H_6\) | \(*\) | \(*\) | \(H_2\) | \(*\) |
| \(U_5\) | \(*\) | \(H_5\) | \(*\) | \(*\) | \(H_7\) | \(*\) | \(H_2\) |
| \(U_6\) | \(*\) | \(*\) | \(H_4\) | \(H_7\) | \(*\) | \(*\) | \(H_3\) |
| \(U_7\) | \(*\) | \(*\) | \(*\) | \(H_5\) | \(H_6\) | \(H_4\) | \(*\) |
Next, we will prove that the array constructed above satisfies the definition of PDA and give its parameters.
Lemma 5. The following relationships hold for the construction we have presented, \[{K=|\mathbb V|={\left[ \begin{array}{l} n\\ v \end{array} \right]_q},}\] \[{F=|\mathbb U|={\left[ \begin{array}{l} \quad n\\ v+h \end{array} \right]_q},}\] \[{Z={\left[ \begin{array}{l} \quad n\\ v+h \end{array} \right]_q}- {\left[ \begin{array}{l} n-v\\ \quad h \end{array} \right]_q}},\] where \(Z\) is the number of elements \(“*"\) in each column of the array P.
Proof. By using the known ideas presented in this section we can write, \[{K=|\mathbb V|=N(v,n)={\left[ \begin{array}{l} n\\ v \end{array} \right]_q},}\] \[{F=|\mathbb U|=N(v+h,n)={\left[ \begin{array}{l} \quad n\\ v+h \end{array} \right]_q}.}\]
Now, we will find the parameter \(Z\). Consider an arbitrary \(V\in \mathbb V\). By lemma 3, we know that the number of \((v+h)\)-dim subspaces of \(\mathbb F_q^n\) containing the fixed \(v\)-dim subspace \(V\) is \({{\left[ \begin{array}{l} n-v\\ \quad h \end{array} \right]_q}}.\) Therefore, we get \[{Z={\left[ \begin{array}{l} \quad n\\ v+h \end{array} \right]_q}- {\left[ \begin{array}{l} n-v\\ \quad h \end{array} \right]_q}.}\] ◻
Lemma 6. There are \({\left[ \begin{array}{l} n\\ h \end{array} \right]_q}\) different non-\(*\) elements in array P.
Proof. If the \(h\)-dim subspace \(H\) of \(U\) appears in array P, \({\left[ \begin{array}{l} n-h\\ \quad v \end{array} \right]_q}\) times will occur. In fact, the number of occurrences of a subspace \(H\) is denoted \(L\): the number of \((v+h)\)-dim subspaces \(U\) containing \(h\)-dim subspaces, then \(L={\left[ \begin{array}{l} \quad n-h\\ (v+h)-h \end{array} \right]_q}={\left[ \begin{array}{l} n-h\\ \quad v \end{array} \right]_q}\) can be seen from the knowledge of vector space, then \[S=\frac {{\left[ \begin{array}{l} v+h\\ \quad v \end{array} \right]_q}\left[ \begin{array}{l} \quad n\\ v+h \end{array} \right]_q}{\left[ \begin{array}{l} n-h\\ \quad v \end{array} \right]_q}={\left[ \begin{array}{l} n\\ h \end{array} \right]_q}.\]
Let \(E\) be the set of \(h\)-dim subspaces, a bijection \(f\) is defined from \(E\) to \([0,S)\), where \(S={\left[ \begin{array}{l}n\\h\end{array} \right]_q}\). Then we can get the array \(\Gamma=(a_{U,V})\) \[a_{U,V}=\begin{cases}f(H)\quad &p_{U,V}=H,\\ \quad *\quad \quad &else.\end{cases}\] ◻
Lemma 7. In array \(\Gamma\), if \(a_{U_{i_1},V_{j_1}}=a_{U_{i_2},V_{j_2}}\)=\(s\in S\), \(U_{i_1}\neq U_{i_2}\), \(V_{j_1}\neq V_{j_2}\), then \(a_{U_{i_1},V_{j_2}}=a_{U_{i_2},V_{j_1}}\)=\(*\).
Proof. If \(a_{U_{i_1},V_{j_1}}=a_{U_{i_2},V_{j_2}}\)=\(H\), then \(V_{j_1}\subset U_{i_1},V_{j_2}\subset U_{i_2}\) and \(H\bigoplus V_{j_1}=U_{i_1},H\bigoplus V_{j_2}=U_{i_2}\). Assume that \(V_{j_1}\subset U_{i_2}=H\bigoplus V_{j_2}\), then \(H\bigoplus V_{j_1}=U_{i_1}\subset H\bigoplus V_{j_2}=U_{i_2}\), so we have \(U_{i_1}=U_{i_2}\), which is not true by the select of \(U_{i_1}\) and \(U_{i_2}\). Thus \(V_{j_1}\not\subset U_{i_2}\). Similarly, \(V_{j_2}\not\subset U_{i_1}\). This completes the proof. ◻
Theorem 1. For any positive integer \(n,v,h\) that satisfies \(v< n,h< n,v+h< n\),
there exists
\(\bigg({\left[ \begin{array}{l}
n\\
v
\end{array} \right]_q},{\left[ \begin{array}{l}
\quad n\\
v+h
\end{array} \right]_q},{\left[ \begin{array}{l}
\quad n\\
v+h
\end{array} \right]_q-{\left[ \begin{array}{l}
n-v\\
\quad h
\end{array} \right]_q}},{\left[ \begin{array}{l}
n\\
h
\end{array} \right]_q}\bigg)\)-PDA, note P. An \({\left[ \begin{array}{l}
\quad n\\
v+h
\end{array} \right]_q}\)–\(\bigg({\left[ \begin{array}{l}
n\\
v
\end{array} \right]_q}, M, N\bigg)\) coded caching scheme can be
implemented, where the cache fraction \(\frac
{M}{N}\) and the transmission rate \(R\) are as follows: \[\frac {M}{N}=1-\frac {{\left[ \begin{array}{l}
n-v\\
\quad h
\end{array} \right]_q}}{{\left[ \begin{array}{l}
\quad n\\
v+h
\end{array} \right]_q}}, R=\frac{{\left[ \begin{array}{l}
n\\
h
\end{array} \right]_q}}{{\left[ \begin{array}{l}
\quad n\\
v+h
\end{array} \right]_q}}.\]
Proof. It can be seen from lemma 5, 6, and 7. ◻
For the coded caching scheme in Theorem 1, let \(t={\left[ \begin{array}{l} n\\ v \end{array} \right]_q}-{\left[ \begin{array}{l} v+h\\ \quad v \end{array} \right]_q}\), We can get an MN coded caching scheme, where the parameters are: \({K={\left[ \begin{array}{l} n\\ v \end{array} \right]_q},}\) \(\frac {M}{N}=1-\frac {{\left[ \begin{array}{l} n-v\\ \quad h \end{array} \right]_q}}{{\left[ \begin{array}{l} \quad n\\ v+h \end{array} \right]_q}}.\)
$${F_{MN}} = \Bigg(\makecell {{\left[ \begin{array}{l} n\\ v \end{array} \right]_q}\\{\left[ \begin{array}{l} n\\ v \end{array} \right]_q}-{\left[ \begin{array}{l} v+h\\ \quad v \end{array} \right]_q}}\Bigg), \;R_{MN}=\frac{{\left[ \begin{array}{l} v+h\\ \quad v \end{array} \right]_q}}{1+{\left[ \begin{array}{l} n\\v \end{array} \right]_q}-{\left[ \begin{array}{l} v+h\\\quad v \end{array} \right]_q}}.$$We know that for the MN scheme, when \(\frac{M}{N}\) is a fixed constant, there are \(F=O(2^K)\) and the rate \(R=O(1)\). In our scheme, we keep the rate upper bounded by a constant, i.e., \(R=O(1)\), then our scheme has subexponential subpacketization, i.e., \(F=q^{O((log_q^K)^2)}\). The analysis proceeds as follows. In the first place, we have \[R={\frac{{\prod\limits_{i = h+ 1}^{h+v} {\left( {{q^i} – 1} \right)}} } {{\prod\limits_{i =n-v-h+1}^{n-h} {\left( {{q^i} – 1} \right)} }}}\leq q^{v(2h-n+v+1)},\] we can assume \(v\) and \(2h-n\) as constants, and we know, \[q^{v(n-v)} \leq K={\left[ \begin{array}{l} n\\ v \end{array} \right]_q}\leq q^{v(n-v+1)},\] consider, \[\frac{F}{K}={\frac{{\prod\limits_{i = n -v- h+ 1}^{n-v} {\left( {{q^i} – 1} \right)}} } {{\prod\limits_{i =v+1}^{v+h} {\left( {{q^i} – 1} \right)} }}}\leq q^{h(n-2v-h+1)}\leq q^{(n-v)(n-2v-h+1)},\] then, \[F\leq Kq^{(n-v)(n-2v-h+1)}=q^{log_q^K}q^{(n-v)(n-2v-2h+1)}q^{(n-v)h}.\]
From \(q^{v(n-v)} \leq K,\) it follows that \(n-v\leq \frac{1}{v}log_q^k\), we have, \[F\leq q^{log_q^K}q^{{\frac{n-2v-2h+1}{v}}log_q^K}q^{\frac{1}{v^2}(log_q^K)^2},\] therefore \(F=q^{O((log_q^K)^2)}\).
The following analysis continues as: \[\begin{aligned} \frac{F}{F_{MN}} & = \frac{{\left[ \begin{array}{l} \quad n\\ v+h \end{array} \right]_q}}{\Bigg(\makecell {{\left[ \begin{array}{l} n\\ v \end{array} \right]_q}\\{\left[ \begin{array}{l} n\\ v \end{array} \right]_q}-{\left[ \begin{array}{l} v+h\\ \quad v \end{array} \right]_q}}\Bigg)} \stackrel{v + h = n – 1}{=} \frac{{\left[ \begin{array}{l} \quad n\\ n-1 \end{array} \right]_q}}{\Bigg(\makecell {{\left[ \begin{array}{l} n\\ v \end{array} \right]_q}\\{\left[ \begin{array}{l} n\\ v \end{array} \right]_q}-{\left[ \begin{array}{l} v+h\\ \quad v \end{array} \right]_q}}\Bigg)} \\ & = \frac{q^{n-1} + q^{n-2} + \dots + 1}{\binom{K}{K – K \frac{q^{n – v} – 1}{q^n – 1}}} < \frac{q^{n-1} + q^{n-2} + \dots + 1}{\alpha^{\frac{K}{\alpha}}} \end{aligned}\]
where \(\alpha=\frac{q^n-1}{q^n-q^{n-v}}.\)
\[\frac{R}{R_{MN}}=\frac{1+{\left[ \begin{array}{l} n\\ v \end{array} \right]_q}-{\left[ \begin{array}{l} v+h\\ \quad v \end{array} \right]_q}}{{\left[ \begin{array}{l} n-h\\ \quad v \end{array} \right]_q}}\stackrel{v+h=n-1}{=} \frac{1+K-K\frac{q^{n-v}-1}{q^n-1}}{q^v+q^{v-1}+\dots+1} \approx K\Bigg(\frac{q^n-q^{n-v}}{(q^v+q^{v-1}+\dots+1)(q^n-1)}\Bigg ).\]
We can see that when the new scheme in Theorem 1 and the MN scheme have the same number of users and cache fraction, we can see that the subpacketization \(F\) of the new scheme is about at least \(\frac{q^{n-1}+q^{n-2}\dots+1}{\alpha^{\frac{K}{\alpha}}}\) times less than \(F_{MN}\), and the transmission rate \(R\) is about at most \(\frac{K}{\alpha (q^v+q^{v-1}+\dots+1)}\) times that of \(R_{MN}\), where \(\alpha=\frac{q^n-1}{q^n-q^{n-v}}.\)
Next, a numerical comparison of the new scheme and the MN scheme is shown in Table 1 (let \(q=2\), \((n,h,v)=(4,1,2), (5,2,2), (6,3,2), (6,2,3), (7,4,2), (7,3,3),(8,2,5)\)), Table 1 shows that the subpacketization \(F\) in the coded caching scheme in Theorem 1 is much smaller than the subpacketization in the MN scheme at the expense of a portion of the transmission rate \(R\), under the same conditions of the number of users \(K\) and the cache fraction \(\frac{M}{N}\).
| \(K\) | \(\frac{M}{N}\) | \(F\) | \(F\) | \(R\) | \(R\) | ||
|---|---|---|---|---|---|---|---|
| \(Th\) | \(MN\) | \(Th\) | \(MN\) | \(Th\) | MN | \(Th\) | MN |
| 35 | 0.8000 | 15 | \(6.7245\times 10^{6}\) | 1 | 0.2414 | ||
| 155 | 0.7742 | 31 | \(6.9284\times 10^{34}\) | 5 | 0.2893 | ||
| 651 | 0.7619 | 63 | \(5.5647\times 10^{153}\) | 22.1429 | 0.3119 | ||
| 1395 | 0.8889 | 63 | \(7.3757\times 10^{209}\) | 10.3333 | 0.1249 | ||
| 2667 | 0.7559 | 127 | inf | 93 | 0.3228 | ||
| 11811 | 0.8819 | 127 | inf | 93 | 0.1339 | ||
| 97155 | 0.9725 | 255 | inf | 42.3333 | 0.0282 | ||
Here we compare the new scheme to the scheme in [12], as shown in Table 2, Table 2 indicates that while surrendering a portion of the transmission rate \(R\), the coded caching scheme presented in Theorem 1 exhibits advantages to a certain extent with regard to the number of users \(K\), subpacketization \(F\), and cache fraction \(\frac{M}{N}\).
| \(scheme\) | \(parameters\) | \(K\) | \(F\) | \(\frac{M}{N}\) | \(R\) |
|---|---|---|---|---|---|
| (n,h,v,q)Th | (4,1,2,2) | 35 | 15 | 0.8000 | 1.0000 |
| (m,a,b,\(\lambda\))[12] | (9,2,3,2) | 28 | 56 | 0.8750 | 0.1607 |
| (n,h,v,q)Th | (5,1,3,2) | 155 | 31 | 0.9032 | 1.0000 |
| (m,a,b,\(\lambda\))[12] | (9,4,3,3) | 126 | 84 | 0.9524 | 0.1071 |
| (n,h,v,q)Th | (6,3,2,2) | 651 | 63 | 0.7619 | 22.1429 |
| (m,a,b,\(\lambda\))[12] | (12,4,3,2) | 495 | 220 | 0.7818 | 3.0000 |
| (n,h,v,q)Th | (6,2,3,2) | 1395 | 63 | 0.8889 | 10.3333 |
| (m,a,b,\(\lambda\))[12] | (13,5,2,2) | 1287 | 78 | 0.8718 | 3.6667 |
| (n,h,v,q)Th | (7,2,4,2) | 11811 | 127 | 0.9449 | 21.0000 |
| (m,a,b,\(\lambda\))[12] | (16,7,3,3) | 11440 | 560 | 0.9375 | 3.2500 |
| (n,h,v,q)Th | (8,2,5,2) | 97155 | 255 | 0.9725 | 42.3333 |
| (m,a,b,\(\lambda\))[12] | (19,8,3,3) | 75582 | 969 | 0.9422 | 12.0000 |
This study presents the construction of PDA in vector space over finite field, which yields a novel coded caching scheme with low subpacketization. A new MN scheme is generated when number of users \(K\) and the cache fraction \(\frac{M}{N}\) are equal. The new scheme has a significant advantage in terms of the subpacketization \(F\) when compared to the new MN scheme based on theoretical and numerical analyses. Upon doing a numerical comparison of the coded caching scheme presented in literature [12], when a portion of transmission rate \(R\), the number of users \(K\), the subpacketization \(F\), and the cache fraction \(\frac{M}{N}\) all demonstrate certain advantages to some degree.
This research was supported partly by the scientific research project of Tianjin Municipal Education Commission (Grant No. 2023ZD041) and the Graduate Student Research and Innovation Fund of Civil Aviation University of China (Grant No. 2023YJSKC06006).
The authors declare no conflict of interest.