We consider the eccentric graph of a graph \(G\), denoted by \(\mathrm{ecc}(G)\), which has the same vertex set as \(G\), and two vertices in the eccentric graph are adjacent if and only if their distance in \(G\) is equal to the eccentricity of one of them. In this paper, we present a fundamental requirement for the isomorphism between \(\mathrm{ecc}(G)\) and the complement of \(G\), and show that the previous necessary condition given in the literature is inadequate. Also, we obtain that the diameter of \(\mathrm{ecc}(T)\) is at most 3 for any tree and get some characterizations of the eccentric graph of trees.
Consider a simple graph \(G = (V, E)\), where the adjacency between vertices \(v_i\) and \(v_j\) is indicated by \(v_iv_j \in E(G)\) or \(v_i\sim v_j\). The distance between two vertices \(u\) and \(v\) in \(G\) is symbolized as \(d_{G}(u, v)\) or, more concisely, as \(d(u,v)\). It signifies the minimum number of edges required to traverse from \(u\) to \(v\) in the graph. The eccentricity \(ecc(u)\) of a vertex \(u\) in \(G\) is the maximum distance between \(u\) and any vertex \(v\) in the graph. In other words, it measures how far apart \(v\) is from the farthest vertex in \(G\). The diameter and radius of any graph \(G\), denoted by \(diam(G)\) and \(rad(G)\), are the maximum and minimum eccentricity among all vertices, respectively. If a graph \(G\) satisfies the condition \(diam(G)=rad(G)=d\) for some value \(d\), it is referred to as a \(d\)-self-centered graph. This means that eccentricities of all vertices in \(G\) are the same.
Consider a collection of mutually disjoint nonempty finite sets \({V_1, \ldots, V_n}\) of any graph \(G\). The construction of a graph, formed by taking the union of the sets \(V_1, \ldots, V_n\), is as follows: for each \(i\), the vertices within \(V_i\) are either all adjacent to each other (forming a clique) or all non-adjacent to each other (forming a coclique). In the graph, two vertices, one from \(V_i\) and another from \(V_j\), are adjacent if and only if \(i\sim j\) in \(G\).
The mixed extension \(\mathcal{ME}_G[\pm p_1, \pm p_2, \ldots, \pm p_n]\) (also referred to as the mixed extension of \(G\) of type (\((\pm p_1, \pm p_2, \ldots, \pm p_n)\)) is constructed by extending the vertex set of \(G\) and specifying the cliques and cocliques according to the given types. In this notation, \(+p_i\) represents a clique of size \(p_i\), and \(-p_i\) represents a coclique of size \(p_i\). If the vertices of \(G\) consist of cocliques (cliques), then the extension will be referred to as a coclique (clique) extension [1].
A tree is a connected undirected graph without any cycles or loops. It consists of vertices (also known as nodes) and edges. In a rooted tree, one vertex is chosen as the root, which serves as the starting point for traversing the tree. Each vertex in the tree has a level, indicating the number of edges in the path from that vertex to the root. The root itself is at level 0. Consider two vertices, denoted as \(v\) and \(w\), in a rooted tree. We say that vertex \(v\) is an ancestor of \(w\) if it lies on the unique path from \(w\) to the root. Similarly, \(w\) is considered a descendant of \(v\). A vertex in a rooted tree is called a leaf if it does not have any children, meaning it is at the end of a branch and has no vertices connected below it.
The eccentric graph \(ecc(G)\) of any graph \(G\) has the same vertex set with \(G\) and two vertices in \(ecc(G)\) are adjacent iff their distance in \(G\) is equal to the eccentricity of one of them. The eccentric graph of a graph has been first introduced by Akiyama et al. in 1985 [2]. Studies on the eccentric graph of some graphs with special type such as unique eccentric point graphs, path graphs, cycle graphs etc. can be seen in [3-7].
One of the fundamental problems in graph theory is to determine when two graphs are isomorphic. In this paper, we focus on the problem of determining when \(ecc(G)\) is isomorphic to the complement of \(G\). This problem has been investigated by Akiyama et. al [2], where they gave a necessary condition for \(ecc(G)\) to be isomorphic to the complement of \(G\). However, we show that this condition is inadequate by presenting an example of a graph \(G\) whose eccentric graph is isomorphic to its complement, but does not satisfy the previous necessary condition.
Motivated by this, we correct the necessary condition for \(ecc(G)\cong \overline{G}\). We prove our result by using the necessary condition given in [2], and show that our condition is stronger than the previous one. We also obtain the structure of \(ecc(T)\) with respect to its center(s). Finally, we show that the diameter of the eccentric graph of any tree is at most \(3\).
We give a more mathematical definition of Akiyama et al. below.
Definition 1. [2] Let \(G\) be a graph with vertex set \(V\) and edge set \(E\). The eccentric graph of \(G\) is denoted by \(ecc(G)= (V, E')\) where \(E'= \{(u, v) :\ d_G(u, v) = ecc(u) \ \text{or}\ \ d_G(u, v) = ecc(v) \ \text{for} \ u, v \in V\}\).
The eccentric graph of some extremal graphs such as path, complete, cycle etc. is given the following table by using the concept of eccentric graph.
| \(G\) | \(ecc(G)\) |
|---|---|
| Complete graph \(K_n\) | Complete Graph \(K_n\) |
| Star graph \(S_n\) | Complete graph \(K_n\) |
| Cycle graph \(C_{2n}\) | Disjoint union of \(K_2\) |
| Cycle graph \(C_{2n-1}\) | Cycle graph \(C_{2n-1}\) |
| Path graph \(P_{2n}\) | Double star |
| Path graph \(P_{2n-1}\) | \(S^*_{\frac{n-3}{2},\frac{n-3}{2}}\) (Figure 1) |
| Complete bipartite graph \(K_{n,m}\) | Disjoint union of \(K_n\) and \(K_m\) |

Theorem 1. [2] \(ecc(G)\cong \overline{G}\) if and only if \(S_i=\emptyset\) for \(i=1,4,5,6\ldots\) and no two vertices in \(S_3\) have a common neighbour , where \(S_i=\{u\in V: ecc(u)=i\}\).
The Akiyama et al. [2] Theorem, labeled as Theorem 1, posits that \(ecc(G)\cong \overline{G}\) under certain conditions. A slight discrepancy exists in the necessary conditions for \(ecc(G)\cong \overline{G}\), as outlined in the theorem. Specifically, if \(S_i=\emptyset\) for \(i=1,4,5,6\ldots\) and vertices in \(S_3\) lack common neighbors, with \(u\) and \(v\) in \(S_3\) having a distance of \(3\) in graph \(G\), the theorem holds. Remarkably, even when vertices in \(S_3\) are adjacent, contrary to the stipulated conditions, the result \(ecc(G)\cong \overline{G}\) persists. Figure 2 illustrates this phenomenon, where the adjacency of vertices \(1\) and \(4\) in \(G\), both within \(S_3\), does not negate the validity of \(ecc(G)\cong \overline{G}\).
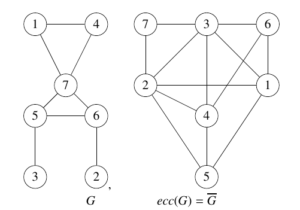
\(G\) \(ecc(G)=\overline{G}\)
Now we give the corrected theorem by also using the proof and also proof.
Theorem 2. Let \(G=(V,E)\) be a graph. \(ecc(G)\) is isomorphic to the complement of \(G\) if and only if \(S_i= \emptyset\) for \(i=1,4,5,\ldots\) and \(d(u,v)\neq 2\) in \(G\) for any \(u,v\in S_3\), where \(S_i=\{u\in V: ecc(u)=i\}\).
Proof. Suppose that \(ecc(G)\cong \overline{G}\). Let \(S_1 \neq \emptyset\) for \(i=1\). It means that \(\overline{G}\) has an isolated vertex. But this contradicts \(ecc(G)\cong \overline{G}\). Now let \(S_i \neq \emptyset\) for some \(i\) greater than or equal to \(4\). In this case, there is a shortest path \(u_1u_2\ldots u_t\) in \(G\). So we have \(ecc(u_{2})\geq t-2\) and \(ecc(u_{t-1})\geq t-2\). Then we have \(d(u_2,u_{t-1})=t-3\) and hence \(u_2\) and \(u_{t-1}\) are adjacent in \(\overline{G}\) but not in \(ecc(G)\). This is also a contradiction. Therefore \(S_i= \emptyset\) for \(i=1\) and \(i\geq 4\).
Similarly assume that \(d(u,v)=2\) for any \(u,v\in S_3\). This implies that \(u\) and \(v\) are not adjacent in \(G\). Moreover, in \(ecc(G)\), they are also not adjacent because \(d_{G}(u,v)\neq 3\). However, this contradicts the assumption that \(ecc(G)\) is isomorphic to the complement of \(G\). Therefore, we can conclude that \(d(u,v)\neq 2\) in \(G\) for any \(u,v\in S_3\).
Conversely, let \(u\) and \(v\) be vertices in \(S_3\). Since \(d_{G}(u,v)\neq 2\), we have \(d_{G}(u,v)=1\) or \(d_{G}(u,v)=3\). If \(d(u,v)=1\) in \(G\), then \(u\not\sim v\) in \(ecc(G)\). If \(d(u,v)=3\) in \(G\) (which means \(u\not\sim v\) in \(G\)), then \(u\sim v\) in \(ecc(G)\). Hence, we can conclude that \(u\sim v\) in \(G\) if and only if \(u\not\sim v\) in \(ecc(G)\) for \(u,v\in S_3\).
Now, let \(u\in S_2\) and \(v\in S_3\). If \(u\sim v\) in \(G\), then \(u\nsim v\) in \(ecc(G)\) since \(d_G(u,v)=1\neq ecc(u)\) (also \(ecc(v)\)). If \(u\nsim v\) in \(G\), we have \(d(u,v)=2=ecc(u)\) in \(G\). This implies that \(u\sim v\) in \(ecc(G)\). Finally, let \(u,v\in S_2\). In this case, \(u\sim v\) in \(G\) if and only if \(u\not\sim v\) in \(ecc(G)\) because \(S_i=\emptyset\) for \(i=1,4,5,\ldots\).
Therefore, in \(ecc(G)\), two vertices are adjacent if and only if they are not adjacent in \(G\). This implies that \(ecc(G)\cong \overline{G}\). ◻
Lemma 1. [3] Every tree has either one or two centers.
Lemma 2. If \(T\) is a tree with two centers, \(ecc(T)\) must be isomorphic to any coclique extension of \(P_4\).
Proof. Let \(T\) be a tree. Assume that \(T\) has two center vertices, denoted as \(c_1\) and \(c_2\).
Consider the bridge in \(T\) connecting \(c_1\) and \(c_2\), denoted as \(c_1c_2\).
We can partite the vertex set of \(T\) into two subsets with respect to this bridge as \(V_1 =\{v \in V : \text{there exists a path in } T \text{ from } v \text{ to } c_1 \text{ that does not cross } c_1c_2\}\) and \(V_2 = \{v \in V : \text{there exists a path in } T \text{ from } v \text{ to } c_2 \text{ that does not cross } c_1c_2\}\). These partitions are disjoint, meaning that no vertex belongs to both \(V_1\) and \(V_2\). Define \(T_{c_1}=\{x\in V_1: d_{T}(x,c_1)< rad(T)\}\) and \(T_{c_2}=\{x\in V_2: d_{T}(x,c_2)< rad(T)\}\). Notice that the remaining vertices are the diametrical vertices in both \(V_1\) and \(V_2\). Now let \(U_1\) and \(U_2\) be the set of diametrical vertices in \(V_1\) and \(V_2\), respectively. Since \(d_{T}(x,y)=diam(T)\) for \(x\in U_{1}, y\in U_2\), by definition of the eccentric graph, they must be adjacent each other. Hence, \(ecc(T)\) contains the complete bipartite graph \(K_{\vert U_1\vert,\vert U_2\vert}\) as an induced subgraph. Also, for any \(x\in T_{c_1}\) and for \(y\in U_2\), we get \(x\sim y\) in \(ecc(T)\) since \(d_T(x,y)=ecc(x)\). Similarly, for any \(x\in T_{c_2}\) and for \(y\in U_1\), we also get \(x\sim y\) in \(ecc(T)\). Therefore \(ecc(T)\) is isomorphic to \(\mathcal{ME}_{P_4}[-p_1,-p_2,-p_3,-p_4]\) where \(p_1=\vert T_{c_1}\vert\), \(p_2=\vert U_2\vert\), \(p_3=\vert U_1\vert\) and \(p_4=\vert T_{c_2}\vert\). ◻
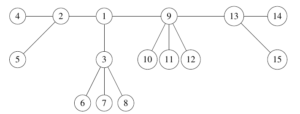
Example 1. \(T'\) in the Figure 3 is a tree with diameter \(5\) and radius \(3\). We have, \(C(T')= \{1,9\}\); \(S_{5}=\{4,5,6,7,8,14,15\}=\{4,5,6,7,8\}\cup \{14,15\}\); \(T_{1}=\{1,2,3\}\) and \(T_{9}=\{9,10, 11,12, 13\}\). Hence \(ecc(T')\cong \mathcal{ME}_{P_4}[-3,-2,-5,-5]\).
Lemma 3. Let \(T\) be a tree with exactly one center vertex. Then \(ecc(T)\) is a \(2\)-self centered graph if and only if among the diametrical leaves, there is at least one triple \((x,y,z)\) such that the distance between each pair of vertices \(x\),\(y\) and \(z\) is equal to \(diam(T)\).
Proof. First, consider \(T\) as a rooted tree with \(c\) as the center vertex.
Let \(ecc(T)\) is a 2-self centered.
This means that for any two vertices \(x, y
\in ecc(T)\), we have \(d_{ecc(T)}(x,
y) = 2\). Suppose that there is no triple \((x, y, z)\) in \(T\) such that the vertices \(x\), \(y\), and \(z\) are diametrical leaves of \(T\), and the distance between every pair of
vertices \(x,y,z\) is equal to the
diameter of \(T\). Note that \(T\) is at least two diametrical pair of
leaves. Let \(x\) and \(y\) be diametrical vertices in \(T\). Now, consider the paths \(P\) and \(Q\) from the root \(c\) to \(x\) and \(y\) respectively. Let \(u\) and \(v\) be any vertices such that \(x \neq u\) and \(y \neq w\) and that are at the same level
in \(P\) and \(Q\), respectively. This implies that \(d_{T}(u,c)=d_{T}(w,c)=k<rad(T)\). Since
\(d_{T}(u,w)=d_{T}(u,c)+d_{T}(w,c)=k+k<k+rad(T)=ecc(u)\),
we have \(u\nsim v\) in \(ecc(T)\). Notice that \(d_{T}(u,y)=ecc(u)\) and \(d_{T}(x,w)=ecc(w)\), so we get \(u\sim y\) and \(x\sim w\) and hence, there is a path \(u-y-x-w\) in \(ecc(T)\). Since there is no other
diametrical vertex which is at distance \(diam(T)\) with both \(x\) and \(y\), \(u\)
and \(w\) have no common neighbour in
\(ecc(T)\). Hence we get \(d_{ecc(T)}(u,w)=3\). But, this contradicts
the assumption that \(ecc(T)\) is a
2-self centered graph. Therefore, there must exist at least one triple
\((x, y, z)\) in \(T\) such that the vertices \(x\), \(y\)
and \(z\) are diametrical leaves of
\(T\) such that the distance between
each pair of vertices \(x,y,z\) is
equal to the diameter of \(T\).
Conversely, let \(x\),\(y\) and \(z\) be the diametrical leaves such that the
distance between each pair of vertices \(x,y,z\) is equal to \(diam(T)\).
Case 1. Let \(x\neq u\) and \(x\neq v\) be vertices that lies on path \(P\) where \(P\) is from the root \(c\) to \(x\) in \(T\). In this case, since \(d_{T}(u,y)=ecc(u)\) and \(d_{T}(v,y)=ecc(v)\), hence \(u\sim y\) and \(v\sim y\) in \(ecc(T)\). This implies that \(d_{ecc(T)}(u,v)=2\).
Case 2. Let \(x \neq u\) and \(y \neq v\) be vertices that lie on the paths \(P\) and \(Q\), respectively, where \(P\) is the path from the root \(c\) to \(x\) and \(Q\) is the path from the root \(c\) to \(y\) in \(T\). If the vertices \(u\) and \(v\) are at the same level (i.e., \(ecc(u) = ecc(v)\)) in \(T\), we have \(u \nsim v\) in \(ecc(T)\) because \(d_{T}(u,c) = d_{T}(v,c) = k < rad(T)\) and \(d_{T}(u,v) = 2k < k+rad(T) = ecc(u) = ecc(v)\) in \({T}\). However, \(u\) and \(v\) have a common neighbour, denoted by \(z\), such that \(u \sim z\) and \(v \sim z\) in \(ecc(T)\), implying that \(d_{ecc(T)}(u,v) = 2\). Without loss of generality, assume that \(u\) and \(v\) are at different levels (i.e., \(ecc(u) \neq ecc(v)\)) in \(T\). Let \(k_1 = d_{T}(u,c) < d_{T}(v,c) = k_2\) in \(T\). Then we have \(d_{T}(u,v) = k_1 + k_2\), but \(ecc(u) = k_1 + rad(T)\) and \(ecc(v) = k_2 + rad(T)\) in \(T\). Hence, \(u\) and \(v\) cannot be adjacent in \(ecc(T)\). Similar to the above argument, \(u\) and \(v\) have a common neighbour \(z\), and thus \(d_{ecc(T)}(u,v) = 2\) in \(ecc(T)\).
Case 3. Let \(u\) and \(v\) be the vertices that have a common ancestor (except for \(c\)) with respect to \(x\) in \(T\). In this case, it is obvious that \(u\) and \(v\) are not adjacent in \(ecc(T)\), that is, \(u \nsim v\) in \(ecc(T)\). Additionally, since \(u\) and \(v\) share a common ancestor in \(T\), they also have at least two common neighbours (\(y\) and \(z\)) in \(ecc(T)\). Furthermore, both \(u\) and \(v\) are not adjacent to their respective ancestors. Therefore, we can conclude that \(d_{ecc(T)}(u,v) = 2\) in \(ecc(T)\).
Case 4. Let \(u\) and \(v\) be any two vertices that have no common ancestor (except for \(c\)) with respect to each of the vertices \(x\), \(y\), and \(z\) in \(T\). Since \(x\), \(y\), and \(z\) are diametrical leaves of \(T\), the paths from the root \(c\) to \(x\), \(y\), and \(z\) in \(T\) are pairwise disjoint. Hence, it is straightforward to observe that \(u\) and \(v\) are adjacent to each of \(x\), \(y\), and \(z\) in \(ecc(T)\). Thus, we can conclude that \(d_{ecc(T)}(u,v) = 2\) in \(ecc(T)\), as there exists a path of length 2 connecting them through either \(x\), \(y\), or \(z\) in \(ecc(T)\).
Therefore, we have shown that for every \(u\) vertex in \(T\), we have \(ecc(u)=2\) in \(ecc(T)\). Thus, we have \(diam(ecc(T)) = rad(ecc(T)) = 2\), which implies that \(ecc(T)\) is a 2-self centered graph. ◻
Corollary 1. Let \(T\) be a tree with exactly one center vertex. If among the diametrical leaves, there does not exist any triple \((x,y,z)\) such that the distance between each pair of vertices \(x,y\) and \(z\) is equal to the diameter of \(T\), \(diam(ecc(T))=3\).
Proof. It is obvious from Lemma 3. ◻
Theorem 3. The diameter of \(ecc(T)\) is at most 3 for any tree \(T\).
Proof. In case there are two centers in \(T\), based on Lemma 2, it can be inferred that \(ecc(T)\) is isomorphic to the coclique extension of \(P_4\), implying that \(diam(ecc(T))=3\). In case there are only one center vertex in \(T\), taking into account Lemma 3 and Corollary 1 , we can conclude directly. ◻
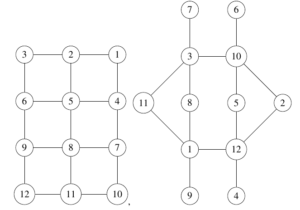
Remark 1. Theorem 3 is applicable only for trees. In general graphs, the diameter of the eccentric graph can exceed 3. For instance, consider the \(3 \times 4\) grid graph \(G\) shown in Figure 4. In this case, we have \(diam(ecc(G)) = 5\), which demonstrates that the diameter can exceed 3 in general graphs.
In this paper, starting from Akiyama’s eccentric graph definition in 1985, we revealed the diametral properties of trees. First, we made a slight correction to a theorem given by Akiyama et. al. Subsequently, we concluded that the diameter of eccentric graphs of any tree at most 3. Despite the limited number of studies on the eccentric graph of a graph until now, it is highly likely that this will shed light on many problems in graph theory and also spectral graph theory. For example, it is clear that the diameter of \(ecc(G)\) cannot be greater than the diameter of \(G\) since \(d_{ecc(G)}(u,v)\leq diam(G)\) for any vertices \(u\) and \(v\). So, we suggest the first problem:
Problem 1. Characterize the graphs which have the same diameter with its eccentric graph.
Building on the motivation of this paper, we can also present the following problem:
Problem 2. Classify the graphs which are isomorphic to its eccentric graph.
The authors declare no conflict of interest
1970-2025 CP (Manitoba, Canada) unless otherwise stated.