A chemical structure specifies the molecular geometry of a given molecule or solid in the form of atom arrangements. One way to analyze its properties is to simulate its formation as a product of two or more simpler graphs. In this article, we take this idea to find upper and lower bounds for the generalized Randić index \(\mathcal{R}_{\alpha}\) of four types of graph products, using combinatorial inequalities. We finish this paper by providing the bounds for \(\mathcal{R}_{\alpha}\) of a line graph and rooted product of graphs.
In chemical graph theory, we identify chemical structures with graphs known as molecular graphs. For \(v\in V_G\), the degree of \(v\) in \(G\) is \(\deg_{G}(v)=N_{G}(v)\), where \(N_{G}(v)\) denotes the set of neighbors of \(v\) in \(G\). The degree of the vertices play an essential role to describe certain chemical properties of a corresponding structure. Every vertex \(v\) in a molecular graph \(G\) has degree smaller than or equal to four. We denote by \(p_G\) and \(q_G\), the number of vertices and number edges of \(G\), respectively. There are many degree-based indices that we associate with a molecular graph. These indices are numbers having an immense amount of applications in Quantitative Structure and Activity Relationships.
There are two oldest topological indices, the Zagreb indices [1,2]. These indices have been used and examined to study the molecular complexity, chirality, ZE-isomerism, and hetero-systems. The first Zagreb index is defined as: \[\label{zag} % \nonumber to remove numbering (before each equation) M_{1}(G) = \sum\limits_{v\in V_G}(\deg_{G}(v))^{2} = \sum\limits_{uv\in E_G}[\deg_{G}(u)+\deg_{G}(v)].\tag{1}\]
One of the most studied topological index, the Randić index, defined in \(1975\) by Milan Randić [3]. See also the survey by Li and Shi [4] and the recent paper Dalfó [5]. This index is essential to measure the level of carbon-atom skeleton in saturated hydrocarbons. In chemistry and pharmacology, the Randić index has significant applications. In particular, it describes boiling points, chromatographic retention times, and several other properties of alkanes.
For a graph \(G\), the general Randić index \(\mathcal{R}_\alpha(G)\) is defined as: \[\label{1} \mathcal{R}_\alpha(G)=\sum_{uv\in E(G)} (\deg_G(u)\deg_G(v))^{\alpha},\tag{2}\] where \(\alpha\) is an arbitrary real number. In [3], Randić proposed both \(\alpha = -1\) and \(\alpha = -1/2\). In [6], Bollobás and Erdős generalized it by replacing \(-1/2\) with any real number \(\alpha\). In 2017, the mathematical background of this index was improved. In [7], the hitherto unnoticed features of the Randić index were pointed out. Due to its innumerable applications, this index is enormously studied [8].
An effective way of better understanding a given chemical graph is to stimulate its formation as a product of two simpler graphs. Many graph operations such as, the Cartesian product, join of graphs, corona product, the edge corona product, the subdivision-vertex join, the subdivision edge join, the neighborhood corona, the subdivision vertex neighborhood corona, and the subdivision edge neighborhood corona are studied in the literature. For more details, we recommend the reader to see [9,17].
In [18], the corona product of two graphs was defined to address associated group isomorphisms. The corona product of two graphs \(G\) and \(H\) is defined as the graph \(G\circ H\) obtained by having \(p_G\) copies \(H_1, H_2, \ldots, H_{p_G}\) of \(H\), and then joining by an edge \(^{i}\)th vertex of \(G\) to every vertex of \(H_i\). Thus, \(p_{G\circ H}=p_G(1+p_H)\) and \(q_{G\circ H}=q_G+p_G(p_H+q_H)\). The degree of a vertex \(v\in V_{G\circ H}\) is given by: \[\label{eq0} \deg_{G\circ H}(v)=\left\{ \begin{array}{ll} \deg_{G}(v)+p_H &\mbox{if $v\in V_G$,}\\ \deg_{H}(v)+1 &\mbox{if $v\in V_H$}. \end{array} \right.\tag{3}\]
The main motivation of this paper is to find the minimum and maximum bounds for the general Randić index of different graph products. In [19], such bounds were computed in the case of the general sum-connectivity index. This paper is divided into four sections. After the introductory section, in Section 2, we calculate bounds on the general Randić index of \(R\)-graphs, including the \(R\)-vertex corona product, \(R\)-edge corona product, \(R\)-vertex neighborhood corona product, and \(R\)-edge neighborhood corona product. In Section 3, we compute the bounds on general Randić index of a line graph \(L^G\) of the graph \(G\). In Section 4, we find the lower and upper bounds for the rooted product of graphs.
In this section, we provide results related to the general Randić index of different \(R\)-graph products. For a graph \(G\), the maximum and minimum degrees of \(G\) are defined as \(\Delta_G =\max\{\deg_G(v)\mid v\in V_G\}\) and \(\delta_G =\min\{\deg_G(v)\mid v\in V_G\}\), respectively. Let \(R^G\) be the \(R\)-graph constructed from \(G\) as follows: to each edge \(e\) of \(G\) we add a new vertex \(v_e\) such that it shares one edge each with the end vertices of \(e\). Thus, \(p_{R^G}=p_G + q_G\). We denote by \(I_G\) the set of the newly added vertices to \(V_G\).
Let \(G\) and \(H\) be two connected and vertex-disjoint graphs. The \(R\)-vertex corona product of two graphs \(R^G\) and \(H\) is defined as the graph \(R^G \odot H\) obtained by having \(p_G\) copies \(H_1, H_2, \ldots, H_{p_G}\) of \(H\) and then joining by an edge \(^{i}\)th vertex of \(G\) to every vertex of \(H_i\). Thus, \(p_{R^G \odot H}=p_G+q_G+p_Gp_H\) and \(q_{R^G \odot H}=3q_G+p_Gq_H+p_Gp_H\). The degree of a vertex \(v\in V_{R^G\odot H}\) is given by: \[\label{eq1} \deg_{R^G\odot H}(v)=\left\{ \begin{array}{ll} 2\deg_{G}(v)+p_H &\mbox{ if $v\in V_G$}, \\ 2 &\mbox{ if $v\in I_G$},\\ \deg_H(v)+1 &\mbox{ if $v\in V_H$}. \end{array} \right.\tag{4}\]
The general Randić index of an \(R\)-vertex corona product of \(R^G\) and \(H\) is given in the following result.
Theorem 1. Let \(G\) and \(H\) be two connected and vertex-disjoint graphs. Then, for \(\alpha <0\), the general Randić index of \(R^G \odot H\) has the following minimum and maximum bounds \[\begin{aligned} \mathcal{R}_{\alpha}(R^G\odot H)&\geq& q_{G}(2\bigtriangleup_{G}+p_{H})^{\alpha}[(2\bigtriangleup_{G}+p_{H})^{\alpha}+2^{\alpha}] +p_{G}q_{H}(\bigtriangleup_{H}+1)^{\alpha}[(\bigtriangleup_{H}+1)^{\alpha}+(2\bigtriangleup_{G}+p_{H})^\alpha],\\ \mathcal{R}_{\alpha}(R^G\odot H)&\leq& q_{G}(2\delta_{G}+p_{H})^{\alpha}[(2\delta_{G}+p_{H})^{\alpha}+2^{\alpha}] +p_{G}q_{H}(\delta_{H}+1)^{\alpha}[(\delta_{H}+1)^{\alpha}+(2\delta_{G}+p_{H})^\alpha]. \end{aligned}\] The above equalities hold if and only if both \(G\) and \(H\) are regular graphs.
Proof. Using (4) in Eq. (2), we get \[\label{qt1} \begin{split} \mathcal{R}_{\alpha}(R^G\odot H)&=\sum\limits_{uv\in E(R^G}(\deg_{R^G}(u)\deg_{R^G}(v))^{\alpha}+p_G\sum\limits_{uv\in E_H}(\deg_{H}(u)\deg_{H}(v))^{\alpha} +\sum\limits_{u\in V_{R^G}}\sum\limits_{v\in V_{H}}(\deg_{R^G}(u)\deg_{H}(v))^{\alpha}\\ &=\sum\limits_{\substack{uv\in E(R^G),\\u,v\in V_G}}[(2\deg_{G}(u)+p_H)(2\deg_{H}(v)+p_{H})]^{\alpha} +\sum\limits_{\substack{uv\in E(R^G),\\u\in V_G,v\in I_G}}[2(2\deg_{G}(u)+p_{H})]^{\alpha}\\ &\quad +p_{G}\sum\limits_{uv\in E_H}[(\deg_{H}(u)+1)(\deg_{H}(v)+1)]^{\alpha} +\sum\limits_{\substack{u\in V_{R^G}\\u\in V_G}}\sum\limits_{v\in V_{H}}[(2\deg_{G}(u)+p_{H})(\deg_{H}(v)+1)]^{\alpha}\\ &\geq q_{G}(2\bigtriangleup_{G}+p_{H})^{2\alpha}+2^{\alpha}q_{G}(2\bigtriangleup_{G}+p_{H})^{\alpha} +p_{G}q_{H}(\bigtriangleup_{H}+1)^{2\alpha} +p_{G}p_{H}(2\bigtriangleup_{G}+p_{H})^\alpha(\bigtriangleup_{H}+1)^{\alpha}\\ &=q_{G}(2\bigtriangleup_{G}+p_{H})^{\alpha}[(2\bigtriangleup_{G}+p_{H})^{\alpha}+2^{\alpha}] +p_{G}q_{H}(\bigtriangleup_{H}+1)^{\alpha}[(\bigtriangleup_{H}+1)^{\alpha}+(2\bigtriangleup_{G}+p_{H})^\alpha]. \end{split}\tag{5}\] Similarly we have the following inequality. \[\label{qt2} \begin{split} \mathcal{R}_{\alpha}(R^G\odot H)&\leq q_{G}(2\delta_{G}+p_{H})^{\alpha}[(2\delta_{G}+p_{H})^{\alpha}+2^{\alpha}] + p_{G}q_{H}(\delta_{H}+1)^{\alpha}[(\delta_{H}+1)^{\alpha}+(2\delta_{G}+p_{H})^\alpha]. \end{split}\tag{6}\] The above equalities hold if and only if \(G\) and \(H\) are regular graphs. This completes the proof. ◻
The \(R\)-edge corona product of \(R^G\) and \(H\) is defined as the graph \(R^G\ominus H\) obtained by having \(q_G\) copies \(H_1, H_2, \ldots, H_{q_G}\) of \(H\), and then joining by an edge \(^{i}\)th vertex of \(I_G\) to every vertex of \(H_i\). Thus, \(p_{R^G\ominus H} = p_G+q_G+q_Gp_H\) and \(q_{R^G\ominus H} =3q_G+q_Gq_H+q_Gp_H\). The degree of a vertex \(v\in V_{R^G\ominus H}\) is given by: \[\label{eq2} \deg_{R^G\ominus H}(v)=\left\{ \begin{array}{ll} 2\deg_{G}(v) &\mbox{ if $v\in V_G$}, \\ 2+p_{H} &\mbox{ if $v\in I_G$},\\ \deg_{H}(v)+1 &\mbox{ if $v\in V_H$}. \end{array} \right.\tag{7}\]
The general Randć index of \(R\)-edge corona product of an \(R^G\) and \(H\) is given in the following result.
Theorem 2. Let \(G\) and \(H\) be two connected and vertex-disjoint graphs. Then, for \(\alpha <0\), the general Randić index of \(R^G \ominus H\) has the following minimum and maximum bounds \[\begin{split} \mathcal{R}_{\alpha}(R^G\ominus H)&\geq4^{\alpha}q_{G}\bigtriangleup_{G}^{2\alpha}+2^{\alpha+1}q_{G}\bigtriangleup^{\alpha}_{G}(p_{H}+2)^{\alpha} +q_{G}q_{H}(\bigtriangleup_{H}+1)^{2\alpha}+q_{G}p_{H}(p_{H}+2)^{\alpha}(\bigtriangleup_{H}+1)^\alpha,\\ \mathcal{R}_{\alpha}(R^G\ominus H)&\leq4^{\alpha}q_{G}\delta_{G}^{2\alpha}+2^{\alpha+1}q_{G}\delta^{\alpha}_{G}(p_{H}+2)^{\alpha} +q_{G}q_{H}(\delta_{H}+1)^{2\alpha}+q_{G}p_{H}(p_{H}+2)^{\alpha}(\delta_{H}+1)^\alpha. \end{split}\] The above equalities hold if and only if both \(G\) and \(H\) are regular graphs.
Proof. Using (7) in Eq. (2), we get \[\label{qt3} \begin{split} \mathcal{R}_{\alpha}(R^G\ominus H)&=\sum\limits_{uv\in E_{R^G}}(\deg_{R^G}(u)\deg_{R^G}(v))^{\alpha}+q_G\sum\limits_{uv\in E_H}(\deg_{H}(u)\deg_{H}(v))^{\alpha} +\sum\limits_{u\in V_{R^G}}\sum\limits_{v\in V_{H}}(\deg_{R^G}(u)\deg_{H}(v))^{\alpha}\\ &=4^{\alpha}\sum\limits_{\substack{uv\in E_{R^G},\\u,v\in V_G}}(\deg_{G}(u)\deg_{H}(v))^{\alpha}+\sum\limits_{\substack{uv\in E_{R^G},\\u\in V_G,v\in I_G}}(2\deg_{G}(u)(p_{H}+2))^{\alpha}\\ &\quad +q_{G}\sum\limits_{uv\in E_H}[(\deg_{H}(u)+1)(\deg_{H}(v)+1)]^{\alpha} +\sum\limits_{\substack{u\in V_{R^G}\\u\in I_G}}\sum\limits_{v\in V_{H}}[(p_{H}+2)(\deg_{H}(v)+1)]^{\alpha}\\ &\geq4^{\alpha}q_{G}\bigtriangleup_{G}^{2\alpha}+2^{\alpha+1}q_{G}\bigtriangleup^{\alpha}_{G}(p_{H}+2)^{\alpha} +q_{G}q_{H}(\bigtriangleup_{H}+1)^{2\alpha}+q_{G}p_{H}(p_{H}+2)^{\alpha}(\bigtriangleup_{H}+1)^\alpha. \end{split}\tag{8}\] Similarly, we have the following inequality. \[\label{qt4} \begin{split} \mathcal{R}_{\alpha}(R^G\ominus H)&\leq4^{\alpha}q_{G}\delta_{G}^{2\alpha}+2^{\alpha+1}q_{G}\delta^{\alpha}_{G}(p_{H}+2)^{\alpha} +q_{G}q_{H}(\delta_{H}+1)^{2\alpha}+q_{G}p_{H}(p_{H}+2)^{\alpha}(\delta_{H}+1)^\alpha. \end{split}\tag{9}\] The above equalities hold if and only if \(G\) and \(H\) are regular graphs. This completes the proof. ◻
The \(R\)-vertex neighborhood corona product of \(R^G\) and \(H\) is defined as the graph \(R^G\boxdot H\) obtained by having \(p_G\) copies \(H_1, H_2, \ldots, H_{p_G}\) of \(H\) and then joining by an edge the neighbors of a vertex of \(G\) in \(R^G\) that is on the \(i\)-th position in \(R^G\) to every vertex of \(H_i\). Thus \(p_{R^G\boxdot H} = p_G+q_G+p_Gp_H\) and \(q_{R^G\boxdot H}=3q_G+p_Gq_H+4q_Gp_H\) number of edges. The degree of vertices of \(R^G\boxdot H\) are given by: \[\deg_{R^G\boxdot H}(u)= \left\{ \begin{array}{ll} 2(p_{H}+1), & {\rm if} \ u\in V_G \\[2mm] \frac{5a-4}{2}, & {\rm if} \ u\in I_G \\[2mm] \end{array} \right.\] \[\label{eq3} \begin{array}{ll} \deg_{R^G\boxdot H}(v)=\deg_{H}(v)+2\deg_{G}(u) &\mbox{if $v\in V_H, u\in V_G$}. \end{array}\tag{10}\] Here \(v\in V_{H_i}\) corresponds to the \(^{i}\)th vertex \(v\in V_G\) in \(R^G\).
The general Randić index of an \(R\)-vertex neighborhood corona product of \(R^G\) and \(H\) is given in the following result.
Theorem 3. Let \(G\) and \(H\) be two connected and vertex-disjoint graphs. Then, for \(\alpha <0\), the general Randić index of \(R^G\boxdot H\) has the following minimum and maximum bounds \[\begin{split} \mathcal{R}_{\alpha}(R^G\boxdot H)&\geq q_{G}(p_{H}+2)^{2\alpha}\bigtriangleup_{G}^{2\alpha}+2^{\alpha+1}q_{G}(p_{H}+2)^\alpha(p_{H}+1)^{\alpha} (\bigtriangleup_{G}+2)^\alpha\\ &\quad +p_{G}q_{H}(\bigtriangleup_{H}+2\bigtriangleup_{G})^{2\alpha}\\ &\quad +p_{H}(p_{H}+2)^\alpha\sum\limits_{\substack{u\in V_G,\\w_i\in N_{G}(u), w_i\in V_G}}\bigtriangleup^\alpha_{G}(\bigtriangleup_{H}+2\bigtriangleup_{G})^{\alpha}\\ &\quad +2^\alpha p_{H}(p_{H}+1)^\alpha\sum\limits_{\substack{u\in V_G,\\w_{i}\in N_{G}(u), w_{i}\in I_G}}(\bigtriangleup_{H}+2\bigtriangleup_{G})^\alpha \end{split}\] \[\begin{split} \mathcal{R}_{\alpha}(R^G\boxdot H)&\leq q_{G}(p_{H}+2)^{2\alpha}\delta_{G}^{2\alpha}\\ &\quad +2^{\alpha+1}q_{G}(p_{H}+2)^\alpha(p_{H}+1)^{\alpha} (\delta_{G}+2)^\alpha+p_{G}q_{H}(\delta_{H}+2\delta_{G})^{2\alpha}\\ &\quad +p_{H}(p_{H}+2)^\alpha\sum\limits_{\substack{u\in V_G,\\w_i\in N_{G}(u), w_i\in V_G}}\delta^\alpha_{G}(\delta_{H}+2\delta_{G})^{\alpha}\\ &\quad +2^\alpha p_{H}(p_{H}+1)^\alpha\sum\limits_{\substack{u\in V_G,\\w_{i}\in N_{G}(u), w_{i}\in I_G}}(\delta_{H}+2\delta_{G})^\alpha. \end{split}\] The equalities hold if and only if both \(G\) and \(H\) are regular graphs.
Proof. Using (10) in Eq. (2), we get \[\label{qt5} \begin{split} \mathcal{R}_{\alpha}(R^G\boxdot H)&=\sum\limits_{uv\in E_{R^G}}(\deg_{R^G}(u)\deg_{R^G}(v))^{\alpha}+p_G\sum\limits_{uv\in E_H}(\deg_{H}(u)\deg_{H}(v))^{\alpha}\\ &\quad +\sum\limits_{u\in V_{R^G}}\sum\limits_{v\in V_{H}}(\deg_{R^G}(u)\deg_{H}(v))^{\alpha}\\ &=\sum\limits_{\substack{uv\in E_{R^G},\\u,v\in V_G}}[(\deg_{G}(u)(p_{H}+2))(\deg_{H}(v)(p_{H}+2))]^{\alpha}\\ &\quad +\sum\limits_{\substack{uv\in E_{R^G},\\u\in V_G,v\in I_G}}[(\deg_{G}(u)(p_{H}+2))(2(p_{H}+1))]^{\alpha}\\ &\quad +p_{G}\sum\limits_{uv\in E_H,w_i\in V_G}[(\deg_{H}(u)+2\deg_{G}(w_i))(\deg_{H}(v)+2\deg_{G}(w_{i}))]^{\alpha}\\ &\quad +\sum\limits_{\substack{u\in V_G\\w_i\in N_{G}(u), w_i\in V_G}}\sum\limits_{v\in V_{H}}[(\deg_{G}(w_i)(p_{H}+2))(\deg_{H}(v)+2\deg_{G}(u))]^{\alpha}\\ &\quad +\sum\limits_{\substack{u\in V_G,\\w_{i}\in N_{G}(u), w_{i}\in I_G}}\sum\limits_{h\in V_{H}}[(2(p_{H}+1)(\deg_{H}(v)+2\deg_{G}(u))]^{\alpha} \\ &\geq q_{G}(p_{H}+2)^{2\alpha}\bigtriangleup_{G}^{2\alpha}+2^{\alpha+1}q_{G}(p_{H}+2)^\alpha(p_{H}+1)^{\alpha} (\bigtriangleup_{G}+2)^\alpha\\ &\quad +p_{G}q_{H}(\bigtriangleup_{H}+2\bigtriangleup_{G})^{2\alpha}\\ &\quad +p_{H}(p_{H}+2)^\alpha\sum\limits_{\substack{u\in V_G \\w_i\in N_{G}(u), w_i\in V_G}}\bigtriangleup^\alpha_{G}(\bigtriangleup_{H}+2\bigtriangleup_{G})^{\alpha}\\ &\quad +2^\alpha p_{H}(p_{H}+1)^\alpha\sum\limits_{\substack{u\in V_G\\w_{i}\in N_{G}(u), w_{i}\in I_G}}(\bigtriangleup_{H}+2\bigtriangleup_{G})^\alpha. \end{split}\tag{11}\] Similarly, we have the following inequality. \[\label{qt6} \begin{split} \chi_{\alpha}(R^G\boxdot H)&\leq q_{G}(p_{H}+2)^{2\alpha}\delta_{G}^{2\alpha}+2^{\alpha+1}q_{G}(p_{H}+2)^\alpha(p_{H}+1)^{\alpha} (\delta_{G}+2)^\alpha\\ &\quad +p_{G}q_{H}(\delta_{H}+2\delta_{G})^{2\alpha}\\ &\quad +p_{H}(p_{H}+2)^\alpha\sum\limits_{\substack{u\in V_G,\\w_i\in N_{G}(u), w_i\in V_G}}\delta^\alpha_{G}(\delta_{H}+2\delta_{G})^{\alpha}\\ &\quad +2^\alpha p_{H}(p_{H}+1)^\alpha\sum\limits_{\substack{u\in V_G,\\w_{i}\in N_{G}(u), w_{i}\in I_G}}(\delta_{H}+2\delta_{G})^\alpha. \end{split}\tag{12}\] The above equalities hold if and only if \(G\) and \(H\) are regular graphs. This completes the proof. ◻
The \(R\)-edge neighborhood corona product of \(R^G\) and \(H\) is defined as the graph \(R^G\boxminus H\) obtained by having \(q_G\) copies \(H_1, H_2, \ldots, H_{q_G}\) of \(H\), and then joining by and edge the neighbors of a vertex of \(I_G\) in \(R^G\) that is on the \(^{i}\)th position in \(R^G\), to every vertex in \(H_i\). Thus, \(p_{R^G\boxminus H} = p_G+q_G+q_Gp_H\) and \(q_{R^G\boxminus H}= 3q_G+q_Gq_H+2q_Gp_H\). The degree of a vertex \(v\in V_{R^G\boxminus H}\) is given by: \[\label{eq4} \deg_{R^G\boxminus H}(v)=\left\{ \begin{array}{ll} \deg_{G}(v)(2+p_H) &\mbox{ if $v\in V_G$}, \\ 2 &\mbox{ if $v\in I_G$},\\ \deg_{H}(v)+2 &\mbox{ if $v\in V_H$}. \end{array} \right.\tag{13}\]
The general Randić index of an \(R\)-edge neighborhood corona product of \(R^G\) and \(H\) is given in the following result.
Theorem 4. Let \(G\) and \(H\) be two connected and vertex-disjoint graphs. Then for \(\alpha <0\), the general Randić index of \(R^G\boxminus H\) has the following minimum and maximum bounds \[\begin{split} \mathcal{R}_{\alpha}(R^G\boxminus H)\geq& q_{G}(p_{H}+2)^{2\alpha}\bigtriangleup_{G}^{2\alpha}+2^\alpha q_{G}(p_{H}+2)^\alpha\bigtriangleup^\alpha_{G} +q_{G}q_{H}(\bigtriangleup_{H}+2)^{2\alpha}\\ &+p_{H}(p_{H}+2)^\alpha\sum\limits_{\substack{u\in I_G,\\w_{i}\in N_{G}(u), w_{i}\in V_G}}\bigtriangleup_{G}^\alpha(\bigtriangleup_{H}+2)^\alpha,\\ \mathcal{R}_{\alpha}(R^G\boxminus H)\leq& q_{G}(p_{H}+2)^{2\alpha}\delta_{G}^{2\alpha}+2^\alpha q_{G}(p_{H}+2)^\alpha\delta^\alpha_{G} +q_{G}q_{H}(\delta_{H}+2)^{2\alpha}\\ &+p_{H}(p_{H}+2)^\alpha\sum\limits_{\substack{u\in I_G,\ w_{i}\in N_{G}(u), w_{i}\in V_G}}\delta_{G}^\alpha(\delta_{H}+2)^\alpha. \end{split}\] The equalities hold if and only if both \(G\) and \(H\) are regular graphs.
Proof. Using (13) in Eq. (2), we get \[\label{qt7} \begin{split} \mathcal{R}_{\alpha}(R^G\boxminus H)=&\sum\limits_{uv\in E_{R^G}}(\deg_{R^G}(u)\deg_{R^G}(v))^{\alpha}+q_G\sum\limits_{uv\in E_H}(\deg_{H}(u)\deg_{H}(v))^{\alpha}\\ &+\sum\limits_{u\in V_{R^G}}\sum\limits_{v\in V_{H}}(\deg_{R^G}(u)\deg_{H}(v))^{\alpha}\\ =&\sum\limits_{\substack{uv\in E_{R^G},\\u,v\in V_G}}[(\deg_{G}(u)(p_{H}+2))(\deg_{G}(v)(p_{H}+2))]^{\alpha}\\ &+\sum\limits_{\substack{uv\in E_{R^G},\\u\in V_G,v\in I_G}}(2\deg_{G}(u)(p_{H}+2))^{\alpha}\\ &+q_{G}\sum\limits_{uv\in E_H}[(\deg_{H}(u)+2)(\deg_{H}(v)+2)]^{\alpha}\\ &+\sum\limits_{\substack{u\in I_G,\\w_{i}\in N_{G}(u), w_{i}\in V_G}}\sum\limits_{v\in V_{H}}[(\deg_{G}(w_i)(p_{H}+2))(\deg_{H}(u)+2)]^{\alpha} \\ \geq& q_{G}(p_{H}+2)^{2\alpha}\bigtriangleup_{G}^{2\alpha}+2^\alpha q_{G}(p_{H}+2)^\alpha\bigtriangleup^\alpha_{G} +q_{G}q_{H}(\bigtriangleup_{H}+2)^{2\alpha}\\ &+p_{H}(p_{H}+2)^\alpha\sum\limits_{\substack{u\in I_G,\\w_{i}\in N_{G}(u), w_{i}\in V_G}}\bigtriangleup_{G}^\alpha(\bigtriangleup_{H}+2)^\alpha. \end{split}\tag{14}\] Similarly, we have following bound. \[\label{qt8} \begin{split} \mathcal{R}_{\alpha}(R^G\boxminus H)\leq& q_{G}(p_{H}+2)^{2\alpha}\delta_{G}^{2\alpha}+2^\alpha q_{G}(p_{H}+2)^\alpha\delta^\alpha_{G}+q_{G}q_{H}(\delta_{H}+2)^{2\alpha}\\ &+p_{H}(p_{H}+2)^\alpha\sum\limits_{\substack{u\in I_G,\\w_{i}\in N_{G}(u), w_{i}\in V_G}}\delta_{G}^\alpha(\delta_{H}+2)^\alpha. \end{split}\tag{15}\] The above equalities hold if and only if \(G\) and \(H\) are regular graphs, which completes the proof. ◻
Let \(G\) be a simple graph with vertex set \(V_G=\{v_1,\ldots,v_{p_G}\}\) and edge set \(E_G=\{e_1,\ldots,e_{p_G}\}\). We construct a line graph \(L^G\) to \(G\) as follows. The set of vertices of \(L^G\) is the same as the set of edges of \(G\). Thus, \(V_{L^G}=E_G\). Also, \(E_{L^G}=\{\{e_i,e_j\}\,\,|\,\,e_i, e_j\text{ share a common vertex in }G \}\). Thus \(p_{L^G}=q_G\) and \(q_{L^G}=\frac{1}{2}\sum_{i=1}^{p_G}(\deg(v_i))^2-q_G\). Thus using (1), \(q_{L^G}=\frac{1}{2}M_1(G)-q_G\). The degree of a vertex \(v\in L^G\) is given by: \[\label{eq5} \begin{array}{ll} \deg_{L^G}(v)=\deg_G(v_i)+\deg_G(v_j)-2 &\mbox{ if $v=v_iv_j, ~ \forall ~ v_i,v_j\in V_G$}. \end{array}\tag{16}\]
We compute the lower and upper bounds on the general Randić index of \(L^G\) in the following result.
Theorem 5. Let \(G\) be a connected graph. Then, for \(\alpha<0\), the bounds for the general Randić index of \(L^G\) are given by \[\begin{aligned} 2^{\alpha}(\Delta_{G}-1)^{2\alpha}\left(\frac{1}{2}M_1(G)-q_{G}\right)\leq \mathcal{R}_{\alpha}(L^G)\leq2^{\alpha}(\delta_{G}-1)^{2\alpha}\left(\frac{1}{2}M_1(G)-q_{G}\right). \end{aligned}\] The equality holds if and only if \(G\) is a regular graph.
Proof. Using (16) in Eq. (2), we get \[\label{eqn1} \begin{split} \mathcal{R}_{\alpha}(L^G)&=\sum\limits_{uv\in E_{L^G}}(\deg_{L^G}(u)\deg_{L^G}(v))^{\alpha}\\ &=\sum\limits_{\substack{u=w_iw_j \\v=w_jw_k \in E_G}}[(\deg_{G}(w_i)\deg_{G}(w_j)-2)(\deg_{G}(w_j)+\deg_{G}(w_k)-2)]^\alpha\\ &\geq2^{\alpha}(\bigtriangleup_{G}-1)^{2\alpha}\left(\frac{1}{2}M_1(G)-q_{G}\right). \end{split}\tag{17}\] Similarly, we have the following inequality. \[\label{eqn2} \mathcal{R}_{\alpha}(L^G)\leq2^{\alpha}(\delta_{G}-1)^{2\alpha}\left(\frac{1}{2}M_1(G)-q_{G}\right).\tag{18}\] The above equalities hold if and only if \(G\) is a regular graph. ◻
A rooted graph is a labeled graph with one vertex labeled as the root. Let \(Y\) be a labeled graph with \(p_Y\) number of vertices. Let \(G\) be a sequence of \(p_Y\) rooted graphs \(G_1,G_2,\ldots,G_{p_Y}\). The rooted product of \(Y\) and \(G\) is defined as the graph \(Y^G\) obtained by having \(p_Y\) copies of \(G\) and identifying the rooted vertex of \(G_i\) \((1\leq i\leq p_Y)\) with \(i\)-th vertex of \(Y\). Thus, \(p_{Y^G}= p_G= p_{G_1}+p_{G_2}+\dots+p_{G_{p_Y}}\) and \(q_{Y^G}=q_G+q_Y\). Let \(w_i\) be the rooted vertex of \(G_i\). The degree of a vertex \(v\in V_{Y^G}\) is given by \[\label{eq6} \deg_{Y^G}(v)=\left\{ \begin{array}{ll} \deg_{Y}(v)+\deg_{G_i}(w_i) &\mbox{if $v\in V_Y$}, \\ \deg_Y(v)+\deg_{G_i}(w_i) &\mbox{if $v\in V_G,v=w_i$},\\ \deg_{G_i}(v) &\mbox{if $v\in V_G,v\neq w_i$}. \end{array} \right.\tag{19}\]
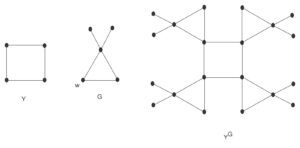
In the following result, the bounds on the general Randić index of a rooted product of given graphs are computed.
Theorem 6. Let \(Y\) be a labeled graph and \(G\) be a sequence of rooted graphs \(G_1, \ldots, G_{p_Y}\). Then, for \(\alpha<0\), we have \[\begin{split} \mathcal{R}_{\alpha}(Y^G)\geq& \sum\limits_{ij\in E_Y}(\bigtriangleup_{Y}+\omega_i)^\alpha(\bigtriangleup_{Y}+\omega_j)^{\alpha}+ \sum\limits_{i=1}^{p_Y}\mathcal{R}_{\alpha}(G_i)\\ &+\sum\limits_{i=1}^{p_Y}|N_{G_i}(w_i)|\bigtriangleup_{G_i}^{\alpha}\left[ (\bigtriangleup_{Y}+\bigtriangleup_{G_i})^{\alpha}-\bigtriangleup_{G_i}^{\alpha}\right],\\ \mathcal{R}_{\alpha}(Y^G)&\leq \sum\limits_{ij\in E_Y}(\delta_{Y}+\omega_i)^\alpha(\delta_{Y}+\omega_j)^{\alpha}\\ &+ \sum\limits_{i=1}^{p_Y}\mathcal{R}_{\alpha}(G_i)+\sum\limits_{i=1}^{p_Y}|N_{G_i}(w_i)|\delta_{G_i}^{\alpha}\left[ (\delta_{Y}+\delta_{G_i})^{\alpha}-\delta_{G_i}^{\alpha}\right]. \end{split}\] The equalities hold if and only if \(Y\) and \(G_i\) are regular graphs.
Proof. The number of neighbors of \(w_i\) is denoted by \(|N_{G_i}(w_i)|\) and the degree of \(w_i\) is denoted by \(\omega_i\) in \(G_i\). Using (19) in Eq. (2), we get \[\begin{aligned} \mathcal{R}_{\alpha}(Y^G)=&\sum\limits_{ij\in E_Y}[(\deg_{Y}(i)+\omega_i)(\deg_{Y}(j)+\omega_j)]^{\alpha}\\ &+\sum\limits_{i=1}^{p_Y}\left[\sum\limits_{\substack{uv\in E_{G_i}\\u,v\neq w_i}}(\deg_{G_i}(u)\deg_{G_i}(v))^{\alpha}\right]\\ &+\sum\limits_{i=1}^{p_Y}\left[\sum\limits_{\substack{uv\in E_{G_i}\\u\in V_{G_i},v=w_i}}[\deg_{G_i}(u)(\deg_{Y}(i)+\omega_i)]^{\alpha}\right]\\ =&\sum\limits_{ij\in E_Y}[(\deg_{Y}(i)+\omega_i)(\deg_{Y}(j)+\omega_j)]^{\alpha}\\ &+\sum\limits_{i=1}^{p_Y}\left[\mathcal{R}_{\alpha}(G_i)-\sum\limits_{\substack{uv\in E_{G_i}\\u\in V_{G_i},v=w_i}}(\deg_{G_i}(u)\omega_i)^{\alpha}\right]\\ &+\sum\limits_{i=1}^{p_Y}\left[\sum\limits_{\substack{uv\in E_{G_i}\\u\in V_{G_i},v=w_i}}[\deg_{G_i}(u)(\deg_{Y}(i)+\omega_i)]^{\alpha}\right]\\ \geq&\sum\limits_{ij\in E_Y}(\bigtriangleup_{Y}+\omega_i)^\alpha(\bigtriangleup_{Y}+\omega_j)^{\alpha}+ \sum\limits_{i=1}^{p_Y}\mathcal{R}_{\alpha}(G_i)\\ &+\sum\limits_{i=1}^{p_Y}|N_{G_i}(w_i)|\bigtriangleup_{G_i}^{\alpha}\left[ (\bigtriangleup_{Y}+\bigtriangleup_{G_i})^{\alpha}-\bigtriangleup_{G_i}^{\alpha}\right]. \end{aligned}\] Similarly, we can show that \[\begin{split} \mathcal{R}_{\alpha}(Y^G)\leq&\sum\limits_{ij\in E_Y}(\delta_{Y}+\omega_i)^\alpha(\delta_{Y}+\omega_j)^{\alpha}+ \sum\limits_{i=1}^{p_Y}\mathcal{R}_{\alpha}(G_i)\\ &+\sum\limits_{i=1}^{p_Y}|N_{G_i}(w_i)|\delta_{G_i}^{\alpha}\left[ (\delta_{Y}+\delta_{G_i})^{\alpha}-\delta_{G_i}^{\alpha}\right]. \end{split}\] The above equalities hold if and only if \(Y\) and \(G_i\) are regular graphs. This completes the proof. ◻
Let the sequence of graphs \(G_1,G_2,G_3,\dots,G_{p_H}\) be isomorphic to a graph \(G\). Then, we denote the rooted product of \(H\) and \(G\) by \(H\{G\}\). This rooted product is called a cluster of \(H\) and \(G\). Thus, using Theorem 6, we get at the following result.
Corollary 1. Let \(H\) be a labeled graph, and \(G\) be a sequence of isomorphic rooted
graphs
\(G_1,G_2,\dots,G_{p_H}\). Then, for
\(\alpha<0\), we have \[\begin{split}
\mathcal{R}_{\alpha}(H\{G\})\geq&
q_{H}(\bigtriangleup_{Y}+\omega)^{2\alpha}+p_H \mathcal{R}_{\alpha}(G)\\
&+p_H|N_{G}(w)|\bigtriangleup_{G_i}^{\alpha}\left[
(\bigtriangleup_{H}+\bigtriangleup_{G_i})^{\alpha}-\bigtriangleup_{G_i}^{\alpha}\right],\\
\mathcal{R}_{\alpha}(H\{G\})\leq&
q_{H}(\delta_{Y}+\omega)^{2\alpha}+p_H \mathcal{R}_{\alpha}(G)\\
&+p_H|N_{G}(w)|\delta_{G_i}^{\alpha}\left[
(\delta_{H}+\delta_{G_i})^{\alpha}-\delta_{G_i}^{\alpha}\right],
\end{split}\] where \(\omega=\deg_{G}(w)\).
We have obtained the lower, and upper bounds for the general Randić index \(\mathcal{R}_{\alpha}\) of four types of graph operations involving an \(R\)-graph. Additionally, we have determined the bounds for the general Randić index of a line graph, and rooted product of graphs.
The authors are grateful to the anonymous referee for their valuable comments and suggestions that improved this paper.
This research is supported by the Soft Scientific Research Foundation of Sichuan Provincial Science and Technology Department(2018ZR0265) and Key Project of Sichuan Provincial Department of Education under grant 18ZA0118.
Also this research is supported by the Start-Up Research Grant 2016 of United Arab Emirates University (UAEU), Al Ain, United Arab Emirates via Grant No. G00002233 and UPAR Grant of UAEU via Grant No. G00002590.
The authors declare no conflict of interest
1970-2025 CP (Manitoba, Canada) unless otherwise stated.