Let \( G=(V,E) \) be a simple connected graph with vertex set \( G \) and edge set \( E \). The harmonic index of graph \( G \) is the value \( H(G)=\sum_{uv\in E(G)} \frac{2}{d_u+d_v} \), where \( d_x \) refers to the degree of \( x \). We obtain an upper bound for the harmonic index of trees in terms of order and the total domination number, and we characterize the extremal trees for this bound.
Let \(G=(V,E)\) be a simple, undirected and connected graph with vertex set \(V=V(G)\) and edge set \(E=E(G)\), respectively. Here, \(uv\) represents an edge in the graph \(G\) that connects two vertices given by \(u\) and \(v\). Moreover, the number of edges incident to having \(u\) in graph \(G\) is indicated by \(deg(u)\) (or \(d_u\)), which is also known as the vertex degree \(u\). Given that \(d_u=1\), a vertex \(u\) in \(G\) is termed a pendant or leaf. In a graph \(G\), the greatest vertex degree is expressed with the notation \(\Delta(G)\) (or simply \(\Delta\)).
The open neighborhood of each vertex \(v \in V\) denotes the \(N(v) = \{u \in V|uv \in E\}\) set. Meanwhile, the closed neighborhood denotes the \(N[v]=N(v)\cup \{v\}\) set. The cycle and the path on \(n\) vertices are expressed as \(C_n\) and \(P_n\), respectively. Assume \(T\) is a tree. Then, the longest path that exists between the two leaves defines a tree’s diameter. Provided that \(v_1, v_2, \ldots, v_d\) denotes a path in which the diameter is obtained, we may state that it resembles a diametrical path in \(T\). To designate the forest generated by \(T\) via eliminating the vertices of \(u_1, u_2, \ldots, u_k\) or the edges \(e_1, e_2, \ldots, e_k\) in \(T\), we employ \(T-\{u_1, u_2, \ldots, u_k\}\) or \(T-\{e_1, e_2, \ldots, e_k\}\). For other notations and terminologies that are not defined here, please refer to the book by West [1].
Provided that every vertex \(V(G) \setminus D\) possesses a neighbor in \(D\), then the subset known as \(D\subseteq V(G)\) is termed a dominating set that belongs to \(G\). On the other hand, the minimal cardinality referring to a \(G\) dominating set is termed the domination number, represented by \(\gamma(G)\). If every vertex \(G\) has a neighbor in \(D\), a subset known as \(D \subseteq V(G)\) is termed the total dominating set, expressed as TDS. The total domination number of \(G\), indicated by \(\gamma_t(G)\), is the minimum cardinality of a TDS [2]. Please see [3] for a summary of the latest findings on the total domination number in graphs. Domination and total domination in graphs has been an active research area in graph theory [4-6]. The harmonic index of graph \(G\) is the value of
\[H(G)=\sum_{uv\in E(G)} \frac{2}{d_u+d_v}.\]
For some results on extremal results and bounds for harmonic index, refer to [7-10].
Recently, the domination number has been studied in relation to some degree based topological indices such as the geometric-arithmetic, Randić, Zagreb, harmonic or Sombor index, respectively, see [9, 11-14]. Mojdeh et al. [15] obtained some upper bounds for the Zagreb indices of trees, unicyclic and bicyclic graphs with the given total domination number. Ahmad Jamri et al. [16,17] determined the upper and lower bounds of the Randić index for trees with a given total domination number. Very recently, Bermudo et al. [18] obtained an upper bound for the geometric-arithmetic index of trees with a given total domination number, and characterized the extremal trees for this bound. This article is a continuation of these studies. Namely, we present a new upper bound of the harmonic index in terms of the order and the total domination number, and we characterize the extremal trees for that bound.
In this section, we present a new upper bound for the harmonic index of trees in terms of order and the total domination number, as well as a characterization of trees that attain this upper bound. We first describe which of these extremal trees.
We define a class of trees \(\mathcal{F}\) by recursion. Let \(\mathcal{F}\) be a family of trees where \(P_{4t} \in \mathcal{F}\) for \(t\geq 1\). We construct new graphs in \(\mathcal{F}\) as follows. If \(T' \in \mathcal{F}\) satisfies that there exists a vertex \(v\) belonging to a minimum total dominating set in \(T'\) such that \(N(v)=\{v_1, v_2\}\) where \(d(v_1)=d(v_2)=2\), then attach a path \(P_{4k+1}\), \(k\geq 1\), to the vertex \(v\) and construct the graph \(T\) with the vertex set \(V(T)=V(T')\cup V(P_{4k+1})\) and the edge set \(E(T)=E(T')\cup E(P_{4k+1})\cup\{vx\}\) where \(x\) is a leaf in \(P_{4k+1}\). Then, \(T \in \mathcal{F}\). An example of a tree in the family \(\mathcal{F}\) is shown in Figure 1.
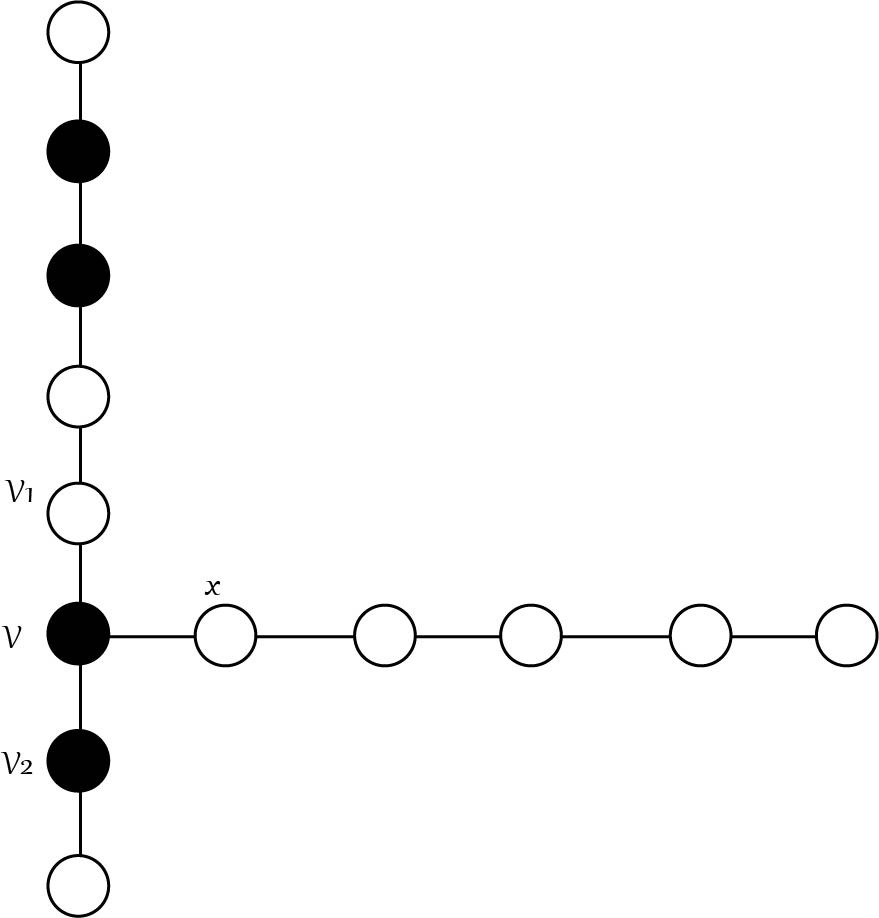
To simplify our calculations, we denote \[f(n,\gamma_t)=\frac{11}{30}n+\frac{4}{15}\gamma_t-\frac{1}{6}.\]
We have the following outcome.
Lemma 1. \(H(T)=f(n(T),\gamma_t(T))\) for every \(T\in \mathcal{F}\).
Proof. Assume that \(n_i\) is the number of vertices with degree \(i\). For any tree \(T \in \mathcal{F}\) with \(n\) vertices and a total domination number \(\gamma_t\), we get \[n_1+n_2+n_3=n, ~~~ n_1+2n_2+3n_3=2(n-1), ~~~ \gamma_t=2n_3+\frac{n-5n_3}{2}=\frac{n-n_3}{2}.\] Therefore, we have \(n_1=n-2\gamma_t+2\), \(n_2=4\gamma_t-n-2\) and \(n_3=n-2\gamma_t\). By the definition of the Harmonic index and the structure of trees \(T \in \mathcal{F}\), we conclude that \[\begin{aligned} H(T)&=\frac{2}{3}n_1+\frac{6}{5}n_3+\frac{1}{2}\left(n-1-n_1-3n_3\right)=\frac{2}{3}n\left(n-2\gamma_t+2 \right)+\frac{6}{5}\left(n-2\gamma_t \right)+\frac{1}{2}\left(8\gamma_t-3n-3\right)\\ &=\frac{11}{30}n+\frac{4}{15}\gamma_t-\frac{1}{6}. \end{aligned}\]
This completes the proof. ◻
Lemma 2. Let \(T\) be any tree with order \(n\) and total domination number \(\gamma_t\). Suppose that there exists a vertex \(v\in V(T)\) such that \(d(v)=i\ge 3\), \(N(v)=\{u_1,u_2,\ldots,u_i\}\), \(d(u_i)=j\ge 2\) and \(d(u_k)=1\) for all \(k\in \{1,2,\ldots,i-1\}\). Set \(T^\prime=T-u_1\), if \(H(T^\prime)\le f(n-1,\gamma_t)\), then \(H(T)<f(n,\gamma_t)\).
Proof. Clearly, the total domination number of \(T^\prime\) is \(\gamma_t\) or \(\gamma_t -1\), so we have \[H(T)=H(T^\prime) + \frac{4}{i(i+1)} – \frac{2}{(i+j)(i+j-1)}.\]
If \(\gamma(T^\prime)=\gamma_t\),
\[ H(T^\prime) + \frac{4}{i(i+1)} – \frac{2}{(i+j)(i+j-1)} \le \frac{11}{30}(n-1)+ \frac{4}{15}\gamma_t -\frac{1}{6} + \frac{4}{i(i+1)} – \frac{2}{(i+j)(i+j-1)}\] \[< f(n,\gamma_t) – \frac{11}{30} + \frac{4}{i(i+1)}\] \[< f(n,\gamma_t),\] and if \(\gamma(T^\prime)=\gamma_t-1\),
\[ H(T^\prime) + \frac{4}{i(i+1)} – \frac{2}{(i+j)(i+j-1)} \le \frac{11}{30}(n-1)+ \frac{4}{15}(\gamma_t -1) -\frac{1}{6} + \frac{4}{i(i+1)} – \frac{2}{(i+j)(i+j-1)}\] \[< f(n,\gamma_t) – \frac{11}{30} -\frac{4}{15} + \frac{4}{i(i+1)}\] \[< f(n,\gamma_t), \] since \(- \frac{11}{30} + \frac{4}{i(i+1)}<0\) and \(- \frac{11}{30} -\frac{4}{15} + \frac{4}{i(i+1)}<0\) for any \(i\ge 3\).
This completes the proof. ◻
Now, we prove that \(f(n(T),\gamma_t(T))\) is the upper bound for the harmonic index of any tree with order \(n\) and total domination number \(\gamma_t\).
Theorem 1. Let \(T\) be a tree of order \(n\) and total domination number \(\gamma_t\). Then \[\label{22} H(T)\leq f(n,\gamma_t), \nonumber%\frac{11}{30}n+\frac{4}{15}\gamma_t-\frac{1}{6},\nonumber\] with equality holds if and only if \(T \in \mathcal{F}\).
Proof. Let us prove the result by using the induction hypothesis on the number of vertices. We denote \(f(n,\gamma_t)=\frac{11}{30}n+\frac{4}{15}\gamma_t-\frac{1}{6}\). If \(n=4\), then \(T\) is path \(P_4\) or star \(S_4\). We have seen that \(H(P_4)=f(4,2)\) and \(H(S_4)=\frac{3}{2}< \frac{11}{30}(4)+\frac{4}{15}(2)-\frac{1}{6}=f(4,2)\). We suppose that the inequality is true for every tree with \((n-1)\) vertices, and consider a tree \(T\) with order \(n\) and total domination number \(\gamma_t\). We take a diameter path \(diam(T)=v_0v_1 \ldots v_d\) in \(T\). By Lemma 2, we can assume that \(d(v_1)=2\). Thus, we only need to discuss the following two cases.
Case 1. \(d(v_2)=m\ge 3\).
Denote \(N(v_2)=\{v_1,v_3,w_1,w_2,\ldots,w_{m-2}\}\), \(d(w_l)=s_l \leq 2\) and \(d(v_3)=k\). We take \(T^{\prime\prime}=T-\{v_0,v_1\}\). It is clear that there exists a total dominating set \(D\) in \(T\) such that \(v_1\in D(T)\) and \(v_2\in N(D \setminus \{v_2\})\), which implies that \(\gamma_t(T^{\prime\prime})=\gamma_t-1\). We get
\[ H(T)= H(T^{\prime\prime}) + \sum^{m-2}_{l=1} \frac{2}{s_l+m} + \frac{2}{m+2} + \frac{2}{1+2} + \frac{2}{m+k} – \frac{2}{m-1+k} – \sum^{m-2}_{l=1} \frac{2}{s_l+m-1}\] \[\le \frac{11}{30}(n-2)+ \frac{4}{15}(\gamma_t-1)-\frac{1}{6} – \sum^{m-2}_{l=1} \frac{2}{(m+s_l)(m-1+s_l)} + \frac{2}{2+m} + \frac{2}{3}\nonumber\] \[\le f(n,\gamma_t) – \frac{1}{3} + \frac{6}{(m+2)(m+1)}\nonumber\] \[< f(n,\gamma_t), \] since \(- \frac{1}{3} + \frac{6}{(m+2)(m+1)}<0\) for all \(m\ge 3\).
Case 2. \(d(v_2)=2\).
Denote \(N(v_3)=\{v_2,v_4,x_1,x_2,\ldots, x_{k-2}\}\) and \(d(v_4)=r\), \(d(x_l)=t_l\) for every \(l\in \{1,2,\ldots, k-2\}\). For any \(l\in \{1,2,\ldots, k-2\}\), if there exist two vertices \(y_1,y_2\) such that \(y_1 \in N(x_1)\) and \(y_2 \in N(y_1)\), then we get a diametrical path of \(T\), i.e., \(y_2y_1x_lx_3x_4\ldots v_d\). So by the above discussion we can assume that \(t_l=d(y_1)=2\).
Subcase 2.1. \(k\ge 3\).
Let \(T^{\prime\prime}=T-\{v_0,v_1,v_2\}\). In such a case, \(\gamma_t(T^{\prime\prime})=\gamma_t-2\). Thus we have \[ H(T)= H(T^{\prime\prime}) + \sum^{k-2}_{l=1} \frac{2}{k+t_l} + \frac{2}{k+r} + \frac{2}{k+2} + \frac{2}{1+2} + \frac{2}{2+2}- \frac{2}{k-1+r}-\sum^{k-2}_{l=1} \frac{2}{k-1+t_l} \]\[ \leq \frac{11}{30}(n-3)+ \frac{4}{15}(\gamma_t-2) -\frac{1}{6} – \frac{2(k-2)}{(k+2)(k+1)}- \frac{2}{(k+r)(k+r-1)} + \frac{2}{k+2}+ \frac{1}{2} + \frac{2}{3}\]\[< f(n,\gamma_t) – \frac{7}{15} – \frac{2(k-2)}{(k+2)(k+1)} + \frac{2}{k+2}\]\[< f(n,\gamma_t), \] since \(- \frac{7}{15} – \frac{2(k-2)}{(k+2)(k+1)} + \frac{2}{k+2}<0\) for all \(k\ge 3\).
Subcase 2.2. Suppose that \(k=2\).
Denote \(N(v_4)=\{ v_3,a_1, a_2,\ldots, a_{r-1}\}\) and \(d(a_l) \geq 2\) for every \(l \in \{1,2,\ldots, r-2\}\). We can assume that \(v_4 \notin D\) for any the total dominating set \(D\) in \(T\). We take \(T_4=T-\{v_0, v_1, v_2, v_3 \}\) such that \(\gamma_t(T_4)=\gamma_t-2\). Therefore, we get \[ H(T)= H(T_4) + \frac{ 2}{3} + \frac{4\times 2}{4}+\frac{2}{r+2}+\sum_{l=1}^{r-1}\frac{2}{r+d(a_l)}-\sum_{l=1}^{r-1}\frac{2}{r+d(a_l)-1} \]\[\leq \frac{11}{30}(n-4)+ \frac{4}{15}(\gamma_t-2) -\frac{1}{6} +\frac{5}{3} +\frac{2}{r+2}+\sum_{l=1}^{r-1}\frac{2}{(r+d(a_l))({r+d(a_l)-1})} \]\[< f(n,\gamma_t)-\frac{1}{3}+\frac{2}{r+2}\]\[<f(n,\gamma_t), \] for any \(r\geq 4\). If \(r=3\), since \(v_4 \notin D\), there are two following cases.
There is a path \(w_2- w_1- w -v_4\) in \(T\) such that \(d(w_2)=1\) and \(d(w_1)=d(w)=2\). We take \(T_3=T-\{w, w_1, w_2\}\) and we have \[ H(T)= H(T_3) + \frac{ 2}{3} + \frac{ 2}{4}+\frac{2\times 2}{5}- \frac{ 2}{4}+\frac{2}{d(v_5)+3}-\frac{2}{d(v_5)+2} \]\[\leq f(n-3, \gamma_t-2) +\frac{2}{3} +\frac{4}{5}-\frac{2}{(d(v_5)+3)(d(v_5)+2))} \]\[= f(n,\gamma_t)-\frac{1}{6}-\frac{2}{(d(v_5)+3)(d(v_5)+2))}\]\[< f(n,\gamma_t). \]
There is a path \(w_3-w_2- w_1- w -v_4\) in \(T\) such that \(d(w_2)=1\) and \(d(w_2)=d(w_1)=d(w)=2\). We take \(T_5=T-\{v_0, v_1, v_2, v_3, w_3\}\). Consequently, we get \[ H(T)= H(T_5) + \frac{ 2}{5} + \frac{ 4}{3}+\frac{1}{2}- \frac{ 2}{4}+\frac{2}{d(v_5)+3}-\frac{2}{d(v_5)+2} \]\[\leq f(n-5, \gamma_t-2) +\frac{67}{30}-\frac{2}{(d(v_5)+3)(d(v_5)+2))} \]\[= f(n,\gamma_t)-\frac{2}{15}-\frac{2}{(d(v_5)+3)(d(v_5)+2))}\]\[< f(n,\gamma_t). \]
If \(d(v_4)=r=2\), then we consider two following subcases.
Subcase 2.2.1 Let \(d(v_5)=2\).
Then we consider the tree \(T_4=T-\{v_0,v_1,v_2, v_3\}\) of order \(n-4\) and \(\gamma_t(T_4)=\gamma_t-2\). Therefore, we get \[ H(T)= H(T_4) + \frac{ 2}{1+2} + \frac{4\times 2}{2+2} – \frac{2}{1+2} \leq \frac{11}{30}(n-4)+ \frac{4}{15}(\gamma_t-2) -\frac{1}{6} +2 \]\[ = f(n,\gamma_t). \] With the equality holds only if \(T_4 \in \mathcal{F}\) of order \(n-4\) and the total domination number \(\gamma_t-2\), which implies that \(T \in \mathcal{F}\) of order \(n\) with \(\gamma_t\).
Subcase 2.2.2 Let \(d(v_5)\geq 3\).
Denote \(N(v_5)=\{v_4, z_1, z_2, \ldots, z_{s-1}\}\). We consider two following subcases.
Subcase 2.2.2.1 For each \(l \in \{1, 2, \ldots, s-1\}\), \(d(z_l)\leq 2\). We take \(T_5=T-\{v_0, v_1, v_2, v_3, v_4\}\) with \(\gamma_t(T_5)=\gamma_t-2\). Therefore, \[ H(T)= H(T_5) + \frac{ 2}{1+2} + \frac{3\times 2}{2+2} + \frac{2}{s+2}+\sum_{l=1}^{s-1}\frac{2}{s+d(z_l)}-\sum_{l=1}^{s-1}\frac{2}{s+d(z_l)-1} \]\[\leq \frac{11}{30}(n-5)+ \frac{4}{15}(\gamma_t-2) -\frac{1}{6} + \frac{13}{6} + \frac{2}{s+2}-\sum_{l=1}^{s-1}\frac{2}{(s+d(z_l))(s+d(z_l)-1)}\]\[\leq f(n,\gamma_t)-\frac{1}{5}+ \frac{2}{s+2}+\frac{2(s-1)}{(s+2)(s+1)}\]\[\leq f(n, \gamma_t), \] for any \(s \ge 3\). The equalities attain if and only if \(T_6 \in \mathcal{F}\) of order \(n-5\) with \(\gamma_t-2\) and \(d(v_5) =s= 3\), \(d(z_1) = d(z_2) = 2\), which implies that \(T \in \mathcal{F}\) of order \(n\) with \(\gamma_t\).
Subcase 2.2.2.2 Let \(p= \mbox{max}\, \{d(z_1), \ldots, d(z_{s-1})\} \ge 3\).
Without loss of generality, we suppose that \(d(z_1)=p\). Denote \(N(z_1)=\{v_5, y_1, \ldots, y_{p-1}\}\). By the above cases and Lemma 2, we assume that for any \(1\leq l \leq p-1\), \(d(y_l)\leq 2\). We take \(T'=T-\{z_1 v_5\}\) with two components \(T_{z_1}\) and \(T_{v_5}\) which contain the vertex \(z_1\) and \(v_5\), respectively. Then \[ H(T)= H(T_{v_5}) + H(T_{z_1})+\frac{2}{p+s} +\frac{2}{s+2}+\frac{2}{s+d(v_6)}-\sum_{l=2}^{s-2}\frac{2}{(d(z_l)+s)(d(z_l)+s-1)}\]\[- \sum_{l=1}^{p-1}\frac{2}{(d(y_l)+p)(d(y_l)+p-1)}- \frac{2}{s-1} -\frac{2}{s+d(v_6)-1}\]\[\le f(n,\gamma_t) – \frac{1}{6} +\frac{2}{p+s}- \frac{6}{(s+2)(s-1)} – \frac{2}{(d(v_6+s)(d(v_6)+s-1)}\]\[- \frac{2(p-1)}{(p+2)(p+1)} -\sum_{l=2}^{s-2}\frac{2}{(d(z_l)+s)(d(z_l)+s-1)} \]\[\leq f(n,\gamma_t) – \frac{1}{6} +\frac{2}{p+s}- \frac{2(p-1)}{(p+2)(p+1)}\]\[< f(n,\gamma_t), \] since \(- \frac{1}{6} +\frac{2}{p+s}- \frac{2(p-1)}{(p+2)(p+1)}<0\) for any \(s\geq 3\) and \(p \geq 3\).
This completes the result. ◻
We have determined an upper bound for the harmonic index of trees and we have characterized the extremal trees for this bound. Now we propose some remarks and conjectures for further discussion.
Remark 1. Let \(T\) be a tree with order \(n\), domination number \(\gamma\) and total domination number \(\gamma_t\). It was proved in [9] that \[\label{1} H(T)\leq \frac{11}{30}n+\frac{2}{5}\gamma-\frac{1}{6}.\tag{1}\] For \(\gamma_t\leq \frac{3}{2}\gamma\), we have \(2\gamma_t \leq 3 \gamma\) and consequently, \(+\frac{4}{15}\gamma_t\leq +\frac{2}{5}\gamma\). Therefore, we get \[H(T)\leq \frac{11}{30}n+\frac{4}{15}\gamma_t-\frac{1}{6} \leq \frac{11}{30}n+\frac{2}{5}\gamma-\frac{1}{6}.\] Consequently, our obtained upper bound in Theorem 1 is stronger than the upper bound (1) obtained in [9].
Remark 2. Zhong [10] presented the following upper bound on the harmonic index of trees in terms of the order \(n\geq 5\). \[\label{2} H(T)\leq \frac{4}{3}+\frac{n-3}{2}.\tag{2}\] For any \(n \geq 5\) and \(\gamma_t \leq \frac{n}{2}\), since \(f(n, \gamma_t)\) is an increasing function on \(\gamma_t\), we have \[ H(T)=\frac{11}{30}n+\frac{4}{15}\gamma_t-\frac{1}{6}=f(n, \gamma_t)\leq f(n, \frac{n}{2})=\frac{11}{30}n+\frac{4}{30}n-\frac{1}{6}\]\[=\frac{n}{2}-\frac{1}{6}=\frac{4}{3}+\frac{n-3}{2}. \] Therefore, for any tree \(T\) and with the condition \(\gamma_t \leq \frac{n}{2}\), the upper bound in [10] is smaller than upper bound in Theorem 1.
For the lower bound, we think that the following conjecture could be true.
Conjecture 1. Let \(T\) be a tree of order \(n\) and total domination number \(\gamma_t\). Then \[\label{3} H(T)\geq \big(n-\frac{1}{2}(3\gamma_t-1)\big)\Big(\frac{2}{n-\gamma_t+1}\Big)+\left(\frac{\gamma_t-1}{2}\right)\Big[\frac{2}{n-\gamma_t+2}+\frac{7}{6}\Big],\tag{3}\] with equality if and only if \(T \in T_{s, r}\) as the tree shown in Figure 2.
The first author (R. Hasni) is grateful to Universiti Malaysia Terengganu (UMT), Terengganu, Malaysia, for granting him the Sabbatical Leave and Universiti Sains Malaysia (USM), Penang, Malaysia, for the hospitality in this research work. The authors would like to thank the referees for their comments and suggestions, which improved the paper.
The authors declare no conflict of interest
1970-2025 CP (Manitoba, Canada) unless otherwise stated.