A modification of Merino-Mǐcka-Mütze’s solution to a combinatorial generation problem of Knuth is proposed in this survey. The resulting alternate form to such solution is compatible with a reinterpretation by the author of a proof of existence of Hamilton cycles in the middle-levels graphs. Such reinterpretation is given in terms of a dihedral quotient graph associated to each middle-levels graph. The vertices of such quotient graph represent Dyck words and their associated ordered trees. Those Dyck words are linearly ordered via a rooted tree that covers all their tight, or irreducible, forms, offering an universal reference point of view to express and integrate the periodic paths, or blocks, whose concatenation leads to Hamilton cycles resulting from the said solution.
In this survey, an alternate form of Merino-Mička-Mütze’s solution [1] to a combinatorial generation problem of Knuth [2] is given that is compatible with a reinterpretation [3] of the proof by Mütze [4] and Gregor, Mütze and Nummenpalo [5] of existence of Hamilton cycles in the middle-levels graph \(M_n\) [6] (\(0<n\in\mathbb{Z}\)). This graph \(M_n\) is induced by the vertices of the \((2n+1)\)-cube that represent the \(n\)– and \((n+1)\)-subsets of the set \(\{0,\ldots,2n\}\) and is further considered from Section 2 on.
The reinterpretation in question is given in terms of the associated dihedral quotient graph \(N_n\) of \(M_n\) whose vertices (here called necklaces, as in [1], see Definition 2, below) represent the Dyck words of length \(2n\) defined in the following alternate way to that of [1]:
Definition 1. The deficiency (not the excess, as in [1]) of a bitstring \(x\) is its number of 0’s minus its number of 1’s. If \(x\) has deficiency 0 and every prefix has negative deficiency, then we say that \(x\) is a Dyck word. Let \(D_n\) be the set of Dyck words of length \(2n\). Let \(D = \cup_{n\ge 0} D_n\).
Such words can be linearly ordered via a castling, or lexical, procedure [3,Section 3] (where the term lexical appears in [3] in relation to Kierstead and Trotter [6]).
The castling procedure uses restricted growth strings or RGSs of length \(n\), namely the \(n\)-strings \(a_1a_2\cdots a_n\) such that \(a_1=0\) and \(a_k\le a_{k-1}+1\), for \(1<k\le n\); see [7,page 325]-[8, page 224], that establish that their number is the Catalan number \(C_n=\frac{1}{n+1}{2n\choose n}\) [9, A100108]. By eliminating the initial zero of each such RGS, we say that the resulting \((n-1)\)-string is an \(n\)–germ \(a_2\cdots a_n=b_{n-1}\cdots b_0\), better denoted \(b_{n-1}\cdots b_0\) in what follows.
Those \(n\)-germs form an ordered tree \(\mathcal T^n\) [3,Theorem 1] whose root is the null \(n\)-germ \(\alpha=0^{n-1}\) and such that each non-null \(n\)-germ \(\alpha=a_{n-1}\cdots a_1\) with rightmost nonzero entry \(a_i\) (\(1\le i<n\)) has as parent in \(\mathcal T_n\) the \(n\)-germ \(\beta=b_{n-1}\cdots b_1\) such that \(b_i=a_i-1\) and \(a_j=b_j\), for \(j\ne i\).
To each non-null \(n\)-germ \(\alpha\) corresponds its tight RGS, or irreducible RGS, obtained by removing its largest null prefix. The ordered trees \(\mathcal T^k\) form a chain \({\mathcal T^1}\subset{\mathcal T^2}\subset\cdots\subset{\mathcal T^n}\subset\cdots\) etc. of ordered trees obtained by identifying each \(n\)-germ \(\alpha\) with the \((n+1)\)-germ obtained from \(\alpha\) by prefixing a zero to it. The limit \(\cup_{i=1}^{\infty}{\mathcal T^i}\) of this chain, denoted \(\mathcal T\), will be considered with each vertex \(v\) written as the tight RGS \(\alpha\) associated to the \(n\)-germs \(\alpha,0\alpha,00\alpha,\ldots\) that \(v\) represents, so we have \[V({\mathcal T^1})=\{\emptyset\}, V({\mathcal T^2})=\{0,1\}, V({\mathcal T^2})=\{00,01,10,11,12\},\mbox{ etc.,}\] that, as subsets of \(\mathcal T\), will be expressed as \[V({\mathcal T^1})=\{\emptyset\}, V({\mathcal T^2})=\{\emptyset,1\}, V({\mathcal T^2})=\{\emptyset,1,10,11,12\}\mbox{ etc.}\] The tree \(\mathcal T\) is partially represented on the lower-right of Table 1 by its subtree \({\mathcal T}^4\).
The castling procedure is realized by an inductively defined bijection \(F\) from the set of \(n\)-germs onto \(D_n\). This yields a natural way of designating the participating necklaces.
We “personalize” each necklace of length \(2n+1\) by taking a representation \(f_0f_1\cdots f_{2n}\) of it such that \(f_0=0\) and \(f_1\cdots f_{2n}\in D_n\), and then applying the following procedure: \[\begin{aligned} \label{ifni}\begin{array}{l} g_0:=0;\\ \mbox{begin}\\ \mbox{ for }k=1\mbox{ to }2k\mbox{ do}\\ \mbox{if }f_{k+1}=0\mbox{ then }g_{k+1}=g_k+1\mbox{ else }g_{k+1}=g_k-1;\\ k:=k+1\\ \mbox{end.} \end{array} \end{aligned}\tag{1}\] The procedure (1) replaces each bit \(f_k\) of the necklace \(f_0f_1\cdots f_{2n}\) with a corresponding integer \(g_k\) (\(0\le g_k\le n\)). We say that the resulting \((2n+1)\)-tuple \(g_0g_1\cdots g_{2n}\) is the neck, more specifically the \(n\)–neck, associated to the necklace \(f_0f_1\cdots f_{2n}\), (with the \(2n\)-string \(f_1\cdots f_{2n}\) denoted as an \(n\)–nest in [10,11]). It happens that the necklace \(f_0f_1\cdots f_{2n}\) has each bit \(f_k\) replaced by the height \(g_k\) it determines in its Dyck path [12, Subsection 3.2], so that each 0-bit is replaced either by the null height at the starting point of the Dyck path or the first appearance of each non-null height, and each 1-bit is replaced by the second appearance of that non-null height. See Remark 4 and Figure 2, below. This “personalized” representation of the necklaces, that we call necks here, are shown as an example of Theorem [3,Theorem 2 ] on the left of Table 1, below, generating \(\mathcal T^4\) via the procedure (1), where each row, except the top one, shows an inductively obtained parent correspondence \(F:n\)-germ\(^{parent}\mapsto n\)-neck\(^{parent}\) assigned to its child correspondence \(F:n\)-germ\(^{child}\mapsto n\)-neck\(^{child}\).
In Table 1, from each parent \(n\)-germ to its child \(n\)-germ, the suffix in bold, shows a unit increase at the rightmost nonzero entry of the child’s \(n\)-germ. Such suffix in bold has the same length as both the prefixes and suffixes in bold of both the parent neck and child neck. Both are to be kept unchanged, while a central-string castling takes place on the non-bold central strings. In fact, the one on the parent side is subdivided into a left Italic substring and a right Roman substring, while the other one, on the child side (i.e., inside \(n\)-neck\(^{child}\)), permutes the order of the two substrings, justifying denoting this procedure as “castling”, like in chess. The Roman substring of a central string starts at the first appearance of the integer \(\ell+1\) subsequent to the integer \(\ell\) starting the Italic side.
The upper-right of Table 1 represents how \(n\)-germs and \(n\)-necks fit for each index \(n\) into the case of the subsequent index \(n+1\), where each zero which is added as a prefix (between auxiliary parentheses) of an RGS results in the corresponding neck into an inserted substring (also between auxiliary parentheses) [10]. As a result, the ordered tree \(\mathcal T\) of RGSs yields a bijection into an ordered tree \(\mathcal T'\) covering all tight necks (namely, where all parenthesized substrings as mentioned above are eliminated).
This section is completed by providing some historical motivation and statement of the main results of [1] as Theorems 1 and 2. In the rest of the paper, we adapt the discourse of [1] to our alternate form. In Section 2 we provide additional information about the middle-levels graphs and necklace graphs. In Section 3, basic flip sequences are presented. In Section 4, periodic paths and gluing pairs are introduced. In Section 5, an initial attempt at proving theorem 1 is given. In Sections 6 and 8, sketches of the proofs of Theorems 1 and 2 are given, while Section 7 provides information about involved efficient computations.
| 0 | F | 000 → 012344321 | (0)(0)(0)∅ → 01(2(3(44)3)2)1 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 000 → 012344321 | 001 → 023443211 | (0)(0)1 → 02(3(44)3)211 | ||||||
| 2 | 000 → 012344321 | 010 → 013443221 | (0)10 → 013(44)3221 | ||||||
| 3 | 010 → 013443221 | 011 → 022134431 | (0)11 → 02213(44)31 | ||||||
| 4 | 011 → 022134431 | 012 → 034432211 | (0)12 → 03(44)32211 | ||||||
| 5 | 000 → 012344321 | 100 → 012443321 | ==== == ======== | ||||||
| 6 | 100 → 012443321 | 101 → 024433211 | |||||||
| 7 | 100 → 012443321 | 110 → 013324421 | 1. 10 | ||||||
| 8 | 110 → 013324421 | 111 → 024421331 | 11 101. 110 | ||||||
| 9 | 111 → 024421331 | 112 → 033244211 | 12. 111 120 | ||||||
| 10 | 110 → 013324421 | 120 → 014433221 | |||||||
| 11 | 120 → 014433221 | 121 → 022144331 | |||||||
| 12 | 121 → 022144331 | 122 → 033221441 | |||||||
| 13 | 122 → 033221441 | 123 → 044332211 | |||||||
An expressed objective of [1] is to generate all \((k,\ell)\)-combinations, i.e. all ways of choosing a subset \(S\) of a fixed size \(k\) from the set \([n]:=\{1,\ldots,n\}\), with \(n=k+\ell\). Each such subset \(S\) is encoded by a bitstring of length \(n\) with exactly \(k\) many 1’s, where the \(i\)-th bit is 1 if and only if the element \(i\) is contained in \(S\).
Buck and Wiedemann conjectured in [13] that all \((n+1,n+1)\)-combinations are generated by
star transpositions, for every \(n\ge 1\), i.e. in each step the element 1
either enters or leaves the set. The corresponding flip
sequence \(\alpha\) records
the position of the bit swapped with the first bit in each step, where
positions are indexed in \([2n+1]\) and
\(\alpha\) has length \(N:={2n+2\choose n+1}.\) Buck-Wiedemann’s
conjecture was independently raised by Havel [14] and became known as the
middle-levels conjecture, name coming from an
equivalent formulation of the problem, which asks for a Hamilton cycle
in the middle-levels graphs, recalled below in Section 2.
In [], Knuth conjectured that there is a star transposition that orders the \((n+1,n+1)\)-combinations, for every \(n\ge 1\), such that the flip sequence \(\alpha\) has a block structure \(\alpha=(\alpha_0,\alpha_1,\ldots,\alpha_{2n})\), where each block \(\alpha_i\) has length \(\frac{N}{2n+1}=\frac{1}{2n+1}{2(n+1)\choose n+1}\) and is obtained from \(\alpha_0\) by element-wise addition of \(i\) mod \(2n+1\), where \(i\in[2n]\). As the entries of \(\alpha\) are from \([2n+1]\), the numbers \(1,\ldots,2n+1\) are chosen as addition residue-class representatives, rather than the usual \(0,\ldots,2n\). Note that \(\frac{N}{2n+1}=2C_n\), where \(C_n=\frac{1}{n+1}{2n\choose n}\) is the n-th Catalan number. Then, [1] proves the following.
Theorem 1. [1,Theorem 1] For any \(n\ge 1\) and \(1\le s\le 2n\) that is coprime to \(2n+1\), there is a star-transposition ordering of all \((n+1,n+1)\)-combinations such that the corresponding flip sequence is of the form \(\alpha=(\alpha_0,\alpha_1,\ldots,\alpha_{2n})\) with each block \(\alpha_i\) obtained from \(\alpha_0\) by element-wise addition of \(i.s\) modulo \(2n+1\), where \(i\in[2n]\).
Remark 1. By omitting the first entry of every \((n+1,n+1)\)-combination, the \((n+1,n+1)\)-combinations are transformed bijectively into the vertices of the middle-levels graphs \(M_n\), so Theorem 1 can be rephrased in terms of Hamilton cycles of \(M_n\), each cycle formed as a concatenation of \(2n+1\) copies of a periodic path representing a block as in the statement of the theorem, presented below in terms of the approach of [3], with lemmas and propositions leading to the proof of Theorem 1 stated in parallel to those of [1].
The proof of Theorem 1 in [1] is constructive and translates into an algorithm that generates all \((n+1,n+1)\)-combinations by star transpositions efficiently, stated in [1] as follows.
Theorem 2. [1,Theorem 2] There is an algorithm that computes for any \(n\ge 1\) and \(1\le s\le 2n\) that is coprime to \(2n+1\), a star transposition ordering of all \((n+1,n+1)\)-combinations as in Theorem 1, with running time \(O(n)\) for each generated combination, using \(O(n)\) memory.
Since \(\mathcal T^n\) is an ordered tree, then its vertex set \(V({\mathcal T_n})\) inherits a natural linear order \(\mathcal L^n\). Thus, we have a chain of linear orders \(\mathcal L^1\subset\mathcal L^2\subset\cdots\subset\mathcal L^n\subset\cdots\) etc. The limit \(\cup_{i=1}^\infty\mathcal L^i\) of such a chain, denoted \(\mathcal L\) and consisting of tight RGSs, induces via the castling operation a linear order \(\mathcal L'\) of the tight necks, offering an universal reference point of view [10]–[11] to express and integrate the periodic paths or blocks whose concatenation leads to Hamilton cycles resulting from Remark 1.
Question 1. Can the Hamilton cycles obtained in the middle-levels graphs, or the periodic paths found for Knuth problem, according to Remark 1, be set in terms of the tight RGSs in the linear order \(\mathcal L\), or their numerical designations via the linear order \(\mathcal L'\)?
Question 2. Is it possible to find a periodic path \(P_n\) in each \(M_n\), for \(n>1\), so that when considering the composing vertices of such paths as elements of \(V({\mathcal T'})\) it happens that \(P_n\) is an initial subpath (prefix) of \(P_{n+1}\), \(\forall n>1\)?
\[1_1 0\]
\[12_3 0{\it 1}_2 0{\it 0}_1 10_2 11\]
\[123_3 0{\it 12}_2 0{\it 01}_1 0{\it 00}_2 0{\it 10}_4 0{\it 11}_1 111_3 110_4 100_2 120_4 122_3 112_4 101_0 121\]
\[1234_4 0{\it 123}_3 0{\it 012}_2 0{\it 001}_1 0{\it 000}_2 0{\it 010}_4 0{\it 011}_1 0{\it 111}_3 0{\it 110}_4 0{\it 100}_2 0{\it 120}_4 0{\it 122}_3 0{\it 112}_4 0{\it 101}_0 0{\it 121}_2\]
\[0121_2 1121_5 1221_2 1232_0 1012_5 1123_0 1230_5 1233_1 1231_0 1201_1 1200_3 1000_5 1100_4 1110_5 1111_3\]
\[1111_3 1220_4 1122_5 1112_4 1101_5 1001_0 1011_5 1120_4 1222_5 1211_3 1210_0 1010_1 1212_2 1223\]
Let \(0<n\in\mathbb{Z}\). Let \(A_n\) (resp. \(B_n\)) be the set of bitstrings of length \(2n+1\) and weight \(n\) (resp. \(n+1\)). The middle-levels graph \(M_n\) can be set as the graph whose vertex set is \(V(M_n)=A_n\cup B_n\) and whose adjacency is given by a single flip. The positions of the bitstrings in \(V(M_n)\) are denoted \(1,2,…,2n+1\) (mod \(2n+1\)), where \(2n+1\) takes the place of additive identity 0. Let \(\sigma^i(x)\) denote the cyclic right-rotation by \(i\) positions ([1] uses left-rotation, while our approach here is compatible with the treatment of [3]). The necklace \(\langle x\rangle\) of \(x\) is defined to be \(\{\sigma^i(x);i\ge 0\}\). For example, if \(x=11000\in A_2\) then \(\langle x\rangle = \{11000, 01100, 00110, 00011, 10001\}\).
Definition 2. Define the necklace graph \(N_n\) to have as vertex set all necklaces \(\langle x\rangle\), (\(x\in V(M_n)\)), with an edge between \(\langle x\rangle\) and \(\langle y\rangle\) if and only if \(x\) and \(y\) differ in a single bit. \(N_n\) is quotient graph of \(M_n\) under the equivalence relation given by cyclically rotating bitstrings. There may be, for each \(\langle x\rangle\), two distinct bits in \(x\) that reach the same \(\langle y\rangle\). But \(N_n\) is to be considered as a simple graph, so in \(N_n\) not all vertices have the same degree. \(N_n\) has less vertices than \(M_n\) by a factor of \(2n+1\).
Definition 3. To obtain a flip sequence for a Hamilton cycle in \(M_n\), we say that a path \(P=\{x_1,…,x_k\}\) in \(M_n\) is periodic if flipping a single bit in \(x_k\) yields a vertex \(x_{k+1}\) that satisfies \(\langle x_{k+1}\rangle = \langle x_1\rangle\).
Operations on sequences \(x=(x_1,\ldots,x_n)\) of integers \(x+a:=(x_1+a,…,x_k+a)\), (\(a\in\mathbb{Z}\)) and \(|x|=\) length of \(x\); of bitstrings: \(\langle x\rangle=(\langle
x_1\rangle,\ldots,\langle x_k\rangle)\mbox{ and }
\sigma^i(x)=(\sigma^i(x_1),\ldots,\sigma^i(x_k)).\)
Remark 2 (Rooted trees). Differing from [1], all rooted trees treated here have a specific right-to-left ordering for the children of each vertex. Every Dyck word \(x\in D_n\) can be interpreted as one such rooted tree on \(n\) edges, as follows, adapting the viewpoint of [1] to the setting of [3], where \(\epsilon\) stands for the empty bitstring: If \(x=\epsilon\), then \(x\) is associated to the tree formed by an isolated root; else, \(x=u0v1\), where \(u,v\in D\). The trees \(R, L\) corresponding to \(v, u\), respectively, have the tree corresponding to \(x\) with \(R\) rooted at the rightmost child of the root, and the edges from the root to all other children except that rightmost child, together with their subtrees, forming the tree \(L\). This yields a bijection from \(D_n\) onto the rooted trees with \(n\) edges.
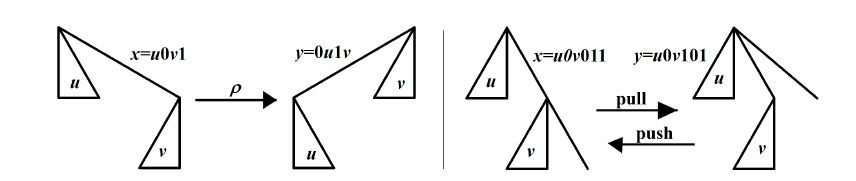
Remark 3. [Rooted-tree rotations] Given a rooted tree \(x\ne\epsilon\), let \(\rho(x)\) denote the tree obtained by rotating \(x\) to the left (in contrast to [1], that rotates it to the right), which corresponds to designating the rightmost child (not leftmost as in [1]) of the root of \(x\) as the root of \(\rho(x)\). In terms of bitstrings, if \(x = u0v1\), with \(u,v\in D\), then \(\rho(x) = 0u1v\). See the left half of Figure 2, which resembles, but differs reflectively from [1,Figure 7].
Definition 4. A plane tree is a tree embedded in the plane with a specified clockwise cyclic ordering for the neighbors of each vertex, (not counterclockwise, shortened as ccw, [1]).
For \(n\ge 1\), let \(PT_n\) be the set of all plane trees with \(n\) vertices. For any rooted tree \(x\), let \([x]\) denote the set of all rooted trees obtained from \(x\) by rotation (that is \([x] = \{\rho^i(x) ; i\ge 0\}\)), to be interpreted as the plane tree underlying \(x\), obtained by “forgetting” the root.
Let \(\lambda(x) = |[x]|\). For \(T=[x]\in PT_n\), define \(\lambda(T) = \lambda(x).\) Note that \[\lambda(x) = \min\{i\ge 1 ; \rho^i(x) = x\},\] the choice of representative of \([x]\) in defining \(\lambda(T)\) being irrelevant, for \(\lambda(T)\) is well defined. Examples for \(\lambda=4,8,2,3\) are given in Figure 2, below, in the notation of [3], meaning that each 0-bit (resp. 1-bit) is represented by the first (resp. second) appearance of each integer, counting appearances rotationally from the red 0 and in the direction indicated by “\(>\)” or by “\(<\)“. See also Remark 4.
Let \(T\in PT_n\). Let \((a,b)\in E(T)\). Let \(T^{(a,b)}\) be \(T\) seen as a rooted tree with root \(a\) and rightmost child \(b\) (not leftmost as in [1]). Let \(T^{(a,b)-}\) be obtained from \(T^{(a,b)}\) by removing all its children and their subtrees except for \(b\) and its descendants. Given \(a\in V(T)\), and all neighbors \(b_i\) of \(a\), (\(i\in[k]\)), let the trees \(t_i=T^{(a,b_i)_-}\) be called the \(a\)-subtrees of \(T\). Then, \(T=[(t_1,\ldots,t_k)]\), where \((t_1,\ldots,t_k)\) is the rooted tree obtained by gluing \(t_1,\ldots,t_k\) at their roots from right to left (in this order, reversed to that of [1]): In terms of bitstrings, \((t_1,\ldots,t_k)\) is obtained by concatenating the bitstring representations of \(t_1,\ldots,t_k\).
Given a (rooted or plane) tree \(T\), the potential \(\phi(a)\) of a vertex \(a\) of \(T\) is the sum of the distances from \(a\) to \(V(T)\). The potential \(\phi(T)\) of \(T\) is \(\phi(T)=\)min\(\{\phi(a);a\in V(T)\}\). A centroid of \(T\) is an \(a\in V(T)\) with \(\phi(a)=\phi(T)\). Merino, Mička and Mütze [1]: (i) mention that a centroid of \(T\) is a vertex whose removal splits \(T\) into subtrees with at most \(\frac{|V(T)|}{2}\) vertices each; (ii) prove in [1] that \(T\) has either one centroid or two adjacent centroids, and that if \(|E(T))|\) is even, then \(T\) has just one centroid.
Lemma 1. [1,Lemma 4] Let \(T\in PT_n\) with \(n\ge 1\) edges. Then, \(\lambda(T)|2n\). If \(T\) has a unique centroid, then \(\lambda(T)\) is even; else, \(\lambda(T) = 2n\) if \(n\) is even, and \(\lambda(T)\in\{n,2n\}\) if \(n\) is odd. For \(n\ge 4\) and any even divisor \(k\) of \(2n\), or for \(k=n\), there is \(T\in PT_n\) with \(\lambda(T) = k\).
Our objective is to define as in [1] basic flip sequences that visit every necklace exactly once in order to obtain a 2-factor (or cycle factor [1]) in \(N_n\), namely a collection of disjoint cycles that visits every vertex of \(N_n\) exactly once.
Lemma 2. Let \(n\ge 1\). For any \(x\in A_n\), there is a unique integer \(\ell = \ell(x)\) with \(0\le\ell\le 2n\) such that the last \(2n\) bits of \(\sigma^\ell(x)\) form a Dyck word. For any \(y\in B_n\), there is a unique integer \(\ell = \ell(y)\) with \(0\le\ell\le 2n\) such that the first \(2n\) bits of \(\sigma^\ell(y)\) form a Dyck word. (Modified from [1,Lemma 5] that refers in turn to [15, Problem 7]).
\(\forall x\in A_n\), let \(t(x)\in D_n\) denote the last \(2n\) bits of \(\sigma^\ell(x)\), where \(\ell =\ell(x)\), i.e. \(\sigma^\ell(x) = 0t(x)\), and \(\forall y\in B_n\), let \(t(y)\in D_n\) denote the first \(2n\) bits of \(\sigma^\ell(y)\), where \(\ell =\ell(y)\), i.e. \(\sigma^\ell(y) = t(y)1\). Then, by Lemma 2, every \(x\in A_n\) (resp. \(y\in B_n\)) can be identified uniquely with the pair \((t(x),\ell(x))\) (resp. \((t(y),\ell(y))\)).
A bijection \(f\) on \(V(M_n)\) is introduced that yields a basic flip sequence visiting every necklace exactly once, however in a different fashion to that of [1] but akin to the treatment of [3].
Let \(x\in A_n\) with \(\ell(x) = 0\), i.e. \(x = 0(u0v1) = 0t(x)\), where \(u,v\in D\). Define \(y:=f(x) = (0u1v)1 = \rho(t(x))1\in B_n\), where \(\ell(y) = 1\) and \(\rho\) is as in Remark 3. Furhter, define \(f(y) = f(f(x)) = (0u1v)0 = \rho(t(x))0\in A_n\), where \(\ell(f(y)) =0\). Extend these definitions of \(f\) for all \(x\in V(M_n)\) via \(f(x) := \sigma^{-\ell}(f(\sigma^\ell))\), where \(\ell := \ell(x)\). Then \(f\) is invertible and \(t(f(f(x)))=t(f(x))=\rho(t(x))\). In our alternate situation (differing from that of [1]), \(\ell(x)=1\), \(\ell(f(x))=0\) and \(\ell(f(f(x)))=0\). Then, for all \(x\in A_n\), \(\ell(f(x))=\ell(x)-1\) and \(\ell(f(f(x)))=\ell(x)-1\).
Definition 5. For any \(x\in V(M_n)\), let \(\kappa(x)=\min\{i>0;\langle f^i(x)\rangle=\langle x\rangle\}\), be the period of \(f\) at \(x\), namely the number of times \(f\) must be applied before returning to the same necklace of \(x\). For any \(x\in V(M_n)\), let \(P(x):=(x,f(x),f^2(x),\ldots,f^{\kappa(x)-1}(x))\) be the periodic path of \(f\) at \(x\) (Definition 3) in \(M_n\), namely a path of period \(\kappa(x)\). Therefore, \(\langle P(x)\rangle\) is a cycle in \(N_n\).
Remark 4. Our definition of \(f\) (differing from the \(f\) in [1, display(6)]) is illustrated in Figure 2, below, in the notation of [3], arising from the Dyck path associated to each vertex \(x\) of \(M_n\), with 0, or the first (resp. second) appearance of each integer in \([n+1]\), corresponding to a 0- (resp. 1-) bit in \(x\), where vertices \(x\in A_n\) (resp. \(x\in B_n\)) are expressed as “\(>\ldots >\)” (resp. “\(<\ldots <\)”), to be read from left to right (resp. right to left). The ordered trees for those vertices \(x\) are drawn to the right of each resulting periodic path in Figure 2.
Lemma 3. [1,Lemaa 6] Let \(n\ge 1\) and let \(x\in V(M_n)\). Then,
\(\forall y\in\langle x\rangle\) and \(\forall 0\le i\in\mathbb{Z}\), \(\langle f^i(x)\rangle=\langle f^i(y)\rangle\). In particular, \(\kappa(y)=\kappa(x)\).
\(\forall 0\le i\in\mathbb{Z}\), \(\langle f^i(x)\rangle=\langle f^{\kappa(x)+i}(x)\rangle\).
\(\forall 0\le i<j\le\kappa(x)\) in \(\mathbb{Z}\), \(\langle f^i(x)\rangle\ne\langle f^j(x)\rangle\).
\(\forall 0\le i\in\mathbb{Z}\), \(\kappa(f^i(x))=\kappa(x)\).
\(\kappa(x)=2\lambda(t(x))\), so \(\lambda(t(x))\) is semi-period of \(f\) at \(x\).
For any \(y\in\langle x\rangle\) and any \(0\le i\in\mathbb{Z}\), we have \(\kappa(f^i(y))=\kappa(x)\), so \(\langle P(x)\rangle=\langle P(f^i(y))\rangle\). This yields a 2-factor of \(N_n\), denoted \({\mathcal F}:=\{\langle P(x);x\in V(M_n)\}\).
Proposition 1. [1,Proposition 7] For any \(n\ge 2\), \({\mathcal F}_n\) has the following properties:
for every \(x\in V(M_n)\) the \((2i)\)-th vertex \(y\) after \(x\) on \(P(x)\) satisfies \(t(y)=\rho^i(t(x))\). Therefore, both \(P(x)\) and \(\langle P(x)\rangle\) can be identified with \([t(x)]\).
\(|V(P(x))|=2\lambda(t(x))\ge 4\) and \(\ell(f^{2i}(x))=\ell(x)+i\), \(\forall i=0,\ldots,\lambda(t(x))\).
The cycles of \({\mathcal F}_n\) are in bijective correspondence with the plane trees on \(n+1\) vertices.

By Proposition 1 item 3, the number of cycles of \({\mathcal F}_n\) fits the sequence [9, A002995]. Also, [1] mentions that the number of plane trees, or cycles of \({\mathcal F}_n\), grows exponentially.
Consider the star \(s_n=0(01)^{n-1}1\in D_n\) for \(n\ge 3\) and the footed-star \(s'_n=01s_{n-1}\in D_n\) for \(n\ge 4\). A gluing pair is a pair \((x,y)\ne(s_n,s'_n)\), with \(x=u0v011\) and \(y=u0v101\), where \(u,v\in D\).
Let \(G_n\) be the set of all gluing pairs \((x,y)\), where \(x,y\in D_n\). By seeing \(x,y\) as rooted trees, [1] declares that \(y\) is obtained from \(x\) by a pull operation, and calls its inverse a push operation. In our treatment, the right half of our Figure 1 resembles, but differs reflectively, from [1, Figure 9]. We write \(y=\mbox{pull}(x)\) and \(x=\mbox{push}(y)\), say that \(x\) is pullable, \(y\) is pushable and that \(u\) and \(v\) are the left and right subtrees of both \(x\) and \(y\).
Lemma 4. [1,Lemma 8] Let \((x,y)\in G_n\). If \(x\) has a centroid in \(u\), then \(u\) is also a centroid of \(y\), so \(\phi(y)=\phi(x)-1\). If \(y\) has a centroid in \(v\), then \(v\) is also a centroid of \(x\), so \(\phi(y)=\phi(x)+1\).
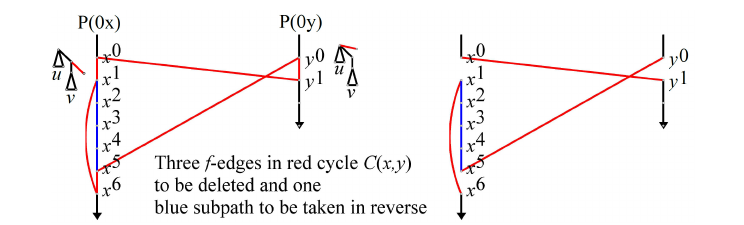
Let \((x,y)\in G_n\). Let \(x^i:=f^i(0x)\) and \(y^i:=f^i(0y)\), for \(i\ge 0\). The resulting sequences agree with the first vertices of \(P(x)\) and \(P(y)\), respectively. In such notation, we notice the 6-cycle \(C(x,y)=(x^0,y^1,y^0,x^5,x^6,x^1)\), where:
\[\begin{aligned} \label{6}\begin{array}{c} x^0=0u0v011,\\ y^1=0u0v111,\\ y^0=0u0v101,\\ x^5=0u1v101,\\ x^6=0u1v001,\\ x^1=0u1v011. \end{array} \end{aligned}\tag{2}\] Then, \(P(x)\) and \(P(y)\) are glued together by removing the alternate edges \((y^0,y^1)\), \((x^0,x^1)\) and \((x^5,x^6)\) via the symmetric difference between \(C(x,y)\) and \(P(x)\cup P(y)\).
Lemma 5. [1,Lemma 9] \((x,y)\in G_n\Rightarrow(|P(x^0)|=\kappa(x^0)\ge 8\mbox{ and }|P(y^0)|=\kappa(y^0)\ge 4)\).
Modifying the proof of Lemma 9 in [1], we get for our Lemma 5 now that \[\alpha(C(x,y))=(|u|+|v|+3,|u|+|v|+4,|u|+2,|u|+|v|+3,|u|+|v|+4,|u|+2).\] On the other hand, if \((x,y)=(s_n,s'_n)\), then \(\kappa(x^0)=4\), so \(\langle x^0\rangle = \langle x^4\rangle\), \(\langle x^2\rangle = \langle x^6\rangle\), and Lemma 5 does not hold.
Remark 5. By Lemma 5, \(\sigma^i(C(x,y))\) shares \(\sigma^i(x^0,x^1)\) and \(\sigma^i(x^5,x^6)\) with \(\sigma^i(P(x^0))\), and \(\sigma^i(y^0,y^1)\) with \(\sigma^i(P(y^0))\). These edges are said to be the \(f\)-edges of the gluing cycle \(\sigma^i(C(i,j))\).
If \([x]\ne[y]\), then \(\langle P(x)\rangle\) and \(\langle P(y)\rangle\) are distinct cycles in \(N_n\) by Proposition 1, so we have that the grafted path \[P(x^0)\nabla P(y^0):=(x^0,y^1,y^2,\ldots,y^{2\lambda(y)-1},\sigma^{-\lambda(y)}(y^0,x^5,x^4,x^3,x^2,x^1,x^6,x^7,\ldots,x^{2\lambda(x)-1}))\] is a periodic path in \(M_n\).
The \(2n+1\) periodic paths \(\sigma^i(P(x^0)\nabla P(y^0))\) form \[\cup_{i\ge0}(\sigma^i(P(x^0)\nabla P(y^0))),\mbox{ that visits all vertices of }\cup_{i\ge 0}(\sigma^i(P(x^0)\cup P(y^0))).\] Indeed, \(|P(x^0)|=2\lambda(x)\), \(|P(y^0)|= 2\lambda(y)\) and \(\sigma^{\lambda(i)}(y^{2\lambda(y)})=y^0\), by Proposition 1, item 2. Then, \(E(\cup_{i\ge0}(\sigma^i(P(x^0)\nabla P(y^0))))\) is the symmetric difference of \[E(\cup_{i\ge 0}(\sigma^i(P(x^0)\cup P(y^0))))\mbox{ with the gluing cycles }\cup_{i\ge 0}\sigma^i(C(x,y)).\]
For all \(i\ge0\), the subpath \(\sigma^i(x^1,\ldots,\sigma^5)\) of \(\sigma^i(P(x^0))\) is said to be reversed by \(\sigma^i(C(x,y))\). Two gluing cycles \(\sigma^i(C(x,y))\) and \(\sigma^j(C(x',y'))\) are compatible if they have no \(f\)-edges in common. They are nested if the edge \(\sigma^i(y^0,y^1))\) of \(\sigma^i(C(x,y))\) belongs to the path reversed by \(\sigma^j(C(x',y'))\) (see Figure 4). They are interleaved if the \(f\)-edge \(\sigma^j(x'^0,x'^1)\) of \(\sigma^j(C(x',y'))\) belongs to the path that is reversed by \(\sigma^i(C(i,j))\).
Proposition 2. [1,Proposition 10]Let \(n\ge 4\). Let \((x,y),(x'y')\in G_n\) with \([x]\ne[y]\), \([x']\ne[y']\) and \(\{[x],[y]\}\ne\{[x'],[y']\}\). Then, \(\forall 0\le i,j\in\mathbb{Z}\), \(\sigma^i(C(x,y))\) and \(\sigma^j(C(x',y'))\) are:
compatible;
interleaving \(\Leftrightarrow\) \(i=j+2\) and \(x'=\rho^2(x)\);
nested \(\Leftrightarrow\) \(i=j-1\) and \(x'=\rho^{-1}(y)\).
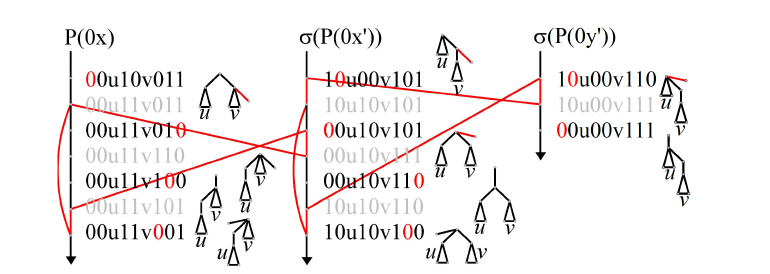
Item 3 here can be interpreted as follows: Starting at the tree \(x\), pull an edge \(e\) towards the root to reach the tree
\(y=\)pull\((x)\), then perform an inverse tree
rotation \(x'=\rho^{-1}(y)\) which
makes \(e\) pullable, and pull it again
to reach \(y'=\)pull\((x')\). Thus, nested gluing cycles
occur if and only if the same edge of the underlying plane trees is
pulled twice in succession.
Definition 6. For \(n\ge 4\), let \({\mathcal H}_n\) be the directed arc-labeled multigraph with vertex set \(PT_n\) and such that for each \((x,y)\in G_n\) there is an arc labeled \((x,y)\) from \([x]\) to \([y]\).
Some pairs of nodes in \({\mathcal H}_n\) may be connected by multiple arcs similarly oriented but with different labels, e.g. \(([0011001101],[0101001101])\) and \(([0011010011],[0101010011])\); oppositely oriented, e.g. \(([00101011],[01001011])\) and \(([00110101],[01010101])\). There may be also loops in \({\mathcal H}_n\), e.g. \(([00101101],[01001101])\).
Remark 6. Let \(\mathcal T\) be a simple subgraph of \({\mathcal H}_n\). Let \(G({\mathcal T})\) be the set of all arc labels of \(\mathcal T\). Since \(\mathcal T\) is simple, then \([x]\ne[y]\), \([x']\ne[y']\) and \(\{[x],[y]\}\ne\{[x'],[y']\}\), for all \(([x],[y]),([x'],[u'])\in G({\mathcal T})\). We say that \(G({\mathcal T})\) is interleaving-free or nesting-free, respectively, if there are no two gluing pairs \((x,y),(x',y')\in G({\mathcal T})\) such that the gluing cycles \(\sigma^i(C(x,y))\) and \(\sigma^j(C(x',y'))\) are interleaved or nested for any \(i,j\ge 0\).
Lemma 6. [1,Lemma 11] If for every \((x,y)\in G({\mathcal T})\) the root of \(x\) is not a leaf, then \(G({\mathcal T})\) is interleaving-free.
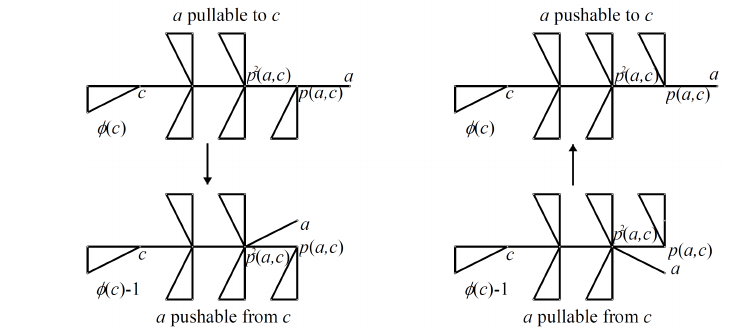
Let \(T\) be a tree, let \(a,c\in V(T)\) and let \(d(a,c)\) be the distance between \(a\) and \(c\). Let \(p^i(a,c)\) be the \(i\)-th vertex in the path from \(a\) to \(c\), (\(i=0,1,\ldots,d(a,c)\)). In particular, \(p^0(a,c)=0\) and \(p^{d(a,c)}(a,c)=c\). (See Figure 5).
Let \(c,a\in V(T)\), where \(a\) is a leaf of \(T\) and \(d(a,c)\ge 2\). Then \(a\) is pullable to \(c\) if \(p^1(a,c)\) has no neighbors between \(p^2(a,c)\) and \(a\) in the clockwise ordering of neighbors. (This and the next concepts differ from the couterclockwise stance in [1]). Also, \(a\) is pushable to \(c\) if \(p^1(a,c)\) has no neighbors between \(a\) and \(p^2(a,c)\) in the clockwise ordering of neighbors.
Let \(d(a,c)\ge 1\). Then, \(a\) is pullable from \(c\) if \(d(a,c)\ge 2\) and \(p^1(a,c)\) has at least one neighbor between \(p^2(a,c)\) and \(a\) in its clockwise ordering of neighbors or if \(c\) is not a leaf and \(d(a,c)=1\). Also, \(a\) is pushable from \(c\) if \(d(a,c)\ge 2\) and \(p^1(a,c)\) has at least one neighbor between \(a\) and \(p^2(a,c)\) in its clockwise ordering of neighbors or if \(c\) is not a leaf and \(d(a,c)=1\).
For odd \(n\ge 5\), consider the dumbbells \(d_n:=(01)^{\frac{n-1}{2}}0(01)^{\frac{n-1}{2}}1\) and \(d'_n:=\rho^{2}(d_n)=010(01)^{(n-1)/2}0(01)^{(n-3)/2}\). Each dumbbell has two centroids of degree \(\frac{n+1}{2}\), while all the remaining vertices are leaves.
If \(T\) has just one centroid \(c\), every \(c\)-subtree of \(T\) is said to be active. If \(T\) has two centroids \(c,c'\), every \(c\)-subtree except the one containing \(c'\) and every \(c'\)-subtree except the one containing \(c\) are also said to be active. For \(n\ge 4\), if \(T\ne[s_n]\) and \(T\ne[d_n]\) for odd \(n\), then \(T\) has a centroid with an active subtree that is not a single edge.
Lemma 7. [1,Lemma 12] Let \(c\) be a centroid of a plane tree \(T\), let \(a\) be a leaf of \(T\) that is pullable to \(c\) and that belongs to an active \(c\)-tree unless \(n\ge 5\) is odd with \(T=d_n\). Then, the rooted tree \(x:=x(T,c,a)=T^{(p^2(a,c),p^1(a,c))}\) is a pullable tree, the rooted tree \(y:={\rm pull}(x)\) satisfies \(\phi(y)=\phi(x)-1\) and the leaf \(a\) is pushable from \(c\) in \([y]\). Moreover, the centroids of \(x\) and \(y\) are identical and contained in the left subtrees of \(x\) and \(y\), unless \(n\ge 5\) is odd with \(x=d_n\), in which case \(x\) has two centroids, namely the roots of its left and right subtrees, and the root of the left subtree is the unique centroid of \(y\).
A leaf of \(T\) is thin if its unique neighbor in \(T\) has degree \(\le 2\); otherwise, it is thick.
Lemma 8. [1,Lemma 13] Let \(c\) be a centroid of a plane tree \(T\), let \(a\) be a thick leaf of \(T\) that is pushable to \(c\) and that belongs to an active \(c\)-subtree unless \(n\ge5\) is odd with \(T=[d'_n]\). Then, the rooted tree \(y:=y[T,c,a]:=T^{(p^1(a,c),a)}\) is a pushable tree, the rooted tree \(x={\rm push}(y)\) satisfies \(\phi(x)=\phi(y)-1\), and the leaf \(a\) is pushable from \(c\) in \([y]\). Moreover, the centroid(s) of \(x,y\) (is) are identical and contained in the right subtrees of \(x,y\), unless \(n\ge 5\) is odd with \(x=d_n\), in which case \(x\) has two centroids, namely the roots of its left and right subtrees, and the leaf of its right subtree is the unique centroid of \(y\).
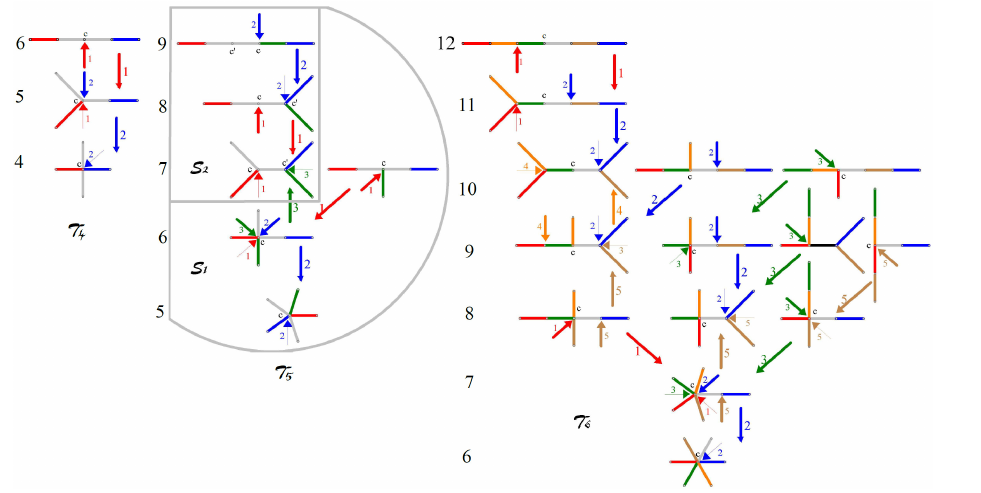
Definition 7. For \(n\ge 4\), let \({\mathcal T}_n\) be a subgraph of \({\mathcal H}_n\) such that: (a) for every \(T\in PT_n\) with \(T\ne[s_n]\), and \(T\ne[d_n]\) if \(n\) is odd, there is a centroid \(c\) of \(T\) with at least one active \(c\)-subtree \(C\) that is not a single edge; the rightmost leaf of every such \(C\) is pullable to \(c\); we fix one such leaf \(a\); (b) If \(n\) is odd and \(T=[d_n]\), let \(c\) be one of its centroids with exactly one \(c\)-subtree \(C\) which is not a leaf, namely the tree \(s_{(n+1)/2}\); the rightmost leaf of \(C\) is pullable to \(c\). In both cases, let \(x:=x(T,c,a)\) be the corresponding pullable rooted tree as defined in Lemma 7 and define \(y:=\mbox{pull}(x)\), yielding the gluing pair \((x,y)\in G_n\). We let \({\mathcal T}_n\) be the spanning subgraph of \({\mathcal H}_n\) given by the union of arcs \(([x],[y])\) labeled \((x,y)\) for all gluing pairs \((x,y)\) obtained this way. Ties between two centroids or multiple \(c\)-subtrees are broken arbitrarily. For any arc \((T,T')\), \(T'\) is an out-neighbor and \(T\) is an in-neighbor.
Lemma 9. [1,Lemma 14] For any \(n\ge 4\), \({\mathcal T}_n\) is a spanning tree of \({\mathcal H}_n\), and for every arc \((T,T')\) in \({\mathcal H}_n\), \(\phi(T')=\phi(T)-1\). Every plane tree \(T\ne[s_n]\) has exactly one neighbor \(T'\) in \({\mathcal T}_n\) with \(\phi(T')=\phi(T)-1\) which is an out-neighbor. Furthermore, \(G({\mathcal T}_n)\) is interleaving-free.
Definition 8. Consider a periodic path \(P=(x_1,\ldots,x_k)\) in \(M_n\). An integer sequence \(\alpha=(a_1,\ldots,a_k)\) is a flip sequence if \(a_i\) is the position at which \(x_{i+1}\) differs from \(x_i\), for each \(i\in[k-1]\), and the vertex \(x_{k+1}\) obtained from \(x_k\) by flipping the bit at position \(a_k\) satisfies \(\langle x_{k+1}\rangle=\langle x_1\rangle\). There is a unique integer \(\lambda\) mod \(2n+1\) given by the relation \(x_1=\sigma^\lambda(x_{k+1})\). Let \(\lambda(\alpha)=\lambda\) be said to be the shift of \(\alpha\).
[1] presents a scaling trick consisting in the construction of a flip sequence \(\alpha_0\) for one particular shift \(s\) coprime to \(2n+1\). From such a shift \(s\), a transformation \(\Upsilon\) yields every shift \(s'\) coprime to \(2n+1\), where \(\Upsilon\) consists in multiplying all entries of \(\alpha_0\) by \(s^{-1}s'\) mod \(2n+1\), with \(s^{-1}\) equal to the multiplicative inverse of \(s\).
Define \(\label{rev}\mbox{rev}(P):=(x_1,\sigma^{\lambda(\alpha)}(x_k,x_{k-1},\ldots,x_2))\) and \(\mbox{rev}(\alpha):=(a_k,a_{k-1},\ldots,a_1)-\lambda(\alpha)\), with indices taken mod \(2n+1\). Note that rev\((\alpha)\) is a flip sequence for the periodic path rev\((P)\) satisfying \(\lambda(\)rev\((\alpha))=-\lambda(\alpha)\).
Define mov\((P):=(x_2,\ldots,x_k,\sigma^{-\lambda(\alpha)}(x_1))\) and mov\((\alpha):=(a_2,\ldots,a_k,a_1+\lambda(\alpha))\), this being a flip sequence for the periodic path mov\((P)\) satisfying \(\lambda(\)mov\((\alpha))=\lambda(\alpha)\), which means that the shift is independent of the choice of the starting vertex along the path. Similarly, \(\alpha +i\) is a flip sequence for \(\sigma^{-i}(P)\) satisfying \(\lambda(\alpha +i)=\lambda(\alpha)\), \(\forall i\in{\mathbb Z}\).
For any \(x\in V(M_n)\), let \(\alpha(x)\) be the sequence of positions at which \(f^{i+1}(x)\) differs from \(f^i(x)\), \(\forall i=0,\ldots,\kappa(x)-1\). Clearly, \(\alpha(x)\) is a flip sequence for \(P(x)\) (Definition 5). By Proposition 1 item 2, \(\lambda(\alpha(x))=\lambda(t(x))\).
For any subtree \({\mathcal T}\) of \({\mathcal H}_n\) with \(G:=G({\mathcal T})\) interleaving-free as in Remark 6, define the set of necklaces \(N({\mathcal T}):=\cup_{[x]\in{\mathcal T}}\langle P(0x)\rangle\). By Proposition 1 item 1, this is the set of necklaces visited by those cycles \(\langle P(0x)\rangle\) in \(N_n\) for which \([x]\in\mathcal T\).
For any \(z\in N({\mathcal T})\) and any \(x\in z\), there is a pair \({\mathcal P}_G(X)=\{P,P'\}\) of two periodic paths \(P\) and \(P'\), both starting at \(x\in V(M_n)\) with flip sequences \(\alpha(P)\) and \(\alpha(P')\) such that \(P'=\)rev\((P)\) and \(\alpha(P')=\)rev\((\alpha(P))\). Moreover, \(\langle P\rangle\) and \(\langle P'\rangle\) are oppositely oriented in the subgraph of \(N_n\) whose vertex set is \(N({\mathcal T})\).
The node set of \({\mathcal T}_n\) is \(PT_n\). By Lemma 9, \(G({\mathcal T}_n)\) is interleaving-free. Fix \(x_1:=0^{n+1}1^n\in V(M_n)\). The pair \({\mathcal P}_{G({\mathcal T}_n)}(x_1)\) contains a periodic path \(P\) with starting vertex \(x_1\) and second vertex \(f(x_1)\) in \(M_n\) such that \(\langle P\rangle\) has vertex set \(N({\mathcal T}_n)=\cup_{[x]\in PT_n}\langle P(0x)\rangle=\{\langle x\rangle |x\in V(M_n)\}\), i.e. \(\langle P\rangle\) is Hamilton cycle in \(N_n\). The corresponding flip sequence \(\alpha(P)\) has a shift \[\begin{aligned} \label{la}\lambda(\alpha(P))=\sum_{T\in PT_n}\gamma_T.\lambda(T), \end{aligned}\tag{3}\] for numbers \(\gamma_T\in\{1,-1\}\) that are determined by which gluing cycles encoded by \({\mathcal T}_n\) are nested.
With \(s:=\lambda(\alpha(P))\), define \(\alpha_0:=\alpha(P)\) and \(\alpha_i:=\alpha_0+i.s\), for \(i\in[2n]\). If we apply the entire flip sequence \((\alpha_0,\alpha_1,\ldots,\alpha_{2n})\) to \(x_1\) in \(M_n\), then the vertex \(\sigma^{i.s}(x_1)\) is reached after applying all flips in \((\alpha_0,\alpha_1,\ldots,\alpha_{i-1})\), \(\forall i\in[2n+1]\). If \(s\) and \(2n+1\) are coprime, then \(x_1\) is reached only after applying the entire flip sequence. Since \(\alpha_0\) is the flip sequence of the Hamilton cycle \(\langle P\rangle\) in \(N_n\), the resulting sequence of bitstrings is a Hamilton cycle in \(M_n\). However, this approach requires that \(s=\lambda(\alpha(P))\) and \(2n+1\) be coprime. A technique is needed to modify \(\alpha(P)\) into another flip sequence \(\alpha'\) such that \(s':=\lambda(\alpha')\) is coprime to \(2n+1\).
Let \(p(x,y)\) indicate a pair \(x,y\in V(M_n)\) that differ in just one position. A triple of vertices \(\tau=(x,y,y')\), where \(x\in A_n\), \(\{y,y'\}\subseteq B_n\) and \(y\ne y'\), is a switch if \(x\) differs from \(y\), (resp. \(y'\)) in a single bit, and \(\langle y\rangle=\langle y'\rangle\). In \(N_n\), a switch may be considered as a multiedge \((\langle x\rangle,\langle y\rangle)=(\langle x\rangle,\langle y'\rangle)\). The shift of a switch \(\tau=(x,y,y')\), denoted \(\lambda(\tau)\), is the integer \(i\) such that \(y=\sigma^i(y')\). Denote a switch \(\tau=(x,y,y')\) compactly by writing \(x\) with the 0-bit at position \(p(x,y)\) underlined and the 0-bit at position \(p(x,y')\) overlined. This way, we write \(\tau=(0000111,1000111,0001111)=\underline{0}00\overline{0}111\). For any switch \(\tau=(x,y,y')\), the inverted switch \(\tau^{-1}=(x,y',y)\) has shift \(\lambda(\tau^{-1})=-\lambda(\tau)\). Clearly, cyclically rotating a switch yields another switch with the same shift. Also, reversing a switch yields another switch with the negated shift. For example, \(\sigma(\tau)=11\overline{0}00\underline{0}1\) has shift 1 while its reversed switch \(1\underline{0}00\overline{0}11\) has shift \(-1\).
Consider a flip sequence \(\alpha=(a_1,\ldots,a_k)\) with shift \(\lambda(\alpha)\) for a periodic path \(P=(x_1,\ldots,x_k)\) and let \(x_{k+1}\) be the vertex obtained from \(x_k\) by flipping the bit at position \(a_k\). If \((x_i,x_{i+1})=(x,y)\) for some \(i\in[k]\), then the modified flip sequence \[\begin{aligned} \label{25a} \alpha'=(a_1,\ldots,a_{i-1},p(x,y'),a_{i+1}+\lambda(\tau),\ldots,a_k+\lambda(\tau)) \end{aligned}\tag{4}\] yields a periodic path \(P'=(x'_1,\ldots,x'_k)\) that visits necklaces in the same order as does \(P\), i.e. \(\langle x_i\rangle=\langle x'_i\rangle\), for \(i\in[a_k]\), and \(\lambda(\alpha')=\lambda(\alpha)+\lambda(\tau)\). The situation where \((x_i,x_{i+1})=(x,y')\) is symmetric and considers the inverted switch \(\tau^{-1}\), with \(\lambda(\tau^{-1})=-\lambda(\tau)\).
Similarly, if \((x_i,x_{i+1})=(y',x)\) for some \(i\in[k]\), then the modified sequence \[\begin{aligned} \label{25c}\alpha':=(a_1,\ldots,a_{i-1},p(x,y)+\lambda(\tau),a_{i+1}+\lambda(\tau),\ldots,a_k+\lambda(\tau)) \end{aligned}\tag{5}\] produces a periodic path \(P'=(x'_1,\ldots,x'_k)\) that visits necklaces in the same order as \(P\), and \(\lambda(\alpha')=\lambda(\alpha)+\lambda(\tau)\). The situation \((x_i,x_{i+1})=(y,x)\) is symmetric and goes to the inverted switch \(\tau^{-1}\), with \(\lambda(\tau^{-1})=-\lambda(\tau)\).
In particular, if \(\langle
P\rangle\) is a Hamilton cycle in \(N_n\), then \(\langle P'\rangle\) is also a Hamilton
cycle in \(N_n\) with shift \(\lambda(\alpha')=\lambda(\alpha)+\lambda(\tau)\).
For any integers \(n\ge 1\), \(d\ge 1\) and \(1\le s\le d\), make the \((s,d)\)-orbit to be the maximal prefix of the sequence \(s+id\), \(i\ge0\), modulo \(2n+1\), in which all the numbers are distinct. Then, the number of distinct \((s,d)\)-orbits for fixed \(d\) and \(s\ge 1\) is \(n_d:=\)gcd\((2n+1,d)\), and the length of each orbit is \(\ell_d:=\frac{2n+1}{n_d}\), where both \(n_d\) and \(\ell_d\) are odd. For example, let \(n=10\) and \(d=6\), so \(n_d=3\), \(\ell_d=7\) and the \((1,6)\)-orbit is \((1,7,13,19,4,10,16)\), the \((2,6)\)-orbit is \((2,8,14,20,5,11,17)\) and the \((3,6)\)-orbit is \((3,9,15,21,6,12,18)\).
For any integer \(d\) (\(2\le d\le n\)) that is coprime to \(2n+1\), let \(\tau_{n,d}\) denote the sequence whose entries at the positions given by the \((1,d)\)-orbit equal \(\tau_{n,1}=\underline{0}0^{n-1}\overline{0}1^n\), including the overlined and underlined entries.
For any \(n\ge 1\), let \(Z_n\) be the set of bitstrings of length \(2n\) and weight \(n\). For any integers \(d\) (\(3\le d\le n\)) not coprime to \(2n+1\), select an arbitrary bitstring \(z=(z_2,\ldots,z_{n_d})\in Z_{(n_d-1)/2}\). Let \(\tau_{n,d,z}\) be the sequence: (a) whose entries at the positions given by the \((1,d)\)-orbit form the sequence \(\tau_{(\ell_d-1)/2,1}\), including the underlined and overlined entries, and (b) for \(j=2,\ldots,n_d\), all entries at the positions given by the \((j,d)\)-orbit form the sequence \(z_j\). Then, the number of choices for \(z\) in such a construction is \({n_d-1\choose (n_d-1)/2}\).
Lemma 10. [1,Lemma 15] Let \(n\ge 1\). For any integer \(d\) (\(1\le d\le n\)) coprime to \(2n+1\), the sequence \(\tau_{n,d}\) is a switch with \(\lambda(\tau_{n,d})=d\). For any integer \(3\le d\le n\) not coprime to \(2n+1\) and any bitstring \(z\in Z_{(n_d-1)/2}\), the sequence \(\tau_{d,n,z}\) is a switch with \(\lambda(\tau_{d,n,z})=d\).
Given a flip bijection \(f\) of \(V(M_n)\) as in Section 3, a switch \(\tau=\tau(x,y,y')\) is said to be \(f\)-conformal if either \(y=f(x)\) or \(x=f(y')\); in such cases, \((x,y)\) or \((y',x)\), respectively, is said to be the \(f\)-edge of \(\tau\). We say that \(\tau\) is \(f^{-1}\)–conformal if \(\tau^{-1}\) is conformal and we refer to the \(f\)-edge of \(\tau^{-1}\) also as an \(f\)-edge of \(\tau\). That a switch is \(f\)-conformal means that its \(f\)-edge belongs to a periodic path, as in Definition 5.
Given a subset \(G\subseteq G_n\), an \(f\)-conformal or \(f^{-1}\)-conformal switch \(\tau\) is usable with respect to \(G\) if for every \((x',y')\in G\) and all \(i\ge 0\), the three \(f\)-edges of \(\sigma^i(C(x',y'))\) in Remark 5 are distinct from the \(f\)-edges of \(\tau\). Those three \(f\)-edges are removed when joining periodic paths.
Lemma 11. [1,Lemma 16] Let \(\tau=(x,y,y')\) be an \(f^{-1}\)-conformal switch with \(f\)-edge \((y,x)\) for which \(t(x)=00\ldots\). Then \(\tau\) is usable with respect to any subset \(G\subseteq G_n\).
Lemma 12. [1,Lemma 17] Let \(n\ge 4\). The switch \(\tau_{n,1}=:(x,y,y')=\underline{0}0^{n-1}\overline{0}1^n\), where \(x\in A_n\) and \(y\in B_n\) differ in the first bit, has \(f\)-edge \((y,x)\) and is \(f^{-1}\)-conformal. The switch \(\tau_{n,2}=:\overline{0}\underline{0}(01)^{n-1}=(x,y,y')=\overline{0}\underline{0}1(01)^{n-1}\), where \(x\in A_n\) and \(y'\in B_n\) differ in the first bit, has \(f\)-edge \((y',x)\) and is \(f\)-conformal. Both switches are usable with respect to any subset \(G\subseteq G_n\).
Lemma 13. [1,Lemma 18] Let \(n\ge 11\) and let \(3\le c,d\in\mathbb{Z}\) be such that \(c.d=2n+1\). The switch \(\tau_{n,d,z}=:(x,y,y')=z\underline{0}(z0)^{(c-3)/2}z\overline{0}(z1)^{(c-1)/2}\), where \(z:=0^{(d-1)/2}1^{(d-1)/2}\in Z_{(d-1)/2}\) has \(f\)-edge \((y,x)\) and is \(f^{-1}\)-conformal and usable with respect to \(G({\mathcal T}_n)\).
Let \(n\ge 1\). Let \({\mathcal P}(n)\) be the set of prime factors of \(n\). For any \(s\in\{0,1,\ldots,n-1\}\), define \({\mathcal P}(n,s):={\mathcal P}(n)\setminus{\mathcal P}(s)\), if \(s>0\), and \({\mathcal P}(n,0):=\emptyset\).
Lemma 14. [1,Lemma 19] Let \(n\ge 1\) be such that \(2n+1\) is not a prime power. Let \(s\in\{0,\ldots,n-1\}\) be not coprime to \(2n+1\). If \({\mathcal P}(2n+1,s)\ne\emptyset\), then both numbers \(s+d\) and \(s-d\), where \(d:=\Pi\{p\in{\mathcal P}(2n+1,s)\}\), are coprime to \(2n+1\). If \({\mathcal P}(2n+1,s)=\emptyset\), then \({\mathcal P}(2n+1,s+d)={\mathcal P}(2n+1,s-d)={\mathcal P}(2n+1))\setminus\{d\}\ne\emptyset\), for any \(d\in{\mathcal P}(2n+1)\).
Lemma 15. [1,Lemma 20] Let \(n\) be an integer such that \(4\le n\le 10\) and let \(s\in\{0,\ldots,2n\}\) be not coprime to \(2n+1\). Then, both numbers in at least one of the pairs \(\{s-1,s+1\}\), \((s-2,s+2\}\), \(\{s-1,s+2\}\), \(\{s+1,s-2\}\) are coprime to \(2n+1\).
Proof. Theorem 1 is established via the scaling trick (Section 5) for each \(n\ge 1\) and any value of \(s\) coprime to \(2n+1\). For \(n=1\), via flip sequence \(\alpha:=32\) starting at \(x_1=001\) and yielding shift \(s=-1\); for \(n=2\), via flip sequence \(\alpha=1531\) starting at \(00011\) and yielding shift \(s=1\); for \(k=3\), via flip sequence \(2635426753\) starting at \(0000111\) and yielding \(s=-1\).
Assume \(n\ge 4\). Consider the spanning tree \({\mathcal T}_n\subseteq{\mathcal H}_n\) (Definition 7). In Section 5, a periodic path \(P\) is defined with starting vertex \(x_1=0^{n+1}1^n\) and second vertex \(f(x_1)\) in \(M_n\) such that \(\langle P\rangle\) is a Hamilton cycle in \(N_n\) and the shift of the corresponding flip sequence \(\alpha(P)\) is given by (3). Denote this shift by \(s:=\lambda(\alpha(P))\). If \(s\) is coprime to \(2n+1\), we are done. Let us consider the case \(s\) not coprime to \(2n+1\).
If \(4\le n\le 10\), consider the switches \(\tau_{n,1}\) and \(\tau_{n,2}\), which are \(f^{-1}\)– and \(f\)-conformal, respectively, both usable with respect to \(G({\mathcal T}_n)\) by Lemma 12. By Lemma 10, their shifts are \(\lambda(\tau_{n,1})=1\) and \(\lambda(\tau_{n,2})=2\), respectively. Consequently, by modifying the flip sequence \(\alpha(P)\) to become like \(\alpha'\) in (4) via one of the two, or both, switches, we obtain a flip sequence \(\alpha'\) with shift \[\begin{aligned} \label{28a}s':=\lambda(\alpha')=s + \chi_1.\gamma_1 + \chi_2.\gamma_2.2, \end{aligned}\tag{6}\] for certain signs \(\gamma_1,\gamma_2\in\{1,-1\}\) and with indicators \(\chi_1,\chi_2\in\{0,1\}\) that are nonzero if the corresponding switches are employed.
If \(n\ge 11\), we distinguish 3 cases: If \(2n+1\) is prime power, then \(s\) is also power of the same prime. Apply the switch \(\tau_{n,1}\) as above, modifying \(\alpha(P)\) so that the resulting flip sequence \(\alpha'\) has shift \[\begin{aligned} \label{28b}s':=\lambda(\alpha')+\gamma_1.1, \end{aligned}\tag{7}\] for some \(\gamma_1\in\{-1,1\}\), with \(s'=s\pm 1\) coprime to \(2n+1\).
If \(2n+1\) is not a prime power and \({\mathcal P}(2n+1,s)\neq\emptyset\), we define \(d:=\Pi\{p\in{\mathcal P}(2n+1,s)\}\) and \(c:=\frac{2n+1}{d}\), and consider the switch \(\tau_{n,d,z}\) from Lemma 13, modifying the flip sequence \(\alpha(P)\) so that the resulting \(\alpha'\) has shift \[\begin{aligned} \label{28c}s':=\lambda(\alpha')=s+\gamma_d.d. \end{aligned}\tag{8}\]
If \(2n+1\) is not a prime power and \({\mathcal P}(2n+1,s)=\emptyset\), then we pick some \(d\in{\mathcal P}(2n+1)\), define \(c=\frac{2n+1}{d}\) and apply switch \(\tau_{n,d,z}\), yielding a flip sequence \(\alpha'\) with shift \(s'\) given as above, which satisfies \({\mathcal P}(2n+1,z)\neq\emptyset\) by the last sentence of Lemma 14. We then modify the flip sequence a second time as in the previous case, and the switch used is distinct from the first one, as \(d':=\Pi\{p\in{\mathcal P}(2n+1,s\pm d)\}=\Pi\{p\in{\mathcal P} (2n+1)\setminus\{d\}\}\) clearly satisfies \(d'\neq d\). ◻
The switches \(\tau_{n,1}\) and \(\tau_{n,2}\) are not sufficient alone for the proof of Theorem 1, starting with \(n=52\) and \(2n+1=105=3\dot 5\dot 7\) and \(s=5\), for which none of the three numbers \(s-2=3\), \(s+1=6\) and \(s+2=7\) is coprime to \(2n+1\), so Lemma 15 cannot be applied and it is necessary to use switches \(\tau_{n,s,z}\).
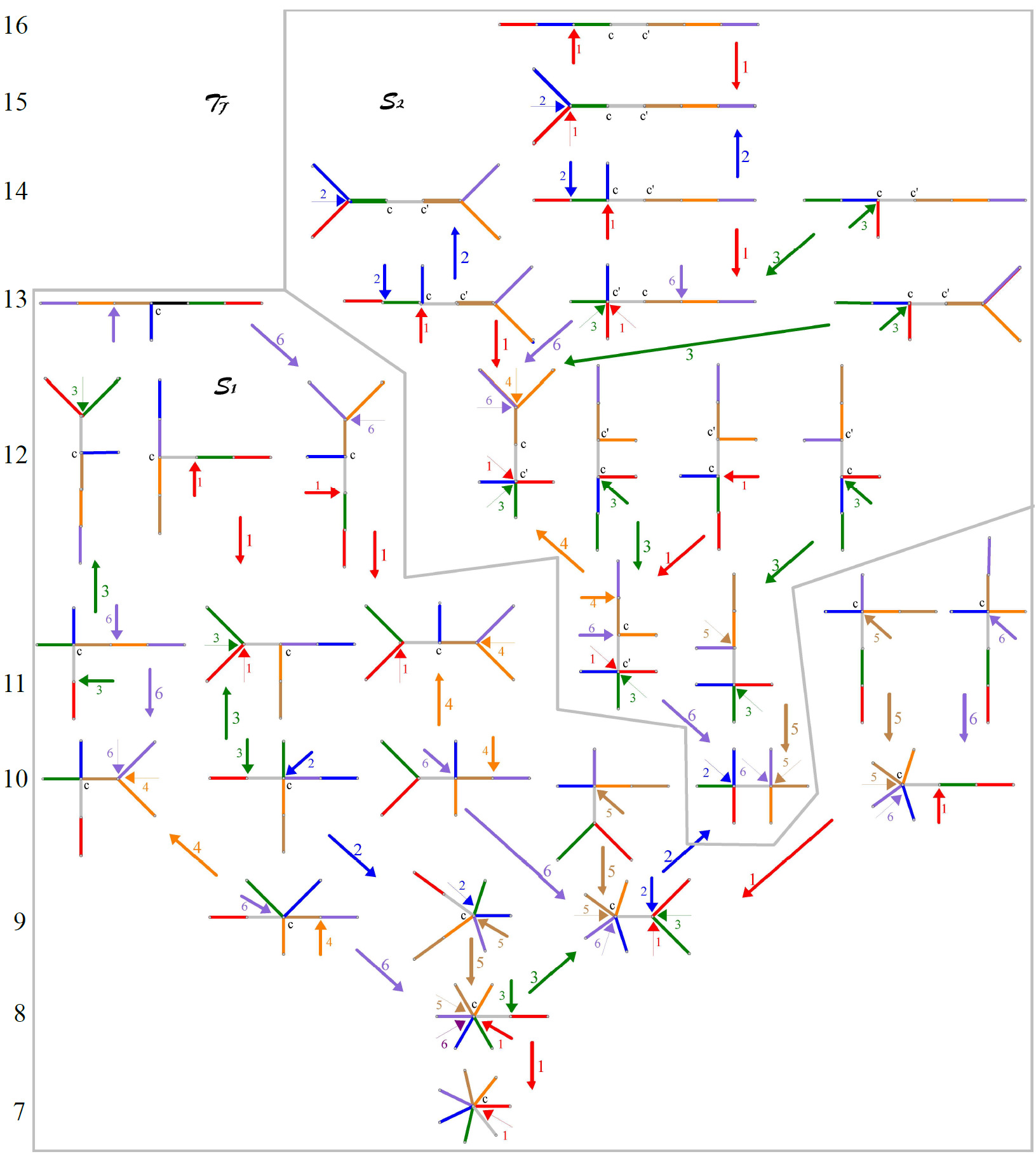
Remark 7. If we knew that \(G({\mathcal T}_n)\) is not only interleaving-free, but also nesting-free, then this would guarantee that all signs \(\gamma_T\) in (3) are positive, yielding \[\begin{aligned} \label{Cat} s=\lambda(\alpha(P))=\sum_{T\in{\mathcal T}_m}\lambda(T)=C_n. \end{aligned}\tag{9}\] Following [1] with the stance of [3], we define now another spanning tree \({\mathcal T}_n\) of \({\mathcal H}_n\) such that \(G({\mathcal T}_n)\) is both interleaving-free and nesting-free.
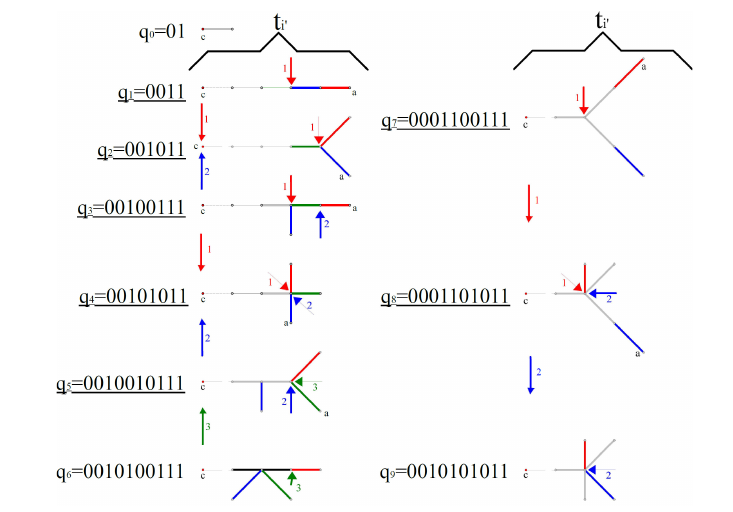
In [1], ten rooted trees are distinguished, that in our alternate viewpoint are expressed as: \[\begin{aligned} \label{eqn}\begin{array}{llll} q_0:=01,&q_1:=0011,&q_2:=001011,&q_3:=00100111,\\ q_4:=00101011,&q_5:=0010010111,&q_6:=0010100111,&q_7:=0001100111,\\ q_8:=00011010111,&q_9:=0010101011.&& \end{array} \end{aligned}\tag{10}\]
For \(n\ge 4\), let \({\mathcal T}_n\) be a subgraph of \({\mathcal H}_n\) given as follows: For each plane tree \(T\in PT_n\) with \(T\ne[s_n]\), consider a gluing pair \((x,y)\in G_n\) with either \(T=[x]\) or \(T=[y]\). Let \({\mathcal T}_n\) be the spanning subgraph of \({\mathcal H}_n\) given by the union of the arcs \(([x],[y])\), labeled \((x,y)\), for all gluing pairs \((x,y)\) obtained this way. The definition of the gluing pair \((x,y)\) for a given plane tree \(T\ne[s_n]\) proceeds as in the following three steps (T1)-(T3), unless \(n\) is odd and \(T=[d_n]\), in which case the special rule (D) is applied.
If \(n\) is odd and \(T=[d_n]\), let \(c\) be one of the centroids of \(T\) having exactly one \(c\)-subtree that is not a single edge, namely the subtree \(s_{(n+1)/2}\). Its leftmost leaf \(a\) is thick and pushable to \(c\) in \(T\), so we define \(y:=y(T,c,a)=d'_n\) and \(x:=push(y)\), as in Lemma 8.
If \(T\) has two centroids, we let \(c\) be a centroid of \(T\) whose active \(c\)-subtrees are not all single edges. If this is true for both centroids, we let \(c\) be the one for which its clockwise-ordered active \(c\)-subtrees \(t_1,\ldots,t_k\) give the lexicographically minimal string \((t_1,\ldots,t_k)\), with \(t_1\) as the first \(c\)-subtree found after the \(c\)-subtree containing the other centroid.
If \(T\) has a unique centroid, we denote it by \(c\) and consider all \(c\)-subtrees of \(T\), denoting them \(t_1,\ldots,t_k\), i.e. \(T=[(t_1,\ldots,t_k)]\) such that among all possible clockwise orderings around \(c\), the string \((t_1,\ldots,t_k)\) is lexicographically minimal.
If \(T\) has two centroids, we let \(t_{i'}\) be the first of the trees \(t_1,\ldots,t_k\) that differs from \(q_0\), in display (10).
If \(T\) has a unique centroid, then for each of the following conditions (i)-(iv), we consider all trees \(t_i\) (\(i\in[k]\)) and determine the first subtree \(t_i\) satisfying the condition, i.e. only check one of these conditions once all trees failed all previous conditions:
\(t_i=q_1\) and \(t_{i-1}=q_0\);
\(t_i\in\{q_2,q_4\}\) and \(t_{i+1}\in\{q_0,q_1,q_2\}\);
\(t_i\notin\{q_0,q_1,q_2,q_4\}\);
\(t_i\neq q_0\).
Conditions (i) and (ii) refer to the previous tree \(t_{i-1}\) and the next tree \(t_{i+1}\) in the clockwise ordering of \(c\)-subtrees, and those indices are considered modulo \(k\). Note that \(T\ne[s_n]\). Thus, at least one \(c\)-subtree is not \(q_0\) and satisfies condition (iv), so this rule to determine \(t_i\) is well defined. Let \(t_{i'}\) be the \(c\)-subtree determined in this way. Clearly, \(t_{i'}\) has at least two edges.
If \(t_{i'}=0^lq_j1^l\), for some \(l\ge 0\) and \(j\in\{1,\ldots,8\}\), i.e. \(t_{i'}\) is a path with one of the trees \(q_j\) attached to it. Then, four cases are distinguished:
(q137) If \(j\in\{1,3,7\}\), let \(a\) be the rightmost leaf of \(t_{i'}\), which is thin, and define \(x:=x(T,c,a)\) and \(y:=\mbox{pull}(x)\), as in Lemma 7. Clearly, \((j=1)\Rightarrow(y=0^{l-1}q_21^{l-1}\), if \(l>0\), and \(y=q_0^2\), if \(l=0)\); also, \((j=3)\Rightarrow (y=0^lq_41^l)\); and \((j=7)\Rightarrow (t=0^lq_81^l)\).
(q24) If \(j\in\{2,4\}\), let \(a\) be the leftmost leaf of \(t_{i'}\), which is thick, and define \(y:=y(T,c,a)\) and \(x:=\mbox{push}(y)\), as in Lemma 8. Clearly, \((j=2)\Rightarrow(x=0^{l-1}q_31^{l-1}\), if \(l>0\), and \(x=q_2q_0\), if \(l=0)\); also, \((j=4)\Rightarrow(x=0^{l-1}q_51^{l-1}\), if \(l>0\), and \(x=q_2q_0\), if \(l=0)\).
(q5) If \(j=5\), let \(a\) be the unique leaf of \(t_{i'}\) that is neither the rightmost nor the leftmost leaf of \(t_{i'}\), where \(a\) is thick, and define \(y:=y(T,c,a)\) and \(y=\mbox{push}(x)\), as in Lemma 8. Clearly, \(x=0^lq_61^l\).
(q8) If \(j=8\), let \(a\) be the leftmost leaf of \(t_{i'}\), which is thin, and define \(x:=x(T,c,a)\) and \(y:=\mbox{pull}(x)\), as in Lemma 7. Clearly, \(y=0^lq_01^l\).
Otherwise, there are three cases to be distinguished:
(e) If the potential \(\phi(T)=\phi(c)\) is even, we let \(a\) be the rightmost leaf of \(t_{i'}\) and define \(x:=x(T,c,a)\) and \(y=\mbox{pull}(x)\), as in Lemma 7.
(o1) If the potential \(\phi(T)=\phi(c)\) is odd and the leftmost leaf \(a\) of \(t_{i'}\) is thin, define \(x:=x(T,c,a)\) and \(y:=\mbox{pull}(y)\), as in Lemma 7.
(o2) If the potential \(\phi(T)=\phi(c)\) is odd and the leftmost leaf \(a\) of \(t_{i'}\) is thick, define \(y:=y(T,c,a)\) and \(x:=\mbox{push}(y)\), as in Lemma 8.
This completes the definition of \({\mathcal T}_n\). [1] refers to rules (q137), (q8), (e) and (o1) in step (T3) as pull rules and to rules (q24), (q5) and (o2) as push rules. The leaf to which one of the pull rules (q137), (q8) or (o1) is applied is always thin, whereas the leaf to which any push rule is applied is always thick.
Lemma 16. [1,Lemma 21] If \(T\) has a unique centroid \(c\), then the \(c\)-subtree \(t_{i'}\) selected in Step (T2) satisfies the following conditions:
If \(t_{i'}=q_1\), then \(t_{i'-1}=q_0\) or \(t_1=t_2=\cdots=t_k=q_1\).
If \(t_{i'}=\in\{q_2,q_4\}\), then \(t_{i'+1}\in\{q_0,q_1,q_2\}\) or \(t_1=t_2=\cdots=t_k=q_4\).
Lemma 17. [1,Lemma 22] For any \(n\ge 4\), the graph \({\mathcal T}_n\) is a spanning tree of \({\mathcal H}_n\). For every arc \((T,T')\) in \({\mathcal T}_n\), either \(\phi(T')=\phi(T)- 1\) or \(\phi(T)=\phi(T')- 1\). Every plane tree \(T\ne[s_n]\) has exactly one neighbor \(T'\) in \({\mathcal T}_n\) with \(\phi(T')=\phi(T)-1\) which is either an out-neighbor or in-neighbor. Moreover, \(G({\mathcal T}_n)\) is interleaving-free and nesting-free.
Illustrations for the spanning trees \({\mathcal T}_i\) for \(i=4,5,6,7\) are in Figures 7-8, the versions of [1, Figures 15-16] for the alternate viewpoint in this survey.
Assume \(G\subseteq G_n\) is nesting-free. A usable switch \(\tau\) is reversed if the \(f\)-edge of \(\tau\) lies on the reversed path of one of the gluing cycles \(\sigma^i(C(x',y'))\), \((x',y')\in G\), for some \(i\ge 0\), i.e. on the path \(\sigma^i(x'^1,\ldots,x'^5)\).
Lemma 18. [1,Lemma 23] Let \({\mathcal T}_n\) be the spanning tree of \({\mathcal H}_n\) of Section 7. For \(n\ge 4\), the switch \(\tau_{n,1}\) is reversed with respect to \(G({\mathcal T}_n)\) and the switch \(\tau_{n,2}\) is not reversed with respect to any set of gluing pairs \(G\subseteq G_n\). For \(n,d,z\) as in Lemma 13, the switch \(\tau_{n,d,z}\) is usable and not reversed with respect to \(G({\mathcal T}_n)\).
The algorithm in Theorem 2 is a faithful implementation of the constructive proof of Theorem 1 sketched in Section 6 which also works with the spanning tree \({\mathcal T}_n\) of Section 7. In particular, the switch \(\tau_{n,d,z}\) is usable by Lemma 18. The effective shifts of the switches \(\tau_{n,1}\), \(\tau_{n,2}\) and \(\tau_{n,d,z}\) used in the proof, i.e. the signs \(\gamma_1\), \(\gamma_2\) and \(\gamma_d\) in displays (6)-(8), can now be computed explicitly. Specifically, from Lemmas 12, 13 and 18, it is obtained: \[\begin{aligned} \label{gam}\gamma_1=(-1)(-1)=+1,\gamma_2=(+1)(+1)=(+1),\gamma_d=(-1)(+1)=-1. \end{aligned}\tag{11}\] In each product in (11), the first factor is \(-1\) if and only if the switch is \(f^{-1}\)-conformal and the second factor is \(-1\) if and only if the switch is reversed.
Proof. The input of the algorithm is the integer \(n\ge 1\), the initial combination \(x'\) and the desired shift \(\bar{s}\) coprime to \(2n+1\). Then, \(C_n\) mod \(2n+1\) is computed in \(O(n^2)\) time via Segner’s recurrence relation, namely \[C_0=1\;\mbox{ and }\;C_{n+1}=\sum_{i=0}^{n}C_iC_{n-i}.\] By (9), this yields the shift \(s\) of the flip sequence obtained from gluing without modifications. A test of whether \(s\) is coprime to \(2n+1\) proceeds, followed by the computation of one or two switches such that the shift \(s'\) of the modified flip sequence \(s'\), via (6)-(8) and (11), is coprime to \(2n+1\). In particular, the definition of \(d\) in (8) involves computing the prime factorization of \(2n+1\). From \(s'\), the scaling factor \((s')^{-1}\bar{s}\) is computed as well as the corresponding initial combination \(x\), such that \(x'\) is obtained from \(x\) by permuting columns according to the rule \(i\mapsto (s')^{-1}\bar{s}i\) (applying the inverse permutation). These remaining initial steps can be performed in \(O(n)\) time. All further computations are then performed with \(x\), and whenever a flip position is computed for \(x\), it is scaled by \((s')^{-1}\bar{s}\), before applying it to \(x'\).
To decide whether to perform an \(f\)-step or a pull/push step, the following computations are performed on the current plane tree \(T=[t(x)]\), following steps (T1)-)(T3), Section 7:
compute a centroid \(c\) of \(T\) and its potencial \(\phi(c)\), as in (T1), in time \(O(n)\) (see [16]);
compute the lexicographic subtree ordering, as in (T1), in time \(O(n)\); if the centroid is unique, this is done via Booth’s algorithm [17]; specifically, to compute the lexicographically smallest clockwise (differing from ccw in [1]) ordering \((t_1,\ldots,t_k)\) of the \(c\)-subtrees of \(T\), insert \(-1\)’s as separators between the bitstrings \(t_i\); this takes to the string \(z:=(-1,t_1,-1,,\ldots,-1,t_k)\); such trick makes Booth’s algorithm return a cyclic rotation of \(z\) that starts with -1; it follows that such rotation is also the one minimizing the cyclic subtree ordering \((t_1,\ldots,t_k)\);
compute a \(c\)-subtree of \(T\) and one of its leaves, as in steps (T2)-(T3), Section 7.
Overall, the decision of which type of step to perform next takes time \(O(n)\) to compute. Whenever a switch appears in the course of the algorithm, detectable in time \(O(n)\), a modified flip as in (4)-(5) is performed. Each time this occurs, the position \(\ell(c)\) has to be recomputed, with \(T=[t(x)]\) unchanged.
In sum, the algorithm runs in time \(O(n)\) in each step, using \(O(n)\) memory all the time, and it requires time \(O(n^2)\) for initialization. ◻
The author declares no conflicts of interest to this work.