For a graph
All graphs considered here are simple, finite and undirected. Let
A latin square of order
It is worth mentioning that cycle decomposition problems are NP –
complete in general, see [5]. Recently, Paulraja and Srimathi [6,7] proved the
necessary and sufficient conditions for the existence of
The problem of decomposing complete tripartite graphs into cycles
have been studied by different authors [4,10-16]. The
necessary and sufficient conditions for the existence of
Theorem 1. The complete tripartite graph
The main results of [17]
can be deduced as a corollary by substituting
Corollary 1. [17]The complete tripartite
graph
If
If
The value of
If we put
Corollary 2. Let
The corollary 2 subsumes the main result of [3].
Corollary 3. [3] Let
In order to prove our result, we make use of the following
Theorem 2. [18] Let
Lemma 1. [4] Let
Remark 1. Since a cycle of length 3 in a
Throughout this paper, we denote
In this section, we prove the necessary conditions for the existence
of
decomposition of the complete tripartite graphs
Remark 2. [17] A
Lemma 2. The graph
Proof. In this case, all the possible triplets are:
(4, 0, 0):
(0, 3, 0):
(0, 0, 2):
(2, 0, 1):
Thus, the graph
Lemma 3. The graph
Proof. Consider a cyclic idempotent latin square of
order 3. By Remark 2, every entry
Now,
(7, 0, 1):
(5, 0, 2):
(5, 3, 0):
(3, 3, 1):
(3, 0, 3):
(1, 3, 2):
(1, 6, 0):
(1, 0, 4):
The above cases guarantees the existence of
Theorem 3. The graph
Proof. Let the partite sets of
Case 1.
Consider a cyclic latin square of order
|
|
|
|
|
|
|
|
|
|
|
|
The partial latin square of the above form corresponds to 12
edges and can be decomposed into
(4, 0, 0): The four
(2, 0, 1): The two
(0, 3, 0): The required
(0, 0, 2):
Thus each of these
Hence
Case 2.
Consider a cyclic latin square of order
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The edges corresponding to partial latin square of the above form
can be decomposed into
(8, 0, 0): This can be achieved directly from Remark 2.
(6, 0, 1):
(4, 3, 0):
(4, 0, 2):
(2, 3, 1):
(2, 0, 3):
(0, 6, 0):
(0, 0, 4):
(0, 3, 2):
The remaining entries of the latin square can be partitioned into
Hence for all admissible triplets
In this section, we have proved the necessary conditions for the
existence of
Lemma 4. The graph
Proof. The graph
(3, 0, 1):
(1, 3, 0):
(1, 0, 2):
Thus, the graph
Lemma 5. The graph
Proof. The graph
(5, 5, 0):
(5, 2, 2):
(3, 5, 1):
(3, 2, 3):
(1, 8, 0):
(1, 5, 2):
(1, 2, 4):
Thus there exists a
Lemma 6. There exists a
Proof. In order to prove the existence of
(7, 0, 7): Seven
(7, 3, 5): Seven
(7, 6, 3): The seven
(7, 9, 1):
(5, 0, 8):
(5, 3, 6): Three copies of
(5, 6, 4): Five copies of
(5, 9, 2): Five copies of
(5, 12, 0):
(3, 0, 9): Three copies of
(3, 3, 7): Required copies of
(3, 6, 5):
(3, 9, 3): Three copies of
(3, 12, 1): Twelve edge disjoint copies of
(1, 0, 10):
(1, 3, 8):
(1, 6, 6): One copy of
(1, 9, 4):
(1, 12, 2):
(1, 15, 0): Required
Thus the graph
Theorem 4. The graph
Proof. The graph
By Lemma 5, the graph
By Lemmas 5 and 6, the graph
Lemma 7. There exists a
Proof. The graph
It is easy to verify that whenever
Thus the graph
Lemma 8. The graph
Proof. Let
By Lemma 1, the edges corresponding to the entries in the
first
Next, we consider the remaining
| 1 | 2 | 3 | 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Note that each entry in the remaining
This proves the existence of
Lemma 9. For
Proof. Consider the bipartite graph
In order to prove the existence of
Lemma 10. The graph
Proof. In order to prove the existence of
(15, 1, 1): The maximum number of possible
(13, 4, 0): Required edge disjoint copies of
(13, 1, 2): Edge disjoint copies of
(11, 4, 1): Required copies of
(11, 1, 3): Required copies of
(9, 7, 0): Seven copies of
(9, 4, 2): Nine copies of
(9, 1, 4): Required copies of
(7, 7, 1):
(7, 4, 3): Four copies of
(7, 1, 5):
(5, 10, 0): Five copies of
(5, 7, 2): Five copies of
(5, 4, 4):
(5, 1, 6): Five copies of
(3, 1, 7): Edge disjoint copies of
(3, 4, 5): Edge disjoint copies of
(3, 7, 3): Seven copies of
(3, 10, 1):
(1, 10, 2): Ten copies of
(1, 7, 4): Required copies of
(1, 4, 6):
(1, 1, 8):
Thus the graph
Definition 1. [17] In a
|
|
|
|
|
|
Next to prove the existence of
Recall that if the cell
Lemma 11. [17] For any
In the following example, using an idempotent latin square of order
Example 1. Consider the latin square
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
We can obtain the required latin square,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Lemma 12. For
Proof. The proof is splitted into 2 cases.
Case 1.
The graph
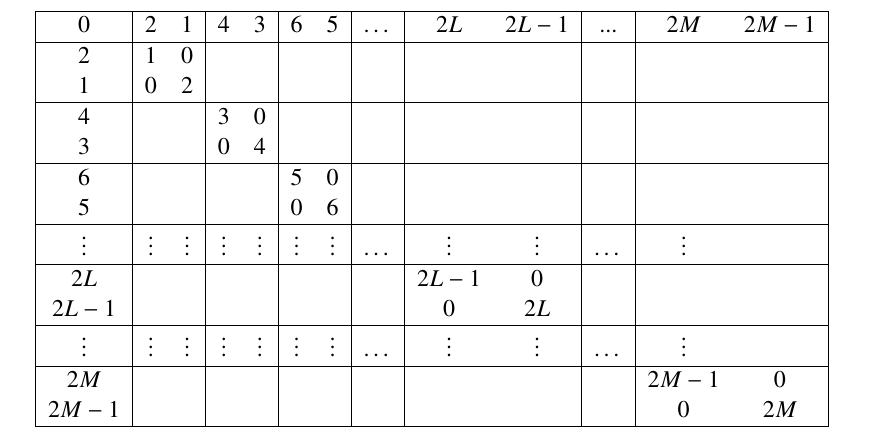
Clearly,
It may be noted that the edges corresponding to the entry
|
|
|
|
|
|
|
|
|
|
|
|
Observe that the edges corresponding to each of the
|
|
|
|
|
|
|
|
|
|
|
|
together with the corresponding entries of row
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
The corresponding edges induce a graph isomorphic to
Now consider the edges corresponding to the entries of the cells
That is, for some
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
The edges corresponding to the entries given in Table 1 can
be either decomposed into three
The remaining edges, corresponding to the last
| 2 | 3 | 4 | |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
| 2 | 3 | 4 | |
|
|
|
||
|
|
|
||
|
|
|
|
|
|
|
|
|
The edges corresponding to the entries as shown in Table 2 can be decomposed into two
Similarly, the edges corresponding to other groups with the above
mentioned condition(4 column and 4 symbols) admits a
Now it remains to show that when
Next, the case
A similar approach can be used to partition the last
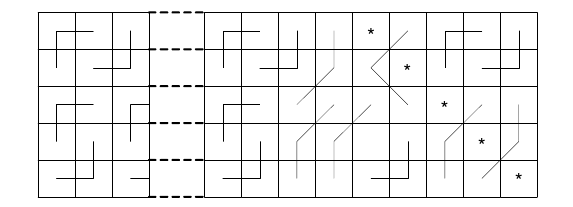
Next, we consider the case
Observe that each of the partial latin square considered in
Figure 3 corresponds to either three
The same approach can be used to partition the last
In the case when
Two such
| 1 | 2 | 3 | 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Consider the highlighted entries in the above Table 4
which correspond to three
It is straightforward to check that similar edge trading is
possible to have all possible
When
Similarly, when
Thus, there exists a
Case 2.
In order to prove this case, we consider a latin square of order
| |
|
|
|
|
|
||
| |
|
|
|
|
|
||
| |
|
|
|
||||
| |
|||||||
| |
|
|
|
|
The first
Theorem 5. The graph
Proof. The graph
Case 1.
Consider the graph
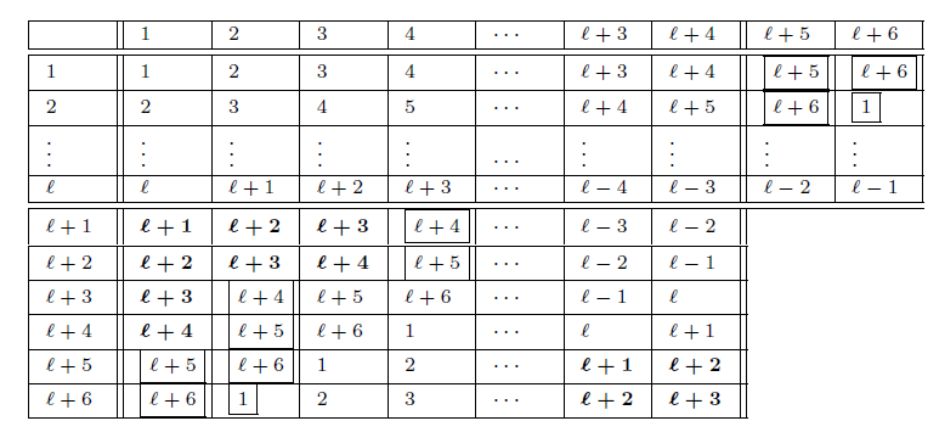
<The first
The edges corresponding to the latin rectangle can be decomposed
into cycles of length
Now, we consider the edges corresponding to the entries outside
the latin rectangle (the remaining edges from partite set
Construction 1. In this type of construction, we use the edges between partite
set
Construction 2. In this type of construction, we consider only the edges between
the partite set
| |
||
| |
||
| |
Thus by using these two types of construction, all the remaining
edges can be decomposed into
In order to obtain all possible
Type 1. This edge trading is similar to
Construction 1, where we use edges between partite set
Type 2. This edge trading is similar to
Construction 2, where we use only the edges between partite set
By using Type 1 and Type 2 edge trading, all the remaining edges
can be decomposed into copies of
Thus, all the remaining edges corresponding to the entries
outside the latin rectangle can be decomposed into copies of
Thus the graph
In this case, let
Similar to Case 1, the first
By the structure of the latin square, the edges corresponding to
the entries in rows
Here, we take
When
Thus the graph
Theorem 1. The complete tripartite graph
Proof. The proof follows from Lemma 7, Theorem 3,
Theorem 4 and Theorem 5.
In this paper, the necessary condition for the existence of
There is no conflict of interest related to this work.
1970-2025 CP (Manitoba, Canada) unless otherwise stated.