For a graph \( G \) and a subgraph \( H \) of a graph \( G \), an \( H \)-decomposition of the graph \( G \) is a partition of the edge set of \( G \) into subsets \( E_i \), \( 1 \leq i \leq k \), such that each \( E_i \) induces a graph isomorphic to \( H \). In this paper, it is proved that every simple connected unicyclic graph of order five decomposes the \( \lambda \)-fold complete equipartite graph whenever the necessary conditions are satisfied. This generalizes a result of Huang, *Utilitas Math.* 97 (2015), 109–117.
For a graph \(G\) and a positive integer \(\lambda,\) \(G(\lambda)\) is the graph obtained from \(G\) by replacing each of its edges by \(\lambda\) parallel edges. Let \(C_k\) denote the cycle of length \(k.\) The complete graph on \(m\) vertices is denoted by \(K_m\) and its complement is denoted by \(\overline K_m.\) If \(H_1,\,H_2,\,\dots,\,H_k\) are edge-disjoint subgraphs of a graph \(G\) such that \(E(G)=\bigcup^{k}_{i\,=\,1}E(H_i),\) then \(H_1,H_2,\dots,H_k\) decompose \(G;\) we write it as \(G\,=\,H_1\,\oplus\,H_2\,\oplus\,\dots\,\oplus\,H_k.\) If each \(H_i\,\cong\,H,\) then \(G\) has an \(H\)-decomposition and we denote it by \(H\,|\,G.\) A graph \(G\) has a \(C_k\)-decomposition or a \(k\)-cycle decomposition whenever \(C_k\,|\,G.\)
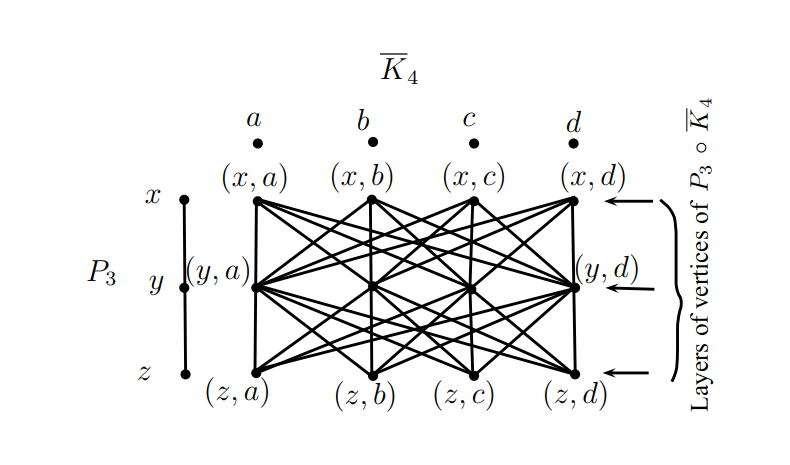
For two graphs \(G\) and \(H\) their wreath product, denoted by \(G\,\circ\,H,\) has vertex set \(V(G)\,\times\,V(H)\) in which two vertices \((g_1,h_1)\) and \((g_2,h_2)\) are adjacent whenever \(g_1g_2\in E(G)\) or, \(g_1=g_2\) and \(h_1h_2\in E(H);\) see Figure 1. Clearly, if \(G\,=\,H_1\,\oplus\,H_2\,\oplus\,\dots\,\oplus\,H_k,\) then \(G\,\circ\,\overline K_n\,=\,H_1\,\circ\,\overline K_n\,\oplus\,H_2\,\circ\,\overline K_n\,\oplus\,\dots\,\oplus\,H_k\,\circ\,\overline K_n.\) It can be observed that \(K_m\,\circ\,\overline K_n\) is isomorphic to the complete \(m\)-partite graph in which each partite set has \(n\) vertices. For graphs \(G\) and \(H,\) and \(x\,\in\,V(G),\) \(x\,\times\,V(H)\,=\,\{(x,\,v)\,|\,v\,\in\,V(H)\}\) is called the layer of vertices of \(G\,\circ\,H\) corresponding to \(x.\)
A latin square \(L\) of order \(n\) is an \(n\,\times\,n\) array, each cell of which contains exactly one of the symbols in \(\{0,\,1,\,2,\,\dots,\,n-1\},\) such that each row and each column of the array contains each of the symbols in \(\{0,\,1,\,2,\,\dots,\,n-1\}\) exactly once, see [1]. A quasigroup of order \(n\) is a pair \((Q,*),\) where \(Q\) is a set of size \(n\) and \(*\) is a binary operation on \(Q\) such that for every pair of elements \(a,b\in Q,\) the equations \(a\,*\,x=b\) and \(y\,*\,a=b\) have unique solutions. We consider a quasigroup is just a latin square with a headline and a sideline, see [1].
Let \(G\) be a bipartite graph with bipartition \((X,\,Y),\) where \(X\,=\,\{x_0,\,x_1,\)\(x_2,\,\dots,\,x_{n-1}\},\) \(Y\,=\,\{y_0,\,y_1,y_2,\dots,\,y_{n-1}\};\) if \(G\) contains the set of edges \(F_i(X,\,Y)=\{x_jy_{j+i}\,|\,0\,\leq\,j\,\leq\,n-1,\) where addition in the subscript is taken modulo \(n\)}, \(0\,\leq\,i\,\leq\,n-1,\) then \(G\) has the \(1\)-factor of distance \(i\) from \(X\) to \(Y.\) It is important to note that for \(0\leq i\leq n-1,\) \(F_i(X,\,Y)\,=\,F_{n-i}(Y,\,X).\) An edge \(e\in F_i(X,Y)\) is an edge of distance \(i\) from \(X\) to \(Y\) or it is an edge of distance \(n-i\) from \(Y\) to \(X.\) Clearly, if \(G\,=\,K_{n,\,n},\) then \(E(G)\,=\,\bigcup^{n-1}_{i\,=\,0}F_i(X,\,Y).\)
We denote the graphs of Figure 2 by \(H_i,\) \(1\leq i\leq 4\) and \(C_5.\) For all \(i\) such that \(1\leq i\leq 4,\) \(H_i\) has the vertex set \(\{a,b,c,d,e\}.\) The graph \(H_1\) with the edge set \(\{ab,bc,ca,bd,ce\}\) is denoted by \(((a,b,c);bd,ce)\) or \((C;bd,ce),\) where \(C\) denotes the cycle \((a,b,c);\) the graph \(H_2\) with the edge set \(\{ab,bc,ca,cd,ce\}\) is denoted by \(((a,b,c);cd,ce)\) or \((C;cd,ce),\) where \(C\) denotes the cycle \((a,b,c);\) the graph \(H_3\) with the edge set \(\{ab,bc,ca,cd,de\}\) is denoted by \(((a,b,c);cd,de)\) or \((C;cd,de),\) where \(C\) denotes the cycle \((a,b,c);\) the graph \(H_4\) with the edge set \(\{ab,bc,cd,da,de\}\) is denoted by \(((a,b,c,d);de)\) or \((C;de),\) where \(C\) denotes the cycle \((a,b,c,d)\) and the cycle \(C_5\) with the edge set \(\{ab,bc,cd,de,ea\}\) is denoted by \((a,b,c,d,e).\)
In the future, for \(1\leq i\leq 4,\) \(H_i,\) stands for the graphs in Figure 2.
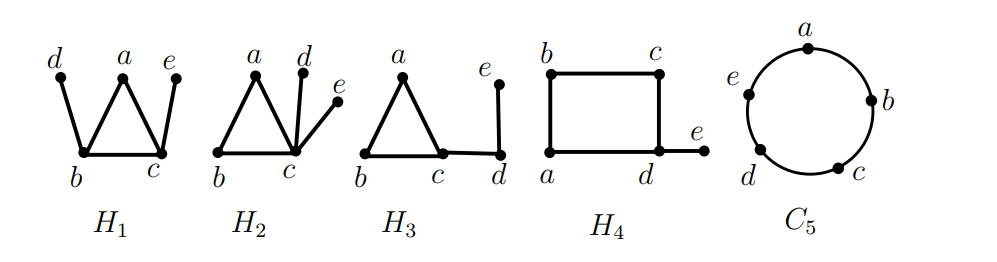
Decomposition of a graph into a specified subgraph is an interesting area of research in graph theory. In particular \(K_k\)-decomposition of \(K_n\) (\(BIBD\)) has received much attention, see [2]. The \(K_3\)-design of order \(n\) is known as the Steiner triple system. Decompositions of \(K_n\) into complete subgraphs, complete bipartite graphs, complete equipartite graphs, linear forests have been studied, see [3-6]. Decomposition of \((K_m\,\circ\,\overline K_n)(\lambda)\) (\(GDD\)) into \(K_3\) (resp. \(K_4\)) is studied in [7,8]. Cycle decompositions of the graphs \(K_n(\lambda)\), \(K_n-F,\) where \(F\) is a perfect matching of \(K_n\), \(K_{n,m}(\lambda)\) and \((K_m\,\circ\,\overline K_n)(\lambda)\) are considered in [9-13].
Bermond et al. [14] studied the decompositions of complete graphs into isomorphic subgraphs with five vertices. Further, Bermond and Sch\(\ddot{\rm o}\)nheim [15] obtained \(G\)-decompositions of \(K_n,\) where \(G\) has four vertices or less. Moreover, in [16], Huang obtained decompositions of the complete equipartite graphs into connected unicyclic graphs of size five. Here we obtain decompositions of the \(\lambda\)-fold complete equipartite graphs into connected unicyclic graphs of size five, whenever the necessary conditions are satisfied. This generalizes a result of Huang [16].
The main result of this paper is the following:
Theorem 1. If \(m\) and \(n\) are at least \(3,\) then for \(1\,\leq\,i\,\leq\,4,\) \(H_i\,|\,(K_m\,\circ\,\overline K_n)(\lambda)\) if and only if \(5\,|\,\lambda nm(m-1).\)
In this section, we prove that every simple connected unicyclic graph on five vertices decomposes the graph \((K_m\,\circ\,\overline K_n)(\lambda),\) whenever the necessary conditions are satisfied.
Lemma 1. If \(n\,\geq\,3\) and \(H_i\,|\,G,\) \(1\leq i\leq 3,\) then \(H_i\) decomposes the graph \(G\,\circ\,\overline K_n.\)
Proof. Consider the graph \(G\,\circ\,\overline K_n=(H_i\,\oplus\,H_i\,\oplus\dots\oplus\,H_i)\,\circ\,\overline K_n=H_i\,\circ\,\overline K_n\,\oplus\,H_i\,\circ\,\overline K_n\,\oplus\,\cdots\,\oplus\,H_i\,\circ\,\overline K_n.\) We need to prove that for all \(i\) such that \(1\leq i\leq 3,\) \(H_i\,|\,H_i\,\circ\,\overline K_n.\) Let \((L,*)\) be a quasigroup of order \(n,\) where \(L=\{0,1,2,\dots,n-1\}.\) Let the vertices of \(H_i\) be as shown in Figure 2 and let the vertex set of \(\overline K_n\) be \(\{0,1,2,\dots,n-1\}.\) Let \(\{(a,j); 0\leq j\leq n-1\}\) be the layer of \(H_i\,\circ\,\overline K_n\) corresponding to the vertex \(a\) in \(V(H_i).\) Then the graphs in \(\big\{\big(((a,\ell),(b,k),(c,\ell*k));(b,k)(d,\ell),(c,\ell*k)(e,\ell)\big)\,|\,\forall\,\ell,k\in L\big\},\) each one of them is isomorphic to \(H_1,\) decompose the graph \(H_1\,\circ\,\overline K_n,\) the graphs in \(\big\{\big(((a,\ell),(b,k),(c,\ell*k));(c,\ell*k)(d,\ell),(c,\ell*k)(e,\ell)\big)\,|\,\forall\,\ell,k\in L\big\},\) each one of them is isomorphic to \(H_2,\) decompose the graph \(H_2\,\circ\,\overline K_n\) and the graphs in \(\big\{\big(((a,\ell),(b,k),(c,\ell*k));(c,\ell*k)(d,\ell),(d,\ell)(e,k)\big)\,|\,\forall\,\ell,k\in L\big\},\) each one of them is isomorphic to \(H_3,\) decompose the graph \(H_3\,\circ\,\overline K_n.\) ◻
Lemma 2. If \(n\,\geq\,2\) and \(H_4\,|\,G,\) then \(H_4\) decomposes the graph \(G\,\circ\,\overline K_n.\)
Proof. Consider the graph \(G\,\circ\,\overline K_n=(H_4\,\oplus\,H_4\,\oplus\dots\oplus\,H_4)\,\circ\,\overline K_n=H_4\,\circ\,\overline K_n\,\oplus\,H_4\,\circ\,\overline K_n\,\oplus\,\dots\,\oplus\,H_4\,\circ\,\overline K_n.\) We need to prove that \(H_4\,|\,H_4\,\circ\,\overline K_n.\) Let \((L,*)\) be a quasigroup of order \(n,\) where \(L=\{0,1,2,\dots,n-1\}.\) Let the vertices of \(H_4\) be as shown in Figure 2 and let the vertex set of \(\overline K_n\) be \(\{0,1,2,\dots,n-1\}.\) Let \(\{(a,j); 0\leq j\leq n-1\}\) be the layer of \(H_4\,\circ\,\overline K_n\) corresponding to the vertex \(a\) in \(V(H_4).\) Then the graphs in \(\big\{\big(((a,\ell),(b,k),(c,\ell),(d,k));(d,k)(e,\ell*k)\big)\,|\,\forall\,\ell,k\in L\big\},\) each one of them is isomorphic to \(H_4,\) decompose the graph \(H_4\,\circ\,\overline K_n.\) ◻
Lemma 3. \(K_4\setminus\{e\}\,|\,K_4(5),\) where \(e\) is an edge of \(K_4.\)
Proof. Let \(V(K_4)=\{a,b,c,d\}.\) A \(K_4\setminus\{e\}\) decomposition of \(K_4(5)\) is given by the edge induced subgraphs \(\langle bc,cd,da,ac,bd\rangle,\) \(\langle ab,cd,da,ac,bd\rangle,\) \(\langle ab,bc,da,ac,bd\rangle,\) \(\langle ab,bc,cd,ac,bd\rangle,\) \(\langle ab,bc,cd,da,bd\rangle,\) \(\langle ab,bc,cd,da,ac\rangle.\) ◻
Lemma 4. For \(i\in\{1,3,4\},\) \(H_i\) decomposes the graph \((K_4\,\circ\,\overline K_n)(5).\)
Proof. Let \(V(K_4)=\{a,b,c,d\}\) and let \(V(\overline K_n)=\{0,1,2,\dots,n-1\}.\) By Lemma 3, \(K_4\,\setminus\,\{e\}\,|\,K_4(5);\) hence it is enough to prove that for \(i\in\{1,3,4\},\) \(H_i\,|\,(K_4\,\setminus\,\{e\})\,\circ\,\overline K_n.\) Let the edge \(e=ad.\) Let \((L,*)\) be a quasigroup of order \(n,\) where \(L=\{0,1,2,\dots,n-1\}.\) We have \(V((K_4\,\setminus\,\{e\})\,\circ\,\overline K_n)=\displaystyle\bigcup^{n-1}_{j=0}\{(a,j),(b,j),(c,j),(d,j)\}.\) Then the graphs in \(\big\{\big(((a,\ell),(b,k),(c,\ell*k));(b,k)(d,\ell),(c,\ell*k)(d,\ell+1)\big)\,|\,\forall\,\ell,k\in L\big\},\) each one of them is isomorphic to \(H_1,\) decompose the graph \((K_4\,\setminus\,\{e\})\,\circ\,\overline K_n,\) the graphs in \(\big\{\big(((a,\ell),(b,k),(c,\ell*k));(c,\ell*k)(d,\ell),(d,\ell)(b,k+1)\big)\,|\,\forall\,\ell,k\in L\big\},\) each one of them is isomorphic to \(H_3,\) decompose the graph \((K_4\,\setminus\,\{e\})\,\circ\,\overline K_n\) and the graphs in \(\big\{\big(((a,\ell),(b,k),(d,\ell*k),(c,k));(c,k)(b,k+1)\big)\,|\,\forall\,\ell,k\in L\big\},\) each one of them is isomorphic to \(H_4,\) decompose the graph \((K_4\setminus \{e\})\circ\overline K_n.\) ◻
For the rest of the paper, we fix the layers of the graph \(G\,\circ\,\overline K_m\) as follows: let \(V(G)=\{a,b,c,d,\dots,w,x\}\) and let \(V(\overline K_m)=\{0,1,2,\dots,m-1\}.\) Then \(V(G\,\circ\,\overline K_m)=V(G)\,\times\,V(\overline K_m)=\{a\times V(\overline K_m)\}\cup\{b\times V(\overline K_m)\}\cup\{c\times V(\overline K_m)\}\cup\dots\cup\{x\times V(\overline K_m)\}.\) For convenience, we write \(A=a\,\times\,V(\overline K_m)=\{(a,0),(a,1),(a,2),\dots,(a,m-1)\}=\{a_0,a_1,a_2,\dots,a_{m-1}\},\) where for all \(i\) such that \(0\leq i\leq m-1,\) \(a_i,\) denotes the vertex \((a,i).\) Similarly, \(B,C,\dots,X\) are defined. \(A,B,C,\dots,X\) are the layers of \(G\,\circ\,\overline K_m,\) see Figure 1.
Lemma 5. For \(n\,\geq\,2,\) the graph \((K_4\,\circ\,\overline K_n)(5)\) has an \(H_2\)-decomposition.
Proof. We complete the proof in two cases.
Case 1 \(n\) is odd.
Let \(V(K_4)=\{a,b,c,d\}\) and let
\(V(\overline
K_n)=\{0,1,2,\dots,n-1\}.\) By Lemma 3, \(K_4\,\setminus\,\{e\}\,|\,K_4(5)\) and
hence it is enough to to prove that \(H_2\,|\,(K_4\,\setminus\,\{e\})\,\circ\,\overline
K_n.\) Let the edge \(e=ad.\)
Let \(\sigma\) be the cyclic
permutation \((0,1,2,3,\dots ,n-1)\) on
\(\{0,1,2,\dots,n-1\}.\)
Subcase 1.1. \(n=3.\)
Let \(H_2^1=((a_0,b_0,c_0);c_0a_2,c_0d_1),\)
\(H^2_2=((a_0,b_1,c_2);b_1a_2,b_1d_0)\)
and \(H_2^3=((b_0,c_2,d_1);d_1c_1,d_1b_1)\) be
three edge-disjoint copies of \(H_2\)
in \((K_4\,\setminus\,\{e\})\,\circ\,\overline
K_3.\) Then the graphs in \(\big\{\sigma^0(H^j_2)=H^j_2,\,\sigma^1(H^j_2),\,\sigma^2(H^j_2)\,|\,1\leq
j\leq 3\big\},\) each one of them is isomorphic to \(H_2,\) decompose the graph \((K_4\,\setminus\,\{e\})\,\circ\,\overline
K_3,\) where \(\sigma^i\) acts
on the subscripts of the vertices of \(H^j_2.\)
Subcase 1.2. \(n\geq 5.\)
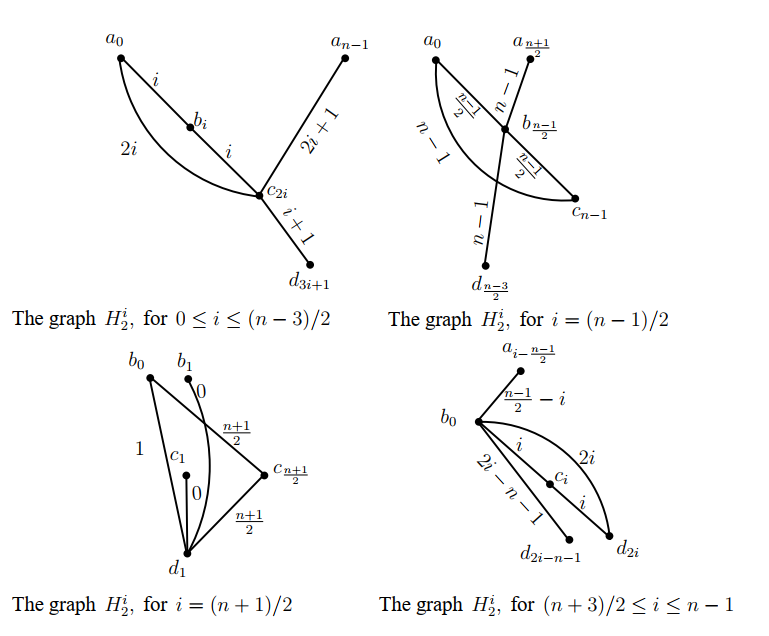
For all \(i\) such that \(0\leq i\leq (n-3)/2,\) let \(H^i_2=((a_0,b_i,c_{2i});c_{2i}a_{n-1},c_{2i}d_{3i+1});\) for \(i=(n-1)/2,\) let \(H^i_2=((a_0,b_{\frac{n-1}{2}},c_{n-1});b_{\frac{n-1}{2}}a_{\frac{n+1}{2}},b_{\frac{n-1}{2}}d_{\frac{n-3}{2}});\) for \(i=(n+1)/2,\) let \(H^i_2=((b_0,c_{\frac{n+1}{2}},d_1);d_1c_1,d_1b_1)\) and for all \(i\) such that \((n+3)/2\leq i\leq n-1,\) let \(H^i_2=((b_0,c_i,d_{2i});b_0a_{i-\frac{n-1}{2}},b_0d_{2i-n-1}),\) where the subscripts are taken modulo \(n,\) see Figure 3. Then the graphs in \(\big\{\sigma^i(H^j_2)\,|\,0\leq i,j\leq n-1\big\},\) each one of them is isomorphic to \(H_2,\) decompose the graph \((K_4\,\setminus\,\{e\})\,\circ\,\overline K_n.\) The ( base ) graphs \(H^i_2,\) \(0\leq i\leq n-1\) are described in Figure 3.
Case 2. \(n\) is even.
The graph \((K_4\,\circ\,\overline K_n)(5)=\big((K_4\,\circ\,\overline K_2)\,\circ\,\overline K_{\frac{n}{2}}\big)(5)\,\cong\,(K_4\,\circ\,\overline K_2)(5)\,\circ\,\overline K_{\frac{n}{2}}.\) We shall prove that \(H_2\,|\,(K_4\,\circ\,\overline K_2)(5)\) and apply Lemma 1. Let \(V(K_4)=\{a,b,c,d\}\) and let \(V(\overline K_2)=\{0,1\}.\) Let \(\sigma=(0,1)\) be a permutation on \(\{0,1\}.\) Let \(H^1_2=((a_0,b_0,c_1);b_0c_0,b_0d_1),\) \(H^2_2=((b_0,c_0,d_1);b_0a_0,b_0a_1),\) \(H^3_2=((a_1,c_0,d_0);d_0a_0,d_0b_1),\) \(H^4_2=((a_0,b_1,d_0);a_0c_1,a_0d_1),\) \(H^5_2=((a_0,c_0,d_1);\) \(d_1a_1,d_1b_1),\) \(H^6_2=((a_1,b_0,d_0);a_1c_0,a_1d_1),\) \(H^7_2=((a_1,b_0,c_1);c_1a_0,c_1d_0),\) \(H^8_2=((b_0,c_1,d_0);c_1a_1,c_1d_1),\) \(H^9_2=((b_1,c_0,d_1);b_1a_1,b_1c_1),\) \(H^{10}_2=((b_0,c_0,d_0);\) \(d_0a_1,d_0b_1),\) \(H^{11}_2=((a_0,b_0,c_0);c_0b_1,c_0d_0)\) and \(H^{12}_2=((a_0,c_0,d_0);a_0b_0,a_0b_1)\) be twelve edge-disjoint copies of \(H_2\) in \((K_4\,\circ\,\overline K_2)(5).\) Then the graphs in \(\big\{\sigma^0(H^j_2)=H^j_2,\,\sigma^1(H^j_2)\,|\,1\leq j\leq 12\big\},\) each one of them is isomorphic to \(H_2,\) decompose the graph \((K_4\,\circ\,\overline K_2)(5).\) ◻
Lemma 6. For \(n\geq 2,\) the graph \((K_3\,\circ\,\overline K_n)(5)\) has an \(H_1\)-decomposition.
Proof. We complete the proof in two cases.
Case 1. \(n\) is odd.
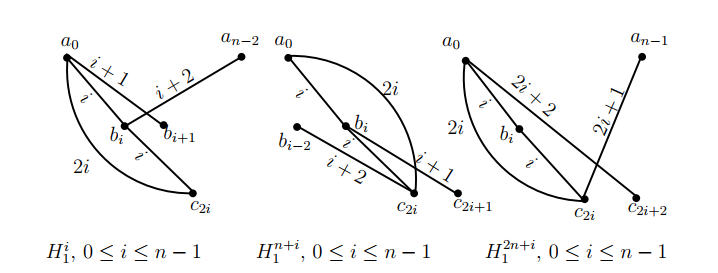
Let \(V(K_3)=\{a,b,c\}\) and let \(V(\overline K_n)=\{0,1,2,3,\dots,n-1\}.\) Let \(\sigma=(0,1,2,3,\dots,n-1)\) be a permutation on \(\{0,1,2,3,\dots,n-1\}.\) For \(0\leq i\leq n-1,\) let \(H^i_1=((a_0,b_i,c_{2i});a_0b_{i+1},b_ia_{n-2});\) for \(0\leq i\leq n-1,\) let \(H^{n+i}_1=((a_0,b_i,\) \(c_{2i});b_ic_{2i+1},c_{2i}b_{(n+i)-2})\) and for \(0\leq i\leq n-1,\) let \(H^{2n+i}_1=((a_0,b_i,\) \(c_{2i});a_0c_{2i+2},c_{2i}a_{n-1}),\) where the subscripts are taken modulo \(n,\) see Figure 4. Then the graphs in \(\big\{\sigma^i(H^j_1)\,|\,0\leq i\leq n-1,\,0\leq j\leq 3n-1\big\},\) each one of them is isomorphic to \(H_1,\) decompose the graph \((K_3\,\circ\,\overline K_n)(5),\) where \(\sigma^i\) acts on the subscripts of the vertices of \(H^j_1.\) The ( base ) graphs \(H^i_1,\) totally \(3n\) in number, with the distances of their edges are shown in the graph of Figure 4.
Case 2. \(n\) is even.
The graph \((K_3\,\circ\,\overline K_n)(5)=\big((K_3\,\circ\,\overline K_2)\,\circ\,\overline K_{\frac{n}{2}}\big)(5)\,\cong\,(K_3\,\circ\,\overline K_2)(5)\,\circ\,\overline K_{\frac{n}{2}}.\) We shall prove that \(H_1\,|\,(K_3\,\circ\,\overline K_2)(5)\) and apply Lemma 1. Let \(V(K_3)=\{a,b,c\}\) and let \(V(\overline K_2)=\{0,1\}.\) Let \(\sigma=(0,1)\) be a permutation on \(\{0,1\}.\) Let \(H^1_1=((a_0,b_0,c_1);b_0c_0,a_0b_1),\) \(H^2_1=((a_1,b_0,c_0);c_0a_0,b_0c_1),\) \(H^3_1=((a_0,b_1,c_0);a_0c_1,b_1a_1),\) \(H^4_1=((a_0,b_0,c_0);b_0a_1,a_0b_1),\) \(H^5_1=((a_0,b_0,c_0);c_0b_1,b_0c_1)\) and \(H^6_1=((a_0,b_0,c_0);a_0c_1,c_0a_1)\) be six edge-disjoint copies of \(H_1\) in \((K_3\,\circ\,\overline K_2)(5).\) Then the graphs in \(\big\{\sigma^i(H^j_1)\,|\,0\,\leq\,i\,\leq\,1,\,1\,\leq\,j\,\leq\,6\big\},\) each one of them is isomorphic to \(H_1,\) decompose the graph \((K_3\,\circ\,\overline K_2)(5).\) ◻
Lemma 7. For \(n\geq 2,\) the graph \((K_3\,\circ\,\overline K_n)(5)\) has an \(H_2\)-decomposition.
Proof. We complete the proof in two cases.
Case 1. \(n\) is odd.
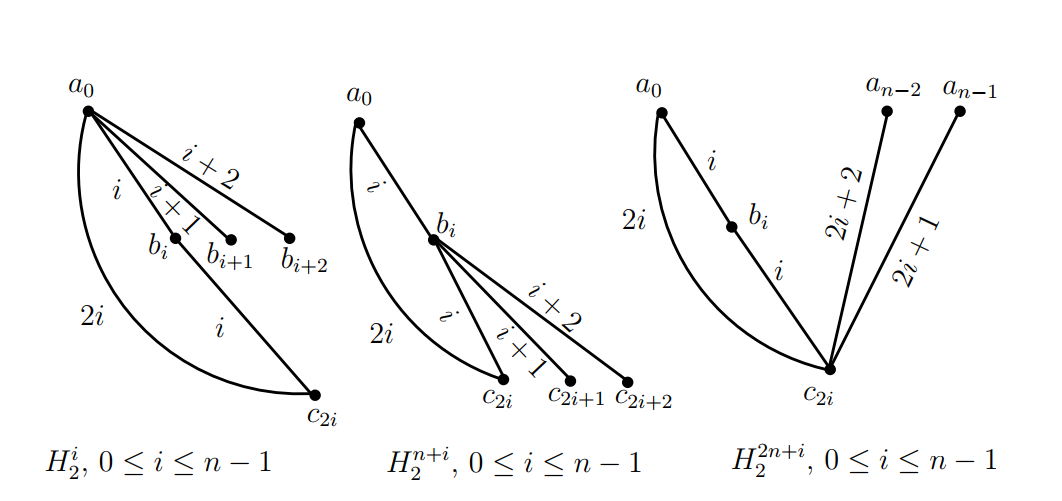
Let \(V(K_3)=\{a,b,c\}\) and let \(V(\overline K_n)=\{0,1,2,3,\dots,n-1\}.\) Let \(\sigma=(0,1,2,3,\dots,n-1)\) be a permutation on \(\{0,1,2,3,\dots,n-1\}.\) For \(0\leq i\leq n-1,\) let \(H^i_2=((a_0,b_i,c_{2i});a_0b_{i+1},a_0b_{i+2});\) for \(0\leq i\leq n-1,\) let \(H^{n+i}_2=\) \(((a_0,b_i,c_{2i});b_{i}c_{2i+1},b_{i}c_{2i+2})\) and for \(0\leq i\leq n-1,\) let \(H^{2n+i}_2=((a_0,b_i,\) \(c_{2i});c_{2i}a_{n-2},c_{2i}a_{n-1}),\) where the subscripts are taken modulo \(n,\) see Figure 5. Then the graphs in \(\big\{\sigma^i(H^j_2)\,|\,0\leq i\leq n-1,\,0\leq j\leq 3n-1\big\},\) each one of them is isomorphic to \(H_2,\) decompose the graph \((K_3\,\circ\,\overline K_n)(5),\) where \(\sigma^i\) acts on the subscripts of the vertices of \(H^j_2.\) The ( base ) graphs \(H^i_2,\) totally \(3n\) in number, with the distances of their edges are shown in the graph of Figure 5.
Case 2. \(n\) is even.
The graph \((K_3\,\circ\,\overline K_n)(5)=\big((K_3\,\circ\,\overline K_2)\,\circ\,\overline K_{\frac{n}{2}}\big)(5)\,\cong\,(K_3\,\circ\,\overline K_2)(5)\,\circ\,\overline K_{\frac{n}{2}}.\) We shall prove that \(H_2\,|\,(K_3\,\circ\,\overline K_2)(5)\) and apply Lemma 1. Let \(V(K_3)=\{a,b,c\}\) and let \(V(\overline K_2)=\{0,1\}.\) Let \(\sigma=(0,1)\) be a permutation on \(\{0,1\}.\) Let \(H^1_2=((a_0,b_0,c_1);a_0c_0,a_0b_1),\) \(H^2_2=((a_1,b_0,c_0);b_0a_0,b_0c_1),\) \(H^3_2=((a_0,b_1,c_0);c_0b_0,c_0a_1),\) \(H^4_2=((a_0,b_0,c_0);a_0b_1,a_0c_1),\) \(H^5_2=((a_0,b_0,c_0);b_0a_1,b_0c_1)\) and \(H^6_2=((a_0,b_0,c_0);c_0a_1,c_0b_1)\) be six edge-disjoint copies of \(H_2\) in \((K_3\,\circ\,\overline K_2)(5).\) Then the graphs in \(\big\{\sigma^i(H^j_2)\,|\,0\,\leq\,i\,\leq\,1,\,1\,\leq\,j\,\leq\,6\big\},\) each one of them is isomorphic to \(H_2,\) decompose the graph \((K_3\,\circ\,\overline K_2)(5).\) ◻
Lemma 8. For \(n\geq 2,\) the graph \((K_3\,\circ\,\overline K_n)(5)\) has an \(H_3\)-decomposition.
Proof. We complete the proof in two cases.
Case 1. \(n\) is odd.
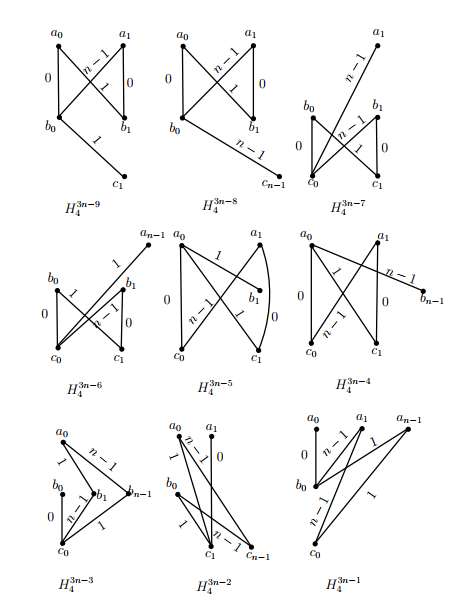
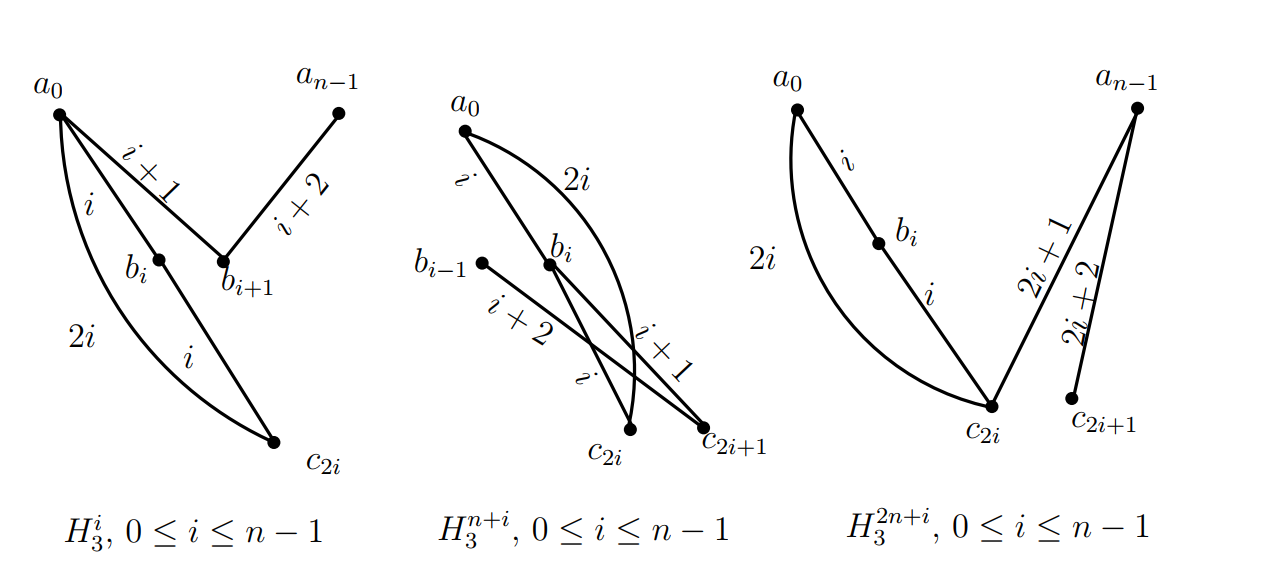
Let \(V(K_3)=\{a,b,c\}\) and let \(V(\overline K_n)=\{0,1,2,3,\dots,n-1\}.\) Let \(\sigma=(0,1,2,3,\dots,n-1)\) be a permutation on \(\{0,1,2,3,\dots,n-1\}.\) For \(0\leq i\leq n-1,\) let \(H^i_3=((a_0,b_i,c_{2i});a_0b_{i+1},b_{i+1}a_{n-1});\) for \(0\leq i\leq n-1,\) let \(H^{n+i}_3=((a_0,b_i,c_{2i});b_{i}c_{2i+1},c_{2i+1}b_{i-1})\) and for \(0\leq i\leq n-1,\) let \(H^{2n+i}_3=((a_0,b_i,c_{2i});c_{2i}a_{n-1},a_{n-1}c_{2i+1}),\) where the subscripts are taken modulo \(n,\) see Figure 6. Then the graphs in \(\big\{\sigma^i(H^j_3)\,|\,0\leq i\leq n-1,\,0\leq j\leq 3n-1\big\},\) each one of them is isomorphic to \(H_3,\) decompose the graph \((K_3\,\circ\,\overline K_n)(5),\) where \(\sigma^i\) acts on the subscripts of the vertices of \(H^j_3.\) The ( base ) graphs \(H^i_3,\) totally \(3n\) in number, with the distances of their edges are shown in the graph of Figure 6.
Case 2. \(n\) is even.
The graph \((K_3\,\circ\,\overline K_n)(5)=\big((K_3\,\circ\,\overline K_2)\,\circ\,\overline K_{\frac{n}{2}}\big)(5)\,\cong\,(K_3\,\circ\,\overline K_2)(5)\,\circ\,\overline K_{\frac{n}{2}}.\) We shall prove that \(H_3\,|\,(K_3\,\circ\,\overline K_2)(5)\) and apply Lemma 1. Let \(V(K_3)=\{a,b,c\}\) and let \(V(\overline K_2)=\{0,1\}.\) Let \(\sigma=(0,1)\) be a permutation on \(\{0,1\}.\) Let \(H^1_3=((a_0,b_0,c_1);a_0b_1,b_1c_0),\) \(H^2_3=((a_1,b_0,c_0);b_0c_1,c_1a_0),\) \(H^3_3=((a_0,b_1,c_0);c_0a_1,a_1b_0),\) \(H^4_3=((a_0,b_0,c_0);a_0b_1,b_1a_1),\) \(H^5_3=((a_0,b_0,c_0);b_0c_1,c_1b_1)\) and \(H^4_3=((a_0,b_0,c_0);c_0a_1,a_1c_1)\) be six edge-disjoint copies of \(H_3\) in \((K_3\,\circ\,\overline K_2)(5).\) Then the graphs in \(\big\{\sigma^i(H^j_3)\,|\,0\,\leq\,i\,\leq\,1,\,1\,\leq\,j\,\leq\,6\big\},\) each one of them is isomorphic to \(H_3,\) decompose the graph \((K_3\,\circ\,\overline K_2)(5).\) ◻
Lemma 9. For \(n\geq 2,\) the graph \((K_3\,\circ\,\overline K_n)(5)\) has an \(H_4\)-decomposition.
Proof. We complete the proof in two cases.
Case 1. \(n\) is odd.
Let \(V(K_3)=\{a,b,c\}\) and let \(V(\overline K_n)=\{0,1,2,3,\dots,n-1\}.\)
Let \(\sigma=(0,1,2,3,\dots,n-1)\)
be a permutation on \(\{0,1,2,3,\dots,n-1\}.\)
Subcase 1.1. \(n\,\equiv\,3\) (mod \(4\)).
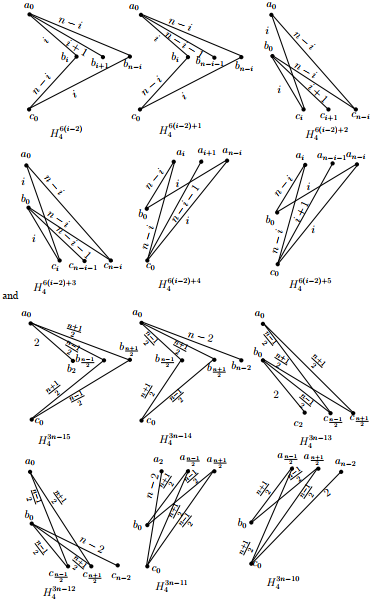
For all \(i\) such that \(2\,\leq\,i\,\leq\,(n-1)/2,\) let \(H^{6(i-2)}_4=((b_{i},c_0,b_{n-i},a_0);a_0b_x),\) \(H^{6(i-2)+1}_4=((b_{i},c_0,b_{n-i},a_0);a_0b_y),\) \(H^{6(i-2)+2}_4=((c_{n-i},a_0,c_{i},b_0);b_0c_x),\) \(H^{6(i-2)+3}_4=((c_{n-i},a_0,c_{i},b_0);b_0c_y),\) \(H^{6(i-2)+4}_4=((a_{n-i},b_0,a_{i},c_0);c_0a_x)\) and \(H^{6(i-2)+5}_4=((a_{n-i},b_0,a_{i},c_0);c_0a_y),\) where
\(x=\begin{cases}
i+1& \text{if $i\,\neq\,(n-1)/2,$}\\
2& \text{if $i=(n-1)/2.$}
\end{cases},\) \(y=\begin{cases}
n-i-1& \text{if $i\,\neq\,(n-1)/2,$}\\
n-2& \text{if $i=(n-1)/2.$}
\end{cases}\)
and the subscripts are taken modulo \(n;\) let \(H^{3n-9}_4=((a_0,b_1,a_1,b_0);b_0c_1),\)
\(H^{3n-8}_4=((a_0,b_1,a_1,b_0);b_0c_{n-1}),\)
\(H^{3n-7}_4=((b_0,c_1,b_1,c_0);c_0a_1),\)
\(H^{3n-6}_4=((b_0,c_1,b_1,c_0);c_0a_{n-1}),\)
\(H^{3n-5}_4=((c_0,a_1,c_1,a_0);a_0b_1),\)
\(H^{3n-4}_4=((c_0,a_1,c_1,a_0);\)
\(a_0b_{n-1}),\) \(H^{3n-3}_4=((b_1,a_0,b_{n-1},c_0);c_0b_0),\)
\(H^{3n-2}_4=((b_0,c_{n-1},a_0,c_1);c_1a_1)\)
and \(H^{3n-1}_4=((a_1,c_0,a_{n-1},b_0);b_0a_0).\)
Then the graphs in \(\big\{\sigma^i(H^j_4)\,|\,0\leq i\leq n-1,\,0\leq
j\leq 3n-1\big\},\) each one of them is isomorphic to \(H_4,\) decompose the graph \((K_3\,\circ\,\overline K_n)(5),\) where
\(\sigma^i\) acts on the subscripts of
the vertices of \(H^j_4.\)
The ( base ) graphs \(H^i_4,\)
totally \(3n\) in number, with the
distances of their edges are shown in the graphs of Figure 7
and Figure 8 of the appendix. In the union of the
graphs of Figure 8, the edges with distances in \(\{2,3,4,\dots,n-3,n-2\}\) from \(A\) to \(B,\) \(B\)
to \(C\) and \(A\) to \(C\) appear exactly five times. In the union
of the graphs of Figure 7, the edges with distances \(0,1\) and \(n-1\) from \(A\) to \(B,\) \(B\)
to \(C\) and \(A\) to \(C\) appear exactly five times.
Subcase 1.2. \(n\,\equiv\,1\) (mod \(4\)).
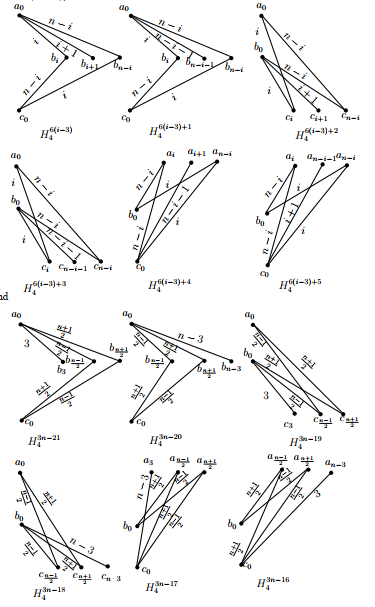
For all \(i\) such that \(3\,\leq\,i\,\leq\,(n-1)/2,\) let \(H^{6(i-3)}_4=((b_{i},c_0,b_{n-i},a_0);a_0b_x),\) \(H^{6(i-3)+1}_4=((b_{i},c_0,b_{n-i},a_0);a_0b_y),\) \(H^{6(i-3)+2}_4=((c_{n-i},a_0,c_{i},b_0);b_0c_x),\) \(H^{6(i-3)+3}_4=((c_{n-i},a_0,c_{i},b_0);b_0c_y),\) \(H^{6(i-3)+4}_4=((a_{n-i},b_0,a_{i},c_0);c_0a_x)\) and \(H^{6(i-3)+5}_4=((a_{n-i},b_0,a_{i},c_0);c_0a_y),\) where
\(x=\begin{cases}
i+1& \text{if $i\,\neq\,(n-1)/2,$}\\
3& \text{if $i=(n-1)/2.$}
\end{cases},\) \(y=\begin{cases}
n-i-1& \text{if $i\,\neq\,(n-1)/2,$}\\
n-3& \text{if $i=(n-1)/2.$}
\end{cases}\)
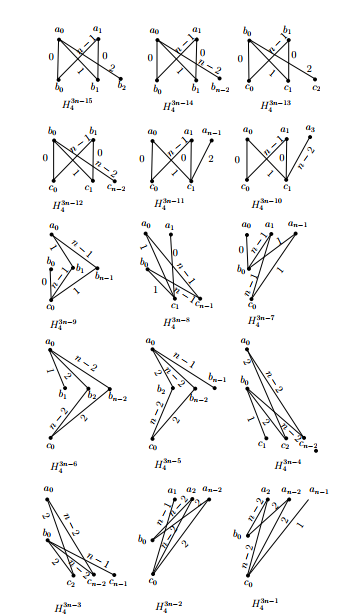
and the subscripts are taken modulo \(n;\) let \(H^{3n-15}_4=((b_0,a_1,b_1,a_0);a_0b_2),\)
\(H^{3n-14}_4=((b_0,a_1,b_1,a_0);a_0b_{n-2}),\)
\(H^{3n-13}_4=((c_0,b_1,c_1,b_0);b_0c_2),\)
\(H^{3n-12}_4=((c_0,b_1,c_1,b_0);b_0c_{n-2}),\)
\(H^{3n-11}_4=((a_0,c_0,a_1,c_1);c_1a_{n-1}),\)
\(H^{3n-10}_4=((a_0,c_0,a_1,c_1);c_1a_3),\)
\(H^{3n-9}_4=((b_1,a_0,b_{n-1},c_0);c_0b_0),\)
\(H^{3n-8}_4=((b_0,c_{n-1},a_0,\) \(c_1);c_1a_1),\) \(H^{3n-7}_4=((a_1,c_0,a_{n-1},b_0);b_0a_0),\)
\(H^{3n-6}_4=((b_2,c_0,b_{n-2},a_0);a_0b_1),\)
\(H^{3n-5}_4=((b_2,c_0,b_{n-2},a_0);a_0b_{n-1}),\)
\(H^{3n-4}_4=((c_{n-2},a_0,c_2,b_0);b_0c_1),\)
\(H^{3n-3}_4=((c_{n-2},a_0,c_2,b_0);b_0c_{n-1}),\)
\(H^{3n-2}_4=((a_{n-2},b_0,a_2,c_0);c_0a_1)\)
and \(H^{3n-1}_4=((a_{n-2},b_0,a_2,c_0);c_0a_{n-1}).\)
Then the graphs in \(\big\{\sigma^i(H^j_4)\,|\,0\leq i\leq n-1,\,0\leq
j\leq 3n-1\big\},\) each one of them is isomorphic to \(H_4,\) decompose the graph \((K_3\,\circ\,\overline K_n)(5).\)
The ( base ) graphs \(H^i_4,\) totally \(3n\) in number, with the distances of their edges are shown in the graphs of Figure 9 and Figure 10 of the appendix. In the union of the graphs of Figure 9, the edges with distances in \(\{3,4,\dots,n-4,n-3\}\) from \(A\) to \(B,\) \(B\) to \(C\) and \(A\) to \(C\) appear exactly five times. In the union of the graphs of Figure 10, the edges with distances \(0,1,2,n-1\) and \(n-2\) from \(A\) to \(B,\) \(B\) to \(C\) and \(A\) to \(C\) appear exactly five times.
Case 2. \(n\) is even.
The graph \((K_3\,\circ\,\overline K_n)(5)=\big((K_3\,\circ\,\overline K_2)\,\circ\,\overline K_{\frac{n}{2}}\big)(5)\,\cong\,(K_3\,\circ\,\overline K_2)(5)\,\circ\,\overline K_{\frac{n}{2}}.\) We shall prove that \(H_4\,|\,(K_3\,\circ\,\overline K_2)(5)\) and apply Lemma 2. Let \(V(K_3)=\{a,b,c\}\) and let \(V(\overline K_2)=\{0,1\}.\) Let \(\sigma=(0,1)\) be a permutation on \(\{0,1\}.\) Let \(H^1_4=((b_0,a_1,b_1,a_0);a_0c_0),\) \(H^2_4=((b_0,a_0,b_1,a_1);a_1c_0),\) \(H^3_4=((c_0,b_1,c_1,b_0);b_0a_0),\) \(H^4_4=((c_0,b_0,c_1,b_1);b_1a_0),\) \(H^5_4=((a_0,c_1,a_1,c_0);c_0b_0)\) and \(H^6_4=((a_1,c_0,a_0,c_1);c_1b_0)\) be six edge-disjoint copies of \(H_4\) in \((K_3\,\circ\,\overline K_2)(5).\) Then the graphs in \(\big\{\sigma^i(H^j_4)\,|\,0\,\leq\,i\,\leq\,1,\,1\,\leq\,j\,\leq\,6\big\},\) each one of them is isomorphic to \(H_4,\) decompose the graph \((K_3\,\circ\,\overline K_2)(5).\) ◻
We use the following two theorems and a lemma in the proof of Theorem 1.
Theorem 2. (see [2]).For \(n\,\geq\,3,\,K_n\) can be decomposed into \(K_3, K_4, K_5, K_6\) and \(K_8.\)
Theorem 3. [16].If \(m\) and \(n\) are at least \(3,\) then for \(1\leq i\leq 4,\) \(H_i\,|\,K_m\,\circ\,\overline K_n\) if and only if \(5\,|\,mn(m-1).\)
Lemma 10. [17] For \(1\,\leq\,i\,\leq\,4,\) \(H_i\,|\,K_8(5).\)
Observation 4. It is clear that if \(\lambda_1\,|\,\lambda\) and \(G(\lambda_1)\) has an \(H\)-decomposition, then \(G(\lambda)\) also has an \(H\)-decomposition.
Proof of Theorem 1. The proof of the necessity is
obvious and we prove the sufficiency in two cases.
Case 1. \(g.c.d\)\((\lambda,5)=1.\)
The result follows by Theorem 3 and Observation
4.
Case 2. \(g.c.d\)\((\lambda,5)=5.\)
First we prove this case for \(\lambda=5.\) By Theorem 2 and the tensor product is distributive over edge-disjoint union of subgraphs, it is enough to prove that for \(m\in\{3,4,5,6,8\}\) and for \(1\leq i\leq 4,\) \(H_i\,|\,(K_m\,\circ\,\overline K_n)(5).\) If \(m\in\{3,4\},\) then the result follows by Lemmas 4, 5, 6, 7, 8 and 9 and if \(m\in\{5,6\},\) then the result follows by Theorem 3. If \(m=8,\) then \((K_8\,\circ\,\overline K_n)(5)=K_8(5)\,\circ\,\overline K_n=H_i\,\circ\,\overline K_n\,\oplus\,H_i\,\circ\,\overline K_n\,\oplus\,\dots\,\oplus\,H_i\,\circ\,\overline K_n,\) by Lemma 10 and for \(1\leq i\leq 4,\) \(H_i\,|\,H_i\,\circ\,\overline K_n,\) by Lemmas 1 and 2. If \(\lambda>5,\) the result follows by Observation 4.\(\) ◻
Theorem 5. [12].If \(m\) and \(n\) are at least \(3,\) then \(C_5\,|\,(K_m\,\circ\,\overline K_n)(\lambda)\) if and only if \(\lambda(m-1)n\) is even and \(5\,|\,\lambda m(m-1)n.\)
Combining Theorems 1 and 5, we obtain a complete solution to the decomposition of the \(\lambda\)-fold complete equipartite graphs into any simple connected unicyclic graph of order five.
There is no conflict of interest related to this work.
The author is grateful to Professor P. Paulraja for his valuable suggestion. The author would like to thank the referees for their careful reading and suggestions which improved the presentation of the paper.