The secure edge dominating set of a graph \( G \) is an edge dominating set \( F \) with the property that for each edge \( e \in E-F \), there exists \( f \in F \) adjacent to \( e \) such that \( (F-\{f\})\cup \{e\} \) is an edge dominating set. In this paper, we obtained upper bounds for edge domination and secure edge domination number for Mycielski of a tree.
The concept, domination of a graph G was introduced by Claude Berge in 1958. Later, Cockayne and Stephen Hedetniemi introduced edge domination of graphs. The concept of secure domination was introduced by Cockayne [1], which is applied to protect a system, using guards that can defend each vertex of G from an attack. In this paper, we initiate the study of secure edge domination in Mycielski of trees.
Let G(V,E) be a simple graph, with a finite nonempty set V(G)= {\(v_{1},v_{2}….v_{n}\)} called the vertex-set of G and E(G) called the edge-set of G. Degree of a vertex \(v \in\)V(G) is the number of edges adjacent to \(v\). A vertex induced subgraph of G induced by a vertex set S denoted by G[S], is a graph with vertex set S and edge set consists of edges \(uv\), whenever \(u,v \in\)S and \(uv\in\)E(G). The open neighborhood of a vertex \(v \in\) V(G), denoted by \(N(v)\), is the set of all vertices of G which are adjacent to \(v\). \(N[v]\) = \(N(v)\) \(\cup\) \(\{v\}\) is called closed neighborhood of v in the graph G. An edge covering of G is a subset C of E(G) such that every vertex of G is incident to some edges of C and the size of a minimum edge covering of G is \(\beta'(G)\).
A connected acyclic graph is called Tree. Leaf of a tree is a vertex having degree one. Remote vertex of a tree is the vertex having more than one leaf.
The Mycielski graph of G, \(\mu(G)\), is a graph with vertex set V(G) \(\cup\) {\(v'_{1},v'_{2},….v'_{n}\)} \(\cup\) \(\{z\}\) and edge set E(G) \(\cup\) {\(v_{i}v'_{j}\) ,\(v'_{i}v_{j}\) : \(v_{i}v_{j}\) is an edge in G} \(\cup\) {\(v'_{i}z: 1 \leq i \leq n\)} [2].
A set of edges F in graph G is an edge dominating set if every edge \(e\in E-F\) is adjacent to at least one edge in F. The edge domination number, \(\gamma'(G)\) is the minimum cardinality of an edge dominating set of G [3-5]. Secure edge dominating set of G is an edge dominating set F with property that for each edge \(e\in E-F\), there exists \(f\in F\) adjacent to \(e\) such that \((F-\{f\})\cup \{e\}\) is an edge dominating set. The secure edge dominating number, \(\gamma'_{s}(G)\) is the minimum cardinality of a secure edge dominating set.
In 1977, Mitchell and Hedetniemi in [6] constructed an algorithm for edge domination number of a tree. Later many studies have been done in the edge domination number of many graphs. In 2016, Kulli, [7] presented lower bound of secure edge domination of graph G and found secure edge domination number of many classes of graphs.
Related to this ideas, we have initiated our study in secure edge domination of Mycielski graphs. And found upper bounds for edge domination number and secure edge domination number of Mycielski graphs in [8].
In this paper, we obtained an upper bound for the edge domination and secure edge domination number in Mycielski of trees.
Let \(T_{0}\) be the given tree. Now consider the following set of vertices; U={Remote vertices of \(T_{0}\)} and L={leaf adjacent to the remote vertices of \(T_{0}\) }.
Step 1.
Case a. \(T_{0}\) have atleast one remote vertex.
Consider the remote vertices and its neighbors in \(T_{0}\). Since U={remote vertices of \(T_{0}\)}, we denote the number of remote vertices in \(T_{0}\) as \(|U|\). Now construct two graphs, \(T_{1}\) and \(T_{2}\) as follows:
\(T_{1}= G[N[U]-L]\), the graph induced by remote vertices and its neighbors, except the leafs incident to the remote vertices.
\(T_{2}\) = \(T_{0}- N[U]\), obtained by removing all remote vertices and their neighbors from \(T_{0}\).
Case b. \(T_{0}\) have no remote vertex .
In this case consider \(|U|=1\) and proceed to Step2.
Step 2.
Case a. \(T_{0}\) have atleast one remote vertex
Find the minimum edge cover of \(T_{1}\) and \(T_{2}\) and denote the size of minimum edge covers as \(n_{1}\) and \(n_{2}\) respectively. While computing cardinality of edge cover, the isolated vertices are counted once. Here the graphs \(T_{1}\) and \(T_{2}\), may be connected or disconnected.
Case a(1). Both \(T_{1}\) and \(T_{2}\) are connected.
Then, \(n_{1}\) = \(\beta'(T_{1})\) and \(n_{2}\) = \(\beta'(T_{2})\).
Case a(2). Both \(T_{1}\) and \(T_{2}\) are disconnected.
Then,
\(n_{1}= \sum_{i=1}^{r}\beta'_{i}\), where \(\beta'_{i}\) is the edge cover of components, \(C_{1},C_{2},…,C_{r}\) of \(T_{1}\).
\(n_{2}= \sum_{i=1}^{s}\beta'_{i}\), where \(\beta'_{i}\) is the edge cover of components, \(C_{1},C_{2},…,C_{s}\) of \(T_{2}\).
Case a(3). If \(T_{1}\) is connected and \(T_{2}\) is disconnected.
Then, \(n_{1}\) = \(\beta'(T_{1})\) and \(n_{2}= \sum_{i=1}^{s}\beta'_{i}\), where \(\beta'_{i}\) is the edge cover of components, \(C_{1},C_{2},…,C_{s}\) of \(T_{2}\). ( If \(T_{1}\) is disconnected and \(T_{2}\) is connected, then \(n_{1}= \sum_{i=1}^{r}\beta'_{i}\), where \(\beta'_{i}\) is the edge cover of components, \(C_{1},C_{2},…,C_{r}\) of \(T_{1}\) and \(n_{2}\) = \(\beta'(T_{2})\).)
Case b. \(T_{0}\) have no remote vertices
In this case, we denote the minimum cardinality of edge cover of \(T_{0}\) as \(n_{1}\) and \(n_{2}=0\).
Theorem 1. The edge domination number of Mycielski of tree \[\gamma'(\mu(T))\le n_{1} + n_{2} + |U|.\]
Proof. Let \(T_{0}\) be the given tree and \(\mu(T_{0})\) be its Myceilski graph. Let U={\(u_{i},u_{j},u_{q},u_{k}….\)} be the set of all remote vertices of \(T_{0}\) and L={\(u_{i1},u_{i2},…\) \(,u_{j1},u_{j2},…,u_{q1},u_{q2},…,u_{k1},u_{k2}…\)} be the leaves adjacent to remote vertices in U. Consider the neighbors of \(u_{i}\) except leaves adjacent to it, \(N[U]-L\)={\(u_{y},u_{i},u_{m},u_{n},u_{j},u_{q},u_{s},u_{t},u_{k},u_{r},…\) }. Then let \(T_{1}\) be the graph induced by vertex set \(N[U]-L\) and \(D_{1}\) be the edge cover of \(T_{1}\). The edge cover \(D_{1}\) will consists of all the vertices of \(N[U]-L\) as the end vertices of edges in \(D_{1}\).
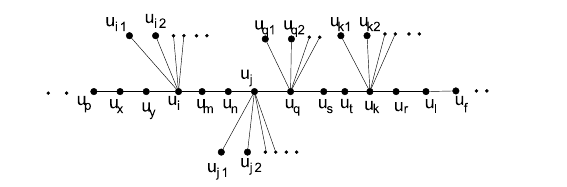
If \(T_{1}\) is disconnected, then let \(C_{1},C_{2},…,C_{r}\) are components of \(T_{1}\). Consider the edges which cover each component \(C_{i}\) of the graph \(T_{1}\). Let \(A{i}\)={\(u_{y}u_{i},u_{m}u_{n}, u_{j}u_{q},u_{s}u_{t}\) \(u_{k}u_{r},…\)} be the edge cover of a component \(C_{i}\). Then vertex set of \(A_{i}\) consists of every vertices of \(C_{i}\) as the end vertex of edges in \(A_{i}\). Thus edge cover of \(T_{1}\) is \(D_{1}=\cup A_{i}\) for i=1,2,3…,\(r\) corresponding to each component in \(C_{i}\) in \(T_{1}\). If any of the component is an isolated vertex then consider an edge incident to it from \(T_{0}\) in \(D_{1}\).
Thus we constructed a set of edges \(D_{1}\) which consists of every vertices in \(N[U]-L\). Hence \(D_{1}\) can dominate every edges incident to remote vertices and its neighbors except the edges adjacent to leafs of remote vertices in \(\mu(T_{0})\). That is, any edge \(u_{y}u_{i}\) in \(D_{1}\) can dominate edges {\(u_{x}u_{y}\), \(u'_{x}u_{y}\), \(u_{i}u_{m}\), \(u_{i}u'_{y}\),… \(u_{i}u_{i1}\),\(u_{i}u_{i2}\),..}.
Now remove all the remote vertices and neighbors from \(T_{0}\) to get the graph \(T_{2}\). To construct a dominating set, find the edge cover \(D_{2}\) of \(T_{2}\). If \(T_{2}\) is disconnected then, let \(B_{i}\)={\(u_{p}u_{x},u_{l}u_{f},…\)} be the edge cover of a component \(C_{i}\) of \(T_{2}\), which can dominate the edges of \(C_{i}\) and edges {\(u'_{p}u_{x}\), \(u_{p}u'_{x},u'_{l}u_{f},u_{l}u'_{f},…\}\) in \(\mu(T_{0})\). Thus any edge \(u_{p}u_{x}\) in edge cover \(D_{2}=\cup B_{i}\) for i=1,2,3,…,\(s\) dominates edges \(u'_{p}u_{x}\), \(u_{p}u'_{x}\) adjacent to \(T_{2}\) in \(\mu(T_{0})\). Thus \(D_{1} \cup D_{2}\) can dominate all the edges \(uv\), \(uv'\) and \(u'v\) except the edges \(u_{i1}u'_{i}\),\(u_{i2}u'_{i}\),.. for each remote vertex \(u_{i}\).
Now let us consider the edges of type \(u'_{i}z\) corresponding to each remote vertex \(u_{i}\) which can dominates \(u_{i1}u'_{i}\),\(u_{i2}u'_{i}\),…and edges \(v'z\) for v be any vertex in tree \(T_{0}\). Thus corresponding to each remote vertex, consider \(D_{3}\)={\(u'_{i}z,u'_{j}z,u'_{q}z,u'_{k}z,…\)}, where \(|D_{3}|\)=\(|U|\). If \(T_{0}\) is a tree without remote vertex then to dominate edges \(v'z\), consider \(D_{3}\)={\(v'z\)}.
Thus D= \(D_{1}\) \(\cup\) \(D_{2}\) \(\cup\) \(D_{3}\) is an edge dominating set of \(\mu(T_{0})\), Where \(|D_{1}|=n_{1}\), \(|D_{2}|=n_{2}\) and \(|D_{3}|= |U|\). Therefore, \(\gamma'(\mu(T))\) \(\le\) \(n_{1} + n_{2} + |U|\). ◻
To construct a secure edge dominating set, we have to create an edge dominating set S such that, for every e\(\in E(T)-S\) there exists a \(f\in S\) such that \((S-\{f\})\cup \{e\}\) is an edge dominating set. That is, we have to replace each edge e not in S with neighbors of e in S, provided that S still dominates \(\mu(T)\). But the edge dominating set \(D=D_{1}\) \(\cup\) \(D_{2}\) \(\cup\) \(D_{3}\) is not a secure edge dominating set. Since, for edge \(u_{y}u'_{i}\) \(\in E(T)-D\), \((D-\{u_{y}u_{i}\}) \cup u_{y}u'_{i}\) is not an edge dominating set. Hence, to make D a secure edge dominating set, we have to add some guards corresponding to each edges in D.
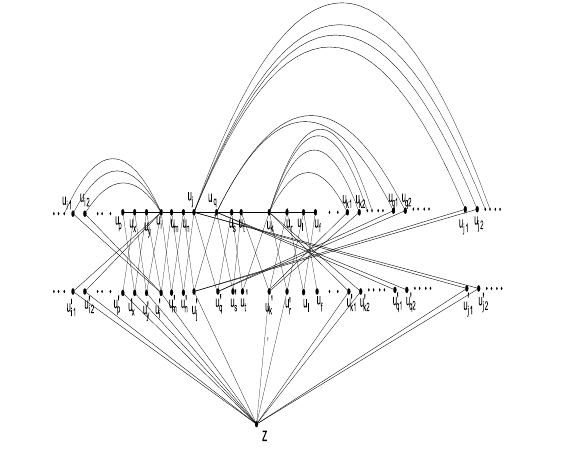
To safeguard each edges of \(D=D_{1}\) \(\cup\) \(D_{2}\) \(\cup\) \(D_{3}\), consider \(D_{1}\), \(D_{2}\) and \(D_{3}\) separately, see Figure 2.
Step 1. Guards for the edges {\(u_{y}u_{i},u_{m}u_{n},u_{j}u_{q}\)…..} in \(D_{1}\).
Consider the remote vertex set U={\(u_{i},u_{j},…\)}, then \(D_{1}\) consists of edges of the form X={\(u_{y}u_{i},u_{j}u_{q},u_{k}u_{r},…\)} corresponding to each remote vertices {\(u_{i},u_{j},u_{q},u_{k},…\)} \(\in U\) and Y={\(u_{m}u_{n}\),\(u_{s}u_{t}\),…} where {\(u_{m}\),\(u_{n}\),\(u_{s}\), \(u_{t}\),…} are neighbors of remote vertices. The number of edges in X is at most \(|U|\) and consider the number of edges in Y as \(n_{3}\). Now set {\(u_{i}u'_{y}\),\(u_{q}u'_{j}\),\(u_{r}u'_{k}\),…} as the guard of each edge in Y and {\(u_{n}u'_{m}\),\(u_{t}u'_{s}\),…} as the guard for each edge in X. Thus number of guards of Y is same as the number of edges in Y, which is equal to \(|U|\). Similarly number of guards for edges in X is \(n_{3}\). Thus, minimum number of guards required to secure \(D_{1}= |U|+ n_{3}\).
Step 2. Guards for the edges {\(u_{p}u_{x}\),\(u_{l}u_{f}\),…}in \(D_{2}\).
For each edge \(u_{p}u_{x}\) in \(D_{2}\), set \(u_{x}u'_{p}\) as guards. Therefore guards for edges of \(D_{2}\) are {\(u_{x}u'_{p}\),\(u_{f}u'_{l}\),…}. Thus number of guards for \(D_{2}\) is same as the number of edges in \(D_{2}\) which is equal to \(n_{2}\). Thus, Minimum number of guards required to secure \(D_{2}= n_{2}\).
Step 3. Guards of edges in \(D_{3}\).
To secure each edges {\(u'_{i}z,u'_{j}z,u'_{q}z,u'_{k}z,…\)} in \(D_{3}\), set the edge \(v'_{k}z\) as guard. Thus, Minimum number of guards required to secure \(D_{3}= 1\). Thus total number of guards required to secure D= \(|U|+ n_{3}+n_{2}+1\).
Theorem 2. Secure edge domination number of Mycielski graph of a tree \(T\) is, \[\gamma'_{s}(\mu(T)) \le 2|U| + n_{1} + 2n_{2}+ n_{3}+1.\]
Proof. By Theorem 1, we know that, edge domination number of Mycielski of tree is \(\gamma'(\mu(T))\) \(\le\) \(n_{1} + n_{2} + |U|\), where D= \(D_{1}\) \(\cup\) \(D_{2}\) \(\cup\) \(D_{3}\) is the edge dominating set of \(\mu(T)\). Now to safe guard D, for each edge in \(D_{1}\) \(\cup\) \(D_{2}\) \(\cup\) \(D_{3}\), we have to find a guard. Let S=\(S_{1} \cup S_{2}\cup S_{3}\) be the secure edge dominating set, where \(S_{1} =\{u_{i}u'_{y},u_{j}u'_{q},…\}\cup \{u_{n}u'_{m},u_{t}u'_{s}…\} \cup D_{1}\), \(S_{2}=\{u_{x}u'_{p},u_{f}u'_{l},…\} \cup D_{2}\) and \(S_{3}= \{v'z\}\cup D_{3}\). Since S contains \(D_{1}\cup D_{2}\cup D_{3}\), clearly S is an edge dominating set. Now we prove that S is a secure edge dominating set.
For, we have to replace each edge f not in \(S\) with adjacent edge e in \(S\) and prove that F= \((S-\{e\})\) \(\cap \{f\}\) is an edge dominating set.
Case 1. Consider the edges \(u_{x}u_{y}\) \(\notin S\) which is adjacent to \(u_{y}u_{i}\) in \(S_{1}\).
Case 1.1. Consider edges \(u_{x}u_{y}\),\(u'_{x}u_{y}\) \(\notin S\) which is adjacent to vertex \(u_{y}\) where \(u_{y}u_{i}\) \(\in\) \(S_{1}\).
Consider edge \(u_{x}u_{y}\) \(\notin S\) and replace \(u_{x}u_{y}\) instead of \(u_{y}u_{i}\) in \(S_{1}\). That is
F= \((S-\{u_{y}u_{i}\})\) \(\cap \{u_{x}u_{y}\}\). Now to check that F
is an edge dominating set, it is enough to verify that the adjacency of
deleted edge is still preserved by F. The edges incident to vertex \(u_{y}\) is dominated by \(u_{x}u_{y}\) and edges adjacent to vertex
\(u_{i}\) is dominated by the guard
\(u_{i}u'_{y}\) in \(S_{1}\). Thus \(S_{1}\) act as a secure edge dominating
set. Similar argument also hold if we replace \(u'_{x}u_{y}\) instead of \(u_{y}u_{i}\).
Case 1.2. Consider edges \(u_{i}u'_{q}\),\(u_{i}u_{i1}\),\(u_{i}u_{i2}\),…,\(u_{i}u'_{i1}\),\(u_{i}u'_{i2}\),… \(\notin S\) which is adjacent to vertex \(u_{i}\) where \(u_{y}u_{i}\) \(\in\) \(S_{1}\). Here each edge \(u_{i}u'_{q}\),\(u_{i}u_{i1}\),\(u_{i}u_{i2}\),…,\(u_{i}u'_{i1}\),\(u_{i}u'_{i2}\),… \(\notin S_{1}\) is not only adjacent to \(u_{y}u_{i}\), but also adjacent to \(u_{i}u'_{y}\), the guard of \(u_{y}u_{i}\). Consider the edge \(u_{i}u'_{q}\) adjacent to vertex \(u_{i}\) of edge \(u_{y}u_{i}\) and F= \((S-\{u_{i}u'_{y}\})\) \(\cap \{u_{i}u'_{q}\}\). Then F act as a dominating set, since edges adjacent to \(u_{i}\) is dominated by \(u_{y}u_{i}\) and \(u_{i}u'_{q}\). Remaining is to prove that F also dominates edges adjacent to \(u'_{y}\). If there exists no edge adjacent to \(u'_{y}\) other than \(u_{i}u'_{y}\) then proof is trivial. If there exists an \(u_{x}u_{y}\), then \(u_{x}u'_{y}\) will be adjacent to \(u'_{y}\). Since S consists of \(D_{1}\cup D_{2}\cup D_{3}\), which cover every vertices of tree T except the leafs. There will exists an edge \(u_{p}u_{x}\) in S which is adjacent to \(u_{x}u'_{y}\). Hence F dominates \(\mu(T)\). Similar conditions hold if we replace \(u_{m}u_{n}\) with adjacent edges not in \(S_{1}\).
Case 2. Consider edges \(u_{r}u_{l}\) \(\notin S\) which is adjacent to \(u_{l}u_{f} \in S_{2}\).
Similar to Case 1, for each edge adjacent to \(u_{l}\), remove \(u_{l}u_{f}\) from \(S_{2}\) and replace the edge adjacent to \(u_{l}\). And for edges adjacent to \(u_{f}\), remove guard \(u_{f}u'_{l}\) from \(S\). Then both F= \((S-\{u_{l}u_{f}\})\) \(\cup \{u_{r}u_{l}\}\) and F= \((S-\{u_{f}u'_{l}\})\) \(\cap \{u_{f}u_{e}\}\) dominates \(\mu(T)\) with similar arguments of Case 1.
Case 3. Consider edges \(u'_{r}z\) and \(u_{i1}u'_{i}\) \(\notin S\) which is adjacent to \(\{u'_{i}z\} \in S_{3}\).
For each edge adjacent to \(u_{i1}u'_{i}\), remove \(u'_{i}z\) from \(S\). Then F= \((S-\{u'_{i}z\})\) \(\cap \{u_{i1}u'_{i}\}\) act as an edge
dominating set, since adjacency of \(u'_{i}\) is preserved by \(u_{i1}u'_{i}\) \(\in F\) and adjacency of \(z\) by \(v'z\). Hence F dominates \(\mu(T)\). For edge \(\{u'_{r}z\} \notin S\), remove \(\{v'z\}\) from S. Then F= \((S-\{v'z\})\) \(\cup \{u'_{r}z\}\) is an edge
dominating set , since adjacency of z is preserved by \(\{u'_{r}z\}\). Now it is only to check
whether adjacency of \(u'_{r}\) is
dominated. Since S consists of all vertices of tree T except leafs, for
an edge \(uv'\) adjacent to \(v'z\) will get dominated by edge \(vu\) in S. Thus F is an edge dominating
set.
Hence S secure \(\mu(T)\), where \(S=|S_{1}\cup S_{2} \cup S_{3}|\) = \(2|U| + n_{1} + 2n_{2} +n_{3}+1\). ◻
There is no conflict of interest related to this work.
1970-2025 CP (Manitoba, Canada) unless otherwise stated.