We introduce a two-player game where the goal is to illuminate all edges of a graph. At each step the first player, called Illuminator, taps a vertex. The second player, called Adversary, reveals the edges incident with that vertex (consistent with the edges incident with the already tapped vertices). Illuminator tries to minimize the taps needed, and the value of the game is the number of taps needed with optimal play. We provide bounds on the value in trees and general graphs. In particular, we show that the value for the path on \( n \) vertices is \( \frac{2}{3} n + O(1) \), and there is a constant \( \varepsilon > 0 \) such that for every caterpillar on \( n \) vertices, the value is at most \( (1 – \varepsilon) n + 1 \).
We consider a game with two players: Illuminator and Adversary. There is a graph, and the goal of Illuminator is to illuminate all the edges of the graph. At each step Illuminator taps one vertex, and Adversary responds by illuminating the edges incident with the tapped vertex. Though Illuminator knows in advance (the isomorphism class of) the graph, Illuminator always sees only the spanning subgraph induced by the illuminated edges, with no labels on the vertices except which have been tapped and which have not. So at the beginning Illuminator sees a collection of isolates (vertices of degree \(0\)). The goal of Illuminator is to minimize the number of taps. The value of the game on graph \(G\), denoted \(ill(G)\), is the number of taps taken if both players play optimally.
Consider for example the case that the graph is the tree on \(5\) vertices of diameter three. At the beginning, Illuminator sees five isolates and the only option is to tap one of the isolates. There are three possible results: Adversary reveals the tapped vertex \(v\) to be either (i) the vertex of degree \(3\), (ii) the vertex of degree \(2\), or (iii) an end-vertex. Here are the three possibilities for what Illuminator sees:
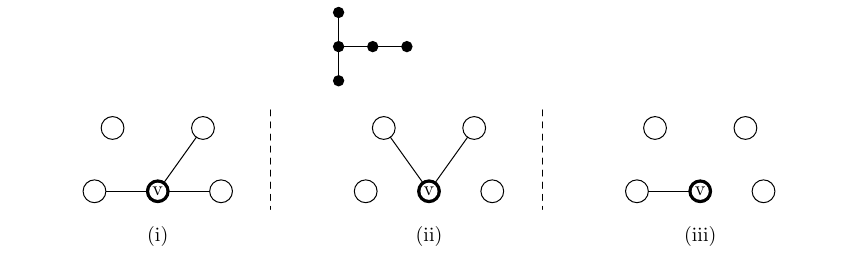
In scenario (i), Illuminator can finish in one tap by tapping the isolated vertex. In scenario (ii), Illuminator can finish in two taps, by for example tapping the two isolates. In scenario (iii), Illuminator can finish in two taps by first tapping the neighbor \(w\) of \(v\): then if \(w\) is revealed to be the vertex of degree \(3\), tapping the remaining isolate, while if \(w\) is revealed to be the vertex of degree \(2\), tapping \(w\)’s other neighbor. Thus Adversary should respond with either (ii) or (iii), and the value of the game is \(3\).
Essentially, at each step Illuminator chooses an orbit of the automorphism group of the current graph (where the vertices are colored as to whether they have been tapped or not), and Adversary reveals the connections of some vertex in this orbit. Thus such a game fits into the framework where decisions have to be made with incomplete information and past choices cannot be undone. The most common version is an online algorithm, where the graph is revealed one vertex at a time. This genre includes online graph coloring [1], independent sets [2] and online vertex covering [3]. Online algorithms are sometimes analyzed by competitive ratio: that is, how well they do compared to an algorithm with complete information. In our case, the natural analog would be to compare it to the vertex cover number. But it is immediate that the graph with \(n\) vertices and exactly one edge has vertex cover number \(1\) while the value of the game is \(n-1\). This observation parallels the linear lower bound of performance ratios for online algorithms for vertex cover.
In this paper we consider the Illumination problem. We provide some general bounds and elementary facts. We show that the path and cycle need approximately \(\frac{2}{3}\) of their vertices. We further show that for caterpillars that the value is at most \(\frac{83}{88} n + 1\), where \(n\) is the order.
We start with some elementary general observations
Lemma 1. For a graph \(G\) of order \(n\ge 3\) with at least one edge, it holds that \(2 \le ill(G) \le n-1\).
Proof. For the upper bound, tapping any \(n-1\) vertices is guaranteed to reveal all edges. For the lower bound, Adversary can ensure that there is an edge that remains not illuminated after the first tap. ◻
Equality in the lower bound in Lemma 1 is attained for the star (and some other small graphs such as \(K_3\) or \(2K_2\)). Equality in the upper bound is attained for the complete graph, and indeed the union of the complete graph with some isolates. (There are many more examples; see the discussion of joins below.)
Lemma 2. If \(T\) is a tree of order \(n\) and maximum degree \(\Delta\), then \(\textit{ill}(T) \le n-\Delta+1\).
Proof. Consider the following strategy for Illuminator. After the first tap there is one nontrivial component. Then repeatedly tap any of the untapped vertices in the nontrivial component, until a vertex \(v\) of the maximum degree is tapped. Then tap every other vertex in the graph. At the end all edges are illuminated, but at least \(\Delta-1\) neighbors of \(v\) are never tapped. ◻
The bound of Lemma 2 is sharp for the star. It is also sharp for the star with one edge subdivided (which for \(n\ge 6\) is the unique tree that needs \(3\) taps).
Here is another simple upper bound. Recall that a support vertex is one that has an end-vertex neighbor.
Lemma 3. If \(G\) is a graph such that every vertex is either an end-vertex or support vertex, then \(\textit{ill}(G) \le 2s\) where \(s\) is the number of support vertices.
Proof. Illuminator starts by tapping an isolate. If this is revealed to be an end-vertex, Illuminator immediately taps its neighbor. In either case, the next step is to tap an isolate and repeat. All support vertices are tapped and at most one end-vertex neighbor for each support vertex. ◻
It can be shown that the bound of Lemma 3 is sharp if \(G\) is a tree where every support vertex has sufficiently many end-vertex neighbors. In particular:
Lemma 4. Let \(T\) be the tree formed by taking the path \(S = v_1, \ldots, v_s\) on \(s\) vertices and attaching to each vertex \(v_i\) a set \(L_i\) of at least two vertices. Then \(\textit{ill}(T) = 2s\).
Proof. By Lemma 3 the value \(2s\) is an upper bound. Observe that for each vertex \(v_i\) of \(S\), if \(v_i\) is not tapped then all of \(L_i\) is tapped.
So consider the following strategy for Adversary. Adversary responds to the tap of an isolate by revealing the next available vertex in the sequence all of \(L_1\), then all of \(L_2\), and so on. If Illuminator taps a vertex of degree one, it is revealed to be the next \(v_i\). If Illuminator taps a neighbor of tapped \(v_i\), then this is revealed to be part of \(L_i\) if possible.
Now, the only way for one tap in \(\{v_i\} \cup L_i\) combined is that Illuminator is able to force Adversary to reveal \(v_i\) without having tapped any of \(L_i\). By the Adversary strategy, this means that \(v_{i-1}\) has been tapped along with all of \(L_{i-1}\). So while there is only one tap on \(\{v_i\} \cup L_i\), there are at least three taps on \(\{v_{i-1} \} \cup L_{i-1}\). Hence the average number of taps per \(\{v_i\} \cup L_i\) is at least two. ◻
We next consider the cycle.
Theorem 1. For the cycle \(\textit{ill}(C_n) = \lfloor 2n/3 \rfloor\).
Proof. A tap of an isolate illuminates two edges, and a tap of a degree-\(1\) vertex illuminates one edge. So the goal of Illuminator is to tap as many isolates as possible, and for Adversary the reverse. Thus Illuminator should tap an isolate if there is one, and Adversary should expend as many isolates as possible. Hence with optimal play there will be \(\lceil n/3 \rceil\) isolate-taps, and the value of the game is \(n – \lceil n/3 \rceil\). ◻
We next consider the path. We use the term “end” to mean an end-vertex of the path.
Theorem 2. For the path on \(n\ge 3\) vertices, it holds that \(\textit{ill}( P_n ) = \lfloor (2n+1)/3 \rfloor\).
Proof. We prove first that this value is an upper bound. A strategy for Illuminator is: tap an isolate if there is one; otherwise tap an (untapped) vertex of degree \(1\), choosing one in a component containing a tapped end if there is such a component.
At each stage, let \(\Phi\) denote the sum of the number of edges that are not illuminated plus the number of ends that have not been tapped. Initially \(\Phi=n+1\). Every time Illuminator taps an isolate, \(\Phi\) goes down by \(2\) (either two edges are illuminated or one edge is illuminated and one end becomes tapped); every time Illuminator taps a degree-\(1\) vertex, \(\Phi\) goes down by \(1\). When \(\Phi=0\) we are guaranteed to be done. Indeed, if the isolates are depleted before both ends are tapped, then Illuminator can ensure that at least one end is never tapped and so the game finishes with \(\Phi \ge 1\).
If Adversary does not reveal both ends during the isolate-tapping phase, then the best they can do is to minimize the number of tapped isolates, namely \(\lceil n/3 \rceil\) taps. Hence in this case the total number of taps is at most \(n – \lceil n/3 \rceil = \lfloor 2n/3 \rfloor\). If Adversary does reveal both ends during the isolate-tapping phase, then again the best they can do is to minimize the number of tapped isolates, but now this is at least \(2 + \lceil (n-4)/3\rceil\) taps, since revealing a tapped isolate to be an end reduces the number of isolates by at most \(2\). Hence in this case the total number of taps is at most \(n+1 – (2 + \lceil (n-4)/3 \rceil ) = \lfloor (2n+1)/3 \rfloor\). This proves the upper bound.
There is a corresponding strategy for Adversary: If possible, reveal the tapped vertex to be an end; in any case, have as many isolates as possible be neighbors of the tapped vertex. If Illuminator only ever taps one isolate, then the total number of taps is \(n-1\). Otherwise, Adversary’s strategy ensures that the game ends with \(\Psi=0\), and the number of taps that decrease \(\Psi\) by \(2\) is at most \(2 + \lceil (n-4)/3 \rceil\); thus the bound follows. ◻
Finally in this section, we make some observations about the join and disjoint union. Let \(G \cup H\) denote the disjoint union of graphs \(G\) and \(H\), and \(G \vee H\) their join.
Lemma 5. If \(G\) is a graph of order \(n_G\) and \(H\) a graph of order \(n_H\), then
(a) \(\textit{ill}( G \cup K_1 ) = \textit{ill}( G \vee K_1) = \textit{ill}(G)+1\).
(b) \(\textit{ill}(G \cup H) \ge \textit{ill}(G) + \textit{ill}(H)\).
(c) \(\textit{ill}(G \vee H) \ge \min \left( \textit{ill}(G) + n_H, \textit{ill}(H)+n_G \right)\).
Proof.
(a) The stated value is a lower bound, since Adversary can respond to the first tap by declaring that the tapped vertex is the \(K_1\), so that what remains is the game on \(G\). The stated value is also an upper bound. Illuminator plays the game as if they are in \(G\); the first time a candidate for the \(K_1\) is revealed, they assign it as such and continue.
(b)(c) Even if the vertices come with labels as to whether they are in \(G\) or \(H\), the game takes at least this long.
◻
In particular, Lemma 5 implies that if both \(G\) and \(H\) have the property that the value of the game is their order minus \(1\), then this is also true about their join.
Perhaps surprisingly, there are cases where \(\textit{ill}( G \cup H)\) is much larger than \(\textit{ill}(G) + \textit{ill}(H)\). For example, let \(G\) be the graph obtained from the star \(S_n\) on \(n\) vertices by adding one edge. Let \(H\) be the disjoint union \(rS_n\). Then \(\textit{ill}(G) = n-1\) and \(\textit{ill} (H) = 2r\). But \(\textit{ill}( G \cup H) = r(n-1)\): Illuminator has to find the component with the extra edge, and it takes \(n-1\) taps of each component to determine whether it has the extra edge or not.
Recall that a caterpillar is a graph such that when one removes all end-vertices, what remains is a path, known as the spine (such as the trees discussed in Lemma 4).
Theorem 3. For a caterpillar on \(n\) vertices, one can illuminate all edges in at most \(\frac{83}{88} n +1\) taps.
The proof is an immediate consequence of two strategies, depending on how the order \(d\) of the spine compares with \(5n/22\).
Lemma 6. For a caterpillar \(G\) with \(n\) vertices and \(d\) vertices on the spine, \(\textit{ill}( G ) \le n – \lfloor d/4 \rfloor\).
Lemma 7. For a caterpillar \(G\) with \(n\) vertices and \(d\) vertices on the spine, \(\textit{ill}( G ) \le \frac{43}{48} n + \frac{5}{24}d\).
The two lemmas are proved below. Note that in several place the constants can be improved by a more careful argument. But since we do not how to achieve an optimal bound for caterpillars, we stick to the basic argument.
To prove Lemma 6, consider the following strategy for Illuminator:
Phase 1: While there is an edge joining two vertices of degree \(1\) or an isolate: If there is an edge joining two vertices of degree \(1\) then tap the untapped end; else tap an isolate.
Phase 2: Repeatedly tap an untapped spinal vertex that does not already have two spinal edges illuminated.
Claim 1. Under the above strategy,
All edges become illuminated.
On the spine there cannot be four tapped vertices in a row.
Proof.
Let \(F\) be the spanning subgraph of the illuminated edges when Phase 1 finishes. Then \(F\) has no isolate, and so every leaf-edge of \(G\) has been illuminated. Furthermore, for every leaf-edge Illuminator knows which end is the end-vertex in \(G\). In particular, in \(F\) Illuminator knows which vertices are on the spine. The only missing edges join vertices of the spine, and so Phase 2 ensures that all remaining edges of \(G\) become illuminated.
Consider the situation after all edges have been illuminated. Assume the spine is \(v_1, \ldots, v_d\) and consider two consecutive vertices on the spine that have been tapped, say \(v_i\) and \(v_{i+1}\), with \(1<i<d-1\). Assume vertex \(v_i\) was tapped before vertex \(v_{i+1}\). Then \(v_{i+1}\) was tapped in Phase 2. So at that moment, the edge \(v_{i+1}v_{i+2}\) was not illuminated. On the other hand, edge \(v_{i+2}v_{i+3}\) was illuminated, since otherwise \(v_{i+2}\) would have been tapped in Phase 1. It follows that after \(v_{i+1}\) is tapped, vertex \(v_{i+2}\) has two spinal neighbors and so is never tapped. Similarly, if \(v_{i-1}\) is tapped, it must have been tapped after \(v_i\), and thus \(v_{i-2}\) was never tapped.
◻
The bound of Lemma 6 follows, as the number of untapped spinal vertices is at least \(\lfloor d/4 \rfloor\).
For the analysis of the strategy on short spines, we need a result that can be viewed as the weighted version of the game on path. Consider the illumination problem on a path, but with the vertices having nonnegative integer weights (visible at all times). Again the goal is to illuminate all the edges, but the cost of a tap is the weight of that vertex.
Theorem 4. One can illuminate a weighted path at cost at most \(\frac{43}{48} W\) where \(W\) is the total weight.
Theorem 4 follows immediately from Lemma 8 below, as the worst case is \(W_E = \frac{7}{12} W\) and \(W_I = W – W_E\).
We prove by induction a bound for the path where some of the edges have already been illuminated, and thus some vertices are isolated and some are not. We do not assume Illuminator knows anything about how the weights are ordered in the overall path, except that they know the weights of the two ends. Let \(\alpha= \frac{1}{2}\) and \(\beta = \frac{3}{4}\). Define \[\Psi = \alpha W_N + \beta W_I + \min ( W_E, zW )\] where \(W_N\) is the total weight of degree-\(1\) vertices other than the ends, \(W_I\) the total weight of isolates other than the ends, \(W_E\) is the total weight of the untapped end(s), \(W=W_N+W_I+W_E\), and \(z\) is \(0\) if no untapped end, \(\frac{1}{3}\) if one untapped end, and \(\frac{7}{12}\) if two untapped ends.
Lemma 8. The partially illuminated path can be fully illuminated at a cost of at most \(\Psi\).
Proof. The proof is by induction on the number of components, and subject to this, on the number of tapped ends. (The base case is one component, i.e., all edges are illuminated.) At each stage let \(F\) be the spanning subgraph of the illuminated edges. Let \(x\) be the smallest weight of an untapped vertex of degree \(1\) (if it exists), say of vertex \(u\). Let \(y\) be the smallest weight of an isolate (if it exists); say of vertex \(v\).
Note that at least one of \(u\) or \(v\) exists, else we are done. We choose a candidate vertex \(C\) as follows. If only one of \(u\) or \(v\) exists, then that vertex is \(C\). Otherwise \(C\) is vertex \(u\) if \(y>2x\) and vertex \(v\) otherwise. Let \(w_C\) denote its weight.
Case 1: It is possible for \(C\) to be an end of the path, and \(w_C > \frac{1}{4}W\) if there are two
untapped ends or \(w_C > \frac{1}{3}
W\) if there is one untapped end.
Then since \(C\) is a candidate, each
component of \(F\) has untapped weight
at least \(w_C\) except possibly the
one containing the tapped end (if there is such a component) which has
weight at least \(w_C/2\). Thus there
are at most three components.
Now, the strategy for Illuminator is to tap all vertices in all components except the component with maximum weight. Say this costs \(X\). Then \(X \le \min( \frac{2}{3} W, W-w_C)\). Assume there is one untapped end. Then \(\Psi \ge \frac{1}{2} ( W- w_C ) + \frac{1}{3}W > X\) since \(W_E = w_C > \frac{1}{3}W\). Assume there are two untapped ends. Then \(W_E > \frac{3}{2} w_C\) and \(\Psi \ge \frac{1}{2} ( W- w_E ) + \min ( W_E, \frac{7}{12}W )\). Again it can be checked that \(\Psi \ge X\). The bound is established in this case.
Case 2: Otherwise. Then tap \(C\). Assume first that \(C\) is revealed to be an end of the path. Then we can induct: If there was only one untapped end, then \(C\) has weight at most \(\frac{1}{3}W\) and \(z\) decreases by \(\frac{1}{3}\), while if there were two untapped vertices, then \(C\) has weight at most \(\frac{1}{4}W\) and \(z\) decreases by \(\frac{1}{4}\).
So assume that \(C\) is revealed to be not an end. If \(C=u\), there are two possibilities:
Vertex \(u\) links to a non-isolate \(u'\), say of weight \(x'\). (Note that \(x'\ge x\).) In that case, the decrease in \(\Psi\) is at least \(\alpha x' + \alpha (x) \ge x\).
Vertex \(u\) links to an isolate, say with weight \(y'\). (Note that \(y'\ge y > 2x\).) In that case, the decrease in \(\Psi\) is at least \(\alpha x + (\beta – \alpha ) y' \ge x\).
If \(C=v\), there are three possibilities.
Vertex \(v\) links to two non-isolates. In that case, the decrease in \(\Psi\) is at least \(\beta y – \alpha (2x) > y\).
Vertex \(v\) links to one isolate, say of weight \(y'\), and one non-isolate, say of weight \(x'\). Then the decrease in \(\Psi\) is \(\beta y + (\beta – \alpha) y' + \alpha x' \ge y\).
Vertex \(v\) links to two isolates. Then the decrease in \(\Psi\) is at least \(\beta y + 2( \beta -\alpha )y \ge y\).
This completes the proof since we can induct in each case. ◻
We are now in a position to prove Lemma 7. We start with the following strategy for Illuminator:
Phase 1. Repeatedly: If there is an untapped vertex with a tapped end-vertex neighbor, then tap it. Else tap an isolate. Else halt.
Let \(F\) be the spanning subgraph of the illuminated edges when Phase 1 halts. The lack of isolates means each leaf-edge of \(G\) has been revealed. If a leaf-edge is revealed through the tap of the end-vertex, then the other end of the edge is tapped next by the condition. Thus all spinal vertices of the original caterpillar that have leaf-edges have been tapped. In particular, every missing edge joins two vertices of the spine both of which have degree \(2\) in \(G\).
Each component \(F_i\) of \(F\) is a caterpillar and thus has a sub-spine \(S_i\). Note that each vertex of \(S_i\) is on the spine of \(G\), but end-vertices in \(F_i\) can be as well. Define a vertex as flailing if it is untapped, of degree one, and adjacent to the end of its sub-spine.
Claim 2. One can complete the illumination of \(G\) in at most \(\frac{43}{48} f\) where \(f\) is the number of flailing vertices.
Proof. Associated with \(F\) we build a weighted auxiliary graph \(A\) as follows. For each \(F_i\) where \(S_i\) is one vertex, there is one isolate in \(A\) with weight the number of flailing vertices in the component. For each \(F_i\) where \(S_i\) is more than one vertex, there is a \(K_2\) in \(A\) with weights the number of flailing neighbors of each ends of the sub-spine. See the following figure.

Then apply Theorem 4 to \(F\). We claim that a strategy on the weighted \(A\) corresponds to a strategy on \(F\). For each vertex tapped on \(A\), tap all the flailing neighbors of the corresponding sub-spine-end in \(F\). This will illuminate the un-illuminated edge(s) incident with that component. ◻
Now, if an untapped vertex has degree one but its neighbor is in the interior of its sub-spine, then that vertex will never be tapped. So it follows that the illumination of \(G\) can be completed in at most \(\frac{43}{48} f^*\) taps where \(f^*\) is the number of untapped vertices of degree one. Observe that \(f^* \ge n-2d\), since for each spinal vertex at most one end-vertex neighbor is tapped in Phase 1. So the total number of taps taken is at most \(n – (1-\frac{43}{48} )(n-2d) = \frac{43}{48} n + \frac{5}{24}d\).
The most obvious and critical question is whether there are trees where the number of taps needed is \(n-o(n)\) where \(n\) is the order. Several attempts by one of the authors to build such a tree, carefully negating a particular strategy of Illuminator, failed when the other author showed that another strategy of Illuminator would work quickly. In another direction, one could hope for better bounds in other family of trees, such as for example complete binary trees, or trees of maximum degree \(3\) in general.
There are also other possible goals for the game. We considered here the task of illuminating all the edges, but one could also consider the task of illuminating a path between two specified vertices. We also assumed the underlying graph was known to Illuminator; but maybe this assumption can be relaxed.
The authors declare no conflicts of interest to this work.