An hourglass \(\Gamma_0\) is the graph with degree sequence \(\{4,2,2,2,2\}\). In this paper, for integers \(j\geq i\geq 1\), the bull \(B_{i,j}\) is the graph obtained by attaching endvertices of two disjoint paths of lengths \(i,j\) to two vertices of a triangle. We show that every 3-connected \(\{K_{1,3},\Gamma_0,X\}\)-free graph, where \(X\in \{ B_{2,12},\,B_{4,10},\,B_{6,8}\}\), is Hamilton-connected. Moreover, we give an example to show the sharpness of our result, and complete the characterization of forbidden induced bulls implying Hamilton-connectedness of a 3-connected {claw, hourglass, bull}-free graph.
In this paper, we basically follow the most common graph-theoretical terminology and notation and for concepts not defined here we refer the reader to [1]. By a graph we always mean a simple finite undirected graph \(G=(V(G),E(G))\); whenever we admit multiple edges, we always speak about a multigraph. For a set \(X\), the cardinality of \(X\) is denoted by \(|X|\). We write \(|G|\) for \(|V(G)|\). For a family of graphs \(\mathcal{F}\), we say that \(G\) is \(\mathcal{F}\)-free if \(G\) does not contain an induced subgraph isomorphic to a member of \(\mathcal{F}\), and the graphs in \(\mathcal{F}\) are referred to in this context as forbidden induced subgraphs. If \(\mathcal{F}=\{F\}\), then we simply say that \(G\) is \(F\)-free. Here, the claw is the graph \(K_{1,3}\).
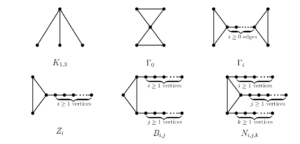
Several further graphs that will be used as forbidden subgraphs are shown in Figure 1 (specifically, the vertex of degree \(2\) in the triangle of the bull \(B_{i,j}\) will be called its mouth and denoted \(\mu(B_{i,j}\))). When listing vertices of an induced subgraph \(F\cong B_{i,j}\), we will always list first \(\mu(F)\), and then vertices of the two paths, starting (if possible) with the shorter one. In addition, let \(P_i\) and \(C_i\) denote the path and cycle with \(i\) vertices.
In this paper, we will consider these questions in 3-connected and claw-free graphs. A graph \(G\) is hamiltonian if \(G\) has a spanning cycle. The hamiltonian problem is generally considered to be determining conditions under which a graph contains a spanning cycle. To determine whether a graph is hamiltonian is very basic and popular problem. There are many results on hamiltonian properties of graphs in classes defined in terms of forbidden induced subgraphs. We first summarize some known results.
(Fujisawa [7]) if \(G\) is \(Z_9\)-free, then either \(G\) is hamiltonian, or \(G\) is isomorphic to the line graph of the graph obtained from the Petersen graph by adding one pendant edge to each vertex.
(Hu and Lin [8], Xiong et al. [23]) if \(G\) is \(N_{i,j,k}\)-free with positive integers \(i+j+k\leq 9\), then \(G\) is hamiltonian.
(Du and Xiong [6]) if \(G\) is \(B_{i,j}\)-free with positive integers \(i+j\leq 9\), then \(G\) is hamiltonian.
In 2002, Brousek [3] start to consider a triples of forbidden subgraphs for a graph to be Hamiltonian. Ryjáček et al. [19] and Du and Xiong [6] continue in this direction by showing that Theorem 1.1 can be substantially strengthened under an additional assumption that \(G\) is \(\Gamma_0\)-free, and it shows that these results of Hamiltonicity are sharp.
(Ryjáček et al. [19]) \(Z_{18}\)-free, or
(Ryjáček et al. [19]) \(N_{2i,2j,2k}\)-free with positive integers \(i+j+k\leq 9\), or
(Du and Xiong [6]) \(B_{2i,2j}\)-free with positive integers \(i+j\leq 9\),
then \(G\) is hamiltonian.
Theorem 1.2 adds the condition that \(G\) is hourglass-free on the basis of Theorem 1.1. Ryjáček and Vrána [17] give the following result.
In 2018, Ryjáček et al. [19] start to consider a triples of forbidden subgraphs for a graph to be Hamilton-connected. Recently, Liu and Xiong [12] also considered a triples of forbidden subgraphs for a 3-connected graph to be Hamilton-connected, this result on Hamilton-connectedness are sharp.
Then \(G\) is Hamilton-connected.
Theorem 1.5 lists known result on pairs of forbidden subgraphs implying Hamilton-connectedness of a \(3\)-connected graph.
By adding the condition “\(\Gamma_0\)-free” to Theorem 1.5, we further prove that every 3-connected, \(\{\)claw, hourglass, bull\(\}\)-free graph is Hamilton-connected.
Proof of Theorem 1.6, consisting in direct case-distinguishing, is postponed to Section 3. In Section 2, we collect necessary known results on line graphs and on closure operations.
In order to state results clearly, we further introduce the following notation. We denote by \(N_G(v)\) (or simply \(N(v)\)) and \(d_G(v)\) (or simply \(d(v)\)) the neighborhood and the degree of a vertex \(v\) in \(G\), respectively. For each integer \(i\geq 0\), define \(V_i(G)=\{v\in V(G): d(v)=i\}\). Let \(N[v]=N(v)\cup \{v\}\). Let \(S\subseteq V(G)\), the subgraph with \(S\) as the vertex set and all the edges with both end-vertices in \(S\) as the edge set is called the subgraph induced from the vertex set \(S\) (or simply induced subgraph), denoted by \(G[S]\). Let \(S'\subseteq E(G)\), the subgraph with \(S'\) as edge set and all the end-vertices of \(S'\) as vertex set is called the subgraph induced from edge set \(S'~(\)or simply edge induced subgraph\()\), denoted as \(G[S']\).
A vertex-cut (edge-cut, respectively) \(X\) of a multigraph \(G\) is essential if \(G-X\) has at least two nontrivial components, and \(G\) is essentially \(k\)-connected (essentially \(k\)-edge-connected, respectively) if every essential vertex-cut (essential edge-cut, respectively) of \(H\) is of size at least \(k\). Let \(\kappa'(G)\), \(c(G)\) denote the edge connectivity and the circumference of \(G\), respectively.
In Subsections 2.1-2.3, we summarize some facts that will be need in our proof of Theorem 1.6.
The line graph of a given \(G\), denoted by \(L(G)\), is a graph with vertex set \(E(G)\) such that two vertices in \(L(G)\) are adjacent if and only if the corresponding edges in \(G\) are incident to a common vertex in \(G\). The induced sub(multi)graph on a set \(M\subset V(G)\), denoted by \(G[M]\).
The multigraph \(H\) will be called the preimage of a line graph \(G\) and denoted \(H=L^{-1}(G)\). We will also use the notation \(a=L(e)\) and \(e=L^{-1}(a)\) for an edge \(e\in E(H)\) and the corresponding vertex \(a\in V(G)\).
A vertex \(x\in V(G)\) is eligible if \(G[N(x)]\) is a connected noncomplete graph, and we use \(V_{EL}(G)\) to denote the set of all eligible vertices of \(G\). The local completion of \(G\) at a vertex \(x\) is the graph \(G^{*}_x\) obtained from \(G\) by adding all edges with both vertices in \(N(x)\) (note that the local completion at \(x\) turns \(x\) into a simplicial vertex, and preserves the \(K_{1,3}\)-free property of \(G\)). The closure \(cl(G)\) of a \(K_{1,3}\)-free graph \(G\) was defined as the graph obtained from \(G\) by recursively performing the local completion operation at eligible vertices, as long as this is possible(more precisely: \(cl(G)=G_k\), where \(G_1,\ldots, G_k\) is a sequence of graphs such that \(G_1=G\), \(G_{i+1}=(G_i)^*_x\) for some \(x\in V_{EL}(G_i), i\in 1,\ldots,k-1\), and \(V_{EL}(G_k)=\emptyset\)). We say that \(G\) is closed if \(G=cl(G)\). The closure \(cl(G)\) of a \(K_{1,3}\)-free graph \(G\) is uniquely determined, is the line graph of a triangle-free graph, and is Hamiltonian if and only if so is \(G\). However, as observed in [2], the closure operation does not preserve (non-)Hamilton-connectedness of \(G\). It is a well-known fact that
We recall that if \(G=L(H)\), then a graph \(F\) is an induced subgraph of \(G\) if and only if \(L^{-1}(F)\) is a subgraph (not necessarily induced) of \(H\).
The core of \(H\) is the multigraph \(H_0\) obtained from \(H\) by deleting all the vertices of degree 1, and replacing the path \(xyz\) by the edge \(xz\) for each \(y\) of degree 2, and denoted \(co(H)\).
Obviously, if \(G\) is \(K_{1,3}\)-free, then so is \(G^*_x\). Note that in the special case when \(G\) is a line graph and \(H=L^{-1}(G)\), \(G^*_x\) is the line graph of the graph obtained from \(H\) by contracting the edge \(L^{-1}(x)\) into a vertex and replacing the created loop(s) by pendant edge(s). The following results show some properties of eligible vertexs.
The following theorem was proved in [4], [5].
A multigraph \(H\) is strongly spanning trailable if for any edge \(e_1, e_2\in E(H)\) (possibly \(e_1=e_2\)), the multigraph \(H(e_1, e_2)\), which is obtained from \(H\) by replacing the edge \(e_1\) by a path \(u_1v_{e_1}v_1\) and the edge \(e_2\) by a path \(u_2v_{e_2}v_2\), has a spanning \((v_{e_1}, v_{e_2})\)-trail. The following theorem establishes a correspondence between a \(IDT\) in \(H\) and a hamiltonian path in \(L(H)\).
\(\mathcal{W}_{0}\) is the family of multigraphs obtained from the Wagner graph \(W_8\) by subdividing one of its edges and adding at least one edge between the new vertex and exactly one of its neighbors (see Figure 2).
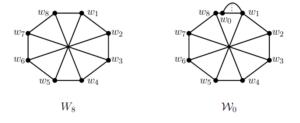
Every 2-connected 3-edge-connected multigraph \(H\) with \(c(H)\leq 8\) other than \(W_8\) is strongly spanning trailable.
Every 3-edge-connected multigraph \(H\) with \(|V(H)|\leq 9\) other than a member of \({W_8}\cup \mathcal{W}_{0}\) is strongly spanning trailable.
\(H_0\) is uniquely defined and \(\kappa'(H_0)\geq 3\),
\(V(H_0)\) dominates all edges of \(H\),
if \(H_0\) has a spanning closed trail, then \(H\) has a DCT,
if \(H_0\) is strongly spanning trailable, then \(L(H)\) is Hamilton-connected.
For a given \(K_{1,3}\)-free graph \(G\), a graph \(G^M\), as introduced in [9], is defined by the following construction.
If \(G\) is Hamilton-connected, we set \(G^M = cl(G)\).
If \(G\) is not Hamilton-connected, we recursively perform the local completion operation at such eligible vertices for which the resulting graph is still not Hamilton-connected, as long as this is possible. We obtain a sequence of graphs \(G_1\), …, \(G_k\) such that
\(G_1=G\),
\(G_{i+1}=(G_i)^{*}_{x_i}\) for some \(x_i\in V_{EL}(G_i)\), \(i=1,…,k-1\),
\(G_k\) has no hamiltonian \((a,b)\)-path for some \(a,b\in V(G_k)\),
for any \(x\in V_{EL}(G_k)\), \((G_k)^{*}_{x}\) is Hamilton-connected,
and set \(G^{M}=G_k\).
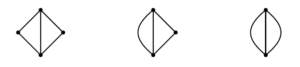
A resulting \(G^{M}\) is called a strong \(M\)-closure (or briefly an \(SM\)-closure) of the graph \(G\), and a graph \(G\) equal to its \(SM\)-closure is said to be \(SM\)-closed. Note that for a given graph \(G\), its \(SM\)-closure is not uniquely determined. As shown in [15] and [9], if \(G\) is \(SM\)-closed, then \(G=L(H)\), where \(H\) does not contain a subgraph\((\)not necessarily induced\()\) isomorphic to any of the graphs in Figure 3.
For \(x,y\in V(G)\), a path (trail) with endvertices \(x,y\) is referred to as an \((x,y)\)-path (\((x,y)\)-trail), a trail with terminal edges \(e,f\in E(G)\) is called an \((e,f)\)-trail, and Int\((T)\) denotes the set of interior vertices of a trail \(T\). A set of vertices \(M\subset V(G)\) dominates an edge \(e\), if \(e\) has at least one vertex in \(M\), and a subgraph \(F\subset G\) dominates \(e\) if \(V(F)\) dominates \(e\). A closed trail \(T\) is a dominating closed trail (abbreviated DCT) if \(T\) dominates all edges of \(G\), and an \((e,f)\)-trail is an internally dominating \((e,f)\)-trail (abbreviated \((e,f)\)-IDT) if Int\((T)\) dominates all edges of \(G\).
The following results show some properties of the \(SM\)-closure.
\(V(G)=V(G^M)\) and \(E(G)\subset E(G^M)\).
\(G^M\) is obtained from \(G\) by a sequence of local completions at eligible vertices.
\(G\) is Hamilton-connected if and only if \(G^M\) is Hamilton-connected.
if \(G\) is Hamilton-connected, then \(G^M=cl(G)\).
if \(G\) is not Hamilton-connected, then either
\(V_{EL}(G^M)=\emptyset\) and \(G^M=cl(G)\), or
\(V_{EL}(G^M)\neq \emptyset\) and \((G^M)^*_x\) is Hamilton-connected for any \(x\in V_{EL}(G^M)\).
\(G^M=L(H)\), where \(H\) contains either
at most \(2\) triangles and no multiedge, or
no triangle, at most one double edge and no other multiedge.
If \(G^M\) contains no hamiltonian \((a,b)\)-path for some \(a,b \in V(G^M)\) and
\(X\) is a triangle in \(H\), then \(E(X)\cap\{L^{-1}_{G^M}(a),L^{-1}_{G^M}(b)\}\neq \emptyset\).
\(X\) is a multiedge in \(H\), then \(E(X)=\{L^{-1}_{G^M}(a),L^{-1}_{G^M}(b)\}\).
We will also need the following lemma on \(SM\)-closed graphs proved in [16].
The concept of \(SM\)-closure can be further strengthened by omitting the eligibility assumption in the local completion operation. Specifically, for a given \(K_{1,3}\)-free graph \(G\), Liu et al. [11] constructed a graph \(G^U\) by the following construction.
If \(G\) is Hamilton-connected, we set \(G^U=K_{|V(G)|}\).
If \(G\) is not Hamilton-connected, we recursively perform the local completion operation at such vertices for which the resulting graph is still not Hamilton-connected, as long as this is possible. We obtain a sequence of graphs \(G_1\), \(\ldots\), \(G_k\) such that
\(G_1=G\),
\(G_{i+1}=(G_i)^{*}_{x_i}\) for some \(x_i\in V(G_i)\), \(i=1,…,k-1\),
\(G_k\) has no hamiltonian \((a,b)\)-path for some \(a,b\in V(G_k)\),
for any \(x\in V(G_k)\), \((G_k)^{*}_{x}\) is Hamilton-connected,
and set \(G^{M}=G_k\).
A resulting \(G^{U}\) is called a ultimate \(M\)-closure (or briefly an \(UM\)-closure) of the graph \(G\), and a graph \(G\) equal to its \(UM\)-closure is said to be \(UM\)-closed. When applying closure techniques to \(\{claw,\Gamma_0, bull\}\)-free graphs, the main problem is that a closure of a \(\{K_{1,3},\Gamma_0,B_{i,j}\}\)-free graph is not necessarily \(\{K_{1,3},\Gamma_0,B_{i,j}\}\)-free (i.e., in the terminology of [14], the class of \(\{K_{1,3},\Gamma_0,B_{i,j}\}\)-free graphs is not stable under the closure operation). Unfortunately, this is the case with all the closure operations mentioned in the previous subsections.
We say that a vertex \(x\in V(G)\) is simplicial if the subgraph induced by \(G[N(x)]\) is complete graph, and we use \(V_{SI}(G)\) to denote the set of all simplicial vertices of \(G\).
It turns out that this difficulty can be overcome by working in a slightly larger class of graphs which contains all the requested \(\{K_{1,3},\Gamma_0,B_{i,j}\}\)-free graphs but is stable under the closure. Ryjáček and Vrána [18] defined the class \(\mathcal{B}_{i,j}\) as follows, and they proved the following properties.
For any positive integers \(i,j\), \(\mathcal{B}_{i,j}\) is the class of all \(K_{1,3}\)-free graphs \(G\) such that every induced subgraph \(F\subset G\), \(F\simeq \mathcal{B}_{i,j}\), satisfies \(\mu(F)\in V_{SI}(G)\).
Clearly, every \(\{K_{1,3},B_{i,j}\}\)-free graph is in \(\mathcal{B}_{i,j}\).
We will always write the list such that integers \(1\leq i\leq j\) and \(i+j=7\), we use \(S_{1,2i+1,2j+1}\) to denote the graph obtained from \(K_{1,3}\) by subdividing two of its edges \(2i\) and \(2j\) times, respectively, where the labeling of vertices as in Figure 4, and the vertex \(o\) will be called the center vertex. It is easy to observe that \(L^{-1}(\Gamma_0)\) is the unique graph with degree sequence \(3,3,1,1,1,1\) and \(L^{-1}(B_{2i,2j})=S_{1,2i+1,2j+1}\). We will use the notation \(S_{1,i,j}(o,a_1,b_1b_2\ldots b_i,c_1\ldots c_j)(S_{1,i,j}\subseteq S(o,a_1, b_1b_2\ldots b_{i'},c_1\ldots c_{j'})\) with integers \(i'\geq i\) and \(j'\geq j)\) to denote the subgraph \(S_{1,i,j}\). Now, we present the proof of Theorem 1.6.
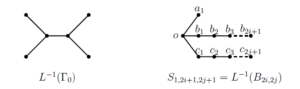
Proof of Theorem 1.6. Let \(G\) be a 3-connected \(\{K_{1,3},\Gamma_0, X\}\)-free graph, where \(X\in \{B_{2,12}\), \(B_{4,10}\), \(B_{6,8}\}\), and suppose, to the contrary, that \(G\) is not Hamilton-connected. By Theorems 2.3 and 2.11, we can assume that \(G\) is \(UM\)-closed and \(G\in \mathcal{B}_{2,12}\cup \mathcal{B}_{4,10}\cup \mathcal{B}_{6,8}\). Obviously, \(G\) is also \(SM\)-closed, implying that \(G\) is a line graph and \(H=L^{-1}(G)\) has special structure (contains no diamond, no multitriangle and triple edge), and let \(H_0\) be the core of \(H\). By Theorem 2.6 (4), \(H_0\) is not strongly spanning trailable. By Lemma 2.2, every induced hourglass in \(G\) is centered at an eligible vertex. By Theorem 2.7, \(H\) has at most two triangles or an multiedge. Hence, we may let \[\begin{aligned} \text{}~E_0~\text{be~the~edge~set~of~two~triangles~or~the~multiedge~in}~H. \end{aligned}\] By Theorem 2.6 (1), \[\begin{aligned} \label{zuixiaodu} \kappa'(H_0)\geq 3. %~\text{i.e.}, \end{aligned} \tg{1}\] For any edge \(e \in E(H_0)\backslash E_0\), \(L(e)\) is not an eligible vertex in \(G\) by Lemma 2.9, i.e., the edge \(e\) cannot be a central edge of an \(L^{-1}(\Gamma_0)\) for some induced hourglass \(\Gamma_0\) of \(G\). Thus we have \[\begin{aligned} \label{subdivided} \text{each~edge~of}~E(H_0)\backslash E_0~\text{should~be~subdivided~by~a~vertex~of~degree}~2~\text{in}~H. \end{aligned} \tag{2}\] It suffices to show that \(H\) contains all possible subgraphs \(S_{1,2i+1,2j+1}\in\{S_{1,3,13}\), \(S_{1,5,11}\), \(S_{1,7,9}\}\), where positive integers \(i+j=7\).
Proof. Assume, to the contrary, that \(c(H_0)\leq 8\) or \(|V (H_0)|\leq 9\). By Theorem 2.5, \(H_0\in \{W_8\}\cup \mathcal{W}_0\). Then \(H_0\) has a \(8\)-cycle \(w_1w_2\ldots w_8w_1\) or \(9\)-cycle \(w_1w_2\ldots w_8w_0w_1\) with \(\{w_1w_5, w_2w_6, w_3w_7\), \(w_4w_8\}\subseteq E(H_0)\) and \(w_0w_1\) is multiple edge. By (2), each edge \(w_mw_n\) of \(H_0\) should be subdivided by a vertex \(w_{m,n}\) of degree \(2\) with integers \(0\leq m< n\leq 8\). Then \(H\) contains subgraphs \[\begin{aligned} %\begin{split} &S_{1,3,13}(w_1,w_{1,5}, w_{1,8}(w_0)w_8w_{4,8},w_{1,2}w_2w_{2,3}w_3w_{3,4}w_4w_{4,5}w_5w_{5,6}w_6w_{6,7}w_7w_{7,8}),\\ &S_{1,5,11}(w_1,w_{1,5}, w_{1,8}(w_0)w_8w_{7,8}w_7w_{3,7},w_{1,2}w_2w_{2,3}w_3w_{3,4}w_4w_{4,5}w_5w_{5,6}w_6w_{6,7}) \end{aligned}\] and \[\begin{aligned} &S_{1,7,9}(w_1,w_{1,5}, w_{1,8}(w_0)w_8w_{7,8}w_7w_{6,7}w_6w_{2,6},w_{1,2}w_2w_{2,3}w_3w_{3,4}w_4w_{4,5}w_5w_{5,6}), %\end{split} \end{aligned}\] a contradiction. This proves Claim 3.1. ◻
Therefore \(c(H_0)\geq 9\) and \(|V(H_0)|\geq 10\). Throughout the proof, we use the following notation:
\(C_{c(H_0)}=v_1v_2\ldots v_{c(H_0)}v_1\) always denotes a longest cycle of \(H_0\), and \(C=PI_H(C_{c(H_0)})\);
Set \(m^{H_0}=|E_0\cap E(C_{c(H_0)})|\);
Set \(\mathcal{D}_{H_0}=V(H_0)\setminus V(C_{c(H_0)})\);
Let \(E_{H_0}^1\) be the set of all edges between \(C_{c(H_0)}\) and \(\mathcal{D}_{H_0}\). Then \(|E_{H_0}^1|\geq 3\);
By (2), \(C_{c(H_0)}\) has at least \(c(H_0)-m^{H_0}\) edges that should be subdivided by \(c(H_0)-m^{H_0}\) vertices of degree \(2\) in \(H_0\), then \(|V(C)|=2c(H_0)-m^{H_0}\). For integers \(1\leq r<s\leq c(H_0)\), we use \(v_{r,s}\) to denote the vertex subdivide edge \(v_rv_s\) in \(C_{c(H_0)}\). An edge \(v_rv_s\in E(C_{c(H_0)})\) is a \(l\)-chord if the shortest one of the two subpaths of \(C_{c(H_0)}\) determined by \(v_r\) and \(v_s\) has \(l\) internal vertices.
For a pair of vertices \(x\) and \(y\) in \(C_{c(H_0)}\), and a path \(P_{H_0\backslash C_{c(H_0)}}(x,y)\) with \(x,y\) as its end vertices and their internal vertices are not in \(C_{c(H_0)}\). Let \(P_{C_{c(H_0)}}(x,y)\) be the subpath of \(C_{c(H_0)}\). Then \(|P_{C_{c(H_0)}}(x,y)|\geq |P_{H_0\backslash C_{c(H_0)}}(x,y)|\).
Proof. Suppose Claim 3.2 false, \(|P_{ C_{c(H_0)}}(x_0,y_0)|< |P_{H_0\backslash C_{c(H_0)}}(x_0,y_0)|\) for some \(x_0,y_0\) satisfying the hypothesis Claim 3.2. Then \[C'=H_0[(E(C_{c(H_0)})\cup E(P_{H_0\setminus C_{c(H_0)}}(x_0,y_0))\setminus E(P_{C_{c(H_0)}}(x_0,y_0)]\] is a cycle of length at least \(c(H_0)+1\), which contradicts the choice of \(C_{c(H_0)}\). This proves Claim 3.2. ◻
Proof. Assume, to the contrary, that \(V(E_0)\cap V(C_{c(H_0)})=\emptyset\). Then \(|V(\mathcal{D}_{H_0})|\geq 2\) and \(E_{H_0}^1\cap E_0=\emptyset\). By (2), \(|V(C)|=2c(H_0)\geq 18\). Moreover, there is at least one edge in \(E_{H_0}^1\) with \(v_{i_0}\) as its end-vertex should be subdivided by a vertex \(x_0\) of degree \(2\) in \(H_0\). Then \(H\) contains all subgraphs \(S_{1,2i+1,2j+1}\subseteq H[V(C)\cup\{x_0\}]\) with its center vertex \(v_{i_0}\), for positive integers \(i+j=7\), a contradiction. This proves Claim 3.2. ◻
Proof. Assume, to the contrary, that \(H_0\) contains multiple edges. By Theorem 2.7 (6), \(H_0\) contains at most two mutiple edges and no other multiple edge. Let \(\{e_1',e_2'\}\subseteq E(H_0)\) be a pair of multiple edges, with \(u_1,u_2\) as their end-vertices.
Suppose first that \(|V(H_0)|=c(H_0)\). Then \(T=%e_1' v_{i_0}e_1'v_{i_0+1}\ldots v_{i_0}e_2'v_{i_0+1}\) is an \((e_1',e_2')\)-IDT in \(H\) with \(\{u_1,u_2\}=\{v_{i_0},v_{i_0+1}\}\), contradicting Theorem 2.7 (7). Now suppose that \(|V(H_0)|>c(H_0)\). Firstly, suppose that \(m^{H_0}=2\), but then \(c(H_0)=2\), contradicting \(c(H_0)\geq 9\). Then, suppose that \(m^{H_0}=0\). By Claim 3.3, \(\{u_1,u_2\}\cap V(C_{c(H_0)})\neq \emptyset\). If \(|\{u_1,u_2\}\cap V(C_{c(H_0)})|=2\) and \(u_1u_2\notin E(C_{c(H_0)})\), since \(H\) is triangle-free, \(e_1'\) is a \(k\)-chord in \(C_{c(H_0)}\) with \(k\geq 2\), then \(\Gamma_0\subseteq L^{-1}(H[u_1,u_1^+,u_1^-,u_2,u_2^+,u_2^-])\), a contradiction; otherwise, \(\{u_1,u_2\}\cap V(C_{c(H_0)})=\{u_1\}=\{v_{i_0}\}(\) say \(v_{i_0}\in V(C_{c(H_0)}))\) and \(u_2\) is not in \(C_{c(H_0)}\), by (2), \(|V(C)|=2c(H_0)\geq 18\). Then \(H\) contains all subgraphs \(S_{1,2i+1,2j+1}\subseteq H[V(C)\cup\{u_2\}]\) with its center vertex \(u_1\), and positive integers \(i+j=7\), a contradiction. Finally suppose that \(m^{H_0}=1\), say \(e_1'=v_{i_0}v_{i_0+1}\in E(C_{c(H_0)})\). By (2), \(|V(C)|=2c(H_0)-1\geq 17\). Moreover, there is at least one edge in \(E_{H_0}^1\) with \(v_{j_0}\) as its end-vertex that should be subdivided a vertex \(x_0\) of degree \(2\) in \(H\). Then \(H\) contains all subgraphs \(S_{1,2i+1,2j+1}\subseteq H[V(C)\cup\{x_0\}]\) with its center vertex \(v_{j_0}\), for positive integers \(i+j=7\), a contradiction. Thus \(H_0\) has no multiple edges. This proves Claim 3.4. ◻
By Claims 3.3 and 3.4, we can get that \(H_0\) is simple graph.
Proof. Assume, to the contrary, that \(H_0\) is a triangle-free simple graph. By (2), \(|V(C)|=2c(H_0)\geq 18\). Since \(\kappa'(H_0)\geq 3\), there is a vertex \(x_0\in N_H(v_{i_0})\) and \(x_0\notin V(C_{c(H_0)})\). Then \(H\) contains all subgraphs \(S_{1,2i+1,2j+1}\subseteq H[V(C)\cup\{x_0\}]\) with center vertex at \(V(C)\), for positive integers \(i+j=7\), a contradiction. This proves Claim 3.5. ◻
By Claims 3.4 and 3.5, \(H_0\) contains at least one triangle.
\(d_{H_0}(u_1)=d_{H_0}(u_2)=d_{H_0}(u_3)=3\).
\(m^{H_0}\in\{2,4\}\) if \(H_0\) contains at least one triangle.
Proof. (1). By Lemma 2.8, suppose to the contrary that \(d_{H_0}(u_1)\geq 4\). Since \(d_{H_0}(u_3)\geq 3\), \(\Gamma_0\subseteq L^{-1}(H[u_1,u_1^+,u_1^-,u_3,u_3^+,u_3^-])%\cong\), a contradiction. Then \(d_{H_0}(u_1)=3\). Similarly, \(d_{H_0}(u_3)=3\). If \(d_{H_0}(u_2)\geq 4\), then \(\Gamma_0\subseteq L^{-1}(H[u_1,u_1^+,u_1^-,u_2,u_2^+,u_2^-])\), a contradiction. We have that \(d_{H_0}(u_2)=3\).
(2). Firstly, suppose that \(m^{H_0}=3\), but then \(c(H_0)=3\), contradicting \(c(H_0)\geq 9\). We can easily get that \(m\notin \{3,5,6\}\). Then, suppose that \(m^{H_0}=0\). By Claim 3.3, \(\{u_1,u_2,u_3\}\cap V(C_{c(H_0)})\neq \emptyset\). Then for some vertex \(u_0\in \{u_1,u_2,u_3\}\), \(d_{H_0}(u_0)\geq 4\), which contradicts \(d_{H_0}(u_0)=3\), a contradiction. Finally, suppose \(m^{H_0}=1\), and \(u_1u_2\in E(C_{c(H_0)})\). By Claim 3.2, \(u_3\in V(C_{c(H_0)})\). Then \(d_{H_0}(u_3)\geq 4\), a contradiction. Therefore \(m^{H_0}\in \{2,4\}\). This proves Claim 3.6. ◻
If \(m^{H_0}=2\), then \(H_0\) has exactly one triangle and \(C_{c(H_0)}\) contains exactly three vertices of the triangle, where the vertices of the triangle are pairwise adjacent in \(H_0\). Without loss of generally, we denote the triangle by \(v_1v_2v_3v_1\). Choose a shortest path \(P^{r,s}\subseteq H[E(\mathcal{D}_{H_0})\cup E_{H_0}^1]\) with two vertices \(v_r,v_s\in V(C_{c(H_0)})\) as its end-vertices, respectively, where the edges incident with vertices \(v_r\) and \(v_s\) in \(P^{r,s}\) are denoted by \(e_{r,s}^r\) and \(e_{r,s}^s\), respectively. For edge \(e_{r,s}^r,e_{r,s}^s\notin E_0\) and \(e_{r,s}^r,e_{r,s}^s\in E_{H_0}^1\), by (2), they should be subdivided by two vertices of degree \(2\) in \(H\), say \(x_{r,s}^r,x_{r,s}^s\in V(H)\), respectively. Let \(\mathcal{P}'\) be the set of all path \(P^{r,s}\) satisfying integer \(1\leq r,s\leq c(H_0)\).
Proof. Assume, to the contrary, that \(m^{H_0}= 2\). Then \(E_{H_0}^1\cap E_0=\emptyset\). By (2), \(|V(C)|=2c(H_0)-2\geq 16\). For any path \(P^{r,s}\in \mathcal{P}'\), if \(r=s\), then \(H\) contains a subgraph \(S_{1,2i+1,2j+1}\subseteq S(v_r,v_{r+1},P^{r,s}v_s\backslash v_s,v_{r-1,r} v_{r-1}\ldots v_{r+1,r+2})\), a contradiction. Therefore integer \(1\leq r< s\leq c(H_0)\) in \(P^{r,s}\). Since \(\kappa'(H_0)\geq 3\), there is at least a vertex \(x_r^0\in N_{H_0}(v_r)\backslash \{v_{r-1},v_{r+1}\}\) for all \(v_r\in V(C_{c(H_0)})\backslash \{v_1,v_3\}\).
Case 1. \(G\in \mathcal{B}_{2,12}\).
Suppose that \(x_r^0\notin V(C_{c(H_0)})\) and \(x_r^0\in V(\mathcal{P}')\). Then \(H\) contains a subgraph \(S_{1,3,13}\subseteq S(v_2,v_1,P_{H}^{2,s}\) \(x_{2,s}^s,v_{2,3}v_3\ldots v_9)\) or \(S_{1,3,13}\subseteq S(v_r,v_{r-1,r},P^{r,s}x_{r,s}^s,v_{r,r+1}v_{r+1}\ldots v_{r-1})\) with \(v_r\in \{v_4,v_5,\ldots v_{c(H_0)}\}\), a contradiction. Now suppose that \(x_r^0\in V(C_{c(H_0)})\) and \(|V(H_0)|=c(H_0)\geq 10\). Then \(v_2v_s\in E(H_0)\), where \(v_s\in \{v_5,\ldots,v_{c(H_0)-1}\}\), and \(H\) contains a subgraph \(S_{1,3,13}(v_2,v_{2,s},v_1\ldots v_{c(H_0)}\), \(v_3v_{3,4}\ldots v_9)\), a contradiction. Therefore \(d_{H_0}(v_2)=2\), contradicting (1). This proves Case 1.
Case 2. \(G\in \mathcal{B}_{4,10}\).
Suppose that \(x_r^0\notin V(C_{c(H_0)})\) and \(x_r^0\in V(\mathcal{P}')\) and \(|P^{r,s}|\geq 4\). Then \(H\) contains a subgraph \(S_{1,5,11}\subseteq S(v_r,v_{r+1},P_{H}^{r,s}x_{r,s}^s,v_{r-1,r}v_{r-1}\ldots v_{r+2})\), where \(v_r\in \{v_2,v_4,v_5,\ldots v_{c(H_0)}\}\), a contradiction. Then, suppose that \(|P^{r,s}|=3\) with \(P_{H}^{r,s}=v_rx_{r,s}^rx_{r,s}(x_r^0)x_{r,s}^sv_s\) and \(c(H_0)\geq 10\). By (2), \(|V(C)|=2c(H_0)-2\geq 18\). Then \(H\) contains a subgraph \(S_{1,5,11}\subseteq H[V(C)\cup \{x_{r,s}^r\}]\) with its center vertex \(v_r\), a contradiction. We have that \(c(H_0)=9\), say \(C_{c(H_0)}=v_1v_2\ldots v_9v_1\). Firstly, suppose \(N_{H_0}(v_6)\backslash \{v_7,v_5\}\subseteq V(\mathcal{D}_{H_0})\). Then there exists a path \(P^{6,r}\) for any possibility \(r\in \{2,4,8,9\}\). Then \(H\) contains a subgraph \[\begin{aligned} &S_{1,5,11}(v_1,v_{1,9}, v_3v_{3,4}\ldots v_5,v_2P_{H}^{2,6}v_6v_{6,7}\ldots v_9),S_{1,5,11}(v_6,v_{5,6}, P_{H}^{4,6}v_4v_{4,5},v_{6,7}v_7\ldots v_{3,4}),\\ &S_{1,5,11}(v_6,v_{6,7}, P_{H}^{6,8}v_8v_{7,8},v_{5,6}v_5\ldots v_{8,9}) \text{~or~}S_{1,5,11}(v_9,v_{1,9}, v_{8,9}v_8\ldots v_{6,7},P_{H}^{6,9}v_6v_{5,6}\ldots v_3v_2), %\end{split} \end{aligned}\] a contradiction. Hence \(v_6\) is on a chord of \(C_{c(H_0)}\) (\(v_2v_6\in E(H_0)\) or \(v_6v_9\in E(H_0)\)). Similarly, \(v_7\) is on a chord of \(C_{c(H_0)}\) (\(v_2v_7\in E(H_0)\) or \(v_4v_7\in E(H_0)\)). Then, suppose \(N_{H_0}(v_2)\backslash \{v_1,v_3\}\subseteq V(\mathcal{D}_{H_0})\), \(\{v_2,v_s\}\subseteq N(\mathcal{D}_{H_0})\cap V(C_{c(H_0)})\), by symmetry, \(s\in \{4,5\}\). Then \(H\) contains a subgraph \[\begin{aligned} S_{1,5,11}(v_4,v_{3,4}, P_{H}^{2,4}v_2v_3, v_5v_{5,6}\ldots v_{1,9}) \end{aligned}\] or \[\begin{aligned} S_{1,5,11}(v_7,v_{4,7}, v_{7,8}v_8\ldots v_{1,9},v_{6,7}\ldots v_5P_{H}^{2,5}v_2v_3v_{3,4}v_4), \end{aligned}\] a contradiction. \(v_2\) is on a chord of \(C_{c(H_0)}\). Then \(N_{H_0}(v_2)\in \{v_5,v_6,v_7,v_8\}\). If \(v_2v_6\in E(H_0)\), then \(H\) contains a subgraph \(S_{1,5,11}(v_6,v_{6,7},v_{5,6}v_5\ldots v_{2,3}, v_{2,6}v_2v_{3,4}v_4\ldots v_7v_{4,7})\), a contradiction. Hence \(v_2v_6\notin E(H_0)\), by symmetry, \(v_2v_7\notin E(H_0)\). Hence \(v_4v_7\in E(H_0)\) and \(v_6v_9\in E(H_0)\), we have that \(H\) contains a subgraph \[S_{1,5,11}(v_9,v_{6,9},v_{1,9}v_1\ldots v_{3,4}, v_{8,9}v_8\ldots v_4v_{4,7}),\] a contradiction. Therefore \(d_{H_0}(v_6)=d_{H_0}(v_7)=2\), contradicting (1). This proves Case 2.
Case 3. \(G\in \mathcal{B}_{6,8}\).
Subcase 3.1. \(c(H_0)\geq 10\) and \(|V(H_0)|\geq 10\).
By (2), \(|V(C)|=2c(H_0)-2\geq 18\). Hence \(d_{H_0}(v_r)\geq 3\), where \(v_r\in V(C_{c(H_0)})\). Then \(H\) contains all subgraphs \(S_{1,2i+1,2j+1}\subseteq H[V(C)\cup \{u\}]\) with its center vertex \(v_r\), positive integers \(i+j=7\), and \(u\in N_H(v_r)\backslash \{v_{r-1,r}, v_{r,r+1}\}\), a contradiction.
Subcase 3.2. \(c(H_0)= 9(\)say \(C_{c(H_0)}=v_1v_2\ldots v_9v_1)\) and \(|V(H_0)|\geq 10\).
By (2), \(|V(C)|=2c(H_0)-2\geq 16\). Firstly, suppose that \(P^{2,s}\in \mathcal{P}'\) for any possibility \(s\in \{4,5,6\}\). Then \(H\) contains a subgraph \[\begin{aligned} S_{1,7,9} &\subseteq S(v_2, v_3, P_{H}^{2,4}v_4v_{4,5}v_5v_{5,6}, v_1v_{1,9}\ldots v_6), \\ S_{1,7,9} &\subseteq S(v_5, x_{2,5}^5, v_{4,5}v_4v_{3,4}v_3v_1v_2x_{2,5}^2, v_{5,6}v_6\ldots v_{1,9}), \\ S_{1,7,9} &\subseteq S(v_6, x_{2,6}^6, v_{6,7}v_7 \ldots v_{1,9}, v_{5,6}v_5 \ldots v_3v_1v_2x_{2,6}^2). \end{aligned}\] a contradiction. Hence \(s\notin \{4,5,6\}\), by symmetry, \(s\notin \{9,8,7\}\). Then, supposed that \(P^{4,s}\in \mathcal{P}'\). Then \(H\) contains a subgraph \(S_{1,7,9}\subseteq S(v_4,v_{4,5},P_{H}^{4,6}v_6v_{5,6}v_5u,v_{3,4}v_3\ldots v_{7,8})\), where \(u\in N_{H}(v_5)\backslash \{v_{4,5}\), \(v_{5,6}\}\), \(S_{1,7,9}\subseteq S(v_4,v_{4,5},P_{H}^{4,7}v_7v_{6,7}v_6v_{5,6},v_{3,4}v_3\ldots v_{7,8})\), \(S_{1,7,9}\subseteq S(v_8,x_{4,8}^8,v_{7,8}v_7\ldots v_{4,5}\), \(v_{8,9}v_9\ldots v_4\) \(x_{4,8}^4)\) or \(S_{1,7,9}\subseteq S(v_9,x_{4,9}^9,v_{1,9}v_1\ldots v_4x_{4,9}^4, v_{8,9}v_8\ldots v_{4,5})\), a contradiction. Hence \(P^{4,s}\notin \mathcal{P}'\), by symmetry, \(P^{r,9}\notin \mathcal{P}'\). Finally, suppose that \(P^{5,s}\in \mathcal{P}'\). Then \(H\) contains a subgraph \(S_{1,7,9}\subseteq S(v_5,v_{5,6},P_{H}^{5,7}v_7v_{6,7}v_6u\), \(v_{4,5}v_4\ldots v_{8,9})\), where \(u\in N_{H}(v_6)\backslash \{v_{6,7},v_{5,6}\}\) or \(S_{1,7,9}\subseteq S(v_5,v_{5,6},P_{H}^{5,8}v_8v_{7,8}\) \(v_7v_{6,7}, v_{4,5}v_4\ldots v_{8,9})\), a contradiction. Hence \(P^{5,s}\notin \mathcal{P}'\), by symmetry, \(P^{r,8}\notin \mathcal{P}'\). Hence \(P^{6,s}\notin \mathcal{P}'\) and \(P^{7,s}\notin \mathcal{P}'\). Therefore \(|V(H_0)|=9\), a contradiction. This proves Claim 3.7. ◻
By Claims 3.6 and 3.7, \(m^{H_0}= 4\). If \(m^{H_0}=4\), then \(C_{c(H_0)}\) contains exactly six vertices of two triangles, where the vertices of each triangle are pairwise adjacent in \(C_{c(H_0)}\). In the following of Theorem 1.6, we denote the another triangle by \(v_{q-1}v_qv_{q+1}v_{q-1}\), by symmetry, \(q\in \{5,6,\ldots, \lceil\frac{c(H_0)+3}{2}\rceil\}\). By Claim 3.6 (1), we have that \(d_{H_0}(v_{q-1})=d_{H_0}(v_q)=d_{H_0}(v_{q-1})=3\).
Proof. Assume, to the contrary, that \(c(H_0)= 9(\)say \(C_{c(H_0)}=v_1v_2\ldots v_9v_1)\). By (2), \(|V(C)|=2c(H_0)-2\geq 14\). In this case, \(v_q\in\{v_5,v_6\}\), and \(|V(\mathcal{D}_{H_0})|\geq 1\) and \(E_{H_0}^1\cap E_0=\emptyset\).
Case 1. \(G\in \mathcal{B}_{2,12}\).
Subcase 1.1. \(v_q=v_5\).
Suppose that \(N_{H_0}(v_8)\backslash \{v_7,v_{9}\}\subseteq V(\mathcal{D}_{H_0})\). Then \(H\) contains a subgraph \(S_{1,3,13}\subseteq S(v_8,v_{8,9},P^{r,8}\) \(x_{r,8}^r,v_{7,8}v_7\ldots v_{9}x)\) with \(x\in N_H(v_9)\), a contradiction. Hence \(v_8\) is on a chord of \(C_{c(H_0)}\), i.e., \[\begin{aligned} \label{v8v2v5} \begin{split} v_8v_2\in E(H_0) \text{~or~} v_8v_5\in E(H_0). \end{split} \end{aligned} \tag{3}\] Suppose that \(N_{H_0}(v_9)\backslash \{v_8,v_1\}\subseteq V(\mathcal{D}_{H_0})\). Then there exists a path \(P^{r,9}\) for any possibility \(r\in \{2,5,7,9\}\), and \(H\) contains a subgraph \(S_{1,3,13}\subseteq S(v_9,v_{1,9},P_{H}^{r,9}x_{r,9}^r, v_{7,8}v_7\ldots v_3v_1v_2x_1)\) with \(x_1\in~N_H(v_2)\backslash\) \(\{v_3,v_1\}\) and \(r\in \{5,7\}\), \(S_{1,3,13}\subseteq(v_4,v_5, v_{3,4}v_3v_2,v_6v_{6,7}\ldots v_9P_{H}^{9,9}v_9\backslash v_9)\) or \(S_{1,3,13}\subseteq(v_1,v_{1,9}, v_3v_{3,4}v_4\), \(v_2P_{H}^{2,9}v_9v_{8,9}\ldots v_5x_2)\) with \(x_2\in~N_H(v_5)\backslash\{v_{4,5},v_{5,6}\}\), a contradiction. Hence \(v_9\) is on a chord of \(C_{c(H_0)}\) (\(v_5v_9\in E(H_0)\)). Similarly, \(v_2v_7\in E(H_0)\). Hence by Claim 3.6 (1), \(v_8v_2\not\in E(H_0)\) and \(v_8v_5\not\in E(H_0)\), contradicting (3).
Subcase 1.2. \(v_q=v_6\).
Suppose that \(N_{H_0}(v_8)\backslash \{v_7,v_{9}\}\subseteq V(\mathcal{D}_{H_0})\). Then there exists a path \(P^{r,8}\) for any possibility \(r\in \{2,4,6,8\}\). Then \(H\) contains a subgraph \[\begin{aligned} S_{1,3,13} &\subseteq (v_1, v_2, v_{1,9}v_9v_{8,9}, v_3v_{3,4,7} \ldots v_8P_{H}^{8,8}v_8 \setminus v_8) \end{aligned}\] or \[\begin{aligned} S_{1,3,13} &\subseteq S(v_8, v_{8,9}, P_{H}^{r,8}x_{r,8}^r, v_{7,8}v_7 \ldots v_9x_1) \end{aligned}\] with \(x_1\in N_H(v_9)\backslash\) \(\{v_{1,9},v_{8,9}\}\), a contradiction. Hence \(v_8\) is on a chord of \(C_{c(H_0)}\) . Similarly, \(v_9\) is on a chord of \(C_{c(H_0)}\). Suppose that \(N_{H_0}(v_2)\backslash \{v_3,v_1\}\subseteq V(\mathcal{D}_{H_0})\). Then there exists a path \(P^{2,r}\) for any possibility \(r\in \{4,6\}\), and \(H\) contains a subgraph \(S_{1,3,13}\subseteq(v_5,v_6, v_{4,5}v_4v_{3,4},v_7v_{7,8}\) \(\ldots v_2P_{H}^{2,2}v_2\backslash v_2)\), \(S_{1,3,13}\subseteq(v_9,x_2,v_{8,9}v_8v_{7,8},v_{1,9}v_1\ldots v_5v_7v_6P_{H}^{2,6}x_{2,6}^2)\) with \(x_2\in~N_H(v_9)\backslash\) \(\{v_{8,9},v_{1,9}\}\) or \(S_{1,3,13}\subseteq S(v_4,v_{4,5}, P_{H}^{2,4}x_{2,4}^2, v_{3,4}v_3\ldots v_7v_5v_6x_3)\) with \(x_3\in N_H(v_6)\backslash\) \(\{v_5,v_6\}\), a contradiction. Hence \(v_2\) is on a chord of \(C_{c(H_0)}\). Similarly, \(v_6\) is on a chord of \(C_{c(H_0)}\). Then we have that \(v_4\) is on a chord of \(C_{c(H_0)}\). Therefore, \(|V(H_0)|=9\), a contradiction, this proved Case 1.
In the proof of the following cases, for any path \(P^{r,r}\in \mathcal{P}'\). Then \(H\) contains a subgraph \(S_{1,2i+1,2j+1}\subseteq S(v_r,v_{r+1},P_{H}^{r,r}v_r\backslash v_r,v_{r-1,r} v_{r-1}\ldots v_{r+1,r+2})\), a contradiction. Therefore integer \(1\leq r< s\leq c(H_0)\) in \(P^{r,s}\).
Case 2. \(G\in \mathcal{B}_{4,10}\).
Suppose that \(|P^{r,s}|\geq 4\), \(S_{1,5,11}\subseteq H[V(C)\cup V(P_{H}^{r,s})]\) with its center vertex \(v_r\), a contradiction. Then suppose that \(|P^{r,s}|=3\), say \(P_{H}^{r,s}=v_rx_{r,s}^rx_{r,s}x_{r,s}^sv_s\).
Subcase 2.1. \(v_q=v_5\).
Suppose that \(N_{H_0}(v_8)\backslash \{v_7,v_{9}\}\subseteq V(\mathcal{D}_{H_0})\). Then there exists a path \(P^{r,8}\) for any possibility \(r\in \{2,5\}\), and \(H\) contains a subgraph \(S_{1,5,11}(v_9,x_1,v_{8,9}v_8P_{H}^{r,8}x_{r,8}^r,v_{1,9}v_1\ldots v_{7,8})\) with \(x_1\in N_H(v_9)\) and \(r\in \{2,5\}\) a contradiction. Hence \(v_8\) is in a chord of \(C_{c(H_0)}\), i.e.,
\[\begin{aligned} \label{v8v2v51} \begin{split} v_8v_2\in E(H_0) \text{~or~} v_8v_5\in E(H_0). \end{split} \end{aligned} \tag{4}\] Suppose that \(N_{H_0}(v_9)\backslash \{v_8,v_1\}\subseteq V(\mathcal{D}_{H_0})\). Then there exists a path \(P^{r,9}\) for any possibility \(r\in \{2,5,7\}\), and \(H\) contains a subgraph \(S_{1,5,11}(v_9,v_{1,9},v_{8,9}v_8\ldots v_{6,7},P_{H}^{2,9}v_2v_1v_3v_{3,4}v_4v_6v_5x_2)\) with \(x_2\in N_H(v_5)\), \(S_{1,5,11}(v_9\), \(v_{1,9}, v_{8,9}v_8\ldots v_{6,7},P_{H}^{5,9}v_5v_6v_4v_{3,4}v_3v_1v_2x_3)\) with \(x_3\in N_H(v_2)\) or \(S_{1,5,11}(v_8,x_2, v_{7,8}v_7\) \(P_{H}^{7,9}x_{7,9}^9, v_{8,9}v_9\ldots\) \(v_{6,7})\) with \(x_2\in N_H(v_5)\), a contradiction. Hence \(v_9\) is on a chord of \(C_{c(H_0)}\) (\(v_5v_9\in E(H_0)\)). Similarly, \(v_2v_7\in E(H_0)\). Hence by Claim 3.6 (1), \(v_8v_2\not\in E(H_0)\) and \(v_8v_5\not\in E(H_0)\), contradicting (4).
Subcase 2.2. \(v_q=v_6\).
Suppose that \(N_{H_0}(v_8)\backslash \{v_7,v_{9}\}\subseteq V(\mathcal{D}_{H_0})\). Then there exists a path \(P^{r,8}\) for any possibility \(r\in \{2,4,6\}\), and \(H\) contains a subgraph \(S_{1,5,11}(v_9,x_1, v_{8,9}v_8P_{H}^{r,8}x_{r,8}^r,v_{1,9}v_1\ldots v_{7,8})\) for any possibility \(r\in \{2,4,6\}\) and \(x_1\in N_H(v_9)\), a contradiction. Hence \(v_8\) is on a chord of \(C_{c(H_0)}\) . Similarly, \(v_9\) is on a chord of \(C_{c(H_0)}\). Suppose that \(N_{H_0}(v_2)\backslash \{v_3,v_1\}\subseteq V(\mathcal{D}_{H_0})\). Then there exists a path \(P^{2,s}\) for any possibility \(s\in \{4,6\}\), and \(H\) contains a subgraph \(S_{1,5,11}(v_4,v_{3,4}, v_{4,5}v_5v_7v_6x_2, P_{H}^{2,4}v_2v_3v_1v_{1,9}\ldots v_{7,8})\) with \(x_2\in N_H(v_6)\) or \(S_{1,5,11}(v_4,v_{3,4}, v_{4,5}v_5\ldots v_{7,8},v_{4,8}v_8v_{8,9}v_9v_{1,9}v_1v_3v_2P_{H}^{2,6}x_{2,6}^6)\), a contradiction. Thus \(v_2\) is on a chord of \(C_{c(H_0)}\). Similarly, \(v_6\) is on a chord of \(C_{c(H_0)}\). Hence \(v_4\) is on a chord of \(C_{c(H_0)}\). Therefore \(|V(H_0)|=9\), a contradiction. This proved Case 2.
Case 3. \(G\in \mathcal{B}_{6,8}\).
Suppose that \(|P^{r,s}|\geq 5\), \(S_{1,7,9}\subseteq H[V(C)\cup V(P_{H}^{r,s})]\) with its center vertex \(v_r\), a contradiction. Then suppose that \(|P^{r,s}|=3\) or \(|P^{r,s}|=4\), say \(P_{H}^{r,s}=v_rx_{r,s}^rx_{r,s}x_{r,s}^sv_s\) or \(P_{H}^{r,s}=v_rx_{r,s}^rx_{r,s}^1x_{r,s}^{12}x_{r,s}^2x_{r,s}^sv_s\).
Subcase 3.1. \(v_q=v_5\).
Let \(N_{H_0}(v_8)\backslash \{v_7,v_{9}\}\subseteq V(\mathcal{D}_{H_0})\), there exists a path \(P^{r,8}\) for any possibility \(r\in \{2,5\}\). Then \(H\) contains a subgraph \(S_{1,7,9}\subseteq S(v_8,v_{7,8},v_{8,9}v_9\ldots v_{3,4},P_{H}^{5,8}v_5v_4v_6v_{6,7}v_7x_1)\) with \(~x_1\in~N_H(v_7)\) or \(S_{1,7,9}\subseteq S(v_8,v_{8,9},v_{7,8}v_7\ldots v_{3,4},P_{H}^{2,8}v_2v_3v_1v_{1,9}v_9x_2)\) with \(x_2\in~N_H(v_9)\), a contradiction. Hence \(v_8\) is on a chord of \(C_{c(H_0)}\), i.e., \[\begin{aligned} \label{v8v2v52} \begin{split} v_8v_2\in E(H_0) \text{~or~} v_8v_5\in E(H_0). \end{split} \end{aligned} \tag{5}\] Let \(N_{H_0}(v_9)\backslash \{v_8,v_1\}\subseteq V(\mathcal{D}_{H_0})\), there exists a path \(P^{r,9}\) for any possibility \(r\in \{2,5,7\}\). If \(|P^{r,s}|= 4\), then \(H\) contains a subgraph \(S_{1,7,9}(v_3,v_2,v_{3,4}v_4v_6v_{6,7}\ldots v_8,v_1v_{1,9}v_9P_{H}^{5,9}v_5)\), a contradiction. Hence \(|P^{r,s}|=3\) (\(P_{H}^{r,s}=v_9x_{r,9}^9x_{r,9}x_{r,9}^rv_r\)). Then \(H\) contains a subgraph \[\begin{aligned} S_{1,7,9}(v_9, v_{1,9}, P_{H}^{2,9}v_2v_1v_3v_{3,4}, v_{8,9}v_8 \ldots v_6v_4v_5x_3) \end{aligned}\] with \(x_3 \in N_H(v_5),\) \[\begin{aligned} S_{1,7,9}(v_8, x_4, v_{8,9}v_9 \ldots v_{3,4}, v_{7,8}v_7v_{6,7}v_6v_4v_5P_{H}^{5,9}x_{5,9}^9) & \end{aligned}\] with \(x_4\in N_H(v_8)\) or \(S_{1,7,9}(v_7, v_{7,8},P_{H}^{7,9}v_9v_{8,9}v_8x_5,v_{6,7}v_6\ldots v_{1,9})\) with \(x_5\in N_H(v_8)\), a contradiction. Hence \(v_9\) is on a chord of \(C_{c(H_0)}\) (\(v_5v_9\in E(H_0)\)). Similarly, \(v_2v_7\in E(H_0)\). Hence by Claim 3.6 (1), \(v_8v_2\not\in E(H_0)\) and \(v_8v_5\not\in E(H_0)\), contradicting (5).
Subcase 3.2. \(v_q=v_6\).
Let \(N_{H_0}(v_8)\backslash \{v_7,v_{9}\}\subseteq V(\mathcal{D}_{H_0})\), there exists a path \(P^{r,8}\) for any possibility \(r\in \{2,4,6\}\). If \(|P^{r,s}|= 4\), then \(H\) contains a subgraph \[\begin{aligned} S_{1,7,9}(v_8, v_{7,8}, P_{H}^{4,8} v_4 v_{4,5} v_5 v_6, v_{8,9} v_9 \ldots v_{3,4}) \end{aligned}\] or \[\begin{aligned} S_{1,7,9}(v_2, v_1, v_3 v_{3,4} \ldots v_7, P_{H}^{2,8} v_8 v_{8,9} v_9 v_{1,9}), \end{aligned}\] a contradiction. Hence \(|P^{r,s}|=3\) (\(P_{H}^{r,s}=v_8x_{r,8}^8x_{r,8}x_{r,8}^rv_r\)). Then \(H\) contains a subgraph \[\begin{aligned} S_{1,7,9}(v_4, x_1, v_{4,5}v_5 \ldots v_{8,9}, v_{3,4}v_3 \ldots v_8 P_{H}^{2,8} x_{2,8}^2) &\quad \text{with } x_1 \in N_H(v_4), \\ S_{1,7,9}(v_8, v_{7,8}, v_{8,9}v_9 \ldots v_{3,4}, P_{H}^{4,8}v_4v_{4,5}v_5v_7v_6x_2) &\quad \text{with } x_2 \in N_H(v_6), \\ S_{1,7,9}(v_4, x_3, v_{3,4}v_3 \ldots v_{8,9}, v_{4,5}v_5v_7v_6 P_{H}^{6,8} v_8 v_{7,8}) &\quad \text{with } x_3 \in N_H(v_4), \end{aligned}\] a contradiction. Hence \(v_8\) is on a chord of \(C_{c(H_0)}\). Similarly, \(v_9\) is on a chord of \(C_{c(H_0)}\). Let \(N_{H_0}(v_2)\backslash \{v_3\), \(v_1\}\subseteq V(\mathcal{D}_{H_0})\), there exists a path \(P^{2,r}\) for any possibility \(r\in \{4,6\}\). Then \(H\) contains a subgraph \(S_{1,7,9}\subseteq S(v_9,v_{4,9}, v_{1,9}v_1v_2P_{H}^{2,6}v_6, v_{8,9}v_8v_{7,8}v_7v_5v_{4,5}v_4v_{3,4}v_3)\) or \(S_{1,7,9}\subseteq S(v_8,v_{4,8},v_{8,9}v_9\ldots v_{3,4}, v_{7,8}v_7\ldots v_4P_{H}^{2,4}x_{2,4}^2)\), a contradiction. Hence \(v_2\) is on a chord of \(C_{c(H_0)}\). Similarly, \(v_6\) is on a chord of \(C_{c(H_0)}\). Hence \(v_4\) is on a chord of \(C_{c(H_0)}\). Therefore, \(|V(H_0)|=9\), a contradiction. This proves Claim 3.8. ◻
Thus we can get that \(c(H_0)\geq 10\) and \(|V(H_0)|\geq 10\) and \(m^{H_0}=4\), where \(E_{H_0}^1\cap E_0=\emptyset\). By (2), \(|V(C)|=2c(H_0)-2\geq 16\). For any path \(P^{r,r}\in \mathcal{P}'\). Then \(H\) contains a subgraph \(S_{1,2i+1,2j+1}\subseteq S(v_r,v_{r+1},P_{H}^{r,r}v_r\backslash v_r,v_{r-1,r} v_{r-1}\ldots v_{r+1,r+2})\), a contradiction. Therefore integer \(1\leq r< s\leq c(H_0)\) in \(P^{r,s}\).
Proof. Assume, to the contrary, that \(|V(H_0)|> c(H_0)\geq 10\). If \(c(H_0)\geq 11\), then \(|V(C)|=2c(H_0)-4\geq 18\). Hence \(d_{H_0}(v_r)\geq 3\) with \(v_r\in V(C_{c(H_0)})\), Then \(H\) contains all subgraphs \(S_{1,2i+1,2j+1}\subseteq H[V(C)\cup \{u\}]\) with its center vertex \(v_r\), and \(u\in N_H(v_r)\backslash \{v_{r-1,r}, v_{r,r+1}\}\), a contradiction. Therefore \(c(H_0)=10(\)say \(C_{c(H_0)}=v_1v_2\ldots v_{10}v_1)\).
Case 1. \(G\in \mathcal{B}_{2,12}\).
We can get that \(S_{1,3,13}\subseteq H[V(C)\cup V(P_{H}^{r,s})]\) with its center vertex \(v_r\in V(C_{c(H_0)})\), a contradiction.
Case 2. \(G\in \mathcal{B}_{4,10}\).
If \(|P^{r,s}|\geq 4\), then \(S_{1,5,11}\subseteq H[V(C)\cup V(P_{H}^{r,s})]\) with its center vertex \(v_r\in V(C_{c(H_0)})\), a contradiction. Hence \(|P^{r,s}|=3\), i.e., \(P_{H}^{r,s}=v_rx_{r,s}^rx_{r,s}x_{r,s}^sv_s\).
Subcase 2.1. \(v_q=v_5\).
Firstly, suppose that \(N_{H_0}(v_{10})\backslash \{v_1,v_9\}\subseteq V(\mathcal{D}_{H_0})\). Then \(H\) contains a subgraph \[\begin{aligned} S_{1,5,11}(v_{10}, v_{1,10}, v_{9,10}v_9 \ldots v_{7,8}, P_{H}^{2, 10}v_2v_1v_3 \ldots v_7), \\ S_{1,5,11}(v_{10}, v_{9,10}, v_{1,10}v_1v_2v_3 v_{3,4}, P_{H}^{5, 10}v_5v_4v_6 \ldots v_9), \\ S_{1,5,11}(v_{10}, v_{1,10}, v_{9,10}v_9v_{8,9}v_8v_{7,8}, P_{H}^{7, 10}v_7v_{6,7} \ldots v_1), \\ S_{1,5,11}(v_8, v_{8,9}, P_{H}^{8, 10}v_{10}v_{9,10}, v_{7,8}v_7v_{6,7} \ldots v_{1,10}), \end{aligned}\] a contradiction. Hence \(N_{H_0}(v_{10})\subseteq V(C_{c(H_0)})\), by symmetry, \(N_{H_0}(v_7)\subseteq V(C_{c(H_0)})\). Then, suppose that \(N_{H_0}(v_9)\backslash \{v_8\), \(v_{10}\}\subseteq V(\mathcal{D}_{H_0})\). Then \(H\) contains a subgraph \[\begin{aligned} S_{1,5,11}(v_6, v_5, v_{6,7}v_7 \ldots v_{8,9}, v_4v_{3,4}v_3v_2P_{H}^{2,9}v_9v_{9,10}v_{10}v_{1,10}) \end{aligned}\] or \[\begin{aligned} S_{1,5,11}(v_9, v_{9,10}, v_{8,9}v_8 \ldots v_{6,7}, P_{H}^{5,9}v_5v_4 \ldots v_{10}), \end{aligned}\] a contradiction. Hence \(N_{H_0}(v_9)\subseteq V(C_{c(H_0)})\), by symmetry, \(N_{H_0}(v_8)\subseteq V(C_{c(H_0)})\). Finally, suppose that \(N_{H_0}(v_2)\backslash \{v_1,v_3\}\subseteq V(\mathcal{D}_{H_0})\). Then \(H\) contains a subgraph \[S_{1,5,11}(v_4,v_{3,4}, v_5P_{H}^{2,5}v_2,v_6v_{6,7}\ldots v_1),\] a contradiction. Hence \(N_{H_0}(v_2)\subseteq V(C_{c(H_0)})\), by symmetry, \(N_{H_0}(v_5)\subseteq V(C_{c(H_0)})\). Therefore, \(|V(H_0)|=c(H_0)=10\), a contradiction.
Subcase 2.2. \(v_q=v_6\).
Firstly, suppose that \(N_{H_0}(v_{10})\backslash \{v_1,v_9\}\subseteq V(\mathcal{D}_{H_0})\). Then \(H\) contains a subgraph \(S_{1,5,11}(v_7,v_6, v_{7,8}\) \(v_8v_{8,9}v_9v_{9,10},v_5v_{4,5}v_4\ldots v_{10}P_{H}^{r,10}x_{r,10})\) for any possibility \(r\in \{2,4,6,8\}\), a contradiction. Hence \(N_{H_0}(v_{10})\subseteq V(C_{c(H_0)})\), by symmetry, \(N_{H_0}(v_8)\subseteq V(C_{c(H_0)})\). Secondly, suppose that \(N_{H_0}(v_9)\backslash \{v_8,v_{10}\}\) \(\subseteq V(\mathcal{D}_{H_0})\). Then \(H\) contains a subgraph \[\begin{aligned} S_{1,5,11}(v_7,v_6, v_5v_{4,5}v_4v_{3,4}v_3,v_{7,8}v_8\ldots v_2x_{2,9}^2x_{2,9}), \\ S_{1,5,11}(v_1, v_2, v_3v_{3,4}v_4x_{4,9}^4x_{4,9},v_{1,10}v_{10}\ldots v_{4,5}), \\ S_{1,5,11}(v_1,v_2, v_3v_{3,4}\ldots v_5,v_{1,10}v_{10}v_{9,10}v_9\ldots v_6x_{6,9}^6x_{6,9}), \end{aligned}\] a contradiction. Hence \(N_{H_0}(v_9)\subseteq V(C_{c(H_0)})\). Finally, suppose that \(N_{H_0}(v_2)\backslash \{v_1,v_3\}\subseteq V(\mathcal{D}_{H_0})\). Then \(H\) contains a subgraph \(S_{1,5,11}(v_4,v_{3,4}, P_{H}^{2,4}v_2v_3,v_{4,5}v_5\ldots v_{1,10})\) or \[S_{1,5,11}(v_1,v_2, v_3v_{3,4}v_4v_{4,5}v_5, v_{1,10}v_{10}\ldots v_6x_{2,6}^6x_{2,6}),\] a contradiction. Hence \(N_{H_0}(v_2)\subseteq V(C_{c(H_0)})\), by symmetry, \(N_{H_0}(v_6)\subseteq V(C_{c(H_0)})\). Therefore, \(N_{H_0}(v_4)\subseteq V(C_{c(H_0)})\) and \(|V(H_0)|=c(H_0)=10\), a contradiction.
Subcase 2.3. \(v_q=v_7\).
Suppose that \(N_{H_0}(v_9)\backslash \{v_8,v_{10}\}\subseteq V(\mathcal{D}_{H_0})\), then \(H\) contains a subgraph \[\begin{aligned} S_{1,5,11}(&v_8, v_7, v_{8,9}v_9P_{H}^{r,9}, x_{r,9}^r, v_6v_{5,6} \ldots v_{10}) \quad \text{for any possibility } r \in \{2, 4, 5, 7\}. \end{aligned}\] a contradiction. Hence \(N_{H_0}(v_9)\subseteq V(C_{c(H_0)})\), by symmetry, \(N_{H_0}(v_{10})\subseteq V(C_{c(H_0)})\), \(N_{H_0}(v_5)\subseteq V(C_{c(H_0)})\) and \(N_{H_0}(v_4)\subseteq V(C_{c(H_0)})\). Next, suppose that \(N_{H_0}(v_2)\backslash \{v_1,v_3\}\subseteq V(\mathcal{D}_{H_0})\). Then \(H\) contains a subgraph \(S_{1,5,11}(v_1,v_2\), \(v_{1,10}v_{10}\ldots v_{8,9},v_3v_{3,4}\) \(\ldots v_7P_{H}^{2,7}x_{2,7}^2)\), a contradiction. Hence \(N_{H_0}(v_2)\subseteq V(C_{c(H_0)})\), by symmetry, \(N_{H_0}(v_7)\subseteq V(C_{c(H_0)})\). Therefore, \(|V(H_0)=c(H_0)|=10\), a contradiction. This proves Case 2.
Case 3. \(G\in \mathcal{B}_{6,8}\).
If \(|P^{r,s}|\geq 5\), then \(S_{1,7,9}\subseteq H[V(C)\cup V(P_{H}^{r,s})]\) with its center vertex \(v_r\in V(C_{c(H_0)})\), a contradiction. Hence \(|P^{r,s}|=3\) or \(|P^{r,s}|=4\), i.e., \(P_{H}^{r,s}=v_rx_{r,s}^rx_{r,s}x_{r,s}^sv_s\) or \(P_{H}^{r,s}=v_rx_{r,s}^rx_{r,s}^1x_{r,s}^{12}x_{r,s}^2x_{r,s}^sv_s\).
Subcase 3.1. \(v_q=v_5\).
Firstly, suppose that \(N_{H_0}(v_9)\backslash \{v_8,v_{10}\}\subseteq V(\mathcal{D}_{H_0})\). Then \(H\) contains a subgraph \[\begin{aligned} &S_{1,7,9}(v_9, x_{5,9}^9, v_{9,10}v_{10}\ldots v_{3,4}, v_{8,9}v_8\ldots v_6v_4v_5x_{5,9}^5), \\ &S_{1,7,9}(v_9, x_{2,9}^9, v_{9,10}v_{10}v_{1,10}v_1v_3v_2x_{2,9}^2, v_{8,9}v_8\ldots v_{3,4}), \\ &S_{1,7,9}(v_6, v_5, v_4v_{3,4}\ldots v_{10}, v_{6,7}v_7v_{7,8}\ldots v_{9}P_{H}^{7,9}x_{7,9}^7), \end{aligned}\] a contradiction. Hence \(N_{H_0}(v_9)\subseteq V(C_{c(H_0)})\), by symmetry, \(N_{H_0}(v_8)\subseteq V(C_{c(H_0)})\). Then, suppose that \(N_{H_0}(v_7)\backslash \{v_1,v_9\}\subseteq V(\mathcal{D}_{H_0})\), we can easily get that \(H\) contains a subgraph \[\begin{aligned} S_{1,7,9}(v_7, x_{2,7}^7, v_{7,8}v_8 \ldots v_{1,10}, v_{6,7}v_6 \ldots v_3v_1v_2x_{2,7}^2), \\ S_{1,7,9}(v_7, x_{7,10}^7, v_{7,8}v_8v_{8,9}v_9v_{9,10}v_{10}x_{7,10}^{10}, v_{6,7}v_6 \ldots v_{1,10}), \\ S_{1,7,9}(v_7, v_{6,7}, v_{7,8}v_8 \ldots v_{1,10}, P_{H}^{5,7}v_5v_4v_{3,4} \ldots v_1), \end{aligned}\] a contradiction. Hence \(N_{H_0}(v_7)\subseteq V(C_{c(H_0)})\), by symmetry, \(N_{H_0}(v_{10})\subseteq V(C_{c(H_0)})\). Finally, suppose that \(N_{H_0}(v_2)\backslash \{v_1,v_3\}\subseteq V(\mathcal{D}_{H_0})\). Then \(H\) contains a subgraph \(S_{1,7,9}\subseteq S(v_4,v_5,v_{3,4}v_3v_1v_2P_{H}^{2,5}x_{2,5}^5, v_6v_{6,7}\ldots v_{10})\), a contradiction. Hence \(N_{H_0}(v_2)\subseteq V(C_{c(H_0)})\), by symmetry, \(N_{H_0}(v_5)\subseteq V(C_{c(H_0)})\). Therefore, \(|V(H_0)|=10\), a contradiction.
Subcase 3.2. \(v_q=v_6\).
Firstly, suppose that \(N_{H_0}(v_8)\backslash \{v_7,v_9\}\subseteq V(\mathcal{D}_{H_0})\). Then \(H\) contains a subgraph \[\begin{aligned} S_{1,7,9}(v_1, v_2, v_3v_{3,4} \ldots v_7, v_{1,10}v_{10} \ldots v_8P_{H}^{8,10}x_{8,10}^{10}), \\ S_{1,7,9}(v_1, v_2, v_3v_{3,4}v_4v_{4,5}v_5v_7v_{7,8}, v_{1,10}v_{10}v_{9,10}v_9v_{8,9}v_8P_{H}^{6,8}x_{6,8}^6), \\ S_{1,7,9}(v_8, x_{4,8}^8, v_{7,8}v_7 \ldots v_4x_{4,8}^4, v_{8,9}v_9 \ldots v_{3,4}) \end{aligned}\] or \[\begin{aligned} S_{1,7,9}(v_8, x_{2,8}^8, v_{7,8}v_7 \ldots v_{3,4}, v_{8,9}v_9 \ldots v_1v_3v_2x_{2,8}^2), \end{aligned}\] a contradiction. Hence \(N_{H_0}(v_8)\subseteq V(C_{c(H_0)})\), by symmetry, \(N_{H_0}(v_{10})\subseteq V(C_{c(H_0)})\). Then, suppose that \(N_{H_0}(v_9)\backslash\) \(\{v_{10},v_8\}\) \(\subseteq V(\mathcal{D}_{H_0})\), we have that \(H\) contains a subgraph \[\begin{aligned} S_{1,5,11}(&v_8, v_7, v_{8,9}v_9P_{H}^{r,9}, x_{r,9}^r, v_6v_{5,6} \ldots v_{10}) \quad \text{for any possibility } r \in \{2, 4, 5, 7\}. \end{aligned}\] a contradiction. Hence \(N_{H_0}(v_9)\subseteq V(C_{c(H_0)})\). Finally, suppose that \(N_{H_0}(v_2)\backslash \{v_1,v_3\}\subseteq V(\mathcal{D}_{H_0})\), we can get that \(H\) contains a subgraph \[\begin{aligned} &S_{1,7,9} \subseteq S(v_3, v_{3,4}, v_2P_{H}^{2,4}v_4v_{4,5}v_5v_6, v_1v_{1,10}\ldots v_7), \end{aligned}\] or \[\begin{aligned} &S_{1,7,9}(v_2, x_{2,6}^2, v_3v_{3,4}\ldots v_6x_{2,6}^6, v_1v_{1,10}\ldots v_7), \end{aligned}\] a contradiction. Hence \(N_{H_0}(v_2)\subseteq V(C_{c(H_0)})\), by symmetry, \(N_{H_0}(v_6)\subseteq V(C_{c(H_0)})\). Therefore, \(N_{H_0}(v_4)\subseteq V(C_{c(H_0)})\) and \(|V(H_0)|=10\), a contradiction.
Subcase 3.3. \(v_q=v_7\).
Suppose that \(N_{H_0}(v_9)\backslash \{v_{8},v_{10}\}\subseteq V(\mathcal{D}_{H_0})\). Then \(H\) contains a subgraph \[\begin{aligned} & S_{1,7,9}(v_9, x_{2,9}^9, v_{9,10}v_{10} \ldots v_1v_3v_2x_{2,9}^2, v_{8,9}v_8 \ldots v_{3,4}), \\ & S_{1,7,9}(v_9, x_{4,9}^9, v_{8,9}v_8 \ldots v_{4,5}, v_{9,10}v_{10}v_{1,10} \ldots v_4x_{4,9}^4), \\ & S_{1,7,9}(v_9, x_{5,9}^9, v_{8,9}v_8 \ldots v_5x_{5,9}^5, v_{9,10}v_{10} \ldots v_{4,5}), \\ & S_{1,7,9}(v_1, v_2, v_3v_{3,4} \ldots v_6, v_{1,10}v_{10}v_{9,10}v_9P_{H}^{7,9}v_7v_8), \end{aligned}\] a contradiction. Hence \(N_{H_0}(v_9)\subseteq V(C_{c(H_0)})\), by symmetry, \(N_{H_0}(v_{10})\subseteq V(C_{c(H_0)})\), \(N_{H_0}(v_5)\subseteq V(C_{c(H_0)})\) and \(N_{H_0}(v_4)\subseteq V(C_{c(H_0)})\). Next, we suppose that \(N_{H_0}(v_2)\backslash \{v_1,v_3\}\subseteq V(\mathcal{D}_{H_0})\). Then \(H\) contains a subgraph \(S_{1,7,9}(v_2,x_{2,7}^2,v_3v_{3,4}\ldots v_6, v_1v_{1,10}\ldots v_7x_{2,7}^7)\), a contradiction. Hence \(N_{H_0}(v_2)\subseteq V(C_{c(H_0)})\), by symmetry, \(N_{H_0}(v_7)\subseteq V(C_{c(H_0)})\). Therefore, \(|V(H_0)|=10\), a contradiction. This proves Claim 3.9. ◻
Proof. Assume, to the contrary, that \(|V(H_0)|= c(H_0)=10\).
Case 1. \(G\in \mathcal{B}_{2,12}\).
Firstly, suppose that \(v_q=v_5\). Since \(\kappa'(H_0)\geq 3\), \(N_{H_0}(v_7)\backslash \{v_6,v_8\}\subseteq \{v_2, v_{10}\}\). Then \(H\) contains a subgraph \[\begin{aligned} & S_{1,3,13}(v_7, v_{2,7}, v_{7,8}v_8v_{5,8}, v_{6,7}v_6 \ldots v_{8,9}) \end{aligned}\] or \[\begin{aligned} & S_{1,3,13}(v_7, v_{7,10}, v_{7,8}v_8v_{5,8}(v_{2,8}), v_{6,7}v_6 \ldots v_{8,9}), \end{aligned}\] a contradiction. Therefore \(d_{H_0}(v_7)=2\), a contradiction.
Then, suppose that \(v_q=v_6\). Since \(\kappa'(H_0)\geq 3\), \(N_{H_0}(v_9)\backslash \{v_8,v_{10}\}\subseteq \{v_2,v_4,v_6\}\). We can get that \(H\) contains a subgraph \(S_{1,3,13}(v_9,v_{2,9}, v_{9,10}v_{10}v_{6,10}(v_{4,10}),v_{8,9}v_8\ldots v_{1,10})\), \(S_{1,3,13}(v_9,v_{6,9}, v_{9,10}v_{10}v_{4,10}\), \(v_{8,9}v_8\ldots v_{1,10})\) or \(S_{1,3,13}(v_9,v_{4,9}, v_{9,10}v_{10}v_{r,10},v_{8,9}v_8\ldots v_{1,10})\) for any possibility \(r\in \{2,4,6\}\), a contradiction. Therefore \(d_{H_0}(v_9)=2\), a contradiction.
Finally, suppose that \(v_q=v_7\). Since \(\kappa'(H_0)\geq 3\), \(N_{H_0}(v_7)\backslash \{v_8,v_6\}\subseteq \{v_2,v_4,v_{10}\}\). Then \(H\) contains a subgraph \[\begin{aligned} &S_{1,3,13}\big(v_6, v_{5,6}, v_7v_{2,7}v_2, v_8v_{8,9} \ldots v_1v_3v_{3,4}v_4v_{4,5}v_5v_{5,9}(v_{5,10})\big), \\ &S_{1,3,13}\big(v_4, v_{4,7}, v_{4,5}v_5x_1, v_{3,4}v_3 \ldots v_{5,6}\big) \text{ with } x_1 \in \{v_{2,5}, v_{2,9}, v_{2,10}\}, \\ &S_{1,3,13}\big(v_{10}, v_{7,10}, v_{9,10}v_9x_2, v_{1,10}v_1 \ldots v_{8,9}\big) \text{ with } x_2 \in \{v_{2,9}, v_{4,9}, v_{5,9}\}, \end{aligned}\] a contradiction. Therefore \(d_{H_0}(v_7)=2\), a contradiction. This proves Case 1.
Case 2. \(G\in \mathcal{B}_{4,10}\).
Firstly, suppose that \(v_q=v_5\). Since \(\kappa'(H_0)\geq 3\), \(N_{H_0}(v_7)\backslash \{v_6,v_8\}\subseteq \{v_2, v_{10}\}\).Then \(H\) contains a subgraph \[\begin{aligned} S_{1,5,11}(v_7, v_{2,7}, v_{7,8}v_8 \ldots v_9v_{5,9}, v_{6,7}v_6 \ldots v_{9,10}) \end{aligned}\] or \[\begin{aligned} S_{1,5,11}(v_7, v_{7,10}, v_{7,8}v_8 \ldots v_9v_{5,9}(v_{2,9}), v_{6,7}v_6 \ldots v_{9,10}), \end{aligned}\] a contradiction. Therefore \(d_{H_0}(v_7)=2\), a contradiction.
Then, suppose that \(v_q=v_6\). Since \(\kappa'(H_0)\geq 3\), \(N_{H_0}(v_{10})\backslash \{v_9,v_1\}\subseteq \{v_4,v_6\}\). We can get that \(H\) contains a subgraph \(S_{1,5,11}(v_{10},v_{4,10},v_{9,10}v_9v_{8,9} v_8v_{2,8}(v_{4,8}),v_{1,10}v_1\ldots v_{7,8})\) or \(S_{1,5,11}(v_{10},v_{6,10},v_{9,10}v_9\) \(v_{8,9}v_8v_{2,8}(v_{4,8}),v_{1,10}v_1\ldots v_{7,8})\), a contradiction. Therefore \(d_{H_0}(v_{10})=2\), a contradiction.
Finally, suppose that \(v_q=v_7\). Since \(\kappa'(H_0)\geq 3\), \(N_{H_0}(v_9)\backslash \{v_8,v_{10}\}\subseteq \{v_2,v_4,v_5\}\). Then \(H\) contains a subgraph \[\begin{aligned} & S_{1,5,11}(v_9, v_{2,9}, v_{8,9}v_8v_6v_7v_{4,7}(v_{7,10}), v_{9,10}v_{10} \ldots v_{5,6}), \\ & S_{1,5,11}(v_9, v_{4,9}, v_{8,9}v_8v_6v_7u, v_{9,10}v_{10} \ldots v_{5,6}) \text{ for any possibility } u \in \{v_{7,10}, v_{2,7}, v_{4,7}\} \end{aligned}\] or \[\begin{aligned} & S_{1,5,11}(v_9, v_{5,9}, v_{8,9}v_8v_6v_7u, v_{9,10}v_{10} \ldots v_{5,6}) \text{ for any possibility } u \in \{v_{7,10}, v_{2,7}, v_{4,7}\}, \end{aligned}\] a contradiction. Therefore \(d_{H_0}(v_9)=2\), a contradiction. This proves Case 2.
Case 3. \(G\in \mathcal{B}_{6,8}\).
Firstly, suppose that \(v_q=v_5\). Since \(\kappa'(H_0)\geq 3\), \(N_{H_0}(v_7)\backslash \{v_6,v_8\}\subseteq \{v_2, v_{10}\}\). Then \(H\) contains a subgraph \[\begin{aligned} & S_{1,7,9}(v_7, v_{2,7}, v_{7,8}v_8 \ldots v_{10}v_{5,10}(v_{7,10}), v_{6,7}v_6 \ldots v_{1,10}) \end{aligned}\] or \[\begin{aligned} & S_{1,7,9}(v_7, v_{7,8}, v_{7,10}v_{10}v_{9,10}v_9v_{8,9}v_8 \, v_{5,8}(v_{2,8}), v_{6,7}v_6 \ldots v_{1,10}), \end{aligned}\] a contradiction. Therefore \(d_{H_0}(v_7)=2\), a contradiction.
Then, suppose that \(v_q=v_6\). Since \(\kappa'(H_0)\geq 3\), \(N_{H_0}(v_{10})\backslash \{v_9,v_1\}\subseteq \{v_4,v_6\}\). We can get that \(H\) contains a subgraph \(S_{1,7,9}(v_6,v_{6,10},v_5v_{4,5}\ldots v_2v_{2,8}(v_{2,9}),v_{6,7}v_7\ldots v_1)\) or \(S_{1,7,9}(v_{10},v_{4,10},v_{1,10}v_1\ldots v_{4,5}\), \(v_{9,10}v_9\ldots v_7v_5v_6u)\) for any possibility \(u\in \{v_{2,6},v_{6,9},v_{6,10}\}\), a contradiction. Therefore \(d_{H_0}(v_{10})=2\), a contradiction.
Finally, suppose that \(v_q=v_7\). Since \(\kappa'(H_0)\geq 3\), \(N_{H_0}(v_9)\backslash \{v_8,v_{10}\}\subseteq \{v_2,v_4,v_5\}\). If \(v_4v_9\in E(H_0)\) or \(v_5v_9\in E(H_0)\), then \(H\) contains a subgraphs \[S_{1,7,9}(v_9,v_{4,9}(v_{5,9}),v_{9,10}v_{10}v_{1,10}v_1v_3v_2u,v_{8,9} v_8\ldots v_{3,4})\] for any possibility \(u\in \{v_{2,5},v_{2,9},v_{2,7}\}\), a contradiction. Therefore \(v_4v_9\notin E(H_0)\) and \(v_5v_9\notin E(H_0)\). By symmetry, \(v_4v_{10}\notin E(H_0)\) and \(v_5v_{10}\notin E(H_0)\). Therefore \(v_2v_9\in E(H_0)\) and \(v_7v_{10}\in E(H_0)\), we can get that \(d_{H_0}(v_4)=2\), a contradiction. This proves Claim 3.10.
By Claims 3.1 and 3.4-3.10, we have that \(|V(H_0)|=c(H_0)\geq 11\) and \(m^{H_0}=4\). By (2), \(|V(C)|=2c(H_0)-2\geq 18\). Since \(\kappa'(H_0)\geq 3\), \(v_r\in N_{H_0}(v_2)\backslash \{v_1,v_3\}\). We can get that \(H\) contains subgraphs \(S_{1,3,13}\subseteq S(v_2,v_{2,r},v_1v_{1,c(H_0)}v_{c(H_0)},v_3v_{3,4}\ldots v_{c(H_0)-1})\), \(S_{1,5,11}\subseteq S(v_2,v_{2,r},v_1v_{1,c(H_0)}v_{c(H_0)}\ldots v_{c(H_0)-1}\), \(v_3v_{3,4}v_4v_{4,5}\ldots v_{c(H_0)-2})\) and \[S_{1,7,9}\subseteq S(v_2,v_{2,r},v_1v_{1,c(H_0)}\ldots v_{c(H_0)-2},v_3v_{3,4}\ldots v_{c(H_0)-3}),\] a contradiction. This completes the proof of Theorem 1.6. ◻
| The graph \(X\) | Possible | Best Known | Reference | Open |
| \(P_i\) | \(i \leq 16\) | \(P_{16}\) | [19], [12] | \(-\) |
| \(Z_{2i}\) | \(i \leq 7\) | \(Z_{14}\) | [22] | \(-\) |
| \(B_{2i,2j}\) | \(i + j \leq 7\) | \(i + j \leq 7\) | This paper | \(-\) |
| \(N_{2i,2j,2k}\) | \(i + j + k \leq 7\) | \(i + j + k \leq 7\) | [21] | \(-\) |
The proof of results in [19] depends on the pairs of forbidden subgraphs, while this method of the present paper does not depend on the results of a pair of forbidden subgraphs and we may prove the results directly.
The authors would like to thank the referees for many helpful comments and suggestions. This work is supported by Nature Science Funds of China (No. 12131013).
The authors declare no conflict of interest.
1970-2025 CP (Manitoba, Canada) unless otherwise stated.