The \( n \)-dimensional Möbius cube \( MQ_n \) is an important variant of the hypercube \( Q_n \), which possesses some properties superior to the hypercube. This paper investigates the fault-tolerant edge-pancyclicity of \( MQ_n \), and shows that if \( MQ_n \) (\( n \geq 5 \)) contains at most \( n-2 \) faulty vertices and/or edges then, for any fault-free edge \( uv \) in \( MQ_n^i (i=0,1) \) and any integer \( \ell \) with \( 7-i \leqslant \ell \leqslant 2^n – f_v \), there is a fault-free cycle of length \( \ell \) containing the edge \( uv \), where \( f_v \) is the number of faulty vertices. The result is optimal in some senses.
It is well known that interconnection networks are of interest in parallel and distributed computing systems because they determine the performance of the systems on a large scale. As topological structures, interconnection networks can be represented by a graph \(G=(V, E)\), where \(V\) is the vertex-set of \(G\) and \(E\) is the edge-set of \(G\). \(|V(G)|\) and \(|E(G)|\) denote the numbers of vertices and edges of \(G\), respectively. A path denoted by \((v_{1},v_{2}, \dots ,v_{k})\) is a sequence of vertices where two consecutive vertices are adjacent in \(G\). A cycle is a path \((v_{1},v_{2}, \dots ,v_{k})\) where \(v_{1}=v_{k}\). A graph \(G\) is pancyclic if, for every \(girth\leqslant\ell\leqslant|V(G)|\), \(G\) has a cycle of length \(\ell\). A graph \(G\) is edge-pancyclic if, for any edge \(e\) of \(G\) and every \(girth\leqslant\ell\leqslant|V(G)|\), \(G\) has a cycle of length \(\ell\) containing \(e\). A graph \(G\) is vertex-pancyclic if, for any vertex \(u\) of \(G\) and every \(girth\leqslant\ell\leqslant|V(G)|\), \(G\) has a cycle of length \(\ell\) containing \(u\). Obviously, if a graph is edge-pancyclic, it is also vertex-pancyclic. Edge-pancyclic and vertex-pancyclic on various interconnection networks were studied, including hypercubes, crossed cubes, twisted cubes, locally twisted cubes, augmented cubes, star graphs, and others.
Edge and/or vertex failures are inevitable when a large parallel and distributed computer system is running. Thus, the fault-tolerant capacity of network is an important issue for parallel and distributed computing. A graph \(G\) is \(k\)-fault-tolerant pancyclic(resp., vertex-pancyclic, edge-pancyclic) if \(G-F\) is still pancyclic(resp., vertex-pancyclic, edge-pancyclic) for any \(F\subset E(G)\cup V(G)\) with \(|F|\leqslant k\). Pancyclicity and fault-tolerant pancyclicity have been widely studied for many well-known networks, see Xu and Ma [14] for a detail survey on these topics.
The Möbius cube has many properties superior to the hypercube. Though both the Möbius cubes and the ordinary hypercube have the same number of vertices and the same vertex degree, the diameter of the Möbius cube is approximately half that of the ordinary hypercube. Due to nearly half the diameter and better graph embedding capability as compared with its hypercube counterpart of the same size, the Mö¡§bius cubes have been proposed as promising candidates for interconnection topology, and have received considerable attention [1,2,3,6,7,8,11,13,5,4].
With regard to the fault-tolerant Hamiltonicity of Möbius cubes, Huang et al. [7] showed that an \(n\)-dimensional Möbius cube is Hamiltonian in the presence of up to \(n-2\) node and edge faults. As concerns the pancyclicity and fault-tolerant pancyclicity of Möbius cubes, Fan [3] proved that Möbius cubes are four-pancyclic. Hsieh and Chen [6] found that an \(n\)-dimensional Möbius cube with up to \(n-2\) edge faults is four-pancyclic.
This paper investigates the fault-tolerant edge-pancyclicity of \(MQ_n\), and shows that if \(MQ_n\)(\(n\geq5\)) contains at most \(n-2\) faulty vertices and/or edges then, for any fault-free edge \(uv\) in \(MQ_n^i(i=0,1)\) and any integer \(\ell\) with \(7-i\leqslant\ell\leqslant 2^n-f_v\), there is a fault-free cycle of length \(\ell\) containing the edge \(uv\), where \(f_v\) is the number of faulty vertices.
The remainder of this paper is organized as follows. In Section 2, we recall the definition of \(MQ_n\), and introduce some properties of \(MQ_n\) to be used in our proofs. In Section 3, we give the proof of our result. Finally, we give some concluding remarks in Section 4.
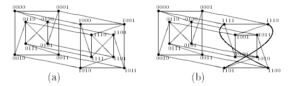
The \(n\)-dimensional Möbius cube, denoted by \(MQ_n\), is such an undirected graph, its vertex set is the same as the vertex set of \(Q_n\), the vertex \(X = x_1x_2 \cdots x_n\) connects to \(n\) other vertices \(Y_i\), (\(1\leq i\leq n\)), where each \(Y_i\) satisfies one of the following equations: \[Y_i= \left\{\begin{array}{ll} \displaystyle x_1x_2\cdots x_{i-1}\bar x_ix_{i+1}\cdots x_n \ & {\rm when}\ x_{i-1}=0,\\ \displaystyle x_1x_2\cdots x_{i-1}\bar x_i\bar x_{i+1}\cdots \bar x_n \ & {\rm when} \ x_{i-1}=1.\\ \end{array}\right.\]
From the above definition, \(X\) connects to \(Y_i\) by complementing the bit \(x_i\) if \(x_{i-1} = 0\) or by complementing all bits of \(x_i, \cdots, x_n\) if \(x_{i-1} = 1\). The connection between \(X\) and \(Y_1\) is undefined, so we can assume that \(x_0\) is either equal to \(0\) or equal to \(1\), which gives us slightly different network topologies. If we assume \(x_0 = 0\), we call the network a ¡®0-Möbius cube¡¯; and if we assume \(x_0 = 1\), we call the network a ¡®1-Möbius cube¡¯, denoted by \(MQ^0_n\) and \(MQ^1_n\), respectively. The graphs shown in Fig.1 are \(MQ^0_4\) and \(MQ^1_4\), respectivily.
According to the above definition, it is not difficult to see that \(MQ^0_n\) (respectively, \(MQ^1_n\)) can be recursively constructed from \(MQ^0_{n-1}\) and \(MQ^1_{n-1}\) by adding \(2^{n-1}\) edges. \(MQ^0_n\) is constructed by connecting all pairs of vertices that differ only in the \(1\)-th bit, and \(MQ^1_n\) is constructed by connecting all pairs of vertices that differ in the \(1\)-th through the \(n\)-th bits. The superscript \(i\) of notation \(MQ^i_n\), \(i=0, 1\), can be omitted if there is no ambiguity arise.
For convenience, we say that \(MQ^0_{n-1}\) and \(MQ^1_{n-1}\) are two sub-Möbius cubes of \(MQ_n\), where \(MQ^0_{n-1}\) (respectively, \(MQ^1_{n-1}\)) is an (\(n-1\))-dimensional \(0\)-Möbius cube (respectively, \(1\)-Möbius cube) which includes all vertices \(0x_2\cdots x_n\) (respectively, \(1x_2\cdots x_n\)), \(x_i\in\{0,1\}\). More simply, let \(L=MQ^0_{n-1}\) and \(R=MQ^1_{n-1}\). In addition, we define the set of crossing edges of \(MQ_n\) to be \(E_C=\{xy\in E(MQ_n)|x\in V(MQ^0_{n-1}) \wedge y\in V(MQ^1_{n-1}) \}\). For any edge \(xy\in E_C\), vertices \(x\) and \(y\) are crossing vertices of each other. Indeed, there are \(2^{n-1}\) crossing edges and \(2^{n-1}\) pairs of crossing vertices in \(MQ_n\).
The Möbius cube \(MQ_n\) was first proposed by Cull and Larson [1]. Like \(Q_n\), \(MQ_n\) is an \(n\)-regular \(n\)-connected graph with \(2^n\) vertices and \(n2^{n-1}\) edges. Moreover, \(MQ_n\) has a diameter of \(\lceil\frac{(n+2)}{2}\rceil\) for \(MQ^0_{n-1}\) and \(\lceil\frac{(n+1)}{2}\rceil\) for \(MQ^1_{n-1}\). However, for \(n\geq4\), \(MQ_n\) is neither vertex-transitive nor edge-transitive.
Cull and Larson[1] first proved the existence of hamiltonian cycles in \(MQ_n\) by proving that in \(MQ^0_{n}\) or \(MQ^1_{n}\), there are \(2^{n-k}\) disjoint cycles of length \(2^k\) for any \(k\geq2\).
We need the following two definitions.
Definition 2.1. For any edge \(e=(x_1x_2\cdots x_{n},y_1y_2\cdots y_{n})\in E(MQ_n)\), let \(\lambda(e)\) be the smallest positive integer \(i\in \{1,2,\ldots,n\}\) such that \(x_i\neq y_i\), then \(e\) is called a \(\lambda\)-dimensional edge.
According to Definition 2.1, if we use \(u_L\) to denote a vertex in \(L\), then \(u_R\) always denotes its unique neighbor in \(R\), that is, \(u_Lu_R\) is an \(1\)-dimensional edge. Let \(e=uv\) be a \(i_1\)-dimensional edge, then denote \(v=u^{i_1}\). Let \(u^{i_1,\ldots,i_{j-1},i_j}={(u^{i_1,\ldots,i_{j-1}})}^{i_j}\) for \(j\geq2\). Let \(P^{t-1}(u_0)=(u_0,u_1,\ldots u_j\ldots u_{t-1})\) be a path of length \(\ell=t-1\), then \(u_j=u_{j-1}^{i_j}\) for \(1\leq j\leq t-1\). We use \((i_1,i_2,\ldots,i_{t-1})\) to denote \(P^{t-1}(u_0)\) for short. If \(u_0u_{t-1}\in E\), then we use \((i_1,i_2,\ldots,i_{t-1})\) to denote cycle \(C^t(u_0)\) of length \(\ell=t\) containing edge \(u_0u_{t-1}\) for short.
For example, for \(C^{7}(000001)=(000001,001001,011001,010110,110110,101001,100001)\) in \(MQ_n^0\), we use \((3, 2, 3, 1, 2,3)\) to denote the cycle \(C^{7}(000001)\).
If \(|F|=n-2\) and there exists a vertex \(w\) with \(N_{MQ_n-F}(w)=\{w_1,w_2\}\), then \(w\) is called a weak 2-degree vertex and \(\{w_1,w_2\}\) is called a \(w\)-weak vertex pair(or a weak vertex pair, for short).
Since there is no triangle in \(MQ_n\), we can obtain the Proposition 2.3 as follows.
If \(xy\in E(MQ_n)\), then \((x,y)\) is not a weak vertex-pair in \(MQ_n-F\) with \(|F|\leq n-2\).
( Xu et al. [9]) If for any vertex \(u_L \in L\)(\(u_R \in R\)), \(v_L\)(\(v_R\)) is a neighbor of \(u_L\)(\(u_R\)) in \(L\)(\(R\)) then, the distance between \(u_R\)(\(u_L\)) and \(v_R\)(\(v_L\)) is 1 or 2.
( Xu et al. [11]) \(MQ_n\) is edge-pancyclic for \(n\geq2\).
( Xu et al. [10]) For any two different vertices \(x\) and \(y\) with distance \(d\) in \(MQ_n\)\((n\geq3)\), there exists an \(xy\)-path of every length \(\ell\) from \(d\) to \(2^n-1\) except for \(d + 1\).
Let \(F\) be a set of faulty elements in \(MQ_n\). We need the following lemmas:
Lemma 2.7. If any edge \(u_Lu_R\in E_C\) in \(MQ^0_n-F\) for \(|F|\leq n-2\), there exists a fault-free \(4\)-cycle or \(5\)-cycle containing the edge \(u_Lu_R\).
Proof. Let \(u_L=0x_2\ldots x_n\), we show the lemma according to the following two cases.
Case 1. \(x_2=0\).
We can find (\(n-2\)) disjoint \(4\)-cycles and a \(5\)-cycle except the common edge \(u_Lu_R\) as follows. \[\begin{array}{llll}\left\{\begin{array}{llllllllllllllll} (i+2, &1, &i+2), &\ \ \ \ \ \ \ \ \ 1\leq i\leq n-2, \\ (2, &1, &3, &2), \ \ \ \ \ \ i=n-1.\\ \end{array} \right . \end{array}\]
Since \(|F|\leq n-2\), there exists a fault-free \(4\)-cycle or \(5\)-cycle containing the edge \(u_Lu_R\). The lemma holds.
Case 2. \(x_2=1\).
There exist at most \(n-2\) disjoint \(4\)-cycles as \(C_i^4(u_L)=(i,1,i)=(u_L,u^i_L,u^{i,1}_L,u_R)\) for \(3\leq i\leq n\) except the common edge \(u_Lu_R\).
If one of \(4\)-cycle \(C_i^4(u_L)\)(\(3\leq i\leq n\)) is fault-free, the lemma holds.
If each \(4\)-cycles \(C_i^4(u_L)\)(\(3\leq i\leq n\)) contains a faulty vertices. Consider \(4\)-cycles \((3,1,3)=(u_L,u^3_L,u^{3,1}_L,u_R)\).
If \(u^{3,1}_L\in F\), then \(u^3_L\notin F\). We can find a fault free \(5\)-cycle \((3,2,1,2)=(u_L,u^3_L, u^{3,2}_L, u^{3,2,1}_L,\\ u_R)\) containing the edge \(u_Lu_R\).
If \(u^3_L\in F\), then \(u^{3,1}_L\notin F\). We can find a fault-free \(5\)-cycle \((2,1,2,3)=(u_L,u^2_L,u^{2,1}_L,u^{3,1}_L,\\u_R )\) containing the edge \(u_Lu_R\).
The proof is completed. ◻
Lemma 2.8. If any edge \(u_Lu_R\in E_C\) in \(MQ^1_n-F\) for \(|F|\leq n-2\), there exists a fault-free \(5\)-cycle containing the edge \(u_Lu_R\).
Proof. Let \(u_L=x_1x_2\ldots x_ix_{i+1}\ldots x_n\). There exist (\(n-2\)) disjoint \(5\)-cycles and a \(4\)-cycle except the common edge \(u_Lu_R\) as follows. \[\begin{array}{llll}\left\{\begin{array}{llllllllllllllll} (i+1, &i+2, &1, &i+1), \ \ 1\leq i\leq n-2\wedge x_{i+1}=0, \\ (i+1, &1, &i+2,&i+1), \ \ 1\leq i\leq n-2\wedge x_{i+1}=1, \\ (n, &1, &n), &\ \ \ \ \ \ \ \ \ \ \ i=n-1.\\ \end{array} \right . \end{array}\]
Since \(|F|\leq n-2\), there exists a fault-free \(4\)-cycle or \(5\)-cycle containing the edge \(u_Lu_R\). ◻
By Lemma 2.7 and 2.8, we can obtain the following result.
If any edge \(u_Lu_R\in E_C\) in \(MQ_n-F\) for \(|F|\leq n-2\), there exists a fault-free \(4\)-cycle or \(5\)-cycle containing the edge \(u_Lu_R\).
(Xu et al. [9]) If \(|F|\leq n-3\) and \(n\geq 3\) then, for any fault-free edge \(e\) in \(MQ_n\) and any integer \(\ell\) with \(6\leq \ell \leq 2^n-f_v\), there is a fault-free cycle of length \(\ell\) containing the edge \(e\) in \(MQ_n\).
(Xu et al. [12]) If \(F\subset V(MQ_n)\cup E(MQ_n)\) and \(|F|\leq n-2\), then for any two distinct fault-free vertices \(u\) and \(v\), there exists a fault-free path \(P_{uv}\) of every length \(\ell\) with \(2^{n-1}-1\leq \ell\leq 2^n-f_v-1-\alpha\), where \(\alpha=0\) if vertices \(u\) and \(v\) is not a weak vertex-pair in \(MQ_n-F\) and \(\alpha=1\) if vertices \(u\) and \(v\) form a weak vertex-pair in \(MQ_n-F\)(\(n\geq5\)).
If \(F\subset V(MQ^1_n)\) with \(|F|\leq n-2\)(\(n\geq6\)), then for any edge \(u_Lv_L\in L\), there exists a fault-free \(6\)-cycle containing the edge \(u_Lv_L\) in \(MQ^1_n-F\).
Proof. By Lemma 2.10, the lemma holds for \(|F|\leq n-3\). We only need to consider the case of \(|F|= n-2\).
Let \(u_L=x_1x_2\ldots x_j \ldots x_n\). We can assume that \(|F_R|\leq |F_L|\). Otherwise, if \(|F_L|\leq|F_R|\), then \(|F_L|\leq\lfloor\frac{n-2}{2}\rfloor\leq n-4(n\geq6)\). By Lemma 2.10, there exists a fault-free \(6\)-cycle containing the edge \(u_Lv_L\) in \(L-F_L\), and so in \(MQ^1_n-F\).
If \(|F_L|\leq n-4\), by Lemma 2.10 , there exists a fault-free \(6\)-cycle containing the edge \(u_Lv_L\).
If \(|F_L|\geq n-3\), then \(|F_R|\leq1\). We can prove the result according to the relationship between the \(v_L\) and \(u_L\) as follows.
Case 1. \(v_L=u^j_L\)(\(j=2\)).
There exist \(n-1\) disjoint \(6\)-cycles as \(C_{i}^{6}(u_L)(1\leq i\leq n-1)\) except the common edge \(u_Lv_L\) as follows. \[\begin{array}{llll}C_{i}^{6}(u_L)=\left\{\begin{array}{llllllllllllllll} (1, &3, &1, &2, &3), & i=1, \\ (i+1, &2, &1, &3, &1), & i=2,\\ (i+1, &5, &2, &5, &4), & i=3,\\ (i+1, &n, &2, &n, &i+1), & 4\leq i\leq n-2\wedge x_4=0,\\ (i+1, &4, &2, &4, &i+1), & 4\leq i\leq n-2\wedge x_4=1,\\ (i+1, &4, &2, &4, &n), & i=n-1.\\ \end{array} \right . \end{array}\]
Since \(|F|\leq n-2\), there exists a fault-free \(6\)-cycle containing the edge \(u_Lv_L\).
Case 2. \(v_L=u^j_L\)(\(3\leq j\leq n\)).
Case 2.1. \(u_R,v_R \notin F\).
For \(3\leq j\leq n-2\), there exist two disjoint \(u_Rv_R\)-paths as \(P_i^3(u_R)\) of length \(\ell=3\) in \(R-F_R\) as follows. \[\begin{array}{llll}P_i^3(u_R)=\left\{\begin{array}{llllllllllllllll} (i+j-2, &j, &j-1), &i=1 ,\\ (i+j-2, &j+1, &j+2), &i=2\wedge x_{j-1}=x_{j+1}, \\ (i+j-2, &j+2, &j+1), &i=2\wedge x_{j-1}\neq x_{j+1}.\\ \end{array} \right . \end{array}\]
For \(j\geq n-1\), there exist two disjoint \(u_Rv_R\)-paths as \(P_i^3(u_R)\) of length \(\ell=3\) in \(R-F_R\) as follows. \[\begin{array}{llll}P_i^3(u_R)=\left\{\begin{array}{llllllllllllllll} (2, &j, &2), &i=1, \\ (j-1, &j, &j-1), &i=2 .\\ \end{array} \right . \end{array}\]
Since \(|F_R|\leq1\), there exists a fault-free \(u_Rv_R\)-path \(P^3(u_R)\) of length \(\ell=3\) in \(R-F_R\). Then \(C=u_Lu_R+P^3(u_R)+v_Rv_L+u_Lv_L\) is a fault-free \(6\)-cycle containing the edge \(u_Lv_L\).
Case 2.2. \(|\{u_R,v_R\}\cap F|=1\). Without loss of generality, assume that \(u_R\in F\). Let \(F^{'}=F-\{u_R\}\), then \(|F^{'}|=n-3\).
For \(j=3\), there exist \(n-2\) \(6\)-cycles as \(C_{i}^{6}(u_L)(1\leq i\leq n-2)\) containing the common edge \(u_Lv_L\) in \(MQ^1_n-F^{'}\) as follows. \[\begin{array}{llll}C_{i}^{6}(u_L)=\left\{\begin{array}{llllllllllllllll} (i+1, &1, &3, &1, &2), & i=1, \\ %(i+1, &3, &1, &4, &1), & i=2\wedge i<j-1.\\ (i+2, &3, &1, &4, &1), & i=2,\\ %(i+1, &n, &3, &n, &i+2), & 3\leq i\leq n-3\wedge x_2=0 \wedge i<j-1.\\ (i+2, &n, &3, &n, &i+2), & 3\leq i\leq n-3\wedge x_2=0,\\ %(i+1, &3, &1, &i+2, &1), & 3\leq i\leq n-3\wedge x_2\neq0 \wedge i<j-1.\\ (i+2, &3, &1, &i+2, &1), & 3\leq i\leq n-3\wedge x_2\neq0,\\ (i+2, &3, &1, &n, &1), & i=n-2.\\ \end{array} \right . \end{array}\]
For \(4 \leq j\leq n-2\), there exist \(n-2\) \(6\)-cycles as \(C_{i}^{6}(u_L)(1\leq i\leq n-2)\) containing the common edge \(u_Lv_L\) in \(MQ^1_n-F^{'}\) as follows: \[\begin{array}{llll}C_{i}^{6}(u_L)=\left\{\begin{array}{llllllllllllllll} (i+1, j, j+1, 2, j+1), i=1, \\ (i+1, n, j, n, i+1),2\leq i\leq j-3\wedge x_i=0,\\ (i+1, j-1, j, j-1, i+1),2\leq i\leq j-3\wedge x_i\neq0,\\ (i+1, j+1, j+2, j, j-1),i=j-2 \wedge x_{j-2}=x_j \wedge x_{j-2}=x_{j+1},\\ (i+1, j+2, j+1, j, j-1),i=j-2 \wedge x_{j-2}=x_j \wedge x_{j-2}\neq x_{j+1},\\ (i+1, j, j+2, j+1, j-1),\\ i=j-2 \wedge x_{j-2}\neq x_j \wedge ((x_{j-1}= x_{j+1}\wedge x_{j-2}=0)\vee (x_{j-1}\neq x_{j+1}\wedge x_{j-2}=1)),\\ (i+1, j, j+1, j+2, j-1),\\ i=j-2 \wedge x_{j-2}\neq x_j\wedge ((x_{j-1}\neq x_{j+1}\vee x_{j-2}\neq0)\wedge (x_{j-1}=x_{j+1}\vee x_{j-2}\neq1)),\\ (i+2, j, 1, j+1, 1), i=j-1,\\ (i+2, 2, j, 2, i+2),j\leq i\leq n-2\wedge x_{j-1}=0,\\ (i+2, j, 1, i+2, 1), j\leq i\leq n-2\wedge x_{j-1}\neq0.\\ \end{array} \right . \end{array}\]
For \(j= n-1\), there exist \(n-2\) \(6\)-cycles as \(C_{i}^{6}(u_L)(1\leq i\leq n-2)\) containing the common edge \(u_Lv_L\) in \(MQ^1_n-F^{'}\) as follows. \[\begin{array}{llll}C_{i}^{6}(u_L)=\left\{\begin{array}{llllllllllllllll} (i+1, &n, &j, &n, &i+1), & i\leq n-4 \wedge x_i=0 ,\\ (i+1, &j-1, &j, &j-1, &i+1), & i\leq n-4 \wedge x_i\neq0, \\ (i+1, &n, &1, &n-2, &1), & i= n-3 \wedge x_{n-2}=0 ,\\ (i+1, &1, &n-1, &1, &n-2), & i= n-3 \wedge x_{n-2}\neq0, \\ (i+2, &n-1, &1, &n, &1), & i= n-2 .\\ \end{array} \right . \end{array}\]
For \(j= n\), there exist \(n-2\) \(6\)-cycles as \(C_{i}^{6}(u_L)=(i+1, i, n, i, i+1)\)\((1\leq i\leq n-2)\) containing the common edge \(u_Lv_L\) in \(MQ^1_n-F^{'}\).
Note that \(n-2\) \(6\)-cycles are disjoint in \(L\) and contain no \(u_R\) in \(MQ^1_n-F^{'}\). Since \(|F^{'}|=n-3\), we have that there exists a fault-free 6-cycles in \(MQ^1_n-F^{'}\), and so in \(MQ^1_n-F\).
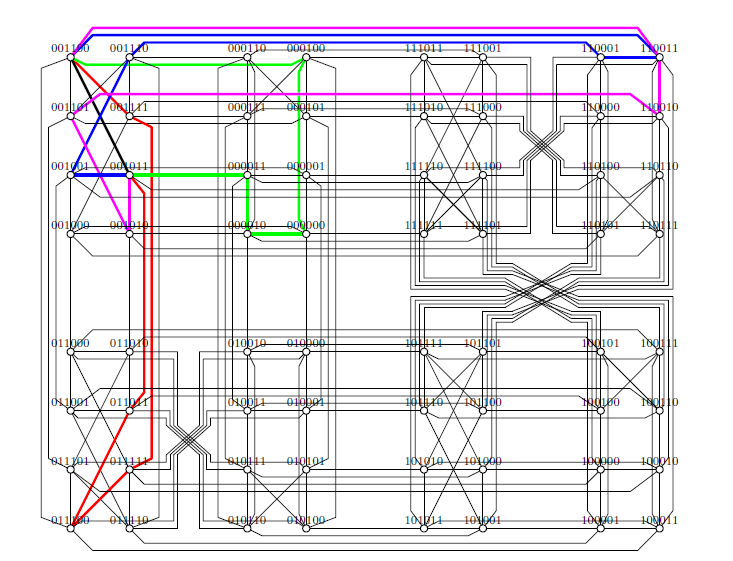
Take edge \(u_Lv_L=(001011,001100)\) in \(MQ^1_6\) for an example. We have \(u_R=110100\),\(v_R=110011\). Assume \(110100\in F\), then \(110011\notin F\). There exist four disjoint \(6\)-cycles in \(L\) except a common edge \(u_Lv_L=(001011,001100)\) as follows(see Figure 2). \[\begin{array}{llll}\left\{\begin{array}{llllllllllllllll} (001011, &011011, &011100, &011111, &001111, &001100),\\ (001011, &000011, &000010, &000000, &000100, &001100),\\ (001011, &001001, &001110, &110001, &110011, &001100),\\ (001011, &001010, &001101, &110010, &110011, &001100).\\ \end{array} \right . \end{array}\]
◻
Lemma 2.13. If \(F\subset R\) with \(|F|= n-2\)(\(n\geq6\)), then for any edge \(u_Rv_R\in R\), there exists a fault-free \(6\)-cycle containing the edge \(u_Rv_R\) in \(MQ^1_n-F\).
Proof. Let \(u_L,v_L\) be the adjacent vertices of \(u_R,v_R\) respectively in \(L\) and \(u_R=x_1x_2\ldots x_i\ldots x_n\). Since \(F\subset R\), \(F_L=0\). There exists a fault-free \(u_Lv_L\)-path \(P\) of length \(\ell=3\) in \(L\) as follows. \[\begin{array}{llll}P=\left\{\begin{array}{llllllllllllllll} (2, &4, &3), & v_R=u^2_R \wedge x_3=0, \\ (2, &3, &4), & v_R=u^2_R \wedge x_3\neq 0,\\ (j-1,&j, &j-1), & v_R=u^j_R(3\leq j\leq n-1),\\ (2, &n, &2), & v_R=u^n_R.\\ \end{array} \right . \end{array}\]
Then \(C=v_Rv_L+P+u_Lu_R+u_Rv_R\) is a fault-free \(6\)-cycle containing the edge \(u_Rv_R\) in \(MQ^1_n-F\). ◻
Lemma 2.14. For any edge \(u_Lu_R\in E_C\) in \(MQ^i_n-F\)(\(i=0,1\))(\(n\geq6\)) with \(|F|\leq n-2\), there exists a fault-free cycle of length \(\ell=7-i,7,8\) containing the edge \(u_Lu_R\) in \(MQ^i_n-F\)(\(i=0,1\)).
Proof. Let \(u_L=x_1x_2x_3\ldots x_i\ldots x_n\). We prove the lemma according to edge \(u_Lu_R\) in \(MQ^0_n\) or \(MQ^1_n\) as follows.
Case 1. \(u_Lu_R\in E(MQ^0_n)\).
Case 1.1. \(\ell=7\).
For \(1\leq i\leq n-1\), we can find \(n-1\) disjoint \(7\)-cycles as \(C_{i}^{7}(u_L)\) except the common edge \(u_Lu_R\) as follows. \[\begin{array}{llll}C_{1}^{7}(u_L)=\left\{\begin{array}{llllllllllllllll} (2, &3, &n-1, &1, &n-1, &2), &x_3=0\wedge x_2=0, \\ (2, &3, &2, &1, &4, &3), &x_3=0\wedge x_2\neq0, \\ (2, &1, &2, &5, &4, &3), &x_3\neq0\wedge x_2=0\wedge x_4=0, \\ (2, &1, &5, &2, &4, &3), &x_3\neq0\wedge x_2=0\wedge x_4\neq0, \\ (2, &n, &1, &n, &2, &3), &x_3\neq0\wedge x_2\neq0 ,\\ \end{array} \right . \end{array}\] \[\begin{array}{llll}C_{2}^{7}(u_L)=\left\{\begin{array}{llllllllllllllll} (3, &2, &3, &1, &2, &3), &x_3=0\wedge x_2=0 ,\\ (3, &2, &3, &1, &3, &2), &x_3=0\wedge x_2\neq0, \\ (3, &4, &2, &1, &5, &2), &x_3\neq0\wedge x_2=0\wedge x_4=0, \\ (3, &5, &2, &1, &4, &2), &x_3\neq0\wedge x_2=0\wedge x_4\neq0, \\ (3, &4, &2, &1, &4, &2), &x_3\neq0\wedge x_2\neq0\wedge x_4=0, \\ (3, &5, &2, &1, &5, &2), &x_3\neq0\wedge x_2\neq0\wedge x_4\neq0, \\ \end{array} \right . \end{array}\] \[\begin{array}{llll}\ C_{i}^{7}(u_L)=\left\{\begin{array}{llllllllllllllll} (i+1, &2, &3, &1, &2, &i+1), &3\leq i\leq n-1 \wedge x_2=0, \\ (i+1, &3, &2, &1, &2, &i+1), &3\leq i\leq n-1 \wedge x_2\neq0.\\ \end{array} \right . \end{array}\]
Since \(|F|\leq n-2\), there exists a fault-free \(7\)-cycle containing the edge \(u_Lu_R\).
Case 1.2. \(\ell=8\).
For \(1\leq i\leq n-1\), we can find \(n-1\) disjoint \(8\)-cycles as \(C_{i}^{8}(u_L)\) except the common edge \(u_Lu_R\) as follows. \[\begin{array}{llll}C_{1}^{8}(u_L)=\left\{\begin{array}{llllllllllllllll} (2, &1, &n-1, &3, &n-1, &2), &x_2=0 ,\\ (2, &3, &2, &1, &2, &3), &x_2\neq0, \\ \end{array} \right . \end{array}\]
\[C_{i}^{8}(u_L)=(i+1,\, \, 2,\, \, n,\, \, 2,\, \, 1,\, \, n), \, \, 2\leq i\leq n-2,\]
\[\begin{array}{llll}C_{n-1}^{8}(u_L)=\left\{\begin{array}{llllllllllllllll} (n, &2, &1, &n-1, &3, &n-1), &x_2=0, \\ (n, &2, &1, &3, &4, &2), &x_2\neq0\wedge x_3=0, \\ (n, &2, &1, &4, &3, &2), &x_2\neq0\wedge x_3\neq0. \\ \end{array} \right . \end{array}\]
Since \(|F|\leq n-2\), there exists a fault-free \(8\)-cycle containing the edge \(u_Lu_R\).
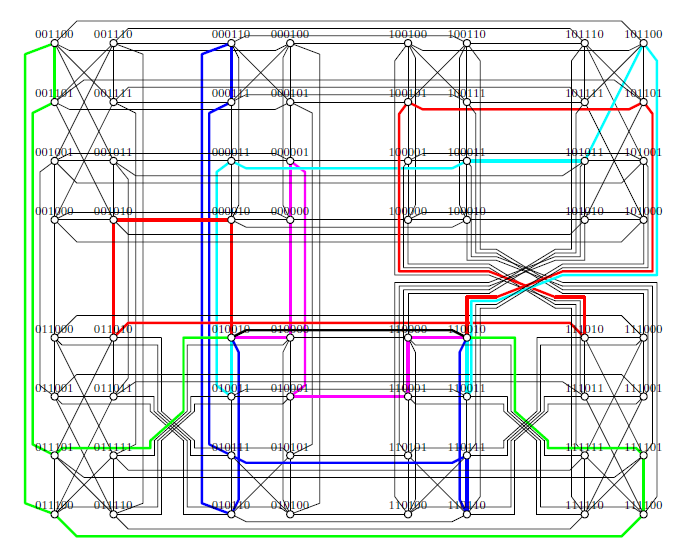
Take edge \((010010,110010)\) in \(MQ^0_6\) for an example, there exist \(5\) disjoint \(8\)-cycles except the common edge \((010010,110010)\) as follows(see Figure 3). \[\begin{array}{llll}\left\{\begin{array}{llllllllllllllll} (010010, 000010, 001010, 011010, 111010, 100101, 101101, 110010),\\ (010010, 011101, 001101, 001100, 011100, 111100, 111101, 110010),\\ (010010, 010110, 000110, 000111, 010111, 110111, 110110, 110010),\\ (010010, 010000, 000000, 000001, 010001, 110001, 110000, 110010),\\ (010010, 010011, 000011, 100011, 101011, 101100, 110011, 110010).\\ \end{array} \right . \end{array}\]
Case 2. \(u_Lu_R\in E(MQ^1_n)\).
Case 2.1. \(\ell=6\).
For \(1\leq i\leq n-1\), we can find \(n-1\) disjoint \(6\)-cycles as \(C_{i}^{6}(u_L)\) except the common edge \(u_Lu_R\) as follows. \[\begin{array}{llll}C_{i}^{6}(u_L)=\left\{\begin{array}{llllllllllllllll} (i+1, 1, i+3, i+2, i+1), 1\leq i\leq n-4\wedge x_i=x_{i+2}\wedge x_{i+1}=0 ,\\ (i+1, i+2, i+3, 1, i+1), 1\leq i\leq n-4\wedge x_i=x_{i+2}\wedge x_{i+1}\neq0, \\ (i+1, i+3, 1, i+2, i+1), 1\leq i\leq n-4\wedge x_i\neq x_{i+2}\wedge x_{i+1}=0 ,\\ (i+1, i+2, 1, i+3, i+1), 1\leq i\leq n-4\wedge x_i\neq x_{i+2}\wedge x_{i+1}\neq0, \\ \end{array} \right . \end{array}\] \[\begin{array}{llll}C_{n-3}^{6}(u_L)=\left\{\begin{array}{llllllllllllllll} (n-2, &n-1, &n-2, &1, &n-1), &x_{n-2}=0 ,\\ (n-2, &n-1, &1, &n-2, &n), &x_{n-2}\neq0, \\ \end{array} \right . \end{array}\] \[\begin{array}{llll}C_{n-2}^{6}(u_L)=\left\{\begin{array}{llllllllllllllll} (n-1, &n-2, &1, &n-2, &n), &x_{n-2}=0, \\ (n-1, &1, &n-2, &n-1, &n-2), &x_{n-2}\neq0, \\ \end{array} \right . \end{array}\] \[\begin{array}{llll}C_{n-1}^{6}(u_L)=\left\{\begin{array}{llllllllllllllll} (n, &n-2, &1, &n-1, &n-2), &x_{n-2}=0 ,\\ (n, &n-2, &1, &n-2, &n-1), &x_{n-2}\neq0. \\ \end{array} \right . \end{array}\]
Since \(|F|\leq n-2\), there exists a fault-free \(6\)-cycle containing the edge \(u_Lu_R\).
Case 2.2. \(\ell=7\).
For \(1\leq i\leq n-1\), we can find \(n-1\) disjoint \(7\)-cycles as \(C_{i}^{7}(u_L)\) except the common edge \(u_Lu_R\) as follows.
\[\begin{array}{llll}C_{i}^{7}(u_L)=\left\{\begin{array}{llllllllllllllll} (i+1, i+3, i+2, 1, i+3, i+1), &1\leq i\leq n-4\wedge x_{i+1}=0,\\ (i+1, i+3, 1, i+2, i+3, i+1), &1\leq i\leq n-4\wedge x_{i+1}\neq0, \\ \end{array} \right . \end{array}\] \[\begin{array}{llll}C_{n-3}^{7}(u_L)=\left\{\begin{array}{llllllllllllllll} (n-2, &1, &n, &n-2, &n, &n-1), &x_{n-2}=0,\\ (n-2, &1, &n, &n-1, &n-2, &n), &x_{n-2}\neq0, \\ \end{array} \right . \end{array}\] \[\begin{array}{llll}C_{n-2}^{7}(u_L)=\left\{\begin{array}{llllllllllllllll} (n-1, n-2, n-3, 1, n-3, n), x_{n-2}=0\wedge x_{n-3}=0,\\ (n-1, n, n-3, 1, n-3, n-2), x_{n-2}=0 \wedge x_{n-3}\neq0\wedge x_{n-4}=0, \\ (n-1, n-3, n-2, 1, n-3, n), x_{n-2}=0\wedge x_{n-3}\neq0\wedge x_{n-4}\neq0,\\ (n-1, 2, n-2, 2, 1, n-2), x_{n-2}\neq0, \\ \end{array} \right . \end{array}\] \[\begin{array}{llll}C_{n-1}^{7}(u_L)=\left\{\begin{array}{llllllllllllllll} (n, n-3, 1, n-3,n, n-2), x_{n-2}=0\wedge x_{n-3}=0,\\ (n, n-2, n-3, 1, n-3,n), x_{n-2}=0 \wedge x_{n-3}\neq0\wedge x_{n-4}=0, \\ (n, n-2, n-1, 1, n, n-2), x_{n-2}=0\wedge x_{n-3}\neq0\wedge x_{n-4}\neq0,\\ (n, 2, n-1, 2, 1, n-1), x_{n-2}\neq0 .\\ \end{array} \right . \end{array}\]
Since \(|F|\leq n-2\), there exists a fault-free \(7\)-cycle containing the edge \(u_Lu_R\).
Case 2.3. \(\ell=8\).
For \(1\leq i\leq n-1\), we can find \(n-1\) disjoint \(8\)-cycles as \(C_{i}^{8}(u_L)\) except the common edge \(u_Lu_R\) as follows. \[\begin{array}{llll}C_{i}^{8}(u_L)=\left\{\begin{array}{llllllllllllllll} (i+1, n, 1, n, i+3, i+2), 1\leq i\leq n-4\wedge x_i=x_{i+2}\wedge x_{i+1}=0, \\ (i+1, i+2, i+3, n, 1, n), 1\leq i\leq n-4\wedge x_i=x_{i+2}\wedge x_{i+1}\neq0, \\ (i+1, i+3, n, 1, n, i+2), 1\leq i\leq n-4\wedge x_i\neq x_{i+2}\wedge x_{i+1}=0, \\ (i+1, i+2, n, 1, n, i+3), 1\leq i\leq n-4\wedge x_i\neq x_{i+2}\wedge x_{i+1}\neq0, \\ \end{array} \right . \end{array}\] \[\begin{array}{llll}C_{n-3}^{8}(u_L)=\left\{\begin{array}{llllllllllllllll} (n-2, &1, &n-1, &1, &n, &1), &x_{n-2}=0, \\ (n-2, &1, &n, &1, &n-1,&1), &x_{n-2}\neq0, \\ \end{array} \right . \end{array}\] \[\begin{array}{llll}C_{n-2}^{8}(u_L)=\left\{\begin{array}{llllllllllllllll} (n-1, &2, &n, &3, &1, &2), &x_{2}=0, \\ (n-1, &2, &n, &1, &3, &2), &x_{2}\neq0, \\ \end{array} \right . \end{array}\] \[\begin{array}{llll}C_{n-1}^{8}(u_L)=\left\{\begin{array}{llllllllllllllll} (n, n-2, 1, 2, n-2, 2), x_{2}=0\wedge x_{n-2}=0 ,\\ (n, n-1, n-2, n-3,1, n-3), x_{2}=0\wedge x_{n-2}\neq0\wedge x_{n-3}=0 ,\\ (n, n-1, n-3, 1, n-3, n-2), x_{2}=0\wedge x_{n-2}\neq0\wedge x_{n-3}\neq0, \\ (n, 2, 3, 2, 1, 3), x_{2}\neq0\wedge x_3=0 ,\\ (n, 2, 4, 3, 1, 2), x_{2}\neq0\wedge x_3\neq0 .\\ \end{array} \right . \end{array}\]
Since \(|F|\leq n-2\), there exists a fault-free \(8\)-cycle containing the edge \(u_Lu_R\).
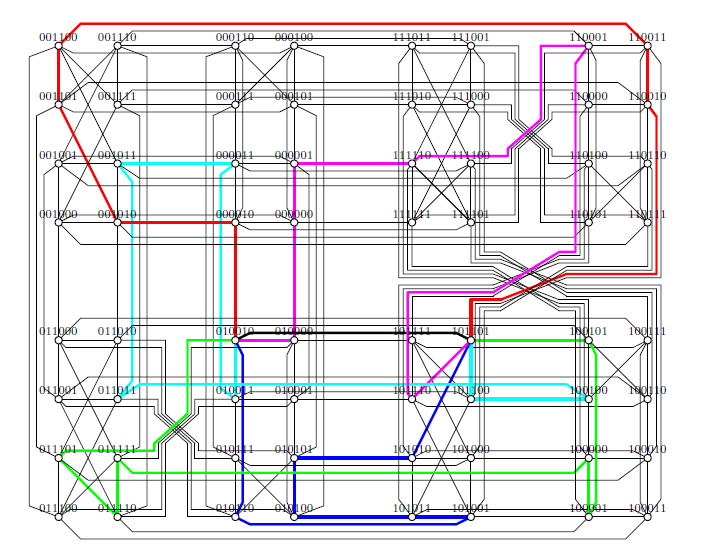
Take edge \((010010,101101)\) in \(MQ^1_6\) for an example, there exist \(5\) disjoint \(8\)-cycles except the common edge \((010010,101101)\) as follows (see Figure 4): \[\begin{array}{llll}\left\{\begin{array}{llllllllllllllll} (010010, 000010, 001010, 001101, 001100, 110011, 110010, 101101),\\ (010010, 011101, 011110, 011111, 100000, 100001, 100101, 101101),\\ (010010, 010110, 101001, 101011, 010100, 010101, 101010, 101101),\\ (010010, 010000, 000000, 000001, 111110, 110001, 101110, 101101),\\ (010010, 010011, 000011, 001011, 011011, 100100, 101100, 101101).\\ \end{array} \right . \end{array}\]
◻
In this section, we investigate the fault-tolerant edge-Pancyclicity of \(MQ_n\) and show that \(MQ_n\) is \((n-2)\)-fault-tolerant edge-Pancyclic.
Let \(F\) be a set of faulty elements in \(MQ_n\), \(F_L=F\cap L\), \(F_R=F\cap R\), \(F_C=F\cap E_C\), \(F^v=F\cap V(MQ_n)\), \(F^e=F\cap E(MQ_n)\) \(F_L^v=F_L\cap V(L)\) and \(F_R^v=F_R\cap V(R)\), \(f_v=|F^v|\), \(f_e=|F^e|\).
Theorem 3.1. If \(f_v+f_e\leq n-2\) and \(n\geq 5\) then, for any fault-free edge \(e\) in \(MQ_n^i(i=0,1)\) and any integer \(\ell\) with \(7-i\leq \ell \leq 2^n-f_v\), there is a fault-free cycle of length \(\ell\) containing the edge \(e\).
In this section, we will give the proof of Theorem 3.1. The theorem follows from Lemma 2.10 if \(|F|\leqslant n-3\). We only need to consider \(|F|=n-2\). Start with the following lemma.
Lemma 3.2. If Theorem 3.1 holds for any subset \(F \subset V(MQ_n)\) with \(| F|=n-2\), then Theorem 3.1 also holds for any subset \(F^{'}\subset V(MQ_n)\cup E(MQ_n)\) with \(|F^{'}|=n-2\).
Proof. The lemma holds for \(f_e=0\) by hypothesis of Lemma 3.2. Assume that the lemma holds for any \(t\) with \(0< t\leq n-3\) and \(f_e=t\). We prove the lemma holds for \(f_e=t+1\). Let \(xy\) be an edge in \(F\).
Case 1. \(x\in F\) or \(y\in F\).
Without loss of generality, assume \(x\in F\). Let \(F^{'}=F-xy\), then \(|F^{'}|=n-3\). By Lemma 2.10, this result has been proved.
Case 2. \(x,y\notin F\).
Let \(F^{'}=F+\{x\}-\{xy\}\), then \(|F^{'}|=n-2\), and \(F^{'}\) contains at most \(t\) edges and \(f_v+1\) vertices. By induction hypothesis, for every integer \(\ell\) with \(7-i \leq \ell\leq 2^n-f_v-1\), there is a fault-free \(\ell\)-cycle containing the edge \(e\) in \(MQ^i_n-F^{'}\)(\(i=0,1\)). By Proposition 2.1, for any \(e=uv\in E(MQ_n-F)\), \((u,v)\) is not a weak vertex-pair in \(MQ_n-F\). For \(\ell=2^n-f_v\), by Lemma 2.11, there is a fault-free \(uv\)-hamiltonian path in \(MQ_n-F\), i.e., there is a fault-free \(\ell\)-cycle containing the edge \(e\) in \(MQ_n-F\).
The proof of lemma is completed. ◻
Proof of Theorem 3.1. By Lemma 3.2, we only need to prove the theorem with \(F\subset V(MQ_n)\). The proof proceeds by induction on \(n\geqslant 5\). The result holds for \(n=5\) by developing computer program using depth first searching technique combining with backtracking and branch and bound algorithm.
Assume that the theorem holds for any \(k\) with \(6\leq k < n\). Then we must show the theorem holds for \(n\).
Let \(e=uv\) be a fault-free edge in \(MQ_n\). By Proposition 2.3, \((u,v)\) is not a weak vertex-pair in \(MQ_n-F\). Let \(2^{n-1}\leq\ell \leq 2^n-f_v\) and \(\ell=\ell'+1\), where \(2^{n-1}-1 \leq \ell'\leq 2^n-f_v-1\) then, by Lemma 2.11, there exists a fault-free \(uv\)-path \(P\) of length \(\ell'\) in \(MQ_n\). Then \(P+uv\) is a fault-free cycle of length \(\ell\) containing the edge \(e\) in \(MQ_n\). Thus, we only need to consider \(\ell\) with \(7-i \leq \ell \leq 2^{n-1}-1\) in \(MQ_n^i(i=0,1)\)(\(n\geq6\)).
Case 1. \(|F_R|\leq |F_L|\).
Case 1.1. \(e\in E(L-F_L)\). Let \(e=u_Lv_L\).
By Lemma 2.12, there exists a fault-free \(6\)-cycle containing the edge \(e\) in \(MQ^1_n-F\). Thus, we only need to consider the length of \(7\leq \ell \leq 2^{n-1}-1\).
Case 1.1.1. \(|F_L|\leq n-3\). Then \(|F_R|\leq n-4\).
Case 1.1.1.1. \(7\leq \ell \leq 2^{n-1}-|F^v_L|\).
By induction hypothesis, there is a fault-free cycle of length \(\ell\) containing the edge \(e\) in \(L\), so in \(MQ_n\).
Case 1.1.1.2. \(2^{n-1}-|F^v_L|+1\leq \ell \leq2^{n-1}-1\).
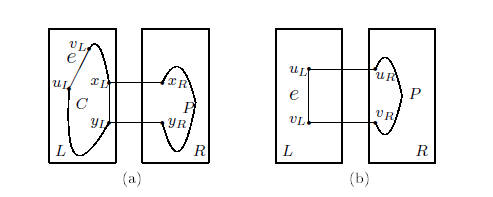
Write \(\ell=\ell_1+1+\ell_2\), where \(2^{n-2}-|F^v_L|+1\leq \ell_1 \leq 2^{n-2}-1\) and \(\ell_2 = 2^{n-2}-1\). Since \(2^{n-2}-|F^v_L|+1\geq 2^{n-2}-|F_L|+1\geq 2^{n-2}-n+4>7\) for \(n\geq 6\) and \(|F_L|\leq n-3\), by induction hypothesis, there is a fault-free cycle \(C\) of length \(\ell_1\) containing the edge \(u_Lv_L\) in \(L\). Note that a cycle of length \(\ell_1\) contains a matching \(M\) with \(|M|=\lfloor \frac{\ell_1}{2}\rfloor\). Consider the following inequality. \[\begin{array}{rl} \left\lfloor\frac{\ell_1}{2}\right\rfloor-|F_C|-|F_R|-|\{e\}| & \geq \left\lfloor\frac{2^{n-2}-|F^v_L|+1}{2}\right\rfloor-|F_C|-|F_R|-1\\ & \geq 2^{n-3}-|F|-1\ \geq 2^{n-3}-n+1. \end{array}\]
Let \(f(x)=2^{x-3}-x+1\). Since \(f'(x)=2^{x-3}\ln2-1\geq 0\) for \(x \geq 6\), \(f(x)\) is an increasing function, which implies that \(\lfloor\frac{\ell_1}{2}\rfloor-|F_C|-|F_R|\geq f(6)=2^{6-3}-6+1= 3\). It follows that, there is such an edge, say \(x_Ly_L\), in \(M\) that \(x_Ly_L\ne u_Lv_L\) and \(|\{x_R,y_R,x_Lx_R,y_Ly_R\}\cap F|=0\). By Lemma 2.1, there is a fault-free \(x_Ry_R\)-path \(P\) of length \(\ell_2\) in \(R\). Then \(C-x_Ly_L+y_Ly_R+P+x_Rx_L\) is a fault-free cycle of length \(\ell\, (=\ell_1+1+\ell_2)\) containing \(e\) (see Figure 5 (a)).
Case 1.1.2. \(|F_L|= n-2\). In this case, \(|F_R|=0\).
Let \(u_R\) and \(v_R\) be neighbors of \(u_L\) and \(v_L\) in \(R\), respectively.
Let \(\ell=\ell'+3\), where \(4 \leq \ell' \leq 2^{n-1}-4\). By Lemma 2.4, \(d_{u_Rv_R}\leq2\). Since \(|F_R|=|F_C|=0\), by Lemma 2.6, there is a fault-free \(u_Rv_R\)-path \(P\) of length \(\ell'\) in \(R\), and so \(P+v_Rv_L+v_Lu_L+u_Lu_R\) is a fault-free cycle of length \(\ell\) containing the edge \(u_Lv_L\) (see Figure 5 (b)).
Case 1.2. \(e\in E(R-F_R)\). Let \(e=u_Rv_R\).
Case 1.2.1. \(|F_L|\leq n-3\). Then \(|F_R|\leq n-4\).
Case 1.2.1.1. \(7-i\leq \ell \leq 2^{n-1}-|F^v_R|\) in \(MQ_n^i(i=0,1)\).
By induction hypothesis, there is a fault-free cycle of length \(\ell\) containing the edge \(e\) in \(R\), so in \(MQ_n^i(i=0,1)\).
Case 1.2.1.2. \(2^{n-1}-|F^v_R|+1\leq \ell \leq2^{n-1}-1\).
The proof is similar to Case 1.1.1.2.
Case 1.2.2. \(|F_L|= n-2\). In this case, \(|F_R|=0\).
Since \(|F_R|=0\), by Lemma 2.5, there exists a fault-free cycle of length \(\ell\) with \(7-i\leq \ell\leq 2^{n-1}-1\) containing the edge \(e\) in \(R\), and so in \(MQ_n^i-F(i=0,1)\).
Case 1.3. \(e\in (E_C-F_C)\). Let \(e=u_Lu_R\).
By Lemma 2.14, there exists a fault-free cycle of length \(\ell=7-i,7,8\) containing the edge \(u_Lu_R\) in \(MQ^i_n-F\)(\(i=0,1\)). Thus, we only need to consider the length \(9\leq\ell \leq 2^{n-1}-1\).
Case 1.3.1. \(|F_L|\leq n-3\). Then \(|F_R|\leq n-4\).
By Corollary 2.1., there exists a fault-free \(4\)-cycle \(C\) (or \(5\)-cycle) containing the edge \(u_Lu_R\).
Case 1.3.1.1. \(C=C^4=(u_L,s_L,s_R,u_R)\).
For \(9\leq \ell \leq 2^{n-1}-|F^v_R|-1\). Let \(\ell=\ell'+2\), where \(7\leq \ell' \leq 2^{n-1}-|F^v_R|-3\). By induction hypothesis, there is a fault-free cycle \(C'\) of length \(\ell'\) containing the edge \(u_Rs_R\) in \(R\). Then \(C=C'-u_Rs_R+s_Rs_L+s_Lu_L+u_Lu_R\) is a fault-free cycle of length \(\ell\) containing the edge \(e=u_Lu_R\).
For \(2^{n-1}-|F^v_R|\leq \ell \leq 2^{n-1}-1\). Let \(\ell=\ell_1+\ell_2\), where \(\ell_1=2^{n-2}\) and \(2^{n-2}-|F^v_R| \leq \ell_2 \leq 2^{n-2}-1\). Since \(2^{n-2}>7\) and \(2^{n-2}-|F^v_R|>7\) for \(n \geq6\), by induction hypothesis, there exists a fault-free cycle \(C_1\) of length \(\ell_1\) containing the edge \(u_Ls_L\) in \(L\) and a fault-free cycle \(C_2\) of length \(\ell_2\) containing the edge \(u_Rs_R\) in \(R\). Then \(C=C_1-u_Ls_L+s_Ls_R+C_2-s_Ru_R+u_Ru_L\) is a fault-free cycle of length \(\ell\) containing the edge \(e=u_Lu_R\) in \(MQ_n\) (see Figure 6(a)).
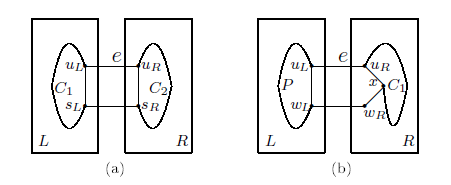
Case 1.3.1.2. \(C=C^5=(u_L,w_L,w_R,x,u_R)\).
Since \(|F_R|\leq n-4\). Let \(F_R^1=F_R-\{w_R\}\), then \(|F_R^1|=|F_R|-1\leq n-3\).
For \(9\leq \ell \leq 2^{n-1}-|F^v_R|-1\). Let \(\ell=\ell'+3\), where \(6\leq \ell' \leq 2^{n-1}-|F^v_R|-4\). By induction hypothesis, there is a fault-free cycle \(C'\) of length \(\ell'\) containing the edge \(u_Rx\) in \(R-F_R^1\). Then \(C=C'-u_Rx+xw_R+w_Rw_L+w_Lu_L+u_Lu_R\) is a fault-free cycle of length \(\ell\) containing the edge \(e=u_Lu_R\).
For \(2^{n-1}-|F^v_R|\leq \ell \leq 2^{n-1}-1\). Let \(\ell=\ell_1+\ell_2+2\), where \(\ell_1=2^{n-2}-1\) and \(2^{n-2}-|F^v_R|-1\leq \ell_2 \leq 2^{n-2}-2\). Since \(2^{n-2}-|F^v_R|-1>7\) for \(n \geq6\), by induction hypothesis, there exists a fault-free cycle \(C_1\) of length \(\ell_2\) containing the edge \(xu_R\) in \(R-F_R^1\) and, by Lemma 2.11, there exists a fault-free \(u_Lw_L\)-path \(P\) of length \(\ell_1\) in \(L\). Then \(C=C_1-u_Rx+xw_R+w_Rw_L+P+u_Lu_R\) is a fault-free cycle of length \(\ell\) containing the edge \(e=u_Lu_R\) in \(MQ_n\) (see 6(b)).
Case 1.3.1.3. \(C=C^5=(u_L,x,w_L,w_R,u_R)\).
For \(9\leq \ell \leq 2^{n-1}-|F^v_R|-1\). Let \(\ell=\ell'+3\), where \(6\leq \ell' \leq 2^{n-1}-|F^v_R|-4\). By induction hypothesis, there is a fault-free cycle \(C'\) of length \(\ell'\) containing the edge \(u_Rw_R\) in \(R\). Then \(C=C'-u_Rw_R+w_Rw_L+w_Lx+xu_L+u_Lu_R\) is a fault-free cycle of length \(\ell\) containing the edge \(e=u_Lu_R\).
For \(2^{n-1}-|F^v_R|\leq \ell \leq 2^{n-1}-1\). Let \(\ell=\ell_1+\ell_2+1\), where \(\ell_1=2^{n-2}\) and \(2^{n-2}-|F^v_R|-1\leq \ell_2 \leq 2^{n-2}-2\). Since \(2^{n-2}-|F^v_R|-1>7\) for \(n \geq6\), by induction hypothesis, there exists a fault-free cycle \(C_1\) of length \(\ell_2\) containing the edge \(u_Rw_R\) in \(R\) and, by Lemma 2.11, there exists a fault-free \(u_Lw_L\)-path \(P\) of length \(\ell_1\) in \(L\). Then \(C=C_1-u_Rw_R+w_Rw_L+P+u_Lu_R\) is a fault-free cycle of length \(\ell\) containing the edge \(u_Lu_R\) in \(MQ_n\) (see Figure 7(a)).
Case 1.3.2. \(|F_L|= n-2\). In this case, \(|F_R|=0\).
Since \(|F_L|=n-2\), there exists a fault-free neighbor \(v_L\) of \(u_L\) in \(L\). Let \(v_R\) be neighbors of \(v_L\) in \(R\).
Let \(\ell=\ell'+3\), where \(6 \leq \ell' \leq 2^{n-1}-4\). By Lemma 2.4, \(d_{u_Rv_R}\leq2\). By Lemma 2.6, there is a fault-free \(u_Rv_R\)-path \(P\) of length \(\ell'\) in \(R\). So \(P+u_Ru_L+u_Lv_L+v_Lv_R\) is a fault-free cycle of length \(\ell\) containing the edge \(u_Lu_R\).
Case 2. \(|F_L|\leq|F_R|\).
Case 2.1. \(e\in E(R-F_R)\). Let \(e=u_Rv_R\).
Case 2.1.1. \(|F_R|\leq n-3\). Then \(|F_L|\leq n-4\).
For \(7-i\leq \ell \leq 2^{n-1}-|F^v_R|\) in \(MQ_n^i(i=0,1)\). By induction hypothesis, there is a fault-free cycle of length \(\ell\) containing the edge \(e\) in \(R\), so in \(MQ_n^i(i=0,1)\).
For \(2^{n-1}-|F^v_R|+1\leq \ell \leq2^{n-1}-1\). The proof is similar to Case 1.1.1.2.
Case 2.1.2. \(|F_R|= n-2\). In this case, \(|F_L|=0\).
By Lemma 2.13, there exists a fault-free \(6\)-cycle containing the edge \(e\) in \(MQ^1_n-F\). Thus, we only need to consider the length of \(7\leq \ell \leq 2^{n-1}-1\).
Let \(u_L\) and \(v_L\) be neighbors of \(u_R\) and \(v_R\) in \(L\), respectively.
Let \(\ell=\ell'+3\), where \(4 \leq \ell' \leq 2^{n-1}-4\). By Lemma 2.4, \(d_{u_Lv_L}\leq2\). Since \(|F_L|=|F_C|=0\), by Lemma 2.6, there is a fault-free \(u_Lv_L\)-path \(P\) of length \(\ell'\) in \(L\), and so \(P+v_Lv_R+v_Ru_R+u_Ru_L\) is a fault-free cycle of length \(\ell\) containing the edge \(u_Rv_R\).
Case 2.2. \(e\in E(L-F_L)\). Let \(e=u_Lv_L\).
Case 2.2.1. \(|F_R|\leq n-3\). Then \(|F_L|\leq n-4\).
For \(7-i\leq \ell \leq 2^{n-1}-|F^v_L|\) in \(MQ^i_n-F\)\((i=0,1)\). Since \(|F_L|\leq n-4\), by Lemma 2.10, there exists a fault-free cycle of length \(\ell\) containing the edge \(e\) in \(MQ^i_n-F\)\((i=0,1)\).
For \(2^{n-1}-|F^v_L|+1\leq \ell \leq2^{n-1}-1\). The proof is similar to Case 1.1.1.2.
Case 2.2.2. \(|F_R|= n-2\). In this case, \(|F_L|=0\).
Since \(|F_L|=0\), by Lemma 2.5, there exists a fault-free cycle of length \(\ell\) with \(7-i\leq \ell\leq 2^{n-1}-1\) containing the edge \(e\) in \(L\), and so in \(MQ_n^i(i=0,1)\).
Case 2.3. \(e\in (E_C-F_C)\). Let \(e=u_Lu_R\).
By Lemma 2.14, there exists a fault-free cycle of length \(\ell=7-i,7,8\) containing the edge \(u_Lu_R\) in \(MQ^i_n-F\)(\(i=0,1\)). Thus, we only need to consider the length \(9\leq\ell \leq 2^{n-1}-1\).
Case 2.3.1. \(|F_R|\leq n-3\). Then \(|F_L|\leq n-4\).
By Corollary 2.1., there exists a fault-free \(4\)-cycle \(C\) (or \(5\)-cycle) containing the edge \(u_Lu_R\).
Case 2.3.1.1. \(C=C^4=(u_L,s_L,s_R,u_R)\).
The proof is similar to Case 1.3.1.1.
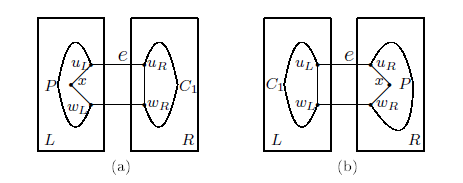
Case 2.3.1.2. \(C=C^5=(u_L,w_L,w_R,x,u_R)\).
For \(9\leq \ell \leq 2^{n-1}-|F^v_L|-1\). Let \(\ell=\ell'+3\), where \(6\leq \ell' \leq 2^{n-1}-|F^v_L|-4\). Since \(|F_L|\leq n-4\), by Lemma 2.10, there is a fault-free cycle \(C'\) of length \(\ell'\) containing the edge \(u_Lw_L\) in \(L-F_L\). Then \(C=C'-u_Lw_L+w_Lw_R+w_Rx+xu_R+u_Ru_L\) is a fault-free cycle of length \(\ell\) containing the edge \(e=u_Lu_R\).
For \(2^{n-1}-|F^v_L|\leq \ell \leq 2^{n-1}-1\). Let \(\ell=\ell_1+\ell_2+1\), where \(2^{n-2}-|F^v_L|-1\leq \ell_1\leq 2^{n-2}-2\) and \(\ell_2=2^{n-2}\). Since \(2^{n-2}-|F^v_L|-1>7\) for \(n \geq6\), by induction hypothesis, there exists a fault-free cycle \(C_1\) of length \(\ell_1\) containing the edge \(u_Lw_L\) in \(L-F_L\) and, by Lemma 2.11, there exists a fault-free \(u_Rw_R\)-path \(P\) of length \(\ell_2\) in \(R\). Then \(C=C_1-u_Lw_L+w_Lw_R+P+u_Ru_L\) is a fault-free cycle of length \(\ell\) containing the edge \(e=u_Lu_R\) in \(MQ_n\) (see Figure 7(b)).
Case 2.3.1.3. \(C=C^5=(u_L,x,w_L,w_R,u_R)\).
The proof is similar to Case 1.3.1.3.
Case 2.3.2. \(|F_R|= n-2\). In this case, \(|F_L|=0\).
Since \(|F_R|=n-2\), there exists a fault-free neighbor \(v_R\) of \(u_R\) in \(R\). Let \(v_L\) be the neighbor of \(v_R\) in \(L\). Let \(\ell=\ell'+3\), where \(6 \leq \ell' \leq 2^{n-1}-4\). By Lemma 2.4, \(d_{u_Lv_L}\leq2\). By Lemma 2.6, there is a fault-free \(u_Lv_L\)-path \(P\) of length \(\ell'\) in \(L\). So \(P+u_Lu_R+u_Rv_R+v_R v_L\) is a fault-free cycle of length \(\ell\) containing the edge \(u_Lu_R\).
The proof of the theorem is completed. ◻
As one of the most fundamental networks for parallel and distributed computation, cycles are suitable for developing simple algorithms with low communication cost. Edge and/or vertex failures are inevitable when a large parallel computer system is put in use. Therefore, the fault-tolerant capacity of a network is a critical issue in parallel computing. The fault-tolerant edge-pancyclicity of an interconnection network is a measure of its capability of implementing ring-structured parallel algorithms in a communication-efficient fashion in the presence of faults.
In view of the fact that the hypercube network \(Q_n\) contains only even cycles, \(MQ_n\) is superior to \(Q_n\) in fault-tolerant pancyclicity. This shows that, when the \(MQ_n\) is used to model the topological structure of a large-scale parallel processing system, our result implies that the system has larger capability of implementing ring-structured parallel algorithms in a communication-efficient fashion in the hybrid presence of edge and vertex failures than one of the hypercube network.
We make some remarks on the optimality of our result in the following sense.
For \(\ell=4\), in \(MQ_5^0\), taking \(e=(11011,11100)\), there are only two cycles: \((11011, 11010,\\ 11101, 11100)\), \((11011, 01011, 01100, 11100)\) of length 4 containing the edge \(e\) (we calculate it by computer).
If \(F=\{01011,11101\}\), then there exists no fault-free cycle of length 4 containing the edge \(e\) in \(MQ_5^0-F\). In \(MQ_5^1\), taking \(e=(11101,11110)\), there exists only one cycle \((11101,11100,11111,11110)\) of length 4 containing the edge \(e\). If \(F=\{11100\}\) or \(F=\{11111\}\), then there exists no fault-free cycle of length 4 containing the edge \(e\) in \(MQ_5^1-F\).
For \(\ell=5\), in \(MQ_5\), taking \(e=(11110,11111)\), the cycles of length 5 containing the edge \(e\) are as \(Table~1\) and \(Table~2\)(we calculate it by computer):
| (11110 11101 11010 11000 11111) | (11110 11101 10010 10000 11111) |
| (11110 11001 11011 11100 11111) | (11110 10001 10011 11100 11111) |
| (11110 11101 11010 11000 11111) | (11110 11101 10010 10000 11111) |
| (11110 11101 00010 00000 11111) | (11110 11001 11011 11100 11111) |
| (11110 10001 10011 11100 11111) | (11110 00001 00011 11100 11111) |
If \(F=\{11100,11101\}\), then there exists no fault-free cycle of length 5 containing the edge \(e\) in \(MQ_5-F\).
For \(\ell=6\), in \(MQ^0_n\), taking \(e=(01011,01100)\), the cycles of length 6 containing the edge \(e\) are as \(Table~3\)(we calculate it by computer):
| (01011 01010 01000 00000 00100 01100) | (01011 01010 01101 01110 01111 01100) |
| (01011 01010 01101 00101 00100 01100) | (01011 01010 01101 11101 11100 01100) |
| (01011 01010 00010 00000 00100 01100) | (01011 01010 11010 11011 11100 01100) |
| (01011 01010 11010 11101 11100 01100) | (01011 01010 11010 11101 01101 01100) |
| (01011 01001 01000 01010 01101 01100) | (01011 01001 01000 00000 00100 01100) |
| (01011 01001 00001 00000 00100 01100) | (01011 01001 00001 00101 00100 01100) |
| (01011 01001 00001 00101 01101 01100) | (01011 01001 11001 11011 11100 01100) |
| (01011 00011 00010 00000 00100 01100) | (01011 00011 00010 01010 01101 01100) |
| (01011 00011 00001 00000 00100 01100) | (01011 00011 00001 00101 00100 01100) |
| (01011 00011 00001 00101 01101 01100) | (01011 11011 11010 11101 11100 01100) |
| (01011 11011 11010 11101 01101 01100) | (01011 11011 11010 01010 01101 01100) |
| (01011 11011 11100 11101 01101 01100) | (01011 11011 11100 11111 01111 01100) |
If \(F=\{00100,01101,11100\}\), then there exists no fault-free cycle of length 6 containing the edge \(e\) in \(MQ_5^0-F\).
The research is supported by National Natural Science Foundation of China under Grant No.U22A2005, No. U21A20491, No. U1936109, No.U1908214, No. KLSA201906 and Key Research and Development Program of Zhejiang (2024SSYS0001).