In this paper, it is pointed out that the definition of `Fibonacci \((p,r)\)-cube’ in many papers (denoted by \(I\Gamma_{n}^{(p,r)}\)) is incorrect. The graph \(I\Gamma_{n}^{(p,r)}\) is not the same as the original one (denoted by \(O\Gamma_{n}^{(p,r)}\)) introduced by Egiazarian and Astola. First, it is shown that \(I\Gamma_{n}^{(p,r)}\) and \(O\Gamma_{n}^{(p,r)}\) have different recursive structure. Then, it is proven that all the graphs \(O\Gamma_{n}^{(p,r)}\) are partial cubes. However, only a small part of graphs \(I\Gamma_{n}^{(p,r)}\) are partial cubes. It is also shown that \(I\Gamma_{n}^{(p,r)}\) and \(O\Gamma_{n}^{(p,r)}\) have different medianicity. Finally, several questions are listed for further investigation.
Let \(B=\{0,1\}\) and for \(n\geq1\) set \[\mathcal{B}_{n}=\{b_{1}b_{2}\ldots b_{n}\mid b_{i}\in B, i\in1:n\}.\]
An element of \(\mathcal{B}_{n}\) is called a binary word of length \(n\) (or simply a word). All words considered of this paper are binary.
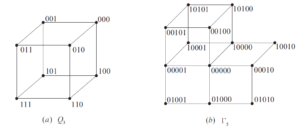
The \(n\)-dimensional hypercube \(Q_{n}\) is the graph whose vertex set is \(\mathcal{B}_{n}\), and two vertices are adjacent if and only if they differ in precisely one coordinate. The cube \(Q_{3}\) is shown in Figure 1\((a)\). Hypercubes play an important role in many areas of discrete mathematics and computer science. An excellent survey on hypercubes can be found in [15].
The Fibonacci cube \(\Gamma_{n}\) [7] can be obtained from \(Q_{n}\) by removing all vertices that contain two consecutive \(1\)s. It is a graph family that have been studied as alternatives for the classical hypercube topology for interconnection networks. The graph \(\Gamma_{5}\) is shown in Figure 1 \((b)\). For more results on application and structure of \(\Gamma_{n}\), see the survey [12] and the recent book [4].
When Fibonacci cubes were introduced, they soon became increasingly popular. Numerous variants and generalizations of Fibonacci cubes, the so called Fibonacci-like cube, are proposed and investigated such as in papers [1,5,8,17,20,26]. Recently, many other Fibonacci-like cubes have also been introduced and studied, such as generalized Fibonacci cubes [9], generalized Lucas cubes [10], daisy cubes [13], Pell graphs [16], Fibonacci-run graph [3], Fibonacci \(p\)-graph [23], Metallic cubes [2] and Lucas-run graph [22].
In the present paper, a special attention is given to the graphs called ‘Fibonacci \((p,r)\)-cubes’. It was first introduced by Egiazarian and Astola [5]. In many papers, such as [12,14,18,19,25] and others, although it is pointed out that the graphs studied comes from [5], we find that it is not the same as given in [5]. For convenience, the graphs studied in [5] are called \(O\)-Fibonacci \((p,r)\)-cubes, and the graphs studied in [12,14,18,19,25] are called \(I\)-Fibonacci \((p,r)\)-cubes.
Let \(p\geq1\) and \(r\geq1\). Then for \(n\geq1\), \(\alpha=a_{1}a_{2}\ldots a_{n}\) is called a \(O\)-Fibonacci \((p,r)\)-word ([5], where it is called Fibonacci \((p,r)\)-code) if the following hold:
(1) if \(a_{i}=1\) then \(a_{i+1}=\ldots=a_{i+(p-1)}=0\), i.e. there is at least \(p-1\) 0s between two 1s (which is called ‘consecutive’ 1s); and
(2) there are no more than \(r\) ‘consecutive’ 1s in \(\alpha\), i.e. ones, between which there are exactly \(p-1\) zeroes.
For examples, \((100)^{4}0^{3}(100)^{3}0(100)^{2}10\) is a \(O\)-Fibonacci \((3,4)\)-word of length \(33\), but \((100)^{4}0^{3}(100)^{5}010\) is not a \(O\)-Fibonacci \((3,4)\)-word.
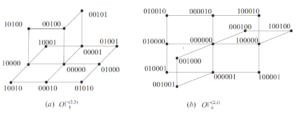
It is easily seen that if \((p,r)=(1,1)\), then a \(O\)-Fibonacci \((p,r)\)-word is a word that contain no two consecutive \(1\)s. Therefore, the \(O\)-Fibonacci \((1,1)\)-cube \(O\Gamma^{(1,1)}_{n}\) is just the classical Fibonacci cube \(\Gamma_{n}\). The graphs \(O\Gamma^{(2,2)}_{5}\) and \(O\Gamma^{(2,1)}_{6}\) are shown in Figure 2 \((a)\) and \((b)\), respectively.
As mentioned above, the ‘Fibonacci \((p,r)\)-cubes’ studied in [12,14,18,19,25] will be called \(I\)-Fibonacci \((p,r)\)-cubes. They are defined as follows.
Let \(p\), \(r\) and \(n\) be any positive integers. Then an \(I\)-Fibonacci \((p,r)\)-word of length \(n\) is a word of length \(n\) in which there are at most \(r\) consecutive 1s and at least \(p\) element \(0\)s between two sub-words composed of (at most \(r\)) consecutive 1s.
Note that the cubes \(I\Gamma_{n}^{(p,r)}\) is considered for \(n\geq p\) and \(n\geq r\) in the above papers. As \(I\Gamma_{n}^{(p,r)}\) is not always trivial for the case \(n<r\) or \(n<p\), we consider the graph \(I\Gamma_{n}^{(p,r)}\) for all \(p\geq1,r\geq1\) and \(n\geq1\) in this paper.
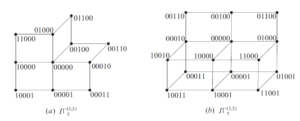
For examples, the graphs \(I\Gamma_{5}^{(3,2)}\) and \(I\Gamma_{5}^{(2,2)}\) are shown in Figure 3 \((a)\) and \((b)\), respectively. Obviously, \(I\)-Fibonacci \((1,1)\)-cube \(I\Gamma^{(1,1)}_{n}\) is just the classical Fibonacci cube \(\Gamma_{n}\).
We think that the main difference between the definitions of \(O\Gamma_{n}^{(p,r)}\) and \(I\Gamma_{n}^{(p,r)}\) is the meaning of ‘consecutive’ 1s: the \(r\) ‘consecutive 1s’ in a vertex of \(O\Gamma_{n}^{(p,r)}\) means the sub-word \((10^{p-1})^{r}\), but the \(r\) ‘consecutive 1s’ in a vertex of \(I\Gamma_{n}^{(p,r)}\) means the sub-word \(1^{r}\).
For a binary word \(\chi\), we set \(\chi^{0}=\lambda\), where \(\lambda\) is the empty word. For convenience, if \(n=0\), then let \(O\Gamma_{n}^{(p,r)}\) and \(I\Gamma_{n}^{(p,r)}\) be the graphs with only one vertex \(\lambda\).
Many Fibonacci like-cubes and some sub-cubes of hypercubes can be obtained from hypercubes by some word forbidden to appear in the words of hypercubes. From the point of view, the following note holds:
From Remark 1.3 and Definitions 1.1 and 1.2, \(O\Gamma_{n}^{(p,r)}\) and \(I\Gamma_{n}^{(p,r)}\) are not isomorphic in general. For example, \(O\Gamma_{5}^{(2,2)}\) (Figure 2 \((a)\)) is not isomorphic to \(I\Gamma_{5}^{(2,2)}\) (Figure 3 \((b)\)). This fact can be further illustrated by the results of Sections 3 and 4 in the paper.
The rest of the paper is organized as follows. In Sect. 2, some necessary definitions and known results are introduced. In Sect. 3, the recursive structures of \(O\Gamma_{n}^{(p,r)}\) and \(I\Gamma_{n}^{(p,r)}\) are given. In Sect. 4, the graphs \(O\Gamma_{n}^{(p,r)}\) and \(I\Gamma_{n}^{(p,r)}\) which are partial cube and median graphs are determined. In the last section, some questions on \(O\Gamma_{n}^{(p,r)}\) and \(I\Gamma_{n}^{(p,r)}\) are listed for further investigation.
In this section, some definitions, notion and results needed in the paper are given. Let \(\mathcal{A}\) be a set of some words. Then \(\alpha\mathcal{A}\) is the set of the words obtained from \(\mathcal{A}\) by appending a fixed word \(\alpha\) in front of each of the elements of \(\mathcal{A}\). Recall that Fibonacci numbers are defined as \(F_{0}=0,F_{1}=1\), and \(F_{n}=F_{n-1}+F_{n-2}\) for \(n\geq2\). Let \(\mathcal{F}_{n}\) be the vertex set of Fibonacci cube \(\Gamma_{n}\). sThen for \(n\geq2\) the well known decomposition of Fibonacci cube can be obtained as follows [7], where \(\mathcal{F}_{0}=\{\lambda\}\) and \(\mathcal{F}_{1}=\{0,1\}\): \[\label{2.1} \mathcal{F}_{n}=0\mathcal{F}_{n-1}\cup 10\mathcal{F}_{n-2}. \tag{1}\]
The name of the cubes \(\Gamma_{n}\) is justified with the fact that for any \(n\geq0\), \(|\mathcal{F}_{n}|=F_{n+2}\) [7]. By Eq. (1), the size of \(\Gamma_{n}\) can be shown in Eq. (2) for \(n\geq2\), and the recursive structure can be illustrated in Figure 4:
\[\label{2.2} |E(\Gamma_{n})|=|E(\Gamma_{n-1})|+|E(\Gamma_{n-2})|+F_{n}. \tag{2}\]
The distance \(d_{G}(\alpha,\) \(\beta)\) between vertices \(\alpha\) and \(\beta\) of a graph \(G\) is the length of a shortest \(\alpha,\beta\)-path. Given two words \(\alpha\) and \(\beta\) of the same length, their Hamming distance \(H(\alpha,\) \(\beta)\) is the number of coordinates in which they differ. Let \(H\) and \(G\) be arbitrary (connected) graphs. Then a mapping \(f: V(H)\rightarrow V(G)\) is an isometric embedding if \(d_{H}(u,v)=d_{G}(f(u),f(v))\) holds for any \(u,v\in V(H)\).
A partial cube is a connected graph that admits an isometric embedding into a hypercube [6]. It is well known that if \(\alpha\) and \(\beta\) are vertices of \(Q_{n}\), then \(d_{Q_{n}}(\alpha,\beta)=H(\alpha,\beta)\). So we know that if \(G\) is a partial cube, then \(d_{G}(\alpha,\beta)=H(\alpha,\beta)\) for any vertices \(\alpha\) and \(\beta\) of \(G\). There are more studies on determining which graphs are partial cubes. For example, some generalized Fibonacci and Lucas cubes [9,10] as partial cubes are shown in [21,24].
Let \(r\geq p+2\) and \(n\geq r\). Then for some \(t\) with \(p\leq t\leq r-2\), there exist vertices \(\alpha\) and \(\beta\) of \(I\Gamma_{n}^{(p,r)}\) such that \(10^{t}1\) and \(11^{t}1\) appear in the same coordinates of \(\alpha\) and \(\beta\), respectively. For convenience, we call there is a distance-barrier between the above vertices \(\alpha\) and \(\beta\). It can be shown that \(d_{I\Gamma_{n}^{(p,r)}}(\alpha,\beta)\neq H(\alpha,\beta)\) by Remark 1.3. By the following result we know that not all \(I\Gamma_{n}^{(p,r)}\) are partial cubes.
A median of vertices \(u, v,w \in V(G)\) is a vertex of \(G\) that simultaneously lies on a shortest \(u,v\)-path, a shortest \(u,w\)-path, and a shortest \(v,w\)-path. The graph \(G\) is called a median graph if every triple of its vertices has a unique median. It is well known that a median graph must be a partial cube ([6], Proposition 12.4), and hypercube \(Q_{n}\) is a median graph for every \(n\geq1\) ([6], Proposition 3.7).
A subgraph \(H\) of a graph \(G\) is median-closed if, with any triple of vertices of \(H\), their median is also in \(H\). The following result gives a useful tool to prove that a graph is a median graph ([6], Corollary 14.9).
It was shown that all Fibonacci cubes \(\Gamma_{n}\) are median graphs (of course are partial cubes) [11]. In this paper, the question for determining which \(O\Gamma_{n}^{(p,r)}\) and \(I\Gamma_{n}^{(p,r)}\) are partial cubes and median graphs is solved completely.
Now we turn to consider some basic properties of \(O\Gamma_{n}^{(p,r)}\) and \(I\Gamma_{n}^{(p,r)}\) in the rest of this section. By Definitions 1.1 and 1.2, the following results hold obviously.
\(O\Gamma_{n}^{(1,r)}\cong I\Gamma_{n}^{(1,r)}\cong Q_{n}\) for \(n\leq r\);
\(O\Gamma_{n}^{(1,1)}\cong I\Gamma_{n}^{(1,1)}\cong \Gamma_{n}\);
\(O\Gamma_{n}^{(p,r)}\cong O\Gamma_{n}^{(p,r')}\) for \(n\leq sp\), and \(O\Gamma_{n}^{(p,r)}\cong O\Gamma_{n}^{(p',r)}\) for \(n\leq t\); and
\(I\Gamma_{n}^{(p,r)}\cong I\Gamma_{n}^{(p,r')}\) for \(n\leq s\), and \(I\Gamma_{n}^{(p,r)}\cong I\Gamma_{n}^{(p',r)}\) for \(n\leq t+1\).
By Proposition 2.3 (1) and (2), \(O\Gamma_{n}^{(p,r)}\cong I\Gamma_{n}^{(p,r)}\) for some special \(p\) and \(r\). For examples, \(O\Gamma^{(1,3)}_{3}\cong I\Gamma_{3}^{(1,3)}\cong Q_{3}\) (as shown in Figure 1 \((a)\)) and \(O\Gamma^{(1,1)}_{5}\cong I\Gamma_{5}^{(1,1)}\cong \Gamma_{5}\) (as shown in Figure 1 \((b)\)). It is obvious that all those graphs are connected. In general, we have the following result.
Proof. First we show that \(I\Gamma_{n}^{(p,r)}\) is connected. It is obvious that \(0^{n}\) is a vertex of \(I\Gamma_{n}^{(p,r)}\) for any \(p,r\) and \(n\). We claim that every vertex \(\alpha\) of \(I\Gamma_{n}^{(p,r)}\) is connected with \(0^{n}\) by a \(\alpha,0^{n}\)-path. In fact, let \(\alpha=a_{1}a_{2}\ldots a_{n}\) be any vertex of \(I\Gamma_{n}^{(p,r)}\) differing from \(0^{n}\), and \(a_{i_{1}}=\ldots=a_{i_{t}}=1\), where \(t\geq1\) and \(i_{1}\leq\ldots\leq i_{t}\). Then the word \(\alpha_{j}\) obtained from \(\alpha\) by changing \(a_{i_{1}},\ldots,a_{i_{j}}\) from \(1\) to \(0\) is also a vertex of \(I\Gamma_{n}^{(p,r)}\), where \(j=1,\ldots,t\). Obviously, \(\alpha_{t}=0^{n}\). If \(j=1\), then \(\alpha\) and \(0^{n}\) are adjacent vertices. Now suppose that \(j\geq2\). Then \(\alpha\rightarrow\alpha_{1}\rightarrow \ldots\rightarrow\alpha_{j-1}\rightarrow 0^{n}\) is a path in \(I\Gamma_{n}^{(p,r)}\), and so \(I\Gamma_{n}^{(p,r)}\) is connected.
Similarly, we can show that \(O\Gamma_{n}^{(p,r)}\) is connected by the facts that \(0^{n}\) is a vertex of \(O\Gamma_{n}^{(p,r)}\), and for any vertex \(\alpha\) of \(O\Gamma_{n}^{(p,r)}\) differing from \(0^{n}\), there exist a \(\alpha,0^{n}\)-path. This completes the proof. ◻
Although some of the structure of \(O\Gamma_{n}^{(p,r)}\) was studied [5], we list them here to show they are different from that of \(I\Gamma_{n}^{(p,r)}\).
Recall that \(O\mathcal{F}_{n}^{(p, r)}\) and \(I\mathcal{F}_{n}^{(p, r)}\) are the vertex sets of \(O\Gamma_{n}^{(p,r)}\) and \(I\Gamma_{n}^{(p,r)}\), respectively.
In paper [5], it is shown that for \(n\geq pr+1\), the set \(O\mathcal{F}_{n}^{(p, r)}\) can be defined recursively by \[\label{3.1} O\mathcal{F}_{n}^{(p, r)}=\mathop{\bigcup}\limits^{r}_{i=0}(10^{p-1})^{i}0O\mathcal{F}_{n-pi-1}^{(p, r)}, \tag{3}\] with \(O\mathcal{F}_{0}^{(p, r)}=\{\lambda\}\). For example, the first five (from \(n=1\)) sets \(O\mathcal{F}_{n}^{(2, 2)}\) are thus:
\(\{0,1\},\)
\(\{00,01,10\},\)
\(\{000,001,010,100,101\},\)
\(\{0000,0001,0010,0100,0101,1000,1001,1010\},\)
\(\{00000,00001,00010,00100,00101,01000,01001,01010,10000,10001,10010,10100\}.\)
If \(p=1\) and \(r=1\), then we have \(O\mathcal{F}_{n}^{(1, 1)} =0O\mathcal{F}_{n-1}^{(1, 1)}\cup 10O\mathcal{F}_{n-2}^{(1, 1)}\) by Eq. (3). This means that Eq. (1) can be obtained from Eq. (3) by Proposition 2.3(2).
For convenience, if \(n\geq1\) and \(-p\leq n-pi-1<0\) for some \(i\) \((1\leq i\leq r)\), then let \((10^{p-1})^{i}0O\mathcal{F}_{n-pi-1}^{(p, r)}\) be the set containing only one word, and this word is the prefix of length \(n\) of \((10^{p-1})^{i}0\); if \(n-pi-1<-p\), then let \((10^{p-1})^{i}0O\mathcal{F}_{n-pi-1}^{(p, r)}=\emptyset\). This means that Eq. (3) also holds for \(1\leq n\leq pr\), and so we have \[\label{3.2} |O\mathcal{F}_{n}^{(p,r)}|=\mathop{\sum}\limits^{r}_{i=0}|O\mathcal{F}_{n-pi-1}^{(p, r)}|, \tag{4}\] where \(|O\mathcal{F}_{n-pi-1}^{(p, r)}|=1\) if \(-p\leq n-pi-1<0\), and \(|O\mathcal{F}_{n-pi-1}^{(p, r)}|=0\) if \(n-pi-1<-p\).
In paper [5], Fibonacci \((p,r)\)-number \(OF_{n}^{(p,r)}\) is defined as follows with \(OF_{n}^{(p,r)}=0\) if \(n\leq0\), and \(OF_{n}^{(p,r)}=1\) if \(1\leq n\leq p+1\): \[\label{3.3} OF_{n}^{(p,r)}=\mathop{\sum}\limits^{r}_{i=0}OF_{n-pi-1}^{(p, r)}. \tag{5}\]
It is easily seen that if \(p=r=1\), then \(OF_{n}^{(p,r)}=F_{n}\). By Eqs. (4) and (5), it is known that \(|V(O\Gamma_{n}^{(p,r)})|\)=\(|O\mathcal{F}_{n}^{(p, r)}|=OF_{n+p+1}^{(p, r)}\). By this result and Proposition 2.3(2), \(|V(\Gamma_{n})|=|\mathcal{F}_{n}|=|O\mathcal{F}_{n}^{(1, 1)}|=OF_{n+1+1}^{(1, 1)}=F_{n+2}\) holds for the classical Fibonacci cubes [7].
On the vertex set of \(I\Gamma_{n}^{(p,r)}\), we have the following result.
Proof. It is easy to see that \(I\mathcal{F}_{n}^{(p,r)} \supseteq 0I\mathcal{F}_{n-1}^{(p,r)}\cup 10^{p}I\mathcal{F}_{n-p-1}^{(p,r)}\cup\ldots \cup 1^{r}0^{p}I\mathcal{F}_{n-p-r}^{(p,r)}\). Let \(\alpha\in I\mathcal{F}_{n}^{(p,r)}\) and suppose that the coordinate of the first 0 of \(\alpha\) is \(i\). Then \(1\leq i\leq r+1\) by the definition of \(I\)-Fibonacci \((p,r)\)-word and then the following holds. If \(i=1\), then \(\alpha=0\beta\) for some \(\beta\in I\mathcal{F}_{n-1}^{(p,r)}\). If \(2\leq i\leq r+1\), then \(\alpha\) has the form of \(1^{i-1}0^{p}\gamma\), where \(\gamma\in I\mathcal{F}_{n-p-(i-1)}^{(p,r)}\). It implies that \(I\mathcal{F}_{n}^{(p,r)} \subseteq 0I\mathcal{F}_{n-1}^{(p,r)}\cup 10^{p}I\mathcal{F}_{n-p-1}^{(p,r)}\cup\ldots \cup 1^{r}0^{p}I\mathcal{F}_{n-p-r}^{(p,r)}\). This completes the proof. ◻
It is easy to see that if \(p=1\) and \(r=1\), then Eq. (1) can be obtained from Eq. (6) by Proposition 2.3 (2).
For convenience, if \(1\leq n<p+i\) for some \(i\in[r]\), then let \(1^{i}0^{p}I\mathcal{F}_{n-p-i}^{(p,r)}\) be the set consisting of only the word which is the prefix of length \(n\) of \(1^{i}0^{p}\). It can be seen that if \(i<j\) and \(n<p+i\), then \(1^{i}0^{p}I\mathcal{F}_{n-p-i}^{(p,r)}=1^{j}0^{p}I\mathcal{F}_{n-p-j}^{(p,r)}\). So for \(n<i\), let \(1^{i}0^{p}I\mathcal{F}_{n-p-i}^{(p,r)}=\emptyset\). Then for \(1\leq n<p+r\), the set \(I\mathcal{F}_{n}^{(p,r)}\) also can be determined by Eq. (6).
For example, the first few \(I\mathcal{F}_{n}^{(2,2)}\) are thus:
\(I\mathcal{F}_{1}^{(2,2)}=\{0,1\},\)
\(I\mathcal{F}_{2}^{(2,2)}=\{00,01,10,11\},\)
\(I\mathcal{F}_{3}^{(2,2)}=\{000,001,010,011,100,110\},\)
\(I\mathcal{F}_{4}^{(2,2)}=\{0000,0001,0010,0011,0100,0110,1000,1001,1100\},\)
\(I\mathcal{F}_{5}^{(2,2)}=\{00000,00001,00010,00011,00100,00110,01000,01001,01100,10000,10001,\)
\(10010,10011,11000,11001\}.\)
By Theorem 3.1 and the above analysis, the following result holds.
By Eqs. (3) and (6), it is easy to see that if \(p=1\) or \(r=1\), then \(O\mathcal{F}_{n}^{(p,r)}= I\mathcal{F}_{n}^{(p,r)}\) and so \(O\Gamma_{n}^{(p,r)}\cong I\Gamma_{n}^{(p,r)}\). For \(p>1\), \(r>1\) and \(n=0\) or \(1\), \(O\mathcal{F}_{n}^{(p,r)}= I\mathcal{F}_{n}^{(p,r)}\) and \(O\Gamma_{n}^{(p,r)}\cong I\Gamma_{n}^{(p,r)}\). But for \(n>1\), \(|I\mathcal{F}_{n}^{(p,r)}|>|O\mathcal{F}_{n}^{(p,r)}|\) by Eqs. (4) and (7). So the following result holds.
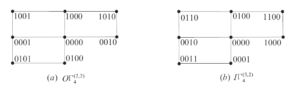
The above result implies that \(O\Gamma_{n}^{(p,r)}\not\cong I\Gamma_{n}^{(p,r)}\) from the general sense. However, there are exist some \(p>1\) and \(p'>1\), \(r>1\) and \(r'>1\), and \(n>1\) and \(n'>1\) such that \(O\Gamma_{n}^{(p,r)}\cong I\Gamma_{n'}^{(p',r')}\). For example, it can be shown that \(O\Gamma_{4}^{(2,2)}\cong I\Gamma_{4}^{(3,2)}\), as illustrated in Figure 5.
The recursive structure on the edge sets of \(O\Gamma_{n}^{(p,r)}\) and \(I\Gamma_{n}^{(p,r)}\) are studied in this subsection.
We show that the iterative formula of the size of \(O\Gamma_{n}^{(p,r)}\) previously given ([5], Property 2) was erroneous and determine its correct expression. First we take \(O\Gamma_{n}^{(2,3)}\) as an example to understand easily the structure of the edge set of \(O\Gamma_{n}^{(p,r)}\). By Eq. (3), for \(n\geq7\), \(O\mathcal{F}_{n}^{(2, 3)} =0O\mathcal{F}_{n-1}^{(2, 3)}\cup 100O\mathcal{F}_{n-3}^{(2,3)}\cup 10100O\mathcal{F}_{n-5}^{(2,3)}\cup 1010100O\mathcal{F}_{n-7}^{(2,3)}\).
Inside each subgraph of \(O\Gamma_{n}^{(p,r)}\) induced by \((10)^{t}0O\mathcal{F}_{n-2t-1}^{(2,3)}\) the edges are inherited from \(O\Gamma_{n-2t-1}^{(2,3)}\), \(t=0,1,2\) and \(3\). We need to determine the edges between these four subgraphs. Let \(0\leq i<j\leq 3\). Then by the fact \(0(10)^{j-i-1}0O\mathcal{F}_{n-2j-1}^{(2,3)}\subseteq O\mathcal{F}_{n-2i-1}^{(2,3)}\), it is known that \((10)^{i}00(10)^{j-i-1}0O\mathcal{F}_{n-2j-1}^{(2,3)}\) is a subset of \((10)^{i}0O\mathcal{F}_{n-2i-1}^{(2,3)}\). It is easily seen that \((10)^{j}0O\mathcal{F}_{n-2j-1}^{(2,3)}=(10)^{i}10(10)^{j-i-1}0O\mathcal{F}_{n-2j-1}^{(2,3)}\). Let \(\alpha\) be a vertex of \((10)^{j}0O\mathcal{F}_{n-2j-1}^{(2,3)}\). Then \(\alpha=(10)^{i}10(10)^{j-i-1}0\beta\) for some \(\beta\in O\mathcal{F}_{n-2j-1}^{(2,3)}\). Obviously, there exist a vertex \(\alpha'=(10)^{i}00(10)^{j-i-1}0\beta\in O\mathcal{F}_{n-2i-1}^{(2,3)}\), and so \(\alpha\) is adjacent to \(\alpha'\). Therefore, there are \(|O\mathcal{F}_{n-2j-1}^{(2,3)}|\) edges between the subsets \((10)^{j}0O\mathcal{F}_{n-2j-1}^{(2,3)}\) and \((10)^{i}0O\mathcal{F}_{n-2i-1}^{(2,3)}\). So we know that the decomposition of \(O\Gamma_{n}^{(2,3)}\) can be shown as in Figure 6, and
\[\begin{aligned} |E(O\Gamma_{n}^{(2,3)})| &= |E(O\Gamma_{n-1}^{(2,3)})| + |E(O\Gamma_{n-3}^{(2,3)})| \\ &\quad + |E(O\Gamma_{n-5}^{(2,3)})| + |E(O\Gamma_{n-7}^{(2,3)})| \\ &\quad + |O\mathcal{F} {n-3}^{(2,3)}| + 2|O\mathcal{F} {n-5}^{(2,3)}| + 3|O\mathcal{F} {n-7}^{(2,3)}| \\ &= \mathop{\sum}\limits^{3} {t=0} \left( |E(I\Gamma_{n-2t-1}^{(2,3)})| + t|V(I\Gamma_{n-2t-1}^{(2,3)})| \right). \end{aligned}\]
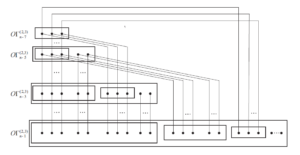
In general, we can get the structure of the edge set of \(O\Gamma_{n}^{(p,r)}\) as follows. By Eq. (3) we know that the vertex set of \(O\Gamma_{n}^{(p,r)}\) can be decomposed into \(r+1\) disjoint subsets for \(n\geq pr+1\): \(O\mathcal{F}_{n}^{(p,r)} =\mathop{\bigcup}\limits^{r}_{t=0}(10^{p-1})^{t}0O\mathcal{F}_{n-pt-1}^{(p,r)}\). So the graph \(O\Gamma_{n}^{(p,r)}\) can be decomposed into \(r+1\) disjoint subgraphs isomorphic to \(O\Gamma_{n-tp-1}^{(p,r)}\) for \(t=0,1,\ldots,r\), respectively. Further, for \(0\leq i< j\leq r\), it can be found that there are \(|V(O\Gamma_{n-jp-1}^{(p,r)})|=|O\mathcal{F}_{n-jp-1}^{(p,r)}|\) edges connecting the subgraphs \(O\Gamma_{n-ip-1}^{(p,r)}\) and \(O\Gamma_{n-jp-1}^{(p,r)}\) (of \(O\Gamma_{n}^{(p,r)}\)). So there are \(\mathop{\sum}\limits^{r}_{t=0}(t|O\mathcal{F}_{n-pt-1}^{(p,r)}|)\) edges between these \(r+1\) subgraphs. So we have the following result.
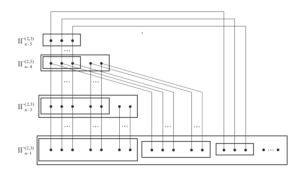
First, we also take \(I\Gamma_{n}^{(2,3)}\) as an example to better understand the structure of the edge set of \(O\Gamma_{n}^{(p,r)}\). By Eq. (6), we know that \(I\mathcal{F}_{n}^{(2,3)}\) can be decomposed into four disjoint subsets for \(n\geq5\): \(0I\mathcal{F}_{n-1}^{(2,3)}\), \(100I\mathcal{F}_{n-3}^{(2,3)}\), \(1100I\mathcal{F}_{n-4}^{(2,3)}\) and \(11100I\mathcal{F}_{n-5}^{(2,3)}\).
Inside each subgraph of \(I\Gamma_{n}^{(p,r)}\) induced by \(0I\mathcal{F}_{n-1}^{(2,3)}\) and \(1^{t}00I\mathcal{F}_{n-2-t}^{(2,3)}\) (\(t\in[3]\)) the edges are inherited from \(I\Gamma_{n-1}^{(2,3)}\) and \(I\Gamma_{n-2-t}^{(2,3)}\), respectively. Now we consider the edges between the above four subsets. It is easily seen that \(01^{t-1}00I\mathcal{F}_{n-2-t}^{(2,3)}\subset 0I\mathcal{F}_{n-1}^{(2,3)}\). So for every vertex \(\alpha\in1^{t}00I\mathcal{F}_{n-2-t}^{(2,3)}\), there exist a vertex \(\alpha'\in01^{t-1}00I\mathcal{F}_{n-2-t}^{(2,3)}\) such that there is an edge between \(\alpha\) and \(\alpha'\). So there are \(|I\mathcal{F}_{n-2-t}^{(2,3)}|\) edges between \(1^{t}00I\mathcal{F}_{n-2-t}^{(2,3)}\) and \(0I\mathcal{F}_{n-1}^{(2,3)}\) for \(t\in[3]\). Suppose \(1\leq i< j\leq 3\), \(\beta\in1^{j}00I\mathcal{F}_{n-2-j}^{(2,3)}\) and \(\beta'\in1^{i}00I\mathcal{F}_{n-2-i}^{(2,3)}\). If \(j-i\geq2\), then \(\beta\) and \(\beta'\) are not adjacent in \(I\Gamma_{n}^{(p,r)}\). If \(j=i+1\), then by the fact \(1^{j-1}000I\mathcal{F}_{n-2-j}^{(2,3)}\subset 1^{i}00I\mathcal{F}_{n-2-i}^{(2,3)}\), we know that there exist a vertex \(\beta''\in1^{i}00I\mathcal{F}_{n-2-i}^{(2,3)}\) such that \(\beta'\) and \(\beta''\) are adjacent in \(I\Gamma_{n}^{(p,r)}\). This implies that for \(1\leq i< j\leq 3\), there exist edges between \(1^{j}00I\mathcal{F}_{n-2-j}^{(2,3)}\) and \(1^{i}00I\mathcal{F}_{n-2-i}^{(2,3)}\) only if \(j=i+1\), and there are \(|I\mathcal{F}_{n-2-j}^{(2,3)}|\) edges between them. Hence, we know that the decomposition of \(I\Gamma_{n}^{(2,3)}\) can be shown as in Figure 7, and \(|E(I\Gamma_{n}^{(2,3)})|=|E(I\Gamma_{n-1}^{(2,3)})|+ \mathop{\sum}\limits^{3}_{t=1}(|E(I\Gamma_{n-2-t}^{(2,3)})|+2|I\mathcal{F}_{n-2-t}^{(2,3)})|) -|I\mathcal{F}_{n-3}^{(2,3)}|\).
In general, we have the following result.
Proof. By Eq. (6), \(I\mathcal{F}_{n}^{(p,r)}=0I\mathcal{F}_{n-1}^{(p,r)}\cup 10^{p}I\mathcal{F}_{n-p-1}^{(p,r)}\cup\ldots \cup 1^{r}0^{p}I\mathcal{F}_{n-p-r}^{(p,r)}\). So the graph \(I\Gamma_{n}^{(p,r)}\) can be decomposed into \(r+1\) disjoint subgraphs isomorphic to \(I\Gamma_{n-1}^{(p,r)}\) (induced by the set \(0I\mathcal{F}_{n-1}^{(p,r)}\)) and \(I\Gamma_{n-p-t}^{(p,r)}\) (induced by the set \(1^{t}0^{p-1}I\mathcal{F}_{n-p-t}^{(p,r)}\)) for \(t\in[r]\), respectively. To achieve the desired result, we need to consider the edges between the above subgraphs. First, we consider \(0I\mathcal{F}_{n-1}^{(p,r)}\) and \(1^{t}0^{p}I\mathcal{F}_{n-p-t}^{(p,r)}\), \(t\in[r]\). Let \(\alpha\) be a vertex of \(1^{t}0^{p}I\mathcal{F}_{n-p-t}^{(p,r)}\). Then \(\alpha=1^{t}0^{p}\alpha'\) for some \(\alpha'\in I\mathcal{F}_{n-p-t}^{(p,r)}\). It can be seen that the vertex \(\beta=01^{t-1}0^{p}\alpha'\in 0I\mathcal{F}_{n-1}^{(p,r)}\), and so there are \(|I\mathcal{F}_{n-p-t}^{(p,r)}|\) edges between \(0I\mathcal{F}_{n-1}^{(p,r)}\) and \(1^{t}0^{p}I\mathcal{F}_{n-p-t}^{(p,r)}\). Now we consider the edges between \(1^{i}0^{p}I\mathcal{F}_{n-p-i}^{(p,r)}\) and \(1^{j}0^{p}I\mathcal{F}_{n-p-j}^{(p,r)}\) for \(1\leq i<j\leq r\). Obviously, if \(j\geq i+2\), then there is not edges between them. Suppose \(j=i+1\) and let \(\alpha\in 1^{j}0^{p}I\mathcal{F}_{n-p-j}^{(p,r)}\). Then \(\alpha=1^{j}0^{p}\alpha'=1^{i}10^{p}\alpha'\) for some \(\alpha'\in I\mathcal{F}_{n-p-j}^{(p,r)}\). As \(\beta=1^{i}00^{p}\alpha'\in 1^{i}0^{p}I\mathcal{F}_{n-p-i}^{(p,r)}\) and \(\alpha\) and \(\beta\) are adjacent, we know that there are \(|I\mathcal{F}_{n-p-j}^{(p,r)}|\) edges between \(1^{i}0^{p}I\mathcal{F}_{n-p-i}^{(p,r)}\) and \(1^{j}0^{p}I\mathcal{F}_{n-p-j}^{(p,r)}\) for \(j=i+1\). Therefore, there are altogether \(2\mathop{\sum}\limits^{r}_{t=1}|I\mathcal{F}_{n-p-t}^{(p,r)}|-|I\mathcal{F}_{n-p-1}^{(p,r)}|\) edges connecting these \(r+1\) subgraphs. This completes the proof. ◻
If \(p=1\) and \(r=1\), then by Eqs. (8) and (9) we have \[\begin{aligned}|E(O\Gamma_{n}^{(1,1)})| =&|E(O\Gamma_{n-1}^{(1,1)})|+|E(O\Gamma_{n-2}^{(1,1)})|+|O\mathcal{F}_{n-2}^{(1,1)}|, and\\ |E(I\Gamma_{n}^{(1,1)})|=&|E(I\Gamma_{n-1}^{(1,1)})|+ |E(I\Gamma_{n-2}^{(1,1)})|+|I\mathcal{F}_{n-2}^{(1,1)}|,\end{aligned}\] respectively. This means that Eq. (2) can be obtained from both Eqs. (8) and (9).
Both partial cubes and median graphs are important and well-studied classes of graphs. The graphs \(I\Gamma_{n}^{(p,r)}\) and \(O\Gamma_{n}^{(p,r)}\) which are partial cubes and median graphs are determined.
Both graphs \(O\Gamma_{n}^{(p,r)}\) and \(I\Gamma_{n}^{(p,r)}\) are induced subgraphs of hypercubes. It is natural to ask whether they can be isometrically embedded into hypercubes. First we consider \(O\Gamma_{n}^{(p,r)}\).
Proof. Let \(\alpha=a_{1}a_{2}\ldots a_{n}\) and \(\beta=b_{1}b_{2}\ldots b_{n}\) be any two vertices of \(O\Gamma_{n}^{(p,r)}\). Suppose that the Hamming distance \(H(\alpha,\beta)\) between \(\alpha\) and \(\beta\) is \(s\), and \(a_{i_{j}}\neq b_{i_{j}}\) for all \(j\in [s].\) The desired result can be obtained by showing \(d_{O\Gamma_{n}^{(p,r)}}(\alpha,\beta)=H(\alpha,\beta)\) for all \(s\geq1\). This can be shown by using induction on \(s\). Obviously if \(s=1\), then \(d_{O\Gamma_{n}^{(p,r)}}(\alpha,\beta)=1=H(\alpha,\beta)\) by Definition 1.1. Suppose that \(s\geq2\) and \(d_{O\Gamma_{n}^{(p,r)}}(\mu,\nu)=H(\mu,\nu)\) holds for any two vertices \(\mu\) and \(\nu\) of \(O\Gamma_{n}^{(p,r)}\) with \(H(\mu,\nu)=s-1\). Without loss of generality, suppose that \(a_{i_{1}}=1\) and \(b_{i_{1}}=0\). Let \(\alpha'\) be the word obtained from \(\alpha\) by changing \(a_{i_{1}}\) from \(1\) to \(0\). Then \(H(\alpha,\alpha')=1\), \(H(\alpha',\beta)=s-1\) and \(\alpha'\) is a \(O\)-Fibonacci \((p,r)\)-word of length \(n\), that is, \(\alpha'\in O\mathcal{F}_{n}^{(p,r)}\). As \(d_{O\Gamma_{n}^{(p,r)}}(\alpha',\beta)=H(\alpha',\beta)=s-1\) by the induction hypothesis, we know \(d_{O\Gamma_{n}^{(p,r)}}(\alpha,\beta)=H(\alpha,\alpha')+H(\alpha',\beta)=1+s-1=s\). This completes the proof. ◻
By Theorem 4.1, all \(O\Gamma_{n}^{(p,r)}\) are partial cubes. However, this does not hold for \(I\Gamma_{n}^{(p,r)}\). For \(n\geq p\) and \(n\geq r\), the cubes \(I\Gamma_{n}^{(p,r)}\) which are partial cubes have been determined [25]. Now for all the cases \(n\geq 1\), \(p\geq1\) and \(r\geq1\), the results are listed as follows.
\((a)\) \(p=1\), \(r\geq1\), and \(n\geq1;\)
\((b)\) \(p \geq 2\), \(r \leq p+1\) and \(n\geq1;\) and
\((c)\) \(p\geq 2\), \(r\geq p+2\) and \(n<r\).
Proof. First we consider the case \(p=1\) and \(r\geq1\). If \(n\geq r\), then \(I\Gamma_{n}^{(1,r)}\) is a partial cube ([25], Lemma 2.2). If \(n< r\), then \(I\Gamma_{n}^{(p,r)}\cong Q_{n}\) by Proposition 2.3, and so \(I\Gamma_{n}^{(p,r)}\) is a partial cube. It means that if \((a)\) holds, then \(I\Gamma_{n}^{(1,r)}\) is a partial cube.
If \(p \geq 2\) and \(r \leq p+1\), then it is obvious that there is not a distance-barrier between any two vertices of \(I\Gamma_{n}^{(p,r)}\). So if \((b)\) holds, then \(I\Gamma_{n}^{(1,r)}\) is partial cube by Lemma 2.1.
Now we turn to consider the case \(p\geq 2\) and \(r\geq p+2\). If \(n\geq r\), then it was shown that \(I\Gamma_{n}^{(p,r)}\) is not a partial ([25], Lemma 2.5). If \(n< r\), then there is not a distance-barrier between any two vertices of \(I\Gamma_{n}^{(p,r)}\), and so \(I\Gamma_{n}^{(p,r)}\) is a partial cube by Lemma 2.1.
According to the above analysis, \(I\Gamma_{n}^{(p,r)}\) is a partial cube if and only if one of \((a),(b)\) and \((c)\) holds. ◻
It is well known that a median graph must be a partial cube. In this subsection, we show that \(O\Gamma_{n}^{(p,r)}\) (resp. \(I\Gamma_{n}^{(p,r)}\)) being median graphs is only a small part of the \(O\Gamma_{n}^{(p,r)}\) (resp. \(I\Gamma_{n}^{(p,r)}\)) which are partial cubes.
Note that for \(n\geq p\) and \(n\geq r\), the graphs \(I\Gamma_{n}^{(p,r)}\) which are median graphs has been determined [8]. For the cases \(p\geq 1\), \(r\geq 1\) and \(n\geq 1\), graphs \(I\Gamma_{n}^{(p,r)}\) as median graphs are list as follows.
\((a)\) \(p=1\), \(r\geq2\) and \(r\geq n\geq1\);
\((b)\) \(p\geq2\), \(r\geq3\) and \(2\geq n\geq1\); and
\((c)\) \(r\leq\) \(p\), \(r\leq\) \(2\) and \(n\geq1\).
Proof. We distinguish three cases: (1) \(p=1\) and \(r\geq2\), (2) \(p\geq2\) and \(r\geq3\), and (3) \(r\leq p\) and \(r\leq\) \(2\). It has been shown that if (1) or (3) holds for \(n\geq p\) and \(n\geq r\), or (2) hold for \(n\geq 3\), then \(I\Gamma_{n}^{(p,r)}\) is not a median graph ([25], Lemma 4.2 and Corollary 4.4).
If (1) holds and \(n<r\), then \(I\Gamma_{n}^{(p,r)}\cong Q_{n}\) by Proposition 2.3(1). It is obvious that if (2) happens and \(2\geq n\geq1\), then \(I\Gamma_{n}^{(p,r)}\cong Q_{n}\). It is well known that \(Q_{n}\) is a median graph. If \(n<p\) and (3) holds, then \(I\Gamma_{n}^{(p,r)}\cong I\Gamma_{n}^{(n,r)}\) by Proposition 2.3 (3). It has been known that \(I\Gamma_{n}^{(n,r)}\) is a median graph if (3) happens ([25], Corollary 4.4). According to the above analysis, \(I\Gamma_{n}^{(p,r)}\) is a median graph if and only if \((a)\), \((b)\), or \((c)\) holds. ◻
The following result determines the graphs \(O\Gamma_{n}^{(p,r)}\) which are median graphs.
\((a')\) \(p\geq1,r=1\) and \(n\geq1\);
\((b')\) \(p=1,r\geq2\) and \(r\geq n\geq1\); and
\((c')\) \(p\geq2\), \(r\geq2\) and \(n\leq pr\).
Proof. We also distinguish three cases by \(p\) and \(r\): \((1')\) \(p\geq1\) and \(r=1\), \((2')\) \(p=1\) and \(r\geq2\), and \((3')\) \(p\geq2\) and \(r\geq2\). By Corollary 3.3, we know that \(O\Gamma_{n}^{(1,r)}\cong I\Gamma_{n}^{(1,r)}\) and \(O\Gamma_{n}^{(p,1)}\cong I\Gamma_{n}^{(p,1)}\). So if \((a')\) or \((b')\) holds, then \(O\Gamma_{n}^{(p,r)}\) is a median graph by Theorem 4.3 \((a)\) and \((c)\). Now we turn to consider case \((3')\). For the case \(p\geq2\), \(r\geq2\) and \(n\leq pr\), let
\[\begin{aligned}\chi=&x_{1}x_{2}\ldots x_{n},\\\eta=&y_{1}y_{2}\ldots y_{n},\\\rho=&p_{1}p_{2}\ldots p_{n},\end{aligned}\] and \[\begin{aligned}\omega=&w_{1}w_{2}\ldots w_{n},\end{aligned}\] where \(\chi,\eta\) and \(\rho\) are vertices of \(O\Gamma_{n}^{(p,r)}\), and \(\omega\) is the median of \(\chi,\eta\) and \(\rho\). It is well known that the median of the triple in \(Q_{n}\) is obtained by the majority rule ([6], Proposition 3.7): the \(i\)th coordinate of the median is equal to the element that appears at least twice among the \(x_{i}\), \(y_{i}\), and \(p_{i}\). Without loss of generality, suppose that among \(x_{1}\), \(y_{1}\) and \(p_{1}\) there at least two \(1s\). Then \(w_{1}=1\). Suppose the second \(1\) contained in \(\omega\) is \(w_{i}\). As \(\chi,\eta\) are vertices of \(O\Gamma_{n}^{(p,r)}\) and there are at least two \(1\) among \(x_{i},y_{i}\) and \(p_{i}\), we know \(i\geq p+1\). By considering the coordinate of the next element 1 in \(\omega\), we can find that the number of \(0s\) between two \(1\) is at least \(p-1\) in \(\omega\). Since the length of \(\omega\) is not more than \(pr\), there are at most \(r\) continue ‘1’ in \(\omega\). Therefore, \(\omega\) is a vertex of \(O\Gamma_{n}^{(p,r)}\), and so \(O\Gamma_{n}^{(p,r)}\) is a median graph for this case.
For any \(p\geq2\), \(r\geq2\) and \(n> pr\), let
\[\begin{aligned}\alpha=&10^{p-1}10^{p-1}0(0^{p-1}1)^{r-2}0^{n-pr-1},\\\beta=&10^{p-1}00^{p-1}1(0^{p-1}1)^{r-2}0^{n-pr-1},\end{aligned}\] and \[\begin{aligned}\gamma=&00^{p-1}10^{p-1}1(0^{p-1}1)^{r-2}0^{n-pr-1}.\end{aligned}\]
Then \(\alpha,\beta\) and \(\gamma\) are vertices of \(O\Gamma_{n}^{(p,r)}\). Set
\[\mu=10^{p-1}10^{p-1}1(0^{p-1}1)^{r-2}0^{n-pr-1}.\]
It is easy to see that \(\alpha,\beta\) and \(\gamma\) are pairwise at distance 2 in \(O\Gamma_{n}^{(p,r)}\). By the majority rule, the unique candidate for their median is \(\mu\). Since there are \(r+1\) ‘consecutive’ 1s in \(\mu\), it does not belong to \(O\Gamma_{n}^{(p,r)}\) and so \(O\Gamma_{n}^{(p,r)}\) is not median-closed induced subgraph of hypercube. Hence, \(O\Gamma_{n}^{(p,r)}\) is not a median graph by Theorem 2.2 for this case. This completes the proof. ◻
In this section, two questions are listed for further study of \(O\Gamma_{n}^{(p,r)}\) and \(I\Gamma_{n}^{(p,r)}\).
Corollary 3.3 shows that \(O\Gamma_{n}^{(p,r)}\not\cong I\Gamma_{n}^{(p,r)}\) for almost all of \(p\) and \(r\). However, there may be some \(p,r,n\) and \(p',r',n'\) such that \(O\Gamma_{n}^{(p,r)}\cong I\Gamma_{n'}^{(p',r')}\). As an example, \(O\Gamma_{4}^{(2,2)}\cong I\Gamma_{4}^{(3,2)}\) is shown in Figure 5. A natural question that arises is the following:
The eccentricity \(e(v)\) of a vertex \(v\) of a graph \(G\) is the maximum of its distances to other vertices in \(G\), and the diameter \(d(G)\) of \(G\) are the maximum of the vertex eccentricities. The diameter of \(O\Gamma_{n}^{(p,r)}\) was determined ([5], Property 4). But the diameter of \(I\Gamma_{n}^{(p,r)}\) has not been studied. So the following questions are listed.
As mentioned above the diameter of a graph \(G\) is the greatest distance between any two vertices in \(G\). Theorem 4.1 shows that every graph \(O\Gamma_{n}^{(p,r)}\) is a partial cube, and so the distance between any two vertices of \(O\Gamma_{n}^{(p,r)}\) is the Hamming distance of them. However, Theorem 4.2 shows that only a small part of all graphs \(I\Gamma_{n}^{(p,r)}\) are partial cube. Therefore, it seems that determining the diameter of \(I\Gamma_{n}^{(p,r)}\) is a rather difficult task.
The author declares no conflict of interest.
1970-2025 CP (Manitoba, Canada) unless otherwise stated.