Let \( G \) be a graph, the zero forcing number \( Z(G) \) is the minimum of \( |Z| \) over all zero forcing sets \( Z \subseteq V(G) \). In this paper, we are interested in studying the zero forcing number of quartic circulant graphs \( C_{p}\left(s,t\right) \), where \( p \) is an odd prime. Based on the fact that \( C_{p}\left(s,t\right) \cong C_{p}\left(1,q\right) \), we give the exact values of the zero forcing number of some specific quartic circulant graphs.
In this paper, all graphs considered are finite, undirected and simple. For any terminology used but not defined here, one may refer to [5].
Graph parameters have many application in some science trends. As one of the most important, it can be zero forcing number. Also, zero forcing number have applications in power domination problem, logic circuits, information in social networks and so on, see [6,4,14]. We now formally introduce its definition. Let \(G\) be a graph and \(Z\) be an subset of \(V(G)\). Color the vertices of \(Z\) and \(V(G)\setminus Z\) black and white initially, respectively. A forcing process is defined as follows: for a black vertex \(u\) of \(V(G)\), if \(u\) has exactly one white neighbor \(v\), then reassign \(v\) black. At the time, we say \(u\) forces \(v\) and denote it by \(u \rightarrow v\). The subset \(Z\) is called a zero forcing set, if all vertices in \(V(G)\setminus Z\) are forced black by repeatedly applying the forcing process. The zero forcing number of \(G\) is the minimum of \(|Z|\) over all zero forcing sets \(Z\subseteq V(G)\), denoted by \(Z(G)\).
The computation of zero forcing number is NP-hard, see [9]. It has attracted many scholars, and a lot of results are obtained in the field. In [1], some elementary results of graphs regarding zero forcing are obtained, such as, trees, Cartesian products of two paths. Kalinowski et al. ([16]) showed that \(Z(G)\geq n(1+\frac{2\lambda_{min}}{d-\lambda_{min}} )\) if \(G\) is \(d\)-regular. In [3], if a graph \(G\) has the minimum and maximum degree \(\delta\) and \(\Delta\) respectively, then the zero forcing number of a graph \(G\) with \(n\) vertices can be as \(\delta \le Z(G)\le\frac{n\Delta}{\Delta +1}\). In addition, Meyer [20] obtained upper and lower bounds for \(Z(G)\) when \(G\) is a bipartite circulant and showed which graphs achieve the equality in the lower bound. From these references, we can find that, even for some special graphs, it seems to be impossible to determine the exact number of zero forcing number. Note that, Riddell [23] obtained some results of the zero forcing number on cubic circulant graphs. Hence determining the zero forcing number for all quartic circulant graphs is an interesting and challenging problem. For more details on zero forcing, see [9,10,12,13,19,24,7,25].
Given an integer \(n\ge2\) and a subset \(S\subseteq\left\{1,2,…,\left\lfloor\dfrac{n}{2}\right\rfloor\right\}\), a circulant graph \(G=C_{n}(S)\) is formally defined as a graph with vertex set \(V(G)=\{0, 1,…, n-1\}\) and edge set \(E(G)=\{\{ i, i \pm j\} \vert i\in\{0,…, {n-1}\}\) and \(j \in S \}\), where \(i\), \(j\) and \(i\pm j\) are taken modulo \(n\). Note that if \(S = \{s_{1},…, s_{t}\}\), then we can always assume that \(s_{1} < s_{2} <…<s_{t}\). In particular, if \(S = \{s,t\}\), the circulant graph \(C_{n}\left( s,t\right)\) is a quartic circulant graph, where \(1\)\(\leq\)\(s<\)\(t\)\(\leq\)\(\left\lfloor\dfrac{n}{2}\right\rfloor\), that is to say, for any \(i\in\{0,…, {n-1}\}\), the neighbours of \(i\) be \(\{i\pm s,i\pm t\}\), where \(\{i\pm s,i\pm t\}\) are taken modulo \(n\).
The distance between two vertices \(u\) and \(v\) is the length of the shortest path from \(u\) to \(v\), denoted by \(d(u,v)\). The diameter of \(G\) is the maximum distance among all pairs of vertices in \(G\), denoted by \(diam\left(G\right)\). If \(u\) is a vertex of \(G\), then let \(N_{i}(u)\) denote the set of vertices at distance \(i\) from \(u\). The partition \(\{N_{0}(u),N_{1}(u),…,N_{d}(u)\}\) is called the distance partition with respect to \(u\). Clearly, \(N_{0}(u)=\{u\}\). The set of neighbours of a vertex \(v\) in a graph \(G\) is denoted by \(N(v)\). Studying the properties of circulant graphs has become an active topic in algebraic graph theory for a long time. Actually, they are close related with graph parameters and networks etc, such as, [15,18,22,27]. Let \(Z_{p}\) be the additive group of integers modulo \(p\), where \(p\) be an odd prime, \(Z^{*}_{p}=Z_{p} \backslash \{0\}\). Some examples of circulant graphs are given in Figure 1.
We first characterize the zero forcing number of quartic circulant graphs \(C_{p}\left(1,q\right)\) on groups \(G\) with some special \(q\).
If \(q=2\), then \(Z\left(C_{p}\left(1,2\right)\right)=4\).
If \(q=3\), then \[Z\left(C_{p}\left(1,3\right)\right)= \begin{cases} 4 \text{,}& p=7,\\ 6 \text{,}& p\geq 11. \end{cases}\]
If \(q=4\), then \[Z\left(C_{p}\left(1,4\right)\right)= \begin{cases} 6 \text{, }& p=11 \, \mathrm{or}\, 13 ,\\ 8 \text{, }& p\geq 17. \end{cases}\]
If \(q=5\), then \[Z\left(C_{p}\left(1,5\right)\right)= \begin{cases} 4 \text{, }& p=11,\\ 6 \text{, }& p=13 \, \mathrm{or}\, 17,\\ 8 \text{, }& p=19 \, \mathrm{or}\, 23,\\ 10 \text{, }& p\geq 29. \end{cases}\]
Motivated by the above result, we have the following conjecture: when \(|p-q|\) is sufficiently large, \(Z(C_{p}(1,q))= 2q\).
The rest of the paper is structured as follows. In Section 2 we give some preliminary results. We focus on the isomorphism of quartic circulant graphs, and conclude that \(C_{p}\left( s,t\right)\cong C_{p}\left( 1,q\right)\) for some \(q\in Z_{p}^{*}\). Inspired by the idea of the isomorphism of those graphs, the zero forcing number of \(C_{p}\left(1,q\right)\) can help us research the zero forcing number of \(C_{p}\left(s,t\right)\). In Section 3 we prove Theorem 1.1.
In this section, we will characterize the isomorphism of (quartic) circulant graphs. Assume that \(C_{p}\left( s_{1},s_{2},…,s_{t}\right)\) be a circulant graph of prime order \(p\) with \(1\leq s_{i}\leq \left\lfloor\dfrac{p}{2}\right\rfloor\ \), \(1\leq i\leq t\). We first propose the following result.
By [8] and [21], together with Lemma 2.1, we have the following useful result, which characterize the isomorphism of circulant graphs with prime vertices.
Based on Theorem 2.2, for quartic circulant graphs, we can get the following conclusion.
As an example of Theorem 2.3, if \(p=11\) and \(s=2\), \(t=5\), then \(C_{11}\left( 2,5\right)\cong C_{11}\left( 1,3\right)\). Therefore, the characterization of the zero forcing number of quartic circulant graphs \(C_{p}\left( s,t\right)\) can be converted into the zero forcing number of quartic circulant graphs \(C_{p}\left( 1,q\right)\).
Motivated by Theorem 2.3, we will characterize the zero forcing number of circulant graphs \(C_{p}\left(1, q\right)\). In this section, we first give the upper bound of the zero forcing number of \(C_{p}\left(1, q\right)\). For the rest of this section, we will give the exact values of the zero forcing number for \(C_{p}\left(1,2\right)\), \(C_{p}\left(1,3\right)\), \(C_{p}\left(1,4\right)\), and \(C_{p}\left(1,5\right)\), respectively.
In this subsection, we characterize the exact values of the zero forcing number of the circulant graphs \(C_{p}\left(1,2\right)\) and \(C_{p}\left(1,3\right)\). For consecutive circulant graphs, we have the following conclusions.
By Lemma 3.2, we can get the following theorem immediately.
Proof. By [8, Lemma 1.2], \(Z\left(C_{n}\left(1,m\right)\right)\geq4\). In the following, we can get a forcing set of size 4, that is to say \(Z\left(C_{n}\left(1,m\right)\right)\leq 4\).
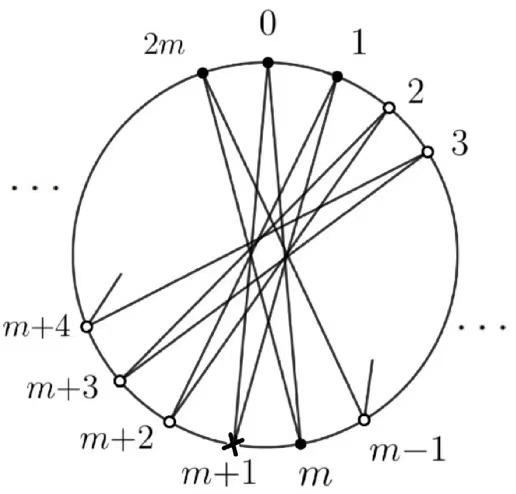
Step 1. Black four vertices \(\{0,1,m,2m\}\), then \(m+1\) be the unique neighbour not be colored black of vertex \(0\), thus \(0 \rightarrow m+1\), see Figure 3.
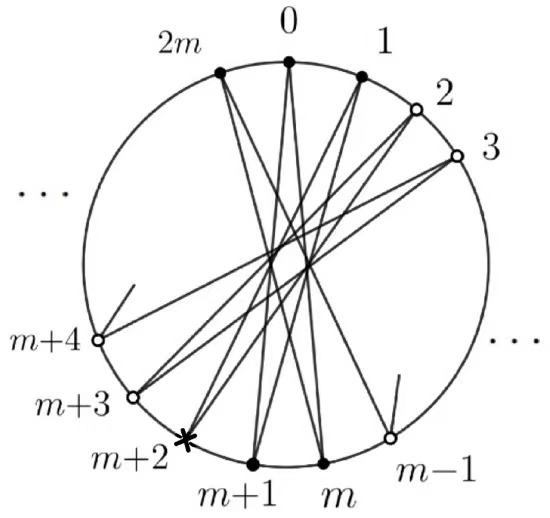
Step 2. After the above forcing process, \(m+1\) has the unique neighbour \(m+2\) not be colored black, thus \(m+1\) \(\rightarrow\) \(m+2\), see Figure 4.
Step 3. After this forcing process, \(1\) has the unique neighbour \(2\) not be colored black, thus \(1\) \(\rightarrow\) \(2\).
Step 4. Similarily, the black vertex \(m+2\) has the unique neighbour \(m+3\) not be colored black, thus \(m+2\) \(\rightarrow\) \(m+3\). Then the black vertex \(2\) has the unique neighbour \(3\) not be colored black, thus \(2\) \(\rightarrow\) \(3\). Continue the similiar analysis, the vertices \(m+4,\) \(4,…,\) \(2m-1,\) \(m-1\) will be colored black by the forcing process of \(m+3,\) \(3,…,\) \(2m-2,\) \(m-2\), respectively.
Then all the vertices of \(G\) be colored black, thus \(\{0,1,m,2m\}\) be a forcing set and \(Z\left(C_{n}\left(1,m\right)\right)\leq 4\). ◻
The girth is the length of the shortest cycle of the graph. It is clearly that the girth of quartic circulant graphs \(C_{p}\left(1,q\right)\) is \(3\) or \(4\). By [11, Theorem 2.4] , if \(G\) is a graph of girth \(g\) at least 3 and minimum degree \(\delta\) at least 2, then \(Z(G)\ge(g-2)(\delta-2)+2\). The next theorem give the exact value of the zero forcing number of \(C_{p}\left(1,3\right)\).
Proof. By Theorem 3.5, we have \(Z\left(C_{7}\left(1,3\right)\right)=4\).
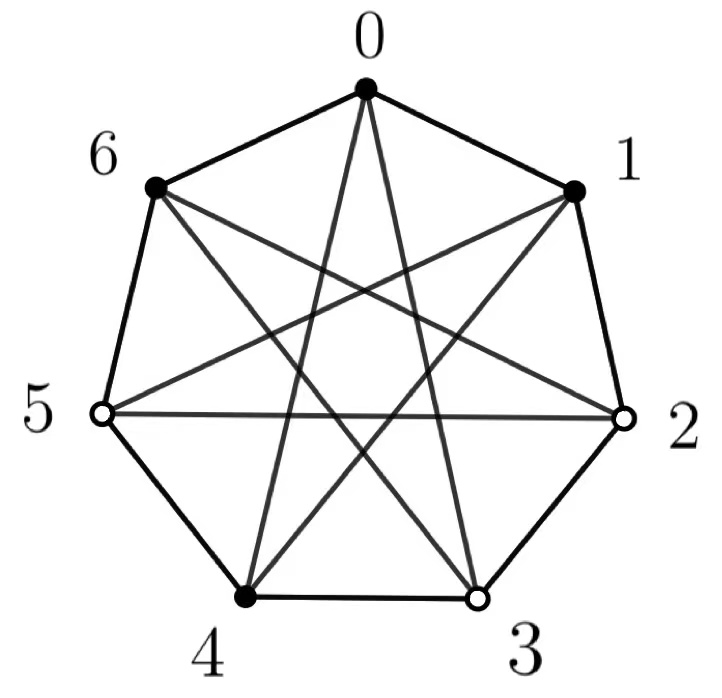
We are going to prove that when \(p\geq 11\), \(Z\left(C_{p}\left(1,3\right)\right)=6\). By Theorem 3.1, \(Z\left(C_{p}\left(1,3\right)\right)\) \(\leq\)\(2\times\)\(3\)\(=\)\(6\). In the following, we prove that \(Z\left(C_{p}\left(1,3\right)\right)\ge 6\). We claim that when \(p\geq 11\), the girth of \(C_{p}\left(1,3\right)\) is 4, that is, \(C_{p}\left(1,3\right)\) is triangle-free. Otherwise, without loss of generality, we can assume that \(C=(0,\) \(x,\) \(y,\) \(0)\) is the \(3\)-cycle containing the identity element \(0\) (the vertex-transitity guarantees the existance of this \(3\)-cycle). That is to say, \(x\) and \(y\) are adjacent. Since \(N(0)=\{1,3,p-3,p-1\}\), under the assumption that \(p\geq 11\), \(3,p-3,p-1\) are not adjacent. Thus \(g \ge 4\). Also we can find a 4-cycle \((0,1,p-2,p-3,0)\). So when \(p\geq 11\), the girth of \(C_{p}\left(1,3\right)\) equal to 4, and \(Z\left(C_{p}\left(1,3\right)\right)\ge (g-2)(\delta-2)+2=(4-2)(4-2)+2=6\).
Hence we conclude that \(Z\left(C_{p}\left(1,3\right)\right)=6\). ◻
In this section, we characterize the exact values of the zero forcing number of the circulant graphs \(C_{p}\left(1,4\right)\). We first propose the following results.
Proof. Since \(u\) and \(v\) be the first and second vertices performing the forcing process and \(d(u,v)\ge 3\), \(|N(u) \cap N(v)|=0\), then \(|Z|\ge 1+(d(u)-1)+1+(d(v)-1)= d(u)+d(v)\). ◻
We will present the first three parts of distance partition \(\{N_{0}(0),N_{1}(0),…,N_{d}(0)\}\) of \(C_{p}\left(1,4\right)\) for \(p>17\), see Figure 6.
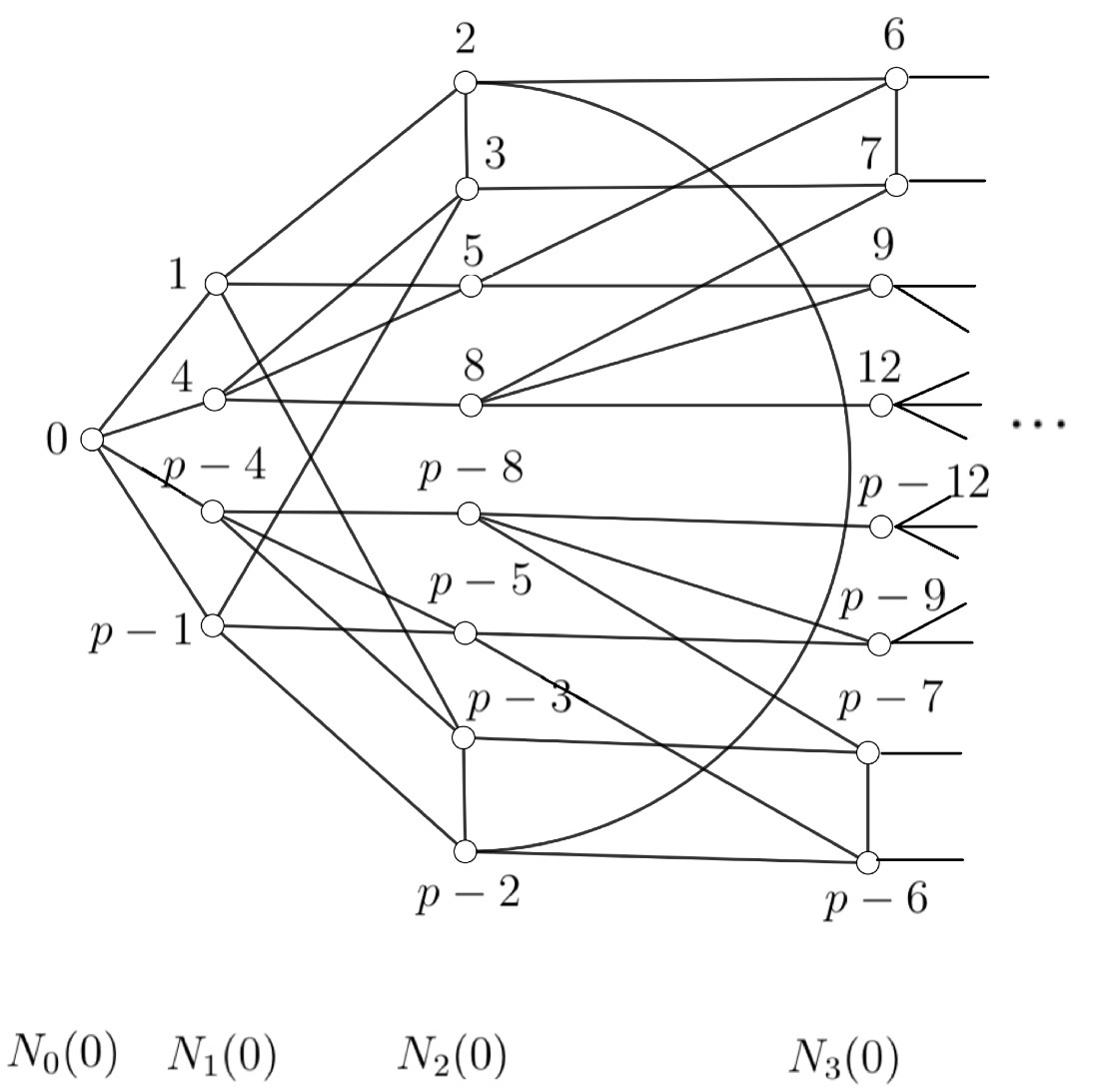
According to the graphs deinition, when \(p>17\), \(N_{0}(0)\), \(N_{1}(0)\), \(N_{2}(0)\) are fixed. Note that when \(p=19\), \(7=p-12\) and \(12=p-7\), then \(N_{3}(0)\) has 6 vertices instead of 8. But this does not affect the following proof, and the proof of \(p=19\) and \(p>19\) is the same. So in the following, we use the Figure 6 as the example graph.
Let \(Z\) be a zero forcing set for \(C_{p}\left(1,4\right)\). Note that \(C_{p}\left(1,4\right)\) is the vertex-transitive graph, with no loss of generality, we assume that \(0\) is the first black vertex which performs the forcing process. Then all but one of the neighbors of \(0\) must be contained in \(Z\). Suppose that \(4\not\in Z\), where \(4\in N_1(0)\). By applying the forcing process, \(0\) \(\rightarrow\) \(4\).
Let \(v\) be the second black vertex which performs the forcing process. According to the symmetry of \(C_{p}\left(1,4\right)\), we only discuss vertex \(v\) as one vertex of the first half of Figure 6, i.e., \(\{1,\) \(4,\) \(2,\) \(3,\) \(5,\) \(8,\) \(6,\) \(7,…\}\). In the following, we say that a set is black, which means that its all vertices are black.
Based on the distance partition, we can get the following lemma of the zero forcing number of \(C_{p}\left(1,4\right)\).
Proof. By the symmetry of \(C_{p}\left(1,4\right)\), we only discuss vertex \(v\) as one vertex of 2, 3, 5, 8.
(1) When \(v=2\).
In this case, \(|N(v)\cap N_{1}(0)|=|\{1\}|=1\), \(|N(v)\cap N_{2}(0)|=|\{3,p-2\}|=2\), \(|N(v)\cap N_{3}(0)|=|\{6\}|=1\). Since \(v\) be the second black vertex which performs the forcing process, \(v\) and its neighbors except one must be included in \(Z\), that is, \(|Z|\ge 7\), and \(0,1,4,p-4,p-1,2,3,p-2,6\) are black. Let \(W_{1}=\{0,1,4,p-4,p-1,2,3,p-2,6\}\).
After the above forcing process, the black vertex \(3,p-1\) have the unique neighbour \(7,p-5\) not be colored black, respectively. Thus \(3 \rightarrow 7\), \(p-1 \rightarrow p-5\), and \(W_{1} \cup \{7,p-5\}\) is black, see Figure 7.
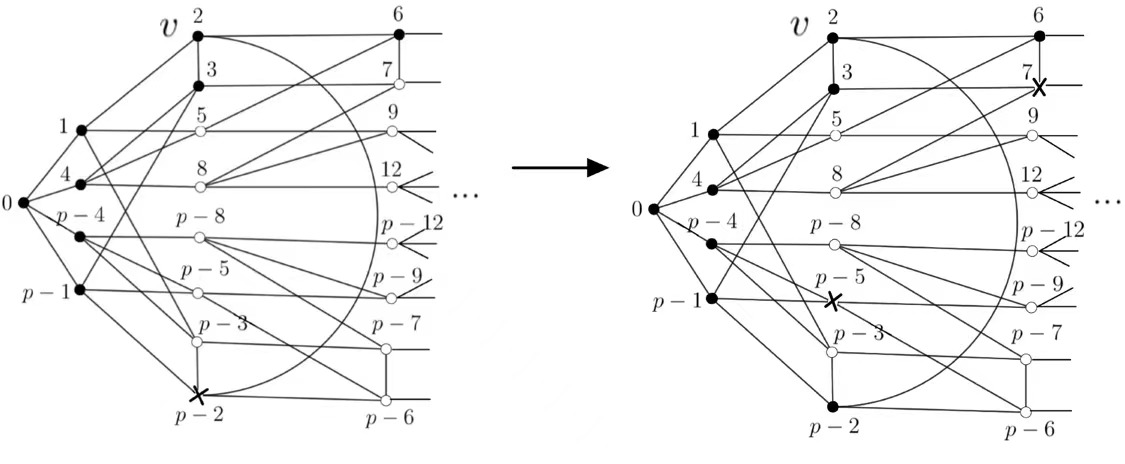
Figure 7 Let \(w\) be the next black vertex which performs the forcing process, \(w\) has the property that \(|(N(w)\cup w)\cap (W_{1} \cup \{7,p-5\})|\le 3\), so we have at least one more vertex belong to \(Z\), which infers that \(|Z|\ge7+1=8\).
When \(v=8\), \(|N(v)\cap N_{1}(0)|=|\{4\}|=1\), \(|N(v)\cap N_{3}(0)|=|\{7,9,12\}|=3\), Since \(v\) be the second black vertex which performs the forcing process, \(v\) and its neighbors except one must be included in \(Z\), that is, \(|Z|\ge 7\). Then we can get the result of \(|Z|\ge 8\) by a similar analysis.
(2) When \(v=3\).
In this case, \(|N(v)\cap N_{1}(0)|=|\{4,p-1\}|=2\), \(|N(v)\cap N_{2}(0)|=|\{2\}|=1\), \(|N(v)\cap N_{3}(0)|=|\{7\}|=1\). Since \(v\) be the second black vertex which performs the forcing process, \(v\) and its neighbors except one must be contained in \(Z\), that is, \(|Z|\ge 6\), and \(0,1,4,p-4,p-1,2,3,7\) are black. Let \(W_{2}=\{0,1,4,p-4,p-1,2,3,7\}\), see Figure 8.
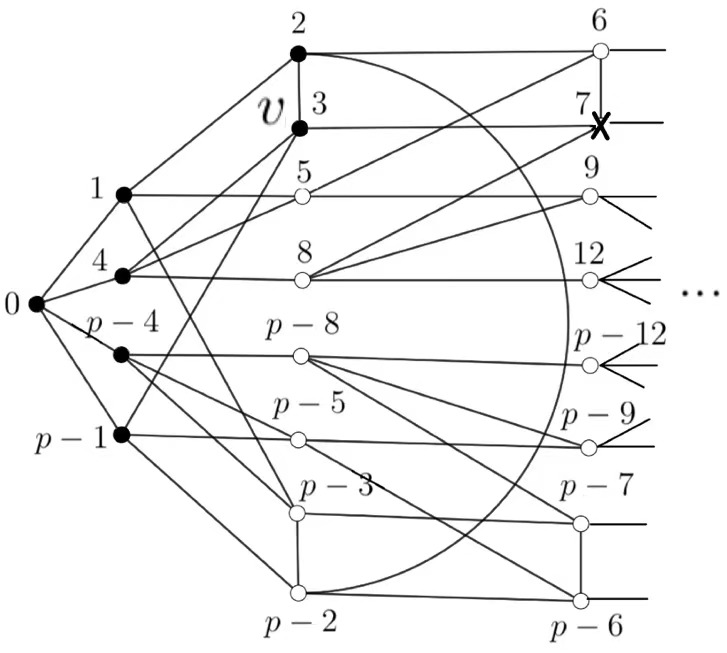
Figure 8 Let \(w\) be the next black vertex which performs the forcing process. The following cases will be considered.
Case i. \(w\in V \backslash\{1,2,4,p-1\}\).
In this case, \(w\) has the property that \(|(N(w)\cup w)\cap W_{2}|\le 2\), there are at least two more vertices belong to \(Z\), which implies that \(|Z|\ge6+2=8\).
Case ii. \(w\in \{1,2,4,p-1\}.\)
When \(w=1\). Without loss of generality, let \(5\in Z\), then \(1 \rightarrow p-3\). At this time, \(|Z|\ge 6+1=7\). Then the black vertex \(4\) has the unique neighbour \(8\) not be colored black, thus \(4\) \(\rightarrow\) \(8\). Let \(u\) be the next black vertex which performs the forcing process, \(u\) has the property that \(|(N(u)\cup u)\cap (W_{2}\cup\{5,8,p-3\})|\le 3\). So there is at least one more vertex contained in \(Z\), and \(|Z|\ge7+1=8\).
When \(w=2\). Without loss of generality, let \(6\in Z\), then \(2 \rightarrow p-2\). At this time, \(|Z|\ge 6+1=7\). Then the black vertex \(p-1\) has the unique neighbour \(p-5\) not be colored black, thus \(p-1\) \(\rightarrow\) \(p-5\). Let \(u\) be the next black vertex which performs the forcing process, \(u\) has the property that \(|(N(u)\cup u)\cap (W_{2}\cup\{6,p-2,p-5\})|\le 3\), so at least one more vertex is added to \(Z\), then \(|Z|\ge7+1=8\).
When \(w=4\). Let \(5\in Z\), then \(4 \rightarrow 8\) and \(|Z|\ge 6+1=7\). The black vertex \(1\) has the unique neighbour \(p-3\) not be colored black, thus \(1\) \(\rightarrow\) \(p-3\). Let \(u\) be the next black vertex which performs the forcing process, \(u\) has the property that \(|(N(u)\cup u)\cap (W_{2}\cup\{5,8,p-3\})|\le 3\), so we have at least one more vertex belonging to \(Z\), which results in \(|Z|\ge7+1=8\).
When \(w=p-1\). Let \(p-2\in Z\), then \(p-1 \rightarrow p-5\) and \(|Z|\ge 6+1=7\). The black vertex \(2\) has the unique neighbour \(6\) not be colored black, thus \(2\) \(\rightarrow\) \(6\). Let \(u\) be the next black vertex which performs the forcing process, \(u\) has the property that \(|(N(u)\cup u)\cap (W_{2}\cup\{6,p-2,p-5\})|\le 3\), then there is at least one more vertex that is included in \(Z\), and \(|Z|\ge7+1=8\).
When \(v=5\), \(|N(v)\cap N_{1}(0)|=|\{1,4\}|=2\), \(|N(v)\cap N_{3}(0)|=|\{6,9\}|=2\). Since \(v\) be the second black vertex which performs the forcing process, \(v\) and its neighbors except one must be included in \(Z\), that is, \(|Z|\ge 6\). Then we can get the result of \(|Z|\ge 8\) by a similar analysis. ◻
Proof. By the symmetry of \(C_{p}\left(1,4\right)\), \(v\) can be regarded as \(1\) or \(4\).
When \(v=1\). In this case, \(|N(v)\cap N_{0}(0)|=|\{0\}|=1\), \(|N(v)\cap N_{2}(0)|=|\{2,5,p-3\}|=3\). Since \(v\) be the second black vertex which performs the forcing process, \(v\) and its neighbors except one must be contained in \(Z\), that is, \(|Z|\geq 4+2=6\), and \(0,1,4,p-4,2,5,p-3\) are black. Let \(W_{3}=\{0,1,4,p-4,2,5,p-3\}\).
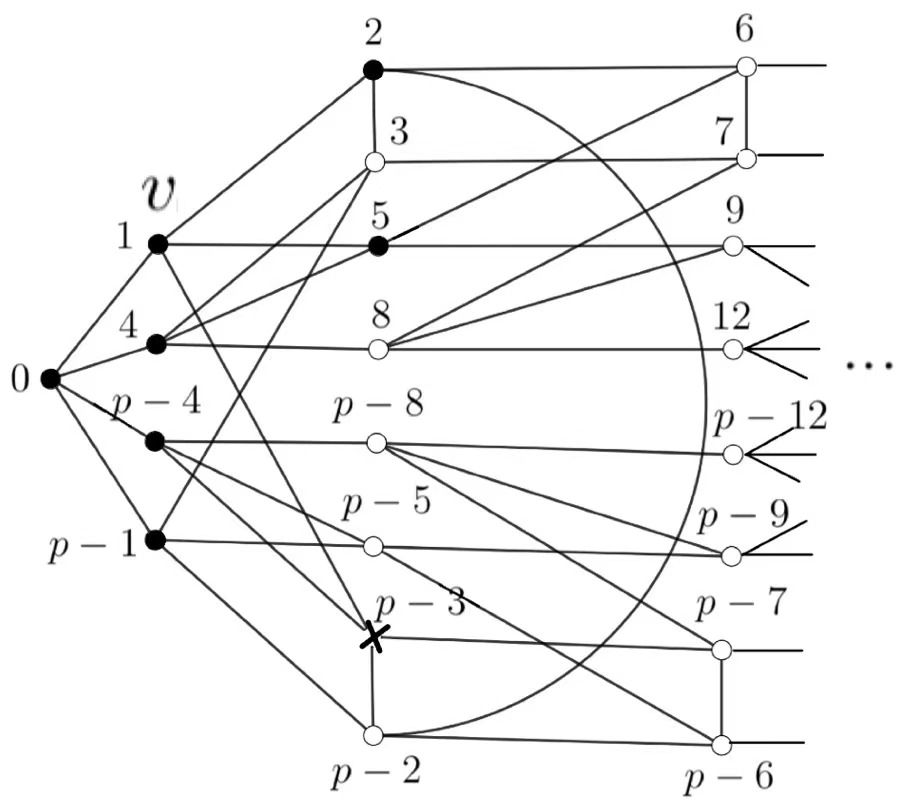
Figure 9 Let \(w\) be the next black vertex which performs the forcing process. The following cases will be considered.
Case i. \(w\in V \backslash\{3,4,p-2,p-4\}\).
In this case, \(|(N(w)\cup w)\cap W_{3}|\le 2\), so there are at least two extra vertices that are added to \(Z\), we thus conclude that \(|Z|\ge6+2=8\).
Case ii. \(w\in \{3,4,p-2,p-4\}.\)
When \(w=3\). Let \(3\in Z\), then \(3 \rightarrow 7\). At this time, \(|Z|\ge 6+1=7\). The black vertex \(4\) has the unique neighbour \(8\) not be colored black, thus \(4\) \(\rightarrow\) \(8\). Let \(u\) be the next black vertex which performs the forcing process, \(u\) has the property that \(|(N(u)\cup u)\cap (W_{3}\cup\{3,7,8\})|\le 3\), then there is at least one more vertex belonging to \(Z\), and \(|Z|\ge7+1=8\).
When \(w=4\). Without loss of generality, let \(3\in Z\), then \(4 \rightarrow 8\) and \(|Z|\ge 6+1=7\). The black vertex \(3\) has the unique neighbour \(7\) not be colored black, thus \(3\) \(\rightarrow\) \(7\). Let \(u\) be the next black vertex performs the forcing process, \(u\) satisfies the property that \(|(N(u)\cup u)\cap (W_{3}\cup\{3,7,8\})|\le 3\), so at least one more vertex belongs to \(Z\), which infers that \(|Z|\ge7+1=8\).
When \(w=p-2\). Let \(p-2\in Z\), then \(p-2 \rightarrow p-6\). At this time, \(|Z|\ge 6+1=7\). Then the black vertex \(p-3\) has the unique neighbour \(p-7\) not be colored black, thus \(p-3\) \(\rightarrow\) \(p-7\). Let \(u\) be the next black vertex which performs the forcing process, we can find that \(|(N(u)\cup u)\cap (W_{3}\cup\{p-2,p-6,p-7\})|\le 3\), so there is at least one extra vertex that is added to \(Z\), we get that \(|Z|\ge7+1=8\).
When \(w=p-4\). Without loss of generality, let \(p-5\in Z\), then \(p-4 \rightarrow p-8\) and \(|Z|\ge 6+1=7\). Let \(u\) be the next black vertex which performs the forcing process, \(u\) has the property that \(|(N(u)\cup u)\cap (W_{3}\cup\{p-5,p-8\})|\le 3\), so we have at least one more vertex belonging to \(Z\), and \(|Z|\ge7+1=8\).
When \(v=4\), \(|N(v)\cap N_{0}(0)|=|\{0\}|=1\), \(|N(v)\cap N_{2}(0)|=|\{3,5,8\}|=3\). Since \(v\) be the second black vertex which performs the forcing process, \(v\) and its neighbors except one must be included in \(Z\), that is, \(|Z|\ge 6\). Then we can obtain the result of \(|Z|\ge 8\) by a similar analysis. ◻
With the above preparations, in the following, we can completely characterize the zero forcing number of \(C_{p}\left(1,4\right)\).
Proof. First, we prove that when \(p=11\), \(Z\left(C_{p}\left(1,4\right)\right)=6\). The circulant graph \(C_{11}\left(1,4\right)\) as follows:
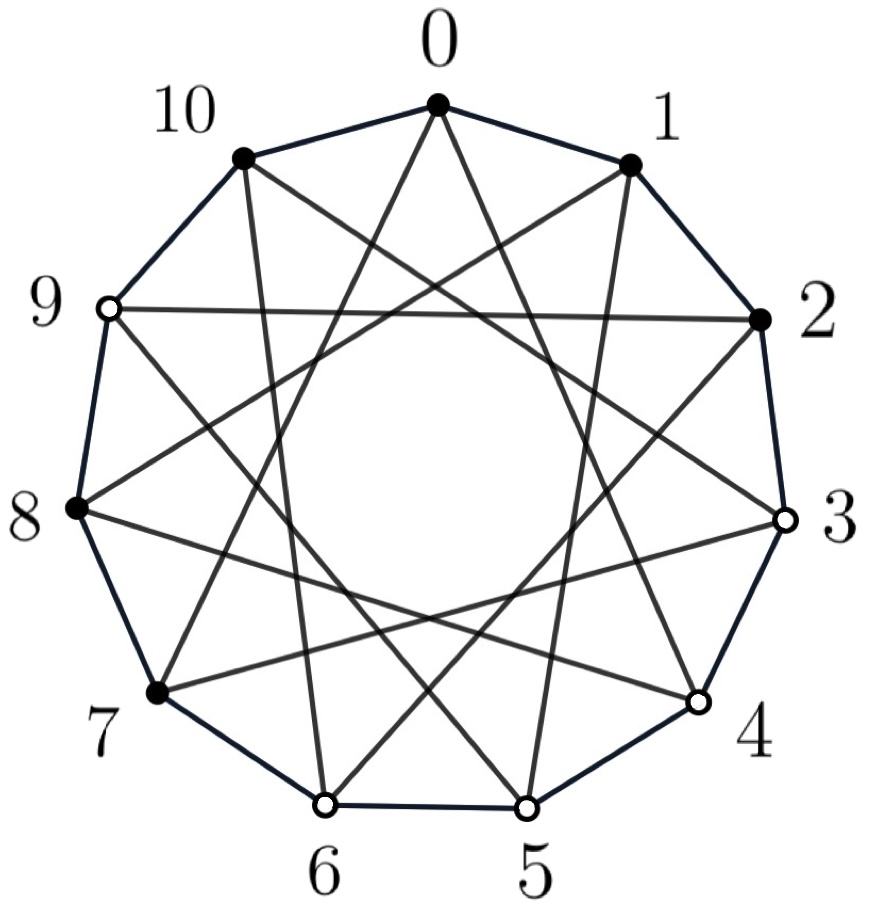
It is easy to check that \(\{0,1,2,7,8,10\}\) is a zero forcing set for \(C_{11}\left(1,4\right)\), that is \(Z\left(C_{11}\left(1,4\right)\right)\le6\). And \(Z(C_{11}\left(1,4\right))\ge(g-2)(\delta-2)+2\ge 6\), hence we conclude that \(Z\left(C_{11}\left(1,4\right)\right)=6\). The forcing processes as follows: \(0\) \(\rightarrow\) \(4\), \(1\) \(\rightarrow\) \(5\), \(4\) \(\rightarrow\) \(3\), \(7\) \(\rightarrow\) \(6\) and \(8\) \(\rightarrow\) \(9\). Similarly, \(Z\left(C_{13}\left(1,4\right)\right)=6\).
Now we prove that when \(p\geq 17\), \(Z\left(C_{p}\left(1,4\right)\right)=8\). By Theorem 3.1, \(Z\left(C_{p}\left(1,4\right)\right)\le8\). In the following, we prove that \(Z\left(C_{p}\left(1,4\right)\right)\ge8\), and hence we conclude that \(Z\left(C_{p}\left(1,4\right)\right)=8\).
Firstly, we show that \(Z\left(C_{p}\left(1,4\right)\right)\ge 8\) for \(p>17\). Let \(0\) be the first black vertex which performs the forcing process, and \(v\) be the second black vertex which performs the forcing process. The following cases will be considered.
Case 1. \(v\in N_i(0)\), \(i\ge 3\).
Since \(C_{p}\left(1,4\right)\) is 4-regular, and \(d(0,v)\ge3\), by Lemma 3.7, \(|Z|\ge d(0)+d(v)=4+4=8\).
Case 2. \(v\in N_2(0)\).
By Lemma 3.3, \(|Z|\ge8\).
Case 3. \(v\in N_1(0)\).
By Lemma 3.4, \(|Z|\ge8\).
Note that when \(p>17\), \(8\) and \(p-8\) are not adjacent, \(8\) and \(p-5\) are not adjacent, \(5\) and \(p-8\) are not adjacent. On the contrary, when \(p=17\), , they are adjacent. Similarly, based on the distance partition, we can prove that when \(p=17\), \(Z\left(C_{p}\left(1,4\right)\right)\ge 8\).
Therefore, when \(p\ge 17\), \(Z(C_{p}\left(1, 4\right))=8\). ◻
Using the similar way of showing \(Z(C_p(1,4))\), we can determine the exact value of \(Z(C_p(1,5))\), but the process of the proof is long and tedious. Hence, we omit it here. But we present the outline of the proof as follows: \(Z(C_{11}\left(1,5\right))\) can be easily obtained through Theorem 3.5; the proof of \(Z(C_{13}\left(1,5\right))\) and \(Z(C_{17}\left(1,5\right))\) is similar to \(Z(C_{11}\left(1,4\right))\); when \(p\ge 19\), the proof of \(Z(C_{p}\left(1,5\right))\) adopts the method of distance partition, and the proof process can be referred to \(C_{p}\left(1,4\right)\), \(p\ge 17\).
| \(C_p\left(1,q\right)\) | diameter | \(\vert Z \vert \) | \(Z\) |
| \(C_11\left(1,5\right)\) | 3 | 4 | \(\{0,1,5,10\}\) |
| \(C_13\left(1,5\right)\) | 2 | 6 | \(\{0,1,2,7,8,12\}\) |
| \(C_17\left(1,5\right)\) | 3 | 6 | \(\{0,1,6,7,12,16\}\) |
| \(C_19\left(1,5\right)\) | 3 | 8 | \(\{0,1,2,4,14,15,17,18\}\) |
| \(C_23\left(1,5\right)\) | 3 | 8 | \(\{0,1,5,6,7,12,13,22\}\) |
In the paper, we have explored the zero forcing number of quartic circulant graphs \(C_{p}\left(s, t\right)\). Firstly, we focus on the isomorphism of quartic circulant graphs, and conclude that \(C_{p}\left( s,t\right)\cong C_{p}\left( 1,q\right)\) for some \(q\in Z_{p}^{*}\). In addition, for \(q=2,3,4,5\), we obtain the zero forcing number of \(C_{p}(1,q)\). When \(|p-q|\) is small, we can use the method of distance partition to get \(Z(G)\). However, for \(|p-q|\) is large, analyzing \(Z(G)\) with distance partition is very complicated. In this case, \(Z(G)\) is still unsolved. For further study, it would be an interesting problem to verify when \(|p-q|\) is sufficiently large, \(Z(C_{p}(1,q))= 2q\).
1970-2025 CP (Manitoba, Canada) unless otherwise stated.