A \(q\)-total coloring of \(G\) is an assignment of \(q\) colors to the vertices and edges of \(G\), so that adjacent or incident elements have different colors. The Total Coloring Conjecture (TCC) asserts that a total coloring of a graph \(G\) has at least \(\Delta+1\) and at most \(\Delta+2\) colors. In this paper, we determine that all members of new infinite families of snarks obtained by the Kochol superposition of Goldberg and Loupekine with Blowup and Semiblowup snarks are Type~1. These results contribute to a question posed by Brinkmann, Preissmann and D. Sasaki (2015) by presenting negative evidence about the existence of Type~2 cubic graphs with girth at least 5.
The study of a particular class of cubic graphs, known as snarks, was sparked by the Four Color Conjecture. Snarks are cyclically 4-edge-connected cubic graphs that cannot have their edges colored with only three colors (no two incident edges have the same color). The Petersen graph is the earliest and smallest example of a snark. Additional snarks, such as the Flower and Loupekine snarks were introduced by Isaacs [8], as well as an operation called dot product, leading to the construction of infinitely many snarks. Snarks have been extensively studied due to their relevance in various problems, including coloring, the cycle double cover conjecture, and the 5-flow conjecture (Esperet and Mazzuoccolo [5]).
In this paper, we focus on finite, undirected and simple graphs \(G = (V, E)\), where \(V\) is the set of vertices and \(E\) is the set of edges. The maximum degree of \(G\) is denoted as \(\Delta(G)\), or simply \(\Delta\).
A \(q\)-total coloring of \(G\) involves assigning \(q\) colors to the vertices and edges of \(G\) in such a way that adjacent or incident elements have distinct colors. The total chromatic number of \(G\), denoted by \(\chi''(G)\) (or simply \(\chi''\)), is the minimum value of \(q\) required for a \(q\)-total coloring of \(G\). We note that if the cardinality of any two color classes differs by at most one, then it is called an equitable \(q\)-total coloring.
The Total Coloring Conjecture (TCC) states that the total chromatic number of a graph \(G\) is at least \(\Delta+1\), but at most \(\Delta+2\) (Behzad [1], Vizing [15]). This conjecture led to the classification of graphs into two types: Type 1, if \(\chi''=\Delta +1\), and Type 2, if \(\chi''=\Delta +2\). While the TCC has been verified for specific graph families, it remains an open problem for many graph classes, spanning over five decades. For cubic graphs \(G\), Rosenfeld [12] and Vijayaditya [14] independently established that \(4\leq \chi''(G)\leq 5\).
The girth of \(G\) is the length of a shortest cycle contained in \(G\). In 2003, Cavicchioli et al. [4] showed, with the assistance of a computer, that all snarks with girth at least 5 and fewer than 30 vertices are Type 1, and asked the following question:
Later, Brinkmann, Preissmann and D. Sasaki [2] divided this problem into two questions to investigate the true obstruction that makes finding these graphs (if they exist at all) challenging: either being snarks or having a girth of at least 5.
In [2], the authors addressed Question 1.3 by finding an infinite number of Type 2 snarks. The question about the existence of a Type 2 cubic graph with girth at least 5 remains open.
In 2011, Campos, Dantas, and Mello [3] provided an equitable total coloring, using four colors for each Flower and Goldberg snark. Notably, all of these graphs have girth 5.
Kochol [10] introduced the concept of the superposition construction, yielding infinite families of snarks with large girth. In 2016, Hägglund [7] defined two additional infinite snark families: Blowup and SemiBlowup. In 2022, Palma et al. [11] proved that the SemiBlowup snarks have equitable total colorings with 4 colors. This work contributes to Question 1.2 by presenting infinite families of Type 1 graph with girth at least 5.
The paper is structured as follows: Section 2 provides the definitions, the construction of Goldberg, Loupekine, \(t\)-SemiBlowup, and \(t\)-Blowup snarks, with their respective known \(4\)-total colorings; and the construction and notation of the Kochol superposition. From Sections 3 to 6, we determine \(4\)-total colorings for all members of the newly derived infinite families obtained through the Kochol superposition of Goldberg and Loupekine snarks with \(t\)-Blowup and \(t\)-SemiBlowup snarks. These results establish that all these members are Type 1.
A semi-graph is a 3-tuple \(G=(V,E, S_{\!E})\), where \(V\) is a finite set of vertices of \(G\), \(E\) is a set of edges with two distinct endpoints in \(V\), and \(S_{\!E}\) is a multiset of semiedges with at most one endpoint in \(V\). A semiedge without endpoints is called an isolated edge. A semiedge with endpoint \(v\) is denoted by \(v\cdot\), and an edge with endpoints \(v\) and \(w\) is denoted by \(vw\). Given two semiedges \(v\cdot\) and \(w\cdot\), the junction of \(v\cdot\) and \(w\cdot\) is formed by replacing \(v\cdot\) and \(w\cdot\) with the edge \(vw\). The definitions applicable for simple graphs can be naturally extended to semi-graphs. Indeed, a graph \(G=(V,E)\) is a semi-graph \(G=(V,E, S_{\!E})\) with an empty set of semiedges \((S_{\!E}=\emptyset)\).
In this subsection, we study the Goldberg family of snarks that was introduced by Goldberg [6] in 1981. Goldberg snarks involves a recursive construction arising from linking basic blocks.
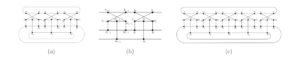
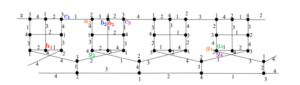
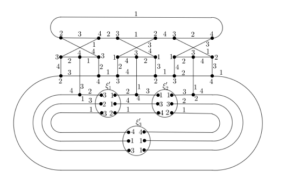
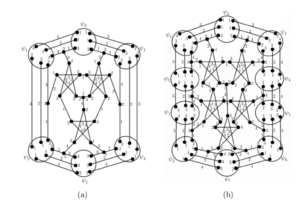
In Figures 1(a) and 1(b), we depict the first Goldberg snark \(G_3\) and the link semi-graph \(\mathcal{L}_i\), with \(V(\mathcal{L}_i)=\{s_{i-1}, t_{i-1}, u_{i-1}, v_{i-1}, w_{i-1}, x_{i-1}, y_{i-1} , z_{i-1}, s_{i}, t_{i},u_{i}, v_{i}, w_{i}, x_{i}, y_{i}, z_{i} \}\), for odd \(i\geq 5\). The second member of this family, Goldberg snark \(G_5\) (see Figure 1(c)), is obtained by deleting the edges \(\{t_3s_1,\) \(y_3x_1,\) \(u_3u_1\}\) from \(G_3\) (depicted as dashed lines in Figure 1(a)); and adding the semiedges \(t_3\cdot\), \(s_1\cdot\), \(y_3\cdot\), \(x_1\cdot\), \(u_3\cdot\), and \(u_1\cdot\); thereafter, we make their corresponding junction with the following semiedges of the link semi-graph \(\mathcal{L}_5\), say \(s_4\cdot\), \(t_5\cdot\), \(x_4\cdot\), \(y_5\cdot\), \(u_4\cdot\), and \(u_5\cdot\), respectively.
All subsequent members in this family, denoted as \(G_i\) with odd \(i\geq 7\), are similarly constructed. This involves the junctions of the semiedges of \(\mathcal{L}_i\) with the corresponding semiedges of the semi-graph obtained from \(G_{i-2}\), with odd \(i\geq 7\). The construction of this semi-graph consists of removing three edges \(\{t_{i-2}s_1,\) \(y_{i-2}x_1,\) \(u_{i-2}u_1\}\) from \(G_{i-2}\), and replacing them with their respective semiedges.
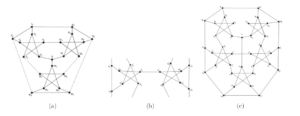
In [3], the Campos, Dantas and Mello showed that Goldberg snarks admit \(4\)-total colorings using the colorings of the first Goldberg snark \(G_3\) and of the link graph \(\mathcal{L}_i\), odd \(i \geq 5\). Figures 2(a) and 2(b) depict \(4\)-total colorings for \(G_3\) and for the link graph \(\mathcal{L}_i\), respectively.
A \(4\)-total coloring for Goldberg snark \(G_5\) is obtained from the \(4\)-total colorings of \(G_3\) and \(\mathcal{L}_i\) presented in Figure 3. For each odd \(i \geq 7\), a \(4\)-total coloring for \(G_i\) is obtained from the \(4\)-total colorings of \(G_{i-2}\) and \(\mathcal{L}_i\), using the recursive definition of Goldberg snarks. That is, to obtain the \(4\)-total coloring for \(G_i\), each element receives the color of its corresponding element in \(G_{i-2}\) or \(\mathcal{L}_i\), odd \(i\geq 5\). The remaining edges are colored as follows: \(t_{i-2}s_{i-1}\), \(t_is_1\), \(y_{i-2}x_{i-1}\) = \(y_ix_1\) receives color 1; \(u_{i-2}u_{i-1}\) and \(u_iu_1\) receives color 4.

Each Goldberg snark \(G_i\), with odd \(i\geq 3\), is Type \(1\).
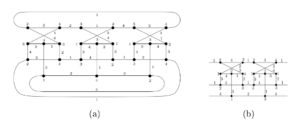
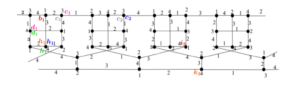
In this subsection, we study the Loupekine family of snarks that was introduced in 1976, by Isaacs [9]. These snarks are also obtained through a recursive construction as follows. In Figures 4(a) and 4(b), we depict the first Loupekine snark \(L_3\) and the link semi-graph \(\mathcal{H}_i\), with \(V(\mathcal{H}_i)=\{v^i_1, \ldots, v^i_7\), \(u^i_1, \ldots, u^i_7\}\), for odd \(i\geq 5\). The second member of this family, Loupekine snark \(L_5\) (see Figure 4(c)), is obtained by deleting the edges \(v_6w_6\), \(v_2w_2\), \(u_2w_3\), \(u_6w_7\) from \(L_3\) (depicted as dashed lines in Figure 4(a)); adding the semiedges \(v_6\cdot\), \(v_2\cdot\), \(u_2\cdot\), \(u_6\cdot\), \(w_6\cdot\), \(w_2\cdot\), \(w_3\cdot\), \(w_7\cdot\), and then making their corresponding junction with the following semiedges of the link semi-graph \(\mathcal{H}_5\), say \(v^5_7\cdot\), \(v^5_3\cdot\), \(u^5_3\cdot\), \(u^5_7\cdot\), \(v^5_6\cdot\), \(v^5_2\cdot\), \(u^5_2\cdot\), \(u^5_6\cdot\), respectively.
All subsequent members in this family, denoted as \(L_i\) with odd \(i\geq 7\), are similarly constructed. This involves the junctions of the semiedges of \(\mathcal{H}_i\) with the corresponding semiedges of the semi-graph obtained from \(L_{i-2}\), with odd \(i\geq 7\). The construction of this semi-graph consists of removing four edges \(v_6v^{i-2}_7\), \(v_2v^{i-2}_3\), \(u_2u^{i-2}_3\), and \(u_6u^{i-2}_7\) from \(L_{i-2}\), and replacing them with their respective semiedges. This procedure is analogous to the construction of \(L_5\) where the dashed edges are removed from \(L_3\).
Sasaki, Dantas, Figueiredo, and Preissmann [13] constructed a \(4\)-total coloring for the Loupekine snarks \(L_i\), with odd \(i\geq 5\).
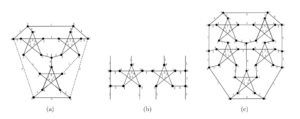
Building upon the proof of this result, we present a \(4\)-total coloring that shows to be useful in simplifying the proof of our main results. This coloring takes advantage of the recursive construction of this class.
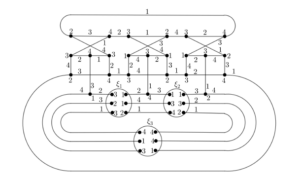
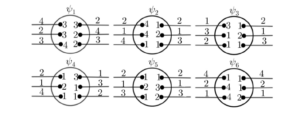
First, we refer to Figures 6(a) and 6(c) for the \(4\)-total colorings of \(L_3\) and \(L_5\), respectively. The \(4\)-total colorings of all subsequent members \(L_i\) with odd \(i\geq 7\), are recursively constructed as follows. We remove four edges \(v_6v^{i-2}_7\), \(v_2v^{i-2}_3\), \(u_2u^{i-2}_3\), and \(u_6u^{i-2}_7\) from the colored \(L_{i-2}\) (replace them with their respective semiedges), and make the junction with the corresponding semiedges of the colored link semi-graph \(\mathcal{H}_i\) of Figure 6(b). It is easy to verify that this construction produces a \(4\)-total coloring for \(L_i\). Indeed, we consider the same coloring for every link semi-graph \(\mathcal{H}_i\) that preserves the coloring of the removed edges and the endpoints of the semiedges. We depict in Figure 7(a) a 4-total coloring of Loupekine \(L_7\). Figure 7(b) highlights the upper part of the Loupekine snarks, demonstrating that the coloring remains the same on the subgraph induced by these vertices in \(L_i\) with odd \(i \geq 5\).
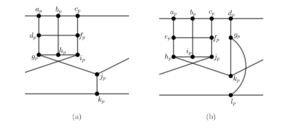
The SemiBlowup family of snarks was introduced in 2016 by Hägglund [7]. Let \(S_{\!\!p}\) be the semi-graph depicted in Figure 8(a), with \(V(S_{\!\!p})=\left\{ a_p, b_p, c_p, d_p, f_p, g_p, h_p, i_p, j_p, k_p \right\}\). The \(t\)-SemiBlowup is a snark constructed by connecting \(t\geq 5\) copies of semi-graph \(S_{\!\!p}\), with \(1 \leq p\leq t\) (as a cycle). Precisely, the \(t\)-SemiBlowup is constructed as follows: for \(2\leq p \leq t\), we make the junctions of semiedges \(a_p\cdot\) with \(c_{p-1}\cdot\), \(i_p\cdot\) with \(j_{p-1}\cdot\), \(k_p\cdot\) with \(k_{p-1}\cdot\); and for \(p=1\), \(a_1\cdot\) with \(c_t\cdot\), \(i_1\cdot\) with \(j_t\cdot\), and \(k_1\cdot\) with \(k_t\cdot\).
Now, let \(S'_{\!\!p}\) be the semi-graph depicted in Figure 8(b), with \[V(S'_{\!\!p})=\left\{ a_p, b_p, c_p, d_p, e_p, f_p, g_p, h_p, i_p, j_p, k_p, l_p \right\}.\]
The \(t\)-Blowup is a snark constructed by connecting \(t\geq 5\) copies of semi-graph \(S'_{\!\!p}\), with \(1 \leq p\leq t\) (as a cycle). That is, the \(t\)-Blowup is constructed as follows: for \(2\leq p \leq t\), we make the junctions of semiedges \(a_p\cdot\) with \(d_{p-1}\cdot\), \(j_p\cdot\) with \(k_{p-1}\cdot\), \(l_p\cdot\) with \(l_{p-1}\cdot\); and for \(p=1\), \(a_1\cdot\) with \(d_t\cdot\), \(j_1\cdot\) with \(k_t\cdot\), and \(l_1\cdot\) with \(l_t\cdot\).
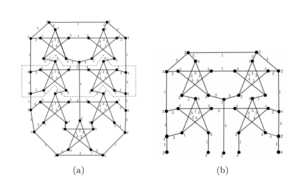
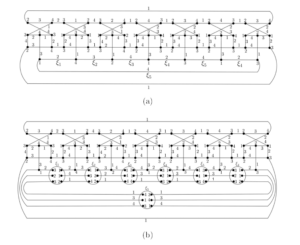
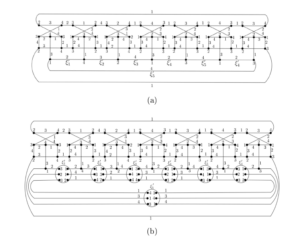
Palma et al. [11] presented equitable \(4\)-total colorings for these graphs proving that these graphs are Type 1. They observed that the \(4\)-total coloring of semi-graph \(B_4\) (a junction of four semi-graphs \(S_{\!\!p}\)), depicted in Figure 9 (resp. semi-graph \(B'_4\), a junction of four semi-graphs \(S'_{\!\!p}\), depicted Figure 10), appears in every \(t\)-SemiBlowup (resp. \(t\)-Blowup) snark, with \(t\geq 6\). We refer to Figures 11(a) and 11(b) for the 6-SemiBlowup and 6-Blowup, and their respective \(4\)-total colorings.
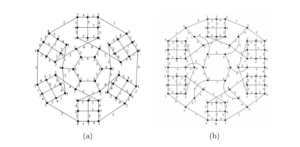
In this section, we define the Kochol superposition construction as presented in [10]. Given a cubic semi-graph \(M(V,E, S_{\!\!E})\), with \(S_{\!\!E}\not=\emptyset\), the set \(S_{\!\!E}\) of semiedges is partitioned into \(q\) pairwise disjoint nonempty sets \(Q_1\), \(Q_2\), \(\ldots\), \(Q_q\) such that \(\vert Q_i\vert = k_i\) with \(i=1, 2,\ldots , q\) and \(\sum_{i=1}^{q} k_i = \vert S_{\!\!E} \vert\). Following the notation of [10], we call the sets \(Q_i\) connectors, and denote the semi-graph \(M\) by (\(k_1\), \(k_2\), \(\ldots\), \(k_q\))-semi-graph \(M\).
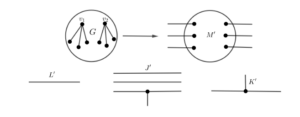
A superedge \(\xi\) is a semi-graph with two connectors, and a supervertex \(\vartheta\) is a semi-graph with three connectors. We consider the following semi-graphs depicted in Figure 12:
\((3, 3)\)-semi-graph \(M'\) (superedge) is obtained by removing two nonadjacent vertices \(v_1\) and \(v_2\) from a snark \(G\), and replacing each edge incident to \(v_1\) or \(v_2\) by semiedges.
\((1, 1)\)-semi-graph \(L'\) (superedge) is an isolated edge (two semiedges);
\((1,3,3)\)-semi-graph \(J'\) (supervertex) consists of two isolated edges and a vertex;
\((1, 1, 1)\)-semi-graph \(K'\) (supervertex) consists of a vertex and three semiedges.
Let \(G'=(V',E')\) be a snark. Replace every edge \(e\in E'\) by a superedge \(\xi_e\), and every vertex \(v\in V'\) by a supervertex \(\vartheta_v\). If \(v\in V'\) is incident to \(e\in E'\) then a connector in \(\vartheta_v\) is linked with a connector in \(\xi_e\) through the junction of semiedges. The obtained cubic graph is called superposition of \(G'\) with \(G\) and it is a snark [10].
Figure 13 depicts an example of isomorphic representations of superedge \(\xi_1\), which are obtained by removing the two nonadjacent vertices \(b_2\) and \(c_1\) from the \(t\)-SemiBlowup snark shown Figure 14. In these representations, every edge incident to \(b_2\) or \(c_1\) is replaced by the corresponding semiedge.
In this section, we present a construction of an infinite family of snarks obtained from a Kochol superposition of Goldberg snarks with \(t\)-SemiBlowup snarks, and show that all members of the presented family are Type 1. For each odd \(i \geq 3\), let \(R_t(i)\) be the snark obtained by a superposition of Goldberg snark \(G_{i}\) with a \(t\)-SemiBlowup snark, \(t\geq 6\).
| Superedge | Deleted | Superedge | Deleted |
| \(\xi_1\) | \(\{c_1,b_2\}\) | \(\xi_4\) | \(\{h_1,b_2\}\) |
| \(\xi_2\) | \(\{g_2,g_4\}\) | \(\xi_5\) | \(\{a_2,g_4\}\) |
| \(\xi_3\) | \(\{c_2,g_4\}\) |
We refer to Table 1 and Figure 14 with the semi-graph \(B_4\) (which appears in every \(t\)-SemiBlowup with \(t\geq 6\)) and the superedges that are necessary for the construction of \(R_t(i)\).
The superedges \(\xi_i\), with \(1\leq i \leq 5\), depicted in Figure 15, are formed by deleting, from the \(t\)-SemiBlowup snark, with \(t\geq 6\), the two nonadjacent vertices of semi-graph \(B_4\) (Figure 14) represented in Table 1, and replacing each edge incident to these vertices with the corresponding semiedge. The superedge \(\xi_1\) is formed by deleting two nonadjacent vertices, \(c_1\) and \(b_2\) , from the \(t\)-SemiBlowup snark (with \(t\geq 6\)), and replacing each edge incident to \(c_1\) and \(b_2\) with the corresponding semiedge. Similarly, the superedges \(\xi_2\), \(\xi_3\), \(\xi_4\), and \(\xi_5\) are obtained by removing, from the \(t\)-SemiBlowup snark (with \(t\geq 6\)), the nonadjacent vertices: \(\{g_2\), \(g_4\}\), \(\{c_2\), \(g_4\}\), \(\{h_1\), \(b_2\}\), and \(\{a_2\), \(g_4\}\) respectively. Again, each edge incident to these vertices is replaced by the corresponding semiedge.
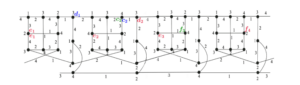
Consider the Goldberg snark \(G_3\) depicted in Figure 1(a). To obtain its superposition \(R_t(3)\), depicted in Figure 16, first replace the following edges by the corresponding superedges: edge \(u_1 u_2\) by a copy of the superedge \(\xi_1\); edge \(u_2 u_3\) by a copy of the superedge \(\xi_2\); and edge \(u_3 u_1\) by a copy of the superedge \(\xi_3\). Second, make the junction of the remaining semiedges (those that are of the same color and whose respective endpoints have different colors), between pairs of consecutive superedges accordingly, say \(\xi_1\) with \(\xi_2\), \(\xi_2\) with \(\xi_3\), and \(\xi_3\) with \(\xi_1\).
We refer to Figures 17 and 18(b), for the superpositions \(R_t(5)\) and \(R_t(7)\) obtained from \(G_5\) (Figure 3) and \(G_7\) (Figure 18 (a)), respectively. Similarly, the superpositions \(R_t(i)\) with odd \(i\geq 5\) and \(t\geq 6\) are obtained by replacing: the edges \(u_1u_2\), \(u_2u_3\), \(u_3u_4\), \(u_4u_5\), by the superedges \(\xi_1\), \(\xi_2\), \(\xi_3\), \(\xi_4\) respectively; the edges \(u_{j}u_{j+1}\), for \(5\leq j \leq i\) and odd \(i\geq 7\) (\(u_{i+1}=u_1\)), by the superedge \(\xi_5\), for odd \(j\); and by the superedge \(\xi_4\) for even \(j\); and make the junctions of the remaining semiedges between pairs of consecutive superedges, respectively.
Following Kochol’s construction, the remaining edges (resp. vertices) are replaced by superedges \(L'\) (resp. supervertices \(K'\)), which is equivalent to maintain the original edges (resp. vertices) of the \(G_{i}\), for odd \(i \geq 5\). Moreover, if \(v\in V\) is incident to \(e\in E\), then a connector in \(\vartheta_v\) is linked with a connector in \(\xi_e\) through the junction of semiedges.

Proof. Let \(t\geq 6\). The proof is by induction. As previously explained, \(R_t(i)\), odd \(i\geq 3\) is obtained from \(G_{i}\) by replacing edges \(u_ju_{j+1}\) with superedges \(\xi\), for \(1\leq j \leq i\), where \(u_{i+1}=u_1\).
It is easy to verify that the assignment presented in Figure 16 (resp. 17) is a \(4\)-total coloring for \(R_t(3)\) (resp. \(R_t(5)\)). Indeed, this coloring preserves the colors of the corresponding elements in \(G_3\) (resp. \(G_5\)); and the junctions are made between semiedges of the same color (say semiedge \(u\cdot\) and a semiedge of superedges \(\xi\) or between semiedges of superedges \(\xi\)), whose endpoints have different colors.
The \(4\)-total coloring of each superedge \(\xi\) is obtained from the \(4\)-total coloring of the \(t\)-SemiBlowup snark with the two deleted nonadjacent vertices of \(B_4\) represented in Table 1 (Figure 14). The colors of the semiedges are the colors of the respective edges incident to these deleted vertices. This is possible since the \(4\)-total coloring of semi-graph \(B_4\) appears in every \(t\)-SemiBlowup, with \(t\geq 6\).
that the coloring of the superposition \(R_t(i-2)\), with odd \(i\geq 7\) and \(t\geq 6\), obtained from \(G_{i}\) by replacing: the edges \(u_1u_2\), \(u_2u_3\), \(u_3u_4\), \(u_4u_5\), by the colored superedges \(\xi_1\), \(\xi_2\), \(\xi_3\), \(\xi_4\) respectively; the edges \(u_{j}u_{j+1}\), for \(5\leq j \leq i-2\) and odd \(i\geq 9\) (\(u_{i+1}=u_1\)), by the colored superedge \(\xi_5\), for odd \(j\); and by the colored superedge \(\xi_4\) for even \(j\) is a \(4\)-total coloring. We depict in Figure 18(b) a \(4\)-total coloring for \(R_t(7)\) satisfying this property.
By the induction hypothesis, we assume that a \(4\)-coloring can be assigned to the superposition \(R_t(i-2)\), where odd \(i\geq 7\) and \(t\geq 6\). This superposition is constructed from \(G_{i}\) by replacing: the edges \(u_1u_2\), \(u_2u_3\), \(u_3u_4\), \(u_4u_5\), by the colored superedges \(\xi_1\), \(\xi_2\), \(\xi_3\), \(\xi_4\) respectively; the edges \(u_{j}u_{j+1}\), for \(5\leq j \leq i-2\) and odd \(i\geq 9\) (\(u_{i+1}=u_1\)), by the colored superedge \(\xi_5\), for odd \(j\); and by the colored superedge \(\xi_4\) for even \(j\) is a \(4\)-total coloring. We depict in Figure 18(b) a \(4\)-total coloring for \(R_t(7)\) satisfying this property.
Now, we construct a \(4\)-total coloring for \(R_t(i)\) from \(R_t(i-2)\) as follows. For \(R_t(i)\), with odd \(i\geq 5\), the edges \(u_{i-1}u_i\) and \(u_iu_1\) are replaced by the colored superedges \(\xi_4\) and \(\xi_5\), respectively. We also note that in the \(4\)-total coloring of \(G_{i}\) with odd \(i\geq 7\): the color of the edge \(u_{i-1}u_i\) is 2; the colors of the vertices \(u_{i-1}\) and \(u_i\) are \(1\) and \(3\), respectively; the color of the edge \(u_iu_1\) is 4; and the colors of the vertices \(u_{i}\) and \(u_1\) are \(3\) and \(1\), respectively.
The \(4\)-total coloring of remaining superedges \(\xi\) in \(R_t(i)\) are obtained from the \(4\)-total coloring of the corresponding superedges in \(R_t(i-2)\). That is, if the colored superedge \(\xi\) of \(R_t(i-2)\) replaced the edge \(u_{j}u_{j+1}\) in \(G_{i-2}\), for \(1\leq j \leq i-2\) and odd \(i\geq 9\), then the coloring of the superedge \(\xi\) of \(R_t(i)\) is also obtained by replacing the same edge in \(G_i\) by this corresponding colored superedge.
The \(4\)-total coloring of the remaining elements \(R_t(i)\), with odd \(i\geq 3\), are obtained from the \(4\)-total coloring of \(G_i\) (presented in Subsection 2.1), without the edges \(\{u_{i-1}u_i, u_iu_1\}\).
Again, the junctions are made between semiedges of the same color: between semiedge \(u\cdot\) and a semiedge of superedge \(\xi_4\) (or \(\xi_5\)) (or between semiedges of superedges \(\xi_4\) and \(\xi_5\)), whose endpoints have different colors. Note that the junctions of these semiedges preserve the colors, since the same junctions are made in the \(4\)-total coloring of \(R_t(7)\) depicted in Figure 18(b).
Finally, by construction this \(4\)-total coloring satisfies the conditions in the inductive hypothesis. This ends the proof. ◻
In this section, we present a construction of an infinite family of snarks obtained from a Kochol superposition of Goldberg snarks with \(t\)-Blowup snarks, and show that all members of the presented family are Type 1. For each odd \(i \geq 3\), let \(R'_t(i)\) be the snark obtained by a superposition of Goldberg snark \(G_{i}\) with a \(t\)-Blowup snark, \(t\geq 6\).
| Superedge | Deleted | Superedge | Deleted |
| \(\xi’_1\) | \(\{c_2,d_1\}\) | \(\xi’_4\) | \(\{c_2,f_3\}\) |
| \(\xi’_2\) | \(\{e_1,e_2\}\) | \(\xi’_5\) | \(\{e_3,f_4\}\) |
| \(\xi’_3\) | \(\{e_1,d_2\}\) |
Similarly to the previous superposition, the superedges \(\xi'\) are formed from the \(t\)-Blowup snark, \(t\geq 6\), by deleting the two nonadjacent vertices of semi-graph \(B'_4\) (Figure 19) represented in Table 2; and replacing each edge incident to these vertices with the corresponding semiedge, see Figure 15.
Consider the Goldberg snark \(G_3\) depicted in Figure 1(a). To obtain its superposition \(R'_t(3)\), depicted in Figure 21, first replace the following edges by the corresponding superedges: edge \(u_1 u_2\) by a copy of the superedge \(\xi'_1\); edge \(u_2 u_3\) by a copy of the superedge \(\xi'_2\); and edge \(u_3 u_1\) by a copy of the superedge \(\xi'_3\). Second, make the junction of the remaining semiedges (which are those of the same color and respective endpoints of different colors), between pairs of consecutive superedges accordingly, say \(\xi'_1\) with \(\xi'_2\), \(\xi'_2\) with \(\xi'_3\), and \(\xi'_3\) with \(\xi'_1\).
We refer to Figures 22 and 23(b) for the superpositions \(R'_t(5)\) and \(R'_t(7)\) obtained from \(G_5\) (Figure 3) and \(G_7\) (Figure 23(a)), respectively. Similarly, the superpositions \(R'_t(i)\) with odd \(i\geq 5\) and \(t\geq 6\) are obtained by replacing: the edges \(u_1u_2\), \(u_2u_3\), \(u_3u_4\), \(u_4u_5\), by the superedges \(\xi'_1\), \(\xi'_2\), \(\xi'_3\), \(\xi'_4\) respectively; the edges \(u_{j}u_{j+1}\), for \(5\leq j \leq i\) and odd \(i\geq 7\) (\(u_{i+1}=u_1\)), by the superedge \(\xi'_5\), for odd \(j\); and by the superedge \(\xi'_4\) for even \(j\); and make the junctions of the remaining semiedges between pairs of consecutive superedges, respectively.
Again, following Kochol’s construction, the remaining edges (resp. vertices) are replaced by superedges \(L'\) (resp. supervertices \(K'\)) which is equivalent to maintain the original edges (resp. vertices) of \(G_{i}\) for \(i\) odd and \(i \geq 5\). Finally, if \(v\in V\) is incident to \(e\in E\), then a connector in \(\vartheta_v\) is linked with a connector in \(\xi_e\) through the junction of semiedges.

Proof. Let \(t\geq 6\). The proof is by induction. As previously explained, \(R'_t(i)\), odd \(i\geq 3\) is obtained from \(G_{i}\) by replacing edges \(u_ju_{j+1}\) with superedges \(\xi'\), for \(1\leq j \leq i\), where \(u_{i+1}=u_1\).
It is easy to verify that the assignment presented in Figure 21 (resp. 22) is a \(4\)-total coloring for \(R'_t(3)\) (resp. \(R'_t(5)\)). Indeed, this coloring preserves the colors of the corresponding elements in \(G_3\) (resp. \(G_5\)); the junctions are made between semiedges of the same color (say semiedge \(u\cdot\) and a semiedge of superedges \(\xi'\) or between semiedges of superedges \(\xi'\)), and whose endpoints have different colors.
The \(4\)-total coloring of each superedge \(\xi'\) is obtained from the \(4\)-total coloring of the \(t\)-Blowup snark with the two deleted nonadjacent vertices of \(B'_4\) represented in Table 2 (Figure 19). The colors of the semiedges are the colors of the respective edges incident to these deleted vertices. This is possible since the \(4\)-total coloring of semi-graph \(B'_4\) appears in every \(t\)-Blowup, with \(t\geq 6\).
The proof is similar to the proof of Theorem 2.3 considering the new colored superedges \(\xi'\). The \(4\)-total coloring of the superedges that replaced the edges \(u_{i-1}u_i\) and \(u_iu_1\) are the same of the coloring of \(\xi'_4\) and \(\xi'_5\), respectively; and the \(4\)-total coloring of the remaining superedges \(\xi'\) in \(R'_t(i)\) is obtained from the \(4\)-total coloring of its corresponding superedge in \(R'_t(i-2)\).
Again, the junctions are made between semiedges of the same color: between semiedge \(u\cdot\) and a semiedge of superedge \(\xi_4\) (or \(\xi_5\)); or between semiedges of superedges \(\xi_4\) and \(\xi_5\). Moreover, the endpoints of the edges corresponding to these junctions have different colors. Note that the junctions of these semiedges preserve the colors, since the same junctions are made in the \(4\)-total coloring of \(R'_t(7)\) depicted in Figure 23(b). This ends the proof. ◻
In this section, we present a construction of an infinite family of snarks obtained from a Kochol superposition of Loupekine snarks with \(t\)-SemiBlowup snarks, and show that all members of the presented family are Type 1. For each odd \(i \geq 3\), let \(L_t(i)\) be the snark obtained by a superposition of Loupekine snark \(L_{i}\) with a \(t\)-SemiBlowup snark, \(t\geq 6\).
| Superedge | Deleted | Superedge | Deleted |
| \(\psi_1\) | \(\{b_1,i_3\}\) | \(\psi_4\) | \(\{c_1, d_1\}\) |
| \(\psi_2\) | \(\{c_2, h_1\}\) | \(\psi_5\) | \(\{h_1, k_3\}\) |
| \(\psi_3\) | \(\{d_1, h_1\}\) | \(\psi_6\) | \(\{c_2, c_1\}\) |
We refer to Table 3 and Figure 24 with the semigraph \(B_4\) (which appears in every \(t\)-SemiBlowup with \(t\geq 6\)) and the superedges that are necessary for the construction of \(R_t(i)\). Similarly to the previous superpositions, the superedges \(\psi_i\) for \(1\leq i \leq 6\), depicted in Figure 25, are formed by deleting, from the \(t\)-SemiBlowup snark, with \(t\geq 6\) (Figure 24), the two nonadjacent vertices represented in Table 3, and replacing each edge incident to these vertices with the corresponding semiedge.
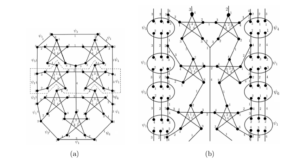
Consider the Loupekine snark \(L_3\) presented in Figure 4(a). To obtain its superposition \(L_t(3)\), depicted in Figure 26(a), replace the following edges by the corresponding superedges: edge \(v_6 v_7\) by a copy of the superedge \(\psi_1\); edge \(v_7 u_7\) by a copy of the superedge \(\psi_3\); edge \(u_7 u_6\) by a copy of the superedge \(\psi_1\); edge \(u_6 w_7\) by a copy of the superedge \(\psi_4\); edge \(w_7 w_6\) by a copy of the superedge \(\psi_1\); and edge \(w_6 v_6\) by a copy of the superedge \(\psi_2\).
Second, make the junction of the remaining semiedges (which are those of the same color and extreme vertices of different colors), between pairs of clockwise consecutive superedges accordingly, say \(\psi_1\) with \(\psi_3\), \(\psi_3\) with \(\psi_1\), \(\psi_1\) with \(\psi_4\), \(\psi_4\) with \(\psi_1\), \(\psi_1\) with \(\psi_2\), \(\psi_2\) with \(\psi_1\).
We refer to Figures 26(b) and 28(b), for the superpositions \(L_t(5)\) and \(L_t(7)\) obtained from \(L_5\) (Figure 4(c)) and \(L_7\) (Figure 5), respectively. Similarly, the superpositions \(L_t(i)\) with odd \(i\geq 5\) and \(t\geq 6\) are obtained by replacing: the edges \(v_6 v_7\), \(v_7 u_7\), \(u_7 u_6\), by a copy of the superedge \(\psi_1\), \(\psi_3\), \(\psi_1\), respectively; the edges \(u_6 u^{i}_7\), \(u^{5}_6 w_7\), \(w_7 w_6\), \(w_6 v^{5}_6\), \(v^{i}_7 v_6\) by a copy of the superedge \(\psi_4\), \(\psi_6\), \(\psi_1\), \(\psi_2\) and \(\psi_5\), respectively; the edges \(u^{j}_6 u^{j}_7\), \(v^{j}_6 v^{j}_7\), odd \(5\leq j \leq i\) by a copy of the superedge \(\psi_1\); the edges \(u^{j-2}_7 u^{j}_6\), \(v^{j}_6 v^{j-2}_7\), for odd \(5\leq j \leq i\) by a copy of the superedges \(\psi_5\), \(\psi_6\), respectively; and make the junctions of the remaining semiedges between pairs of clockwise consecutive superedges, respectively.
Following Kochol’s construction, the remaining edges (resp. vertices) are replaced by superedges \(L'\) (resp. supervertices \(K'\)), which is equivalent to maintain the original edges (resp. vertices) of the \(L_{i}\), for odd \(i \geq 5\). Moreover, if \(v\in V\) is incident to \(e\in E\), then a connector in \(\vartheta_v\) is linked with a connector in \(\xi_e\) through the junction of semiedges.
Proof. Let \(t\geq 6\). The proof is by induction. As previously explained, \(L_t(i)\), odd \(i\geq 3\) is obtained from \(L_{i}\) by replacing certain edges with superedges \(\psi\).
It is easy to verify that the assignment presented in Figure 26(a) (resp. 26(b)) is a \(4\)-total coloring for \(L_t(3)\) (resp. \(L_t(5)\)), since this coloring preserves the colors of the corresponding elements in \(L_3\) (resp. \(L_5\)); the junctions are made between semiedges of the same color; and the extreme vertices of the edges corresponding to these junctions have different colors.
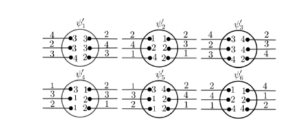
The \(4\)-total coloring of each superedge \(\psi\) is obtained from the \(4\)-total coloring of the \(t\)-SemiBlowup snark with the two deleted nonadjacent vertices of \(B_4\) represented in Table 3 (Figure 24). The colors of the semiedges are the colors of the respective edges incident to these deleted vertices. This is possible since the \(4\)-total coloring of semigraph \(B_4\) appears in every \(t\)-SemiBlowup, with \(t\geq 6\).

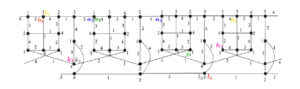
The proof is similar to the previous proofs. For example, it is straightforward to construct \(L_t(7)\) from Figures 27(a), and 27(b). In general, for \(L_t(i)\), the \(4\)-total coloring of the superedges that replaced the edges \(v_6 v^{i}_7\), \(u_6 u^{i}_7\) from \(L_{i-2}\) are the same of the coloring of \(\psi_5\) and \(\psi_4\), respectively; the \(4\)-total coloring of the superedges that replaced the edges \(v^{i}_7 v^{i}_6\), \(u^{i}_7 u^{i}_6\) from the link graph \(L_i\) are the same of the coloring of \(\psi_1\); the \(4\)-total coloring of the superedges that replaced the edges \(v^{i-2}_7 v^{i}_6\), \(u^{i-2}_7 u^{i}_6\) from the link graph \(L_i\) are the same of the coloring of \(\psi_5\) and \(\psi_6\), respectively; and the \(4\)-total coloring of the remaining superedges \(\psi\) in \(L_t(i)\) is obtained from the \(4\)-total coloring of its corresponding superedge in \(L_t(i-2)\).
Again, the junctions are made between semiedges of the same color whose endpoints have different colors. Note that the junctions of these semiedges preserve the colors, since the same junctions are made in the \(4\)-total coloring of \(L_t(7)\) (the superedges of \(L_7\) are indicated in Figure 28(a) and depicted in Figure 28(b)). This ends the proof. ◻
In this section, we present a construction of an infinite family of snarks obtained from a Kochol superposition of Loupekine snarks with \(t\)-SemiBlowup snarks, and show that all members of the presented family are Type 1. For each odd \(i \geq 3\), let \(L'_t(i)\) be the snark obtained by a superposition of Loupekine snark \(L_{i}\) with a \(t\)-Blowup snark, \(t\geq 6\).
| Superedge | Deleted | Superedge | Deleted |
| \(\psi’_1\) | \(\{a_2,a_3\}\) | \(\psi’_4\) | \(\{k_1,l_3\}\) |
| \(\psi’_2\) | \(\{b_1,l_3\}\) | \(\psi’_5\) | \(\{k_1,h_4\}\) |
| \(\psi’_3\) | \(\{a_2,j_3\}\) | \(\psi’_6\) | \(\{b_1,b_4\}\) |
Similarly to the previous superpositions, the superedges \(\psi'_i\) for \(1\leq i\leq 6\), depicted in Figure 30, are formed by deleting, from the \(t\)-Blowup snark, with \(t\geq 6\) (Figure 29), the two nonadjacent vertices represented in Table 4, and replacing each edge incident to these vertices with the corresponding semiedge.
Consider the Loupekine snark \(L_3\) presented in Figure 4(a). To obtain its superposition \(L'_t(3)\), depicted in Figure 31(a), replace the following edges by the corresponding superedges: edge \(v_6 v_7\) by a copy of the superedge \(\psi'_3\); edge \(v_7 u_7\) by a copy of the superedge \(\psi'_4\); edge \(u_7 u_6\) by a copy of the superedge \(\psi'_3\); edge \(u_6 w_7\) by a copy of the superedge \(\psi'_5\); edge \(w_7 w_6\) by a copy of the superedge \(\psi'_1\); and edge \(w_6 v_6\) by a copy of the superedge \(\psi'_2\).
Second, make the junction of the remaining semiedges (which are those of the same color and extreme vertices of different colors), between pairs of clockwise consecutive superedges accordingly, say \(\psi'_3\) with \(\psi'_4\), \(\psi'_4\) with \(\psi'_3\), \(\psi'_3\) with \(\psi'_5\), \(\psi'_5\) with \(\psi'_1\), \(\psi'_1\) with \(\psi'_2\) and \(\psi'_2\) with \(\psi'_3\).
We refer to Figures 31(b) and 33(b), for the superpositions \(L'_t(5)\) and \(L'_t(7)\) obtained from \(L_5\) (Figure 4(c)) and \(L_7\) (Figure 5), respectively. Similarly, the superpositions \(L'_t(i)\) with odd \(i\geq 5\) and \(t\geq 6\) are obtained by replacing: the edges \(v_6 v_7\), \(v_7 u_7\), \(u_7 u_6\), by a copy of the superedge \(\psi'_3\), \(\psi'_4\), \(\psi'_3\), respectively; the edges \(u_6 u^{i}_7\), \(u^{5}_6 w_7\), \(w_7 w_6\), \(w_6 v^{5}_6\), \(v^{i}_7 v_6\) by a copy of the superedge \(\psi'_5\), \(\psi'_6\), \(\psi'_1\), \(\psi'_2\) and \(\psi'_4\), respectively; the edges \(u^{j}_6 u^{j}_7\), \(v^{j}_6 v^{j}_7\), odd \(5\leq j \leq i\) by a copy of the superedge \(\psi'_1\), \(\psi'_3\) respectively ; the edges \(u^{j-2}_7 u^{j}_6\), \(v^{j}_6 v^{j-2}_7\), for odd \(5\leq j \leq i\) by a copy of the superedges \(\psi'_6\), \(\psi'_4\), respectively; and make the junctions of the remaining semiedges between pairs of clockwise consecutive superedges.
Following Kochol’s construction, the remaining edges (resp. vertices) are replaced by superedges \(L'\) (resp. supervertices \(K'\)), which is equivalent to maintain the original edges (resp. vertices) of the \(L_{i}\), for odd \(i \geq 5\). Moreover, if \(v\in V\) is incident to \(e\in E\), then a connector in \(\vartheta_v\) is linked with a connector in \(\xi_e\) through the junction of semiedges.
Proof. Let \(t\geq 6\). The proof is by induction. As previously explained, \(L'_t(i)\), odd \(i\geq 3\) is obtained from \(L_{i}\) by replacing certain edges with superedges \(\psi'\).
It is easy to verify that the assignment presented in Figure 31(a) (resp. 31(b)) is a \(4\)-total coloring for \(L'_t(3)\) (resp. \(L'_t(5)\)), since this coloring preserves the colors of the corresponding elements in \(L_3\) (resp. \(L_5\)); the junctions are made between semiedges of the same color; and the extreme vertices of the edges corresponding to these junctions have different colors.
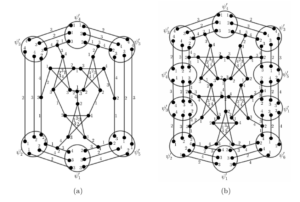
The \(4\)-total coloring of each superedge \(\psi'\) is obtained from the \(4\)-total coloring of the \(t\)-Blowup snark with the two deleted nonadjacent vertices of \(B'_4\) represented in Table 4 (Figure 29). The colors of the semiedges are the colors of the respective edges incident to these deleted vertices. This is possible since the \(4\)-total coloring of semigraph \(B'_4\) appears in every \(t\)-Blowup, with \(t\geq 6\).
The proof is similar to the previous proofs. For example, it is straightforward to construct \(L_t(7)\) from Figures 32(a), and 32(b). In general, for \(L'_t(i)\), the \(4\)-total coloring of the superedges that replaced the edges \(v^{i}_7 v_6\), \(u_6u^{i}_7\) from \(L'_{i-2}\) are the same of the coloring of \(\psi'_4\) and \(\psi'_5\), respectively; the \(4\)-total coloring of the superedges that replaced the edges \(v^{i}_7 v^{i}_6\), \(u^{i}_7 u^{i}_6\) from the link graph \(L_i\) are the same of the coloring of \(\psi'_3\) and \(\psi'_1\), respectively; the \(4\)-total coloring of the superedges that replaced the edges \(v^{i-2}_7 v^{i}_6\), \(u^{i-2}_7 u^{i}_6\) from the link graph \(L_i\) are the same of the coloring of \(\psi'_4\) and \(\psi'_6\), respectively; and the \(4\)-total coloring of the remaining superedges \(\psi'\) in \(L'_t(i)\) is obtained from the \(4\)-total coloring of its corresponding superedge in \(L'_t(i-2)\).
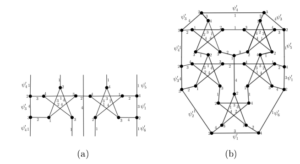
Again, the junctions are made between semiedges of the same color and the extreme vertices of the edges corresponding to these junctions have different colors. Note that the junctions of these semiedges preserve the colors, since the same junctions are made in the \(4\)-total coloring of \(L_t(7)\) (the superedges of \(L_7\) are indicated in Figure 33(a) and depicted in Figure 33(b). This ends the proof. ◻
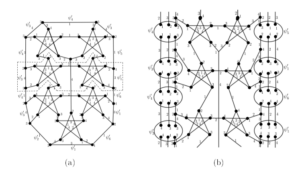
In this paper, we analyze Question 1.2, proposed by Brinkmann, Preissmann and D. Sasaki [2], investigating the Problem 1.1 for cubic graphs. We emphasize that the Loupekine, Goldberg, \(t\)-SemiBlowup and \(t\)-Blowup snarks studied in this paper have girth greater than or equal to \(5\). Hence, once the studied graphs \(R_t(i)\), \(R'_t(i)\), \(L_t(i)\) and \(L'_t(i)\) are obtained by Kochol’s superposition, the girth of the resulting graph is determined by the smallest cycle between the original graphs involved in this operation. Thus, for fixed \(i\) or \(t\), we construct a family of Type 1 cubic graphs with girth greater than or equal to 5, and these results provide evidence of negative answer for the Question 1.2.
This work was partially supported by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior – Brasil (CAPES) – Finance Code 001; the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) 151052/2023-9, 311260/2021-7, 313797/2020-0; and the Fundação Carlos Chagas Filho de Amparo à Pesquisa do Estado do Rio de Janeiro (FAPERJ) Processo SEI 260003/014835/2023, E-26/010.002674/2019, E-26/201.360/2021.
1970-2025 CP (Manitoba, Canada) unless otherwise stated.