In this paper, we identify LWO graphs, f\-ind the minimum \(\lambda\) for decomposition of \(\lambda K_n\) into these graphs, and show that for all viable values of \(\lambda\), the necessary conditions are suf\-f\-icient for LWO–decompositions using cyclic decompositions from base graphs.
Decompositions of graphs into subgraphs is a well–known classical problem. For an excellent survey on graph decompositions, see [1]. Recently, several people including Chan [4], El–Zanati, Lapchinda, Tangsupphathawat and Wannasit [5], Hein [6-9], Hurd [13], Malick [14], Sarvate [10-12], Winter [16,17] and Zhang [18] have results on decomposing \(\lambda K_n\) into multigraphs. In fact, similar decompositions have been attempted earlier in various papers (see [15]). Ternary designs also provide such decompositions (see [2,3]).
Hein [6-9] showed how to decompose \(\lambda K_n\) into LO, LE, LW, OW, LOW and OLW graphs. In this paper’s extension of the previous work, we show how to decompose \(\lambda K_n\) into LWO graphs. Though the main technique used is to construct appropriate base graphs and to develop them cyclically, an additional approach is needed in this type of decomposition.
For simplicity of notation, we use the “alphabetic labeling” used in [6-12,16-18]:
Definition 1. An LWO graph (denoted \(( a, b, c, d)\)) on \(V= \{ a, b\), \(c, d\}\) is a graph with 7 edges where the frequencies of edges \(\{a, b\}\), \(\{b, c\}\) and \(\{c, d\}\) are 1, 4 and 2 (respectively).
Definition 2. For positive integers \(n\ge 4\) and \(\lambda \ge 4\), an LWO–decomposition of \(\lambda K_n\) (denoted LWO\((n, \lambda )\)) is a collection of LWO graphs such that the multiunion of their edge sets contains \(\lambda\) copies of all edges in a \(K_n\).
One of the powerful techniques to construct combinatorial designs is based on difference sets and difference families (see [19] for details). This technique is modified to achieve our decompositions of \(\lambda K_n\) — in general, we exhibit the base graphs, which can be developed to obtain the decomposition.
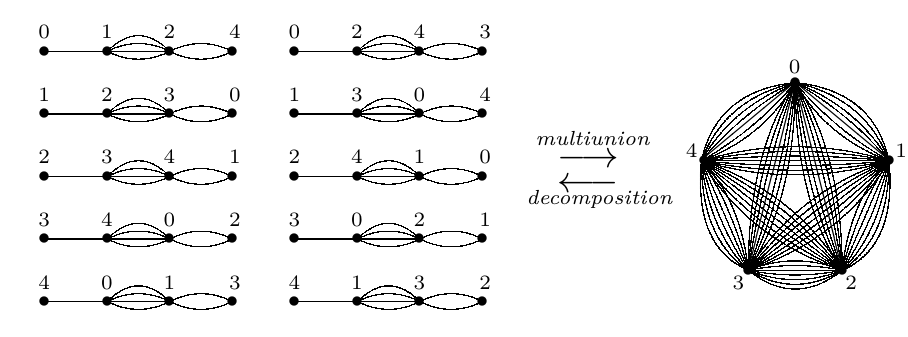
Example 1. Considering the set of points to be \(V= \mathbb{Z}_5\), the LWO base graphs \(( 0, 1, 2, 4)\) and \(( 0, 2, 4, 3)\) when developed modulo 5 constitute an LWO\((5, 7)\).
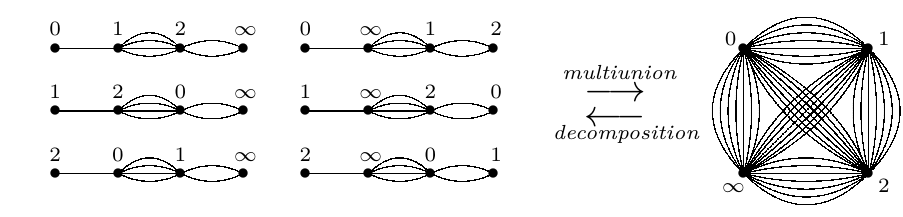
We note that special attention is needed with base graphs containing the “dummy element” \(\infty\). The non–\(\infty\) elements are developed, while \(\infty\) is simply rewritten each time.
Example 2. Considering the set of points to be \(V= \mathbb{Z}_3 \cup \{\infty \}\), the LWO base graphs \(( 0, 1, 2, \infty )\) and \(( 0, \infty , 1, 2)\) when developed modulo 3 constitute an LWO\((4, 7)\).
We first address the minimum values of \(\lambda\) in an LWO\((n, \lambda )\). Recall that \(\lambda \ge 4\).
Theorem 1. Let \(n\ge 4\). The minimum values of \(\lambda\) for which an LWO\((n, \lambda )\) could exist are \(\lambda =4\) when \(n\equiv 0, 1\pmod{7}\) and \(\lambda =7\) when \(n\not\equiv 0, 1\pmod{7}\).
Proof. Since there are \(\frac{\lambda n(n- 1)}{2}\) edges in a \(\lambda K_n\), and 7 edges in an LWO graph, we must have that \(\lambda n(n- 1) \equiv 0 \pmod{14}\) (where \(n\ge 4\) and \(\lambda \ge 4\)) for LWO–decompositions. The result follows from cases on \(n\pmod{14}\). ◻
We are now in a position to prove the main claim of the paper. We first remark that an LWO graph has 4 vertices; that is, we consider \(n\ge 4\). We use difference sets to achieve our decompositions of \(\lambda K_n\). In general, we exhibit the base graphs, which can be developed (modulo either \(n\) or \(n- 1\)) to obtain the decomposition. We also note that the frequency of the edges is fixed by position, as per the LWO graph.
Theorem 2. The minimum number copies of \(K_n\) as given in Theorem 1 can be decomposed into LWO graphs.
Proof. Let \(n\ge 4\). We proceed by cases on \(n \pmod{14}\).
If \(n= 14t\) (for \(t\ge 1\)), we consider the set \(V\) as \(\mathbb{Z}_{14t -1}\cup \{ \infty\}\). The number of graphs required for LWO\((14t, 4)\) is \(\frac{4(14t)(14t -1)}{14}= 4t (14t -1)\). Thus, we need \(4t\) base graphs (modulo \(14t- 1\)). Then, the differences we must achieve (modulo \(14t -1\)) are \(1, 2, \ldots , 7t- 1\). For the first four base graphs, we use \(( \infty , 0, 3t, 6t- 1)\), \(( \infty , 0, 3t+ 1, 6t)\), \(( \infty , 0, 3t+ 2, 6t)\) and \(( \infty, 0, 3t +3, 6t +1)\). We also use the \(4t- 4\) base graphs \(( 0, 1, 3t+ 5, 6t+ 2)\), \(( 0, 1, 3t+ 6, 6t+ 3)\), \(( 0, 1, 3t+ 7, 6t+ 3)\), \(( 0, 1, 3t+ 8, 6t+ 4) , ( 0, 2, 3t+ 10, 6t+ 5)\), \(( 0, 2, 3t+ 11, 6t+ 6)\), \(( 0, 2, 3t+ 12, 6t+ 6)\), \(( 0, 2, 3t+ 13, 6t+ 7) , \ldots , %( 0, t- 2, 8t- 10, 9t- 7)$, $( 0, t- 2, 8t- 9, 9t- 6)$, $( 0, t- 2, 8t- 8, 9t- 6)$, $( 0, t- 2, 8t- 7, 9t- 5)$, $ ( 0, t- 1, 8t- 5, 9t- 4)\), \(( 0, t- 1, 8t- 4, 9t- 3)\), \(( 0, t- 1, 8t- 3, 9t- 3)\) and \(( 0, t- 1, 8t- 2, 9t- 2)\) if necessary. Hence, in this case, LWO\((14t, 4)\) exists.
If \(n= 14t +1\) (for \(t\ge 1\)), we consider the set \(V\) as \(\mathbb{Z}_{14t+ 1}\). The number of graphs required for LWO\((14t+ 1, 4)\) is \(\frac{4(14t+ 1)(14t)}{14}= 4t (14t+ 1)\). Thus, we need \(4t\) base graphs (modulo \(14t+ 1\)). Then, the differences we must achieve (modulo \(14t +1\)) are \(1, 2, \ldots , 7t\). We use the base graphs \(( 0, 1, 3t+ 2, 6t+ 2)\), \(( 0, 1, 3t+ 3, 6t+ 3)\), \(( 0, 1, 3t+ 4, 6t+ 3)\), \(( 0, 1, 3t+ 5, 6t+ 4)\), \(( 0, 2, 3t+ 7, 6t+ 5)\), \(( 0, 2, 3t+ 8, 6t+ 6)\), \(( 0, 2, 3t+ 9, 6t+ 6)\), \(( 0, 2, 3t+ 10, 6t+ 7) , \ldots , %( 0, t- 1, 2t+ 3, 5t+ 11)$, $( 0, t- 1, 2t+ 3, 5t+ 10)$, $( 0, t- 1, 2t+ 2, 5t+ 8)$, $( 0, t- 1, 2t+ 2, 5t+ 7)$, $ ( 0, t, 8t- 3, 9t- 1)\), \(( 0, t, 8t- 2, 9t)\), \(( 0, t, 8t- 1, 9t)\) and \(( 0, t, 8t, 9t+ 1)\). Hence, in this case, LWO\((14t +1, 4)\) exists.
If \(n= 14t +2\) (for \(t\ge 1\)), we consider the set \(V\) as \(\mathbb{Z}_{14t +1}\cup \{ \infty\}\). The number of graphs required for LWO\((14t+ 2, 7)\) is \(\frac{7(14t +2)(14t +1)}{14}= (7t+ 1)(14t +1)\). Thus, we need \(7t+ 1\) base graphs (modulo \(14t+ 1\)). Then, the differences we must achieve (modulo \(14t +1\)) are \(1, 2, \ldots , 7t\). For the first two base graphs, we use \(( 0, \infty , 1, 7t+ 1)\) and \(( 0, 7t, 14t, \infty )\). We also use the \(7t- 1\) base graphs \(( 0, 1, 2, 7t+ 1)\), \(( 0, 2, 4, 7t+ 2)\), \(( 0, 3, 6, 7t+ 3) , \ldots , ( 0, 7t- 3, 14t- 6, 14t- 3)\), \(( 0, 7t- 2, 14t- 4, 14t- 2)\) and \(( 0, 7t- 1, 14t- 2, 14t- 1)\). Hence, in this case, LWO\((14t +2, 7)\) exists.
If \(n= 14t +3\) (for \(t\ge 1\)), we consider the set \(V\) as \(\mathbb{Z}_{14t +3}\). The number of graphs required for LWO\((14t+ 3, 7)\) is \(\frac{7(14t +3)(14t +2)}{14}= (7t+ 1)(14t +3)\). Thus, we need \(7t+ 1\) base graphs (modulo \(14t+ 3\)). Then, the differences we must achieve (modulo \(14t +3\)) are \(1, 2, \ldots , 7t +1\). For the first three base graphs, we use \(( 0, 7t+ 1, 7t+ 2, 14t+ 2 )\), \(( 0, 7t, 14t+ 1, 14t+ 2 )\) and \(( 0, 1, 7t+ 1, 14t+ 2)\). We also use the \(7t- 2\) base graphs \(( 0, 2, 4, 7t+ 3)\), \(( 0, 3, 6, 7t+ 4)\), \(( 0, 4, 8, 7t+ 5) , \ldots , ( 0, 7t- 3, 14t- 6, 14t- 2)\), \(( 0, 7t- 2, 14t- 4, 14t- 1)\) and \(( 0, 7t- 1, 14t- 2, 14t)\). Hence, in this case, LWO\((14t +3, 7)\) exists.
If \(n= 14t+ 4\) (for \(t\ge 0\)), we consider the set \(V\) as \(\mathbb{Z}_{14t+ 3}\cup \{ \infty\}\). The number of graphs required for LWO\((14t+ 4, 7)\) is \(\frac{7(14t+ 4)(14t+ 3)}{14}= (7t+ 2)(14t+ 3)\). Thus, we need \(7t+ 2\) base graphs (modulo \(14t+ 3\)). Then, the differences we must achieve (modulo \(14t +3\)) are \(1, 2, \ldots , 7t+ 1\). For the first two base graphs, we use \(( 0, \infty , 1, 7t+ 2)\) and \(( 0, 7t+ 1, 14t+ 2, \infty )\). We also use the \(7t\) base graphs \(( 0, 1, 2, 7t+ 2)\), \(( 0, 2, 4, 7t+ 3)\), \(( 0, 3, 6, 7t+ 4) , \ldots , ( 0, 7t- 2, 14t- 4, 14t- 1)\), \(( 0, 7t- 1, 14t- 2, 14t)\) and \(( 0, 7t, 14t, 14t+ 1)\) if necessary. Hence, in this case, LWO\((14t +4, 7)\) exists.
If \(n= 14t+ 5\) (for \(t\ge 0\)), we consider the set \(V\) as \(\mathbb{Z}_{14t+ 5}\). The number of graphs required for LWO\((14t+ 5, 7)\) is \(\frac{7(14t+ 5)(14t+ 4)}{14}= (7t+ 2)(14t+ 5)\). Thus, we need \(7t+ 2\) base graphs (modulo \(14t+ 5\)). Then, the differences we must achieve (modulo \(14t +5\)) are \(1, 2, \ldots , 7t+ 2\). When \(t= 0\) (that is, when \(n= 5\)), we use the base graphs \(( 0, 2, 3, 4)\) and \(( 1, 0, 2, 4)\). When \(t\geq 1\) (that is, when \(n\geq 19\)), we use the base graphs \(( 0, 7t+ 2, 7t+ 3, 14t+ 4)\), \(( 0, 7t+ 1, 14t+ 3, 14t+ 4 )\) and \(( 0, 1, 7t+ 2, 14t+ 4)\) as well as the \(7t- 1\) base graphs \(( 0, 2, 4, 7t+ 4)\), \(( 0, 3, 6, 7t+ 5)\), \(( 0, 4, 8, 7t+ 6) , \ldots , ( 0, 7t- 2, 14t- 4, 14t)\), \(( 0, 7t- 1, 14t- 2, 14t+ 1)\) and \(( 0, 7t, 14t, 14t+ 2)\). Hence, in this case, LWO\((14t +5, 7)\) exists.
If \(n= 14t+ 6\) (for \(t\ge 0\)), we consider the set \(V\) as \(\mathbb{Z}_{14t+ 5}\cup \{ \infty \}\). The number of graphs required for LWO\((14t+ 6, 7)\) is \(\frac{7(14t+ 6)(14t+ 5)}{14}= (7t+ 3)(14t+ 5)\). Thus, we need \(7t+ 3\) base graphs (modulo \(14t+ 5\)). Then, the differences we must achieve (modulo \(14t +5\)) are \(1, 2, \ldots , 7t+ 2\). For the first two base graphs, we use \(( 0, \infty , 1, 7t+ 3)\) and \(( 0, 7t+ 2, 14t+ 4, \infty )\). We also use the \(7t+ 1\) base graph(s) \(( 0, 1, 2, 7t+ 3)\), \(( 0, 2, 4, 7t+ 4)%$, $( 0, 3, 6, 7t+ 5) , \ldots , %( 0, 7t- 1, 14t- 2, 14t+ 1)$, $ ( 0, 7t, 14t, 14t+ 2)\) and \(( 0, 7t+ 1, 14t+ 2, 14t+ 3)\). Hence, in this case, LWO\((14t +6, 7)\) exists.
If \(n= 14t+ 7\) (for \(t\ge 0\)), we consider the set \(V\) as \(\mathbb{Z}_{14t+ 6}\cup \{ \infty \}\). The number of graphs required for LWO\((14t+ 7, 4)\) is \(\frac{4(14t+ 7)(14t+ 6)}{14}= (4t+ 2)(14t+ 6)\). Thus, we need \(4t+ 2\) base graphs (modulo \(14t+ 6\)). Then, the differences we must achieve (modulo \(14t +6\)) are \(1, 2, \ldots , 7t+ 3\). For the first two base graphs, we use \(( 0, 7t+ 3, 14t+ 5, \infty )\) and \(( 0, 7t+ 3, 14t+ 4, \infty )\). We also use the \(4t\) base graphs \(( 0, 1, 5t+ 1, 10t+ 2)\), \(( 0, 1, 5t, 10t+ 1)\), \(( 0, 1, 5t- 1, 10t+ 1)\), \(( 0, 1, 5t- 2, 10t)\), \(( 0, 2, 5t- 2, 10t+ 1)\), \(( 0, 2, 5t- 3, 10t)\), \(( 0, 2, 5t- 4, 10t)\), \(( 0, 2, 5t- 5, 10t- 1) , \ldots , %( 0, t- 1, 2t+ 7, 9t+ 4)$, $( 0, t- 1, 2t+ 6, 9t+ 3)$, $( 0, t- 1, 2t+ 5, 9t+ 3)$, $( 0, t- 1, 2t+ 4, 9t+ 2)$, $ ( 0, t, 2t+ 4, 9t+ 3)\), \(( 0, t, 2t+ 3, 9t+ 2)\), \(( 0, t, 2t+ 2, 9t+ 2)\) and \(( 0, t, 2t+ 1, 9t+ 1)\) if necessary. Hence, in this case, LWO\((14t +7, 4)\) exists.
If \(n= 14t+ 8\) (for \(t\ge 0\)), we consider the set \(V\) as \(\mathbb{Z}_{14t+ 8}\). The number of graphs required for LWO\((14t+ 8, 4)\) is \(\frac{4(14t+ 8)(14t+ 7)}{14}= (4t+ 2)(14t+ 8)\). Thus, we need \(4t+ 2\) base graphs (modulo \(14t+ 8\)). Then, the differences we must achieve (modulo \(14t +8\)) are \(1, 2, \ldots , 7t+ 4\). When \(t= 0\) (that is, when \(n= 8\)), we use the base graphs \(( 0, 4, 5, 2)\) and \(( 0, 4, 6, 3)\). When \(t\geq 1\) (that is, when \(n\geq 22\)), we use the base graphs \(( 0, 7t+ 4, 7t+ 5, 7t+ 8)\) and \(( 0, 7t+ 4, 7t+ 6, 7t+ 9)\) as well as \(( 0, 7t+ 3, 13t+ 6, 13t+ 10)\), \(( 0, 7t+ 3, 13t+ 5, 13t+ 9)\), \(( 0, 7t+ 3, 13t+ 4, 13t+ 9)\), \(( 0, 7t+ 3, 13t+ 3, 13t+ 8)\), \(( 0, 7t+ 2, 13t+ 1, 13t+ 7)\), \(( 0, 7t+ 2, 13t, 13t+ 6)\), \(( 0, 7t+ 2, 13t- 1, 13t+ 6)\), \(( 0, 7t+ 2, 13t- 2, 13t+ 5) , \ldots , %( 0, t+ 2, 2t+ 9, 5t+ 20)$, $( 0, t+ 2, 2t+ 9, 5t+ 19)$, $( 0, t+ 2, 2t+ 8, 5t+ 17)$, $( 0, t+ 2, 2t+ 8, 5t+ 16)$, $ ( 0, 6t+ 4, 8t+ 11, 10t+ 13)\), \(( 0, 6t+ 4, 8t+ 10, 10t+ 12)\), \(( 0, 6t+ 4, 8t+ 9, 10t+ 12)\) and \(( 0, 6t+ 4, 8t+ 8, 10t+ 11)\). Hence, in this case, LWO\((14t +8, 4)\) exists.
If \(n= 14t+ 9\) (for \(t\ge 0\)), we consider the set \(V\) as \(\mathbb{Z}_{14t+ 9}\). The number of graphs required for LWO\((14t+ 9, 7)\) is \(\frac{7(14t+ 9)(14t+ 8)}{14}= (7t+ 4)(14t+ 9)\). Thus, we need \(7t+ 4\) base graphs (modulo \(14t+ 9\)). Then, the differences we must achieve (modulo \(14t +9\)) are \(1, 2, \ldots , 7t+ 4\). We use the base graphs \(( 0, 7t+ 4, 7t+ 5, 14t+ 8)\), \(( 0, 7t+ 3, 14t+ 7, 14t+ 8)\) and \(( 0, 1, 7t+ 4, 14t+ 8)\) as well as \(( 0, 2, 4, 7t+ 6)\), \(( 0, 3, 6, 7t+ 7)\), \(( 0, 4, 8, 7t+ 8) , \ldots , ( 0, 7t, 14t, 14t+ 14)\), \(( 0, 7t+ 1, 14t+ 2, 14t+ 5)\) and \(( 0, 7t+ 2, 14t+ 4, 14t+ 6)\). Hence, in this case, LWO\((14t +9, 7)\) exists.
If \(n= 14t+ 10\) (for \(t\ge 0\)), we consider the set \(V\) as \(\mathbb{Z}_{14t+ 9}\cup \{ \infty \}\). The number of graphs required for LWO\((14t+ 10, 7)\) is \(\frac{7(14t+ 10)(14t+ 9)}{14}\) \(=(7t+ 5)(14t+ 9)\). Thus, we need \(7t+ 5\) base graphs (modulo \(14t+ 9\)). Then, the differences we must achieve (modulo \(14t +9\)) are \(1, 2, \ldots , 7t+ 4\). For the first five base graphs, we use \(( 0, 7t+ 4, \infty , 1)\), \(( \infty , 0, 7t+ 4, 14t+ 8)\), \(( 0, 7t+ 3, 7t+ 4, 14t+ 6)\), \(( 0, 7t+ 2, 14t+ 5, 14t+ 6)\) and \(( 0, 1, 7t+ 3, 14t+ 6)\). We also use the \(7t\) base graphs \(( 0, 2, 4, 7t+ 5)\), \(( 0, 3, 6, 7t+ 6)\), \(( 0, 4, 8, 7t+ 7) , \ldots , ( 0, 7t- 1, 14t- 2, 14t+ 2)\), \(( 0, 7t, 14t, 14t+ 3)\) and \(( 0, 7t+ 1, 14t+ 2, 14t+ 4)\) if necessary. Hence, in this case, LWO\((14t +10, 7)\) exists.
If \(n= 14t+ 11\) (for \(t\ge 0\)), we consider the set \(V\) as \(\mathbb{Z}_{14t+ 11}\). The number of graphs required for LWO\((14t+ 11, 7)\) is \(\frac{7(14t+ 11)(14t+ 10)}{14}= (7t+ 5)(14t+ 11)\). Thus, we need \(7t+ 5\) base graphs (modulo \(14t+ 11\)). Then, the differences we must achieve (modulo \(14t +11\)) are \(1, 2, \ldots , 7t+ 5\). For the first three base graphs, we use \(( 0, 7t+ 5, 7t+ 6, 14t+ 10)\), \(( 0, 7t+ 4, 14t+ 9, 14t+ 10)\) and \(( 0, 1, 7t+ 5, 14t+ 10)\). We also use the \(7t+ 2\) base graphs \(( 0, 2, 4, 7t+ 7)\), \(( 0, 3, 6, 7t+ 8)\), \(( 0, 4, 8, 7t+ 9) , \ldots , ( 0, 7t+ 1, 14t+ 2, 14t+ 6)\), \(( 0, 7t+ 2, 14t+ 4, 14t+ 7)\) and \(( 0, 7t+ 3, 14t+ 6, 14t+ 8)\). Hence, in this case, LWO\((14t +11, 7)\) exists.
If \(n= 14t+ 12\) (for \(t\ge 0\)), we consider the set \(V\) as \(\mathbb{Z}_{14t+ 11}\cup \{\infty \}\). The number of graphs required for LWO\((14t+ 12, 7)\) is \(\frac{7(14t+ 12)(14t+ 11)}{14}\) \(=(7t+ 6)(14t+ 11)\). Thus, we need \(7t+ 6\) base graphs (modulo \(14t+ 11\)). Then, the differences we must achieve (modulo \(14t +11\)) are \(1, 2, \ldots , 7t+ 5\). For the first two base graphs, we use \(( 0, 7t+ 5, \infty , 1)\) and \(( \infty , 0, 7t+ 5, 14t+ 10)\). We also use the \(7t+ 4\) base graphs \(( 0, 1, 2, 7t+ 6)\), \(( 0, 2, 4, 7t+ 7)\), \(( 0, 3, 6, 7t+ 8) , \ldots , ( 0, 7t+ 2, 14t+ 4, 14t+ 7)\), \(( 0, 7t+ 3, 14t+ 6, 14t+ 8)\) and \(( 0, 7t+ 4, 14t+ 8, 14t+ 9)\). Hence, in this case, LWO\((14t +12, 7)\) exists.
If \(n= 14t+ 13\) (for \(t\ge 0\)), we consider the set \(V\) as \(\mathbb{Z}_{14t+ 13}\). The number of graphs required for LWO\((14t+ 13, 7)\) is \(\frac{7(14t+ 13)(14t+ 12)}{14}= (7t+ 6)(14t+ 13)\). Thus, we need \(7t+ 6\) base graphs (modulo \(14t+ 13\)). Then, the differences we must achieve (modulo \(14t +13\)) are \(1, 2, \ldots , 7t+ 6\). For the first three base graphs, we use \(( 0, 7t+ 6, 7t+ 7, 14t+ 12 )\), \(( 0, 7t+ 5, 14t+ 11, 14t+ 12)\) and \(( 0, 1, 7t+ 6, 14t+ 12)\). We also use the \(7t+ 3\) base graphs \(( 0, 2, 4, 7t+ 8)\), \(( 0, 3, 6, 7t+ 9)\), \(( 0, 4, 8, 7t+ 10) , \ldots , ( 0, 7t+ 2, 14t+ 4, 14t+ 8)\), \(( 0, 7t+ 3, 14t+ 6, 14t+ 9)\) and \(( 0, 7t+ 4, 14t+ 8, 14t+ 10)\). Hence, in this case, LWO\((14t +13, 7)\) exists. ◻
We now address the sufficiency of existence of LWO\((n, \lambda )\).
Theorem 3. Let \(n\ge 4\) and \(\lambda \ge 4\). For existence of LWO\((n, \lambda )\), the necessary condition for \(n\) is that \(n\equiv 0, 1\pmod{7}\) when \(\lambda\not\equiv 0\pmod{7}\). There is no condition for \(n\) when \(\lambda\equiv 0\pmod{7}\).
Proof. Similar to the proof of Theorem 1, but by cases on \(\lambda \pmod{14}\). ◻
Lemma 1. There exists an LWO\((n, 4)\) for necessary \(n\ge 4\).
Proof. From Theorem 3, the necessary condition is \(n\equiv 0, 1, 7\), \(8\pmod{14}\). In these cases, LWO\((n, 4)\) exists from Theorem 2. ◻
Lemma 2. There does not exist an LWO\((n, 5)\).
Proof. The only edge frequencies in an LWO graph are 1, 2 and 4. The only ways to write \(\lambda =5\) as a sum of \(1\)s, \(2\)s and \(4\)s are as \(5= 4+ 1\), \(5= 2+ 2+ 1\), \(5= 2+ 1+ 1+ 1\) and \(5= 1+ 1+ 1+ 1+ 1\). In an LWO\((n, 5)\), the number of times each edge needs to occur with frequency 4 is always the same as the number of times it needs to occur with frequency 1. Every other way to realize \(\lambda =5\) using edge frequencies of 2 will contribute at least one more unmatched edge frequency of 1. Thus, such a decomposition is not possible. ◻
Lemma 3. There exists an LWO\((n, 6)\) for necessary \(n\ge 4\).
Proof. From Theorem 3, the necessary condition is \(n\equiv 0, 1, 7\), \(8\pmod{14}\).
If \(n= 14t\) (for \(t\ge 1\)), we consider the set \(V\) as \(\mathbb{Z}_{14t- 1} \cup \{ \infty \}\). The number of graphs required for LWO\((14t, 6)\) is \(\frac{6(14t)(14t- 1)}{14} = 6t(14t- 1)\). Thus, we need \(6t\) base graphs (modulo \(14t- 1\)). The differences we must achieve (modulo \(14t- 1\)) are \(1, 2, \dots, 7t- 1\). For the first six base graphs, we use \(( \infty , 0, 7t- 1, 14t- 2)\), \(( \infty , 0, 7t- 2, 14t- 4)\), \(( \infty , 0, 7t- 3, 14t- 6)\), \(( \infty , 0, 7t- 4, 14t- 8)\), \(( \infty , 0, 7t- 5, 14t- 10)\) and \(( \infty , 0, 7t- 6, 14t- 12)\). We also use the \(6t- 6\) base graphs \(( 0, 1, 7t- 6, 14t- 13)\), \(( 0, 1, 7t- 7, 14t- 15)\), \(( 0, 1, 7t- 8, 14t- 17)\), \(( 0, 1, 7t- 9, 14t- 19)\), \(( 0, 1, 7t- 10, 14t- 21)\), \(( 0, 1, 7t- 11, 14t- 23) , \ldots , ( 0, t- 1, 2t+ 4, 3t+ 9)\), \(( 0, t- 1, 2t+ 3, 3t+ 7)\), \(( 0, t- 1, 2t+ 2, 3t+ 5)\), \(( 0, t- 1, 2t+ 1, 3t+ 3)\), \(( 0, t- 1, 2t, 3t+ 1)\) and \(( 0, t- 1, 2t- 1, 3t- 1)\) if necessary. Hence, in this case, LWO\((14t, 6)\) exists.
If \(n= 14t+ 1\) (for \(t\ge 1\)), we consider the set \(V\) as \(\mathbb{Z}_{14t+ 1}\). The number of graphs required for LWO\((14t+ 1, 6)\) is \(\frac{6(14t+ 1)(14t)}{14} = 6t(14t+ 1)\). Thus, we need \(6t\) base graphs (modulo \(14t+ 1\)). The differences we must achieve (modulo \(14t+ 1\)) are \(1, 2, \dots, 7t\). We use the base graphs \(( 0, 1, 7t+ 1, 14t)\), \(( 0, 1, 7t, 14t)\), \(( 0, 1, 7t- 1, 14t- 3)\), \(( 0, 1, 7t- 2, 14t- 5)\), \(( 0, 1, 7t- 3, 14t- 7)\), \(( 0, 1, 7t- 4, 14t- 9) , \ldots , ( 0, t, 2t+ 6, 3t+ 12)\), \(( 0, t, 2t+ 5, 3t+ 10)\), \(( 0, t, 2t+ 4, 3t+ 8)\), \(( 0, t, 2t+ 3, 3t+ 6)\), \(( 0, t, 2t+ 2, 3t+ 4)\) and \(( 0, t, 2t+ 1, 3t+ 2)\). Hence, in this case, LWO\((14t+ 1, 6)\) exists.
If \(n= 14t+ 7\) (for \(t\ge 0\)), we consider the set \(V\) as \(\mathbb{Z}_{14t+ 6} \cup \{ \infty \}\). The number of graphs required for LWO\((14t+ 7, 6)\) is \(\frac{6(14t+ 7)(14t+ 6)}{14} = (6t+ 3)(14t+ 6)\). Thus, we need \(6t+ 3\) base graphs (modulo \(14t+ 6\)). The differences we must achieve (modulo \(14t+ 6\)) are \(1, 2, \dots, 7t+ 3\). When \(t= 0\) (that is, when \(n= 7\)), we use the base graphs \(( 0, 3, \infty , 1)\), \(( 0, 3, 4, 2)\) and \(( 0, 3, 5, 4)\). When \(t\geq 1\) (that is, when \(n\geq 21\)), for the first three base graphs we use \(( 0, 7t+ 3, \infty , 1)\), \(( 0, 7t+ 3, 7t+ 4, 13t+ 6)\) and \(( 0, 7t+ 3, 7t+ 5, 13t+ 6)\). We also use the \(6t\) base graphs \(( 0, 7t+ 2, 7t+ 5, 13t+ 5)\), \(( 0, 7t+ 2, 7t+ 6, 13t+ 5)\), \(( 0, 7t+ 2, 7t+ 7, 13t+ 5)\), \(( 0, 7t+ 2, 7t+ 8, 13t+ 5)\), \(( 0, 7t+ 2, 7t+ 9, 13t+ 5)\), \(( 0, 7t+ 2, 7t+ 10, 13t+ 5) , \ldots , ( 0, 6t+ 3, 12t, 12t+ 6)\), \(( 0, 6t+ 3, 12t+ 1, 12t+ 6)\), \(( 0, 6t+ 3, 12t+ 2, 12t+ 6)\), \(( 0, 6t+ 3, 12t+ 3, 12t+ 6)\), \(( 0, 6t+ 3, 12t+ 4, 12t+ 6)\) and \(( 0, 6t+ 3, 12t+ 5, 12t+ 6)\). Hence, in this case, LWO\((14t+ 7, 6)\) exists.
If \(n= 14t+ 8\) (for \(t\ge 0\)), we consider the set \(V\) as \(\mathbb{Z}_{14t+ 8}\). The number of graphs required for LWO\((14t+ 8, 6)\) is \(\frac{6(14t+ 8)(14t+ 7)}{14} = (6t+ 3)(14t+ 8)\). Thus, we need \(6t+ 3\) base graphs (modulo \(14t+ 8\)). The differences we must achieve (modulo \(14t+ 8\)) are \(1, 2, \dots, 7t+ 4\). When \(t= 0\) (that is, when \(n= 8\)), we use the base graphs \(( 0, 4, 5, 2)\), \(( 0, 4, 7, 5)\) and \(( 0, 4, 6, 7)\). When \(t\geq 1\) (that is, when \(n\geq 22\)), for the first three base graphs we use \(( 0, 7t+ 4, 7t+ 5, 13t+ 8)\), \(( 0, 7t+ 4, 7t+ 6, 13t+ 8)\) and \(( 0, 7t+ 4, 7t+ 7, 13t+ 8)\). We also use the \(6t\) base graphs \(( 0, 7t+ 3, 7t+ 7, 13t+ 7)\), \(( 0, 7t+ 3, 7t+ 8, 13t+ 7)\), \(( 0, 7t+ 3, 7t+ 9, 13t+ 7)\), \(( 0, 7t+ 3, 7t+ 10, 13t+ 7)\), \(( 0, 7t+ 3, 7t+ 11, 13t+ 7)\), \(( 0, 7t+ 3, 7t+ 12, 13t+ 7) , \ldots , ( 0, 6t+ 4, 12t+ 2, 12t+ 8)\), \(( 0, 6t+ 4, 12t+ 3, 12t+ 8)\), \(( 0, 6t+ 4, 12t+ 4, 12t+ 8)\), \(( 0, 6t+ 4, 12t+ 5, 12t+ 8)\), \(( 0, 6t+ 4, 12t+ 6, 12t+ 8)\) and \(( 0, 6t+ 4, 12t+ 7, 12t+ 8)\) if necessary. Hence, in this case, LWO\((14t+ 8, 6)\) exists. ◻
Lemma 4. There exists an LWO\((n, 7)\) for any \(n\ge 4\).
Proof. From Theorem 3, there is no condition for \(n\). We consider cases when \(n\ge 4\) is odd or even.
If \(n= 2t+ 1\) (for \(t\ge 2\)), we consider the set \(V\) as \(\mathbb{Z}_{2t+ 1}\). The number of graphs required for LWO\((2t+ 1, 7)\) is \(\frac{7(2t+ 1)(2t)}{14}= t(2t+ 1)\). Thus, we need \(t\) base graphs (modulo \(2t+ 1\)). The differences we must achieve (modulo \(2t+ 1\)) are \(1, 2, \dots, t\). When \(t= 2\) (that is, when \(n= 5\)), we use the base graphs \(( 0, 1, 2, 4)\) and \(( 0, 2, 4, 3)\). When \(t\geq 3\) (that is, when \(n\geq 7\)), for the first three base graphs we use \(( 0, t, 2t- 1, 2t)\), \(( 0, 1, t+ 1, 2t)\) and \(( 0, t- 1, t, 2t)\). We also use the \(t- 3\) base graphs \(( 0, 2, 4, t+ 2)\), \(( 0, 3, 6, t+ 3)\), \(( 0, 4, 8, t+ 4) , \dots, ( 0, t- 4, 2t- 8, 2t- 4)\), \(( 0, t- 3, 2t- 6, 2t- 3)\) and \(( 0, t- 2, 2t- 4, 2t- 2)\) if necessary. Hence, in this case, LWO\((2t +1, 7)\) exists.
If \(n= 2t\) (for \(t\ge 2\)), we consider the set \(V\) as \(\mathbb{Z}_{2t- 1} \cup \{ \infty\}\). The number of graphs required for LWO\((2t, 7)\) is \(\frac{7(2t)(2t- 1)}{14} = t(2t- 1)\). Thus, we need \(t\) base graphs (modulo \(2t- 1\)). The differences we must achieve (modulo \(2t- 1\)) are \(1, 2, \dots, t- 1\). For the first two base graphs, we use \(( 0, t- 1, \infty , t)\) and \(( \infty , 0, t- 1, 2t- 2)\). We also use the \(t- 2\) base graphs \(( 0, 1, 2, t)\), \(( 0, 2, 4, t+ 1)\), \(( 0, 3, 6, t+ 2) , \ldots , ( 0, t- 4, 2t- 8, 2t- 5)\), \(( 0, t- 3, 2t- 6, 2t- 4)\) and \(( 0, t- 2, 2t- 4, 2t- 3)\) if necessary. Hence, in this case, LWO\((2t, 7)\) exists. ◻
The following examples play important roles in this paper.
Example 3. The LWO graphs \(( 1, 2, 6, 4)\), \(( 1, 3, 5, 7)\), \(( 1, 4, 2, 5)\), \(( 1, 7, 2, 5)\), \(( 2, 3, 4, 5)\), \(( 2, 5, 1, 4)\), \(( 2, 5, 7, 6)\), \(( 2, 7, 1, 5)\), \(( 3, 6, 4, 7)\), \(( 4\), \(2, 1, 3)\), \(( 4, 3, 2, 1)\), \(( 4, 5, 6, 7)\), \(( 4, 6, 7, 5)\), \(( 4, 7, 2, 5)\), \(( 5, 1, 6, 3)\), \(( 5, 2\), \(6, 1)\), \(( 5, 3, 1, 4)\), \(( 6, 1, 7, 4)\), \(( 6, 2, 3, 4)\), \(( 6, 3, 7, 4)\), \(( 6, 3, 7, 4)\), \(( 6, 4, 1\), \(5)\), \(( 6, 4, 2, 1)\), \(( 6, 5, 4, 3)\), \(( 7, 3, 6, 1)\), \(( 7, 5, 3, 1)\) and \(( 7, 6, 5, 4)\) constitute an example of an LWO\((7, 9)\) with point set \(V= \{ 1, \ldots , 7\} \,\).
Example 4. The LWO graphs \(( 1, 2, 3, 4)\), \(( 1, 3, 4, 6)\), \(( 1, 5, 2, 6)\), \(( 1, 6, 8, 2)\), \(( 1, 7, 2, 8)\), \(( 2, 5, 7, 8)\), \(( 2, 6, 1, 4)\), \(( 2, 6, 4, 8)\), \(( 3, 2, 4, 1)\), \(( 3\), \(7, 1, 4)\), \(( 3, 8, 5, 6)\), \(( 4, 1, 5, 7)\), \(( 4, 2, 1, 3)\), \(( 4, 2, 3, 6)\), \(( 4, 2, 8, 1)\), \(( 4, 3\), \(5, 6)\), \(( 4, 5, 1, 6)\), \(( 4, 5, 3, 6)\), \(( 4, 5, 6, 7)\), \(( 4, 6, 3, 7)\), \(( 5, 3, 1, 4)\), \(( 5, 6, 7\), \(8)\), \(( 5, 8, 1, 6)\), \(( 6, 2, 5, 4)\), \(( 6, 3, 7, 2)\), \(( 6, 7, 8, 1)\), \(( 6, 8, 5, 7)\), \(( 7, 2, 1, 3)\), \(( 7, 3, 8, 4)\), \(( 7, 3, 8, 6)\), \(( 7, 4, 8, 6)\), \(( 7, 5, 4, 3)\), \(( 8, 1, 7, 6)\), \(( 8, 2, 6, 4)\), \(( 8\), \(4, 7, 2)\) and \(( 8, 7, 4, 2)\) constitute an example of an LWO\((8, 9)\) with point set \(V= \{ 1, \ldots , 8\}\).
Example 5. The LWO graphs \(( a, 1, b, 2)\), \(( a, 2, b, 3)\), \(( a, 3, b, 4)\), \(( a, 4, b, 6)\), \(( a, 5, b, 4)\), \(( a, 7, b, 6)\), \(( b, 2, a, 4)\), \(( b, 3, a, 4)\), \(( b, 4, a, 3)\), \(( b\), \(5, a, 7)\), \(( b, 6, a, 5)\), \(( b, 7, a, 6)\), \(( 1, b, 7, a)\), \(( 3, a, 1, b)\), \(( 3, a, 2, b)\), \(( 3, b, 5\), \(a)\), \(( 3, b, 6, a)\) and \(( 6, a, 1, b)\) constitute an example of an LWO–decomposition of \(9 K_{\{ a, b\} , \{ 1, 2, 3, 4, 5, 6, 7\} }\).
Sarvate, Winter and Zhang [16,17] have obtained several results on such multigraph decompositions of bipartite graphs.
Lemma 5. There exists an LWO\((n, 9)\) for necessary \(n\ge 4\).
Proof. From Theorem 3, the necessary condition is \(n\equiv 0, 1, 7\), \(8\pmod{14}\).
If \(n= 14t\) (for \(t\ge 1\)), we consider the set \(V\) as \(\mathbb{Z}_{14t- 1} \cup \{ \infty \}\). The number of graphs required for LWO\((14t, 9)\) is \(\frac{9(14t)(14t- 1)}{14} = 9t(14t- 1)\). Thus, we need \(9t\) base graphs (modulo \(14t- 1\)). The differences we must achieve (modulo \(14t- 1\)) are \(1, 2, \dots, 7t- 1\). For the first nine base graphs, we use \(( 0, \infty , 1, 7t)\), \(( 0, 7t- 1, 14t- 3, \infty )\), \(( 0, 7t- 2 , 14t- 4, \infty )\), \(( 0, 1, 2, 7t+ 1)\), \(( 0, 7t- 1, 14t- 4, 14t- 3)\), \(( 0, 7t- 3, 14t- 6, 14t- 5)\), \(( 0, 2, 4, 7t+ 3)\), \(( 0, 7t- 1, 14t- 5, 14t- 3)\) and \(( 0, 7t- 4, 14t- 8, 14t- 6)\). We also use the \(9t- 9\) base graphs \(( 0, 3, 6, 7t+ 1)\), \(( 0, 7t- 5, 14t- 11, 14t- 8)\), \(( 0, 7t- 6, 14t- 12, 14t- 9)\), \(( 0, 4, 8, 7t+ 3)\), \(( 0, 7t- 5, 14t- 12, 14t- 8)\), \(( 0, 7t- 7, 14t- 14, 14t- 10)\), \(( 0, 5, 10, 7t+ 5)\), \(( 0, 7t- 5, 14t- 13, 14t- 8)\), \(( 0, 7t- 8, 14t- 16, 14t- 11) , \ldots , ( 0, 3t- 3, 6t- 6, 9t- 3)\), \(( 0, 3t+ 3, 6t+ 5, 9t+ 2)\), \(( 0, 3t+ 2, 6t+ 4, 9t+ 1)\), \(( 0, 3t- 2, 6t- 4, 9t- 1)\), \(( 0, 3t+ 3, 6t+ 4, 9t+ 2)\), \(( 0, 3t+ 1, 6t+ 2, 9t)\), \(( 0, 3t- 1, 6t- 2, 9t+ 1)\), \(( 0, 3t+ 3, 6t+ 3, 9t+ 2)\) and \(( 0, 3t, 6t, 9t- 1)\) if necessary. Hence, in this case, LWO\((14t, 9)\) exists.
If \(n= 14t+ 1\) (for \(t\ge 1\)), we consider the set \(V\) as \(\mathbb{Z}_{14t+ 1}\). The number of graphs required for LWO\((14t+ 1, 9)\) is \(\frac{9(14t+ 1)(14t)}{14} = 9t(14t+ 1)\). Thus, we need \(9t\) base graphs (modulo \(14t+ 1\)). The differences we must achieve (modulo \(14t+ 1\)) are \(1, 2, \dots, 7t\). We use the base graphs \(( 0, 1, 2, 7t+ 2)\), \(( 0, 7t, 14t- 1, 14t)\), \(( 0, 7t- 1, 14t- 2, 14t- 1)\), \(( 0, 2, 4, 7t+ 4)\), \(( 0, 7t, 14t- 2, 14t)\), \(( 0, 7t- 2, 14t- 4, 14t- 2)\), \(( 0, 3, 6, 7t+ 6)\), \(( 0, 7t, 14t- 3, 14t)\), \(( 0, 7t- 3, 14t- 6, 14t- 3)\), \(( 0, 4, 8, 7t+ 4)\), \(( 0, 7t- 4, 14t- 9, 14t- 5)\), \(( 0, 7t- 5, 14t- 10, 14t- 6)\), \(( 0, 5, 10, 7t+ 6)\), \(( 0, 7t- 4, 14t- 10, 14t- 5)\), \(( 0, 7t- 6, 14t- 12, 14t- 7)\), \(( 0, 6, 12, 7t+ 8)\), \(( 0, 7t- 4, 14t- 11, 14t- 5)\), \(( 0, 7t- 7, 14t- 14, 14t- 8) , \ldots , ( 0, 3t- 2, 6t- 4, 9t)\), \(( 0, 3t+ 4, 6t+ 7, 9t+ 5)\), \(( 0, 3t+ 3, 6t+ 6, 9t+ 4)\), \(( 0, 3t- 1, 6t- 2, 9t+ 2)\), \(( 0, 3t+ 4, 6t+ 6, 9t+ 5)\), \(( 0, 3t+ 2, 6t+ 4, 9t+ 3)\), \(( 0, 3t, 6t, 9t+ 4)\), \(( 0, 3t+ 4, 6t+ 5, 9t+ 5)\) and \(( 0, 3t+ 1, 6t+ 2, 9t+ 2)\). Hence, in this case, LWO\((14t+ 1, 9)\) exists.
If \(n= 14t+ 7\) (for \(t\ge 0\)), we consider the set \(V\) as \(\{ a_1 , a_2, \ldots , a_{14t}\), \(b_1 , b_2 , \ldots , b_7 \}\). To obtain an LWO\((14t+ 7, 9)\), we use an LWO\((14t, 9)\) on \(\{ a_1 , a_2 , \ldots , a_{14t}\}\) (given two cases above) if necessary, an LWO\((7, 9)\) on \(\{ b_1 , b_2 , \ldots , b_7 \}\) (as in Example 3), and an LWO–decomposition of \(9 K_{\{ a_{2i -1}, a_{2i}\} , \{ b_1 , b_2 , b_3 , b_4 , b_5 , b_6 , b_7 \} }\) for all \(i= 1, 2\), \(\ldots , 7t\) (as in Example 5) if necessary. Hence, in this case, LWO\((14t+ 7, 9)\) exists.
If \(n= 14t+ 8\) (for \(t\ge 0\)), we consider the set \(V\) as \(\{ a_1 , a_2, \ldots , a_8\), \(b_1 , b_2 , \ldots , b_{14t}\}\). To obtain an LWO\((8+ 14t, 9)\), we use an LWO\((8, 9)\) on \(\{ a_1 , a_2, \ldots , a_8 \}\) (as in Example 4), an LWO\((14t, 9)\) on \(\{ b_1 , b_2 , \ldots\), \(b_{14t}\}\) (given three cases above) if necessary, and an LWO–decomposition of \(9 K_{\{ a_{2i -1}, a_{2i}\} , \{ b_{7j- 6}, b_{7j- 5}, b_{7j- 4}, b_{7j- 3}, b_{7j- 2}, b_{7j- 1}, b_{7j}\} }\) for all \(i= 1, 2\), \(3, 4\) and for all \(j= 1, 2, \ldots , 2t\) (as in Example 5) if necessary. Hence, in this case, LWO\((14t+ 8, 9)\) exists. ◻
Theorem 4. An LWO\((n, \lambda )\) exists for all \(\lambda \ge 4\) except \(\lambda =5\) (according to Lemma 2), for corresponding necessary \(n\ge 4\).
Proof. We proceed by cases on \(\lambda \pmod{7}\).
For \(\lambda \equiv 0 \pmod{7}\) (so that \(\lambda =7t\) for \(t\ge 1\)), by taking \(t\) copies of an LWO\((n, 7)\) (given in Lemma 4), we have an LWO\((n, 7t)\).
For \(\lambda \equiv 1 \pmod{7}\) (so that \(\lambda =7t+ 1= 7(t- 1)+ 8\) for \(t\ge 1\)), we first take two copies of an LWO\((n, 4)\) (given in Lemma 1). (This gives us \(\lambda =8\) thus far.) We then adjoin this to \(t- 1\) copies of an LWO\((n, 7)\) (given in Lemma 4) if necessary. Hence, we have an LWO\((n, 7t+ 1)\).
For \(\lambda \equiv 2 \pmod{7}\) (so that \(\lambda =7t+ 2= 7(t- 1)+ 9\) for \(t\ge 1\)), we first take an LWO\((n, 9)\) (given in Lemma 5). (This gives us \(\lambda =9\) thus far.) We then adjoin this to \(t- 1\) copies of an LWO\((n, 7)\) (given in Lemma 4) if necessary. Hence, we have an LWO\((n, 7t+ 2)\).
For \(\lambda \equiv 3 \pmod{7}\) (so that \(\lambda =7t+ 3= 7(t- 1)+ 10\) for \(t\ge 1\)), we first take an LWO\((n, 4)\) (given in Lemma 1) and an LWO\((n, 6)\) (given in Lemma 3). (This gives us \(\lambda =10\) thus far.) We then adjoin this to \(t- 1\) copies of an LWO\((n, 7)\) (given in Lemma 4) if necessary. Hence, we have an LWO\((n, 7t+ 3)\).
For \(\lambda \equiv 4 \pmod{7}\) (so that \(\lambda =7t+ 4\) for \(t\ge 0\)), we first take an LWO\((n, 4)\) (given in Lemma 1). (This gives us \(\lambda =4\) thus far.) We then adjoin this to \(t\) copies of an LWO\((n, 7)\) (given in Lemma 4) if necessary. Hence, we have an LWO\((n, 7t+ 4)\).
For \(\lambda \equiv 5 \pmod{7}\) (so that \(\lambda =7t+ 5= 7(t- 1)+ 12\) for \(t\ge 1\)), we first take two copies of an LWO\((n, 6)\) (given in Lemma 3). (This gives us \(\lambda =12\) thus far.) We then adjoin this to \(t- 1\) copies of an LWO\((n, 7)\) (given in Lemma 4) if necessary. Hence, we have an LWO\((n, 7t+ 5)\).
For \(\lambda \equiv 6 \pmod{7}\) (so that \(\lambda =7t+ 6\) for \(t\ge 0\)), we first take an LWO\((n, 6)\) (given in Lemma 3). (This gives us \(\lambda =6\) thus far.) We then adjoin this to \(t\) copies of an LWO\((n, 7)\) (given in Lemma 4) if necessary. Hence, we have an LWO\((n, 7t+ 6)\). ◻
We have identified LWO graphs, found the minimum \(\lambda\) for decomposition of \(\lambda K_n\) into these graphs, and shown that for all viable values of \(\lambda\), the necessary conditions are sufficient for LWO–decompositions.
We leave it as an open problem to find decompositions of \(\lambda K_n\) into the (unnamed) graphs

The author declares no conflict of interest.
1970-2025 CP (Manitoba, Canada) unless otherwise stated.