To fulfil the requirements of task scheduling for processing massive amounts of graph data in cloud computing environments, this thesis offers the LGPPSO method, which is based on Particle Swarm Optimisation. The LGPPSO algorithm considers the task’s overall structure when initialising numerous particles in order to broaden the search range and raise the likelihood of finding an approximation optimal solution. We evaluated it in large-scale simulation trials with 100 performance-heterogeneous virtual machines (VMs) using both randomly generated and real application graphs, and evaluated its effectiveness against the CCSH and HEFT algorithms. The experimental findings demonstrate that, in both randomly generated graphs and real graph structure applications, significantly reducing the scheduling duration of large-scale graph data is the LGPPSO algorithm. For randomly generated 200 and 400 node tasks, respectively, the scheduling length is shortened by approximately 8.3% and 9.7% on average when compared to the HEFT algorithm. The LGPPSO technique minimises the scheduling length for actual graphical structure applications by an average of 14.6% and 16.9% for the Gaussian 100 and 200 node examples, respectively.
The study and use of large-scale graph data processing techniques in cloud computing environments has drawn more attention as the information era progresses. Graph data is a naturally occurring, complex data structure that is widely used in traffic management, bioinformatics, social networks, and other domains. Processing graph data efficiently and in real time has become a major challenge for both commercial and scientific applications and research[1,2].
While cloud computing offers numerous benefits for managing huge amounts of graph data, as a generic processing framework, since cloud computing is still in its infancy, processing large amounts of graph data involves a number of important technological challenges [3]. It is challenging to directly apply traditional techniques to graph data processing, particularly for applications like online transaction processing, because graph computation and distributed parallel processing involve intricate processes that call for numerous iterations and data communications.There are two primary obstacles for large-scale graph processing in cloud computing settings:
First off, processing huge graphs computationally takes a while. For example, computing PageRank takes roughly thirty processing iterations, which can be very time- and resource-consuming[4,5]. Common PCs are used as cloud computing nodes, and because of the lengthy processing durations, individual node failures are unavoidable. Thus, in order to lower the fault recovery overhead during large-scale graph processing and to increase computing stability and efficiency, efficient fault-tolerance management techniques are required[6].
Secondly, because graph computing subtasks are strongly coupled, the failure of one subtask might cause other subtasks to fail as well, adding to the complexity of recovery processing[7]. Thus, in order to minimise the overhead associated with fault recovery during large-scale graph processing, minimise the need for repetitive calculation, and enhance the computing stability and efficiency of large-scale graph processing, an efficient fault tolerance management method must be taken into consideration [8].
By adding several particle initializations, the LGPPSO algorithm broadens the scope of the solution space search and raises the probability that the algorithm will find a nearly optimum solution [9]. Using both real application graphs and randomly generated graphs in a large-scale simulation experiment with 100 performance-heterogeneous virtual machines, we verify the efficacy of the LGPPSO algorithm in scheduling large-scale graph data processing tasks. The LGPPSO algorithm successfully lowers the resource leasing cost and schedule duration, as demonstrated by the experimental findings [10]. The advantage of the LGPPSO algorithm in increasing task scheduling efficiency and decreasing resource overhead is demonstrated by comparison with the HEFT and CCSH algorithms. This provides a workable solution for cloud computing environments’ scheduling of large-scale graph data processing activities.
Graph theory is a significant area of mathematics that uses a graph as its research topic. Supergraph theory, polar graph theory, topological graph theory, and other ideas that aid in the graph’s ability to depict the real world from a number of perspectives can all be built from a basic graph[11]. Large-scale graph data management nowadays uses a wide variety of data models. For example, simple and complex node graph models are categorised based on the complexity of the nodes in the graph, while hypergraph and simple graph models are categorised based on the number of vertices that can connect to an edge. The vertices and edges of any model, be it a simple graph model, hypergraph model, simple node model, or sophisticated node model, may have properties [12].
basic graph models. We refer to simple graphs as hypergraphs, not the simple graphs of graph theory. An edge in a basic graph can only join two vertices, which makes loops possible. Processing and storing simple graphs is comparatively simple, and for general applications like PageRank computation and shortest path queries, the expression capabilities of the simple graph are perfectly capable of handling them. Large-scale graph data processing and storage have been organised using the simple graph model by Pregel, Hama, and other systems [13].
Model of hypergraph. A graph’s edges can link any number of vertices. In this approach, the graph’s edges are referred to as hyperedges. Hypergraphs are more useful and hold more data than the straightforward graphs shown above because of this characteristic. An article, for instance, is represented by a graph vertex, and two articles with the same author are represented by each edge. A is the author of three different articles: \({v_1}\) (authors A and B), \({v_2}\) (authors A and C), and \({v_3}\) (authors A and D).
The basic graph storage model is shown in Figure 1, where three independent edges \({e_1},{e_2},{e_3} = \left\{ {{v_1},{v_2}} \right\},\left\{ {{v_1},{v_3}} \right\},\left\{ {{v_2},{v_3}} \right\}\) , cannot immediately remember that author A is the writer of three articles \({v_1}\),\({v_2}\) ,\({v_3}\) at the same time. The hypergraph storage concept is shown in Figure 1, where the hyperedge \({e_1} = \{ {v_1},{v_2},{v_3}\}\) directly preserves the information that A is the author of 3 articles \({v_1}\),\({v_2}\) ,\({v_3}\). Hypergraph models can be used to model applications with complex connections, such as social networks, bioinformatics networks, etc. Hypergraph models are supported by graph database systems like Trinity to handle massive amounts of graph data.
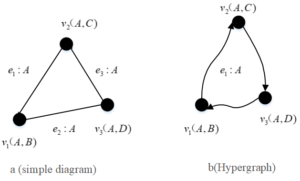
Currently, simple graph and hypergraph, two primary data models with somewhat different organisational storage formats, are employed in large-scale graph data management systems. Both models are capable of handling directed and undirected graphs; directed graphs are the default. An undirected graph is a kind of directed graph since its edges are equivalent to two directed edges[14]. The orientation of edges in a graph will not be the subject of the discussion that follows.
The data models used by NoSQL databases mostly fall into the following categories: graph storage, key-value storage, document storage (Document Store), column family storage (Column Family Store), and additional categories [15]. CouchDB and MongoDB are two common systems that use this store architecture. The document storage model in the storage format is more versatile and better suited for storing system logs and other unstructured data [16]. On the other hand, graph data arranged according to adjacency tables or adjacency matrices is less well-suited for the document storage approach. Furthermore, the document storage model’s reduced processing efficiency, which is intended to facilitate flexibility, may potentially impede large-scale graph data management operations. While the standard row-oriented storage model performs better for exhaustive traversal, the column family storage model is better suited for processing random queries on a column. This storage model is commonly used by BigTable, Hbase, Cassandra, and other systems. Only a few distributed graph databases, like [17], employ the associated research on graph storage model, which is still not ideal, to store graph data.
Large-scale graph data storage is better suited for the Key-Value storage paradigm when compared to the other three storage formats. While the Key-Value storage architecture is ideal for querying or traversing through primary keys, it is not well suited for complicated conditional queries. Its basic storage model allows enormous data storage and high concurrency query execution. Systems like as SimpleDB and Dynamo are typical users of this paradigm. The Key-Value paradigm is ideal from the perspective of graph processing, such as PageRank computation, which doesn’t require intricate queries. If the graph data is organised in an adjacency table, the source vertices of the graph can be used as the Key and the source vertex values, outgoing edges and edge information can be used as the Value. The Key-Key-Value storage model was proposed in literature [18] by fusing the standard Key-Value storage architecture with the Semantic Web. The Key-Key-Value model arranges Alice and Bob’s friendship into a ternary connection, <Alice, Bob, FriendShip>, using the social network as an example. Because this architecture stores richer data than the conventional Key-Value model, it is possible to increase spatial locality by performing data migration and merging in a way that minimises the number of remote reads required for query processing, hence increasing the efficiency of data reading.
Additionally, in order to address the consistency control issue in a distributed context when the graph data is modified, distributed graph databases must have a transaction function. Trinity, HyperGraphDB, and other entities assert that they facilitate consistency control and transaction mechanisms . There is no consistency maintenance issue if the graph data is kept on an HDFS-type distributed file system because it does not permit update and random insertion operations .
The four primary storage models for NoSQL databases were covered above. Figure 2 shows how these four fundamental storage models are compared in literature[19] based on the amount of data to be managed and the two-dimensional model’s complexity.
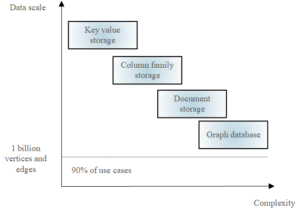
As can be seen from Figure 2, the graph database based on the graph storage model has the highest complexity and stores the graph data at a lower size, although it can also manage more than 1 billion vertices and their corresponding edges. In contrast, Key-Value storage has the lowest complexity and can store data in very large sizes.
In traditional relational databases, indexing is a crucial technology. It includes bitmap, hash, and B + tree indexes, among others. As the technology matures, it can increase the efficiency of processing data queries, particularly when the amount of data returned by the query is significantly less than the original data. If the query results in a larger amount of data, the processing performance is better; however, if the query results in a very small number of access to a lot of useless data, resulting in a waste of computational resources and query inefficiency, you can traverse all the subgraph data according to the query conditions. Therefore, by creating the appropriate indexes, you can effectively solve Appropriate index creation is a good way to tackle this problem.
In a cloud computing environment, the source data of a large-scale graph is kept on a distributed storage system, and the created indexes likewise need to be distributed. The graph’s index file will be very massive if the graph’s original data set was very large. The remote environment and data update latency further compound the problem of index maintenance. As a result, maintaining and storing graph data indexing in a cloud computing environment is a highly challenging task. Based on intended use and actual impact, the index can be divided into two main groups: In cloud computing environments, the first is to make generic queries and index construction easier,which helps to enhance the effectiveness of data search, primarily in distributed graph databases; the second is to expedite computation and index creation, primarily in the context of computational processing of the application’s graph, including clustering analysis, shortest path computation, and PageRank computation.
Graph data is not particularly well-suited to many of the indexing strategies now in use in cloud computing settings. Nevertheless, graph data storage can make use of the majority of these indexing strategies. There are two categories within the existing indexing structure for cloud data management: sharing-nothing cluster structure and indexing for P2P network structure. A secondary indexing method called CG-index was proposed in literature[20] for handling large-scale data queries in cloud computing environments. In order to create a global index, or CG-index, it first creates a local B +tree on each data slice to serve as an index slice. Next, it arranges the computing nodes into an Overlay structure and publishes each computing node’s B + tree slices to the Overlay in accordance with the Overlay’s routing protocol. This index is both scalable and adaptable. A multidimensional indexing system called RT-CAN was developed by literature[21] to offer effective query services in cloud computing environments by combining the capabilities of R-tree and the CAN protocol. A multidimensional index called MIDAS, which is built on distributed KD-tree, was also proposed in literature [22] to handle range, multidimensional, and k-nearest-neighbor queries in P2P environments. A distributed B-tree index structure that is scalable, adaptable, fault-tolerant, and general is suggested in literature [23]. The literature [24] suggests EMINC, a multidimensional index for cloud data management that offers quick query processing and effective index maintenance, along with using R-tree and KD-tree to arrange data records.
The impact of the generic indexing method in the cloud computing environment is not immediately apparent while processing graph queries since it does not take the graph structure’s properties into account. The distributed graph database is optimised for graph data, whether it is used for indexing or data storage.Neo4j indexes fall into two kinds [18]: full-text indexing and indexing hit rate sorting are provided by a standalone Lucene index, which can also be used in conjunction with the database’s tree-structured index to increase query efficiency. Neo4j may be set up on the graph’s edges and vertices, and by using the cache’s index, you can quicken the search even more. The transaction management method must be used for index maintenance activities like deletion and updating. Prior to adding a new index value for the update, the old index value must be deleted.
Similar to Neo4j, InfiniteGraph offers Lucene indexing as well as built-in indexing. at the two-tier storage architecture of HyperGraphDB, the index is an essential component of the storage layer; at the model layer, the Key is sorted and numbered by UUID and an index is constructed upon it. A Key can correspond to many sorted Values and supports Value sharing. The index file contains a caching mechanism that can offer persistent metadata information for querying and other operations. It is stored in B-tree format. In order to retrieve the names of graph vertices, edges, and other associated information, Trinity database offers two index structures: Hash and Trie tree. This can help to narrow down the number of matches for strings that share prefixes.
Cloud computing platforms are the primary implementation of indexing to facilitate graph computation processing. The Hadoop system’s Shuffle process and Reduce process are discussed in literature [14]. These processes improve dynamic incremental hash indexing and caching technology to lower disc IO costs during the Shuffle process and increase CPU utilisation. In contrast, HaLoop increases the performance of Hadoop iterative processing by indexing and caching the inputs and outputs of the Map task as well as the Reduce operation. In the literature [20], a Trojan indexing technique for MapReduce connection operations is proposed. This technique establishes an index by reconstructing the slice information and Key value, ensuring that the data that needs to be connected is located in the same slice. The goal is to reduce the amount of network communication required for the connection operation. Since the MapReduce model is a general computing paradigm, the Hadoop processing platform’s index is likewise general and not particularly tailored to the large-scale graph iterative processing.
Large-scale graph processing in cloud computing environments requires distributed parallel processing. Reducing the coupling between the subgraphs of distributed processing is crucial to accomplishing effective parallel processing because of the inherent connectivity of graph data and the strong coupling of graph computing. Effective graph splitting is a key tactic for establishing decoupling. A logically complete graph is first divided into multiple pieces, one of which is installed on each distributed storage system node that is in operation. The next step in processing the graph is to begin a compute task for each subgraph that has been saved in the distributed storage system. Once each subgraph has undergone the identical processing procedure, the processing of the entire large graph is finished.
Even though parallel processing can boost efficiency, message transmission between jobs during or after task execution is required due to the connection between subgraphs. This message communication is costly and a bottleneck in the efficiency of graph processing. Before the large graph is stored or processed, it can be divided into multiple subgraphs of manageable sizes using a good graph partitioning algorithm, provided that the subgraphs have low connectivity between each other and high connectivity within the subgraphs. This way, a significant portion of the messages can be processed locally and directly, saving on communication costs and increasing the system’s overall operational efficiency.
Achieving greater partitioning impact and realising massive graph partitioning is a difficult task in cloud computing environments. When dividing a large graph into multiple subgraphs, it is crucial to follow two basic principles: the first is to reduce connectivity between subgraphs and increase connectivity within subgraphs, which is particularly appropriate for the distributed parallel processing method used in cloud computing; the second step involves considering the subgraph scale balance, ensuring that each subgraph’s data scale is balanced and free from significant skewness. This will help to reduce the impact of the “bucket effect” during task synchronisation control and prevent an excessive difference in the execution times of the parallel tasks from the data scale perspective. Minimise the “bucket effect”’s influence on the task synchronisation control procedure. It is, of course, necessary to manage the time complexity of large-image segmentation within a tolerable range. The outcomes of three distinct graph partitioning methods are contrasted in Figure 3. The effect is not optimal if one only takes into account the connectivity or data balance of subgraphs; however, by taking these two factors into account simultaneously, the efficiency of distributed parallel processing can be greatly increased.
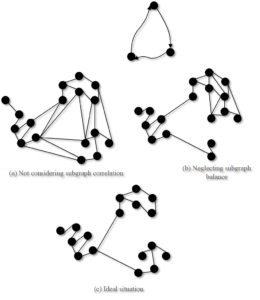
The simplest graph partitioning method, if we limit our analysis to data load balancing as a single measure, is the hash approach. In this method, the graph vertex IDs are hashed to divide the data into a predetermined number of slices once the number of slices is set. This segmentation technique is particularly effective; its time complexity is O(n), and it can be finished before the slice operation is finished in the graph processing or graph data loading process. A well-thought-out hash algorithm can, in some cases, prevent data skewness and bring each subgraph’s data size very close to the same. The locality of the graph data is not taken into consideration by Hash, and even the original data’s locality cannot be maintained. The frequent message exchanges between the jobs processing subgraphs will result in a significant network communication overhead, notwithstanding the Hash approach’s ease of implementation in cloud computing environments.
You may employ clustering techniques to minimise the correlation between subgraphs and raise the correlation within them, if you see the convergence of subgraphs as a single indication. The impact is rather evident. Mahout, an open-source project from Apache, provides a detailed explanation of the distributed clustering technique in a cloud computing environment. However, time costs are a crucial factor to take into account because clustering is usually an iterative process. Furthermore, the skewness of the data size between the clusters is typically ignored by clustering techniques, which increases the “bucket effect” in graph processing by potentially causing a significant disparity in the data size of the partitioned subgraphs. Yahoo Research revealed that even if the initial size of the graph data is quite vast, the final clusters are still significantly smaller, It reduces the subgraph segmentation’s temporal complexity. This finding led Yahoo Research to develop the “Local Partition” technique, whose running time is directly proportional to the size of the cluster in the final output and independent of the size of the graph’s initial input data, enabling the division of larger networks.
Several researchers have also attempted to take into account multiple indexes, such as subgraph data size balance and subgraph convergence simultaneously. A k-graph partitioning technique for distributed P2P networks was published in the literature[18]. A three-step procedure is used in the literature [19] to accomplish large-scale graph segmentation: (1) create a weighted depth-first search tree; (2) divide the big graph into a number of equal subgraphs; and (3) use iterative processing to reduce the correlation between subgraphs.By rearranging rows and columns and aligning the rows and columns of a big graph in a consistent manner, the GBASE system clusters the adjacency matrix of the stored graph data by utilising segmentation methods that are already in use, such as METIS and Disco. Rearranging a large matrix into several uniform regions, forming chunks, and assigning each block to a processing task helps to partially solve the data balancing problem by ensuring that the subgraphs within the block are closely linked and the link between the blocks is loose.
The HEFT algorithm, which was introduced in[20], is a well-liked option since it might result in a shorter scheduling period for large-scale graphical data processing task scheduling algorithms. The large-scale graphical data processing scheduling length and resource leasing cost can be balanced for the characteristics of on-demand resource leasing in a cloud computing environment by using the CCSH algorithm, which was first presented by [21]. Therefore, in order to verify the effectiveness of the LGPPSO algorithm, the heuristics found in [20] and [21] are chosen as the baseline algorithms for comparison. The main metrics for evaluation are the scheduling time of the activity and the resource leasing cost.
One hundred virtual machines with varying processor performance and a fully connected mesh topology make up the cloud computing simulation environment. There is a uniform distribution of CPU frequencies between 1.33GHz and 4.0GHz, and there is a 100Mb/s network bandwidth. The cheapest virtual machine costs $0.5 per compute unit. Real application graphs and randomly generated graphs were the test data utilised in this paper to analyse the performance of the algorithms. Every graph’s node computational demands are created at random between the range of 200–1000 nodes. For experimental testing, the transmission-to-computation load ratio (RCC) is assumed to be 0.1, 0.3, 0.5, or 1.5. The Gaussian elimination graph model, which is frequently used in network topology analysis and picture clustering analysis, is the actual application graph that has been chosen.
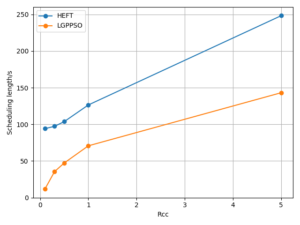
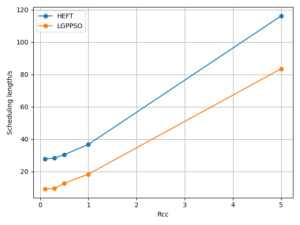
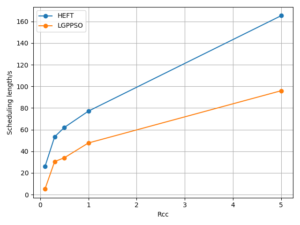
The LPGPSO method has two parameters: the maximum number of algorithm iterations (30) and the initial population size (8) of the particle swarm. The average of all experimental outcomes is calculated across multiple runs. The experimental results of the LGPPSO algorithm for randomly generating graphs and the real graph structure with the dispatch length as the fitness function are shown in Figure 4 to Figure 7. Figure 4 through Figure 7 display the experimental results of the LGPPSO method for randomly generated graphs and real graphical structures, using scheduling length and resource leasing cost as the fitness function. Figure 8 to Figure 11 display the experimental outcomes of the LGPPSO algorithm using scheduling length and resource leasing cost as the fitness function.
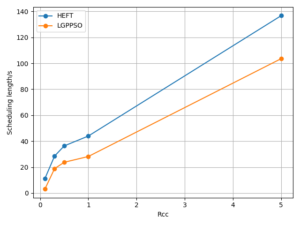
Comparing the LGPPSO algorithm against the HEFT algorithm, Figure 4 and Figure 5 demonstrate how much shorter the scheduling length is for randomly generated large-scale graph data. For random 200 and 400 node tasks, the average scheduling length decrease is around 8.3% and 9.7%, respectively. The real graph structure application can also use the LGPPSO algorithm developed in this paper, as demonstrated by Figure 6 and Figure 7, which also show that the scheduling duration is decreased by an average of 14.6% and 16.9% for the Gaussian 100 nodes and 200 nodes examples, This is primarily because the LGPPSO algorithm suggested in this paper is not appropriate for the large-scale graph structure, and the HEFT only schedules the tasks with the highest priority to the earliest machine to execute them. It does not take the graph data structure as a whole into consideration. The approach for scheduling tasks based on particle swarm optimisation presented in this study initialises many particles, this increases the possibility of discovering a nearly perfect solution and widens the search area in the solution space. On the other hand, the job scheduling technique based on particle swarm optimisation presented in this study initialises numerous particles, expands the range of the solution space search, and raises the probability of finding a close to optimal solution. The task with the highest priority is scheduled to be executed by the earliest completed machine without taking the graphical data structure as a whole into consideration.
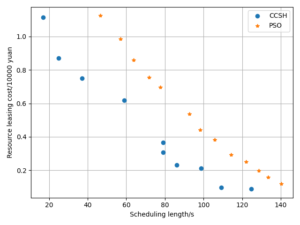
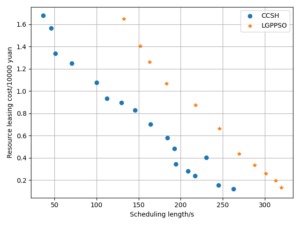
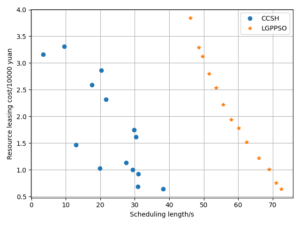
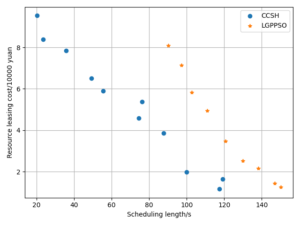
The objective function designed in this paper using Pareto optimality theory is able to solve this problem effectively, while the CCSH algorithm is able to save about 40% of the resource leasing cost but extends the scheduling length by about 10% when compared with the HEFT algorithm designed in the literature . Figures 8 and 9 demonstrate how the algorithm in this study reduces the resource leasing cost by about 0.16% and 0.28% and the scheduling length by approximately 9.3% and 5.6% on average, respectively, when compared to the CCSH algorithm with RCC = 1 and randomly generated nodes of 200 and 400. The LGPPSO technique developed in this paper can also be used to real-world graphical structures, as Figures 10 and 11 demonstrate. The approach reduces the resource leasing cost by approximately 0.13 percent and 0.27 percent for RCC = 1 and the scheduling length by 11.14 percent and 13.85 percent on average for Gaussian elimination graph nodes 200 and 100.
In order to address the issue of effective scheduling and resource leasing for large-scale graphical data processing jobs in a cloud computing environment, we suggest LGPPSO in this work. By initialising many particles and broadening the solution space search range, the LGPPSO method increases the likelihood of obtaining a near-optimal solution when compared to classical heuristics. Based on experimental results, the LGPPSO method efficiently lowers the resource leasing cost while reducing the scheduling length in applications including real and randomly generated graphical structures.The LGPPSO algorithm outperforms the HEFT and CCSH algorithms in terms of reducing resource leasing costs and finding a better balance between job scheduling duration. This demonstrates the efficiency and superiority of the LGPPSO algorithm for handling large-scale graphical data processing jobs and offers a workable optimisation plan for cloud computing environments’ task scheduling. Prospective avenues for investigation may encompass additional refinement of the algorithm and its verification over an expanded array of use cases.
In order to address the issue of effective scheduling and resource leasing for large-scale graphical data processing jobs in a cloud computing environment, we suggest LGPPSO in this work. By initialising many particles and broadening the solution space search range, the LGPPSO method increases the likelihood of obtaining a near-optimal solution when compared to classical heuristics. Based on experimental results, the LGPPSO method efficiently lowers the resource leasing cost while reducing the scheduling length in applications including real and randomly generated graphical structures.The LGPPSO algorithm outperforms the HEFT and CCSH algorithms in terms of reducing resource leasing costs and finding a better balance between job scheduling duration. This demonstrates the efficiency and superiority of the LGPPSO algorithm for handling large-scale graphical data processing jobs and offers a workable optimisation plan for cloud computing environments’ task scheduling. Prospective avenues for investigation may encompass additional refinement of the algorithm and its verification over an expanded array of use cases.
The experimental data used to support the findings of this study are available from the author upon request.
The author declared no conflicts of interest regarding this work.
This work was supported by the patent development project of universities and research institutes in Heilongjiang Province. (201905).
Fu, X., Sun, Y., Wang, H. and Li, H., 2023. Task scheduling of cloud computing based on hybrid particle swarm algorithm and genetic algorithm. Cluster Computing, 26(5), pp.2479-2488.
1970-2025 CP (Manitoba, Canada) unless otherwise stated.