In this paper, we study the \( A_\alpha \)-spectral radius of graphs in terms of given size \( m \) and minimum degree \( \delta \geq 2 \), and characterize the corresponding extremal graphs completely. Furthermore, we characterize extremal graphs having maximum \( A_\alpha \)-spectral radius among (minimally) \( 2 \)-edge-connected graphs with given size \( m \).
All graphs considered here are simple and undirected. For a graph \(G\), \(A(G)\) denotes its adjacency matrix and \(D(G)\) denotes the diagonal matrix of its degrees. The matrix \(Q(G)=D(G)+A(G)\) is called the signless Laplacian matrix of \(G\). The largest eigenvalue of \(A(G)\) is called the spectral radius of \(G\), and the largest eigenvalue of \(Q(G)\) is called the signless Laplacian spectral radius of \(G\). For any real number \(\alpha \in[0,1]\), Nikiforov [1] defined the \(A_{\alpha}\)-matrix of \(G\) as \(A_{\alpha}(G)=\alpha D(G)+(1-\alpha)A(G)\), which can be regarded as a common generalization of \(A(G)\) and \(Q(G)\). The largest eigenvalue of \(A_{\alpha}(G)\) is called the \(A_{\alpha}\)-spectral radius of \(G\), denoted by \(\rho_{\alpha}(G)\). For a connected graph \(G\), by the Perron-Frobenius theory of non-negative matrices [1], \(\rho_\alpha(G)\) has multiplicity one and there exists a unique positive unit eigenvector corresponding to \(\rho_\alpha(G)\). We shall refor to such an eigenvector as the Perron vector of \(A_\alpha(G)\).
The investigation on the extremal problems of the spectral radius and the signless Laplacian spectral radius of graphs is an important topic in the theory of graph spectra. For related results, one may refer to [2-5] and the references therein. Specially, the problem of characterizing the graph with maximal spectral radius for given size is initiated by Brualdi and Hoffman [6], and completely solved by Rowlinson [7]. For further investigation, one may refer to [8-13] and the references therein. Just recently, one of the hot topics in the study of the \(Q\)-spectrum is to characterize the spectral extreme under the conditions of given size and graph parameters. Zhai et al. [14] determined the graph with maximal \(Q-\)spectral radius among all graphs with given size, and characterized the graph with maximal \(Q-\)spectral radius among all graphs with given size and clique number (resp., chromatic number). Lou et al. [15] determined the maximal signless Laplacian spectral radius (Laplacian spectral radius) of connected graphs with fixed size and diameter. For more results, one may refer to [16-19].
The \(A_{\alpha}\)-spectral radius of a graph has been widely concerned. However, the results on the \(A_{\alpha}\)-spectral radius under edge-condition are still relatively little known. Li and Qin [20] generalized the conclusion in [14] to \(A_{\alpha}\)-spectral radius for \(1/2\le \alpha\le 1\). Feng et al. [21] and Huang et al. [22] determined independently the graph having the maximum \(A_{\alpha}\)-spectral radius for \(1/2\le \alpha\le 1\) among all connected graphs of size \(m\) and diameter (at least) \(d\).
A friendship graph is one in which every pair of vertices has exactly one common neighbour, denoted by \(F_{\frac{m}{3}}\) for given \(m \equiv 0(mod3)\). The join of graphs \(G\) and \(H\), denoted by \(G \vee H\), is the graph obtained from \(G \cup H\) by joining each vertex of \(G\) with every vertex of \(H\). In this paper, we completely characterize the graphs attaining the maximal \(A_\alpha\)-index among all graphs with given size \(m\) and minimum degree \(\delta \ge 2\) for \(\frac{1}{2} \le \alpha < 1\).
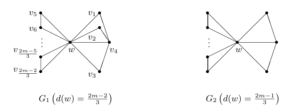
Theorem 1. Let \(\frac{1}{2} \le \alpha < 1\) and \(G\) be a graph with \(m\) edges and minimum degree \(\delta \ge 2\), and \(G_1, G_2\) be the graphs shown in Figure 1.
If \(m \ge 24\) and \(m \equiv 0(mod3)\), then \(\rho_\alpha(G)\le \rho_\alpha(F_{\frac{m}{3}})\), with equality if and only if \(G=F_{\frac{m}{3}}\).
If \(m \ge 37\) and \(m \equiv 1(mod3)\), then \(\rho_\alpha(G) \le \rho_\alpha(G_1)\), with equality if and only if \(G=G_1\), where \(G_1=K_1\vee(\frac{m-7}{3}K_2 \cup K_{1,3})\).
If \(m \ge 29\) and \(\equiv 2(mod3)\), then \(\rho_\alpha(G) \le \rho_\alpha(G_2)\), with equality if and only if \(G=G_2\), where \(G_2=K_1\vee(\frac{m-5}{3}K_2 \cup P_3)\).
A graph is \(2\)-edge-connected if removing fewer than \(2\) edges always leaves the remaining graph connected, and is minimally \(2\)-edge-connected if it is \(2\)-edge-connected and deleting any arbitrary chosen edge always leaves a graph which is not \(2\)-edge-connected. For graphs of order \(n\), Chen and Guo [23] showed that \(K_{2,n-2}\) attained the maximal spectral radius among all the minimally \(2\)-(edge)-connected graphs. Fan et al. [24] proved that \(K_{3,n-3}\) has the largest spectral radius over all minimally \(3\)-connected graphs. For graphs of size \(m\), Guo and Zhang [16,19] gave sharp upper bounds on the \(Q(L)\)-index of (minimally) \(2\)-connected graphs with given size and characterized the corresponding extremal graphs completely. Noting that a connected graph having no cut edges is \(2\)-edge-connected, we have following corollary.
Corollary 1. Let \(\frac{1}{2} \le \alpha < 1\) and \(G\) be a \(2\)-edge-connected graph with \(m\) edges.
If \(m \ge 24\) and \(m \equiv 0(mod3)\), then \(\rho_\alpha(G)\le \rho_\alpha(F_{\frac{m}{3}})\), with equality if and only if \(G=F_{\frac{m}{3}}\).
If \(m \ge 37\) and \(m \equiv 1(mod3)\), then \(\rho_\alpha(G) \le \rho_\alpha(G_1)\), with equality if and only if \(G=G_1\), where \(G_1=K_1\vee(\frac{m-7}{3}K_2 \cup K_{1,3})\).
If \(m \ge 29\) and \(\equiv 2(mod3)\), then \(\rho_\alpha(G) \le \rho_\alpha(G_2)\), with equality if and only if \(G=G_2\), where \(G_2=K_1\vee(\frac{m-5}{3}K_2 \cup P_3)\).

In this paper, we further study the problem of characterizing graphs among minimally \(2\)-edge-connected graph with maximal \(A_\alpha\)– spectral radius. For \(m\equiv1(mod3)\), let \(G_3\) (shown in Figure 2) be the graph obtained from the friendship graph \(F_\frac{m-1}{3}\) by subdividing an edge once. For \(m\equiv2(mod3)\), let \(G_4\) (shown in Figure 2) be the graph obtained from the friendship graph \(F_\frac{m-2}{3}\) by subdividing an edge twice. Employing Theorem 1, we can prove the following theorem.
Theorem 2. Let \(\frac{1}{2} \le \alpha < 1\) and \(G\) be a minimally \(2\)-edge-connected graph with \(m\) edges.
If \(m \ge 24\) and \(m \equiv 0(mod3)\), then \(\rho_\alpha(G)\le \rho_\alpha(F_{\frac{m}{3}})\), with equality if and only if \(G=F_{\frac{m}{3}}\).
If \(m \ge 37\) and \(m \equiv 1(mod3)\), then \(\rho_\alpha(G) \le \rho_\alpha(G_3)\), with equality if and only if \(G=G_3\).
If \(m \ge 50\) and \(m \equiv 2(mod3)\), then \(\rho_\alpha(G) \le \rho_\alpha(G_4)\), with equality if and only if \(G=G_4\).
The remainder of the paper is organized as follows. In Section 2, we recall some useful notions and lemmas that will be used later. In Section 3, we give proofs of Theorems 1 and 2 respectively.
For a graph \(G\), \(V(G)\) and \(E(G)\) denote the vertex set and edge set of \(G\) respectively, and \(e(G)=|E(G)|\) denotes the number of edges in \(G\). For \(v\in V(G),\) \(d_G(v)\) or \(d(v)\) denotes the degree of \(v\), \(N_G(v)\) or \(N(v)\) denotes the set of all neighbors of \(v\) in \(G\), and \(N[v]=N(v)\cup \{v\}\). For a subset \(S\) of \(V(G)\), \(G[S]\) denotes the subgraph of \(G\) induced by \(S\), \(e(S)\) denotes the number of edges in \(G[S]\), and \(N_S(v)\) denotes the set of all neighbors of \(v\) in \(S\). For two disjoint subsets \(S\) and \(T\) of \(V(G)\), \(e(S,\,T)\) denotes the number of edges with one endpoint in \(S\) and the other in \(T\). Let \(G-uv\) denote the graph obtained from \(G\) by deleting the edge \(uv\in E(G).\) Similarly, \(G+uv\) is the graph obtained from \(G\) by adding an edge \(uv\notin E(G),\) where \(u, v\in V(G).\) The average degree of the neighbors of a vertex \(v_i\) of \(G\) is \(m(v_i)=\frac{1}{d(v_i)}\sum \limits_{v_iv_j \in E(G)} d(v_j)\). The degree sequence of \(G\) is the non-increasing sequence of its vertex degrees. Whenever necessary, the vertices of \(G\) can be renumbered so that \(d_i \ge d_{i+1}\) for \(1 \le i \le n\). In that case, we say that \(G\) has degree sequence \((d_1,d_2,\cdots,d_n)\), denoted by \(\mathbb{D}(G)=(d_1,d_2,\cdots,d_n)\).
Let \(G\) be a connected graph on \(n\) vertices and \(X=(x_1,x_2,\cdots,x_n)^T \in R^n\). Then \(X\) can be considered as a function defined on \(V(G)\), that is, each vertex \(x_i\) is mapped to \(x_i=x(v_i)\). One can find in [1] that \[X^TA_\alpha(G)X=(2\alpha-1)\sum \limits_{u \in V(G)}x_u^2d(u)+(1-\alpha)\sum \limits_{uv \in E(G)}(x_u+x_v)^2,\] and for arbitrary unit vector \(X \in R^n\), \[\label{e1}\rho_\alpha(G) \ge X^TA_\alpha(G)X, \tag{1}\] with the equality if and only if \(X\) is the Perron vector of \(A_\alpha(G)\).
In order to prove our main results, we need the following lemmas.
Lemma 1. ([1])If \(G\) is a graph with no isolated vertices, then \[\label{e2}\rho_\alpha(G)\le \max\{\,\alpha d(u)+(1-\alpha)m(u)\,|\,\, u\in V(G)\,\}. \tag{2}\]
Lemma 2. ([1])Let \(G\) be a graph with \(n\) vertices and \(\Delta(G)=\Delta\). If \(\alpha \in [\frac{1}{2},1)\), then \[\label{e3}\rho_\alpha(G) \ge \alpha \Delta+\frac{(1-\alpha)^2}{\alpha}. \tag{3}\] The equality holds if and only if \(\alpha=\frac{1}{2}\) and \(G\) is the star \(K_{1,n-1}\).
Lemma 3. ([1])Let \(G\) be a connected graph with \(\alpha \in [0,1)\) and \(H\) be a proper subgraph of \(G\), then \(\rho_{\alpha}(H) < \rho_{\alpha}(G)\).
Lemma 4. ([25])Let \(G\) be a connected graph, \(u\) and \(v\) be two vertices of \(G\). Suppose that \(v_i\in N_G(v)\setminus N_G(u)\) \((1\le i\le s)\) and \(x =(x_1, x_2, \ldots, x_n)^T\) is the Perron vector of \(Q(G)\), where \(x_i\) corresponds to the vertex \(v_i\) \((1\le i \le n)\). Let \(G^*\) be the graph obtained from \(G\) by deleting the edges \(vv_i\) and adding the edges \(uv_i\) \((1\le i\le s)\). If \(x_u\ge x_v\), then \(\rho_\alpha(G)<\rho_\alpha(G^*)\).
An internal path in some graph is a path \(v_0 v_1 \ldots v_s\) (\(s\ge 1\), or \(s\ge 3\) whenever \(v_s=v_0\)) such that \(d(v_0)>2\), \(d(v_s)>2\), and \(d(v_i)=2\) for \(0<i<s\). Li, Chen and Meng [26] proved the following subdivision theorem.
Lemma 5. ([26])Let \(G\) be a connected graph with \(\alpha \in [0,1)\) and \(uv\) be some edge on an internal path of \(G\). Let \(G_{uv}\) denote the graph obtained from \(G\) by subdivision of edge \(uv\) into edges \(uw\) and \(wv\). Then \(\rho_{\alpha}(G_{uv}) < \rho_{\alpha}(G)\).
A cycle \(C\) of a graph \(G\) is said to have a chord if there is an edge of \(G\) that joins a pair of non-adjacent vertices of \(C\).
Lemma 6. ([11])If \(G\) is a minimally \(2\)-edge-connected graph, then no cycle of \(G\) has a chord.
For a connected graph, Yu, Wu and Shu [27] gave a sharp upper bound on \(Q\)-index in terms of its degree sequence. The authors of the current paper [28] generalized their result to \(A_{\alpha}\)-index of a connected graph. The following Lemma is a corollary of our result.
Lemma 7. ([28])Let \(G\) be a simple connected graph with \(n\) vertices and degree sequence \(d_1\ge d_2\ge \cdots\ge d_n\). If \(d_1\ge s\ge d_2\), then \(\rho_\alpha(G)\le A(d_1, s)\), where \[A(d_1, s)=\frac{1}{2}(\alpha d_1+s+\alpha-1+\sqrt{(s-\alpha d_1+1-\alpha)^2+4(1-\alpha)(d_1-s)}\,).\]
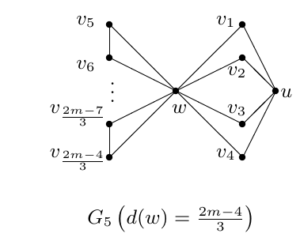
Lemma 8. Let \(\frac{1}{2} \le \alpha < 1, m \ge 50\), and \(G_5\) be the graph shown in Figure 3. Then \(\rho_\alpha(G_5)<\rho_\alpha(G_4)\).
Proof. Label the vertices is as shown in Figure 1. Let \(X=(x_w,x_1,x_2,\cdots,x_{\frac{2m-2}{3}},x_u)^T\) be a unit eigenvector corresponding to \(\rho=:\rho_\alpha(G_5)\) where \(x_w\) corresponds to \(w\) and \(x_i\) corresponds to \(v_i(1 \le i \le \frac{2m-4}{3})\) and \(x_u\) corresponds to \(u\). By the eigenvalue equation \(\rho X=A_\alpha(G_5)X\), we have \(x_1=x_2=x_3=x_4\) and \(\rho x_u=4\alpha x_u+4(1-\alpha)x_1\). It follows that \(x_1=\frac{\rho-4\alpha}{4(1-\alpha)}x_u\). Define \(Y=(y_w,y_1,y_2,\cdots,y_{\frac{2m-4}{3}},y_u,y_v)^T\) such that \(y_w=x_w,y_i=x_i\) for \(1 \le i \le \frac{2m-4}{3}\), and \(y_u=y_v=\frac{\sqrt2}{2}x_v\). Clearly, \[\sum\limits_{i=1}^{\frac{2m-4}{3}}y_i^2+y_w^2+y_u^2+y_v^2=\sum\limits_{i=1}^{\frac{2m-4}{3}}x_i^2+x_w^2+x_u^2=1.\] Noting that \(m \ge 50\) and \(d_1(G_5)=d(w)=\frac{2m-4}{3}\), by Lemma 2, we have \(\rho=\rho_\alpha(G_5)>\frac{2m-4}{3}\alpha \ge 16\). By (1), we have \[\begin{aligned} \rho_\alpha(G_4)-\rho \ge& \ Y^TA_\alpha(G_7)Y-X^TA_\alpha(G_6)X \\ =& \ (2\alpha-1)(-2x_u^2)+(1-\alpha)((x_1+x_2)^2+(x_3+\frac{x_u}{\sqrt{2}})^2\\ & +(x_4+\frac{x_u}{\sqrt{2}})^2+(\frac{x_u}{\sqrt{2}}+\frac{x_u}{\sqrt{2}})^2-4(x_1+x_u)^2)\\ =& \ (2\alpha-1)(-2x_u^2)+(1-\alpha)((2\frac{\rho-4\alpha}{4(1-\alpha)}x_u)^2+2(\frac{\rho-4\alpha}{4(1-\alpha)}x_u+\frac{x_u}{\sqrt{2}})^2\\ &+2x_u^2-4(\frac{\rho-4\alpha}{4(1-\alpha)}x_u+x_u)^2)\\ =& \frac{\rho^2-(4\sqrt2 \alpha-8\alpha-4\sqrt2+16)\rho+16\sqrt2 \alpha^2-24\alpha^2+32\alpha-16\sqrt2 \alpha+8}{8(1-\alpha)}x_u^2\\ >&\frac{\rho^2-(4\sqrt2 \alpha-8\alpha-4\sqrt2+16)\rho}{8(1-\alpha)}x_u^2\\ >&0. \end{aligned}\] Therefore \(\rho_\alpha(G_5)<\rho_\alpha(G_4)\). This completes the proof. ◻
Proof of Theorem 1. We may assume that \(G\) is connected. Otherwise, suppose that \(H_i(i=1,2,\cdots,k)\) are \(k\) connected components of \(G\), where \(k \ge 2\). Since \(\delta(G) \ge 2\), then \(\delta(H_i) \ge 2(1 \le i \le k)\). For \(i=1,2,\cdots,k\), let \(v_i\) be a vertex of \(H_i\), and \(G^*\) be the graph obtained from \(H_i\) by identifying vertices \(v_i\). Clearly, \(\rho_\alpha(G)<\rho_\alpha(G^*)\), and \(G^*\) is a connected graph with \(m\) edges and minimum degree \(\delta \ge 2\). So, in order to complete the proof of Theorem 1, we may assume that \(G\) is connected.
Furthermore, we may assume that \(G\) is \(2\)-edge-connected. Otherwise, suppose that \(u_1v_1 \in E(G)\) is a cut edge of \(G\). Since \(\delta(G) \ge 2\), then there exist a path \(P=u_ku_{k-1} \cdots u_2u_1v_1v_2 \cdots v_{l-1}v_l\), where \(k,l \ge 1\), such that \(d(u_k) \ge 3(d(v_l) \ge 3)\) and \(u_k(v_l)\) belongs to a cycle \(C_1=u_ku_{k+1}\cdots u_{k+p}u_k(C_2=v_lv_{l+1}\cdots v_{l+q}v_1)\). Suppose that \(|V(G)|=n\). Let \(X=(x_{u_1},x_{u_2},\cdots,x_{u_{k+p}},x_{v_1},x_{v_2},\cdots,x_{v_{l+q}}, \cdots, x_n)^T\) be a unit eigenvector corresponding to \(\rho_\alpha(G)\) where \(x_{u_i}\) corresponds to \(u_i(1 \le i \le k+p)\), \(x_{v_j}\) corresponds to \(v_j(1 \le j \le l+q)\). If \(x_{u_{k}} \ge x_{v_{l}}\), let \(G^*=G-v_lv_{l+1}+u_{k}v_{l+1}\); Otherwise, let \(G^*=G-u_ku_{k+1}+v_lu_{k+1}\). In the both cases, \(G^*\) is a connected graph with \(m\) edges and minimum degree \(\delta \ge 2\) and \(uv\) is not a cut edge of \(G^*\) any more. By Lemma 4, we have \(\rho_\alpha(G)<\rho_\alpha(G^*)\). So we may assume that \(G\) is \(2\)-edge-connected.
Let \(\mathcal{G}_m^{2}\) denote the set of all \(2\)-edge-connected graphs with \(m\) edges. For \(G\in\mathcal{G}_m^{2}\) and \(v\in V(G)\), it is easy to see that \(d(v) \ge 2\) and \(G-v\) has no isolated vertices. Noting that \(|E(G-v)|=m-d(v)\), we have \[d(v)\le |V(G-v)|\le 2(m-d(v)).\] It follows that \(d(v)\le \frac{2m}{3}\) with equality if and only if \(G=F_{\frac{m}{3}}\).
For \(G \in \mathcal{G}_m^{2}\), let \(w\) be a vertex of \(G\) such that \[\max_{u\in V(G)}\left \{\alpha d(u)+(1-\alpha)m(u)\right\}=\alpha d(w)+(1-\alpha)m(w)=\alpha d(w)+\frac{1-\alpha}{d(w)}\sum_{wv\in E(G)}d(v).\] Noting that \(e(N(w)) \le m-e(N(w),V(G) \setminus N(w))\) and \(e(N(w),V(G) \setminus N(w)) \ge d(w)\), we have \[\sum_{wv\in E(G)}d(v)=2e(n(w))+e(N(w),V(G) \setminus N(w)) \le 2m-d(w).\] By Lemma 1, we have \[\label{e4}\rho_\alpha(G)\leq \alpha d(w)+\frac{2m}{d(w)}(1-\alpha)-1+\alpha. \tag{4}\]
Let \(m \ge 24\) and \(m \equiv 0(mod 3)\). It is easy to see that \(F_{\frac{m}{3}} \in \mathcal{G}_m^{2}\). By Lemma 2, we have \(\rho_\alpha(F_{\frac{m}{3}})>\frac{2m\alpha}{3}+\frac{(1-\alpha)^2}{\alpha}\).
If \(d(w)=2\), noting that \(e(N(w)) \le 1\), we have \[\sum_{wv\in E(G)}d(v)=2e(N(w))+e(N(w), V(G)\setminus N(w))\le 2+m-1=m+1.\] By (2), we have \[\rho_\alpha(G)\le 2\alpha+\frac{m+1}{2}(1-\alpha) \le \frac{2m\alpha}{3}+\frac{(1-\alpha)^2}{\alpha} <\rho_\alpha(F_{\frac{m}{3}})\] for \(m\ge 9\) and \(\frac{1}{2} \le \alpha <1\).
If \(d(w)=3\), noting that \(e(N(w))\le 3\), we have \[\sum_{wv\in E(G)}d(v)=2e(N(w))+e(N(w), V(G)\setminus N(w))\le 6+m-3=m+3.\] By (2), we have \[q(G)\le 3\alpha+\frac{m+3}{3}(1-\alpha) \le \frac{2m\alpha}{3}+\frac{(1-\alpha)^2}{\alpha} <\rho_\alpha(F_{\frac{m}{3}})\] for \(m\ge 9\) and \(\frac{1}{2} \le \alpha <1\).
If \(4\le d(w)\le \frac{2m-6}{3}\), let \(f(x)=\alpha x+\frac{2m}{x}(1-\alpha)\). It is easy to see that the function \(f(x)\) is convex for \(x>0\) and its maximum in any closed interval is attained at one of the ends of this interval. Combining this and (4), we have \[\begin{aligned} &\rho_\alpha(G) & \le \max\left\{4\alpha+\frac{2m}{4}(1-\alpha),\,\, \frac{2m-6}{3}\alpha+\frac{3m}{m-3}(1-\alpha)\right\}-1+\alpha \\ & &\le \ \frac{2m\alpha}{3}+\frac{(1-\alpha)^2}{\alpha} <\rho_\alpha(F_{\frac{m}{3}}). \end{aligned}\] for \(m\ge 12\) and \(\frac{1}{2} \le \alpha <1\).
If \(d(w)=\frac{2m-3}{3}\), then \(d_1=d_1(G)=\frac{2m-3}{3}\). Let \(|V(G-w)|= \frac{2m-3}{3}+s\), then \(2m\ge \frac{2m-3}{3}+2(\frac{2m-3}{3}+s)\). It follows that \(0 \le s \le 1\). This implies that \(d_2=d_2(G) \le 2+3=5\). By Lemma 7, we have \[\rho_\alpha(G) \le A(\frac{2m-3}{3},5)<\frac{2m\alpha}{3}+\frac{(1-\alpha)^2}{\alpha} <\rho_\alpha(F_{\frac{m}{3}})\] for \(m \ge 24\) and \(\frac{1}{2} \le \alpha <1\).
If \(d(w)=\frac{2m}{3}\), then \(G=F_{\frac{m}{3}}\), completing the proof of (i).
Let \(m \ge 37\) and \(m \equiv 1(mod3)\). It is easy to see that \(G_1=K_1\vee(\frac{m-2}{3}K_2 \cup K_{1,3}) \in \mathcal{G}_m^{2}\). By Lemma 2, we have \(\rho_\alpha(G_1)>\frac{2m-2}{3}\alpha+\frac{(1-\alpha)^2}{\alpha}\).
For \(2 \le d(w) \le \frac{2m-8}{3}\), by similar reasoning as in the proof of (i), we can derived that \[\rho_\alpha(G) \le \frac{2m-2}{3}\alpha+\frac{(1-\alpha)^2}{\alpha}< \rho_\alpha(G_1)\] for \(m \ge 16\) and \(\frac{1}{2} \le \alpha <1\).
If \(d(w)=\frac{2m-5}{3}\), then \(d_1=d_1(G)=\frac{2m-5}{3}\). Let \(|V(G-w)|= \frac{2m-5}{3}+s\), then \(2m\ge \frac{2m-5}{3}+2\left(\frac{2m-5}{3}+s\right)\). It follows that \(0 \le s \le 2\). This implies that \(d_2=d_2(G) \le 2+5=7\). By Lemma 7, we have \[\rho_\alpha(G) \le A\left(\frac{2m-5}{3},7\right)<\frac{2m-2}{3}\alpha+\frac{(1-\alpha)^2}{\alpha} <\rho_\alpha(G_1)\] for \(m \ge 37\) and \(\frac{1}{2} \le \alpha <1\).
If \(d(w)=\frac{2m-2}{3}\), then \(d_1=d_1(G)=\frac{2m-2}{3}\). Let \(|V(G-w)|= \frac{2m-2}{3}+s\), then \(2m\ge \frac{2m-2}{3}+2\left(\frac{2m-2}{3}+s\right)\). It follows that \(0 \le s \le 1\).
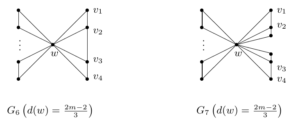
Case 1. \(s=0\), it follows that \(|V(G-w)|=\frac{2m-2}{3}\). Noting that \(|E(G)|=m\), it is well known that \(\sum \limits_{i=1}^{|V(G)|}d_i=2m\). Since \(\delta \ge 2\), then we known that \(\mathbb{D}(G)\) might be \[\left(\,\frac{2m-2}{3}, 4, 2, 2, 2, 2, \ldots, 2\,\right) \;\;\; \text{or} \;\;\; \left(\,\frac{2m-2}{3}, 3, 3, 2, 2, 2, \ldots, 2\,\right).\]
If \(\mathbb{D}(G)=(\,\frac{2m-2}{3}, 4, 2, 2, 2, 2, \ldots, 2\,)\), then \(G=G_1\).
If \(\mathbb{D}(G)=(\,\frac{2m-2}{3}, 3, 3, 2, 2, 2, \ldots, 2\,)\), then \(G=G_6=K_1 \vee(\frac{m-7}{3}K_2 \cup p_4)\) or \(G=G_7=K_1 \vee (\frac{m-10}{3}K_2 \cup 2P_3)\), shown in Figure 4. Let \(X=(x_w, x_1, x_2, x_3, x_4,\cdots, x_{\frac{2m-2}{3}})^T\) be a unit eigenvector corresponding to \(\rho_\alpha(G_6)\) where \(x_w\) corresponds to \(w\) and \(x_i\) corresponds to \(v_i(1 \le i \le \frac{2m-2}{3})\). If \(x_2 \ge x_3\), let \(G^*=G_6-v_4v_3+v_4v_2\); Otherwise, let \(G^*=G_6-v_1v_2+v_1v_3\). In the both cases, \(G^*=G_1\). By Lemma 4, we have \(\rho_\alpha(G_6)<\rho_\alpha(G_1)\). Applying Lemma 4 to the vertices \(v_2\) and \(v_3\) of \(G_7\), we can similarly derive that \(\rho_\alpha(G_7)<\rho_\alpha(G_1)\).
Case 2. \(s=1\), then \(|V(G-w)|=\frac{2m+1}{3}\). Noting that \(|E(G)|=m\), then \(G\) has degree sequence \((\,\frac{2m-2}{3}, 2, 2, 2, 2, 2, \ldots, 2\,)\). It follows that \(G=G_3\). Noting that \(wv_2v_3v_1\) is an internal path of \(G_3\), by Lemma 5, we have \(\rho_\alpha(G_3)< \rho_\alpha(F_{\frac{m-1}{3}})\). Furthermore, noting that \(F_{\frac{m-1}{3}}\) is a proper subgraph of \(G_6\), by Lemma 3, we have \(\rho_\alpha(F_{\frac{m-1}{3}})<\rho_\alpha(G_6)\). Therefore, we have \(\rho_\alpha(G_3)< \rho_\alpha(G_6)<\rho_\alpha(G_1)\).
Let \(m \ge 29\) and \(m \equiv 2(mod3)\). It is easy to see that \(G_2 \in \mathcal{G}_m^{2}\). By Lemma 2, we have \(\rho_\alpha(G_2)>\frac{2m-1}{3}\alpha+\frac{(1-\alpha)^2}{\alpha}\).
For \(2 \le d(w) \le \frac{2m-7}{3}\), by similar reasoning as in the proof of (i), we can similarly derived that \[\rho_\alpha(G) < \frac{2m-1}{3}\alpha+\frac{(1-\alpha)^2}{\alpha}<\rho_\alpha(G_2)\] for \(m \ge 14\) and \(\frac{1}{2} \le \alpha <1\).
If \(d(w)=\frac{2m-4}{3}\), let \(|V(G-w)|= \frac{2m-4}{3}+s\), then \[2m\ge \frac{2m-4}{3}+2\left(\frac{2m-4}{3}+s\right).\] It follows that \(s\le 2\). This implies that \(d_2=d_2(G)\le 2+4=6\). By Lemma 7, we have \[\rho_\alpha(G) \le A\left(\frac{2m-4}{3},6\right)\le \frac{2m-1}{3}\alpha+\frac{(1-\alpha)^2}{\alpha}<\rho_\alpha(G_2)\] for \(m \ge 29\) and \(\frac{1}{2} \le \alpha <1\).
If \(d(w)=\frac{2m-1}{3}\), let \(|V(G-w)|= \frac{2m-1}{3}+s\), then \[2m\ge \frac{2m-1}{3}+2\left(\frac{2m-1}{3}+s\right).\] It follows that \(s=0\). Noting that \(|E(G)|=m\), we known that \(G\) has degree sequence \((\,\frac{2m-1}{3}, 3, 2, 2, 2, 2, \ldots, 2\,)\). It follows that \(G=G_2\), completing the proof of (iii).
◻
Proof of Theorem 2. Let \(\mathcal{H}_m^{2}\) denote the set of all minimally \(2\)-edge-connected graphs with \(m\) edges.
Let \(m \ge 24\) and \(m \equiv 0(mod 3)\). It is easy to see that \(F_{\frac{m}{3}} \in \mathcal{H}_m^{2} \subseteq \mathcal{G}_m^{2}\). By Theorem 1(i), we have \(\rho_\alpha(G) \le \rho_\alpha(F_{\frac{m}{3}})\) for \(G \in \mathcal{H}_m^{2}\) and the equality holds if and only if \(G=F(\frac{m}{3})\).
Let \(m \ge 37\) and \(m \equiv 1(mod 3)\). It is easy to see that \(G_4 \in \mathcal{H}_m^{2} \subseteq \mathcal{G}_m^{2}\). By Lemma 2, we have \(\rho_\alpha(G_3)>\frac{2m-2}{3}\alpha+\frac{(1-\alpha)^2}{\alpha}\). From the proof of Theorem 1(ii), we know that \(\rho_\alpha(G) \le \frac{2m-2}{3}\alpha+\frac{(1-\alpha)^2}{\alpha}\) for \(G \in \mathcal{G}_m^{2} \setminus \{G_1, G_3, G_6, G_7\}\). This implies that \(\rho_\alpha(G) \le \rho_\alpha(G_3)\) for \(G \in \mathcal{H}_m^{2}\), and the equality holds if and only if \(G=G_3\).
Let \(m \ge 50\) and \(m \equiv 2(mod 3)\). It is easy to see that \(G_4 \in \mathcal{H}_m^{2} \subseteq \mathcal{G}_m^{2}\). By Lemma 2, we have \(\rho_\alpha(G_4)>\frac{2m-4}{3}\alpha+\frac{(1-\alpha)^2}{\alpha}\). For \(G \in \mathcal{H}_m^{2}\), let \(w\) be a vertex of \(G\) such that \[\max_{u\in V(G)}\left \{\alpha d(u)+(1-\alpha)m(u)\right\}=\alpha d(w)+(1-\alpha)m(w)=\alpha d(w)+\frac{1-\alpha}{d(w)}\sum_{wv\in E(G)}d(v),\] where \(2 \le d(w) \le \frac{2m-4}{3}\).
For \(2 \le d(w) \le \frac{2m-10}{3}\), by similar reasoning as in the proof of Theorem 1(i), we can prove that \[\rho_\alpha(G) \le \alpha d(w)+(1-\alpha)m(w) \le \frac{2m-4}{3}\alpha+\frac{(1-\alpha)^2}{\alpha}<\rho_\alpha(G_4)\] for \(m \ge 20\) and \(\frac{1}{2} \le \alpha <1\).
If \(d(w)=\frac{2m-7}{3}\), let \(|V(G-w)|= \frac{2m-7}{3}+s\), then \[2m\ge \frac{2m-7}{3}+2\left(\frac{2m-7}{3}+s\right).\] It follows that \(0 \le s \le 3\). This implies that \(d_2=d_2(G)\le 2+7=9\). By Lemma 7, we have \[\rho_\alpha(G) \le A\left(\frac{2m-7}{3},9\right)\le \frac{2m-4}{3}\alpha+\frac{(1-\alpha)^2}{\alpha}<\rho_\alpha(G_4)\] for \(m \ge 50\) and \(\frac{1}{2} \le \alpha <1\).
If \(d(w)=\frac{2m-4}{3}\). let \(|V(G-w)|= \frac{2m-4}{3}+s\), then \[2m\ge \frac{2m-4}{3}+2\left(\frac{2m-4}{3}+s\right).\] It follows that \(0 \le s \le 2\). We consider the following three cases.
Case 1. \(s=0\), then \(|V(G-w)|=\frac{2m-4}{3}\) and \(|E(G-w)|=\frac{m+4}{3}\). Since \(G\) is minimally \(2\)-edge-connected, it follows that \(G-w=pK_2 \cup qK_1\), where \(p\) nd \(q\) are nonnegative integers with \(2p+q=\frac{2m-4}{3}\). This implies that \(|E(G-w)| \le \frac{m-2}{3}\), a contradiction.
Case 2. \(s=1\). Let \(V(G)\setminus N[w]=\{u\}\). Then \(|V(G-w)|=\frac{2m-1}{3}\), and \(\mathbb{D}(G)=(\,\frac{2m-4}{3}, 4, 2, 2, 2, 2, \ldots, 2)\) or \((\frac{2m-4}{3}, 3, 3, 2, 2, 2, \ldots, 2\,)\). If \(\mathbb{D}(G)=(\,\frac{2m-4}{3}, 4, 2, 2, 2, 2, \ldots, 2\,)\) and there exist a vertex \(v_i \in N(w)\) such that \(d(v_i)=4\), then there exist at least two vertices \(v_j,v_k \in N(w)\) such that \(v_iv_j, v_iv_k \in E(G)\). Obviously, we obtain a cycle \(wv_kv_iv_jw\) with a chord \(wv_i\), a contradiction to Lemma 6.
If \(\mathbb{D}(G)=(\,\frac{2m-4}{3}, 4, 2, 2, 2, 2, \ldots, 2\,)\) and \(d(u)=4\), then \(G=G_5\), shown in Figure 3. By Lemma 8, we have \(\rho_\alpha(G_5)<\rho_\alpha(G_4)\).
If \(\mathbb{D}(G)=(\,\frac{2m-4}{3}, 3, 3, 2, 2, 2, \ldots, 2\,)\), then exists a vertex \(v_i \in N(w)\) such that \(d(v_i)=3\). By Lemma 6, we know that \(G[N(w)]=pK_2 \cup qK_1\). It follows that \(u \in N(v_i)\). Suppose \(N(v_i)=\{w,u,v_j\}\). Noting that \(d(u) \ge 2\), we deduce that there exists another vertex \(v_k \in N(w)\) such that \(uv_k \in E(G)\). If \(v_k=v_j\), we obtain a cycle \(wv_iuv_jw\) with a chord \(v_iv_j\); if \(v_k \neq v_j\), we obtain a cycle \(wv_jv_iuv_kw\) with a chord \(wv_i\). This contracts Lemma 6.
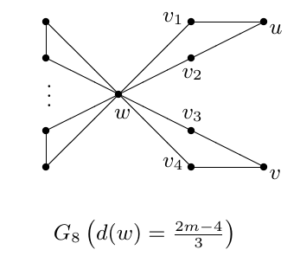
Case 3. \(s=2\). Let \(V(G) \setminus N[w]=\{u,v\}\). Then \(|V(G-w)|=\frac{2m+2}{3}\) and the degree sequence of \(G\) must be \((\,\frac{2m-4}{3}, 2, 2, 2, 2, 2, \ldots, 2\,)\). Noting that \(E(G)=m\) and \(d(w)=\frac{2m-4}{3}\), it follows that \(G=G_4\) or \(G=G_8\), shown in Figure <5. Applying Lemma 4 to vertices \(u\) and \(v\) of \(G_8\), we can derive \(\rho_\alpha(G_8)<\rho_\alpha(G_5)\). By Lemma 8, we have \(\rho_\alpha(G_5)<\rho_\alpha(G_4)\). Therefore \(\rho_\alpha(G_8)<\rho_\alpha(G_4)\).
Combining the above arguments, we complete the proof.
◻
The authors are grateful to the anonymous referees for valuable suggestions and corrections which result in an improvement of the original manuscript.
The author declares no conflict of interest.
This research is supported by the National Natural Science Foundation of China (Nos. 12071411, 12171222).
1970-2025 CP (Manitoba, Canada) unless otherwise stated.