Let \( G \) be a simple finite graph. A \( k \)-coloring of \( G \) is a partition \(\pi = \{ S_1, \cdots, S_k \}\) of \( V(G) \) so that each \( S_i \) is an independent set and any vertex in \( S_i \) takes color \( i \). A \( k \)-coloring \(\pi = \{ S_1, \cdots, S_k \}\) of \( V(G) \) is a neighbor locating coloring if for any two vertices \( u, v \in S_i \), there is a color class \( S_j \) for which one of them has a neighbor in \( S_j \) and the other does not. The minimum \( k \) with this property is said to be the neighbor locating chromatic number of \( G \), denoted by \(\chi_{NL}(G)\). We initiate the study of the neighbor locating coloring of graphs resulting from three types of product of two graphs. We investigate the neighbor locating chromatic number of Cartesian, lexicographic, and corona products of two graphs. Finally, we untangle the neighbor locating chromatic number of any of the aforementioned three products of cycles, paths, and complete graphs.
Let \(G=(V,E)\) be a simple, finite, connected and undirected graph with the vertex set \(V=V(G)\) and the edge set \(E=E(G)\). The open neighborhood of \(v\), \(N(v)\) is the set of vertices adjacent to \(v\) and closed neighborhood of \(v\) is \(N[v]=N(v)\cup \{v\}\). The minimum and the maximum degree of \(G\) is the smallest and largest number of neighbors of a vertex in \(G\) and denoted by \(\delta =\delta(G)\) and \(\Delta =\Delta(G)\) respectively. For the terminologies and notation not herein, see [1].
For two standard products (Cartesian and lexicographic product) of graphs \(G\) and \(H\), the vertex set is \(V(G)\times V(H)\) and the adjacency of two vertices are defined as follows. In the Cartesian product \(G\Box H\), two vertices \((g,h)\) and \((g',h')\) are adjacent if \(g\) is adjacent to \(g'\) in \(G\) and \(h=h'\) in \(H\), or if \(g=g'\) in \(G\) and \(h\) is adjacent to \(h'\) in \(H\). In lexicographic product \(G[H]\), two vertices \((g,h)\) and \((g',h')\) are adjacent if either \(gg'\in E(G)\) or \(g=g'\) and \(hh'\in E(H)\). The corona product \(G\circ H\) of two graphs \(G\) and \(H\) is obtained by tacking one copy of \(G\) and \(|V(G)|\) copies of \(H\) and by joining each vertex of the \(i\)-th copy of \(H\) to the \(i\)-th vertex of \(G\), where \(1\le i\le |V(G)|\). We use \(P_n\), \(C_n\) and \(K_n\) to display the path, cycle and complete graph of order \(n\), respectively. The Cartesian product of \(C_m\square C_n\), \(P_m\square P_n\), \(K_m \square C_n\), and \(K_m \square P_n\), are said to be tori graph, grid graph, perfect tori graph and perfect grid graph respectively.
A proper \(k\)-coloring of \(G\), (\(k\in \mathbb{N}\)), is a function \(f\) defined from \(V(G)\) to a set of colors \([K]=\{1,2,\cdots,k\}\) in which every two adjacent vertices have different colors. Minimum \(k\) for coloring of a graph \(G\) is called the chromatic number of \(G\) denoted by \(\chi(G)=k\), and the color classes is denoted by \(\pi=\{S_1,\cdots,S_k\}\). The color-degree of a vertex \(v\) is defined to be the number of different colors of \(\pi\) comprising some vertex of \(N(v)\). For a connected graph \(G\), a vertex \(v\in V(G)\) and a set of vertices \(S\subseteq V(G)\), the distance between \(v\) and \(S\) is \(d(v,S)=\min\{d(v,w):w\in S\}\).
A \(k\) coloring \(\pi=\{S_1,S_2,\cdots,S_k\}\) is said to be a metric locating (\(ML\)) coloring if for every \(i\in \{1,2,\cdots,k\}\) and for every pair of distinct vertices \(u,v\in S_i\), there exists \(j\in \{1,2,\cdots,k\}\) such that \(d(u,S_j)\neq d(v,S_j)\). Minimum \(k\) for \(ML\)-coloring of a graph \(G\), is called (metric-)locating number \(\chi_L(G)\) of \(G\), [2-4]. Recently, some authors worked on edge-locating coloring of a graph, which is not without pleasure to see [5].
A \(k\)-neighbor locating coloring of a graph \(G\) is a partition of \(V(G)\) to \(\pi=\{S_1,S_2, \cdots, S_k\}\) so that for two vertices \(u_1,u_2\in S_i\), the set of colors of the neighborhood of \(u_1\) is different from the set of colors of the neighborhood of \(u_2\). Minimum \(k\) for a neighbor locating coloring (an \(NL\)-coloring) of a graph \(G\) is called the neighbor locating chromatic number (\(NL\)-chromatic number) of \(G\) denoted by \(\chi_{NL}(G)=k\). This concept has been defined under the name of adjacency locating coloring (\(L_2\)-coloring) of \(G\) in [6] and briefly worked on. Also, its chromatic number was named \(L_2\)-chromatic number of \(G\) (\(\chi_{L_2(G)}\) of \(G\)). For more information on this area see [2, 6-11].
In this paper, we observe some preliminaries results on \(NL\)-coloring in Section 2. In Section 3, the \(NL\)-chromatic number of Cartesian product of two graphs are studied, in particular the \(NL\)-chromatic number of some tori graphs, grid graphs, perfect tori graphs, and perfect grid graphs are determined. In Section 4, the \(NL\)-chromatic number of lexicographic product of two graphs are investigated and finally, \(NL\)-chromatic number of corona product of two graphs are experimented in Section 5.
In this section, we explore some preparatory results related to \(NL\)-coloring of graphs.
Remark 1. ( [8] Remark 1)Let \(G\) be a graph of order \(n\) and maximum degree \(\Delta\). Let \(\Pi= \{S_1,\cdots, S_k\}\) be a \(k\)-NL-coloring of \(G\). There exist at most \(\binom{k-1}{j}\) vertices in \(S_i\) of color-degree \(j\), for every \(1\le i \le k\), where \(1 \le j \le k-1\) and consequently, \(|S_i| \le \sum_{j=1}^{\Delta}\binom{k-1}{j}\). For \(\chi_{NL}(G)=k\ge 3\) and \(1 \le j \le \Delta\), we denote by \(a_j(k)\) the maximum number of vertices of color-degree \(j\), and we denote by \(\ell(k)\) the maximum number of vertices of color-degree \(1\) or \(2\) that is (\(\ell(k)=a_1(k)+a_2(k)\)). Therefore, we have. \[a_1(k)=k(k-1),\ \ \ \ \ a_2(k)=\frac{k(k-1)(k-2)}{2}, \ \ \ \ \ell(k)= k\binom{k}{2}=\frac{k^3-k^2}{2}.\]
Theorem 1. ([7] Theorem 1)Let \(G\) be a non-trivial graph of order \(n\) and maximum degree \(\Delta\). Let \(\chi_{N L}(G) = k\). If \(G\) has no isolated vertices and \(\Delta \le k-1\), then \[n \le k\sum_{j=1}^{\Delta}\binom{k-1}{j}.\]
From Theorem 1 and this fact, for positive integers \(l\ge k\), \(\binom{l}{t} \ge \binom{k}{t}\) (\(t\le k\)), then we have.
Corollary 1. Let \(G\) be a non-trivial graph of order \(n\) and maximum degree \(\Delta\). Let \(k=\chi_{N L}(G) \le l\). If \(G\) has no isolated vertices, then \[n \le l\sum_{j=1}^{\Delta}\binom{l-1}{j}.\]
Let \(G\) be a graph of order \(n\) and maximum degree \(\Delta\). From Corollary 1, if \(m\) is a positive integer in which \(\Delta \le m-1\) and \(n > m\sum_{j=1}^{\Delta}\binom{m-1}{j}\), then \(\chi_{N L}(G)> m\). Therefore we have the following.
Corollary 2. Let \(G\) be a graph of order \(n\) and maximum degree \(\Delta\). Then \[\chi_{N L}(G)\ge \min \left\{l: n \le l\sum_{j=1}^{\Delta}\binom{l-1}{j}\right\}.\] This bound is sharp for nontrivial path \(P_n\) from Theorem 3.6 of [6] or Theorem 17 of [8].
There needs the following.
Theorem 2. ([6] Theorem 3.6). For a positive integer \(n \ge 2\), \(\chi_{L_2(P_n)} = m\), where \(m = min\{k: k \in \mathbb{N}, n \le \frac{1}{2}(k^3-k^2)\}\). More precisely, there exist an adjacency locating \(m\)-coloring \(f_n\) of the path \(P_n = v_1v_2\cdots v_n\) with the color set \(\{1, 2, \cdots, m\}\), and two specified colors (say “1” and “2”) such that \(f_n\) satisfies the following properties.
(a) \(f_n(v_{n-1}) = 2\) and \(f_n(v_n) = 1\).
(b) If \(n \ge 9\), then \(f_n(v_{n-2}) = m\).
(c) If \(n \ge 9\) and \(n \ne\frac{1}{2}(m^3-m^2)-1\), then \(f_n(v_1) = 2\) and \(f_n(v_2) = 1\).
Theorem 3. ([8] Theorem 17). Let \(k, n\) be integers such that \(k \ge 4\) and \(\ell(k-1)< n \le \ell(k)\). Then,
\(\chi_{NL}(P_n) = k\).
\(\chi_{NL}(Cn) = k,\ {if}\ n \ne \ell(k)-1\).
\(\chi_{NL}(Cn) = k + 1,\ {if}\ n = \ell(k)-1\).
In this section we discuss on the neighbor locating coloring of Cartesian product of two graphs and obtain neighbor locating chromatic number of some tori graphs, grid graphs, complete tori and complete grid graphs.
Theorem 4. Let \(G\) and \(H\) be two graphs. Then \(\chi_{NL}(G\square H)\le \chi_{NL}(G)\chi_{NL}(H)\). This Bound is sharp.
Proof. Let \(V(G)=\{v_1, v_2,
\cdots, v_m\}\) and \(V(H)=\{u_1, u_2,
\cdots, u_n\}\). Let \(\chi_{NL}(G)=k'\) and \(\chi_{NL}(H)=k''\) with \({C}_1={CNL}(G)=\{1,2,\cdots,k^\prime\}\) as
an \(NL\)-coloring of \(G\) and \({C}_2={CNL}(H)=\{1,2,\cdots,k^{\prime\prime}\}\)
as an \(NL\)-coloring of \(H\). Now we give rise an \(NL\)-coloring of \(G\square H\). Let \(\{w_{ij}=(v_i,u_j): 1\leq i \leq m, 1\leq j \leq
n\}\) be the set of vertices \(G
\square H\). We make an \(NL\)-coloring of \(G\square H\) with \(k^\prime k^{\prime \prime}\) colors. Let
\[C=\{rs: 1\le r\le k'\ {and}\ 1\le
s\le k''\}=\{11,21,\cdots,k^\prime 1,\ 12,22,\cdots,k^\prime2,\
\cdots,\ 1k'', 2k'',\cdots, k^\prime k^{\prime
\prime}\}\] be a set of \(k'k''\) labels in which the
vertex \(w_{ij}\) is assigned by the
label \(rs\) whenever the vertex \(v_i\) has been assigned with label \(r\) and \(u_j\) with label \(s\). It is sufficient to show that for both
vertices with the same color, their color neighbors are different.
For this, we bring up three positions.
If we have two or more similar colors in a row, for instance
\(w_{ik}\) and \(w_{il}\) are assigned with same color \(rs\) in a \(i\)th row. Then vertex \(v_i\) is assigned by \(r\) and \(u_k\), \(u_l\) are assigned by \(s\). Since \(u_k\), \(u_l\) has same color in \(H\), \(N(u_k)\cap
C_2\ne N(u_l)\cap C_2\). Assume that the label \(t\) is in \(N(u_k)\cap C_2\setminus N(u_l)\cap C_2\),
then \(rt\) is in \(N(w_{ik})\) and is not in \(N(w_{il})\). This shows that, the color
neighbors of \(w_{ik}\) and \(w_{il}\) are different.
If we have two or more similar colors in a column, that is the
vertices \(w_{kj}\) and \(w_{lj}\) have similar color, then we can
observe the proof as part 1.
Let \(w_{ij}\) and \(w_{lk}\) have same color where \(i\ne l\) and \(j\ne k\). Let \(rs\) be the color of \(w_{ij}\) and \(w_{lk}\). Then the vertices \(v_i\), \(v_k\) are assigned with color \(r\) and the vertices \(u_j\), \(u_l\) are assigned with color \(s\). Assume that \(t\) is the color of one of the neighbors of
\(v_i\) say \(v_{p}\) while no neighbors of \(v_l\) are assigned by \(t\). Thus \(w_{pj}\) has color \(ts\). On the other hand, no vertex like
\(w_{qz}\) with color \(ts\) cannot be appeared in \(N(w_{lk})\) since otherwise, \(v_q\) is assigned with color \(t\) in \(N_H(v_l)\). This denotes, the color
neighbors of \(w_{ij}\) and \(w_{lk}\) are different. Therefore \(C\) is a neighbor locating coloring of
\(G\square H\).
For observing the sharpness, consider \(G=H=P_2\), then \(\chi_{NL}(P_2)=2\), \(P_2\square P_2=C_4\) and \(\chi_{NL}(C_4)=4\). ◻
The tori graph \(C_m\square C_n\) has maximum degree \(\Delta=4\) and is a free isolated vertices graph. Therefore we have.
Theorem 5. Let \(G=C_m\square C_n\) be a tori graph. Then, \[\min\{k: \dfrac{\ell(k)+k \binom{k}{4}}{mn}\ge 1\}\leq \chi_{NL}(C_m\square C_n)\leq \chi_{NL}(C_m)\chi_{NL}(C_n).\]
Proof. The upper bound is resulted from Theorem 4.
The lower bound. By definition of Cartesian product, the tori graph \(C_m\square C_n\) is a regular graph with degree \(\Delta(G)=\delta(G)=4\), and \[\begin{split} &k\sum_{j=1}^{4}\binom{k-1}{j}= k \left( \binom{k-1}{1}+\binom{k-1}{2}+\binom{k-1}{3}+\binom{k-1}{4}\right)\\ &= k \binom{k}{2}+k \binom{k}{4} = \ell (k)+k\binom{k}{4}. \end{split}\] Therefore the Corollary 2 prove the lower bound. ◻
Now we investigate the neighbor locating chromatic number of some special tori graphs.
Proposition 1. The following holds.
(i) \(\chi_{NL}(C_3 \square C_3)=5\),
(ii) \(\chi_{NL}(C_3 \square C_4)=4\),
(iii) \(\chi_{NL}(C_3 \square C_5)=5\),
(iv) \(\chi_{NL}(C_4 \square C_4)=5\),
(v) \(5\leq \chi_{NL}(C_4 \square C_5)\leq 6\),
(vi) \(5\leq \chi_{NL}(C_5 \square C_5)\leq 6\),
(vii) \(5\leq \chi_{NL}(C_6 \square C_6)\leq 6\),
(viii) \(6 \leq \chi_{NL}(C_9 \square C_9)\leq 7\).
Proof.
(i) On the contrary, suppose that \(\chi_{NL}(C_3 \square C_3)<5\). It is
clear, \(\chi_{NL}(C_3 \square C_3)\ge
4\). Let \(\{u_{ij} :1\leq i \leq 3,
1\leq j \leq 3\}\) be the set of vertices of \(C_3 \square C_3\). If \(\pi=\{S_1,S_2,S_3,S_4\}\) be the set of
colors, then it is well known that \(u_{22}\) cannot have color-degree \(1\) or \(2\). So there are at least three colors in
its neighbors. Let \(\{u_{22}\}\subseteq
S_1\), \(\{u_{12}\} \subseteq
S_2\), \(\{u_{23},u_{32}\}\subseteq
S_3\) and \(\{u_{21}\}\subseteq
S_4\). Then it is easy to check that \(u_{11}\) does not accept color \(1\) or \(3\) and it must be labeled with fifth
color, a contradiction.
(ii) Let \(\{u_{ij}: 1\leq i \leq 3, 1\leq j
\leq 4\}\) be the set of vertices \(C_3
\square C_4\). It is clear \(\chi_{NL}(C_3 \square C_4)\ge 4\). On the
other hand, if \(\pi=\{S_1,S_2,S_3,S_4\}\) is the set of
colors, and consider \(S_1=\{u_{24},u_{31},u_{33}\}\), \(S_2=\{u_{21},u_{32},u_{34}\}\), \(S_3=\{u_{11},u_{13},u_{22}\}\), \(S_4=\{u_{12},u_{14},u_{23}\}\). then it can
be an \(NL\)-coloring of \(C_3 \square C_4\). Therefore \(\chi_{NL}(C_3 \square C_4)=4\).
(iii) It is well known that \(\chi_{NL}(C_3
\square C_5)\ge 4\). On the contrary, assume that, \(\chi_{NL}(C_3 \square C_5)= 4\). Let \(\pi=\{S_1,S_2,S_3,S_4\}\). Then any vertex
of \(C_3 \square C_5\) has color degree
\(2\) or \(3\) and from Observation 1 for \(m=3\) and \(n=5\), there exist at most \(10\) vertices of color degree \(2\) in \(C_3
\square C_5\). On the other hand, there exist at most \(4\binom{3}{3}=4\) vertices of color degree
\(3\), thus there must exist at least
\(11\) vertices of color degree \(2\) in \(C_3
\square C_5\), a contradiction. Therefore \(\chi_{NL}(C_3 \square C_5)\ge 5\). Now we
give an \(NL\)-coloring of \(C_3 \square C_5\) with \(5\) colors. Let \(\pi=\{S_1,S_2,S_3,S_4,S_5\}\) with \(S_1=\{u_{22}, u_{25}, u_{31},u_{33}\}\),
\(S_2=\{u_{23},u_{34}\}\), \(S_3=\{u_{12}, u_{15} ,u_{24}\}\), \(S_4=\{u_{11},u_{14},u_{32},u_{35}\}\) and
\(S_5=\{u_{13},u_{21}\}\) is an \(NL\) coloring of \(C _3 \square C_5\). Therefore \(\chi_{NL}(C_3 \square C_5)=5\).
(iv) On the contrary, assume that \(\chi_{NL}(C_4 \square C_4)=4\). At first,
we can easy to see that, there does not exist any vertex of color degree
\(1\) in \(C_4 \square C_4\). Also by a routine
investigation, there exist at most two vertices of color degree \(2\) in each column of \(C_4 \square C_4\). On the other hand, since
\(k=4\), there must exist at least
\(4\binom{3}{2}=12\) vertices of color
degree \(2\), a contradiction.
Therefore \(\chi_{NL}(C_4 \square
C_4)\ge5\). Now we give an \(NL\)-coloring with \(5\) colors as follows. Let \(\pi=\{S_1,S_2,S_3,S_4,S_5\}\) with \(S_1=\{u_{22},u_{31},u_{33},u_{44}\}\),
\(S_2=\{u_{14},u_{34}\}\), \(S_3=\{u_{12},u_{24},u_{41},u_{43}\}\),
\(S_4=\{u_{11},u_{23},u_{32}\}\) and
\(S_5=\{u_{13},u_{21},u_{42}\}\).
Therefore \(\chi_{NL}(C_4 \square
C_4)=5\).
(v) At first we assert \(\chi_{NL}(C_4
\square C_5)\ge 5\). Assume on the contrary that, \(\chi_{NL}(C_4 \square C_5)= 4\). Since
\(C_4 \square C_5\) has only the
vertices of color degree \(2\) or \(3\) with \(4\) colors, from Theorem 5 \(\chi_{NL}(C_4 \square C_5)> 4\). The
following denotes \(\chi_{NL}(C_4 \square
C_5)\le 6\). Let \(\pi=\{S_1,S_2,S_3,S_4,S_5,S_6\}\) with
\(S_1=\{u_{22},u_{25},u_{31},u_{33}\}\),
\(S_2=\{u_{23},u_{34},u_{41}\}\), \(S_3=\{u_{12},u_{15},u_{24}\}\), \(S_4=\{u_{14},u_{32},u_{35},u_{43}\}\),
\(S_5=\{u_{13},u_{21},u_{45}\}\) and
\(S_6=\{u_{11},u_{42},u_{44}\}\).
Therefore \(5 \leq \chi_{NL} (C_4 \square C_5)
\leq 6\).
(vi) It is clear that, \(\chi_{NL} (C_5
\square C_5)\ge 5\). Now, consider \(\pi=\{S_1,S_2,S_3,S_4,S_5,S_6\}\) with
\(S_1=\{u_{22},u_{25},u_{31},u_{33},u_{45}\}\),
\(S_2=\{u_{23},u_{34},u_{51}\}\), \(S_3=\{u_{12},u_{15},u_{24},u_{42},u_{44}\}\),
\(S_4=\{u_{14},u_{32},u_{35},u_{53}\}\),
\(S_5=\{u_{13},u_{21},u_{43},u_{55}\}\)
and \(S_6=\{u_{11},u_{41},u_{52},u_{54}\}\). Then
\(\pi\) is an \(NL\)-coloring of \(C_5 \square C_5\). Therefore \(5\leq \chi_{NL}(C_5 \square C_5)\leq
6\).
(vii) It is easy to see that, \(\chi_{NL}(C_6
\square C_6)\ge 5\). We show an \(NL\)-coloring of \(C_6 \square C_6\) with \(6\) colors. Consider the coloring \(\pi=\{S_1,S_2,S_3,S_4,S_5,S_6\}\) with
\(S_1=\{u_{25},u_{33},u_{42},u_{51},u_{53},u_{66}\}\),
\(S_2=\{u_{21},u_{23},u_{32},u_{34},u_{41},u_{55},u_{62}\}\),
\(S_3=\{u_{11},u_{15},u_{22},u_{43},u_{45},u_{54}\}\),
\(S_4=\{u_{13},u_{24},u_{26},u_{35},u_{44},\\
u_{52},u_{61},u_{64}\}\), \(S_5=\{u_{14},u_{16},u_{31},u_{46},u_{63},u_{65}\}\)
and \(S_6=\{u_{12},u_{36},u_{56}\}\).
Therefore \(5\leq \chi_{NL}(C_6 \square C_6)
\leq 6\).
(viii) And finally we investigate \(\chi_{NL}(C_9 \square C_9)\). From Theorem 5, \(\chi_{NL}(C_9 \square C_9)\ge 6\). Consider \(\pi=\{S_1,S_2,S_3,S_4,S_5,S_6,S_7\}\) with
\[\begin{split} &S_1=\{u_{11},u_{14},u_{34},u_{47},u_{53},u_{55},u_{62},u_{73},u_{75},u_{82},u_{88}\},\\ &S_2=\{u_{16},u_{24},u_{36},u_{45},u_{54},u_{56},u_{59},u_{71},u_{83},u_{95},u_{97}\},\\ &S_3=\{u_{17},u_{21},u_{38},u_{42},u_{44},u_{49},u_{61},u_{65},u_{67},u_{76},u_{87},u_{99}\},\\ &S_4=\{u_{13},u_{19},u_{26},u_{28},u_{33},u_{39},u_{47},u_{52},u_{57},u_{66},u_{68},u_{74},u_{79},u_{94},u_{96}\},\\ &S_5=\{u_{32},u_{35},u_{37},u_{41},u_{43},u_{58},u_{63},u_{78},u_{84},u_{86},u_{92}\},\\ &S_6=\{u_{22},u_{25},u_{27},u_{48},u_{64},u_{69},u_{81},u_{93},u_{98}\} \, \, and \\ &S_7=\{u_{12},u_{15},u_{18},u_{23},u_{29},u_{31},u_{51},u_{72},u_{77},u_{85},u_{89},u_{91}\}. \end{split}\] This coloring is an \(NL\)-coloring of \(C_9 \square C_9\) with \(7\) colors. Therefore \(6 \leq \chi_{NL}(C_9 \square C_9)\leq 7\). ◻
Regarding to the Theorem 5, the following problem can be explored.
Problem 1. Let \(n\ge 3\) be a positive integer. For \(k\ge 5\), if \[\ell(k-1)+(k-1)\binom{k-1}{4} < n^2 \le \ell(k)+(k)\binom{k}{4},\] then \(\chi_{NL}(C_n\square C_n)\in \{k, k+1\}.\)
In this subsection we discuss on \(NL\)-coloring of grid graphs. The grid graph \(P_m\square P_n\) has maximum degree \(\Delta=4\) for \(n,m\ge 3\), and has maximum degree \(\Delta=3\) for \(m=2\) and \(n\ge 3\), furthermore, any grid graph is free isolated vertices graph. Therefore we have.
Proposition 2. Let \(G=P_2 \square P_n\) be grid graph (lader graph) where \(n\ge 3\). Then \[\min\{k: \dfrac{k^2-k +k\binom{k}{3}}{2n}\ge 1\}\leq \chi_{NL}(P_2\square P_n)\leq 2\chi_{NL}(P_n).\] The lower bound is sharp for \(P_2\square P_n\) \((n\in \{3,4,5\})\) and the upper bound is sharp for \(P_2\square P_2\).
Proof. The upper bound and its sharpness are resulted from Theorem 4.
For lower bound, since \(\Delta(P_2\square P_n)=3\), \[\begin{split} k\sum_{j=1}^{3}\binom{k-1}{j}&= k \left( \binom{k-1}{1}+\binom{k-1}{2}+\binom{k-1}{3}\right)\\ &= k^2-k +k\binom{k}{3}. \end{split}\] Now using Corollary 2, we observe the proof. ◻
For grid graphs \(P_m\square P_n\) for \(m,n\ge 3\), we have \(\Delta(P_m\square P_n)=4\). Therefore using similar proof of Theorem 5 we have the following.
Theorem 6. Let \(G=P_m \square P_n\) be the grid graph obtained from Cartesian product of \(P_m\) and \(P_n\). Then \[\min\{k: \dfrac{\ell(k)+k \binom{k}{4}}{mn}\ge 1\}\leq \chi_{NL}(P_m\square P_n)\leq \chi_{NL}(P_m)\chi_{NL}(P_n).\] The lower bound is sharp for \(P_m\square P_n\) where \(m=n\in \{3,4, 5,6\}\), see Proposition 3.
Proposition 3. For grid graphs \(P_n\square P_n\), \(n\in \{3,4,6,9\}\), we have.
(i) \(\chi_{NL}(P_3\square P_3)=4\),
(ii) \(\chi_{NL}(P_4\square P_4)=4\),
(iii) \(\chi_{NL}(P_6\square P_6)=5\),
(iv) \(\chi_{NL}(P_9\square P_9)=6\).
Proof. At first, assume that \(V(P_n)=\{v_1,v_2, \cdots, v_n\}\) and \(v_{ij}=(v_i,v_j)\) for \(1\leq i \leq n\) and \(1\leq j \leq n\) be the vertex in a \(i\)th row and \(j\)th column of \(P_n\square P_n\).
(i) Suppose to the contrary that \(\chi_{NL}(P_3\square P_3)\leq 3\). It is easy to see that, \(v_{22}\) has color-degree \(1\) or \(2\). If the color degree of \(v_{22}\) is \(1\), then \(v_{12},v_{21},v_{23},v_{32}\) have same color. According to the definition of neighbor locating coloring \(v_{11},v_{13},v_{31},v_{33}\) should be assigned with different colors, a contradiction.
If the color degree of \(v_{22}\) is
\(2\) and without loss of generality,
the color of \(v_{22}\) is \(1\) and \(v_{12},
v_{21}, v_{23}\) and \(v_{32}\)
accept two colors \(2\) or \(3\). So, at least one of the vertices of
\(v_{11}, v_{13}, v_{31}\) and \(v_{33}\) for example \(v_{31}\), should be assigned with color
\(1\), and so \(v_{22}\) and \(v_{31}\) with color \(1\) have same color neighbor, which is a
contradiction. On the other hand, it is easy to see that \(\chi_{NL}(P_3\square P_3)\le 4\).
Therefore \(\chi_{NL}(P_3\square P_3)=4\).
(ii) For \(4\)–\(NL\) coloring of \(P_4\square P_4\), from Theorem 6, \(\chi_{NL}(P_4\square P_4)\ge 4\). On the
other hand, the tables \(T_1\) and
\(T_2\) show that \(\chi_{NL}(P_4\square P_4)= 4\).
(iii) Theorem 6 denotes \(\chi_{NL}(P_6\square P_6)\ge 5\). On the
other hand, the tables \(T_2\) and
\(T_3\) show that \(\chi_{NL}(P_6\square P_6)= 5\).
(iv) From Theorem 6 we have \(\chi_{NL}(P_9\square P_9)\ge 6\). Now tables \(T_3\) and \(T_4\) show that \(\chi_{NL}(P_9\square P_9)= 6\).
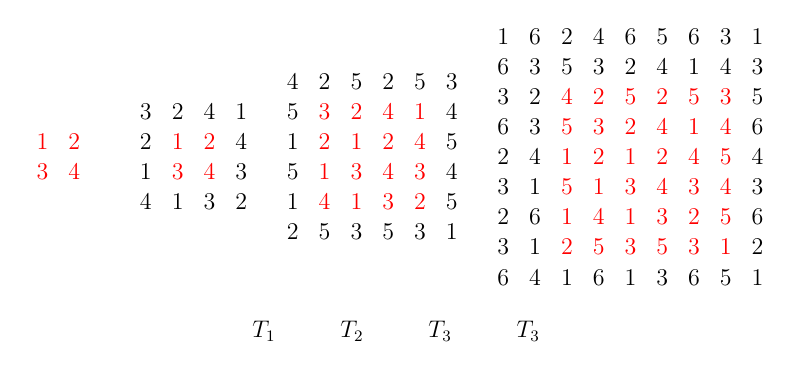
Therefore the results hold. ◻
According to Theorem 6 and Proposition 3, we expect to have the following problem.
Problem 2. Let \(n\ge 3\) be a positive integer. For \(k\ge 5\), if \[\ell(k-1)+(k-1)\binom{k-1}{4} < n^2 \le \ell(k)+(k)\binom{k}{4},\] then \(\chi_{NL}(P_n\square P_n)=k.\)
For neighbor locating coloring of perfect tori graph and perfect grid graph, we have.
Lemma 1. Let \(\chi_{NL}(K_m \square C_n)=k\). If \(m+1\le k\le 2m-1\), then at least one vertex of any column have color degree at least \(m\).
Proof. Let \(u_{1i}\) be the \(i\)-th vertex of the first column with color in \(S_i\). Suppose on the contrary, the first column has the property that, every vertex has color degree \(m-1\), then the second and end columns must be colored with colors \(S_j,\ 1\le j\le m\) which have already used for the \(1\)st column. Now, each vertex in the second column with color in \(S_i\), must have a neighbor in the third column with a color in \(S_t\) where \(t\ge m+1\). Since \(S_t\) can be nominated for at most \(m-1\) colors, one vertex in the third column can be in \(S_j,\ 1\le j\le m\). Let vertex \(u_{3l}\) be in \(S_1\). Then two vertices \(u_{2l}\) and \(u_{1r}\) with same color in \(S_r\) (\(1\le r\le m\)) find same neighbor colors \(\{S_1,S_2,\cdots,S_{r-1}, S_{r+1}, \cdots S_m \}\), that is a contradiction. ◻
The following give us an upper sharp bound for neighbor locating chromatic number for \(K_m\square P_n\) and \(K_m\square C_n\).
Proposition 4. Let \(G=K_m\square P_n\) be the perfect grid graph obtained from Cartesian product of \(K_m\) and \(P_n\) with \(m\geq 3\), \(n\geq 1\). Then \(\chi_{NL}(K_m\square P_n)\leq m+n-1\). This bound is sharp for \(K_3\square P_3\).
Proof. Each vertex in \(K_m\square P_n\) has \(m-1\) neighbors in its column and at most
two neighbors in its row. There is also \(n\) copy of \(K_m\) in \(K_m\square P_n\). We color the graph by
the columns.
The first column must accept \(m\)
colors. By assigning a new color to every other column, we will clearly
have a neighbor locating coloring for \(K_m\square P_n\). We consequently, will
have \(\chi_{NL}(K_m\square P_n)\leq
m+n-1\). ◻
Using similar proof of Proposition 4, we have.
Proposition 5. Let \(G=K_m\square C_n\) be the perfect tori graph obtained from Cartesian product of \(K_m\) and \(C_n\) with \(m, n\geq 3\). Then \(\chi_{NL}(K_m\square C_n)\leq m+n-1\) if \(3\le m\le 6\). This bound is sharp for \(K_3\square C_3\).
In the fallow, we display some Cartesian product of \(K_m\square C_3\) which \(m+1\le \chi_{NL}(K_m\square C_n)\le m+2\). For \(m=3\), with an easy calculation is verifiable that \(\chi_{NL}(K_3\square C_n)=5=3+2\), and for the \(m\ge 7\), we have \(\chi_{NL}(K_m\square C_n)=m+1\) according to the table shown below.
\[%\chi_{NL}(K_8 \square C_3) \begin{matrix} 2 & m+1 & 4\\ 3 & 1 & 5\\ 4 & 5 & 6\\ 5 & 6 & 7\\ . & . & .\\ . & . & .\\ . & . & .\\ m-2 & m-1 & m\\ m-1 & m & m+1\\ m & 3 & 1\\ m+1 & 4 & 2\\ \end{matrix}\] \(T_5\)
\(\chi_{NL}(K_m\square C_n)=m+1\)
Regarding to the table \(T_5\) and
\(\chi_{NL}\)-coloring of \(K_3 \square C_3\) we have.
Corollary 3. For \(m\ge 3\),
\(\chi_{NL}(K_m\square C_3)\le m+2\) if \(3\le m\le 6\). This bound is sharp.
\(\chi_{NL}(K_m\square C_3)= m+1\) if \(m\ge 7\).
According to the Corollary 3, one can
have.
Problem 3. For \(4\le m \le 6\), \(\chi_{NL}(K_{m} \square C_3)=m+2\).
In this section we discuss on the neighbor locating coloring of lexicographic product of two graphs with emphasis on paths, cycles and complete graphs. We start with the following.
Taking the proof of Theorem 4 as a plan, we can have the following theorem.
Theorem 7. Let \(G\) and \(H\) be two graphs. Then \(\chi_{NL}(G[H])\le \chi_{NL}(G)\chi_{NL}(H)\). This bound is sharp.
Proof. The proof is quite similar to the proof of Theorem 4. For sharpness consider \(G=P_2\) and \(H=P_n\) for any \(n\) or \(H=C_n\) for \(n\ge 3\), and see Proposition 6. ◻
For \(n=1\) and \(n=2\), \(P_2 [ P_1]=K_2\) and \(P_2 [ P_2]=K_4\), and next \(\chi_{NL}(K_2)=2\), \(\chi_{NL}(K_4)=4\). We hence deduce \(\chi_{NL}(P_2 [ P_1])=2\chi_{NL}(P_1)\) and \(\chi_{NL}(P_2 [ P_2])=2\chi_{NL}(P_2)\). Now we extend the mentioned results for any \(P_n\) and \(C_n\).
Proposition 6. Let \(n\ge 3\). Then,
\(\chi_{NL}(P_2 [ P_n])=2\chi_{NL}(P_n)\).
\(\chi_{NL}(P_2 [ C_n])=2\chi_{NL}(C_n)\).
Proof. (i) Let \(v_1,v_2,\cdots, v_n\) be the vertices of \(P_n\) and \(u_1, u_2\) be the vertices of \(P_2\). Then \(V(P_2 [ P_n])=\{(u_1,v_i), (u_2,v_i): 1\le i \le n\}\). Since any \((u_1,v_i)\) is adjacent to any \((u_2,v_j)\), hence they receive distinct colors. Therefore, we must use \(\chi_{NL}(P_n)=k\) colors for first row and \(\chi_{NL}(P_n)=k\) colors for the second row and then \(\chi_{NL}(P_2 [ P_n])=2k=2\chi_{NL}(P_n)\).
(ii) It is proved such as the proof of part (i). ◻
It is expected we nurture the Proposition 6 as.
Theorem 8. If \(k\geq 3\) and \(n\geq 4\) are integers and \(\chi_{NL}(P_n)=k\), then
\(\chi_{NL}(P_n[P_n])= 2\chi_{NL}(P_n)=6\), if \(n\in \{3,4\}\),
\(\chi_{NL}(P_n[P_n])= 2\chi_{NL}(P_n)+ \lfloor\frac{n-2}{2}\rfloor\), if \(n\in \{5,6\}\),
\(\chi_{NL}(P_n[P_n])\leq 2\chi_{NL}(P_n)+ \lfloor\frac{n-2}{2}\rfloor\), if \(n\geq 7\).
Proof. Let \(V(P_n)=\{v_1, v_2, \cdots, v_n\}\) and \(V(P_n[P_n])=\{u_{ij}: 1\le i,j\le n\}\). From the definition of the Lexicographic product, each vertex of the first row is adjacent to the vertices of the second row, each vertex of the last row is adjacent to the vertices of the \(n-1\)-th row and each vertex of the \(i\)-th row is adjacent to the vertices of the \(i-1\)-th and \(i+1\)-th rows for \(2\le i\le n-1\).
For \(n=3\), it is easy to see that, \(\chi_{NL}(P_3[P_3])= 2\chi_{NL}(P_3)=6\).
Let \(n=4\). From the relation
between vertices mentioned as above, we need at least \(6\) colors for \(NL\)-coloring of \(P_4[P_4]\). Let \(\pi=\{S_1, S_2, S_3, S_4, S_5, S_6\}\)
where \(S_1=\{u_{22},u_{24},u_{44}\}\),
\(S_2=\{u_{12},u_{14},u_{34}\}\), \(S_3=\{u_{21},u_{41},u_{43}\}\), \(S_4=\{u_{11},u_{31},u_{33}\}\), \(S_5=\{u_{23},u_{42}\}\) and \(S_6=\{u_{13},u_{32}\}\). This gives an
\(NL\)-coloring of \(P_4[P_4]\) with \(6\) colors. Therefore \(\chi_{NL}(P_4[P_4])=6\).
Let \(n\in\{ 5,6\}\). We show that \(\chi_{NL}(P_n[P_n])= 2\chi_{NL}(P_n)+ \lfloor\frac{n-2}{2}\rfloor\).
\(\chi_{NL}(P_5[P_5])\). It is obvious that, the first and second rows needs at least \(6\) colors for \(NL\)-coloring. On the other hand, for avoiding to the same color neighbors for vertices of the first and third rows or for vertices of the second and fourth rows, we need at lest one color that has not been used for first and second rows. Thus \(\chi_{NL}(P_5[P_5])\ge7\). Let \(\pi=\{S_1, S_2, S_3, S_4, S_5, S_6,S_7\}\) where \(S_1=\{u_{11}, u_{14}, u_{31}, u_{34}\}\), \(S_2=\{u_{12}, u_{32}, u_{52}\}\), \(S_3=\{u_{13}, u_{15}, u_{33}, u_{34}, u_{51}, u_{54}\}\), \(S_4=\{u_{21},u_{24}, u_{53}, u_{55}\}\), \(S_5=\{u_{21}, u_{42}, u_{44}\}\), \(S_6=\{u_{23}, u_{25}, u_{41}\}\) and \(S_7=\{u_{43}, u_{45}\}\). Then \(\pi\) is an \(NL\)-coloring of \(P_5[P_5]\) with \(7\) colors. This shows that, \(\chi_{NL}(P_5[P_5])\leq7\). Therefore \(\chi_{NL}(P_5[P_5])=7= 2\chi_{NL}(P_5)+ \lfloor\frac{5-2}{2}\rfloor\).
\(\chi_{NL}(P_6[P_6])\). The first
and second rows need \(6\) colors for
\(NL\)-coloring of \(P_6[P_6]\). If the third row take the
colors of the first row, then the fourth row must take at least one
color that has not been used for the second row. As well, if the fifth
row take the color of the third row, then the sixth row must take at
least one color that has not been used for the second and fourth rows.
Thus for \(NL\)-coloring of \(P_6[P_6]\) we need at least \(8\) distinct colors. That is \(\chi_{NL}(P_6[P_6])\ge 8\). Now we give an
\(NL\)-coloring of \(P_6[P_6]\) with \(8\) colors. Let \(\pi=\{S_1, S_2, S_3, S_4, S_5,
S_6,S_7,S_8\}\) where \(S_1=\{u_{11},u_{16},u_{31},u_{36},u_{64},u_{66}\}\),
\(S_2=\{u_{12},u_{14},u_{32},u_{34},u_{51},u_{53}\}\),
\(S_3=\{u_{13},u_{15},u_{33},u_{35}\}\),
\(S_4=\{u_{21},u_{26},u_{54},u_{56}\}\),
\(S_5=\{u_{22},u_{24},u_{44},u_{46}\}\),
\(S_6=\{u_{23},u_{25},u_{41},u_{43},u_{62},u_{65}\}\),
\(S_7=\{u_{52},u_{55}\}\) and \(S_8=\{u_{42}, u_{45},u_{61},u_{63}\}\).
Then \(\pi\) is an \(NL\)-coloring of \(P_6[P_6]\) with \(8\) colors. This shows that, \(\chi_{NL}(P_6[P_6])\leq8\). Therefore,\(\chi_{NL}(P_6[P_6])=8=2\chi_{NL}(P_6)+
\lfloor\frac{6-2}{2}\rfloor\).
(iii) We want to show that for \(n\geq7\), \(\chi_{NL}(P_n[P_n])\leq 2\chi_{NL}(P_n)+
\lfloor\frac{n-2}{2}\rfloor\). If \(n\ge 7\), then we use \(\chi_{NL}(P_n)=k\) colors \(\{1,2,\cdots,k\}\) for odd rows and we
assign \(k\) colors \(\{k+1, k+2, \cdots, 2k\}\) for second row,
and for any other even row, we use a new color beside the colors have
been used for the second row. Since we have \(\lfloor\frac{n}{2}\rfloor\) even rows, we
need at most \(\lfloor\frac{n-2}{2}\rfloor\) new colors.
This coloring is an \(NL\)-coloring for
\(P_n[P_n]\) with \(2k+\lfloor\frac{n-2}{2}\rfloor\). Therefore
\(\chi_{NL}(P_n[P_n])\leq 2\chi_{NL}(P_n)+
\lfloor\frac{n-2}{2}\rfloor\). ◻
Regarding to the Theorem 8, maybe have the following problem.
Problem 4. For which integers \(n\ge 7\), \(\chi_{NL}(P_n[P_n])= 2\chi_{NL}(P_n)+ \lfloor\frac{n-2}{2}\rfloor\)?
In \(G[H]\), if \(G=C_3\) and \(H\in \{C_n, P_n\}\), then from definition of lexicographic product of two graphs, any two vertices of \(C_3[C_n]\) or of \(C_3[P_n]\) are adjacent. Let \(G_{in}\) represent the \(i\)-th row of \(C_3[C_n]\) or of \(C_3[P_n]\). Then, there needs \(\chi_{NL}(C_n)\) or \(\chi_{NL}(P_n)\) colors for \(NL\)-coloring of \(G_{in}\). Therefore \(\chi_{NL}(C_3[C_n])\ge 3\chi_{NL}(C_n)\) or \(\chi_{NL}(C_3[P_n])\ge 3\chi_{NL}(P_n)\). Now from Theorem 7 we have.
Observation 9. Let \(n\ge 3\). Then,
\(\chi_{NL}(C_3 [ C_n])=3\chi_{NL}(C_n)\).
\(\chi_{NL}(C_3 [ P_n])=3\chi_{NL}(P_n)\).
Remark 2.
In the graph \(G[H]\), if \(G=P_3\) and \(H\in \{C_n, P_n\}\), then from definition of lexicographic product of two graphs, any vertex of second row of \(P_3[C_n]\) or of \(P_3[P_n]\) is adjacent to any vertex of the first and third rows of \(P_3[C_n]\) or \(P_3[P_n]\) respectively. Thus there need at least \(2\chi_{NL}(C_n)\) or \(2\chi_{NL}(P_n)\) for \(NL\)-coloring of \(P_3[C_n]\) or of \(P_3[P_n]\) respectively. On the other hand, each vertex of first and third rows have all colors of the second row in their color neighbors. Therefore if \({u_{1j}}\) and \({u_{3l}}\) of the first and third rows are in a same color class, then it must \(\{u_{1(j+1)}, u_{1(j-1)}\}\ne \{u_{3(l+1)}, u_{3(l-1)}\}\ ({mod}\ n)\). Therefore we can adapt the \(NL\)-coloring of \(P_{1_n}\), and \(P_{3_n}\), from the \(NL\)-coloring of \(P_{2n}\) and also adapt the \(NL\)-coloring of \(C_{1_n}\), and \(C_{3_n}\), from the \(NL\)-coloring of \(C_{2n}\).
Now from the Remark 2, we can have.
Theorem 10. Let \(n\ge 3\). If \(\ell(k-1)< n \le \ell(k)\) and \(\ell(k+t-1)< 2n \le \ell(k+t)\), then
\(\chi_{NL}(P_3 [ P_n])\le2\chi_{NL}(P_n)+t+2\).
\(\chi_{NL}(P_3 [ C_n])\le2\chi_{NL}(C_n)+t+2\).
Proof.
Let \(P_{i_n}=u_{i1}u_{i2}\cdots u_{in}\) be the \(i\)-th row of \(P_3[P_n]\). Let \(\chi_{NL}(P_n)=k\). Then \(\ell(k-1)< n \le \ell(k)\), and \(\ell(k+t-1)< 2n \le \ell(k+t)\). Hence \(\chi_{NL}(P_{2n})=k+t=m\) for \(t\ge 0\). We partition the path \(P_{2n}\) with the set of vertices \(\{v_1,v_2,\cdots, v_{n-1}, v_n,v_{n+1},v_{n+2},\cdots, v_{2n-1}, v_{2n}\}\) with \(\chi_{NL}\)-colors, to two paths \(P_{1_n}=u_{11}u_{12}\cdots u_{1n}\) and \(P_{3_n}=u_{31}u_{32}\cdots u_{3n}\) where \(u_{1j}=v_j\) and \(u_{3j}=v_{n+j}\).
Suppose that, \(c(x)\) denote the
color of \(x\). From the \(NL\)-coloring of \(P_{2n}\), \((c(u_{11}),c(u_{12}))\ne
(c(u_{3n}),c(u_{3(n-1)}))\). Now we bring up a few
situations.
If \((c(u_{11}),\ c(u_{12})) \notin \{(c(u_{1n}), c(u_{1(n-1)})),\ (c(u_{31}), c(u_{32}))\}\ {and}\ (c(u_{3n}), c(u_{3(n-1)}))\notin \{(c(u_{1n}),\ c(u_{1(n-1)})),\ (c(u_{31}),c(u_{32}))\}\), then the colors assigned to \(P_{1_n}\) and \(P_{3_n}\) are \(NL\)-coloring.
If \((c(u_{11}),c(u_{12}))=(c(u_{1n}),c(u_{1(n-1)}))\), then \((c(u_{3n}),c(u_{3(n-1)}))\ne (c(u_{1n}),c(u_{1(n-1)}))\). Thus in this situation, we assign a new color to \(u_{11}\) and the rest of the colors remain unchanged. Therefore \(P_{1_n}\) and \(P_{3_n}\) are \(NL\)-colored with at most \(m+1\) colors.
If \((c(u_{11}),c(u_{12}))=(c(u_{1n}),c(u_{1(n-1)}))\) and \((c(u_{3n}),c(u_{3(n-1)}))= (c(u_{1n}),c(u_{1(n-1)}))\), then we assign two new colors, one to \(u_{11}\), and one other to \(u_{31}\). These coloring is an \(NL\)-coloring for \(P_{1_n}\) and \(P_{3_n}\) with at most \(m+2\) colors.
Now we discuss on \(\chi_{NL}(P_3[C_n])\). Let \(C_{i_n}=u_{i1}u_{i2}\cdots u_{in}\) be the \(i\)-th row of \(P_3[C_n]\). Let \(\chi_{NL}(C_n)\in\{k,k+1\}\). Then \(\ell(k-1)< n \le \ell(k)\), and \(\ell(k+t-1)< 2n \le \ell(k+t)\). Hence \(\chi_{NL}(C_{2n})=k+t=m\) for \(t\ge 0\). We partition the cycle \(C_{2n}\) with the set of vertices \(\{v_1,v_2,\cdots, v_{n-1}, v_n,v_{n+1},v_{n+2},\cdots, v_{2n-1}, v_{2n}\}\) with \(NL\)-colors, to two cycles \(C_{1_n}=u_{11}u_{12}\cdots u_{1n}\) and \(C_{3_n}=u_{31}u_{32}\cdots u_{3n}\) where \(u_{1j}=v_j\) and \(u_{3j}=v_{n+j}\). From the \(NL\)-coloring of \(C_{2n}\), we bring up a few situations.
If \(c(u_{1n})=c(u_{3n})\), then \(C_{1_n}\) has no same color vertices with same color neighbors. In this situation \((c(u_{11}),c(u_{12}))\ne (c(u_{31}),c(u_{32}))\), and it observes that \(C_{3_n}\) also has no same color vertices with same color neighbors. Therefore this \(NL\)-coloring of \(C_{2n}\) can be used for \(C_{1_n}\) and \(C_{3_n}\).
Let \(c(u_{1n})\ne c(u_{3n})\). If \((c(u_{11}),c(u_{12}))= (c(u_{31}),c(u_{32}))\), then \(C_{1_n}\) has no same color vertices with same color neighbors. But maybe, \(C_{3_n}\) has same color vertices with same color neighbors, for this problem, we assign a new color to \(u_{31}\).
Let \(c(u_{1n})\ne c(u_{3n})\) and \((c(u_{11}),c(u_{12}))\ne (c(u_{31}),c(u_{32}))\), to avoid finding vertices with the same color that have same color neighbors, we use two new colors for \(u_{11}\) and \(u_{31}\). These coloring is an \(NL\)-coloring for \(C_{1_n}\) and \(C_{3_n}\) with at most \(m+2\) colors.
◻
Here we give some examples \(P_3 [ P_n]\) and \(P_3 [ C_n]\) with \(\chi_{NL}(P_3 [ P_n])=2\chi_{NL}(P_n)+1\), \(\chi_{NL}(P_3 [ P_n])=2\chi_{NL}(P_n)+2\), \(\chi_{NL}(P_3 [ C_n])=2\chi_{NL}(C_n)\) and \(\chi_{NL}(P_3 [ C_n])=2\chi_{NL}(C_n)+1\).
Example 1.
\(\bullet\) For \(n=4\), \(\chi_{NL}(P_3 [ P_4])=6=2\chi_{NL}(P_4)\)
with \(c(u_{11},u_{12}, u_{13},
u_{14})=(3,1,2,1)\), \(c(u_{21},u_{22},
u_{23}, u_{24})=(4,5,6,5)\) and \(c(u_{31},u_{32}, u_{33},
u_{34})=(3,2,3,1)\).
\(\bullet\) For \(n=4\), \(\chi_{NL}(P_3 [ C_4])=8=2\chi_{NL}(C_4)\)
with \(c(u_{11},\ u_{12},\ u_{13},\
u_{14})=(1,2,3,4)\), \(c(u_{21},\
u_{22},\ u_{23},\ u_{24})=(5,6,7,8)\) and \(c(u_{31},u_{32}, u_{33},
u_{35})=(1,3,2,4)\).
\(\bullet\) For \(n=5\), \(\chi_{NL}(P_3 [ P_5])=7=2\chi_{NL}(P_5)+1\)
with \(c(u_{11},u_{12}, u_{13}, u_{14},
u_{15})=(1,2,3,1,2)\), \(c(u_{21},u_{22}, u_{23},
u_{24}, u_{25})=(4,5,6,4,5)\) and \(c(u_{31},u_{32}, u_{33}, u_{34},
u_{35})=(7,2,3,7,2)\).
\(\bullet\) For \(n=5\), \(\chi_{NL}(P_3 [ C_5])=7=2\chi_{NL}(C_5)+1\)
with \(c(u_{11},u_{12}, u_{13}, u_{14},
u_{15})=(1,2,1,2,3)\), \(c(u_{21},u_{22}, u_{23},
u_{24}, u_{25})=(4,5,4,5,6)\) and \(c(u_{31},u_{32}, u_{33}, u_{34},
u_{35})=(7,2,7,1,2)\).
\(\bullet\) For \(n=6,\ \ \chi_{NL}(P_3 [ P_6])=\ 7=\
2\chi_{NL}(P_6)+1\) with \(c(u_{11},u_{12}, u_{13}, u_{14}, u_{15},
u_{16})=(1,2,3,2,3,1)\), \(c(u_{21},u_{22}, u_{23}, u_{24}, u_{25},
u_{26})=(4,5,6,5,6,4)\) and \(c(u_{31},u_{32}, u_{33}, u_{34}, u_{35},
u_{36})=(2,7,2,3,7,3)\).
\(\bullet\) For \(n=6\), \(\chi_{NL}(P_3 [ C_6])=9\ =2\
\chi_{NL}(C_6)+1\) with \(c(u_{11},u_{12}, u_{13}, u_{14}, u_{15}, u_{16})\
=\ (1,3,4,2,3,2)\), \(c(u_{21},u_{22},
u_{23}, u_{24}, u_{25}, u_{26})=(5,6,7,8,6,8)\) and \(c(u_{31},u_{32}, u_{33}, u_{34}, u_{35},
u_{36})=(1,9,2,3,9,3)\).
In the same way we can obtain \(\chi_{NL}(P_3
[ P_7])=\chi_{NL}(P_3 [ P_8])=\chi_{NL}(P_3 [ P_9])=7\), \(\chi_{NL}(P_3 [C_7])=\chi_{NL}(P_3 [
C_9])=7\) and \(\chi_{NL}(P_3 [
C_8])=9\).
In the next example, it is displayed a \(\chi_{NL}(P_3 [
C_{24}])=10=2\chi_{NL}(C_{24})+2\).
Example 2. \(\chi_{NL}(P_3
[P_{49}])=12=2\chi_{NL}(P_{49})+2\) and \(\chi_{NL}(P_3
[C_{49}])=13=2\chi_{NL}(C_{49})+1\). Since \(\ell(4)< 49 \le \ell(5)\) and \(49=\ell(5)-1\), \(\chi_{NL}(P_{49})=5\) and \(\chi_{NL}(P_{98})=7\) and \(\chi_{NL}(C_{49})=6\) and \(\chi_{NL}(C_{98})=7\), the vertices of
\(P_{1_{49}}\), \(P_{3_{49}}\), \(C_{1_{49}}\) and \(C_{3_{49}}\) cannot be \(NL\)-colored with \(6\) colors, otherwise \(\chi_{NL}(P_{98}) ,\ \chi_{NL}(C_{98}) \le
6\) which is impossible. The following is an \(\chi_{NL}\)-coloring of \(P_3 [P_{49}]\) with \(12\) colors and \(P_3 [C_{49}]\) with \(13\) colors.
\(P_{2_{49}}\) is \(NL\) colored with colors \(8,9,10,11,12\) as usual.
The \(NL\)-colors of the vertices of
\(P_{1_{49}}\) is
\(7,1,5,\ 6,1,6,\ 1,5,4,\ 1,3,5,\ 1,3,2,\
6,7,2,\ 6,3,2,\ 4,6,4,\ 6,2,4,\ 5,2,5,\ 2,6,5,\ 6,5,2,\ 4,7,2,\ 4,3,6,\\
3,6,4,\ 3,5,3,\ 7\) for the vertices \(u_{11}, \cdots, u_{1(49)}\)
respectively.
The \(NL\)-colors of the vertices of
\(P_{3_{49}}\) is
\(7,5,6,\ 3,5,4,\ 5,4,6,\ 5,4,3,\ 4,3,2,\
5,3,2,\ 7,3,2,\ 1,5,2,\ 1,2,1,\ 4,2,1,\ 6,2,1,\ 7,3,1,\ 3,6,1,\ 3,4,1,\\
4,1,6,\ 4,1,7,\ 5\) for the vertices \(u_{31}, \cdots, u_{4(49)}\)
respectively.
\(C_{2_{49}}\) is \(NL\) colored with colors \(8,9,10,11,12,13\) as usual. By changing the
color \(u_{11}\) from \(7\) to \(4\) in \(\chi_{NL}\)-coloring of \(P_3 [P_{49}]\), we attain a \(\chi_{NL}\)-coloring of \(P_3 [C_{49}]\) with \(13\) colors.
If we use the Remark 2,
and Theorem 10, for \(C_4 [ P_n]\) and \(C_4 [ C_n]\) we can adopt.
Theorem 11. Let \(n\ge 4\). If \(\ell(k-1)< n \le \ell(k)\) and \(\ell(k+t-1)< 2n \le \ell(k+t)\), then
\(\chi_{NL}(C_4 [ P_n])\le2\chi_{NL}(P_n)+2t+4\).
\(\chi_{NL}(C_4 [ C_n])\le2\chi_{NL}(C_n)+2t+4\).
Proof. Let Let \(P_{i_n}\) and \(C_{i_n}\) respectively be the \(i\)-th row of \(C_4 [ P_n]\) and \(C_4 [ C_n]\) for \(1\le i \le 4\).
By definition all vertices \(P_{2_n}\) and \(P_{4_n}\) are adjacent to all vertices of \(P_{1_n}\) and \(P_{3_n}\) and vice versa. Therefore, if two vertices \(u_{1j}\) and \(u_{3t}\) respectively in \(P_{1_n}\) and \(P_{3_n}\) have same colors under any \(NL\)-coloring, then \(\{c(u_{1(j-1)}), c(u_{1(j+1)})\}\ne \{c(u_{3(t-1)}), c(u_{1(t+1)})\}\) (\(mod\ n\)), and in the same way, if two vertices \(u_{2j}\) and \(u_{4t}\) respectively in \(P_{2_n}\) and \(P_{4_n}\) have same colors under any \(NL\)-coloring, then \(\{c(u_{2(j-1)}), c(u_{2(j+1)})\}\ne \{c(u_{4(t-1)}), c(u_{4(t+1)})\}\) (\(mod\ n\)). Now using the Remark 1 we need at most \(\chi_{NL}(P_n)+t+2\) colors for \(NL\)-coloring of \(P_{1_n}\) and \(P_{3_n}\) and we need at most \(\chi_{NL}(P_n)+t+2\) colors for \(NL\)-coloring of \(P_{2_n}\) and \(P_{4_n}\).
There is a same way for part 2 and we left the proof.
◻
From the Examples 1, 2, maybe the Theorems 10 and 11 regulated as.
Problem 5. For path \(P_n\) and cycle \(C_n\), we have.
\(\chi_{NL}(P_3 [ P_n])\le2\chi_{NL}(P_n)+t+1\).
\(\chi_{NL}(P_3 [ C_n])\le2\chi_{NL}(C_n)+t+1\).
\(\chi_{NL}(C_4 [ P_n])\le2\chi_{NL}(P_n)+2t+2\).
\(\chi_{NL}(C_4 [ C_n])\le2\chi_{NL}(C_n)+2t+2\).
In this section we investigate neighbor locating coloring of the corona product of two graphs in terms of neighbor locating coloring of each of them. We start with a general result.
Theorem 12. Let \(G\) and \(H\) be two graphs. Then \(\chi_{NL}(G\circ H)\le |V(G)|+\chi_{NL}(H)\). This bound is sharp.
Proof. For this, if we assign distinct colors to the vertices of \(G\) and from definition of corona of two graphs the color of the \(i\)-th vertex of \(G\) must be different to the colors of the vertices of \(i\)-th copy of \(H\). On the other hand, if any two vertices in a copy of \(H\) have same color, then it is clear, they have different color neighbors in this copy. If two vertices of two copies of \(H\) have same color, then one of them is in \(i\)-th copy and the other is in \(j\)-th copy where the color of \(i\)-th vertex in \(G\) and the color of \(j\)-th vertex in \(G\) are different and then two vertices in two copies of \(H\) with same color find different color neighbors. This bound is sharp for \(K_2\circ K_n\), see Theorem 13. ◻
Theorem 13. Let \(n\geq 3\) and \(m\geq 1\) be integers. Then \(\chi_{NL}(K_n\circ K_m)=\begin{cases}n & m\leq n-2 \\ m+2 & m\geq n-1 \end{cases}.\)
Proof. Suppose that \(m\leq n -2\). Since \(\chi_{NL}(K_n)=n\), let \(\pi=\{S_1, S_2, \cdots, S_n\}\) be the set of colors assigned to \(K_n\). Let the \(i\)-th vertex of \(K_n\) is assigned by color \(i\) and \({K^i_m}\) be the \(i\)-th copy of \(K_m\). Then we consider \(\pi(K^i_m)=\{S_{i+1},\cdots, S_{i+m}\}\ (1{mod}\ n)\) for \(1\le i\le n\). We assert that these assignments give us an \(NL\)-coloring of \(K_n\circ K_m\). For this, every vertex of \({K^i_m}\) has at most \(m\) color neighbors and any vertex in \(K_n\) has \(n-1\ge m+1\) color neighbors.
As well we say \(\pi_i= \pi(K^i_m)=
\{S_{i+1}, S_{i+2}, \cdots, S_{i+m}\}\ (1{mod}\ n)\). Then
\(\pi_i\) can be have common colors at
most with \(\pi_{i+1}, \pi_{i+2}, \cdots,
\pi_{i+m}, \pi_{i-1}, \pi_{i-2}, \cdots, \pi_{i-m}\) and \(\pi_i\) does not have common color with
\(\pi_j\) for \(j\ge i+m+1\) or \(j\le i-m-1\) if any. On the other hand, for
any \(1\le k\le m\), every vertex of
\(K^{i+k}_m\) does not have the color
\(i+k-1\ (1{mod}\ n)\) as a color
neighbor but any vertex of \(K^i_m\)
has this property, also for any \(1\le k\le
m\), every vertex of \(K^{i-k}_m\) does not have the color \(i+m-k+1\ (1{mod}\ n)\) as a color
neighbor but any vertex of \(K^i_m\)
has this property. Therefore, \(\pi\)
is a minimum-\(NL\)-coloring of \(K_n\circ K_m\) for \(m\le n-2\), and then \(\chi_{NL}(K_n\circ K_m)=n\).
Suppose that \(m\geq n-1\), then \(\omega(K_n\circ K_m)=m+1\). Same as part 1,
we need \(n\) distinct color for \(K_n\) and since \(m\ge n-1\) at least \(m+1\) distinct color must be used for the
\(i\)-th vertex of \(K_n\) and the vertices of \({K^i_m}\). Therefore, we need at least
\(m+2\) colors for \(NL\)-coloring of \(K_n\circ K_m\). Now we give an \(NL\) coloring of \(K_n\circ K_m\) with \(m+2\) colors. For this, we bring up three
situations.
Suppose that \(m=n-1\) and \(\pi=\{S_1, S_2, \cdots , S_n, S_{n+1}\}\). Then we assign the colors as follows.
\(\pi(K_n)=\{S_1,S_2, \cdots,
S_n\}\), where \(i\)-th color
has been used for \(i\)-th vertex of
\(K_n\). Then \[\pi({K^i_m})=\{S_1, S_2, \cdots, S_{i-2},
S_{i+1}, \cdots, S_{n}, S_{n+1}\}\ 1{for}\ 1\le i \le n.\]
We show that \(\pi\) is a minimum \(NL\)-coloring of \(G\) with \(m+2=n+1\) colors. We straightforward
understand, any vertex of \(K^i_m\)
does not have color \(i-1\) in its
color neighbors and any vertex of \(K_n\) with \(j\)-th color (\(j\ne i-1\)) has \(i-1\) as a color neighbor. On the other
hand, every vertex of \(K^i_m\) has
color \(j-1\) in the color neighbor and
every vertex of \(K^j_m\) has color
\(i-1\) in the color neighbor for \(i\ne j\). Therefore the mentioned coloring
is a minimum \(NL\)-coloring.
Suppose that \(m=n\) and \(\pi=\{S_1, S_2, \cdots , S_n, S_{n+1}, S_{n+2}\}\). We show that \(\pi\) is a minimum \(NL\)-coloring for \(K_n\circ K_m\) with \(m+2=n+2\) colors. Then we consider the assigned colors as follows.
\(\pi(K_n)=\{S_1, S_2, \cdots,
S_n\}\), where \(i\)-th color
has been used for \(i\)-th vertex of
\(K_n\), and \[\pi({K^i_m})=\{S_1, S_2, \cdots, S_{i-2},
S_{i+1}, \cdots, S_{n+1}, S_{n+2}\}\ 1{for}\ 1\le i \le n.\]
It is straightforward to understand, any vertex of \(K^i_m\) (\(1\le
i\le n\)) has color \(n+1\) or
\(n+2\) in its color neighbors and any
vertex of \(K_n\) does not have one as
a color neighbor. On the other hand, every vertex of \(K^i_m\) has color \(j-1\) in the color neighbor and every
vertex of \(K^j_m\) has color \(i-1\) in the color neighbor for \(i\ne j\). Therefore the mentioned coloring
is a minimum \(NL\)-coloring.
Suppose that \(m\geq n+1\) and \(m=n+r\) and \(\pi=\{S_1, S_2,S_3\cdots , S_{n+r+1},S_{n+r+2}\}\). Then, from part 2, consider \(\pi(K_n)=\{S_1, S_2, \cdots, S_n\}\), and \[\pi({K^i_m})=\{S_1, S_2, \cdots, S_{i-2}, S_{i+1}, \cdots, S_{m+1}, S_{m+2}\}\ 1{for}\ 1\le i \le n.\] Now similar proof of part 2, shows that \(\pi\) is a minimum \(NL\)-coloring of \(K_n\circ K_m\) for \(m\ge n+1\).
◻
Theorem 14. Let \(G=P_m \circ P_n\) be a graph. Then, \[\min \{k+m:\dfrac{(k+m)\left(\binom{k+m}{3}+ \binom{k+m}{k+2}\right)}{m+mn} \geq 1\}\leq \chi_{NL}(P_m\circ P_n) \le m+\chi_{NL}(P_n).\] The upper bounds is sharp.
Proof. For upper bound, use Theorem 12 and for the
sharpness, consider \(P_3 \circ P_n\)
for \(n\ge 1\).
Lower bound; in graph \(P_m \circ
P_n\), the vertices of a copy of \(P_n\) have color-degree \(2\) or \(3\) and the vertices of \(P_m\) have color-degree \(k+2\) or \(k+3\), where \(k=\chi_{NL}(P_n)\). On the other hand \(\chi_{NL}(P_m\circ P_n) \le m+k\). From
Corollary 1, we have \[m+mn\le (k+m)\left(\binom{k+m-1}{2}+
\binom{k+m-1}{3} + \binom{k+m-1}{k+1}+
\binom{k+m-1}{k+2}\right)=\] \[(k+m)\left(\binom{k+m}{3}+
\binom{k+m}{k+2}\right).\] Now using Corollary 2 the lower bound
is observed. ◻
In the following, for any integer \(k\ge 3\), we construct a graph \(G\) in which \(\chi_{NL}(G \circ P_2)=k\).
Proposition 7. For every \(k\geq 3\), \(\chi_{NL}(P_{\frac{k(k-1)(k-2)}{6}} \circ P_2)=k\).
Proof. For any positive integer \(m\), there are \(m\) \(K_3\) in \(P_m \circ P_2\) in which \(2m\) vertices have exactly color-degree \(2\). Therefore, from Corollary 1 \[n(P_m \circ P_2)=m+2m \le l \binom{l-1}{2}+m\le \dfrac{3}{2}\binom{l-1}{2}.\] Since \(\frac{l(l-1)(l-2)}{6}\le l \binom{l-1}{2}\), from Corollary 2, \(\chi_{NL}(P_{\frac{k(k-1)(k-2)}{6}})\ge k\). Now we give an \(NL\)-coloring for \(P_{\frac{k(k-1)(k-2)}{6}} \circ P_2\) with \(k\)-colors. It is well known that, \(6\mid k(k-1)(k-2)\). Thus there exist two situations as follows.
Let \(6\mid (k-1)(k-2)\) and \(t=\frac{(k-1)(k-2)}{6}\). Then we have a path with \(tk\) vertices and \(tk\) paths \(P_2\) which each of them is adjacent to a vertex of \(P_{tk}\) and the vertices of \(P_{tk}\) with \(V(P_{tk})=\{v_{jk+i}: 1\le i \le k\ 1{and}\ 0\le j\le t-1\}\) and the vertices of \(V(mP_2)= \{u_{jk+i}, w_{jk+i}: 1\le i \le k\ 1{and}\ 0\le j\le t-1\}\).
For coloring of \(P_{tk}\circ P_2\),
we assign color \(i\) to the vertex
\(v_{jk+i}\) for \(1\le i \le k\) and \(0\le j\le t-1\) of \(P_{tk}\), and assign color \(i+1\), \(j+i+2\) to the vertices \(u_{jk+i}, w_{jk+i}\) for \(1\le i\le k\) and \(1\le j \le t-2\) and assign color \(i+2,i+3\) to the vertices \(u_{(t-1)k+i}, w_{(t-1)k+i}\) (\(mod\ k\)) respectively. This coloring is an
\(NL\)-coloring with \(k\) colors. Therefore, in this position
\(\chi_{NL}(P_{\frac{k(k-1)(k-2)}{6}} \circ
P_2)=k\)
Let \(6\nmid (k-1)(k-2)\) and \(\frac{k(k-1)(k-2)}{6}=sk+r\) where \(1\le r \le k-1\). Then we have a path with \(sk+r\) vertices and \(sk+r\) paths \(P_2\) which each of them is adjacent to a vertex of \(P_{sk+r}\) and the vertices of \(P_{sk+r}\) with \(V(P_{sk+r})=\{v_{jk+i}: 1\le i \le k\ 1{and}\ 0\le j\le s-1\} \cup \{v_{sk+i}: 1\le i\le r \}\) and the vertices of \(V(mP_2)= \{u_{jk+i}, w_{jk+i}: 1\le i \le k\ 1{and}\ 0\le j\le s-1\} \cup \{u_{sk+i}, w_{sk+i}: 1\le i \le r\}\).
For coloring of \(P_{sk+r}\circ P_2\), we assign color \(i\) to the vertex \(v_{jk+i}\) for \(1\le i \le k\) and \(0\le j\le s\) of \(P_{sk+r}\) and assign color \(i+1,j+i+2\) to the vertices \(u_{jk+i}, w_{jk+i}\) for \(1\le i\le k\) and \(1\le j \le s-1\) and assign color \(i+2,i+3\) to the vertices \(u_{sk+i}, w_{sk+i}\) (\(1\le i \le r\)), (\(mod\ k\)) respectively. This coloring is an \(NL\)-coloring with \(k\) colors. Therefore, in this position \(\chi_{NL}(P_{\frac{k(k-1)(k-2)}{6}} \circ P_2)=k\). Consequently, the result holds. ◻
One of the relation in \(NL\) coloring of corona product, attaining \(\chi_{NL}(K_m\circ P_n)\). For this, at first we state a proposition.
Proposition 8. \[\chi_{NL}(K_m\circ P_n)=\begin{cases} m+2 & m=n=3\\n+1 & 4\le m=n \le 5,\ 1{or}\ m=4\ 1{and}\ n\le 3,\ 1{or}\ m=3\ 1{and}\ n\le 2.\end{cases}\]
Proof.
If \(m=n=3\), then it is clear
\(\chi_{NL}(K_3\circ P_3)\ge 4\).
Assume contradictorily, \(\chi_{NL}(K_3\circ
P_3)= 4\) and vertices of \(K_3\) are assigned with colors \(1,2,3\). Then the path \(P_3\) adjacent to the vertex with color
\(1\), are \(2,3,4\) and two other \(P_3\), take colors \(1,2,4\) and \(1,3,4\) respectively. With this coloring,
either two vertices with color \(4\)
attain a same color neighbor or two vertices with one of colors \(1,2\) or \(3\) attain a same color neighbor, that is a
contradiction. Therefore \(\chi_{NL}(K_3\circ
P_3)\ge 5\). Now we assign colors \(1,4,5\); \(2,4,5\) and \(3,4,5\) to the vertices \(P_3\) adjacent to the vertices with color
\(2\), \(3\) and \(1\) respectively. The former coloring is an
\(NL\)-coloring of \(K_3\circ P_3\).
Let \(m=n=4\). Then \(\chi_{NL}(K_4\circ P_4)\ge 5\). Now we give an \(NL\) coloring with \(5\) colors. Let \(v_i\) (\(1\le i \le 4\)) be the vertices of \(K_4\) and \(u_{ji}\), (\(1\le j\le 4\) be the vertices of \(P_{4_i}\), the path \(P_4\) adjacent to \(v_i\). The assignment color \(i\) to \(v_i\); color \(i-1\) (\(1{mod}\ 4\)) to \(u_{1i}\); color \(i+1\) (\(1{mod}\ 4\)) to \(u_{2i}\); color \(5\) to \(u_{3i}\); and color \(i+2\) (\(1{mod}\ 4\)) to \(u_{4i}\) give an \(NL\)-coloring for \(1\le i \le 4\). Therefore \(\chi_{NL}(K_4\circ P_4)= 5\).
Let \(m=n=5\). Then \(\chi_{NL}(K_5\circ P_5)\ge 6\). We give an \(NL\) coloring with \(6\) colors. Let \(v_i\) (\(1\le i \le 5\)) be the vertices of \(K_5\) and \(u_{ji}\), (\(1\le j\le 5\)) be the vertices of \(P_{5_i}\), the path \(P_5\) adjacent to \(v_i\). The assignment color \(i\) to \(v_i\); color \(i-1\) (\(1{mod}\ 5\)) to \(u_{1i}\); color \(i+1\) (\(1{mod}\ 5\)) to \(u_{2i}\); color \(6\) to \(u_{3i}\); color \(i+2\) (\(1{mod}\ 5\)) to \(u_{4i}\); and color \(i+3\) (\(1{mod}\ 5\)) to \(u_{5i}\) give an \(NL\)-coloring for \(1\le i \le 4\). Therefore \(\chi_{NL}(K_5\circ P_5)= 6\).
For \(m=4\) and \(n\le 3\); or \(m=3\) and \(n\le 2\), there exist similar reason, and we left the proof. ◻
Theorem 15. Let \(m\) and \(n\) be positive integers, \(\ell(k-1)+1\le n \le \ell(k)\), and \(n=tk+r\ (0\le r\le k-1)\). \[1{If}\ m>k\ 1{and}\ \binom{m-1}{3}\ge 3(r\lceil \frac{n}{k} \rceil + (k-r)\lfloor \frac{n}{k} \rfloor),\ 1{then}\ \chi_{NL}(K_m\circ P_n)=m\]
Proof. Since \(\ell(k-1)+1\le n \le \ell(k)\), \(\chi_{NL}(P_n)=k\). Let the vertex \(v_i\) of \(K_m\) be assigned by color \(i\) for \(1\le i\le m\). Let \(P_{n_i}\) be the path \(P_n\) adjacent to \(v_i\), and \(V(P_{n_i})=\{u_{ji}: 1\le j\le n\}\). From the data, we assign colors \(i+1, i+2, \cdots, i+k\) (\(1{mod}\ n\)) to the vertices of \(V(P_{n_i})\) (\(1\le i\le m\)). There has been used \(mn\) colors for all \(P_{ni}\)s so that every color is appeared in \(k\) paths \(P_{ni}\)s, and is iterated \(n\) times. In addition to that, each vertex is iterated \(\lceil\frac{n}{k}\rceil\) times in \(r\) paths \(P_{ni}\)s and is iterated \(\lfloor\frac{n}{k}\rfloor\) times in \(k-r\) paths \(P_{ni}\)s. On the other hand, each vertex has color degree at most \(3\). Hence, each vertex with color \(i\) has at most \((r\lceil \frac{n}{k} \rceil + (k-r)\lfloor \frac{n}{k} \rfloor)\) clusters of three colors. In the other words, there exist \((r\lceil \frac{n}{k} \rceil + (k-r)\lfloor \frac{n}{k} \rfloor)\) clusters of four colors in which one of colors is \(i\). Also, if we consider the \(m\) colors of \(K_m\), for each vertex with color \(i\), there exist \(\binom{m-1}{3}\) clusters of three colors so that \(i\) forms clusters of four colors that one of colors is \(i\). Since by the data, \(\binom{m-1}{3}\ge 3(r\lceil \frac{n}{k} \rceil + (k-r)\lfloor \frac{n}{k} \rfloor)\), there does not exist two same color vertices with same color neighbors. Therefore \(\chi_{NL}(K_m\circ P_n)=m\). ◻
We greatly appreciate the valuable suggestions made by Jamie Hallas that resulted in an improved paper.
Behtoei, A. and Anbarloei, M., 2015. A bound for the locating chromatic numbers of trees. Transactions on Combinatorics, 4(1), pp.31-41.
Behtoei, A. and Omoomi, B., 2016. On the locating chromatic number of the Cartesian product of graphs. Ars Combinatoria, 126, pp.221-235.
Chartrand, G., Erwin, D., Henning, M. A., Slater, P. J. and Zhang, P., 2002. The locating-chromatic number of a graph. Bulletin of the Institute of Combinatorics and Its Applications, 36, pp.89-101.
Korivand, M., Mojdeh, D. A., Baskoro, E. T. and Erfanian, A., 2024. Edge-locating coloring of graphs. Electronic Journal of Graph Theory and Applications, 12(1), pp.55-73.
Behtoei, A. and Anbarloei, M., 2014. The locating chromatic number of the join of graphs. Bulletin of the Iranian Mathematical Society, 40(6), pp.1491-1504.
Alcon, L., Gutierrez, M., Hernando, C., Mora, M. and Pelayo, I. M., 2020. Neighbor-locating colorings in graphs. Theoretical Computer Science, 806, pp.144-155.
Alcon, L., Gutierrez, M., Hernando, C., Mora, M. and Pelayo, I. M., 2019. The neighbor-locating-chromatic number of pseudotrees. arXiv:1903.11937v1 [math.CO].
Alcon, L., Gutierrez, M., Hernando, C., Mora, M. and Pelayo, I. M., 2023. The neighbor-locating-chromatic number of trees and unicyclic graphs. Discussiones Mathematicae Graph Theory, 43, pp.659-675.
Hernando, C., Mora, M., Pelayo, I. M., Alcon, L. and Gutierrez, M., 2018. Neighbor-locating coloring: graph operations and extremal cardinalities. Electronic Notes in Discrete Mathematics, 68, pp.131-136.
Mojdeh, D. A., 2022. On the conjectures of neighbor-locating coloring of graphs. Theoretical Computer Science, 922, pp.300-307.
1970-2025 CP (Manitoba, Canada) unless otherwise stated.