The λ-fold complete symmetric directed graph of order v, denoted λKv*, is the directed graph on v vertices and λ directed edges in each direction between each pair of vertices. For a given directed graph D, the set of all v for which λKv* admits a D-decomposition is called the λ-fold spectrum of D. In this paper, we settle the λ-fold spectrum of each of the nine non-isomorphic orientations of a 6-cycle.
If \(a\) and \(b\) are integers with \(a \leq b\), we let \([a,b]\) denote the set \(\{a, a+1, \ldots, b\}\). For a graph (or directed graph) \(D\), we use \(V(D)\) and \(E(D)\) to denote the vertex set of \(D\) and the edge set (or arc set) of \(D\), respectively. Furthermore, we use \({\mbox{$\vphantom{D}$}^{\lambda\!}D}\) to denote the multigraph (or directed multigraph) with vertex set \(V(D)\) and \(\lambda\) copies of each edge (or arc) in \(E(D)\). For a simple graph \(G\), we use \(G^*\) to denote the symmetric digraph with vertex set \(V(G^*)=V(G)\) and arc set \(E(G^*)= \bigcup_{\{u,v\}\in E(G)} \bigl\{ (u,v), (v,u) \bigr\}\). Hence, \({}^{\lambda}K_{v}^{\ast}\) is the \(\lambda\)-fold complete symmetric directed graph of order \(v\).
A decomposition of a directed multigraph \(K\) is a collection \(\Delta =\{D_1, D_2,\ldots, D_t\}\) of subgraphs of \(K\) such that each directed edge, or arc, of \(K\) appears in exactly one \(D_i \in \Delta\). If each \(D_i\) in \(\Delta\) is isomorphic to a given digraph \(D\), the decomposition is called a \(D\)-decomposition of \(K\). A \(D\)-decomposition of \(K\) is also known as a \((K, D)\)-design. The set of all \(v\) for which \(K_{v}^{\ast}\) admits a \(D\)-decomposition is called the spectrum of \(D\). Similarly, the set of all \(v\) for which \({\mbox{$\vphantom{K}$}^{\lambda\!}K}_{v}^{\ast}\) admits a \(D\)-decomposition is called the \(\lambda\)-fold spectrum of \(D\).
The reverse orientation of \(D\), denoted \(\mathop{\mathrm{Rev}}D\), is the digraph with vertex set \(V(D)\) and arc set \(\bigl\{ (v,u) : (u,v)\in E(D) \bigr\}\). We note that the existence of a \(D\)-decomposition of \(K\) necessarily implies the existence of a \(\mathop{\mathrm{Rev}}D\)-decomposition of \(\mathop{\mathrm{Rev}}K\). Since \(K_{v}^{\ast}\) is its own reverse orientation, we note that the spectrum of \(D\) is equal to the spectrum of \(\mathop{\mathrm{Rev}}D\).
The necessary conditions for a digraph \(D\) to decompose \({\mbox{$\vphantom{K}$}^{\lambda\!}K}_{v}^{\ast}\) include
(a) ]\(|V(D)|\leq v\),
(b) ]\(|E(D)|\) divides \(\lambda v(v-1)\), and
(c) ]\(\gcd\{\mathop{\mathrm{outdegree}}(x) : x\in V(D)\}\) and \(\gcd\{\mathop{\mathrm{indegree}}(x) : x\in V(D)\}\) both divide \(\lambda (v-1)\).
The spectrum problem for certain subgraphs (both bipartite and non-bipartite) of \(K^{*}_{4}\) has already been studied. When \(D\) is a cyclic orientation of \(K_{3}\), then a \(( K_{v}^{\ast},D)\)-design is known as a Mendelsohn triple system. The spectrum for Mendelsohn triple systems was found independently by Mendelsohn [1]and Bermond [2]. When \(D\) is a transitive orientation of \(K_{3}\), then a \(( K_{v}^{\ast},D)\)-design is known as a transitive triple system. The spectrum for transitive triple systems was found by Hung and Mendelsohn [3]. There are exactly four orientations of a 4-cycle (i.e., a quadrilateral). It was shown in [4]that if \(D\) is a cyclic orientation of a 4-cycle, then a \(( K_{v}^{\ast},D)\)-design exists if and only if \(v\equiv 0\) or \(1\pmod{4}\) and \(v\neq 4\). The spectrum problem for the remaining three orientations of a 4-cycle were setled in [5]. In [6], Alspach et al. showed that \(K_{v}^{\ast}\) can be decomposed into each of the four orientations of a \(5\)-cycle (i.e., a pentagon) if and only if \(v\equiv 0\) or \(1\pmod{5}\). In [7], it is shown that for positive integers \(m\) and \(v\) with \(2\leq m\leq v\) the directed graph \(K_{v}^{\ast}\) can be decomposed into directed cycles (i.e., with all the edges being oriented in the same direction) of length \(m\) if and only if \(m\) divides the number of arcs in \(K_{v}^{\ast}\) and \((v,m)\notin \bigl\{ (4,4), (6,3), (6,6) \bigr\}\). Also recently [8], Odabaşı settled the spectrum problem for all possible orientations of a \(7\)-cycle.
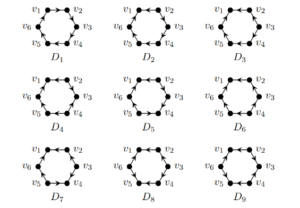
There are nine non-isomorphic orientations of a \(6\)-cycle. We denote these with \(D_1\), \(D_2\), …, \(D_9\) as seen in Figure 1. The \(\lambda\)-fold spectrum problem was settled for the directed \(6\)-cycle (i.e., \(D_1\)) in [9]. In this work, we settle this problem for the remaining eight orientations. Our main result, which is proved in Section 3, is as follows.
Theorem 1. Let \(D\) be an orientation of a \(6\)-cycle and let \(\lambda\) and \(v\) be positive integers such that \(v\geq6\). There exists a \(D\)-decomposition of \({}^{\lambda} K_{v}^{\ast}\) if and only if \(\lambda v(v-1) \equiv 0\pmod{3}\) and neither of the following hold
\((D,\lambda,v)=(D_1,1,6)\) or
\(D=D_9\) and \(\lambda (v-1)\) is odd.
From the necessary conditions stated earlier, we have the following.
Lemma 1. Let \(D \in \{D_2,D_3,\ldots, D_8\}\) and let \(\lambda\) and \(v\) be positive integers such that \(v\geq6\). There exists a \(D\)-decomposition of \({}^{\lambda} K_{v}^{\ast}\) only if \(\lambda v(v-1) \equiv 0\pmod{3}\). Furthermore, there exists a \(D_9\)-decomposition of \({}^{\lambda} K_{v}^{\ast}\) only if \(\lambda v(v-1) \equiv 0\pmod{3}\) and \(\lambda (v-1) \equiv 0\pmod{2}\).
In 1978, Bermond, Huang, and Sotteau [9]showed that with the exception that there is no \(D_1\)-decomposition of \(K^*_6\), these necessary conditions are sufficient for \(D_1\).
Theorem 2. For integers \(v\geq 6\) and \(\lambda \geq 1\), there exists a \(D_1\)-decomposition of \({\mbox{$\vphantom{K}$}^{\lambda\!}K}_{v}^{\ast}\) if and only if \(\lambda v(v-1)\equiv 0\pmod{6}\) and \((\lambda,v)\neq(1,6)\).
The remainder of this paper is dedicated to establishing sufficiency of the above necessary conditions. We achieve this by exhibiting constructions for the desired decompositions (see Section 3) using certain small examples (see Section 2). Henceforth, each of the graphs in Figure 1, with vertices labeled as in the figure, will be represented by \({D_i}[v_1, v_1,\ldots, v_6]\).
For \(m \geq 2\), the following result of Sotteau proves the existence of \(2m\)-cycle decompositions of complete bipartite graphs.
Theorem 3 ([10]). Let \(x\), \(y\), and \(m\) be positive integers such that \(m \geq 2\). There exists a \(2m\)-cycle decomposition of \(K_{2x,2y}\) if and only if \(m \mid 2xy\) and \(\min\{2x,2y\} \geq m\).
Consider an orientation of a 6-cycle that is isomorphic to its own reverse, i.e. any \(D_i\) in Figure 1 such that \(i\notin\{7,8\}\). By definition of reverse orientation, the set \(\{D_i, \mathop{\mathrm{Rev}}D_i\}\) is an obvious \(D_i\)-decomposition of \(C^*_6\) (the symmetric digraph with a 6-cycle as the underlying simple graph). Since a \(G\)-decomposition of a graph \(K\) necessarily implies a \(G^*\)-decomposition of the digraph \(K^*\), we get the following corollary from the case \(m=3\) in Theorem 3.
Corollary 1. Let \(D\in \{D_1,D_2,D_3,D_4,D_5,D_6,D_9\}\). There exists a \(D\)-decomposition of \(K^*_{2x,2y}\) if \(3 \mid xy\) and \(\min\{x,y\}\geq2\).
We first present several \(D_i\)-decompositions of various graphs for \(i \in [2,9]\). Beyond establishing existence of necessary base cases, these decompositions are used extensively in the general constructions seen in Section 3.
If \(i,v_1,v_2,\ldots,v_6\) are integers and \(D\in\{D_1, D_2,\dots, D_9\}\), we define \(D[v_1,v_2,\ldots, v_6]+i\) to indicate \(D[v_1+i,{$ $}v_2+i,{$ $}\ldots,{$ $}v_6+i]\). Similarly, if the vertices of \(D\) are ordered pairs in \({\mathbb{Z}}_m\times{\mathbb{Z}}_n\), then \(D\bigl[(u_1,v_1),{$ $}(u_2,v_2),{$ $}\ldots,{$ $}(u_6,v_6)\bigr]+(i,0)\) means the digraph \(D\bigl[(u_1+i,v_1),{$ $}(u_2+i,v_2),{$ $}\ldots,{$ $}(u_6+i,v_6)\bigr]\). We also use the convention that both \(\infty+i\) and \(\infty+(i,0)\) result in simply \(\infty\).
Example 1. Let \(V\bigl( K^*_6 \bigr) = {\mathbb{Z}}_{5} \cup \{\infty\}\) and let \[\begin{aligned} \Delta_2 = \{& D_2 [0,3,4,2,1,\infty] +i : i \in {\mathbb{Z}}_{5} \} , \\* \Delta_3 = \{& D_3 [0,4,1,3,2,\infty] +i : i \in {\mathbb{Z}}_{5} \} , \\ \Delta_4 = \{& D_4 [0,1,2,4,\infty,3] +i : i \in {\mathbb{Z}}_{5} \} , \\ \Delta_5 = \bigl\{& D_5 [0,1,3,2,\infty,4], \, D_5 [1,3,4,\infty,2,0], \, D_5 [2,4,1,\infty,3,0], \\*& D_5 [4,1,2,3,\infty,0], \, D_5 [3,0,\infty,1,2,4] \bigr\}, \\[3pt] \Delta_6 = \{& D_6 [0,1,3,2,4,\infty] +i : i \in {\mathbb{Z}}_{5} \} , \\ \Delta_7 = \{& D_7 [0,1,3,4,2,\infty] +i : i \in {\mathbb{Z}}_{5} \} , \\* \Delta_8 = \{& D_8 [0,\infty,1,3,2,4] +i : i \in {\mathbb{Z}}_{5} \} . \end{aligned}\] Then \(\Delta_i\) is a \(D_i\)-decomposition of \(K^*_{6}\) for \(i \in [2,8]\).
Example 2. Let \(V\bigl( {\mbox{$\vphantom{K^*}$}^{2\!}K^*}_6 \bigr) = {\mathbb{Z}}_{5} \cup \{\infty\}\) and let \[\Delta_9 = \textstyle\bigcup_{i\in{\mathbb{Z}}_5} \bigl\{ D_9 [0,1,2,3,4,\infty] +i, \, D_9[\infty,0,2,4,1,3] +i \bigr\} .\] Then \(\Delta_9\) is a \(D_9\)-decomposition of \({\mbox{\(\vphantom{K^*}\)}^{2\!}K^*}_{6}\).
Example 3. Let \(V\bigl( K^*_7 \bigr) = {\mathbb{Z}}_{7}\) and let \[\begin{aligned} %B_1 = {}& \{\{{D_1}[0,1,3,2,6,4]\}+i: i \in \Z_{7}\},\\ \Delta_2 = \bigl\{& D_2 [0,1,4,6,5,2], \, D_2 [0,4,1,5,3,6], \, D_2 [0,5,4,2,6,3], \\*& D_2 [1,6,4,3,2,5], \, D_2 [4,0,3,1,6,2], \, D_2 [5,0,1,2,3,4], \\*& D_2 [6,0,2,1,3,5] \bigr\}, \\[3pt] \Delta_3 = \bigl\{& D_3 [3,1,0,6,2,4], \, D_3 [4,5,1,0,3,6], \, D_3 [2,0,6,5,3,1], \\*& D_3 [1,6,5,2,0,4], \, D_3 [0,5,4,2,6,3], \, D_3 [5,3,2,1,4,0], \\*& D_3 [6,4,3,2,5,1] \bigr\}, \\[3pt] \Delta_4 = \{& D_4 [0,1,3,2,6,4] +i : i \in {\mathbb{Z}}_{7} \} , \\ \Delta_5 = \{& D_5 [0,1,3,6,5,2] +i : i \in {\mathbb{Z}}_{7} \} , \\ \Delta_6 = \bigl\{& D_6 [0,1,2,3,4,5], \, D_6 [0,2,1,3,5,6], \, D_6 [0,3,1,6,2,4], \\*& D_6 [3,2,4,5,1,6], \, D_6 [3,4,6,0,2,5], \, D_6 [5,1,4,0,3,6], \\*& D_6 [6,2,5,0,1,4] \bigr\}, \\[3pt] \Delta_7 = \{& D_7 [0,1,3,5,2,6] +i : i \in {\mathbb{Z}}_{7} \} , \\ \Delta_8 = \{& D_8 [0,6,2,5,3,1] +i : i \in {\mathbb{Z}}_{7} \} , \\* \Delta_9 = \{& D_9 [0,1,2,4,6,3] +i : i \in {\mathbb{Z}}_{7} \} . \end{aligned}\] Then \(\Delta_i\) is a \(D_i\)-decomposition of \(K^*_{7}\) for \(i \in [2,9]\).
Example 4. Let \(V\bigl( {\mbox{$\vphantom{K^*}$}^{3\!}K^*}_8 \bigr) = {\mathbb{Z}}_{7}\cup \{\infty\}\) and let \[\begin{aligned} %B_1 = {} \{\{ %& {D_1}[0,1,2,3,5,4],{D_1}[0,2,1,3,6,\infty],{D_1}[0,3,1,5,2,\infty], \\ %& {D_1}[0,4,2,1,6,\infty]\}+i: i \in \Z_{7}\},\\ \Delta_2 = \textstyle\bigcup_{i\in{\mathbb{Z}}_7} \bigl\{& D_2 [0,1,2,3,5,4] +i, \, D_2 [0,2,1,3,6,\infty] +i, \\*&\quad D_2 [0,3,1,5,2,\infty] +i, \, D_2 [0,4,2,3,5,\infty] +i \bigr\}, \\[3pt] \Delta_3 = \textstyle\bigcup_{i\in{\mathbb{Z}}_7} \bigl\{& D_3 [0,1,2,3,5,6] +i, \, D_3 [0,2,3,5,1,\infty] +i, \\*&\quad D_3 [0,3,1,6,4,\infty] +i, \, D_3 [0,4,1,5,2,\infty] +i \bigr\}, \\[3pt] \Delta_4 = \textstyle\bigcup_{i\in{\mathbb{Z}}_7} \bigl\{& D_4 [0,1,2,3,5,6] +i, \, D_4 [0,2,1,3,6,\infty] +i, \\*&\quad D_4 [0,3,1,5,2,\infty] +i, \, D_4 [0,5,2,6,1,\infty] +i \bigr\}, \\[3pt] \Delta_5 = \textstyle\bigcup_{i\in{\mathbb{Z}}_7} \bigl\{& D_5 [0,1,2,3,5,4] +i, \, D_5 [0,2,1,3,6,\infty] +i, \\*&\quad D_5 [0,3,5,2,6,\infty] +i, \, D_5 [0,4,6,3,2,\infty] +i \bigr\}, \\[3pt] \Delta_6 = \textstyle\bigcup_{i\in{\mathbb{Z}}_7} \bigl\{& D_6 [0,1,2,3,4,5] +i, \, D_6 [0,2,4,3,6,\infty] +i, \\*&\quad D_6 [0,3,5,2,6,\infty] +i, \, D_6 [0,4,2,5,1,\infty] +i \bigr\}, \\[3pt] \Delta_7 = \textstyle\bigcup_{i\in{\mathbb{Z}}_7} \bigl\{& D_7 [0,1,2,3,5,6] +i, \, D_7 [0,2,3,5,1,\infty] +i, \\*&\quad D_7 [0,3,1,2,4,\infty] +i, \, D_7 [0,4,1,5,2,\infty] +i \bigr\}, \\[3pt] \Delta_8 = \textstyle\bigcup_{i\in{\mathbb{Z}}_7} \bigl\{& D_8 [0,1,2,3,4,5] +i, \, D_8 [0,2,6,\infty,4,3] +i, \\*&\quad D_8 [0,3,1,\infty,5,2] +i, \, D_8 [0,3,1,\infty,5,2] +i \bigr\}. \end{aligned}\] Then \(\Delta_i\) is a \(D_i\)-decomposition of \({\mbox{\(\vphantom{K^*}\)}^{3\!}K^*}_{8}\) for \(i \in [2,8]\).
Example 5. Let \(V\bigl( {\mbox{$\vphantom{K^*}$}^{6\!}K^*}_8 \bigr) = {\mathbb{Z}}_{7}\cup \{\infty\}\) and let \[\begin{aligned} \Delta_9 = \textstyle\bigcup_{i\in{\mathbb{Z}}_7} \bigl\{& D_9 [0,1,2,3,4,5] +i, \, D_9 [0,1,2,3,4,5] +i, \\*&\quad D_9 [0,2,6,3,\infty,5] +i, \, D_9 [0,2,6,3,\infty,5] +i, \\&\quad D_9 [0,2,6,3,\infty,5] +i, \, D_9 [0,3,1,6,2,\infty] +i, \\*&\qquad D_9 [0,3,1,5,6,\infty] +i, \, D_9 [0,3,1,5,6,\infty] +i \bigr\}. \end{aligned}\] Then \(\Delta_9\) is a \(D_9\)-decomposition of \({\mbox{$\vphantom{K^*}$}^{6\!}K^*}_{8}\).
Example 6. Let \(V\bigl(K^*_{9}\bigr) = ({\mathbb{Z}}_{4}\times{\mathbb{Z}}_{2}) \cup \{\infty\}\). For brevity we use \(i_j\) to denote the ordered pair \((i,j)\in V\bigl(K^*_{9}\bigr)\), and we (continue to) use the convention that \(\infty+i_0=\infty\). Let \[\begin{aligned} \Delta_2 = \textstyle\bigcup_{i\in{\mathbb{Z}}_4} \bigl\{& D_2 [0_0,3_0,\infty,3_1,1_1,1_0] +i_0, \, D_2 [0_0,2_0,3_1,\infty,3_0,2_1] +i_0, \\*&\quad D_2 [0_1,3_1,2_1,1_0,1_1,2_0] +i_0 \bigr\}, \\[3pt] \Delta_3 = \textstyle\bigcup_{i\in{\mathbb{Z}}_4} \bigl\{& D_3 [0_0,3_1,0_1,3_0,2_1,\infty] +i_0, \, D_3 [0_0,2_0,1_0,\infty,3_1,0_1] +i_0, \\*&\quad D_3 [0_1,2_0,3_0,3_1,1_0,2_1] +i_0 \bigr\}, \\[3pt] \Delta_4 = \textstyle\bigcup_{i\in{\mathbb{Z}}_4} \bigl\{& D_4 [0_0,3_0,2_0,0_1,1_1,3_1] +i_0, \, D_4 [0_1,3_0,1_0,\infty,1_1,0_0] +i_0, \\*&\quad D_4 [0_1,1_1,\infty,3_0,2_1,2_0] +i_0 \bigr\}, \\[3pt] \Delta_5 = \textstyle\bigcup_{i\in{\mathbb{Z}}_4} \bigl\{& D_5 [0_0,3_0,0_1,2_0,2_1,3_1] +i_0, \, D_5 [0_0,2_0,1_0,1_1,2_1,\infty] +i_0, \\*&\quad D_5 [0_1,2_1,1_0,3_1,0_0,\infty] +i_0 \bigr\}, \\[3pt] \Delta_6 = \textstyle\bigcup_{i\in{\mathbb{Z}}_4} \bigl\{& D_6 [0_0,1_1,2_0,\infty,2_1,3_1] +i_0, \, D_6 [\infty,3_0,0_0,0_1,2_0,3_1] +i_0, \\*&\quad D_6 [0_1,0_0,2_0,1_0,3_1,1_1] +i_0 \bigr\}, \\[3pt] \Delta_7 = \textstyle\bigcup_{i\in{\mathbb{Z}}_4} \bigl\{& D_7 [0_0,3_0,0_1,2_0,2_1,3_1] +i_0, \, D_7 [0_0,2_0,3_0,3_1,0_1,\infty] +i_0, \\*&\quad D_7 [0_1,2_1,1_0,3_1,0_0,\infty] +i_0 \bigr\}, \\[3pt] \Delta_8 = \textstyle\bigcup_{i\in{\mathbb{Z}}_4} \bigl\{& D_8 [0_0,\infty,0_1,2_1,1_0,3_1] +i_0, \, D_8 [0_1,3_0,0_0,3_1,2_1,2_0] +i_0, \\*&\quad D_8 [0_1,\infty,0_0,2_0,3_0,3_1] +i_0 \bigr\}, \\[3pt] \Delta_9 = \textstyle\bigcup_{i\in{\mathbb{Z}}_4} \bigl\{& D_9 [0_0,\infty,2_1,3_0,0_1,3_1] +i_0, \, D_9 [0_0,3_0,1_1,3_1,2_0,0_1] +i_0, \\*&\quad D_9 [0_1,0_0,3_0,1_0,\infty,1_1] +i_0 \bigr\}. \end{aligned}\] Then \(\Delta_i\) is a \(D_i\)-decomposition of \(K^*_9\) for \(i \in [2,9]\).
Example 7. Let \(V\bigl(K^*_{10}\bigr) = {\mathbb{Z}}_{5}\times{\mathbb{Z}}_{2}\). For brevity we use \(i_j\) to denote the ordered pair \((i,j)\in V\bigl(K^*_{10}\bigr)\). Let \[\begin{aligned} \Delta_2 = \textstyle\bigcup_{i\in{\mathbb{Z}}_5} \bigl\{& D_2 [0_0,1_1,1_0,0_1,4_1,2_1] +i_0, \, D_2 [0_0,1_0,4_1,1_1,2_1,3_0] +i_0, \\*&\quad D_2 [0_1,3_0,1_0,2_1,4_0,0_0] +i_0 \bigr\}, \\[3pt] \Delta_3 = \textstyle\bigcup_{i\in{\mathbb{Z}}_5} \bigl\{& D_3 [0_0,4_1,1_1,2_1,1_0,4_0] +i_0, \, D_3 [0_1,0_0,1_0,3_0,4_1,1_1] +i_0, \\*&\quad D_3 [0_1,1_0,3_1,0_0,2_1,2_0] +i_0 \bigr\}, \\[3pt] \Delta_4 = \textstyle\bigcup_{i\in{\mathbb{Z}}_5} \bigl\{& D_4 [0_0,4_1,0_1,2_0,1_1,3_0] +i_0, \, D_4 [0_0,2_0,3_1,3_0,0_1,2_1] +i_0, \\*&\quad D_4 [0_0,1_0,2_0,3_1,2_1,0_1] +i_0 \bigr\}, \\[3pt] \Delta_5 = \textstyle\bigcup_{i\in{\mathbb{Z}}_5} \bigl\{& D_5 [0_0,4_0,2_0,3_1,4_1,2_1] +i_0, \, D_5 [0_0,3_0,2_1,3_1,1_1,1_0] +i_0, \\*&\quad D_5 [0_0,4_1,3_0,1_1,1_0,3_1] +i_0 \bigr\}, \\[3pt] \Delta_6 = \textstyle\bigcup_{i\in{\mathbb{Z}}_5} \bigl\{& D_6 [0_0,4_0,2_1,1_0,3_0,0_1] +i_0, \, D_6 [0_0,1_1,1_0,0_1,4_1,2_1] +i_0, \\*&\quad D_6 [0_1,4_1,2_1,4_0,3_0,1_0] +i_0 \bigr\}, \\[3pt] \Delta_7 = \textstyle\bigcup_{i\in{\mathbb{Z}}_5} \bigl\{& D_7 [0_0,1_0,0_1,3_1,4_1,3_0] +i_0, \, D_7 [0_0,2_1,3_0,0_1,2_0,3_1] +i_0, \\*&\quad D_7 [0_0,0_1,4_1,1_1,1_0,4_0] +i_0 \bigr\}, \\[3pt] \Delta_8 = \textstyle\bigcup_{i\in{\mathbb{Z}}_5} \bigl\{& D_8 [0_0,1_0,1_1,0_1,2_1,2_0] +i_0, \, D_8 [0_0,4_1,1_1,2_1,1_0,4_0] +i_0, \\*&\quad D_8 [0_1,4_0,2_1,0_0,4_1,2_0] +i_0 \bigr\}. \end{aligned}\] Then \(\Delta_i\) is a \(D_i\)-decomposition of \(K^*_{10}\) for \(i \in [2,8]\).
Example 8. Let \(V\bigl( {\mbox{$\vphantom{K^*}$}^{2\!}K^*}_{10} \bigr) = {\mathbb{Z}}_{10}\) and let \[\begin{aligned} \Delta_9 = \textstyle\bigcup_{i\in{\mathbb{Z}}_{10}} \bigl\{& D_9 [0,4,8,7,9,1] +i, \, D_9 [0,5,2,3,1,4] +i, \\*&\quad D_9 [0,9,2,7,1,8] +i \bigr\}. \end{aligned}\] Then \(\Delta_9\) is a \(D_9\)-decomposition of \({\mbox{$\vphantom{K^*}$}^{2\!}K^*}_{10}\).
Example 9. Let \(V\bigl( {\mbox{$\vphantom{K^*}$}^{3\!}K^*}_{11} \bigr) = {\mathbb{Z}}_{11}\) and let \[\begin{aligned} %B_1 = {} \{\{ %& {D_1}[0,1,3,6,10,4],{D_1}[0,1,3,6,10,4],{D_1}[0,1,3,6,10,4], \\ %& {D_1}[0,6,1,7,4,3], {D_1}[0,8,6,4,2,1]\}+i: i \in \Z_{11}\},\\ \Delta_2 = \textstyle\bigcup_{i\in{\mathbb{Z}}_{11}} \bigl\{& D_2 [0,5,1,2,4,7] +i, \, D_2 [0,5,1,2,4,7] +i, \\*&\quad D_2 [0,6,1,2,4,7] +i, \, D_2 [0,2,1,10,9,3] +i, \\*&\qquad D_2 [0,4,1,6,3,2] +i \bigr\}, \\[3pt] \Delta_3 = \textstyle\bigcup_{i\in{\mathbb{Z}}_{11}} \bigl\{& D_3 [0,2,1,3,6,5] +i, \, D_3 [0,2,1,3,6,5] +i, \\*&\quad D_3 [0,2,1,5,9,3] +i, \, D_3 [0,1,7,2,10,6] +i, \\*&\qquad D_3 [0,3,1,8,4,7] +i \bigr\}, \\[3pt] \Delta_4 = \textstyle\bigcup_{i\in{\mathbb{Z}}_{11}} \bigl\{& D_4 [0,1,7,10,2,6] +i, \, D_4 [0,1,7,10,2,6] +i, \\*&\quad D_4 [0,1,7,10,2,6] +i, \, D_4 [0,4,6,10,1,2] +i, \\*&\qquad D_4 [0,9,10,3,1,2] +i \bigr\}, \\[3pt] \Delta_5 = \textstyle\bigcup_{i\in{\mathbb{Z}}_{11}} \bigl\{& D_5 [0,1,2,5,10,4] +i, \, D_5 [0,1,2,5,10,4] +i, \\*&\quad D_5 [0,1,2,5,10,4] +i, \, D_5 [0,2,4,1,3,7] +i, \\*&\qquad D_5 [0,2,4,1,10,3] +i \bigr\}, \\[3pt] \Delta_6 = \textstyle\bigcup_{i\in{\mathbb{Z}}_{11}} \bigl\{& D_6 [0,1,3,6,10,4] +i, \, D_6 [0,1,3,6,10,4] +i, \\*&\quad D_6 [0,1,3,6,10,4] +i, \, D_6 [0,5,3,2,4,10] +i, \\*&\qquad D_6 [0,10,4,2,5,8] +i \bigr\}, \\[3pt] \Delta_7 = \textstyle\bigcup_{i\in{\mathbb{Z}}_{11}} \bigl\{& D_7 [0,1,3,6,10,7] +i, \, D_7 [0,1,3,6,10,7] +i, \\*&\quad D_7 [0,1,3,6,10,7] +i, \, D_7 [0,6,5,10,4,9] +i, \\*&\qquad D_7 [0,10,4,5,3,9] +i \bigr\}, \\[3pt] \Delta_8 = \textstyle\bigcup_{i\in{\mathbb{Z}}_{11}} \bigl\{& D_8 [0,1,3,6,2,5] +i, \, D_8 [0,1,3,6,2,5] +i, \\*&\quad D_8 [0,1,3,6,2,5] +i, \, D_8 [0,6,4,8,10,9] +i, \\*&\qquad D_8 [0,6,5,9,3,10] +i \bigr\}, \\[3pt] \Delta_9 = \textstyle\bigcup_{i\in{\mathbb{Z}}_{11}} \bigl\{& D_9 [0,1,2,4,6,3] +i, \, D_9 [0,1,2,4,6,3] +i, \\*&\quad D_9 [0,1,2,4,6,3] +i, \, D_9 [0,5,1,8,2,6] +i, \\*&\qquad D_9 [0,5,1,8,2,7] +i \bigr\}. \end{aligned}\] Then \(\Delta_i\) is a \(D_i\)-decomposition of \({\mbox{$\vphantom{K^*}$}^{3\!}K^*}_{11}\) for \(i \in [2,9]\).
Example 10. Let \(V\bigl(K^*_{3,4}\bigr) = {\mathbb{Z}}_7\) with vertex partition \(\bigl\{ \{0,1,2\},{$ $}\{3, 4, 5, 6\} \bigr\}\) and let \[\begin{aligned} \Delta_7 = \bigl\{& D_7 [0,3,1,4,2,6], \, D_7 [3,0,5,1,6,2], \, D_7 [2,5,1,6,0,4], \\*& D_7 [5,2,3,1,4,0] \bigr\}, \\[3pt] \Delta_8 = \bigl\{& D_8 [0,4,2,5,1,6], \, D_8 [3,2,5,0,4,1], \, D_8 [1,3,0,6,2,4], \\*& D_8 [6,2,3,0,5,1] \bigr\}. \end{aligned}\] Then \(\Delta_i\) is a \(D_i\)-decomposition of \(K^*_{3,4}\) for \(i \in \{7,8\}\).
Example 11. Let \(V\bigl(K^*_{6,6}\bigr) = {\mathbb{Z}}_{6}\times{\mathbb{Z}}_{2}\) with the obvious vertex bipartition. For brevity we use \(i_j\) to denote the ordered pair \((i,j)\in V\bigl(K^*_{6,6}\bigr)\). Let \[\begin{aligned} \Delta_7 = \textstyle\bigcup_{i\in{\mathbb{Z}}_6} \bigl\{& D_7 [0_0,5_1,1_0,1_1,5_0,2_1] +i_0, \, D_7 [0_1,5_0,3_1,0_0,1_1,1_0] +i_0 \bigr\}, \\[3pt] \Delta_8 = \textstyle\bigcup_{i\in{\mathbb{Z}}_6} \bigl\{& D_8 [0_0,4_1,5_0,1_1,4_0,0_1] +i_0, \, D_8 [0_1,0_0,5_1,4_0,2_1,5_0] +i_0 \bigr\}. \end{aligned}\] Then \(\Delta_i\) is a \(D_i\)-decomposition of \(K^*_{6,6}\) for \(i \in \{7,8\}\).
For two edge-disjoint graphs (or digraphs) \(G\) and \(H\), we use \(G\cup H\) to denote the graph (or digraph) with vertex set \(V(G)\cup V(H)\) and edge (or arc) set \(E(G)\cup E(H)\). Furthermore, given a positive integer \(x\), we use \(xG\) to denote the edge-disjoint union of \(x\) copies of \(G\), which are not necessarily vertex-joint. If \(G\) and \(H\) are vertex-disjoint, then we use \(G \vee H\) to denote the join of \(G\) and \(H\), which has vertex set \(V(G) \cup V(H)\) and edge (or arc) set \(E(G) \cup E(H) \cup \{\,\{u,v\} : u\in V(G), v\in V(H) \}\). To illustrate the different types of notation described here, consider that \(K_{13}\) can be viewed as \(\bigl( K_6 \cup K_6 \bigr) \vee K_1 \cup K_{6,6} = K_7 \cup K_7 \cup K_{6,6}\). (Note that the join precedes the union in the order of operations.)
We first prove a result about decompositions of \(K^*_{4,6}\), \(K^*_{6,6}\), and \(K^*_{6,8}\).
Lemma 2. For \(D \in \{D_2, D_3,\ldots, D_9\}\), then there exists a \(D\)-decomposition of \(K^*_{4,6}\), \(K^*_{6,6}\) and \(K^*_{6,8}\).
Proof. Let \(D\in\{D_2, D_3,\ldots, D_9\}\). The result follows from Corollary 1 for \(D\notin\{D_7,D_8\}\). For \(i\in\{7,8\}\), a \(D_i\)-decomposition of \(K^*_{3,4}\) (and hence of \(K^*_{6,4}\) and \(K^*_{6,8}\)) exists by Example 10. Moreover, \(D_7\)– and \(D_8\)-decompositions of \(K^*_{6,6}\) are given in Example 11. ◻
We now give our constructions for decompositions of \({}^{\lambda} K_{v}^{\ast}\) in the following lemmas, which cover values of \(v\) working modulo \(6\). The main result is summarized in Theorem 4.
Lemma 3. Let \(\lambda\) and \(v\) be positive integers such that \(v\equiv0\pmod{6}\). If \(D \in \{D_2, D_3,\ldots, D_8\}\), then there exists a \(D\)-decomposition of \({}^{\lambda} K_{v}^{\ast}\). Furthermore, if \(\lambda\) is even, then there exists a \(D_9\)-decomposition of \({}^{\lambda} K_{v}^{\ast}\).
Proof. Let \(D\in\{D_2, D_3,\ldots, D_9\}\). If \(v=6\) and \(D\neq D_9\), then the result follows from \(\lambda\) copies of a \(D\)-decomposition of \(K^*_6\) (see Example 1). If \(v=6\), \(\lambda\) is even, and \(D=D_9\), then the result follows from \(\lambda/2\) copies of a \(D_9\)-decomposition of \({\mbox{$\vphantom{K^*}$}^{2\!}K^*}_6\) (see Example 2). For the remainder of the proof, we let \(v=6x\) for some integer \(x\geq2\), and we assume \(\lambda\) is even whenever \(D=D_9\). Finally,
we note that \(K_{6x} = x K_6 \cup \binom{x}{2} K_{6,6}\). Thus \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{6x} = x\bigl({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_6\bigr) \cup \binom{x}{2}\bigl({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{6,6}\bigr)\), and the result follows from the existence of \(D\)-decompositions of \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_6\) and \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{6,6}\), where the latter decomposition follows from \(\lambda\) copies of a \(D\)-decomposition of \(K^*_{6,6}\) (see Lemma 2). ◻
Lemma 4. Let \(\lambda\) and \(v\) be positive integers such that \(v\equiv1\pmod{6}\) and \(v\geq7\). If \(D \in \{D_2, D_3,\ldots, D_9\}\), then there exists a \(D\)-decomposition of \({}^{\lambda} K_{v}^{\ast}\).
Proof. If \(v=7\), then the result follows from \(\lambda\) copies of a \(D\)-decomposition of \(K^*_7\) (see Example 3). For the remainder of the proof, we let \(v=6x+1\) for some integer \(x\geq2\). We note that \(K_{6x+1} = (x K_6) \vee K_1 \cup \binom{x}{2} K_{6,6} = x K_7 \cup \binom{x}{2} K_{6,6}\). Thus \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{6x+1} = x\bigl({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_7\bigr) \cup \binom{x}{2}\bigl({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{6,6}\bigr)\), and the result follows from the existence of \(D\)-decompositions of \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_7\) and \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{6,6}\). ◻
Lemma 5. Let \(\lambda\) and \(v\) be positive integers such that \(\lambda\equiv0\pmod{3}\), \(v\equiv2\pmod{6}\), and \(v\geq8\). If \(D \in \{D_2, D_3,\ldots, D_8\}\), then there exists a \(D\)-decomposition of \({}^{\lambda} K_{v}^{\ast}\). Furthermore, if \(\lambda\equiv0\pmod{6}\), then there exists a \(D_9\)-decomposition of \({}^{\lambda} K_{v}^{\ast}\).
Proof. Let \(D\in\{D_2, D_3,\ldots, D_9\}\). If \(v=8\) and \(D\neq D_9\), then the result follows from \(\lambda/3\) copies of a \(D\)-decomposition of \({\mbox{$\vphantom{K^*}$}^{3\!}K^*}_8\) (see Example 4). If \(v=8\), \(\lambda\equiv0\pmod{6}\), and \(D=D_9\), then the result follows from \(\lambda/6\) copies of a \(D_9\)-decomposition of \({\mbox{$\vphantom{K^*}$}^{6\!}K^*}_8\) (see Example 5).
Next, for \(v=14\), we note that \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{14} = {\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_8 \cup {\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_6 \cup {\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{8,6}\). Thus the result follows from the existence of \(D\)-decompositions of \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_8\), \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_6\) and and \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{8,6}\).
For the remainder of the proof, we let \(v=6x+8\) for some integer \(x\geq2\) and \(\lambda=3y\) for some integer \(y\geq1\), and we assume \(y\) is even whenever \(D=D_9\). Finally, we note that \(K_{6x+8} = K_8 \cup x K_6 \cup x K_{8,6} \cup \binom{x}{2} K_{6,6}\). Thus \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{6x+8} = {\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_8 \cup x\bigl({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_6\bigr) \cup x \bigl({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{8,6}\bigr) \cup \binom{x}{2}\bigl({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{6,6}\bigr)\), and the result follows from the existence of \(D\)-decompositions of \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_8\), \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_6\), \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{8,6}\), and \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{6,6}\). ◻
Lemma 6. Let \(\lambda\) and \(v\) be positive integers such that \(v\equiv3\pmod{6}\) and \(v\geq9\). If \(D \in \{D_2, D_3,\ldots, D_9\}\), then there exists a \(D\)-decomposition of \({}^{\lambda} K_{v}^{\ast}\).
Proof. If \(v=9\), then the result follows from \(\lambda\) copies of a \(D\)-decomposition of \(K^*_9\) (see Example 6). For \(v=15\), we note that \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{15} = \bigl({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_8 \cup {\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_6\bigr)\vee{\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_1 \cup {\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{8,6} = {\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_9 \cup {\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_7 \cup {\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{8,6}\), and the result follows from the existence of \(D\)-decompositions of \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_9\), \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_7\) (see Lemma 4), and \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{8,6}\).
For the remainder of the proof, we let \(v=6x+9\) for some integer \(x\geq2\). Finally, we note that \(K_{6x+9} = \bigl( K_8 \cup x K_6 \bigr) \vee K_1 \cup x K_{8,6} \cup \binom{x}{2} K_{6,6} = K_9 \cup x K_7 \cup x K_{8,6} \cup \binom{x}{2} K_{6,6}\). Thus \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{6x+9} = {\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_9 \cup x\bigl({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_7\bigr) \cup x \bigl({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{8,6}\bigr) \cup \binom{x}{2}\bigl({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{6,6}\bigr)\), and the result follows from the existence of \(D\)-decompositions of \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_9\), \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_7\), \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{8,6}\), and \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{6,6}\). ◻
Lemma 7. Let \(\lambda\) and \(v\) be positive integers such that \(v\equiv4\pmod{6}\) and \(v\geq10\). If \(D \in \{D_2, D_3,\ldots, D_8\}\), then there exists a \(D\)-decomposition of \({}^{\lambda} K_{v}^{\ast}\). Furthermore, if \(\lambda\) is even, then there exists a \(D_9\)-decomposition of \({}^{\lambda} K_{v}^{\ast}\).
Proof. Let \(D\in\{D_2, D_3,\ldots, D_9\}\). If \(v=10\) and \(D\neq D_9\), then the result follows from \(\lambda\) copies of a \(D\)-decomposition of \(K^*_{10}\) (see Example 7). If \(v=10\), \(\lambda\) is even, and \(D=D_9\), then the result follows from \(\lambda/2\) copies of a \(D_9\)-decomposition of \({\mbox{$\vphantom{K^*}$}^{2\!}K^*}_{10}\) (see Example 8). For the remainder of the proof, we let \(v=6x+4\) for some integer \(x\geq2\), and we assume \(\lambda\) is even whenever \(D=D_9\).
Next, we note that \(K_{6x+4} = K_4 \cup x K_6 \cup x K_{4,6} \cup \binom{x}{2} K_{6,6} = K_{10} \cup (x-1) K_6 \cup (x-1) K_{4,6} \cup \binom{x}{2} K_{6,6}\). Thus \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{6x+4} = {\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{10} \cup (x-1) \bigl({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_6\bigr) \cup (x-1) \bigl({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{4,6}\bigr) \cup \binom{x}{2}\bigl({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{6,6}\bigr)\), and the result follows from the existence of \(D\)-decompositions of \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{10}\), \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_6\) (see Lemma 3), \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{4,6}\), and \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{6,6}\). ◻
Lemma 8. Let \(\lambda\) and \(v\) be positive integers such that \(\lambda\equiv0\pmod{3}\), \(v\equiv5\pmod{6}\), and \(v\geq11\). If \(D \in \{D_2, D_3,\ldots, D_9\}\), then there exists a \(D\)-decomposition of \({}^{\lambda} K_{v}^{\ast}\).
Proof. If \(v=11\), then the result follows from \(\lambda/3\) copies of a \(D\)-decomposition of \({\mbox{$\vphantom{K^*}$}^{3\!}K^*}_{11}\) (see Example 9). For the remainder of the proof, we let \(v=6x+5\) for some integer \(x\geq2\). Finally, we note that \(K_{6x+5} = \bigl(K_4 \cup x K_6 \bigr) \vee K_1 \cup x K_{4,6} \cup \binom{x}{2} K_{6,6} = K_{11} \cup (x-1) K_7 \cup (x-1) K_{4,6} \cup \binom{x}{2} K_{6,6}\). Thus \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{6x+5} = {\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{11} \cup (x-1) \bigl({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_7\bigr) \cup (x-1) \bigl({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{4,6}\bigr) \cup \binom{x}{2}\bigl({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{6,6}\bigr)\), and the result follows from the existence of \(D\)-decompositions of \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{11}\), \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_7\) (see Lemma 4), \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{4,6}\), and \({\mbox{$\vphantom{K^*}$}^{\lambda\!}K^*}_{6,6}\). ◻
Combining the previous results from Lemmas 3 through 8 with Theorem 2 and Lemma 1, we obtain our main theorem, which we restate here.
Theorem 4. Let \(D\) be an orientation of a \(6\)-cycle and let \(\lambda\) and \(v\) be positive integers such that \(v\geq6\). There exists a \(D\)-decomposition of \({}^{\lambda} K_{v}^{\ast}\) if and only if \(\lambda v(v-1) \equiv 0\pmod{3}\) and neither of the following hold
\((D,\lambda,v)=(D_1,1,6)\) or
\(D=D_9\) and \(\lambda (v-1)\) is odd.
1970-2025 CP (Manitoba, Canada) unless otherwise stated.