In secret sharing, the relationships between participants and the information they hold can be modeled effectively using graph structures. Graphs allow us to visualize and analyze these relationships, making it easier to define access structures, optimize share distributions, and ensure security. This paper provides the first comprehensive review of existing research on the application of graph theory to secret sharing comparing different classic and modern approaches and analyzing the current litterature. Through this study we highlight the key advances and methodologies that have been developed, underscoring the pivotal role of graph theoretic approaches in enhancing the security and efficiency of secret sharing schemes. Furthermore, the review identifies open challenges and future research directions, providing insights into potential innovations that could further strengthen cryptographic practices. This work serves as a foundational resource for researchers and practitioners seeking to deepen their understanding of the intersection between graph theory and secret sharing, fostering the development of more robust and sophisticated cryptographic solutions.
Secret sharing emerges as a fundamental technique in information security designed to enhance data protection and ensure reliability across various applications. This cryptographic technique involves dividing a secret into multiple pieces or shares, then distributed among a group of participants. The primary objective is that only some authorized subsets of participants can reconstruct the original secret, while unauthorized subsets are left with no useful information.
First formalized independently by Adi Shamir [37] and George Blakley [7] in 1979. Shamir’s scheme is based on polynomial interpolation over a finite field, where a secret is encoded as the constant term of a polynomial. In contrast, Blakley’s approach utilizes a geometric approach, where the secret is represented as a point of intersection in a multidimensional space. Both schemes laid the groundwork for a wide array of secret sharing protocols, each tailored to specific requirements and security constraints. Ito et al. [25] generalized the idea of secret sharing by presenting the notion of access structure that specifies which groups of participants are authorized to reconstruct the secret. Formally, an access structure \(\Gamma\) is a collection of subsets of a participant set \(P\) verifying the monotonicity property, that is if \(A \in \Gamma\) is an authorized set and \(A \subseteq B \subseteq P\), then \(B\) is also authorized \(B \in \Gamma\) . In particular, In Shamir’s scheme, the access structure is determined by a threshold \(t\). Let \(P = \{x_1, x_2, \dots, x_n\}\) be the set of participants. The access structure \(\Gamma\) is defined as the collection of all subsets of participants that contain at least \(t\) members \(\Gamma = \{ A \subseteq P : |A| \geq t \}\). This access structure ensures that any subset of participants of size \(t\) or greater is authorized to reconstruct the secret, while subsets with fewer than \(t\) participants are unauthorized. An authorized set \(A\in \Gamma\) is said to be minimal if \(B\not\subset A\) for any \(B\in \Gamma\setminus \{A\}\).If minimal authorized subsets contains two participants then their correspondant access structures can be modeled as graphs. In the general case, access structures can be viewed as hypergraphs.
Secret sharing has since been applied in diverse areas such as secure multiparty computation [33,35], oblivious transfer [44] and distributed systems [39,21], etc. Its versatility makes it an essential tool in scenarios where trust and security are paramount. For instance, in financial institutions, secret sharing is employed to protect cryptographic keys, ensuring that no single individual holds complete control over sensitive operations. Similarly, in cloud computing, it facilitates secure data storage and access control [29,36], mitigating the risks associated with single points of failure. It was shown that any access structure can be realized by a perfect secret sharing scheme [25,6], but the size of shares was not seriously been taken in consideration. Secret sharing presents several challenges, particularly in terms of efficiency and scalability. As the size of the participant group grows, managing the distribution and reconstruction of shares becomes increasingly complex. This has prompted ongoing research into optimizing secret sharing schemes to balance security with practical implementation.
Many reviews and surveys on secret sharing has been appeared in the litterature over the years [5,34,13,38], Beimel [5] surveyed secret sharing schemes in cryptography and distributed computing, more specified reviews appeared later in the litterature, Sarosh et al [34] explore secret sharing schemes based on polynomials, the Chinese Remainder Theorem, matrix projections, and visual secret sharing for secure communication and image sharing, while threshold secret sharing (TSS) and its extensions like multi-secret sharing and verifiable secret sharing were reviewed in [13], but as the best as we know, no one of those reviews explicitly studied the graph theory approach. This gap in the literature highlights a lack of comprehensive analysis of how graph theory can be applied to secret sharing schemes. Therefore, there appears to be no existing review that addresses this perspective, presenting an opportunity for future research to explore the intersection of graph theory and secret sharing.
We categrize the use of graph theory in secret sharing into classical and modern approaches, each bringing unique insights and methodologies. The classical approach primarily revolves around matrix characterizations of SSS and decomposition constructions, where the focus is on breaking down the graph into simpler components that facilitate efficient secret distribution and recovery. These techniques leverage the structural properties of graphs to ensure minimal and secure access structures. On the other hand, the modern approach encompasses more advanced methods, such as multipartite secret sharing, linear secret sharing schemes, and an emphasis on computational complexity. These modern techniques provide more flexibility and efficiency, particularly in scenarios requiring fine-tuned control over share sizes, information rates, and security guarantees, aligning well with contemporary cryptographic needs.
We start in Section 2 with highlighting some needed preliminaries for the rest of the paper. In the Section 3, we compare the strengths and limitations of each delves into the classical approach, highlighting, comparing and analysing seminal works and key theorems that have shaped the understanding of graph based secret sharing schemes. Modern approaches, showcasing recent advancements and innovative methods in the field are discussed in fourth section. In addition, the focus shifts to hypergraph construction, presenting advanced techniques and their applications in improving the efficiency of secret sharing schemes. Finally, the last section summarizes the main points and reflecting on the broader implications of the research. he complex landscape of secret sharing and graph theory.
In the remainder of the paper, we will use the notations listed in Table 1 below:
| Description | |
| \(G = (V, E)\) | Graph \(G\) with vertex set \(V\) and edge set \(E\) |
| \(K_n\) | The complete graph on \(n\) vertices |
| \(K{n_1,n_2,…,n_p}\) | The complete multipartite graph |
| \(C_n\) | Cycle on \(n\) vertices |
| \(P_n\) | Path on \(n+1\) vertices |
| \(T\) | Tree |
| \(\Delta(G)\) | The maximum degree of the graph \(G\) |
| \(H(X)\) | Entropy of random variable \(X\) |
| \(SSS\) | Secret Sharing Scheme |
| \(LSSS\) | Linear Secret Sharing Scheme |
| \(CMC\) | Complete Multipartite Covering |
| \(\Gamma\) | Access structure in a secret sharing scheme |
| \(\mathcal{K}\) | The set of possible secrets |
| \(\mathcal{S}\) | The set of possible shares |
| \(n\) | Number of participants in the scheme |
| \(\rho(G)\) | Information rate of a SSS realizing \(G\) |
| \(\tilde{\rho}(G)\) | Average Information rate of a SSS realizing \(G\) |
This section provides a brief overview of the key concepts necessary for understanding the results discussed in this paper. These foundational topics form the basis for exploring the connections between cryptographic secret sharing schemes and graph theory or more generally combinatorial structures. Readers interested in a deeper dive into these subjects are encouraged to consult standard texts on graph theory [9,20,24], information theory [15], and matroid theory [30].
A simple graph \(G=(V,E)\) consists of a finite non empty set \(V\) of vertices together with a set \(E\) of unordered pairs of distinct vertices called edges. Two vertices \(u,v\in V\) are adjacent if \(\{u,v\}\in E\).The degree of a vertex \(v\) is the numbre of vertices adjacent to \(v\), the maximum of degrees in a graph \(G\) is called the maximum degree of \(G\) denoted by \(\Delta(G)\). The graph is regular if all vertices have the same degree. A graph of \(n\) vertices in which any two vertices are adjacent is called the complete graph \(K_n\). A graph is said to be complete multipartite \(K_{n_1,n_2,…,n_p}\) if its vertex set can be partitionned into \(p\) subsests of \(n_i\) vertices \((1\leq i\leq p)\) such that for any edge \(uv\), the vertices \(u\) and \(v\) are in different subsets. If \(p=2\), the graph is called bipartite. A walk of a graph \(G\) is a sequence of adjacent vertices \(v_0, v_1, \ldots, v_{n-1}, v_n\). The length of the walk \(n\). If \(v_0 = v_n\), the walk is said to be closed, a closed walk with \(n\geq 3\) vertices is called a cycle, and we denote it by \(C_n\). A walk is called a path \(P_n\) if all the vertices are distinct. A graph \(G\) is said to be connected if any two vertices are joined by a path. The girth of \(G\) is the length of its smallest cycle. A subgraph \(G_1=(V_1,E_1)\) of \(G\) is a graph such that \(V_1\subseteq V\) and \(E_1\subseteq E\). A tree is a connected acyclic graph in which every two vertices are connected by a unique path, any tree with \(n\) vertices has \(n-1\) edges.
A secret sharing scheme allows a secret to be distributed among \(n\) participants, ensuring that only authorized subsets can reconstruct the secret. Moreover, if unauthorized subsets gain no information about then the secret sharing scheme is called perfect. Let \(\Gamma\) be an access structure on a set \(P\) of \(n\) participants, and let \(s\) be a secret from \(\mathcal{K}\) the set of possible secrets (keys), assign to each participant \(x\in P\) a random share from a set of possible shares \(\mathcal{S}_x\). The shares are then considered random variables with a joint distribution that is determined by the secret \(s\). A secret sharing scheme is a collection of \(n+1\) random variables, one for the secret itself and one for each participant \(x \in P\). The information rate of the share given to \(x\in P\) is defined to be \(\rho_i=\dfrac{log\ |\mathcal{K}|}{log\ |\mathcal{S}_x|}\) and the information rate of the \(SSS\) is \(\rho=min_{x\in P}\ \rho_i\). It is necessary in a perfect scheme that \(|\mathcal{K}|\leq |\mathcal{S}_x|\) for any \(x\in P\), because if it is not the case multiple different secrets could correspond to the same set of shares. This would create ambiguity during reconstruction. One can remark that \(\rho\leq 1\), in the case of equality the SSS is called ideal. The average information rate is defined to be \(\tilde{\rho}=\dfrac{n.log\ |\mathcal{K}|}{\sum_{x\in P}log\ |\mathcal{S}_x|}\), where \(\mathcal{S}_x\) is the set of possible shares for the participant \(x\). A perfect \(SSS\) on a graph is a \(SSS\) realizing an access structures that allows some pairs of participants, edges of the graph, to reconstruct the key. A SSS is linear if \(\mathcal{K}\) is a field, the sets \(\mathcal{S}_x\) of possible shares are vector spaces over \(\mathcal{K}\), and the secret secret can be recovered by \(A\in \Gamma\) using a \(\mathcal{K}\)-linear mapping.
Ito et al. [25] proved that for any access structure there exists a perfect SSS realizing it. The optimal information rate \(\rho^*(G)\) of a graph \(G\) is the supremum of informatiom rates of SSS realizing the access structure on \(G\).
Let \(X\) be a finite set and \(\{p(x)\}_{x \in X}\) a probability distribution. The entropy of \(X\), denoted by \(H(X)\), is defined to be the nonnegative quantity \(H(X) = – \sum_{x \in X} p(x) \log p(x)\). It is an information theoritic tool that measures the average information content of the elements in \(X\), and approximates the average number of bits needed to represent the elements of \(X\) faithfully. If \(X\) and \(Y\) are two finite sets and \(\{p(x, y)\}_{x \in X, y \in Y}\) is a joint probability distribution on the Cartesian product \(X\times Y\), then the conditional entropy \(H(X|Y)\) of \(X\) assuming \(Y\) is defined as \(H(X|Y) = \sum_{y \in Y} p(y) H(X|Y = y)\), where \(H(X|Y = y)\) represents the entropy of \(X\) given a specific value \(Y = y\).
A \(SSS\) is perfect if the following two conditions are satisfied: \(H(s|A)=0\) for any \(A\in\Gamma\), and \(H(s|A)=H(s)\) for any \(A\notin \Gamma\).
The entropy \(H(s)\) of the secret can be viewed as the “length” of the secret. Any lower bound on the entropy of \(x \in P\) immediately gives a lower bound on the size of \(x\)’s share: if \(H(x) \geq \alpha H(s)\), then \(x\)’s share is at least \(\alpha\) times the size of the secret. The concept of entropy is widely used to study the information ratios.
Secret sharing schemes (SSS) where charcterized in terms of matrices of \(\mathcal{M}_{|\mathcal{K}|,n+1}\) with \(n+1\) columns [10], the first one is indexed by the dealer \(D\) (the secret) and each of the remaining \(n\) columns are indexed by the \(n\) participants (shares). each row is indexed by a key and \(n\) possible shares. The dealer \(D\) distributes shares for a key \(K\) by choosing randomly a row of the matrix and distributes them in that row. Brickell and Stinson [11] employed this linear algebraic definition mixed with the theory of matroids considered as combinatorial generalizations of graphs to obtain characterizations of ideal SSS, this approach yields intriguing results that inspired the use of graph structures to classify SSS in particular, and motivating later works based on the integration of graph theoretic approach into the domain of secret sharing. The characterization is articulated in the following theorem.
Brickell and Stinson used the matrix characterization to deduce that for any graph \(G\), there exists a \(SSS\) with information rate \(\rho=\dfrac{1}{\Delta(G)}\), as a consequence, any path \(P_n\) admits a \(SSS\) with \(\rho=\dfrac{1}{2}\). This lower bound was generalized in the following theorem, and even shown that this is the optimal lower bound for some classes of graphs such as regular graphs of girth at least \(5\).
In his paper “the size of a share must be large” [18], Csirmaz improved the upper bound found by Capocelli et al. [12], and introduced tighter lower bounds using polymatroids. He defined a polymatroid function to model the entropy relationships between the secret and the participants’ shares. The paper further explores the properties of this polymatroid function to derive the following result.
Based on the same entropy-theoretical arguments, another improvement of these results [17] was achieved by constructing a graph with average information rate less than \(4/log\ n\), this result was first obtained for a special type of graphs called \(d\)-dimensional cube, which is a bipartite graph with \(2^d\) vertices indexed by elements of \(GF(2)^d\), two vertices are adjacent if they differ at exactly one position.
Blundo et al. [8] developped a construction called graph decomposition that consists of decomposing a graph \(G\) into smaller graphs, whose union covers \(G\), introduced at first in [11] and aims to obtain optimal information rate and average information rate of secret sharing schemes realizing access structures based on graphs and to analyze the results for specific classes of graphs. This construction and variations are discussed also in [41,12,28,11,40]. Here explained the construction:
Let \(G\) be a graph, a complete multipartite covering (CMC) of \(G\) is a family \(\Pi= \{G_1, \dots, G_n\}\) of complete multipartite subgraphs of \(G\), such that each edge of \(G\) occurs in at least one of the \(G_i\)’s.
This construction can be generalized into multiple CMC’s of the same graph instead of a single CMC, it was shown that for \(k\) different CMC’s \(\Pi_j\),\(1\leq j\leq k\), there exists a SSS with \(\rho=\dfrac{k}{R}\), where \(R=max\{ \sum_{j=1}^{k}R_{jv}\:v\in V(G)\}\). Theorem 3.6 is proved using this technique by decomposing \(G\) into complete bipartite graphs \(K{1,m}\).
For the path \(P_3\), we have seen that there is a SSS with \(\rho=\dfrac{1}{2}\), the same result can be obtained with one CMC. However, usinh two CMCs one can get \(\rho=\dfrac{2}{3}\) which is the optimal information rate for \(P_3\) [12]. The decomposition construction is used to obtain the following results:
For paths \(P_n\) with \(n\geq 3\), the optimal information rate is \(\rho^*(P_n)=\frac{2}{3}\) and the optimal average information rate is \(\tilde{\rho}^*(P_n)=\begin{cases} \frac{2(n+1)}{3n}\ \ &\text{if $n$ is even,}\\ \frac{2(n+1)}{3n+1}\ & \text{if $n$ is odd.} \end{cases}\)
For cycles \(C_{n}\) where \(n\geq 5\), the optimal information rate is \(\rho^*(C_n)=\begin{cases} \frac{2}{3}\ & \text{if $n$ is even,}\\ \frac{2n+1}{3n+2}\ & \text{if $n$ is odd,} \end{cases}\) and the optimal average information rate is \(\begin{cases} \tilde{\rho}^*(C_n)=\frac{2}{3}\ & \text{if $n$ is even,}\\ \frac{2n}{3n+1}\leq \tilde{\rho}^*(C_n)\leq \frac{2}{3}\ & \text{if $n$ is odd.} \end{cases}\)
For any tree \(T\) with \(n\) vertices, the information rate is \(\rho(T)\geq \frac{1}{2}\), and the optimal average information rate is \(\tilde{\rho}^*(T)\geq \frac{2n}{3n-2}\).
For any connected graph hich is not complete multipartite, the average information rate \(\tilde{\rho}(G)\leq \frac{n}{n+1}\).
For the 30 connected graphs on at most 5 vertices, and using the CMC construction, the exact optimal information rate and average information rate are determined in most cases, with good upper and lower bounds for the remaining cases.
This construction uses small secret sharing schemes as building blocks in the construction of larger schemes, the number of such “small” schemes is typically exponential in the number of the participant. Sun et al. [42] developped a scheme in such a way that the number of “small” schemes is polynomial in the size of the participants, which in turn gives rise to a polynomial time construction without changing the information rate.
These results about information ratios improve limited ones in [12] which states that there are access structures with four participants for which any secret sharing scheme must give some participant a share that is at least \(50 \%\) larger than the secret size. Despite the interesting results provded in [8], authors did not address some practical aspects of secret sharing schemes, such as protecting against cheating, dealing with disenrollment of participants, and handling multiple secrets. Many developements in this area appeared in the literature over the years leading to interesting achievements [43,45,16,23,1].
The concept of graph decomposition was extended to hypergraphs by Di Crescenzo and Galdi [16]. A hypergraph is a generalization of a graph in the sens that a hyperedge can join any number of vertices, while an edge joins two vertices of a graph. More formally, a hypergraph \(H=(V,E)\) where \(V\) is the vertex set and \(E\) a set of subsets of \(V\). The advantage of hypergraphs is that they can represent any access structures, not only those with minimal authorized sets of two participants (which is the case for graph-based access structures), considering the vertex set as the set of participants and the hyperedges as minimal authorized sets. This approach revealed a novel and elementary characterization of a class of ideal access structures, specifically hyperstars. The key idea behind the hypergraph decomposition technique is to decompose a hypergraph into smaller hypergraphs whose union covers the original hypergraph, and then represent the ideal access structures using these smaller hypergraphs. Beimel [1] used this technique to construct specific \(k\)-hypergraph access structures and prove new lower bounds on the total share size. They define two families of k-hypergraph access structures, \(k-CSI_n\) and \(k-TotCSI_n\), and analyze the share size requirements for realizing these access structures.
Even the problem of finding optimal hypergraph decomposition can be solved efficiently for certain special types of hypergraphs, namely hyperpaths, hypercycles, hyperstars and acyclic hypergraphs, it is \(NP\)-complete for general hypergraphs.
The Table 2 compares different decomposition constructions on different types of graphs and hypergraphs with their contributions to the field.
| Paper | Construction Method | Types of Graphs | Contribution |
| Blundo et al. [8], (1995) | graph decomposition | connected graphs | Optimal information rate for paths and even-length cycles is 2/3. Optimal average information rate schemes are constructed for paths and even-length cycles. For any tree, schemes with information rate at least 1/2 and average information rate at least 2/3. Study of the 30 connected graphs on at most 5 vertices. |
| Sun et al. [43], (2002) | Weighted decomposition construction | connected graphs on six vertices | improve the information rates in four cases of graphs on six vertices \(G_9, G_22, G_40, and G_61\) out of the 18 cases |
| Van Dijk et al. [45], (2006) | \((\lambda,\omega)\)-decomposition | connected graphs on six vertices | (6, 1)-decomposition with optimal worst-case information rate of 5/9 (4, 1)-decomposition with optimal worst-case information rate of 3/5 (7, 3)-decomposition with optimal worst-case information rate of 4/7 |
| Di Crescenzo et al. [16], (2009) | Hypergraph decomposition | Hypergraphs | optimal SSS for hyperpaths and hypercycles characterization of ideal hyperstars upper and lower bounds on the information rate and average information rate for hyperpaths, hypercycles, hyperstars and acyclic hypergraphs optimal hypergraph decomposition is NP-complete for general hypergraphs |
| Garahi et al. [23] (2019) | \((\lambda,\omega)\)-Weighted decomposition | connected graphs on six vertices | Exact value of optimal linear information rate of the remaining seven graphs provide a new upper bound on the optimal information rate |
| Beimel [1] (2023) | \(k\)-hypergraph construction | Hypergraphs | the share size of two families of k-hypergraphs, \(k\)-CSI\(_n\) and \(k\)-TotCSI\(_n\) |
Qi Chen et al. [14] extended this study to ideal uniform multipartite secret sharing schemes based on polymatroids, their main idea was to construct ideal linear secret sharing schemes using two different approaches, the first one uses Gabidulin codes[22] leading to schemes where the size of the shares and secret is polynomial in the number of participants, the second approach consists of using linear algebraic techniques results in efficient schemes when the number of parts is small compared to the number of participants. As an application, authors mention their own ongoing work aiming the design of practical distributed cryptographic protocols in the scenario of blockchain by these schemes. Table 3 provides a comparison between two recent approaches represented by Qi Chen et al. [14] (2024) and Csirmaz et al. [19] (2024).
| Aspect | Qi Chen et al. [14] (2024) | Csirmaz et al. [19] (2024) |
| Graph structure | Multipartite | Bipartite |
| Paper investigation | Construction of ideal linear schemes for ideal uniform multipartite access structures. | Exploring the use of bipartite constructions through matroid theory in \(SSS\). |
| Techniques | Polymatoids, Gabidulin codes and linear algebraic techniques | Matroids, polymatroids and submodular optimization |
| Applications | threshold cryptography, secure multiparty computations, and oblivious transfer | group signatures, secure file storage, and secure multiparty computation |
Multipartite access structures motivated by [27], are a generalization of threshold secret sharing, where participants are divided into different classes, participants in the same class play an equivalent role. If the number of these classes is two, we are then talking about bipartite access structure.
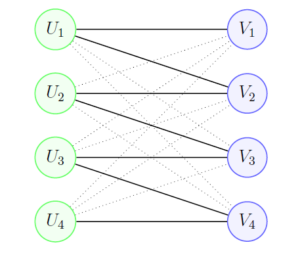
Bipartite access structures divide the set of participants into two classes, where all participants in the same class play an equivalent role (Figure 2). Pàdro et al. [31] completely characterized ideal secret sharing schemes realizing bipartite access structures, while the optimal information rate of a non-ideal bipartite access structure is at most \(1/2\). One can conclude that there is no bipartite access structure that can be realized with an optimal information rate between \(1/2\) to 1. A technical mistake in [31] was noticed by Michael J. Collins concerning the characterization of a class of threshold access structures, and was corrected by the same authors in [32].
For more than two decades, the lower bound \(\Omega(n^2/log\ n)\) provided by Csirmaz [18] on the average information rate remained the best but still far from the upper bound. In the special case of dense graphs on \(n\) vertices [2] that contains at least \(\begin{pmatrix} n\\2 \end{pmatrix}-n^{1+\beta}\) edges with \(0\leq \beta < 1\), there exists a SSS with average information rate \(\tilde{O}(n^{\frac{5}{4}+\frac{3\beta}{4}})\). If \(0\leq \beta<\frac{1}{2}\), then there is a linear SSS [4] with average information rate \(O\left(n^{\frac{7}{6}+\frac{2\beta}{3}}\right)\).
Beimel et al. [3] constructed efficient linear SSS for graph access structures, which include sparse and dense graphs. Recall that a sparse graph of \(n\) vertices is a graph \(n^{1+\beta}\) edges, with \(0\leq \beta < 1\). Their constructions took in consideration at first the bipartite cases and then obtained the following result in the general case.
Adding or removing at most \(n^{1+\beta}\) edges, for some constant \(0 \leq \beta < 1\) from a graph \(G = (V, E)\) with \(n\) vertices that can be realized by a secret-sharing scheme in which the maximum share size is \(\ell\), and the total share size is \(m\), results a graph \(G_0\) that can be realized by a SSS with the following properties:
The total share size \(m + O\left( n^{1 + \beta/2} \log^3 n \right)\) and maximum share size \(\ell + O\left( n^{1/3 + \beta/6} \log^3 n \right)\)
The maximum share size \(\ell + O\left( n^{1/4 + \beta/4} \log^3 n \right)\).
If the scheme that realizes \(G\) is linear, then these schemes are also linear.
To our knowledge, this is the first review that explored the intricate relationship between secret sharing schemes and graph theory, two domains that have witnessed significant advancements in recent years. The convergence of these fields has led to new approaches that not only enhance the theoretical understanding of secret sharing but also improve its practical applications. Our results identified several key developments, including the use of graph theoretic properties to optimize secret sharing schemes. These approaches have demonstrated potential in minimizing the number of shares required for secret reconstruction and enhancing the security of the sharing process. By leveraging the inherent properties of graphs, several researches have developed more efficient and robust secret sharing protocols that are resilient to various attacks. Furthermore, the synthesis of the literature highlighted the importance of interdisciplinary collaboration, as the integration of graph theory into secret sharing has opened new avenues for research and application. The review also underscored the need for continued exploration of complex graph structures and their potential to address existing challenges in secret sharing, such as scalability and dynamic participant management.
Despite the progress made, several gaps remain, particularly in the application of advanced graph theoretic techniques to real world scenarios. Future research should focus on bridging these gaps, with an emphasis on developing adaptive and scalable secret sharing models that can accommodate the ever-evolving landscape of digital communication and data security. One promising direction lies in leveraging advanced graph structures, such as hypergraphs, Cayley graphs, and Schreier graphs in their relationship to \(SSS\) characterized in terms of group structures [26], to design more efficient and scalable \(SSS\). The growing complexity of distributed systems and multi-party computations also invites further investigation into the trade-offs between share size, information rate, and security in both classical and modern graph-theoretic approaches. Additionally, as cryptographic demands evolve with applications in quantum computing and homomorphic encryption, there is an increasing need to refine linear secret-sharing schemes to accommodate more sophisticated access structures and improve computational efficiency. In conclusion, future research will likely focus on pushing the boundaries of existing methods while exploring new ways to harness the rich structure of graphs for cutting-edge cryptographic solutions.
1970-2025 CP (Manitoba, Canada) unless otherwise stated.